Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c
Abstract
1. Introduction
- Does adding nanoparticles affect how a nanofluid transfers heat over a stretched sheet?
- To what extent is the governing flow behavior effectively addressed by the ANN approach?
- How much does thermal radiation affect the thermal characteristics of nanofluids used in technical applications?
- What effect does the Prandtl fluid parameter have on the thermal profile and fluid flow?
- What is the relationship between the outcomes predicted by the ANN and those derived from the bvp4c solver?
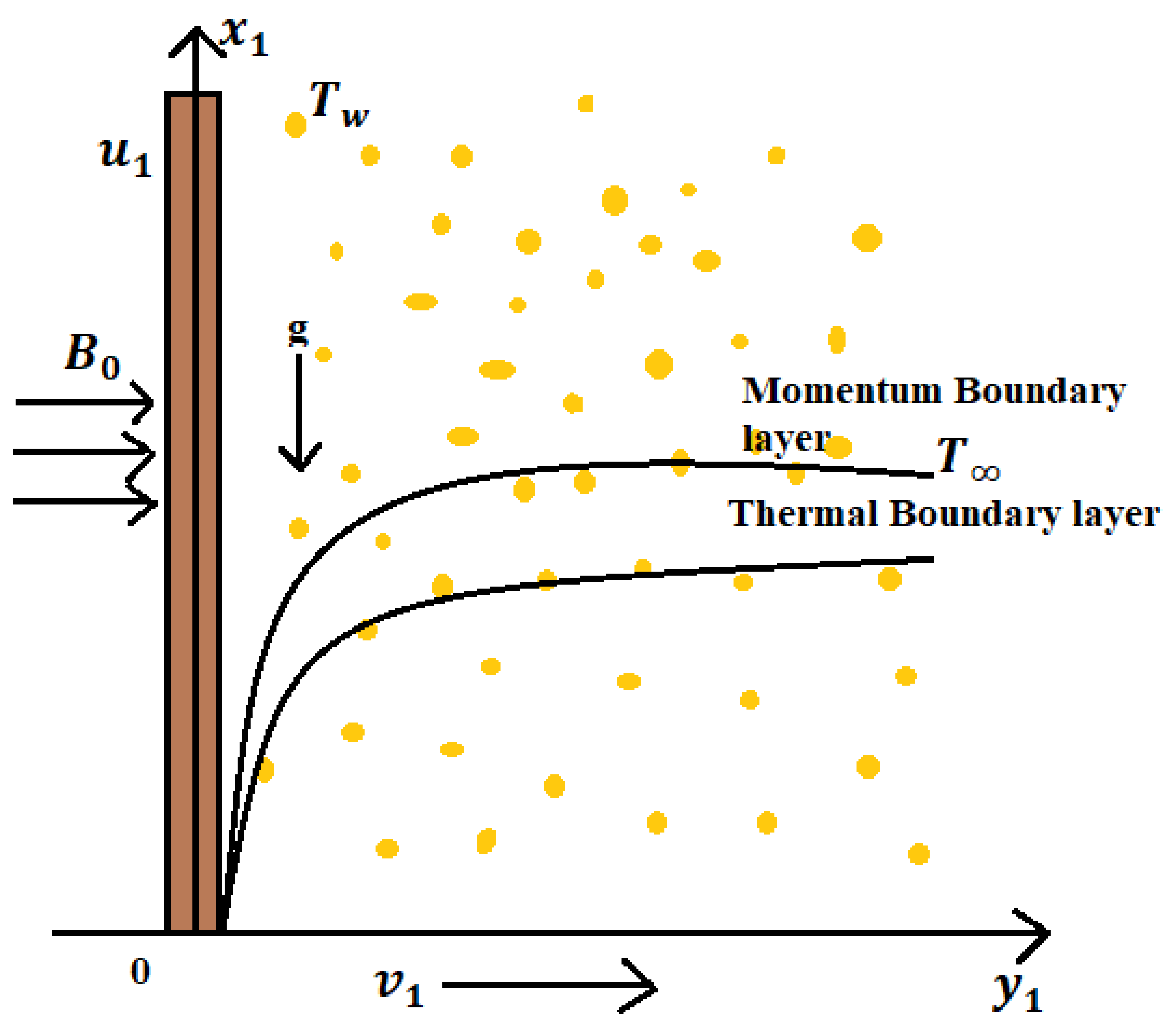
2. Mathematical Modeling
3. Numerical Solution
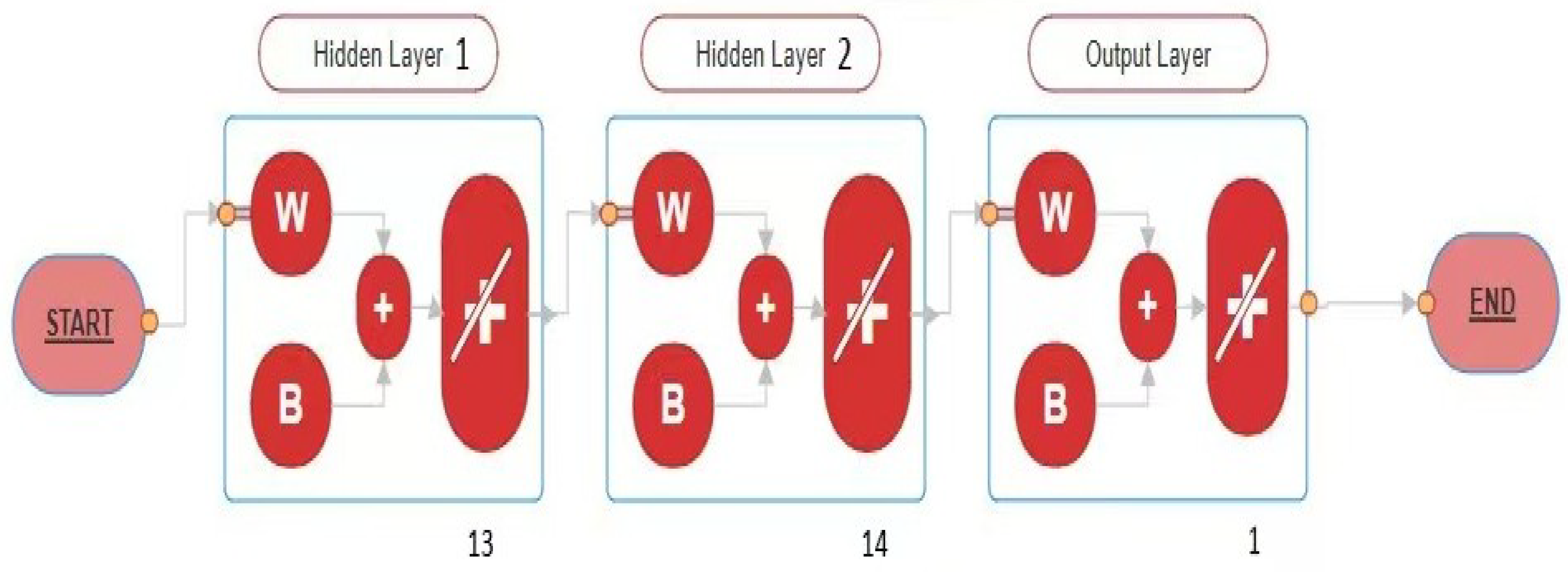
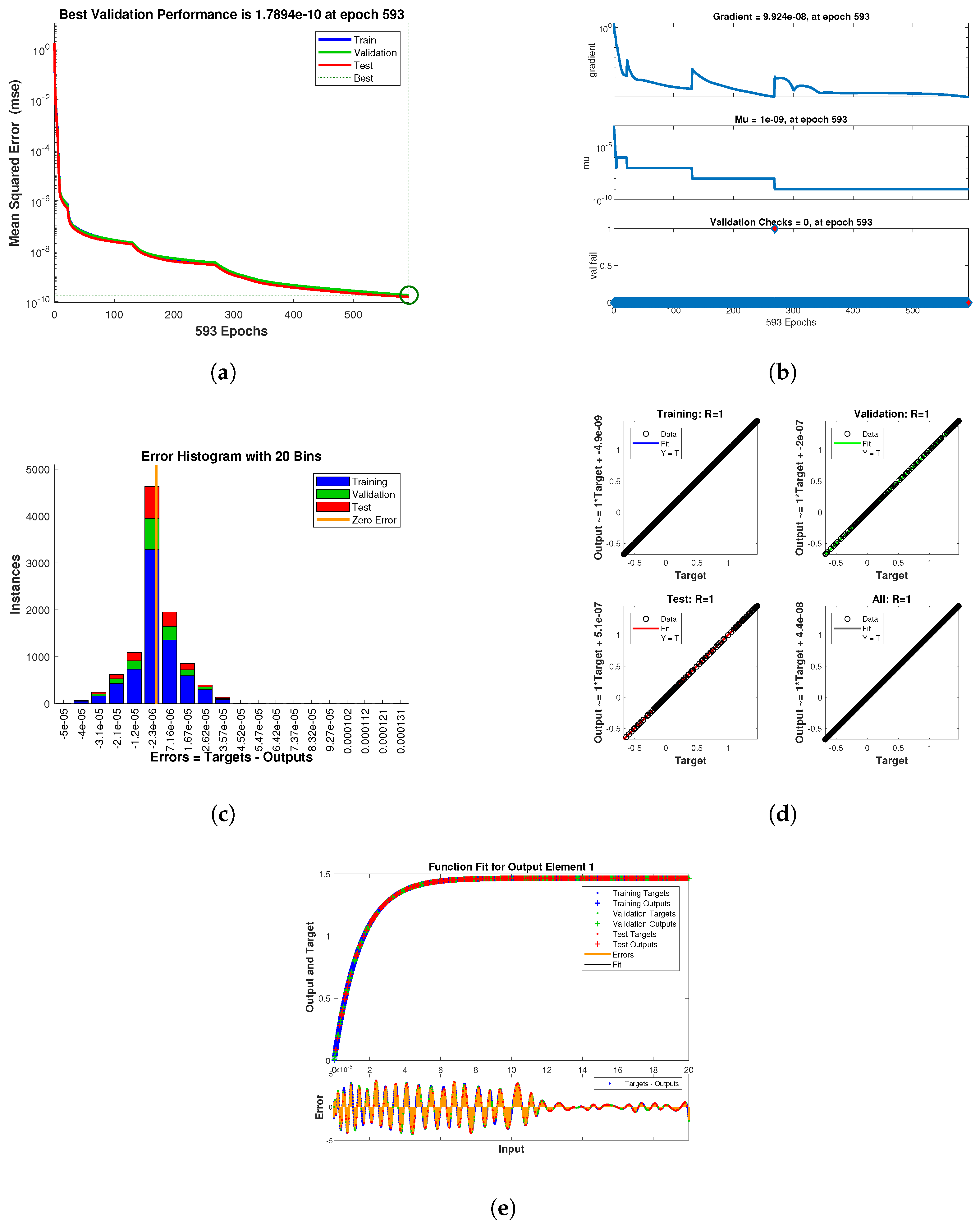
4. Artificial Neural Network (ANN) Modeling
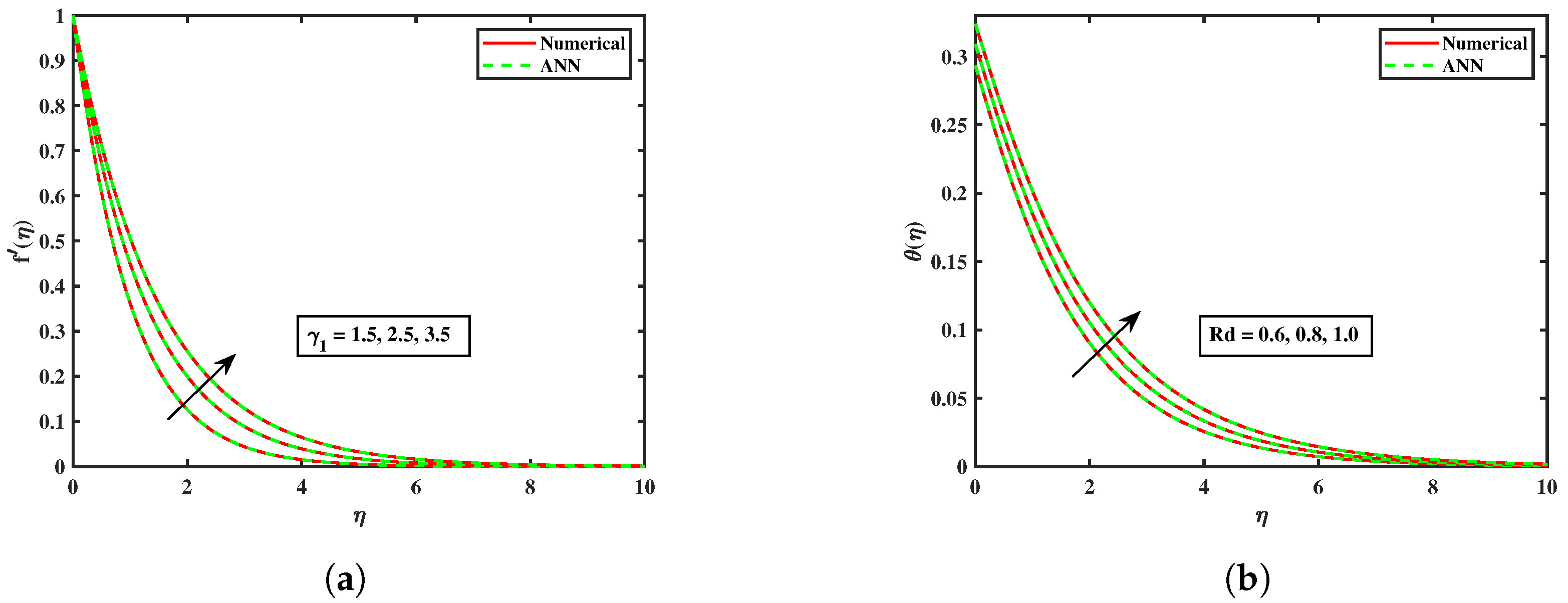
5. Results and Discussion
6. Conclusions
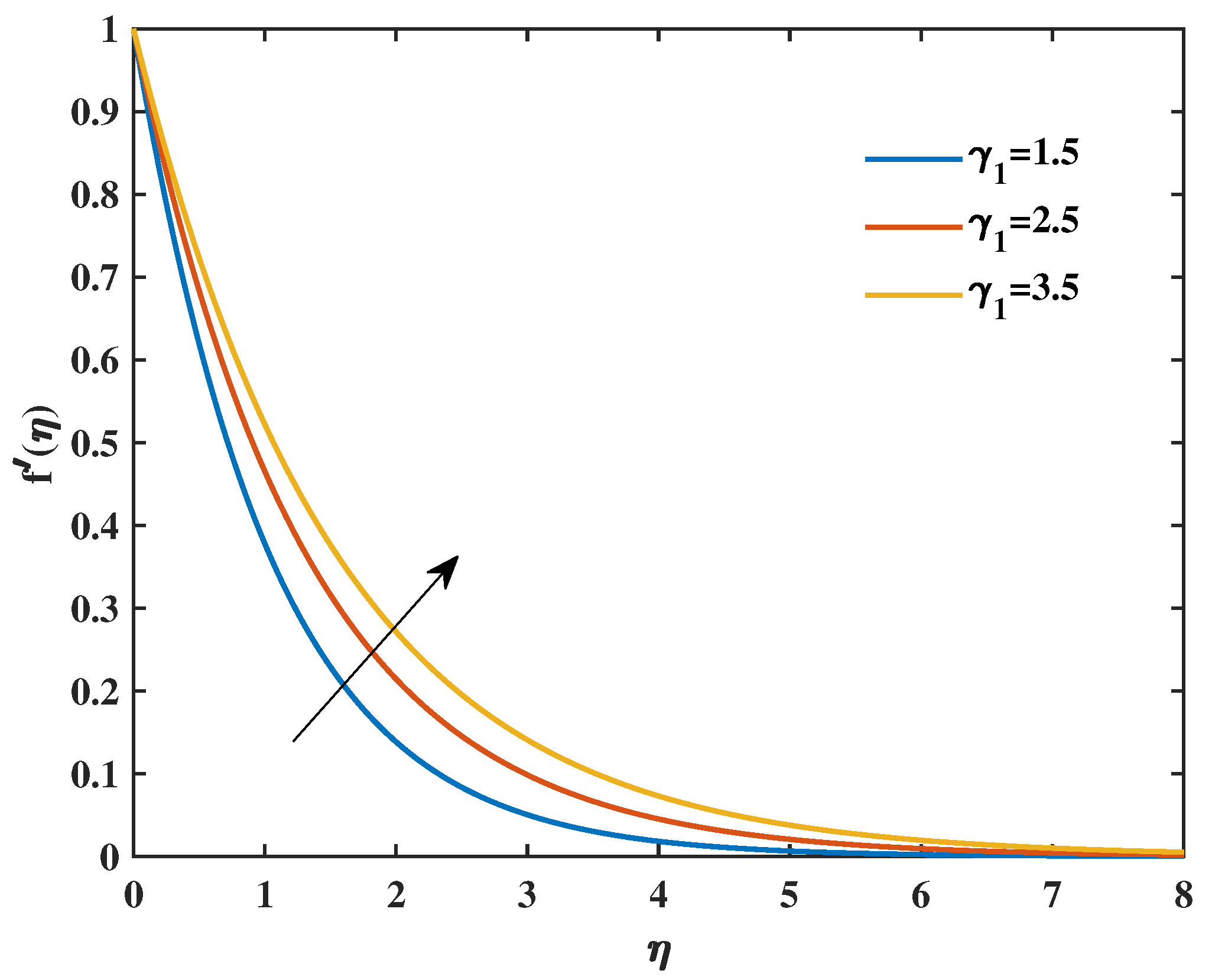
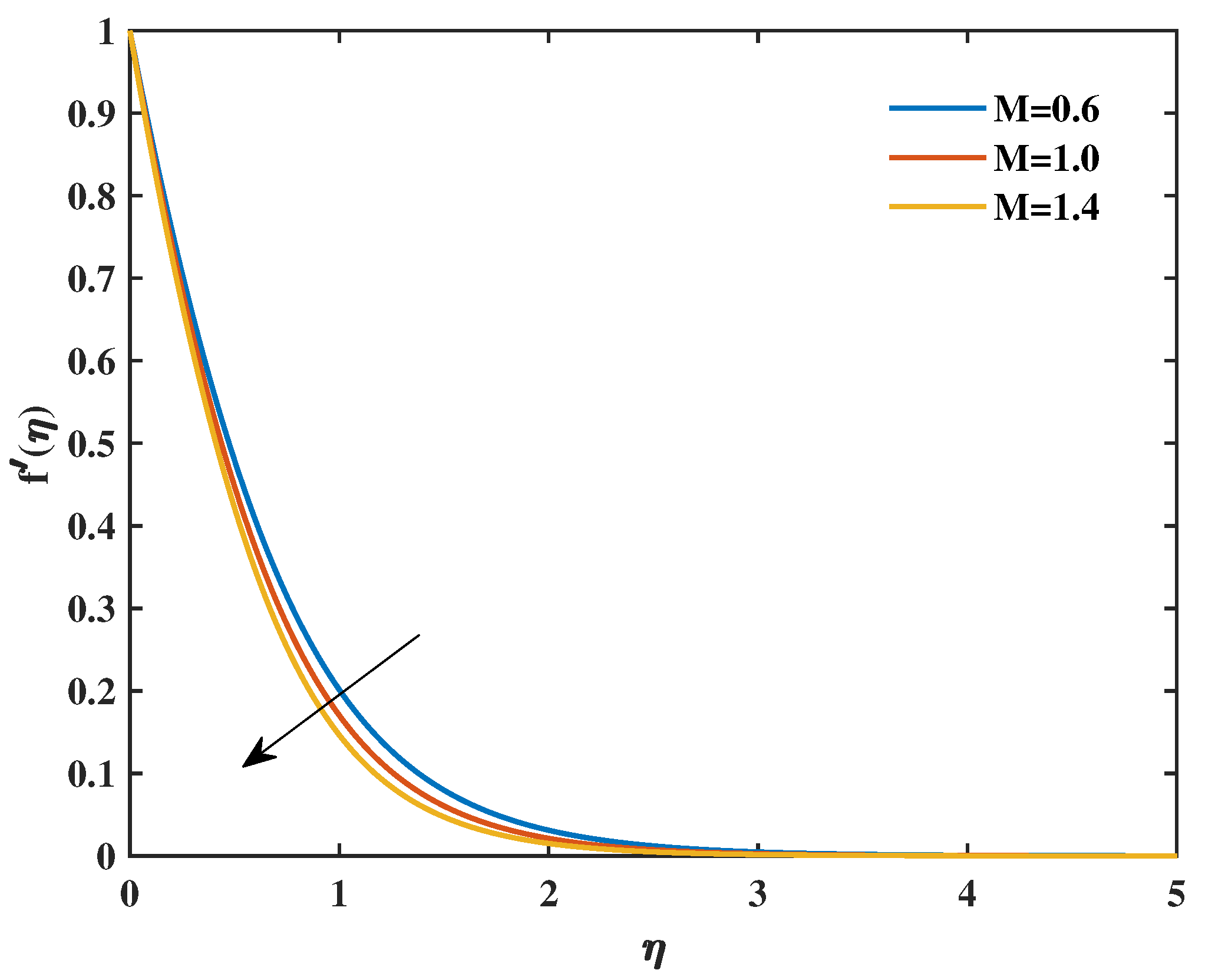
- Higher Prandtl fluid parameter values resulted in an increase in the velocity distribution, whereas higher magnetic parameter values produced the opposite effect.
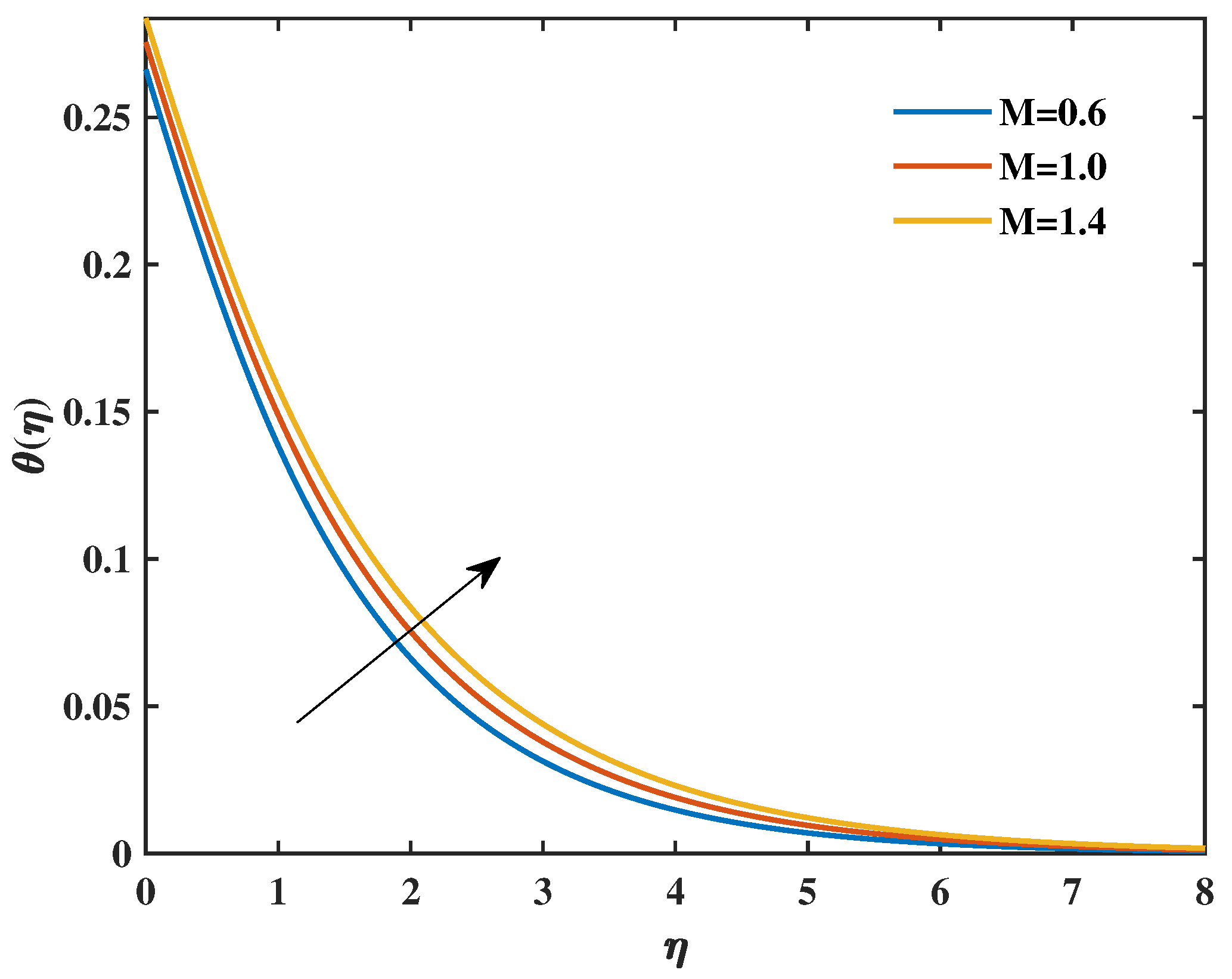
- Increases in the Biot number, radiation parameter, and magnetic parameter caused the temperature profile to rise.
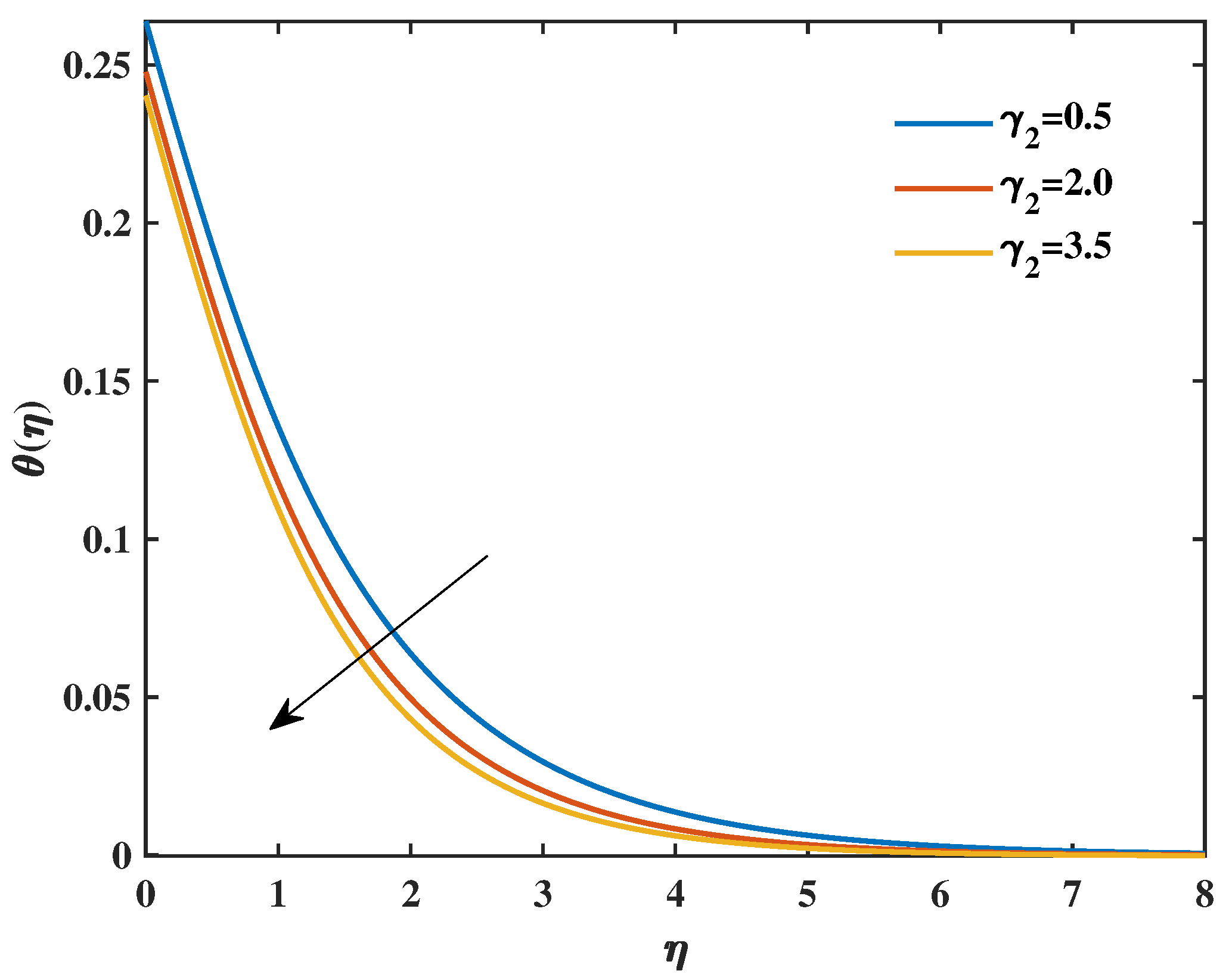
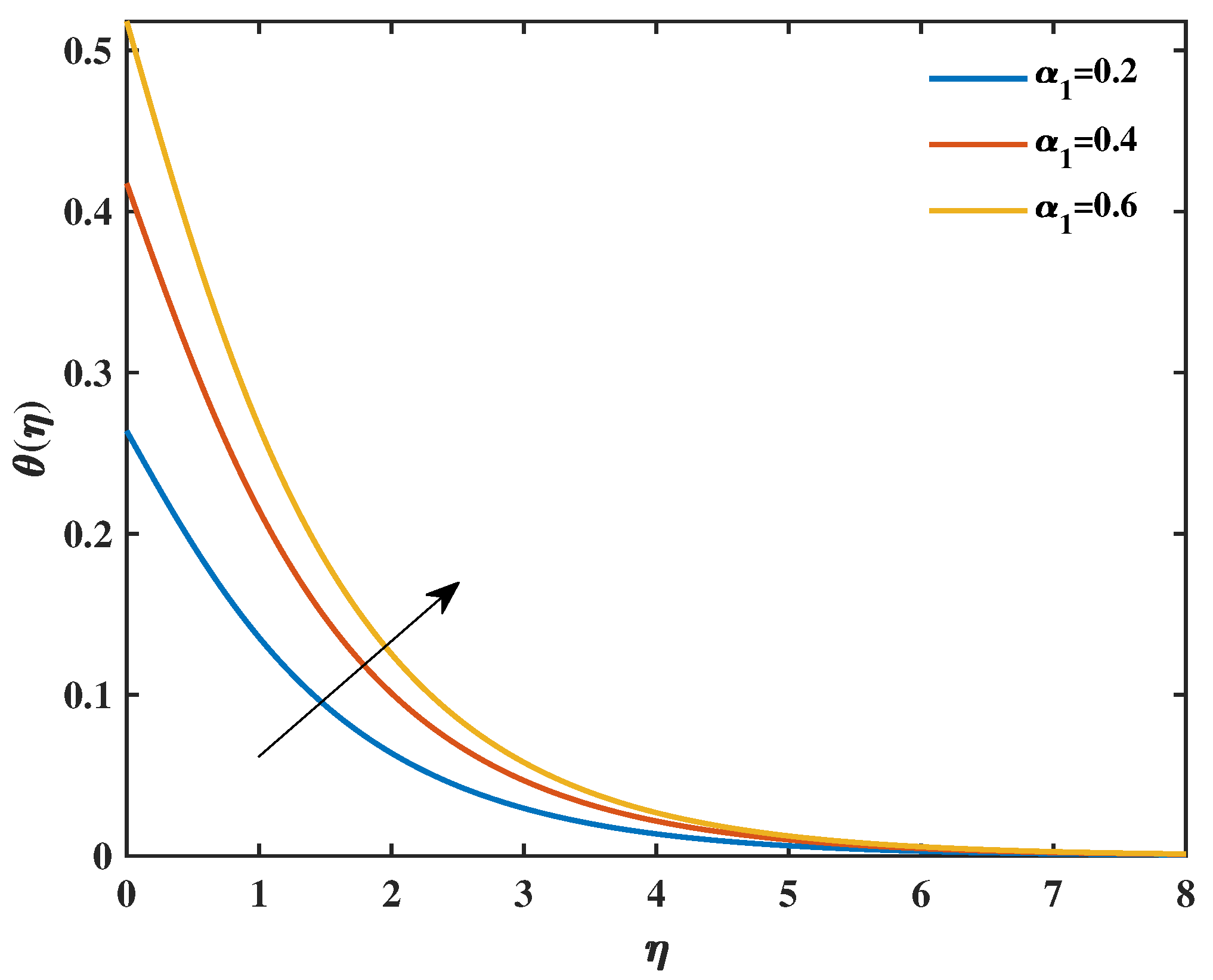
- Increases in the Prandtl fluid parameters reduced the temperature distribution.
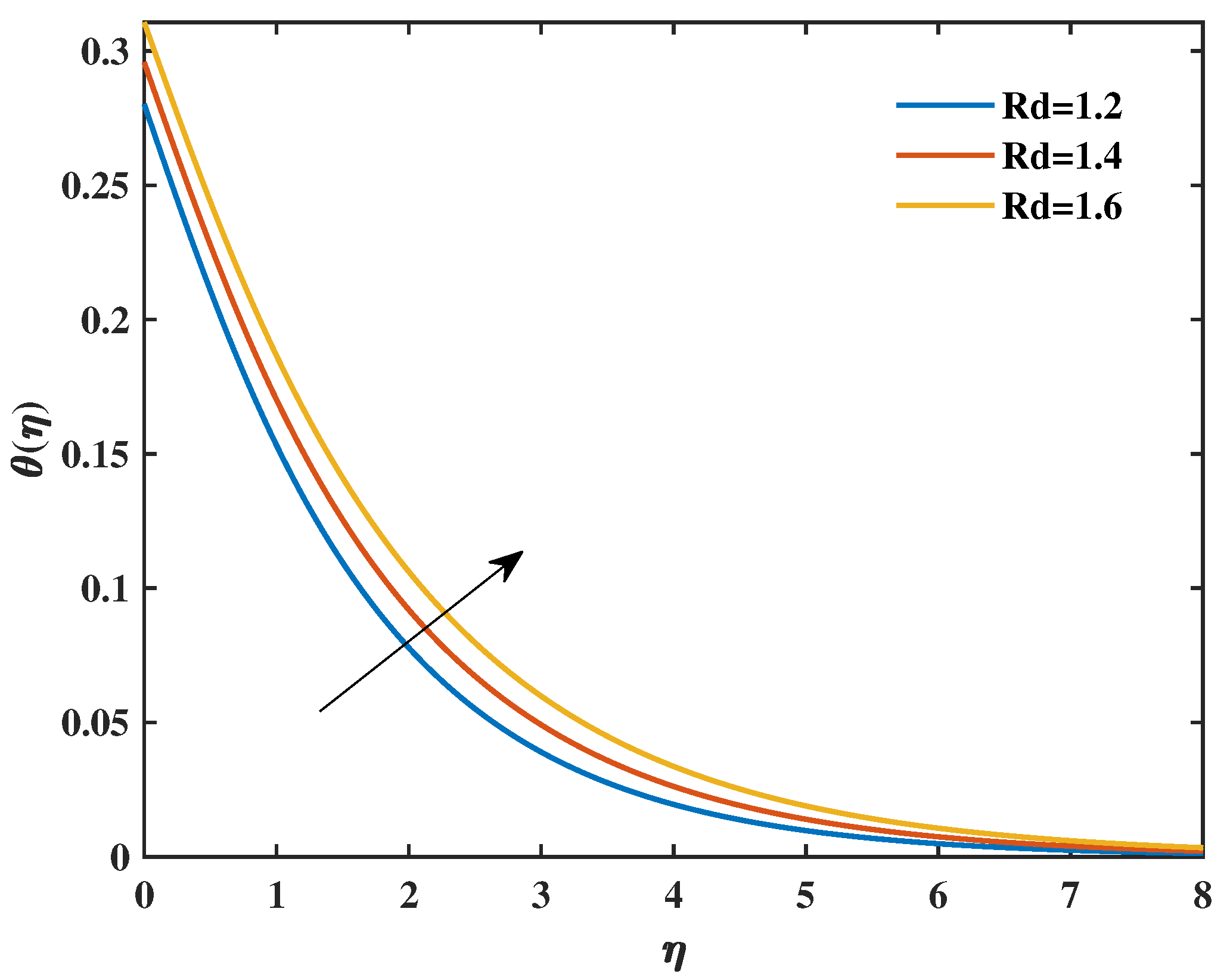
- Temperature profiles were enhanced by increasing the values of the magnetic parameter, thermal radiation, and thermal Biot number.
- As the magnetic parameter and Prandtl fluid parameters increased, the skin friction decreased.
- As the magnetic parameter increased, the Nusselt number decreased, but increases in the radiation parameters, Prandtl fluid parameters, and Biot number increased it.
- The bvp4c methodology’s convergence features were demonstrated, and the findings were validated through numerical comparison with the present ANN model, which showed strong agreement in this scenario.
7. Limitations and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab. (ANL): Lemont, IL, USA, 1995. [Google Scholar]
- Qureshi, M.A. Numerical simulation of heat transfer flow subject to MHD of Williamson nanofluid with thermal radiation. Symmetry 2020, 13, 10. [Google Scholar] [CrossRef]
- Raghu, A.; Gajjela, N.; Aruna, J.; Niranjan, H. Significance of modified Fourier heat flux on Maxwell hybrid (Cu-Al2O3/H2O) nanofluid transport past an inclined stretching cylinder. J. Therm. Anal. Calorim. 2024, 149, 12983–13001. [Google Scholar] [CrossRef]
- Long, J.; Liu, Z.; Cao, Z.; Wu, J.; Xie, X. Highly efficient pool boiling heat transfer on surfaces with zoned rose-petal-inspired hierarchical structures. Appl. Therm. Eng. 2024, 241, 122330. [Google Scholar] [CrossRef]
- Kumar, M.A.; Reddy, Y.D.; Rao, V.S.; Goud, B.S. Thermal radiation impact on MHD heat transfer natural convective nano fluid flow over an impulsively started vertical plate. Case Stud. Therm. Eng. 2021, 24, 100826. [Google Scholar] [CrossRef]
- Gajjela, N.; Balakrishnan, A.S.; Garvandha, M.; Niranjan, H.; Raju, A. Impact on induced magnetic field over a second-grade hybrid nanofluid in unsteady thermal systems. Case Stud. Therm. Eng. 2025, 69, 105956. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud. Therm. Eng. 2022, 37, 102247. [Google Scholar] [CrossRef]
- Zou, H.; Chen, C.; Zha, M.; Zhou, K.; Xiao, R.; Feng, Y.; Wang, Z. A neural regression model for predicting thermal conductivity of CNT nanofluids with multiple base fluids. J. Therm. Sci. 2021, 30, 1908–1916. [Google Scholar] [CrossRef]
- Waqas, H.; Fida, M.; Liu, D.; Manzoor, U.; Alghamdi, M.; Muhammad, T. Heat transport of nanofluid flow through a porous channel with thermal radiation effects. Int. Commun. Heat Mass Transf. 2022, 138, 106376. [Google Scholar] [CrossRef]
- Wang, H.; Hou, Y.; He, Y.; Wen, C.; Giron-Palomares, B.; Duan, Y.; Gao, B.; Vavilov, V.P.; Wang, Y. A Physical-constrained decomposition method of infrared thermography: Pseudo restored heat flux approach based on Ensemble Bayesian Variance Tensor Fraction. IEEE Trans. Ind. Inform. 2023, 20, 3413–3424. [Google Scholar] [CrossRef]
- Tarakaramu, N.; Satya Narayana, P.V.; Sivakumar, N.; Harish Babu, D.; Bhagya Lakshmi, K. Convective conditions on 3D magnetohydrodynamic (MHD) non-Newtonian nanofluid flow with nonlinear thermal radiation and heat absorption: A numerical analysis. J. Nanofluids 2023, 12, 448–457. [Google Scholar] [CrossRef]
- Yan, X.; Feng, Y.; Qiu, L.; Zhang, X. Thermal conductivity and phase change characteristics of hierarchical porous diamond/erythritol composite phase change materials. Energy 2021, 233, 121158. [Google Scholar] [CrossRef]
- Basit, M.A.; Imran, M.; Akgül, A.; Hassani, M.K.; Alhushaybari, A. Mathematical analysis of heat and mass transfer efficiency of bioconvective Casson nanofluid flow through conical gap among the rotating surfaces under the influences of thermal radiation and activation energy. Results Phys. 2024, 63, 107863. [Google Scholar] [CrossRef]
- Vinutha, K.; Sajjan, K.; Madhukesh, J.K.; Ramesh, G.K. Optimization of RSM and sensitivity analysis in MHD ternary nanofluid flow between parallel plates with quadratic radiation and activation energy. J. Therm. Anal. Calorim. 2024, 149, 1595–1616. [Google Scholar] [CrossRef]
- Shoaib, M.; Raja, M.A.Z.; Sabir, M.T.; Islam, S.; Shah, Z.; Kumam, P.; Alrabaiah, H. Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep. 2020, 10, 18533. [Google Scholar] [CrossRef] [PubMed]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 858–879. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Ali, B.; Guedri, K.; Awan, A.U.; Gamaoun, F.; Tag-ElDin, E.M. Significance of bio-convection, MHD, thermal radiation and activation energy across Prandtl nanofluid flow: A case of stretching cylinder. Int. Commun. Heat Mass Transf. 2022, 137, 106299. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Saadeh, R.; Madhukesh, J.K.; Qazza, A.; Khan, U.; Zaib, A.; Abed, A.M. Neural network algorithms of a curved riga sensor in a ternary hybrid nanofluid with chemical reaction and Arrhenius kinetics. J. Radiat. Res. Appl. Sci. 2024, 17, 101078. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Goud, B.S. Comprehensive analysis of thermal radiation impact on an unsteady MHD nanofluid flow across an infinite vertical flat plate with ramped temperature with heat consumption. Results Eng. 2023, 17, 100796. [Google Scholar] [CrossRef]
- Krishna, M.V.; Kumar, A.V. Chemical reaction, slip effects, and non-linear thermal radiation on unsteady MHD Jeffreys nanofluid flow over a stretching sheet. Case Stud. Therm. Eng. 2024, 55, 104129. [Google Scholar] [CrossRef]
- Pourpasha, H.; Farshad, P.; Heris, S.Z. Modeling and optimization the effective parameters of nanofluid heat transfer performance using artificial neural network and genetic algorithm method. Energy Rep. 2021, 7, 8447–8464. [Google Scholar] [CrossRef]
- Qiu, L.; Li, Y.; Feng, Y.; Chen, Z.; Zhang, X. Three-dimensional fluid-solid coupling heat transfer simulation based on the multireference frame for a side-blown aluminum annealing furnace. Eng. Appl. Comput. Fluid Mech. 2019, 13, 1036–1048. [Google Scholar] [CrossRef]
- Akbar, A.; Ullah, H.; Raja, M.A.Z.; Nisar, K.S.; Islam, S.; Shoaib, M. A design of neural networks to study mhd and heat transfer in two phase model of nano-fluid flow in the presence of thermal radiation. Waves Random Complex Media 2022, 1–24. [Google Scholar] [CrossRef]
- Roopa, G.S.; Vishalakshi, C.S.; Madhukesh, J.K.; Ramesh, G.K. Thermal investigation of Tiwari–Das and Xue nanofluid model on space and thermal-dependent heat source/sink over a spinning disk: A numerical study. Numer. Heat Transf. Part Appl. 2025, 1–16. [Google Scholar] [CrossRef]
- Rehman, K.U.; Çolak, A.B.; Shatanawi, W. Artificial neural networking (ANN) model for convective heat transfer in thermally magnetized multiple flow regimes with temperature stratification effects. Mathematics 2022, 10, 2394. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Shehzad, S.A.; Izadi, M. Falkner–Skan flow of aqueous magnetite–graphene oxide nanoliquid driven by a wedge. Chin. J. Phys. 2022, 77, 733–746. [Google Scholar] [CrossRef]
- Hou, Q.; Li, Y.; Singh, V.P.; Sun, Z. Physics-informed neural network for diffusive wave model. J. Hydrol. 2024, 637, 131261. [Google Scholar] [CrossRef]
- Nasir, S.; Berrouk, A.S.; Gul, T.; Ali, A. Develop the artificial neural network approach to predict thermal transport analysis of nanofluid inside a porous enclosure. Sci. Rep. 2023, 13, 21039. [Google Scholar] [CrossRef]
- Mishra, S.R.; Pattnaik, P.K.; Baithalu, R.; Ratha, P.K.; Panda, S. Predicting heat transfer performance in transient flow of CNT nanomaterials with thermal radiation past a heated spinning sphere using an artificial neural network: A machine learning approach. Partial. Differ. Equ. Appl. Math. 2024, 12, 100936. [Google Scholar] [CrossRef]
- Aruna, J.; Niranjan, H. An artificial neural network approach to comparative aspects: A predictive analysis of magnetic dipole on the heat transfer of maxwell hybrid nano coolants flow in an inclined cylinder. Case Stud. Therm. Eng. 2025, 68, 105825. [Google Scholar] [CrossRef]
- Awan, A.U.; Qayyum, S.; Nadeem, S.; Ahammad, N.A.; Gepreel, K.A.; Alharthi, M.; Alosaimi, M. Analysis of chemical characteristics of engine-oil-based Prandtl hybrid nanofluid flow. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, 104, e202400050. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Qayyum, S.; Nadeem, S.; Alzubadi, H.; Ahammad, N.A.; Awan, A.U.; Alroobaea, R. Thermal characterization of Sutterby nanofluid flow under Riga plate: Tiwari and Das model. Mod. Phys. Lett. B 2024, 39, 2450421. [Google Scholar] [CrossRef]
- Cao, W.; Animasaun, I.L.; Yook, S.J.; Oladipupo, V.A.; Ji, X. Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid. Int. Commun. Heat Mass Transf. 2022, 135, 106069. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer (in SI Units); Mcgraw-Hill Education-Europe: London, UK, 2014. [Google Scholar]
- Awan, A.U.; Shah, S.A.A.; Qayyum, S.; Alzubadi, H.; Ahammad, N.A.; Alroobaea, R. Mixed convected synchronization of gyrotactic microorganism flow of an Eyring–Powell nanofluid over a riga plate. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2024, 104, e202301055. [Google Scholar] [CrossRef]
- Gupta, D.; Kumar, L.; Anwar Bég, O.; Singh, B. Finite element analysis of MHD flow of micropolar fluid over a shrinking sheet with a convective surface boundary condition. J. Eng. Thermophys. 2018, 27, 202–220. [Google Scholar] [CrossRef]




| Properties | Nanofluid |
|---|---|
| Viscosity | |
| Density | |
| Heat Capacity | |
| Thermal Conductivity |
| Properties | ||
|---|---|---|
| () | 997.1 | 8933 |
| () | 4179 | 385.0 |
| 0.6130 | 401.0 | |
| (Ωm) | 0.05 |
| M | |||||
|---|---|---|---|---|---|
| Bvp4c | ANN | Error | |||
| 0.50 | 0.5 | 0.5 | −1.7282 | −1.7579 | 0.0297 |
| 0.75 | 0.5 | 0.5 | −1.7007 | −1.7003 | 0.0004 |
| 1.00 | 0.5 | 0.5 | −1.7164 | −1.7023 | 0.0141 |
| 1.25 | 0.5 | 0.5 | −1.7581 | −1.7571 | 0.001 |
| 1.50 | 0.5 | 0.5 | −1.8153 | −1.817 | 0.0017 |
| 1.75 | 0.5 | 0.5 | −1.8813 | −1.8792 | 0.0021 |
| 2.0 | 0.5 | 0.5 | −1.9522 | −1.9528 | 0.0006 |
| 2.25 | 0.5 | 0.5 | −2.0257 | −2.0284 | 0.0027 |
| 2.50 | 0.5 | 0.5 | −2.1001 | −2.0986 | 0.0015 |
| 2.75 | 0.5 | 0.5 | −2.1746 | −2.1717 | 0.0029 |
| 3.00 | 0.5 | 0.5 | −2.2485 | −2.2469 | 0.0016 |
| 3.25 | 0.5 | 0.5 | −2.3216 | −2.3205 | 0.0011 |
| 0.5 | 0.50 | 0.5 | −1.7282 | −1.7579 | 0.0297 |
| 0.5 | 0.75 | 0.5 | −1.9412 | −1.9408 | 0.0004 |
| 0.5 | 1.00 | 0.5 | −2.1105 | −2.1368 | 0.0263 |
| 0.5 | 1.25 | 0.5 | −2.2525 | −2.2517 | 0.0008 |
| 0.5 | 1.50 | 0.5 | −2.3755 | −2.3419 | 0.0336 |
| 0.5 | 1.75 | 0.5 | −2.4847 | −2.4848 | 0.0003 |
| 0.5 | 2.00 | 0.5 | −2.5830 | −2.5836 | 0.0006 |
| 0.5 | 2.25 | 0.5 | −2.6728 | −2.6272 | 0.0456 |
| 0.5 | 2.50 | 0.5 | −2.7555 | −2.7202 | 0.0353 |
| 0.5 | 2.75 | 0.5 | −2.8323 | −2.8355 | 0.0032 |
| 0.5 | 3.00 | 0.5 | −2.9041 | −2.9056 | 0.0015 |
| 0.5 | 3.25 | 0.5 | −2.9716 | −2.9573 | 0.0143 |
| 0.5 | 0.5 | 0.5 | −1.8177 | −1.7579 | 0.0598 |
| 0.5 | 0.5 | 0.7 | −2.0000 | −1.9998 | 0.0002 |
| 0.5 | 0.5 | 0.9 | −2.1780 | −2.2114 | 0.0334 |
| 0.5 | 0.5 | 1.1 | −2.3521 | −2.4175 | 0.0654 |
| 0.5 | 0.5 | 1.3 | −2.5227 | −2.5847 | 0.0620 |
| 0.5 | 0.5 | 1.5 | −2.6902 | −2.704 | 0.0138 |
| 0.5 | 0.5 | 1.7 | −2.8548 | −2.8529 | 0.0019 |
| 0.5 | 0.5 | 1.9 | −3.0168 | −3.0172 | 0.0004 |
| 0.5 | 0.5 | 2.1 | −3.1764 | −3.1545 | 0.0219 |
| 0.5 | 0.5 | 2.3 | −3.3339 | −3.3235 | 0.0104 |
| 0.5 | 0.5 | 2.5 | −3.4892 | −3.5006 | 0.0114 |
| 0.5 | 0.5 | 2.7 | −3.6426 | −3.5879 | 0.0547 |
| Bvp4c | ANN | Error | |||
|---|---|---|---|---|---|
| 0.50 | 0.5 | 1.4 | 0.3436 | 0.3523 | 0.0087 |
| 0.75 | 0.5 | 1.4 | 0.3496 | 0.3512 | 0.0016 |
| 1.00 | 0.5 | 1.4 | 0.3536 | 0.3587 | 0.0051 |
| 1.25 | 0.5 | 1.4 | 0.3565 | 0.3607 | 0.0042 |
| 1.50 | 0.5 | 1.4 | 0.3587 | 0.3561 | 0.0026 |
| 1.75 | 0.5 | 1.4 | 0.3604 | 0.3616 | 0.0012 |
| 2.0 | 0.5 | 1.4 | 0.3618 | 0.3696 | 0.0078 |
| 2.25 | 0.5 | 1.4 | 0.3630 | 0.3668 | 0.0038 |
| 2.50 | 0.5 | 1.4 | 0.3639 | 0.3628 | 0.0011 |
| 2.75 | 0.5 | 1.4 | 0.3648 | 0.3652 | 0.0004 |
| 3.00 | 0.5 | 1.4 | 0.3655 | 0.3647 | 0.0008 |
| 3.25 | 0.5 | 1.4 | 0.3661 | 0.3594 | 0.0067 |
| 0.5 | 0.50 | 1.4 | 0.3436 | 0.3587 | 0.0151 |
| 0.5 | 0.75 | 1.4 | 0.3455 | 0.3542 | 0.0087 |
| 0.5 | 1.00 | 1.4 | 0.3470 | 0.3478 | 0.0008 |
| 0.5 | 1.25 | 1.4 | 0.3483 | 0.3453 | 0.003 |
| 0.5 | 1.50 | 1.4 | 0.3493 | 0.3464 | 0.0029 |
| 0.5 | 1.75 | 1.4 | 0.3503 | 0.3492 | 0.0011 |
| 0.5 | 2.00 | 1.4 | 0.3511 | 0.3513 | 0.0002 |
| 0.5 | 2.25 | 1.4 | 0.3518 | 0.3512 | 0.0006 |
| 0.5 | 2.50 | 1.4 | 0.3524 | 0.3509 | 0.0015 |
| 0.5 | 2.75 | 1.4 | 0.3530 | 0.3532 | 0.0002 |
| 0.5 | 3.00 | 1.4 | 0.3536 | 0.3532 | 0.0029 |
| 0.5 | 3.25 | 1.4 | 0.3541 | 0.3565 | 0.0003 |
| 0.5 | 0.5 | 1.2 | 0.3743 | 0.3627 | 0.0116 |
| 0.5 | 0.5 | 1.4 | 0.4037 | 0.3587 | 0.045 |
| 0.5 | 0.5 | 1.6 | 0.4320 | 0.4096 | 0.0224 |
| 0.5 | 0.5 | 1.8 | 0.4591 | 0.4661 | 0.007 |
| 0.5 | 0.5 | 2.0 | 0.4851 | 0.5002 | 0.0151 |
| 0.5 | 0.5 | 2.2 | 0.5102 | 0.5169 | 0.0067 |
| 0.5 | 0.5 | 2.4 | 0.5343 | 0.5319 | 0.0024 |
| 0.5 | 0.5 | 2.6 | 0.5576 | 0.5526 | 0.005 |
| 0.5 | 0.5 | 2.8 | 0.5800 | 0.5778 | 0.0022 |
| 0.5 | 0.5 | 3.0 | 0.6017 | 0.6043 | 0.0026 |
| 0.5 | 0.5 | 3.2 | 0.6226 | 0.6285 | 0.0059 |
| 0.5 | 0.5 | 3.4 | 0.6429 | 0.6421 | 0.0008 |
| M | ||||
|---|---|---|---|---|
| Bvp4c | ANN | Error | ||
| 0.2 | 1.5 | 0.3436 | 0.3587 | 0.0151 |
| 0.4 | 1.5 | 0.5438 | 0.5352 | 0.0086 |
| 0.6 | 1.5 | 0.6748 | 0.6755 | 0.0007 |
| 0.8 | 1.5 | 0.7673 | 0.7711 | 0.0038 |
| 1.0 | 1.5 | 0.8360 | 0.8328 | 0.0032 |
| 1.2 | 1.5 | 0.8891 | 0.8819 | 0.0072 |
| 1.4 | 1.5 | 0.9314 | 0.9292 | 0.0022 |
| 1.6 | 1.5 | 0.9658 | 0.9677 | 0.0019 |
| 1.8 | 1.5 | 0.9944 | 0.9936 | 0.0008 |
| 2.0 | 1.5 | 1.0185 | 1.0152 | 0.0033 |
| 2.2 | 1.5 | 1.0391 | 1.0383 | 0.0008 |
| 2.4 | 1.5 | 1.0569 | 1.0574 | 0.0005 |
| 0.2 | 0.5 | 0.3436 | 0.3416 | 0.002 |
| 0.2 | 0.7 | 0.3413 | 0.3417 | 0.0004 |
| 0.2 | 0.9 | 0.3391 | 0.3339 | 0.0052 |
| 0.2 | 1.1 | 0.3371 | 0.3347 | 0.0024 |
| 0.2 | 1.3 | 0.3352 | 0.3482 | 0.013 |
| 0.2 | 1.5 | 0.3334 | 0.3587 | 0.0253 |
| 0.2 | 1.7 | 0.3317 | 0.3464 | 0.0147 |
| 0.2 | 1.9 | 0.3301 | 0.3248 | 0.0053 |
| 0.2 | 2.1 | 0.3286 | 0.3205 | 0.0091 |
| 0.2 | 2.3 | 0.3271 | 0.3269 | 0.0002 |
| 0.2 | 2.5 | 0.3257 | 0.3252 | 0.0005 |
| 0.2 | 2.7 | 0.3244 | 0.3240 | 0.0004 |
| M | Gupta et al. [36] | Our Results |
|---|---|---|
| 0.0 | −1.0000084 | −0.999306073 |
| 1.0 | 1.41421356 | 1.414213264 |
| 5.0 | 2.44948974 | 2.449489744 |
| 10.0 | 3.31662479 | 3.316627156 |
| 50.0 | 7.14142843 | 7.141424060 |
| 100.0 | 10.0498756 | 10.049871347 |
| 500.0 | 22.3830293 | 22.383023555 |
| 1000.0 | 31.6385840 | 31.638576868 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.A.A.; Alshammari, F.S.; Malik, M.F.; Batool, S. Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c. Symmetry 2025, 17, 1347. https://doi.org/10.3390/sym17081347
Shah SAA, Alshammari FS, Malik MF, Batool S. Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c. Symmetry. 2025; 17(8):1347. https://doi.org/10.3390/sym17081347
Chicago/Turabian StyleShah, Syed Asif Ali, Fehaid Salem Alshammari, Muhammad Fawad Malik, and Saira Batool. 2025. "Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c" Symmetry 17, no. 8: 1347. https://doi.org/10.3390/sym17081347
APA StyleShah, S. A. A., Alshammari, F. S., Malik, M. F., & Batool, S. (2025). Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c. Symmetry, 17(8), 1347. https://doi.org/10.3390/sym17081347







