Exotic Heavy Hadrons

Abstract

We review our recent findings on the structure and properties of exotic heavy hadrons, focusing on two main topics. First, we examine the role of correlations driven by the short-range Coulomb-like color interaction in hidden heavy-flavor pentaquarks. We show how this framework consistently accounts for the observed pattern of $P_c$ and $P_{cs}$ states in the hidden-charm sector and enables predictions for the hidden-bottom sector, where experimental data are still lacking. The second topic explores the possibility of forming stable multihadron molecules from deeply bound two-hadron exotic states. In this context, a bound state of three B mesons, denoted as $T_{bbb}$, with quantum numbers $\left(I\right)J^P=(1/2)2^{-}$, is presented. We find that the binding energy generally decreases as the number of hadrons increases, primarily due to effects of the Pauli principle and the appearance of new decay thresholds. Nonetheless, resonances may still arise in specific cases, depending on the internal thresholds of the system. Finally, we discuss how the decay width of an exotic multihadron resonance can offer valuable insights into its internal structure and underlying dynamics.

1. Introduction

Hadronic spectroscopy has become an essential tool for improving our understanding of Quantum Chromodynamics (QCD) in the low-energy regime. Broadly speaking, at the beginning of the 21st century, two distinct approaches coexisted for describing the phenomenology of the strong interaction in this domain.

On one hand, there was the traditional approach to hadronic spectroscopy, which focused on studying the spectra of mesons and baryons in the spirit of Gell-Mann’s model [1], where hadrons are treated as systems of constituent (anti)quarks. However, it soon became clear that certain states could not be easily accommodated within this simple picture. Examples include mesons with explicitly exotic quantum numbers that cannot be described as a simple quark–antiquark pair, such as the ${\pi }_1\left(1400\right)$ [2], or the long-standing puzzle of the scalar mesons [3,4]. Anomalies have also emerged in the baryon sector, with early indications of more complex dynamics. One prominent example has been the $\Lambda \left(1405\right)$, whose mass lies significantly below the predictions of many quark models [5]. This discrepancy led to the theoretical prediction of a double-pole structure [6], although some models interpret it as a conventional three-quark state [7]. Predictions of dibaryon candidates have also been made, though in some cases there is still no consensus regarding their internal structure, whether they are bound states of two baryons or genuine hexaquark configurations [8]. Finally, one cannot overlook the controversial case of the ${\Theta }^{+}\left(1540\right)$ [9]. From a theoretical perspective, even relatively simple models that captured the essential features of QCD had already predicted the possible existence of more complex configurations, know as multiquarks [10].

On the other hand, an alternative view was based on the use of asymptotic hadronic states, effective field theories (EFTs) [11]. EFTs provide a suitable theoretical framework for describing low-energy physics, where “low” is defined relative to a characteristic energy scale $\Lambda$. These theories retain only the relevant degrees of freedom and states with mass $m\ll \Lambda$, while heavier states with $m\gg \Lambda$ are systematically integrated out. This leads to a non-renormalizable theory organized as a power expansion in energy ($\Lambda$). EFTs have been successfully employed to describe hadronic interactions and to explore the emergence of higher-mass resonances beyond the effective theory’s cutoff [12].

Over the past two decades, the number of newly observed states in the heavy-hadron spectrum has increased significantly. This has lead to the growing consensus that the heavy-hadron spectrum includes contributions from configurations beyond the simplest quark–antiquark (meson) or three-quark (baryon) structures proposed by Gell-Mann [1]. This is particularly evident in the recent discovery of doubly heavy tetraquarks with manifestly exotic quantum numbers [13,14]. Nonetheless, many of the newly reported states possess ordinary quantum numbers, suggesting that they may arise from more intricate internal structures allowed by QCD [15].

These experimental advances have sparked substantial theoretical efforts aimed at understanding the spectroscopy and internal structure of these novel states [16,17,18,19,20,21,22,23,24,25,26,27,28,29]. A wide range of models has been proposed, including hadronic molecules, diquarks, hadroquarkonium, hybrids, threshold effects, …, each providing valuable insights yet none offering a complete description. No single framework has succeeded in fully accounting for all the observed states. A comprehensive understanding may require the interplay of multiple mechanisms, with different combinations being relevant for different cases.

A central open question in this context is whether states with genuinely complex quark substructures, so-called multiquarks, can be unambiguously identified. For hadrons with manifestly exotic quantum numbers, recent experimental discoveries [13,14] provide a clear affirmative answer. However, for states with non-exotic quantum numbers, the question remains unresolved [3,4]. A striking feature of non-conventional hadrons with standard quantum numbers is the rarity of bound states, which appear only in very specific configurations. This observation is supported by both lattice QCD simulations [30,31,32] and constituent quark models [33,34].

In Section 2, we will address the observed difficulty in forming stable multiquark states that do not undergo prompt decay, which may signal the presence of nontrivial internal correlations, dynamical constraints that restrict the allowed quantum numbers of their constituent subsystems. Multiquark systems (tetraquarks, pentaquarks, etc.) necessarily contain internal color-singlet components. Nevertheless, in contrast to atomic or nuclear physics, their dominant Fock-space components may correspond to color-connected configurations that are not asymptotically separable into isolated hadrons. This opens the possibility for theoretical frameworks in which multiquark dynamics is governed by QCD-induced correlations [15]. Within this context, we recently investigated hidden-flavor pentaquarks by examining the correlations arising from the Coulomb-like behavior of the short-range color interaction [35,36]. Our analysis yields a spectral pattern that aligns with current experimental observations.

The ongoing theoretical efforts in hadron spectroscopy have also underscored another important aspect of low-energy QCD phenomenology: the prediction of stable two-baryon states containing multiple heavy quarks, as suggested both by lattice QCD simulations [37,38,39,40] and by various phenomenological models [41,42,43,44,45]. Nonetheless, several of these predictions have been challenged by rigorous few-body calculations, which argue against the formation of such bound states [46].

Section 3 is motivated by theoretical predictions of deeply bound states involving heavy flavors, specifically the doubly bottom tetraquark $T_{bb}$ [31,32] and the ${\Omega }_{bbb}{\Omega }_{bbb}$ dibaryon [40]. Thus, we review the viability of forming multihadron molecular states composed of such heavy-flavor constituents [43,45]. Our analysis indicates that several dynamical effects contribute to a progressive reduction in the binding energy as the number of hadrons increases, thereby disfavoring the existence of stable multihadron configurations with heavy quarks.

In Section 4, we will address the properties of resonances that often emerge near the various physical thresholds intrinsic to the multiquark system given the inherent difficulty in forming bound multiquark states. One particularly intriguing phenomenon in this context is the appearance of narrow resonances despite the presence of ample phase space for decay. This seemingly paradoxical behavior can be understood as a consequence of the orthogonality between the color wave functions of the physical thresholds, which effectively provides a stabilizing mechanism [47,48].

Finally, Section 5 offers a concise summary of our main findings.

2. Hidden-Flavor Pentaquarks

Table 1. Summary of established $P_c^{+}$ and $P_{cs}$ pentaquark candidates [49,50,51,52].

State	M (MeV)	$\mathbf{\Gamma }$ (MeV)
$P_c{\left(4312\right)}^{+}$	$4311.9\pm 0.7_{-0.6}^{+6.8}$	$9.8\pm 2.7_{-4.5}^{+3.7}$
$P_c{\left(4380\right)}^{+}$	$4380\pm 8\pm 29$	$205\pm 18\pm 86$
$P_c{\left(4440\right)}^{+}$	$4440.3\pm 1.3_{-4.7}^{+4.1}$	$20.6\pm 4.9_{-10.1}^{+8.7}$
$P_c{\left(4457\right)}^{+}$	$4457.3\pm 0.6_{-1.7}^{+4.1}$	$6.4\pm 2.0_{-1.9}^{+5.7}$
$P_{\Psi s}^{\Lambda }\left(4338\right)$	$4338.2\pm 0.7\pm 0.4$	$7.0\pm 1.2\pm 1.3$
$P_{cs}\left(4459\right)$	$4458.8\pm 2.9_{-1.1}^{+4.7}$	$17.3\pm 6.5_{-5.7}^{+8.0}$
$P_{cs}\left(4459\right)$ 1	$4454.9\pm 2.7$	$7.5\pm 9.7$
	$4467.8\pm 3.7$	$5.2\pm 5.3$

¹ Alternative assignment of Ref. [52].

summarizes the currently known hidden-charm pentaquarks, including both nonstrange and strange candidates [49,50,51,52]. The first four entries, collectively referred to as $P_c$ states, are consistent with a minimal quark configuration of $c\overline{c}qqq$, where $q=u$ or d [49,50]. The subsequent entries correspond to candidates for strange hidden-charm pentaquarks, characterized by a minimal quark content of $c\overline{c}uds$.

Recent reviews have extensively covered both experimental results and theoretical interpretations of the nonstrange sector [16,17,18,19,20,21,22,23,24,25,26,27]. More recently, the LHCb Collaboration reported the observation of a new strange pentaquark, $P_{\Psi s}^{\Lambda }\left(4338\right)$, identified as a resonance in the $J/\psi \Lambda$ invariant mass spectrum from the decay $B^{-}\to J/\psi \Lambda \overline{p}$ [51]. This state has a mass of $4338.2\pm 0.7\pm 0.4$ MeV. Additionally, LHCb presented evidence for another structure in the $J/\psi \Lambda$ invariant mass distribution from an amplitude analysis of ${\Xi }_b^{-}\to J/\psi \Lambda K^{-}$ decays [52]. This feature appears at $4458.8\pm 2.9_{-1.1}^{+4.7}$ MeV, although the data are also consistent with two nearby resonances at masses of $4454.9\pm 2.7$ MeV and $4467.8\pm 3.7$ MeV. These alternative interpretations are reflected in the final entry of Table 1. If confirmed, the existence of two strange pentaquarks would parallel the pattern observed in the nonstrange sector, exemplified by the $P_c{\left(4440\right)}^{+}$ and $P_c{\left(4457\right)}^{+}$ states.

It is worth noting that recent studies by the Belle Collaboration rule out the production of $P_c^{+}$ pentaquarks in ${\rm Y}(1,2S)$ decays [53] but provide evidence for the existence of $P_{cs}$ pentaquarks [54]. In particular, for the $P_{cs}\left(4459\right)$ state, Belle reports a mass of $4471.7\pm 4.8\pm 0.6$ MeV/c².

2.1. Coulomb-like Color Correlations

As noted earlier, a central theoretical challenge in the study of multiquarks is identifying multiquark hadrons that do not promptly decay through their fall-apart channel into lighter hadrons. This challenge has motivated proposals emphasizing internal correlations, dynamical mechanisms that constrain the allowed quantum numbers of subsystems, thereby enhancing stability. Notable among these are diquark models [55,56], which restrict the color degree of freedom of quark pairs to specific configurations.

Various diquark models exist, but all impose constraints on the color states of quark–quark or quark–antiquark pairs. For example, some models require diquarks to be in a color $\overline{\mathbf{3}}$ state [57,58,59,60], while others focus on quark–antiquark pairs restricted to a color $\mathbf{8}$ [61]. If a multiquark contains color structures not found in asymptotic hadron states, this could act as a stabilizing mechanism, enhancing the possibility of bound-state formation. Compared to uncorrelated models, these approaches generally predict a richer spectrum of exotic hadrons.

We have employed dynamical correlations induced by the Coulomb-like short-range color interaction between heavy quarks to study hidden-flavor pentaquarks of the form $Q\overline{Q}qq{q}^{\prime }$, where $Q=b$ or c, $q=u$ or d, and $q^{\prime }=u,d,s$ [35,36]. While traditional diquark models often emphasize attractive $qq$ interactions in a color-$\overline{\mathbf{3}}$ state, we argue that the $Q\overline{Q}$ color singlet is even more favorable due to binding energy scaling with the heavy quark mass $M_Q$. In natural units, the binding energy of a $Qq$ diquark scales with the light quark mass $m_q$, whereas that of the color-singlet $Q\overline{Q}$ pair scales as $2M_Q$. 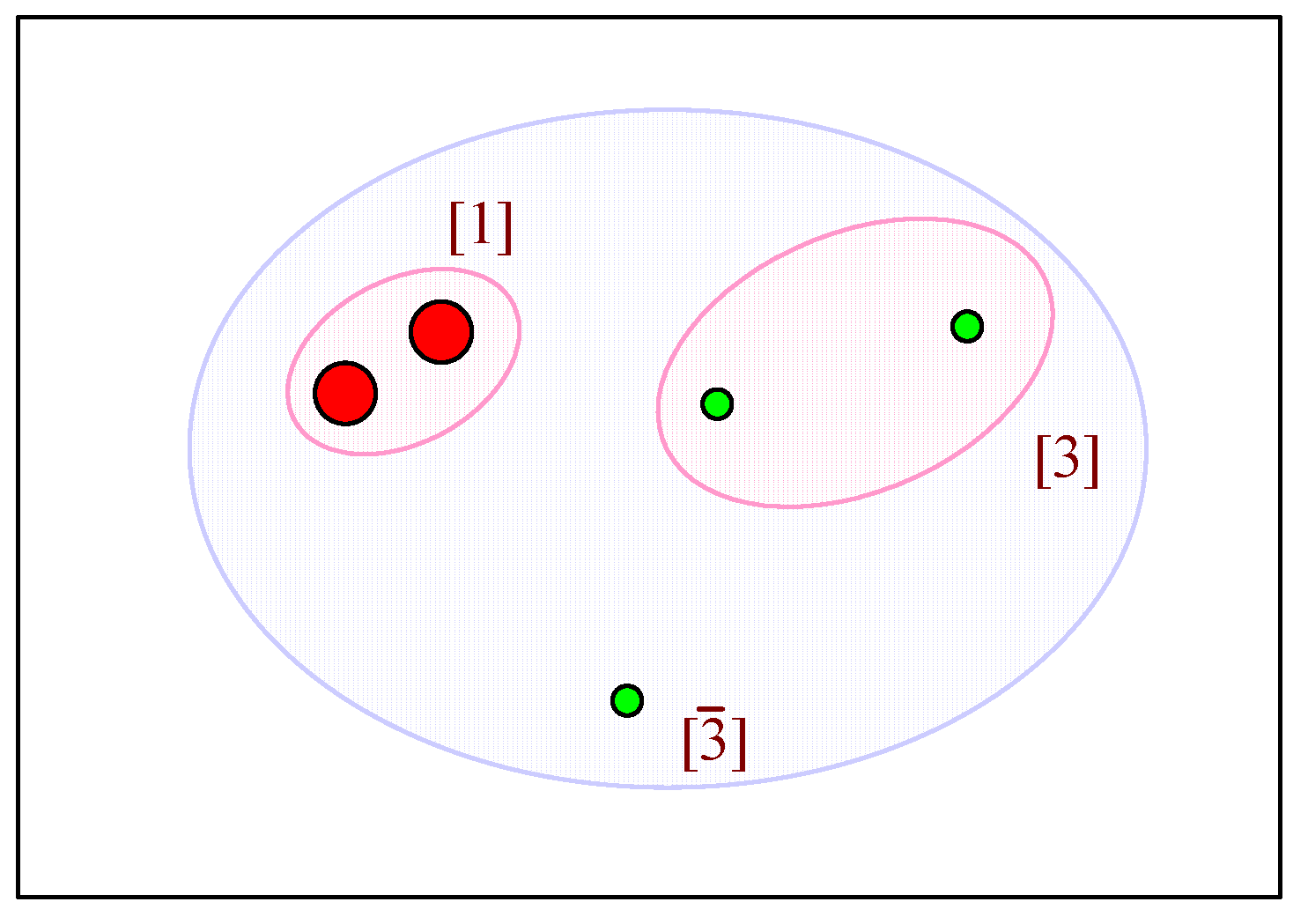This favors an internal structure dominated by a color-singlet $Q\overline{Q}$ pair rather than a color-octet [15], as illustrated in Figure 1. Taking into account the isospin-zero nature of the heavy quarks and the antisymmetry of the color-$\overline{\mathbf{3}}$$qq$ wave function (which enforces matching spin and isospin), we construct the wave function for the lowest-lying states, that is, those with a fully symmetric radial wave function, of any $(I,J)$ pentaquark:

$${\Psi }_{\mathrm{Pentaquark}}^{(I,J)}={\{{\mathbf{3}}_c,i_1,s_1=1/2\}}_q\otimes {\{{\mathbf{1}}_c,i_2=0,s_2\}}_{\left(Q\overline{Q}\right)}\otimes {\{{\overline{\mathbf{3}}}_c,i_3=s_3,s_3\}}_{\left(qq\right)},$$

(1)

where $i_n$ and $s_n$ denote the the isospin and spin of the different components. $i_1=1/2$ for $Q\overline{Q}qqq$ and $i_1=0$ for $Q\overline{Q}qqs$. The Coulomb-like correlations between the heavy quarks help to avoid repulsive interactions associated with color-octet $Q\overline{Q}$ configurations. Notably, these constraints also arise naturally in constituent quark models for doubly heavy tetraquarks [62,63].

QCD favors certain quark configurations over others [15]. As discussed above, the strongest quark–antiquark correlation occurs in the color-, flavor-, and spin-singlet channel $\left\{{\mathbf{1}}_c,{\mathbf{1}}_f,0_s\right\}$. The next most favorable configuration is the color-antitriplet, flavor-antisymmetric, spin-singlet channel $\left\{{\overline{\mathbf{3}}}_c,{\overline{\mathbf{3}}}_f,0_s\right\}$, which underlies the structure of diquarks.

Table 2. Quantum numbers of $Q\overline{Q}qqq$ hidden-flavor pentaquarks containing spin-zero diquarks. Numbers in parentheses denote the isospin of $Q\overline{Q}qqs$ pentaquarks. See Equation (1) for notation.

I	J	${\mathit{s}}_1$	${\mathit{s}}_2$	${\mathit{s}}_3$	Vector
$1/2\left(0\right)$	$1/2$	$1/2$	0	0	$v_1$
	$1/2$		1	0	$v_2$
	$1/2$		0	1	$v_3$
	$3/2$		1	0	$w_1$
$3/2\left(1\right)$	$3/2$	$1/2$	0	1	$w_3$

lists hidden-flavor pentaquark states containing at least one such favorable QCD channel, i.e., a spin-zero diquark.

To analyze the effects of Coulomb-like correlations on the structure of hidden-flavor pentaquarks, we employ the generic constituent quark model known as the AL1 potential [64]. This model has been widely used in studies of multiquark systems [33,34,62,65,66,67,68]. It features a central potential combining a Coulomb term with a linear confinement term, complemented by a smeared chromomagnetic spin–spin interaction:

$$\begin{array}{cc}\hfill V\left(r\right)& =-{\displaystyle \frac{3}{16}}{\tilde{\lambda }}_i·{\tilde{\lambda }}_j\left[\lambda r-{\displaystyle \frac{\kappa }{r}}-\Lambda +{\displaystyle \frac{V_{SS}\left(r\right)}{m_i{m}_j}}{\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j\right],\hfill \\ \hfill V_{SS}& ={\displaystyle \frac{2\pi {\kappa }^{\prime }}{3{\pi }^{3/2}{r}_0^3}}exp\left(-{\displaystyle \frac{r^2}{r_0^2}}\right),r_0=A{\left({\displaystyle \frac{2m_i{m}_j}{m_i+m_j}}\right)}^{-B}.\hfill \end{array}$$

(2)

The model parameters are set as follows: $\lambda =0.1653{\mathrm{GeV}}^2$, $\Lambda =0.8321\mathrm{GeV}$, $\kappa =0.5069$, ${\kappa }^{\prime }=1.8609$, $A=1.6553{\mathrm{GeV}}^{B-1}$, and $B=0.2204$. The constituent quark masses are as follows: $m_u=m_d=0.315\mathrm{GeV}$, $m_s=0.577\mathrm{GeV}$, $m_c=1.836\mathrm{GeV}$, and $m_b=5.227\mathrm{GeV}$. The color factor ${\tilde{\lambda }}_i·{\tilde{\lambda }}_j$ is adapted to differentiate between quark–quark and quark–antiquark interactions.

Notably, the smearing of the spin–spin interaction depends on the reduced mass of the interacting quark pair, thereby maintaining the flavor dependence of the interaction. The AL1 potential parameters were finely tuned through a global fit to 36 mesons and 53 baryons, achieving excellent agreement with experimental data, as detailed in Table 2 of Ref. [64]. Although the reported ${\chi }^2$ value is slightly higher than that of some other models, this is largely due to the inclusion of high-angular-momentum resonances. Nevertheless, the AL1 model remains highly effective for analyzing low-energy hadron spectra [69]. The color–spin algebra pertinent to five-quark systems has been systematically developed in Refs. [66,70].

In multiquark dynamics, binding can arise either from medium- to long-range attraction, often modeled through Goldstone boson exchange between color-singlet clusters [71,72,73], or from short-range dynamics driven by one-gluon exchange. While the latter typically generates strong repulsion in nucleon–nucleon ($NN$) S-waves, it does not universally apply to all hadronic channels. For example, certain configurations in the $\Delta \Delta$ and $N\Delta$ sectors display short-range attraction, as evidenced by their low-energy phase shifts [74]. This attraction has underpinned predictions of resonances in these systems [75,76,77,78], some of which may have experimental support [8]. For a detail discussion on the interplay between Goldstone boson and one-gluon exchange mechanisms within hybrid constituent models, particularly regarding tetraquark stability, see Refs. [71,79].

2.2. The Three-Body Problem

Multiquark systems may exhibit internal clustering, which can significantly simplify their computational treatment. This is especially evident in tetraquark studies, where a diquark–antidiquark approximation reduces the original four-body problem to an effective two-body one [80,81]. For hidden-flavor pentaquarks, the factorization of color degrees of freedom (as discussed in Section 2.1), combined with the flavor independence of the quark–quark interaction, reduces the five-body problem to an effective three-body system, as illustrated in Figure 1. This effective system can be solved exactly using Faddeev equations [82,83], thereby avoiding the convergence difficulties often encountered with variational methods, particularly near thresholds. Our numerical approach follows the formalism outlined in Ref. [84].

The structure of the Faddeev equations is governed by conservation laws. In particular, three-body states in which a particle has a fixed spin can only couple to other states with the same spin due to the orthogonality of spinors. An analogous rule applies to isospin. Consequently, the integral equations decouple into separate sets, each characterized by conserved individual spin and isospin values. The sets relevant to total spin $J=1/2$ and $J=3/2$ are presented in

Table 3. Channels contributing to $J=1/2$ and $J=3/2$ states, denoted by $v_i$ and $w_i$, respectively, in Table 2.

$\mathit{J}=1/2$
	$s_1$	$s_2$	$S_3$	$s_3$	I	F
$v_1$	$1/2$	0	$1/2$	0	$1/2$	$9/8$
$v_2$	$1/2$	1	$1/2$	0	$1/2$	$3/8$
$v_3$	$1/2$	0	$1/2$	1	$1/2$	$9/8$
	$s_2$	$s_3$	$S_1$	$s_1$
$v_1$	0	0	0	$1/2$	$1/2$	0
$v_2$	1	0	1	$1/2$	$1/2$	0
$v_3$	0	1	1	$1/2$	$1/2$	0
	$s_3$	$s_1$	$S_2$	$s_2$
$v_1$	0	$1/2$	$1/2$	0	$1/2$	$9/8$
$v_2$	0	$1/2$	$1/2$	1	$1/2$	$9/8$
$v_3$	1	$1/2$	$1/2$	0	$1/2$	$3/8$
$\mathbf{J}=\mathbf{3}/\mathbf{2}$
	$s_1$	$s_2$	$S_3$	$s_3$	I	F
$w_1$	$1/2$	1	$3/2$	0	$1/2$	$3/2\sqrt{2}$
$w_3$	$1/2$	0	$1/2$	1	$3/2$	$9/8$
	$s_2$	$s_3$	$S_1$	$s_1$
$w_1$	1	0	1	$1/2$	$1/2$	0
$w_3$	0	1	1	$1/2$	$3/2$	0
	$s_3$	$s_1$	$S_2$	$s_2$
$w_1$	0	$1/2$	$1/2$	1	$1/2$	$9/8$
$w_3$	1	$1/2$	$3/2$	0	$3/2$	$3/2\sqrt{2}$

. Here, $S_i$ denotes the spin of the pair $jk$. Because the individual isospin is determined by the spin configuration, it is not explicitly listed in the tables. The matrix element $F=\langle {\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j\rangle$ represents the coupling strength between two-body amplitudes mediated by the spin–spin interaction.

We briefly review the solution of the Faddeev equations in the case where the three constituents are in S-wave configuration. The generalization to states with orbital angular momentum $L\ne 0$ results in a coupled-channel problem, as detailed in Ref. [35]. Accordingly, the Faddeev equations for a bound state with total isospin I and total spin J can be expressed as

$$\begin{array}{ccc}\hfill T_{i;IJ}^{I_i{S}_i}\left(p_i{q}_i\right)=& & \sum _{j\ne i}\sum _{I_j{S}_j}{\displaystyle \frac{1}{2}}{\int }_0^{\infty }{q}_j^{2}d{q}_j{\int }_{-1}^{1}d\cos \theta t_{i;I_i{S}_i}(p_i,p_i^{\prime };E-q_i^2/2{\nu }_i)\hfill \\ & & \times h_{ij;IJ}^{I_i{S}_i;I_j{S}_j}{\displaystyle \frac{1}{E-p_j^2/2{\eta }_j-q_j^2/2{\nu }_j}}{T}_{j;IJ}^{I_j{S}_j}\left(p_j{q}_j\right),\hfill \end{array}$$

(3)

where $t_{i;I_i{S}_i}$ are the two-body scattering amplitudes, and ${\eta }_i$, ${\nu }_i$ are the reduced masses:

$$\begin{array}{ccc}\hfill {\eta }_i& =& {\displaystyle \frac{m_j{m}_k}{m_j+m_k}},\hfill \\ \hfill {\nu }_i& =& {\displaystyle \frac{m_i(m_j+m_k)}{m_i+m_j+m_k}}.\hfill \end{array}$$

(4)

${\overrightarrow{p}}_i^{\prime }$ is the momentum of the pair $jk$ (with $ijk$ an even permutation of 123) and ${\overrightarrow{p}}_j$ is the momentum of the pair $ki$ which are given by

$$\begin{array}{ccc}\hfill {\overrightarrow{p}}_i^{\prime }& =& -{\overrightarrow{q}}_j-{\alpha }_{ij}{\overrightarrow{q}}_i,\hfill \\ \hfill {\overrightarrow{p}}_j& =& {\overrightarrow{q}}_i+{\alpha }_{ji}{\overrightarrow{q}}_j,\hfill \end{array}$$

(5)

where

$$\begin{array}{ccc}\hfill {\alpha }_{ij}& =& {\displaystyle \frac{{\eta }_i}{m_k}},\hfill \\ \hfill {\alpha }_{ji}& =& {\displaystyle \frac{{\eta }_j}{m_k}},\hfill \end{array}$$

(6)

so that

$$\begin{array}{ccc}\hfill p_i^{\prime }& =& \sqrt{q_j^2+{\alpha }_{ij}^2{q}_i^2+2{\alpha }_{ij}{q}_i{q}_j\cos \theta },\hfill \\ \hfill p_j& =& \sqrt{q_i^2+{\alpha }_{ji}^2{q}_j^2+2{\alpha }_{ji}{q}_i{q}_j\cos \theta }.\hfill \end{array}$$

(7)

$h_{ij;IJ}^{I_i{S}_i;I_j{S}_j}$ are the spin–isospin coefficients,

$$\begin{array}{ccc}\hfill h_{ij;IJ}^{I_i{S}_i;I_j{S}_j}=& & {(-)}^{I_j+i_j-I}\sqrt{(2I_i+1)(2I_j+1)}W(i_j{i}_{k}I{i}_i;I_i{I}_j)\hfill \\ & & \times {(-)}^{S_j+s_j-J}\sqrt{(2S_i+1)(2S_j+1)}W(s_j{s}_{k}J{s}_i;S_i{S}_j),\hfill \end{array}$$

(8)

where W is a Racah coefficient and $i_i$, $I_i$, and I ($s_i$, $S_i$, and J) are the isospins (spins) of particle i of the pair $jk$ and of the three-body system.

To facilitate numerical treatment, we map the momentum variable $p_i\in [0,\infty )$ to $x_i\in [-1,1]$ via

$$x_i={\displaystyle \frac{p_i-b}{p_i+b}},$$

(9)

where b is an arbitrary scaling parameter. This transforms the Faddeev equations into

$$\begin{array}{ccc}\hfill T_{i;IJ}^{I_i{S}_i}\left(x_i{q}_i\right)=& & \sum _{j\ne i}\sum _{I_j{S}_j}{\displaystyle \frac{1}{2}}{\int }_0^{\infty }{q}_j^{2}d{q}_j{\int }_{-1}^{1}d\cos \theta t_{i;I_i{S}_i}(x_i,x_i^{\prime };E-q_i^2/2{\nu }_i)\hfill \\ & & \times h_{ij;IJ}^{I_i{S}_i;I_j{S}_j}{\displaystyle \frac{1}{E-p_j^2/2{\eta }_j-q_j^2/2{\nu }_j}}{T}_{j;IJ}^{I_j{S}_j}\left(x_j{q}_j\right).\hfill \end{array}$$

(10)

The kernel can be further simplified by expanding the two-body amplitude in Legendre polynomials:

$$t_{i;I_i{S}_i}(x_i,x_i^{\prime };e)=\sum _{nr}{P}_n\left(x_i\right){\tau }_{i;I_i{S}_i}^{nr}\left(e\right)P_r\left(x_i^{\prime }\right),$$

(11)

where the expansion coefficients are given by

$${\tau }_{i;I_i{S}_i}^{nr}\left(e\right)={\displaystyle \frac{2n+1}{2}}{\displaystyle \frac{2r+1}{2}}{\int }_{-1}^{1}d{x}_i{\int }_{-1}^{1}d{x}_i^{\prime }{P}_n\left(x_i\right)t_{i;I_i{S}_i}(x_i,x_i^{\prime };e)P_r\left(x_i^{\prime }\right).$$

(12)

Substituting this expansion yields

$$T_{i;IJ}^{I_i{S}_i}\left(x_i{q}_i\right)=\sum _n{P}_n\left(x_i\right)T_{i;IJ}^{n{I}_i{S}_i}\left(q_i\right),$$

(13)

where $T_{i;IJ}^{n{I}_i{S}_i}\left(q_i\right)$ satisfies the one-dimensional integral equation

$$T_{i;IJ}^{n{I}_i{S}_i}\left(q_i\right)=\sum _{j\ne i}\sum _{m{I}_j{S}_j}{\int }_0^{\infty }d{q}_j{K}_{ij;IJ}^{n{I}_i{S}_i;m{I}_j{S}_j}(q_i,q_j;E)T_{j;IJ}^{m{I}_j{S}_j}\left(q_j\right),$$

(14)

with

$$\begin{array}{ccc}\hfill K_{ij;IJ}^{n{I}_i{S}_i;m{I}_j{S}_j}(q_i,q_j;E)=& & \sum _r{\tau }_{i;I_i{S}_i}^{nr}(E-q_i^2/2{\nu }_i){\displaystyle \frac{q_j^2}{2}}\hfill \\ & & \times {\int }_{-1}^{1}d\cos \theta h_{ij;IJ}^{I_i{S}_i;I_j{S}_j}{\displaystyle \frac{P_r\left(x_i^{\prime }\right)P_m\left(x_j\right)}{E-p_j^2/2{\eta }_j-q_j^2/2{\nu }_j}}.\hfill \end{array}$$

(15)

The three amplitudes $T_{1;IJ}^{r{I}_1{S}_1}\left(q_1\right)$, $T_{2;IJ}^{m{I}_2{S}_2}\left(q_2\right)$, and $T_{3;IJ}^{n{I}_3{S}_3}\left(q_3\right)$ in Equation (14) are coupled together.

2.3. Results and Discussion

We solved the three-body problem for various $(I,J)$ configurations of the $Q\overline{Q}qq{q}^{\prime }$ pentaquark systems discussed in Section 2.1. The resulting binding energies for the different hidden-flavor pentaquark configurations are summarized in

Table 4. Binding energies (in MeV) of the different $Q\overline{Q}qq{q}^{\prime }$ pentaquark states.

Q	q	${\mathit{q}}^{\prime }$	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	${\mathit{w}}_1$	${\mathit{w}}_3$
c	$u,d$	$u,d$	7	17	24	12	12
c	$u,d$	s	133	138	143	134	134
b	$u,d$	$u,d$	39	41	52	40	40
b	$u,d$	s	165	167	175	166	166

.

We first observe an apparent degeneracy between the $w_1$ and $w_3$ vectors. These correspond to $I=1/2$ and $I=3/2$$Q\overline{Q}qqq$ pentaquarks with $J=3/2$, and to $I=0$ and $I=1$$Q\overline{Q}qqs$ states with $J=3/2$. This behavior aligns with the isospin-independent character of the interaction model described in Equation (2). Nevertheless, this degeneracy is nontrivial because of the constraints imposed by the Pauli principle.

The dominant quark correlations governed by QCD dynamics, as summarized in Table 2, allow us to infer general features of the multiquark spectrum. The mass splitting between the spin-triplet and spin-singlet $Q\overline{Q}$ configurations corresponds to the $J/\psi -{\eta }_c$ mass difference in the charmonium sector and the ${\rm Y}-{\eta }_b$ difference in the bottomonium sector. Additionally, the mass splitting between spin-triplet and spin-singlet $qq$ diquarks, with color–flavor configurations $\{{\overline{\mathbf{3}}}_c,{\mathbf{6}}_f\}$ and $\{{\overline{\mathbf{3}}}_c,{\overline{\mathbf{3}}}_f\}$, respectively, has been estimated from lattice QCD simulations to lie between 100 and 200 MeV [85,86,87]. Based on these findings, we adopt the following effective values for these mass differences:

$$\begin{array}{cc}\hfill \Delta M^{c\overline{c}}=M_{\{{\mathbf{1}}_c,{\mathbf{1}}_f,1_s\}}^{c\overline{c}}-M_{\{{\mathbf{1}}_c,{\mathbf{1}}_f,0_s\}}^{c\overline{c}}& =86\mathrm{MeV},\hfill \\ \hfill \Delta M^{b\overline{b}}=M_{\{{\mathbf{1}}_c,{\mathbf{1}}_f,1_s\}}^{b\overline{b}}-M_{\{{\mathbf{1}}_c,{\mathbf{1}}_f,0_s\}}^{b\overline{b}}& =61\mathrm{MeV},\hfill \\ \hfill \Delta M^{qq}=M_{\{{\overline{\mathbf{3}}}_c,{\mathbf{6}}_f,1_s\}}^{qq}-M_{\{{\overline{\mathbf{3}}}_c,{\overline{\mathbf{3}}}_f,0_s\}}^{qq}& =146\mathrm{MeV}.\hfill \end{array}$$

(16)

Thus, the mass of a $Q\overline{Q}qqq$ pentaquark state can be written as

$$M_i^{Q\overline{Q}qqq}=M_0^{Q\overline{Q},q}-B_i+\Delta M^{Q\overline{Q}}{\delta }_{s_2,1}+\Delta M^{qq}{\delta }_{s_3,1},$$

(17)

where $B_i$ is the binding energy given in Table 4 and $M_0^{Q\overline{Q},q}$ denotes the sum of the masses of a spin-zero $Q\overline{Q}$ pair, a spin-zero $qq$ diquark, and a light quark. A similar expression holds for the $Q\overline{Q}qqs$ states, where the light quark is replaced by a strange quark, and the corresponding mass term is denoted $M_0^{Q\overline{Q},s}$:

$$M_i^{Q\overline{Q}qqs}=M_0^{Q\overline{Q},s}-B_i+\Delta M^{Q\overline{Q}}{\delta }_{s_2,1}+\Delta M^{qq}{\delta }_{s_3,1}.$$

(18)

Using $M_0^{c\overline{c},q}=4319$ MeV, we compute the predicted masses listed in

Table 5. Predicted properties of $c\overline{c}qqq$ pentaquark states compared to experimental data.

Vector	$\left(\mathit{I}\right){\mathit{J}}^{\mathit{P}}$	${\mathit{M}}_{\mathbf{Th}}$ (MeV)	State	${\mathit{M}}_{\mathbf{Exp}}$ (MeV) [49,50]
$v_1$	$(1/2)1/2^{-}$	4312	$P_c{\left(4312\right)}^{+}$	$4311.9\pm 0.7_{-0.6}^{+6.8}$
$v_2$	$(1/2)1/2^{-}$	4388	$P_c{\left(4380\right)}^{+}$	$4380\pm 8\pm 29$
$w_1$	$(1/2)3/2^{-}$	4393
$v_3$	$(1/2)1/2^{-}$	4441	$P_c{\left(4440\right)}^{+}$	$4440.3\pm 1.3_{-4.7}^{+4.1}$
$w_3$	$(3/2)3/2^{-}$	4453	$P_c{\left(4457\right)}^{+}$	$4457.3\pm 0.6_{-1.7}^{+4.1}$

. The recent observation of a hidden-charm pentaquark with strangeness [51] allows for the calibration of the free parameter in the strange sector. Adopting $M_0^{c\overline{c},s}=4471$ MeV, we obtain the results shown in

Table 6. Predicted properties of $c\overline{c}qqs$ pentaquark states compared to experimental data.

Vector	$\left(\mathit{I}\right){\mathit{J}}^{\mathit{P}}$	${\mathit{M}}_{\mathbf{Th}}$ (MeV)	State	${\mathit{M}}_{\mathbf{Exp}}$ (MeV) [51,52]
$v_1$	$\left(0\right)1/2^{-}$	4338	$P_{\Psi s}^{\Lambda }\left(4338\right)$	$4338\pm 0.7$
$v_2$	$\left(0\right)1/2^{-}$	4419
$w_1$	$\left(0\right)3/2^{-}$	4423
$v_3$	$\left(0\right)1/2^{-}$	4474	$P_{cs}\left(4459\right)$	$4454.9\pm 2.7$
$w_3$	$\left(1\right)3/2^{-}$	4483		$4467.8\pm 3.7$

. For completeness,

Table 7. Mass predictions (in MeV) of $c\overline{c}qqs$ pentaquarks from various models.

$\left(\mathit{I}\right){\mathit{J}}^{\mathit{P}}$	This work	Ref. [61]	Ref. [88]	Ref. [89]	Ref. [90]
$\left(0\right)1/2^{-}$	4338	4362.3	$4319.4_{-3.0}^{+2.8}$	4330	4474
$\left(0\right)1/2^{-}$	4419	4548.2	$4456.9_{-3.3}^{+3.2}$	4475	4522
$\left(0\right)3/2^{-}$	4423	4556.1	$4423.7_{-6.8}^{+6.4}$	4440	4522
$\left(0\right)1/2^{-}$	4474	4571.4	$4463.0_{-3.0}^{+2.8}$	4476	−
$\left(1\right)3/2^{-}$	4483	4846.4	−	−	−

presents a comparison of our predictions with those from other theoretical approaches.

We are now in a position to make parameter-free predictions for the lowest-lying nonstrange and strange hidden-bottom pentaquarks, for which no experimental observations currently exist. These predictions are presented in

Table 8. Mass predictions (in MeV) of nonstrange $b\overline{b}qqq$ pentaquarks from various models.

$\left(\mathit{I}\right){\mathit{J}}^{\mathit{P}}$	This Work	Ref. [61]	Ref. [91]	Ref. [92]
$(1/2)1/2^{-}$	11062	11137.1	11080 (11078)	10605
$(1/2)1/2^{-}$	11121	11148.9	11115 (11043)	10629
$(1/2)3/2^{-}$	11122	11237.5	11124 (11122)	10629
$(1/2)1/2^{-}$	11195	11205.0	−	−
$(3/2)3/2^{-}$	11207	11370.6	11112 (10999)	−

and

Table 9. Mass predictions (in MeV) of $b\overline{b}qqs$ pentaquarks from various models.

$\left(\mathit{I}\right){\mathit{J}}^{\mathit{P}}$	This Work	Ref. [61]	Ref. [90]
$\left(0\right)1/2^{-}$	11088	11117.7	10671
$\left(0\right)1/2^{-}$	11147	11183.8	10695
$\left(0\right)3/2^{-}$	11148	11180.2	10695
$\left(0\right)1/2^{-}$	11224	11301.2	−
$\left(1\right)3/2^{-}$	11233	11509.0	−

, alongside results from other theoretical frameworks. Together, they provide a consistent set of spin-parity assignments for the lightest hidden-flavor pentaquark states and serve as useful benchmarks for future experimental investigations, particularly in the hidden-bottom sector.

The spin-parity quantum numbers of hidden-flavor pentaquarks remain experimentally undetermined [27]. Nevertheless, a range of theoretical models offer predictions that can be confronted with our results summarized in Table 5, Table 6, Table 7, Table 8 and Table 9. We begin our discussion with the hidden-charm sector for subsequent analysis of the remaining systems.

Although the quantum numbers of the $P_c{\left(4312\right)}^{+}$ remain uncertain [93], the majority of theoretical works favor a $J^P=1/2^{-}$ assignment [94,95,96,97,98,99]. The two narrow overlapping structures $P_c{\left(4440\right)}^{+}$ and $P_c{\left(4457\right)}^{+}$ [50] were initially interpreted as a single resonance, $P_c{\left(4450\right)}^{+}$ [49]. Before the experimental resolution of this doublet, theoretical models had already predicted the existence of two nearly degenerate states with quantum numbers $J^P=1/2^{-}$ and $3/2^{-}$ in this mass region. These states were interpreted either as hidden-charm pentaquarks dynamically generated through ${\Sigma }_c{\overline{D}}^{*}$ interactions [94,98,100] or as bound states of charmonium $\Psi \left(2S\right)$ and the nucleon [101]. In both scenarios, the predicted quantum numbers are consistent with our findings.

Our model also predicts two candidate states corresponding to the broad $P_c{\left(4380\right)}^{+}$ resonance: one with $J=1/2$ and another with $J=3/2$. The true nature of this state remains uncertain and represents a significant challenge for future experimental investigations [102]. While earlier studies proposed various spin assignments, ranging from $J=3/2$ to $J=5/2$ [49], a more recent analysis of $B_s\to J/\psi p\overline{p}$ decays favors a $J^P=3/2^{-}$ assignment [103]. Based on this evidence, we tentatively associate the $P_c{\left(4380\right)}^{+}$ with the $J^P=3/2^{-}$ state predicted by our model. This identification naturally suggests the existence of a nearby $J^P=1/2^{-}$ partner state, with an estimated mass around 4390 MeV. It is worth noting that for strange hidden-charm pentaquarks, our results are in good agreement with the recent experimental measurement by Belle [54], which reports a mass of $4471.7\pm 4.8\pm 0.6$ MeV/c² for the $P_{cs}\left(4459\right)$. Our model predicts a mass 4474 MeV/c² for the $J^P=1/2^{-}$ state. This consistency is particularly encouraging.

Ref. [72] investigates hidden-charm pentaquarks within the framework of a quark delocalization color screening model. The most deeply bound configurations, corresponding to $J=1/2$ and $J=3/2$, are dominated by a $\left(Q\overline{Q}\right)\left(qqq\right)$ structure, reflecting strong short-range Coulomb-like correlations between the heavy quarks. In contrast, configurations of the form $\left(q\overline{Q}\right)\left(Qqq\right)$ result only in quasi-bound states. Ref. [73] investigates hidden-charm pentaquarks within a chiral quark model. In contrast to Ref. [72], the dominant configuration found here is $\left(q\overline{Q}\right)\left(Qqq\right)$. This difference may be attributed to the absence of shared light quarks between the quarkonium and baryon components in the $\left(Q\overline{Q}\right)\left(qqq\right)$ configuration, which suppresses meson exchanges due to the Okubo–Zweig–Iizuka (OZI) rule [104]. This rationale also underlies the tendency of hadronic molecular models to describe hidden-flavor pentaquarks as bound states of open-flavor hadrons [19,24,105,106,107,108]. In such models, D-meson exchange is too short-ranged to effectively compete with the medium-range attraction generated by light-meson exchanges, which is more naturally realized in the $\left(q\overline{Q}\right)\left(Qqq\right)$ configuration. Consequently, hybrid and purely gluonic models tend to yield different multiquark spectra. Several studies also predict the existence of $I=3/2$ pentaquarks. Within the hadroquarkonium framework, Ref. [109] provides robust predictions of isospin-3/2 $\Psi \left(2S\right)-\Delta$ bound states near 4.5 GeV. From the constituent quark model perspective, Ref. [66] similarly supports the existence of $I=3/2$ hidden-flavor pentaquarks, including a $J=5/2$ state located close to threshold. Ref. [61] explores compact hidden-flavor pentaquarks constructed from the repulsive color-octet–octet configuration $\mathbf{8}\left(Q\overline{Q}\right)\otimes \mathbf{8}\left(qqq\right)$. In this framework, negative-parity states are predicted to remain bound only with respect to the heavier $\left(q\overline{Q}\right)\left(Qqq\right)$ threshold. A distinctive feature of this model is the strong suppression of branching ratios into hidden-flavor channels, which serves to differentiate compact color-octet pentaquarks from meson–baryon molecular states. Ref. [110] employs an extended chromomagnetic model that augments the conventional color–spin interaction with effective quark-pair mass parameters, fitted to reproduce known meson and baryon spectra. The $I=1/2$ spectrum, as presented in Figure 1 of Ref. [110], aligns well with our findings. However, it does not reproduce the near-degeneracy between $I=1/2$ and $I=3/2$ states observed in our model, likely a consequence of the method used to extract the effective parameters, since the underlying interaction is isospin independent.

Beyond constituent quark models, a variety of other theoretical frameworks have been employed to study hidden-flavor pentaquarks. Predictions from diquark-based models exhibit significant variation, largely depending on the assumptions made regarding diquark dynamics [57,58,59,60,111]. QCD sum rule approaches also lead to diverse outcomes, predicting both molecular-like states [112,113,114,115] and hidden-color configurations [116]. For a thorough overview of recent progress in QCD sum rule techniques and their relevance to exotic hadrons, see Ref. [117]. Hadronic molecular models based on effective chiral Lagrangians or one-boson exchange potentials depend on low-energy constants and couplings that are often poorly known. These parameters are typically estimated using quark model relations [94,118,119,120,121].

For the hidden-bottom pentaquarks listed in Table 8, only theoretical predictions are available for comparison. Ref. [61] employs a color-magnetic interaction model, estimating mass splittings relative to a reference mass fitted to experimental data. Ref. [91] uses a chiral quark model and solves the five-body bound-state problem via the Gaussian expansion method. We cite results from the color-singlet calculation, which is theoretically closest to our framework, and list in parentheses those from the coupled-channel calculation that includes hidden-color configurations. Ref. [92] provides predictions from a hadroquarkonium model for isospin-$1/2$ baryons, considering two scenarios with different chromoelectric polarizabilities. We report the results corresponding to the weaker interaction strength, in which hidden-bottom pentaquarks appear in the 10.6–10.9 GeV range. The alternative model, based on a purely Coulombic treatment of charmonia, predicts more deeply bound states in the 10.4–10.7 GeV range. In this case, positive-parity states are less bound and lie approximately 150 MeV above their negative-parity counterparts. It is noteworthy that quark-based approaches [61,91] place hidden-bottom pentaquarks in the 11.0–11.2 GeV mass range, whereas the hadroquarkonium model [92] predicts more deeply bound states.

In the strange hidden-charm sector, the perturbative color-magnetic model of Ref. [61] predicts large mass splittings among the lowest-lying states. In contrast, the chiral effective field theory potentials of Ref. [88] produce results more consistent with ours, locating the lowest states in the 4.3–4.4 GeV region. Notable, these authors find no bound states in $I=1$ channels. Ref. [89] employs a chiral quark model combined with a variational method, expanding radial wave functions in Gaussian bases. This approach, which has proven effective in describing nonstrange pentaquarks, predicts small binding energies across various baryon–meson channels. A complementary study of $c\overline{c}qqs$ tetraquarks within a similar chiral quark framework, utilizing the Gaussian expansion approach in combination with the complex-scaling technique, is presented in Ref. [122]. By contrast, the hadroquarkonium model of Ref. [90] predicts higher masses for strange hidden-charm pentaquarks while yielding lower masses than quark-based models for nonstrange and strange hidden-bottom systems.

The predicted strange hidden-bottom pentaquark states lie close in mass to their nonstrange counterparts, within the 11.1–11.3 GeV range. This aligns with the perturbative chromomagnetic model of Ref. [61]. As in the nonstrange sector, the hadroquarkonium model of Ref. [90] predicts significantly lower masses, with the most deeply bound states appearing near 10.4 GeV under the strong-attraction scenario. Consequently, hidden-bottom pentaquarks, both strange and nonstrange, offer a valuable testing ground for distinguishing between different multiquark interaction mechanisms. In particular, models based on quark substructure suggest that experimental searches should concentrate around the 11 GeV region.

Alternative theoretical frameworks have also been employed to study both strange and nonstrange hidden-flavor pentaquarks. One such approach is the diquark–triquark model of Ref. [93], which leverages attractive color configurations involving non-pointlike triquarks and uses a light-cone distribution amplitude to describe the internal structure of the pentaquark. The model incorporates an effective Hamiltonian with spin–orbit interactions and predicts, among other states, the $P_c{\left(4380\right)}^{+}$ as a $J^P=3/2^{-}$ resonance with a mass of 4349 MeV and the originally reported $P_c{\left(4450\right)}^{+}$ [35] as a $J^P=5/2^{+}$ state with a mass of 4453 MeV. The lightest predicted state is a $J^P=3/2^{-}$ hidden-charm pentaquark at 4085 MeV. Although the model discusses $J^P=1/2^{-}$, their masses are not explicitly provided. Extending this framework, the same authors also explore strange hidden-charm and hidden-bottom pentaquarks. The lightest states in each sector for each spin-parity assignment are

$$\left\{\begin{array}{cc}\mathrm{Hidden-charm}:\hfill & (3/2^{-},5/2^{-},5/2^{+})=(4085,4433,4453)\mathrm{MeV}\hfill \\ \\ \mathrm{Strange} \mathrm{hidden-charm}:\hfill & (3/2^{-},5/2^{-},5/2^{+})=(4314,4624,4682)\mathrm{MeV}\hfill \\ \\ \mathrm{Hidden-bottom}:\hfill & (3/2^{-},5/2^{-},5/2^{+})=(10723,11045,1146)\mathrm{MeV}\hfill \\ \\ \mathrm{Strange} \mathrm{hidden-bottom}:\hfill & (3/2^{-},5/2^{-},5/2^{+})=(10981,11264,11413)\mathrm{MeV}.\hfill \end{array}\right.$$

Preliminary analyses of experimental data in the hidden-charm sector suggest the coexistence of both negative- and positive-parity states within the same energy region [49]. We calculated the mass of the lowest positive-parity state, which corresponds to two nearly degenerate configurations with quantum numbers $J^P=1/2^{+}$ and $3/2^{+}$. This excitation arises from the most strongly correlated internal structure, featuring a $Q\overline{Q}$ pair in the color–flavor–spin configuration $\{{\mathbf{1}}_c,{\mathbf{1}}_f,0_s\}$, and a $qq$ subsystem in $\{{\overline{\mathbf{3}}}_c,{\overline{\mathbf{3}}}_f,0_s\}$. The lightest positive-parity hidden-charm pentaquark states are found above 4.5 GeV, specifically 4527 MeV for $c\overline{c}udd$ and 4552 MeV for $c\overline{c}uds$. In contrast, excitation energies in the hidden-bottom sector are significantly lower, resulting in positive-parity states that lie closer in mass to their negative-parity ground-state counterparts: 11,273 MeV for $b\overline{b}udd$ and 11,291 MeV for $b\overline{b}uds$. Nearly degenerate opposite-parity states may originate from distinct internal mechanisms, for example, a negative-parity state formed by coupling a radially excited quarkonium to a nucleon versus a positive-parity state generated through orbital excitation of a ground-state quarkonium–nucleon system [101]. This pattern of parity assignments is also consistent with the Born–Oppenheimer interpretation proposed in Ref. [58].

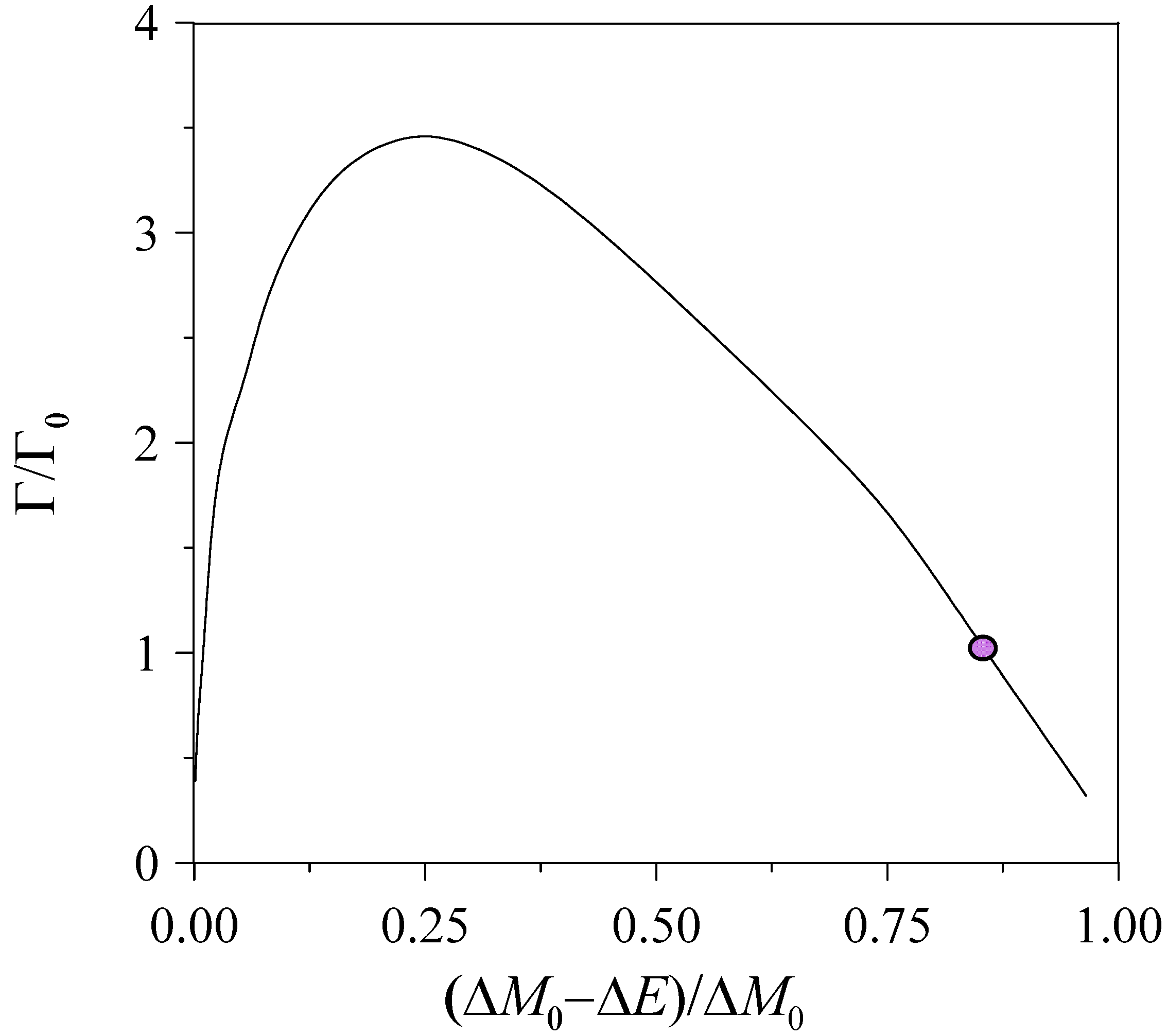
The decay properties of multiquark states are highly sensitive to their internal structure [61]. Transitions into heavy meson–heavy baryon channels are generally expected to be strongly suppressed, primarily due to the need for heavy meson exchange in t-channel processes. Given their quark composition, these exotic states may decay in a manner analogous to excited quarkonia such as $\Psi \left(nS\right)$, ${\rm Y}\left(nS\right)$, ${\eta }_c\left(nS\right)$, or ${\eta }_b\left(nS\right)$. As a result, configurations containing a spin-zero $Q\overline{Q}$ pair (e.g., $v_1$, $v_3$, $w_3$ in Table 2) are predicted to exhibit narrower decay widths than those containing a spin-one $Q\overline{Q}$ pair (such as $v_2$, $w_1$). This pattern is consistent with current empirical findings (see Table 1). Nonetheless, the total decay width also depends critically on the internal structure of the bound state [47,48], a topic discussed in detail in Section 4.

It should be emphasized that the correlation mechanisms employed in our framework do not universally guarantee the stability of multiquark systems across all flavor configurations. Just as the short-range repulsion in the nucleon–nucleon interaction, originating from one-gluon exchange, is not a general feature of all hadronic systems, our QCD-based model does not impose constraints on the color configurations of pentaquarks containing an anticharm or antibottom quark, such as $\overline{Q}qqqq$. As discussed in Ref. [123], these states are unlikely to be bound due to the competing effects of chromoelectric and chromomagnetic interactions, which tend to disfavor binding in such configurations.

Our findings also contribute to the ongoing discussion regarding the possibility of charmonium forming bound states with atomic nuclei, a scenario originally proposed by Brodsky [104]. Since charmonium contains no valence u and d quarks, its interaction with nucleons via light meson exchange is suppressed by the OZI rule. This limitation has led to the development of alternative models to generate sufficient attraction, including those based on chromoelectric polarizability and the energy–momentum tensor distributions of the nucleon [101,109,124]. Additional support comes from studies of in-medium modifications of hadronic structure, such as the predicted formation of $J/\psi$-nucleus bound states [125], and similar theoretical expectations for ${\eta }_c$-nucleus systems across various nuclear targets [126]. Our approach introduces a distinct mechanism, driven by short-range one-gluon exchange between the charmonium and the constituent quarks of the nucleon. This mechanism, originally proposed in the context of dibaryon resonances [74,75,76,77,78], represents, to our knowledge, the first derivation of such bound-state behavior solely from quark–gluon dynamics within a truncated Hilbert space.

3. Molecules of Heavy Hadrons

A striking prediction of the quark model was the possible existence of doubly heavy tetraquarks, $QQ\overline{q}\overline{q}$ [10]. Their stability was shown to depend on the mass ratio $M_Q/m_q$. The mechanism that stabilizes such states at large $M_Q/m_q$ is analogous to that which makes the hydrogen molecule significantly more stable than positronium in atomic physics [127]. This prediction was confirmed by the LHCb Collaboration, which reported the discovery of a very narrow peak in the $DD\pi$ spectrum, identified as the $T_{cc}^{+}$ state [13,14]. It corresponds to a minimal quark content $cc\overline{u}\overline{d}$. The $T_{cc}^{+}$ lies just above the strong interaction threshold, missing binding by a very small amount. Consequently, it is widely believed that its heavier counterparts, $T_{bc}=bc\overline{u}\overline{d}$ and $T_{bb}=bb\overline{u}\overline{d}$, could be stable against both strong and electromagnetic decays [13,32]. Theoretical estimates of the binding energy of the $T_{bb}$ tetraquark vary, with reported values ranging from 90 to 214 MeV [10,34,80,81,128,129,130,131,132,133,134].

As shown in Ref. [34], the probability of the color $\mathbf{6}\overline{\mathbf{6}}$ component in a $QQ\overline{q}\overline{q}$ tetraquark tends to zero as $M_Q\to \infty$. Consequently, doubly heavy tetraquarks are expected to approach a pure $\overline{\mathbf{3}}\mathbf{3}$ color configuration rather than forming a single color-singlet meson–meson $\mathbf{11}$ molecular state [62]. These two-body color components can be expanded into a mixture of several physical meson–meson channels [135]. For instance, in the case of the isoscalar axial-vector $bb\overline{u}\overline{d}$ tetraquark, the relevant channels are $B{B}^{*}$ and $B^{*}{B}^{*}$, see Table II of Ref. [136]. As a result, $QQ\overline{q}\overline{q}$ tetraquarks are naturally generated through a coupled-channel system of colorless meson–meson states [137,138].

Another area that has recently garnered significant attention is the study of heavy baryon bound states, particularly motivated by advances in lattice QCD. The HAL QCD Collaboration [37] investigated the $\Omega \Omega$ system in the ${}^1{S}_0$ channel, finding an overall attractive interaction and reporting a binding energy of $B_{\Omega \Omega }^{\mathrm{QCD}}=1.6\left(6\right)\left(\begin{array}{c}+0.7\\ -0.6\end{array}\right)$ MeV. When Coulomb repulsion is included, the binding energy is reduced by approximately half, yielding $B_{\Omega \Omega }^{\mathrm{QCD}+\mathrm{Coulomb}}=0.75\left(5\right)\left(5\right)$ MeV. The ${\Omega }_{ccc}{\Omega }_{ccc}$ system was also studied using the HAL QCD method [39]. The results show weak short-range repulsion surrounded by a relatively strong attractive potential well, resulting in a bound state with a binding energy of $B_{{\Omega }_{ccc}{\Omega }_{ccc}}^{\mathrm{QCD}}=5.68\left(0.77\right)\left(\begin{array}{c}+0.46\\ -1.02\end{array}\right)$ MeV. When Coulomb interaction is taken into account, a scattering length of $a_0^C=-19\left(7\right)\left(\begin{array}{c}+7\\ -6\end{array}\right)$ fm is obtained. More recently, a lattice QCD study of the ${\Omega }_{bbb}{\Omega }_{bbb}$ system in the ${}^1{S}_0$ channel [40] reported a deeply bound state with a binding energy of $B_{{\Omega }_{bbb}{\Omega }_{bbb}}^{\mathrm{QCD}}=81\left(\begin{array}{c}+16\\ -14\end{array}\right)$ MeV. At this depth, Coulomb repulsion acts merely as a perturbative correction, reducing the binding energy by approximately 5 and 10 MeV.

The possible existence of deuteron-like hadronic molecular states composed of vector–vector or pseudoscalar–vector meson pairs was first proposed in Ref. [139]. This framework, in which meson–meson systems are stabilized through some form of interhadron potential, has since become a common approach to interpreting potential hadronic molecules [140,141,142] (see Ref. [16] for a recent review). Moreover, insights from nuclear physics indicate that if an attractive interaction exists between two baryons, the presence of additional nucleons, provided no severe Pauli principle constraints are introduced, can enhance the overall binding. Simple examples highlight this effect: the deuteron, with quantum numbers $\left(I\right)J^P=\left(0\right)1^{+}$, has a binding energy of $2.225$ MeV; the triton, $\left(I\right)J^P=(1/2)1/2^{+}$, is bound by $8.480$ MeV; and the $\alpha$ particle, $\left(I\right)J^P=\left(0\right)0^{+}$, has a binding energy of $28.295$ MeV. Consequently, the binding energy per nucleon, $B/A$, increases roughly in the ratio 1:3:7. A comparable trend is observed in systems with strangeness $-1$. The hypertriton ${}_{\Lambda }{}^3\mathrm{H}$, with $\left(I\right)J^P=\left(0\right)1/2^{+}$, is weakly bound with a separation energy of $130\pm 50$ keV [143], whereas the ${}_{\Lambda }{}^4\mathrm{H}$, $\left(I\right)J^P=\left(0\right)0^{+}$, has a significantly higher separation energy of $2.12\pm 0.01\left(\mathrm{stat}\right)\pm 0.09\left(\mathrm{syst}\right)$ MeV [144].

Thus, an important and challenging question is whether the existence of deeply bound two-hadron systems, like the $T_{bb}$ tetraquark or the ${\Omega }_{bbb}{\Omega }_{bbb}$ dibaryon predicted by lattice QCD, could lead to the formation of bound states in systems involving more than two hadrons [41,42,43,44,145,146,147]. This issue is particularly relevant in the bottom sector, where the predicted binding energies for two-body systems are exceptionally large. In the following, we analyze the three-meson and three-baryon cases separately.

3.1. The Three-Meson System

We solve the Faddeev equations for the three-meson bound-state problem, using as input the two-body $t—$matrices from Refs. [134,136]. These interactions give rise to an isoscalar axial-vector $bb\overline{u}\overline{d}$ bound state, the $T_{bb}$, which emerges from a coupled-channel system involving both pseudoscalar–vector and vector–vector combinations of two B mesons.

The three-body channels most conducive to generating bound states are those that include the $T_{bb}$ tetraquark and exclude two-B-meson components, due to the lack of attraction in the $BB$ interaction [10,34,80,81,128,129,130,131,132,133,134]. Channels with total angular momentum $J=0$ or 1 would necessarily involve $BB$ subsystems and are therefore disfavored. In contrast, channels with $J=3$ do not contain two-body subsystems with $j=1$, which are required for the $T_{bb}$ quantum numbers, making them unsuitable as well. A similar exclusion applies to channels with isospin $I=3/2$. Consequently, the three-body channel with quantum numbers $\left(I\right)J^P=(1/2)2^{-}$ is the only configuration that satisfies all the conditions necessary to maximize the likelihood of binding. The two-body channels contributing to this state are listed in

Table 10. Different two-body channels $(i,j)$ contributing to the $\left(I\right)J^P=(1/2)2^{-}$ configuration of the $B{B}^{*}{B}^{*}-B^{*}{B}^{*}{B}^{*}$ three-body system.

Interacting Pair	$(\mathit{i},\mathit{j})$	Spectator
$B{B}^{*}$	$(0,1)$	$B^{*}$
	$(1,1)$
$B^{*}{B}^{*}$	$(0,1)$	$B^{*}$
	$(1,2)$
$B^{*}{B}^{*}$	$(1,2)$	B

.

The Faddeev equations for the bound-state three-meson problem [82,83] can be written as

$$T_i=t_i{G}_0(T_j+T_k),$$

(19)

with

$$t_i=V_i+V_i{G}_0{t}_i,$$

(20)

where $t_i$ denotes the two-body t-matrices, which already account for the coupling among all two-body channels that contribute to a given three-body state. For coupled three-meson systems such as $B{B}^{*}{B}^{*}$ and $B^{*}{B}^{*}{B}^{*}$, the resulting equations are illustrated in Figure 2. In these diagrams, solid lines represent $B^{*}$ mesons and dashed lines correspond to B mesons.

If the last term on the right-hand side of the second equation in Figure 2 is omitted, the first and second equations reduce to the Faddeev equations for a system consisting of two identical bosons and a third distinguishable particle [145]. Likewise, by omitting the last two terms in the third equation, one recovers the Faddeev equation for a system of three identical bosons, as in this case all three coupled Faddeev equations become identical [145]. The additional terms shown in Figure 2 are, naturally, those responsible for the coupling between the $B{B}^{*}{B}^{*}$ and $B^{*}{B}^{*}{B}^{*}$ components.

Figure 3 displays the results of our calculation. The solid blue lines correspond to the strong decay thresholds of the three-B-meson system $B{B}^{*}{B}^{*}-B^{*}{B}^{*}{B}^{*}$ with quantum numbers $\left(I\right)J^P=(1/2)2^{-}$. These thresholds include the $B^{*}{B}^{*}{B}^{*}$, $B{B}^{*}{B}^{*}$, and $T_{bb}{B}^{*}$ channels. Dashed green lines indicate electromagnetic decay thresholds involving three B mesons, specifically the $BB{B}^{*}$ and $BBB$ channels with quantum numbers $\left(I\right)J^P=(1/2)1^{-}$ and $(1/2)0^{-}$, respectively. The thick purple line represents the energy of the $T_{bbb}$ state, located 90 MeV below the lowest decay threshold. These results are derived using the binding energy of the axial-vector $T_{bb}$ tetraquark reported in Ref. [128].

There also exists a baryon–antibaryon threshold, ${\Omega }_{bbb}\overline{p}$, which is clearly decoupled from the $T_{bbb}$ state. This decoupling arises from the dominant tetraquark–meson structure of $T_{bbb}$ and the orthogonality of its color wave functions to that of the baryon–antibaryon system. Based on the $T_{bb}$ binding energy reported in Ref. [128], the mass of the ${\Omega }_{bbb}$ baryon is estimated to be 14.84 GeV, placing the ${\Omega }_{bbb}\overline{p}$ threshold at approximately 15.78 GeV, well above the mass of the $T_{bbb}$ state. Although theoretical predictions of the ${\Omega }_{bbb}$ mass vary considerably (see Table 1 of Ref. [148]), even if the ${\Omega }_{bbb}\overline{p}$ threshold were to lie below the $T_{bbb}$ mass, the latter would still manifest as a narrow resonance. This is because $\left|{\Psi }_{T_{bbb}}\right.〉$ is an eigenstate of the Hamiltonian H, and the transition operator T, approximated by $e^{iH}$, cannot induce a decay into a baryon ($B_1$) and an antibaryon (${\overline{B}}_2$) if the matrix element $〈B_1{\overline{B}}_2\left|T\right|{\Psi }_{T_{bbb}}〉$ vanishes. This occurs when the overlap $〈B_1{\overline{B}}_2|{\Psi }_{T_{bbb}}〉$ is zero [149]. The formation of the $T_{bbb}$ state is driven by the attractive dynamics of the three-meson system, whereas the weakly interacting baryon–antibaryon channel would primarily serve as a detection mode. As we will discuss in Section 4, this situation is analogous to the case of the $P_c^{+}\left(4380\right)$ pentaquark, which decays into the $J/\psi p$ channel with a width of $\Gamma =205\pm 18\pm 86$ MeV despite having a phase space of about 345 MeV.

We estimated the binding energy of the three-body $T_{bbb}$ system over a range of input binding energies for the $T_{bb}$ tetraquark, starting from the lowest reported value of approximately 90 MeV, as cited in Ref. [129]. Our calculations indicate that the $T_{bbb}$ three-meson bound state remains robustly stable throughout the entire range considered. The binding energy of $T_{bbb}$ decreases from 90 MeV to 43 MeV as the $T_{bb}$ binding energy is varied between 180 MeV and 87 MeV. The binding energy of the $T_{bbb}$ system is calculated relative to the lowest strong decay threshold, defined as $m_B+2m_{B^{*}}-B\left(T_{bb}\right)$. However, if the $T_{bb}$ binding energy is reduced further to around 50 MeV, the $T_{bbb}$ system would remain bound by only about ∼23 MeV, placing it approximately 19 MeV above the lowest $BBB$ threshold.

The situation is notably less favorable in the charm sector, primarily due to the larger mass difference between vector and pseudoscalar mesons: 141 MeV in the charm sector compared to only 45 MeV in the bottom sector. As a consequence, the $DDD$ and $DD{D}^{*}$ thresholds lie 282 MeV and 141 MeV, respectively, below the $D{D}^{*}{D}^{*}$ configuration. In other words, when the internal two-body thresholds of a three-body system are widely separated, they tend to destabilize the overall system. This is a well-known phenomenon observed in studies of three-body systems comprising either two identical baryons or two identical mesons along with a bound two-body subsystem. Even when strong attractive forces exist within some subsystems, the full three-body configurations often remain unbound and may even display a pronounced repulsive character [145].

Finally, it is worth noting that several studies in the literature have been developed within theoretical frameworks that are not directly related to the consistent approach adopted in this review. For instance, Ref. [150] predicts the existence of $DDK$ and $DDDK$ molecules under the assumption that the $DK$ interaction is sufficiently strong to generate a bound state, identified with the $D_{s0}^{*}\left(2317\right)$. Likewise, Ref. [151] predicts a $D^{*}{D}^{*}{D}^{*}$ bound state based on the hypothesis that the $T_{cc}^{+}$ is itself a $D^{*}{D}^{*}$ bound state, thereby neglecting contributions from $D{D}^{*}$ channels and the corresponding thresholds. Moreover, no mention is made of baryon–antibaryon thresholds in that work.

3.2. The Three-Baryon System

A situation analogous to that described for the three-meson system also arises in the context of the three-baryon systems. The key distinction, however, is that in the baryonic case, the binding of the two-body subsystems does not originate from coupled-channel dynamics. Given the bound-state nature of systems composed of two–$\Omega$ baryons, predicted across different heavy-flavor sectors by lattice QCD calculations [37,39,40], a natural question emerges: could systems containing more than two such $\Omega$-like baryons also form bound states [43,44,45]? We will henceforth use the notation ${\Omega }^i$ to refer to the $\Omega$ for $i=s$, the ${\Omega }_{ccc}$ for $i=c$, and the ${\Omega }_{bbb}$ for $i=b$.

Owing to Fermi–Dirac statistics, the ${\Omega }^i{\Omega }^i$ system is restricted to two $L=0$ partial waves: the spin-singlet ${}^1{S}_0$ and the spin-quintet ${}^5{S}_2$. Moreover, there exists only one fully antisymmetric three-body ${\Omega }^i{\Omega }^i{\Omega }^i$ state with all three baryons in relative S-wave: the $J^P=3/2^{+}$ state. In terms of an arbitrary Jacobi coordinate system, denoted as $\left|s_{12},s_3;S\right.〉$, the fully antisymmetric $J^P=3/2^{+}$ wave function includes two spin components corresponding to $s_{12}=0$ and $s_{12}=2$. These components must be recoupled using alternative Jacobi bases, such as $\left|s_1,s_{23};S\right.〉$, to properly account for particle exchange symmetry. The relevant recoupling coefficients between different Jacobi coordinate systems are provided in

Table 11. Recoupling coefficients between different Jacobi coordinate systems for the fully antisymmetric ${\Omega }^i{\Omega }^i{\Omega }^i$ state with quantum numbers $J^P=3/2^{+}$ state.

		$\left|s_{12},s_3;S\right.〉$
		$s_{12}=0$	$s_{12}=2$
$\left|s_1,s_{23};S\right.〉$	$s_{23}=0$	$-{\displaystyle \frac{1}{4}}$	$-{\displaystyle \frac{\sqrt{5}}{4}}$
	$s_{23}=2$	$-{\displaystyle \frac{\sqrt{5}}{4}}$	${\displaystyle \frac{3}{4}}$

.

This table highlights two key features of the ${\Omega }^i{\Omega }^i{\Omega }^i$ state with $J^P=3/2^{+}$. First, it demonstrates the dominant contribution of the ${}^5{S}_2$ partial wave, which significantly outweighs that of the attractive ${}^1{S}_0$ channel. Second, it reveals the strong mixing between the ${}^1{S}_0$ and ${}^5{S}_2$ components within the fully antisymmetric three-body wave function.

We solved the three-body ${\Omega }^i{\Omega }^i{\Omega }^i$ system using the Faddeev formalism, as described in detail in Ref. [152]. For the two-body input potentials in the ${}^1{S}_0$${\Omega }^i{\Omega }^i$, we employed the parametrization from Refs. [37,39] for the cases $i=s$ and c. For the $i=b$ sector, we parametrized the potential depicted in Figure 4 of Ref. [40] by fitting it to a sum of three Gaussian functions, following the same methodology applied in Refs. [37,39].

As a first exploratory step, we consider only the contribution of the attractive ${}^1{S}_0$${\Omega }^i{\Omega }^i$ interaction. Within this one-channel approximation, no three-body bound state with $J^P=3/2^{+}$ is found in any of the investigated flavor sectors. This notable outcome is a direct manifestation of the Pauli principle at the baryonic level. Specifically, the recoupling coefficient between the two spin-zero Faddeev amplitudes is negative (see Table 11), which effectively converts the attractive two-body interaction into a repulsive one in the three-body system [153]. Interestingly, enhancing the strength of the attraction in the ${}^1{S}_0$ channel further amplifies this effective repulsion in the three-body configuration. This behavior is a generic feature of systems composed of three identical fermions and is, in particular, known to apply to the three-neutron system. However, unlike neutrons, which are spin $1/2$ fermions, the ${\Omega }^i$ baryons are spin-$3/2$ particles. As a result, in addition to spin-zero two-body amplitudes, spin-two contributions are also allowed in the $L=0$ three-body state, as discussed above. Crucially, the recoupling coefficient associated with the spin-two amplitudes is positive and thus unaffected by the antisymmetry constraints that effectively makes repulsive the spin-zero channel. This makes the inclusion of the spin-two component essential for a realistic description of the three-${\Omega }^i$ system.

A comprehensive calculation of the ${\Omega }^i{\Omega }^i{\Omega }^i$S-wave state with quantum numbers $J^P=3/2^{+}$ must account for contributions from both relevant two-body partial waves: ${}^1{S}_0$ and ${}^5{S}_2$. A naive assumption of spin-independence in the ${\Omega }^i{\Omega }^i$ interaction [44], motivated, for instance, by a Fermi–Breit-like potential at the baryonic level, can lead to the prediction of deeply bound three-body states. In particular, when applying the ${}^1{S}_0$ lattice QCD interaction from Ref. [40] in the $i=b$ sector, such an approach yields binding energies on the order of several hundred MeV. However, it is crucial to recognize that the ${\Omega }^i$ baryons are identical particles, each composed of three identical quarks. As a result, the overall two-baryon wave function must remain antisymmetric under the exchange of quarks between baryons, particularly within their spatial overlap region. This fundamental symmetry constraint limits the validity of spin-independent models and must be properly incorporated to ensure a physically meaningful description of the system.

The consequences of having identical quark constituents in the baryons manifest themselves in the normalization of the two-baryon wave function [77], which plays a crucial role in the calculation of observables, most notably, in the effective interaction potential. The effect is encoded in the normalization kernel, which can be formally expressed as [45]

$$\begin{array}{ccc}\hfill {\mathcal{N}}_{{\Omega }^i{\Omega }^i}^{LS}\left(R\right)\overrightarrow{R\to 0}& & 4\pi \left[1-{\displaystyle \frac{3R^2}{4{\alpha }^2}}\right]{\displaystyle \frac{1}{1·3\dots (2L+1)}}{\left[{\displaystyle \frac{R^2}{4{\alpha }^2}}\right]}^L\hfill \\ & & \times \left\{\left[3^L-3C\left(S\right)\right]+{\displaystyle \frac{\left[3^{L+2}-3C\left(S\right)\right]}{2(2L+3)}}{\left[{\displaystyle \frac{R^2}{4{\alpha }^2}}\right]}^2+\dots \right\}.\hfill \end{array}$$

(21)

$C\left(S\right)$ is a flavor-independent spin coefficient given by

$$C\left(S\right)=\left.〈{\Omega }^i\left(123\right),{\Omega }^i\left(456\right);S\right|P_{36}^S\left|{\Omega }^i\left(123\right),{\Omega }^i\left(456\right);S\right.〉.$$

(22)

The spin coefficients for the various ${\Omega }^i{\Omega }^i$ two-body states are presented in

Table 12. $C\left(S\right)$ spin coefficients for the ${\Omega }^i{\Omega }^i$ states.

S	0	1	2	3
$C\left(S\right)$	$-{\displaystyle \frac{1}{3}}$	$-{\displaystyle \frac{1}{9}}$	${\displaystyle \frac{1}{3}}$	1

.

As seen from Equation (21), in S-wave configurations, the closer the coefficient $C\left(S\right)$ is to $1/3$, the more strongly the normalization of the two-baryon wave function is suppressed at short distances. This suppression reflects an effective Pauli repulsion, which originates from the presence of a quasi-forbidden state [154].

To derive the ${}^5{S}_2$${\Omega }^i{\Omega }^i$ interaction from the underlying quark dynamics, we employed the Born–Oppenheimer approximation [77,155,156]. Within this framework, the effective baryon–baryon potential is defined as

$$V_{B^{\alpha }{B}^{\beta }\left(LS\right)\to B^{\alpha }{B}^{\beta }\left(L^{\prime }{S}^{\prime }\right)}\left(R\right)={\xi }_{LS}^{L^{\prime }{S}^{\prime }}\left(R\right)-{\xi }_{LS}^{L^{\prime }{S}^{\prime }}(\infty ),$$

(23)

where

$${\xi }_{LS}^{L^{\prime }{S}^{\prime }}\left(R\right)={\displaystyle \frac{〈{\Psi }_{B^{\alpha }{B}^{\beta }}^{L^{\prime }{S}^{\prime }}\left(\overrightarrow{R}\right)\mid {\sum }_{i<j=1}^6{V}_{q_i{q}_j}\left({\overrightarrow{r}}_{ij}\right)\mid {\Psi }_{B^{\alpha }{B}^{\beta }}^{LS}\left(\overrightarrow{R}\right)〉}{{\mathcal{N}}_{B^{\alpha }{B}^{\beta }}^{L^{\prime }{S}^{\prime }}\left(R\right){\mathcal{N}}_{B^{\alpha }{B}^{\beta }}^{LS}\left(R\right)}}.$$

(24)

By inserting the spin coefficients from Table 12 into the normalization expression of the two-baryon wave function in Equation (21), we find that the ${}^5{S}_2$${\Omega }^i{\Omega }^i$ partial wave satisfies the condition $C\left(S\right)={\displaystyle \frac{1}{3}}$. This value leads to a significant suppression of the wave function normalization at short distances, manifesting as a strong Pauli repulsion. Crucially, this repulsive behavior arises from the quark-level antisymmetrization constraints and cannot be captured by baryonic models alone. Consequently, a prominent short-range repulsive core is predicted in the ${}^5{S}_2$${\Omega }^i{\Omega }^i$ interaction across all flavor sectors, purely as a consequence of the quark substructure regardless of the specific details of the interaction dynamics [157,158].

In contrast, the ${}^1{S}_0$${\Omega }^i{\Omega }^i$ partial wave does not fulfill the Pauli blocking condition, i.e., $C\left(S\right)=1/3$ (see Table 12). As a result, its wave function normalization remains essentially constant at short distances, indicating that no additional Pauli-induced repulsion arises beyond what is already present in the interaction dynamics. This conclusion aligns well with existing lattice QCD results [37,39,40], which also show that the ${}^1{S}_0$ channel exhibits genuine attractive behavior not masked by antisymmetrization effects.

The repulsive character of the ${}^5{S}_2$${\Omega }^i{\Omega }^i$ interaction is illustrated in Figure 4, based on the parametrization and potential model of Ref. [159]. The dominant contribution to this repulsion originates from the Coulomb-like term of the one-gluon exchange potential, which is inherently flavor-independent. As a result, the spatial range of the repulsive core is determined by the Gaussian parameter $\alpha$ of the quark wave function, which characterizes the spatial extension of the ${\Omega }^i$ baryons [160]. This behavior is, in fact, expected: constructing a total spin-2 state from six identical spin-1/2 quarks of the same flavor (three per ${\Omega }^i$ baryon) while satisfying the color-singlet constraint is not possible within the ground-state configuration. At least two quarks would be forced to occupy the same quantum state, in direct violation of the Pauli principle. Therefore, this strong short-range repulsion is a model-independent result, arising as a fundamental consequence of the antisymmetry requirements at the quark level.

This repulsive effect, as previously reported in earlier works [158], is a generic feature of baryonic systems subject to Pauli blocking. It manifest as a short-range repulsive core at distances of approximately 0.75–0.78 fm in light-quark systems, corresponding to a Gaussian parameter $\alpha \simeq 0.5$ fm. Crucially, such repulsion does not arise unless the antisymmetry of the baryon constituents is explicitly imposed. This is not the case in phenomenological approaches that disregard the underlying quark substructure, such as those extrapolating from unrelated two-baryon systems or from the same system in quantum-number sectors unaffected by Pauli constraints. Ref. [44] provides a clear example of this issue: assuming spin independence in the ${\Omega }^i{\Omega }^i$ interaction while using the lattice QCD results of Ref. [40] yields artificially deeply bound states, with binding energies on the order of several hundred MeV in the $i=b$ sector. Even if a strong repulsive core is introduced in the ${}^5{S}_2$ ${\Omega }^i{\Omega }^i$ channel but with the same effective range as the ${}^1{S}_0$ channel (i.e., neglecting the full effect of Pauli blocking), the resulting three-body binding energy varies only mildly. This still leads to bound states with energies in the range of 250–350 MeV for systems with $i=b$.

Additional support for these conclusions comes from preliminary lattice QCD studies of S-wave scattering between strangeness $-3$ baryons [161]. Conducted at a pion mass of $m_{\pi }\sim 390$ MeV across two lattice volumes, these studies indicate that the ${}^1{S}_0$$\Omega \Omega$ interaction is at most weakly attractive, yielding an extrapolated scattering length of $a_{S=0}^{\Omega \Omega }=0.16\pm 0.22$ fm. In contrast, states in the $S=2$ channel appear at significantly higher energies, suggesting strong repulsion. Notably, it was proposed that none of the observed states correspond to the $S=2$ ground state, highlighting the need for future simulations at lower pion masses.

To assess the combined effect of both spin channels, we solved the full three-body ${\Omega }^i{\Omega }^i{\Omega }^i$ problem, incorporating both the ${}^1{S}_0$ and ${}^5{S}_2$ two-body interactions. The ${}^1{S}_0$ interactions were taken from lattice QCD results [37,39,40], while the ${}^5{S}_2$ interaction corresponds to the strongly repulsive potential shown in Figure 4. The repulsive character of the single-channel calculation, driven by Pauli effects at the baryon level, is significantly enhanced by the quark-level antisymmetry that dominates the ${}^5{S}_2$ channel. As a result, despite the attractive nature of the ${}^1{S}_0$ interaction in the two-body sector, we find no evidence of a $J^P=3/2^{+}$ bound state in the ${\Omega }^i{\Omega }^i{\Omega }^i$ system for any flavor sector.

4. Decay Width of a Resonance Between Two Thresholds

A recurring feature among many of the proposed multiquark candidates discussed in the preceding sections is their theoretical interpretation as bound states of higher-energy configurations situated near the observed mass yet experimentally detected in lower-energy decay channels [162]. This leads to a nontrivial relationship between the decay width and the available phase space, challenging the conventional explanation that larger phase spaces generally result in broader widths. A notable example is provided by the $P_c^{+}$ pentaquark states discussed in Section 2.

Table 13. Summary of the $P_c^{+}$ properties decaying to $J/\psi p$ [49,50].

State	M (MeV)	$\mathbf{\Gamma }$ (MeV)	Phase Space (MeV)
$P_c{\left(4380\right)}^{+}$	$4380\pm 8\pm 29$	$205\pm 18\pm 86$	345 ± 30
$P_c{\left(4312\right)}^{+}$	$4311.9\pm 0.7_{-0.6}^{+6.8}$	$9.8\pm 2.7_{-4.5}^{+3.7}$	276.7 ± 6.8
$P_c{\left(4440\right)}^{+}$	$4440.3\pm 1.3_{-4.7}^{+4.1}$	$20.6\pm 4.9_{-10.1}^{+8.7}$	405.1 ± 4.9
$P_c{\left(4457\right)}^{+}$	$4457.3\pm 0.6_{-1.7}^{+4.1}$	$6.4\pm 2.0_{-1.9}^{+5.7}$	422.1 ± 4.1

presents the phase space available for the $J/\psi p$ decay, along with the corresponding widths. Interestingly, the state with the largest phase space exhibits the narrowest decay width, whereas other states with nearly identical phase space show widths that differ by orders of magnitude. This counterintuitive behavior is both intriguing and concerning, as it highlights the limitations of a purely kinematic interpretation and suggests the presence of more intricate dynamical mechanisms at play. Similar patterns have been observed in the meson sector, reinforcing that this phenomenon is not exclusive to baryonic resonances. A comprehensive discussion, along with additional examples, is available in Ref. [162] and the references therein.

If the quark dynamics within a $Q\overline{Q}q\overline{q}$ multiquark system is not constrained by the presence of correlated substructures, then two distinct color-singlet configurations can contribute to the total wave function,

$${\Psi }_{4q}={\alpha }_1\left|\left[Q\overline{Q}\right]\left[q\overline{q}\right]\right.〉+{\alpha }_2\left|\left[Q\overline{q}\right]\left[q\overline{Q}\right]\right.〉,$$

(25)

where, in general, ${\alpha }_1$ and ${\alpha }_2$, determined by the underlying quark dynamics, are both nonzero. A similar decomposition holds for $Q\overline{Q}qqq$ multiquark baryons,

$${\Psi }_{5q}={\beta }_1\left|\left[Q\overline{Q}\right]\left[qqq\right]\right.〉+{\beta }_2\left|\left[q\overline{Q}\right]\left[Qqq\right]\right.〉.$$

(26)

The properties of such states should be addressed by means of a coupled-channel calculation, as detailed in Section 3.1. Consequently, it becomes relevant to analyze the masses of the various thresholds and identify the dominant color-singlet components across different flavor sectors. This threshold structure not only constrains the dynamics of the system but also governs the coupling strength between channels, thereby playing a central role in determining the formation, binding mechanism, and decay patterns of the multiquark states.

Multiquark systems with a flavor content of $Q\overline{Q}q\overline{q}$ can form two types of color-singlet configurations: $\left[Q\overline{q}\right]\left[q\overline{Q}\right]$ and $\left[Q\overline{Q}\right]\left[q\overline{q}\right]$. For the $Q=c$ case, the masses of these two configurations are relatively close. In contrast, for $Q=b$, the $\left[Q\overline{Q}\right]\left[q\overline{q}\right]$ state lies significantly lower in mass, as shown in Figure 5. In the strange sector, the situation is reversed, where the $\left[Q\overline{q}\right]\left[q\overline{Q}\right]$ component becomes the lowest in energy, potentially leading to the formation of stable meson–antimeson molecular states [163]. A similar pattern arises in multiquark systems of the form $Q\overline{Q}qqq$. In the charm sector, for spin $J=1/2$, the mass difference between the two possible color-singlet configurations is $\Delta M=M_{\left[q\overline{Q}\right]\left[Qqq\right]}-M_{\left[Q\overline{Q}\right]\left[qqq\right]}=M_{\overline{D}{\Sigma }_c}-M_{J/\psi p}=$ 288 MeV. However, in the bottom sector, this difference increases significantly to $\Delta M=M_{\left[q\overline{Q}\right]\left[Qqq\right]}-M_{\left[Q\overline{Q}\right]\left[qqq\right]}=M_{\overline{B}{\Sigma }_b}-M_{{\rm Y}p}=$ 692 MeV [164]. This behavior is illustrated in Figure 6 for multiquark baryons with quantum numbers $J^P=1/2^{+}$ and $J^P=3/2^{+}$ in both the charm and bottom sectors. Several of the proposed multiquark states correspond to resonances that lie between the masses of the two color-singlet configurations.

The scenario described above can be modeled using a coupled-channel framework involving two distinct two-body color-singlet configurations, with a resonance emerging between them, as illustrated in Figure 7. Channel 1, which is lower in mass, consists of two color singlets: $\left[Q\overline{Q}\right]\left[q\overline{q}\right]$ for systems with baryon number $B=0$ and $\left[Q\overline{Q}\right]\left[qqq\right]$ for $B=1$. We denote the mass of the $Q\overline{Q}$ state as $m_1$ and that of the $q\overline{q}$ (or $qqq$) state as $m_2$. Channel 2, which is higher in mass, also comprises two color singlets: $\left[Q\overline{q}\right]\left[q\overline{Q}\right]$ for $B=0$ and $\left[q\overline{Q}\right]\left[Qqq\right]$ for $B=1$. The mass of the $Q\overline{q}$ state is denoted by $m_3$ and that of the $q\overline{Q}$ (or $Qqq$) state by $m_4$.

Specifically, we model the system as a coupled-channel problem governed by the non-relativistic Lippmann–Schwinger equation, where the two-body potentials consist of a combination of attractive and repulsive Yukawa terms, i.e.,

$$V^{ij}\left(r\right)=-A^{ij}{\displaystyle \frac{e^{-{\mu }_A^{ij}r}}{r}}+B^{ij}{\displaystyle \frac{e^{-{\mu }_B^{ij}r}}{r}}.$$

(27)

We consider scenarios in which a resonance occurs at an energy $E=E_R$, defined by the condition that the scattering phase shift satisfies $\delta \left(E_R\right)={90}^{\circ }$, corresponding to a Breit–Wigner resonance. This resonances lies between the mass thresholds of channels 1 and 2, i.e., $0<E_R<\Delta M$. The physical mass of the resonance is then given by $W_R=E_R+m_1+m_2$. The width of the resonance is calculated using the Breit–Wigner formula, as described in Refs. [165,166,167],

$$\Gamma \left(E\right)=\underset{E\to E_R}{lim}{\displaystyle \frac{2(E_R-E)}{\cot \mathrm{g}\left[\delta \right(E\left)\right]}}.$$

(28)

We begin by requiring that in a single-channel calculation, the upper channel (channel 2) supports a bound state with energy close to zero. In contrast, when both channels are coupled, the system develops a bound state just below the threshold of the lower channel (channel 1). By increasing, for instance, the strength of the repulsive component in the lower channel, this bound state can be shifted upward, eventually becoming a resonance embedded in the continuum. This framework allows for the study of how the resonance width evolves as its mass transitions from the vicinity of the lower channel to that of the upper channel. The initial configuration is illustrated in Figure 7, representing a resonance near the upper-channel threshold, corresponding to the parameters listed in

Table 14. Parameters of the interaction as defined in Equation (27). The coefficients $A^{ij}$ and $B^{ij}$ are given in MeV·fm, while the inverse ranges ${\mu }_A^{ij}$ and ${\mu }_B^{ij}$ are expressed in ${\mathrm{fm}}^{-1}$.

${\mathit{V}}^{\mathbf{ij}}$	${\mathit{A}}^{\mathbf{ij}}$	${\mathit{\mu }}_{\mathit{A}}^{\mathbf{ij}}$	${\mathit{B}}^{\mathbf{ij}}$	${\mathit{\mu }}_{\mathit{B}}^{\mathbf{ij}}$
$V^{11}$	100	$2.68$	3000	$5.81$
$V^{22}$	680	$4.56$	642	$6.73$
$V^{12}=V^{21}$	200	$1.77$	195	$3.33$

. Numerically, $\Delta E_0=$ 3.64 MeV, ${\Gamma }_0=$ 9.6 MeV, and $\Delta M_0=$ 25.6 MeV.

Let us examine how the decay width of the resonance evolves as its position shifts between the lower, $\Delta E\to \Delta M_0$, an the upper, $\Delta E\to 0$, channels. In other words, both the phase space available for decay and the binding energy relative to the formation channel change simultaneously. Since the resonance is generated by the attraction in the upper channel, we vary the repulsion in the detection (lower) channel to adjust its position. The results, shown in Figure 8, reveal how the resonance width initially increases rapidly as it approaches the lower channel despite the decreasing phase space. However, roughly two-thirds of the way toward the lower channel, the width begins to decrease. This behavior highlights an important point: for resonances significantly separated from their detection channel, it is the mass difference relative to the formation channel that predominantly governs the resonance width. Specifically, a larger binding energy corresponds to a larger width, even though the available phase space diminishes. As the resonance nears the upper channel, it becomes narrow and appears to largely ignore the lower channel. This is because the wave function of the nearly zero-energy bound in channel 2 has minimal overlap with the configuration of channel 1. Consequently, in this region, the dynamics are dominated by the attraction within the upper channel, with the second channel serving primarily as a detection mechanism.

The results presented in Figure 8 align well with recent observations by the LHCb Collaboration. In

Table 15. Suggested molecular structures for the $P_c^{+}$ pentaquarks [49,50,108,168].

State	Suggested Molecule	${\mathit{M}}_{\mathbf{Molecule}}$ (MeV)	$\mathit{\Delta }\mathit{E}$ (MeV)
$P_c{\left(4380\right)}^{+}$	${{\Sigma }_c^{*}}^{+}{\overline{D}}^0$	$4382.3\pm 2.3$	2.3 ± 30.1
$P_c{\left(4312\right)}^{+}$	${\Sigma }_c^{+}{\overline{D}}^0$	$4317.7\pm 0.4$	5.8 ± 6.8
$P_c{\left(4440\right)}^{+}$	${\Sigma }_c^{+}{\overline{D^{*}}}^0$	$4459.8\pm 0.4$	19.5 ± 4.9
$P_c{\left(4457\right)}^{+}$	${\Sigma }_c^{+}{\overline{D^{*}}}^0$	$4459.8\pm 0.4$	2.5 ± 4.1

, we summarize the most commonly proposed molecular interpretations of the $P_c^{+}$ pentaquarks. Focusing first on the latest LHCb results, listed in the last three rows of Table 15, we note that these resonances lie far from their detection channel, $J/\psi p$, with the corresponding phase space values given in Table 13. As demonstrated in Figure 8, when a resonance is distant from its detection channel, the key factor determining its decay width is the mass difference relative to the formation channel. The binding energies of the recent $P_c^{+}$ states increase as follows (see Table 15): 2.5 MeV, 5.8 MeV, and 19.5 MeV. Correspondingly, their observed decay widths (from Table 13) are 6.4 MeV, 9.8 MeV, and 20.6 MeV, respectively, showing excellent agreement with the trends predicted by our model.

5. Summary and Outlook

We present a summary of our recent findings on the structure and properties of exotic hadrons, focusing on two complementary research directions.

The first line of investigation addresses hidden-flavor pentaquark states, incorporating dynamical correlations arising from the Coulomb-like behavior of the short-range color interaction. These correlations effectively “freeze” the color wave function, allowing the reduction of the original five-body problem to a simplified three-body system. This reduced system is solved exactly using Faddeev equations. Our results provide a coherent description of the observed spectrum in the hidden-charm sector and offer predictive insights for the hidden-bottom sector, where experimental data are still unavailable. It is important to note that the color correlations employed here do not universally lead to bound multiquark states for all quark configurations. In particular, for pentaquarks containing anticharm or anti bottom quarks, the color wave function remains unconstrained within this framework. Finally, our model yields a dynamical mechanism for the possible formation of quarkonium bound to nuclear matter, an outcome not previously derived from quark–gluon dynamics within a restricted Hilbert space.

The second part of our study explores recent developments from lattice QCD and phenomenological analyses that suggest the potential stability of hadronic molecules containing multiple heavy quarks. These results indicate that few-body systems involving heavy flavors may inherently favor bound-state formation. As illustrative examples, we consider extreme configurations such as multiquark systems incorporating the doubly bottom tetraquark $T_{bb}$ or the $\Omega \Omega$ dibaryon states predicted by lattice QCD. In three-meson systems, we observe a general trend in which the binding energy diminishes with an increasing number of hadronic constituents. This decrease arises from the combined effects of the Pauli principle and the emergence of additional kinematic thresholds. Furthermore, the binding is weakened as the heavy-quark mass is reduced, due to the increasing mass differences among internal two-body subsystems, which act to destabilize potential bound configurations. Turning to three-baryon systems, we find that the Pauli principle again plays a critical role, particularly in suppressing the formation of bound states composed of three ${\Omega }^i$ baryons. Two dominant effects are identified. First, for spin-zero two-body subsystems, a negative spin recoupling coefficient transforms attractive ${}^1{S}_0$ interactions into effectively repulsive ones when extended to the full three-body system. Second, while spin-two configurations are not constrained by the Pauli principle at the baryon level, they still encounter strong short-range repulsion at the quark level due to antisymmetrization. Together, these effects significantly hinder the formation of S-wave three-$\Omega$ bound states regardless of the specific flavor content.

Finally, we examine the decay width of multiquark resonances composed of multiple color-singlet substructures. We have illustrated how narrow resonances can exist even when a large phase space for decay is available. In particular, for resonances located far from the experimental detection threshold, the decay width is primarily determined by the mass difference between the resonance and its formation channel rather than by the available phase space in the decay channel. As a result, more deeply bound states can exhibit broader widths despite having limited phase space for decay. We also explore the potential existence of multiquark analogs across different flavor sectors. Our analysis reveals that structural similarities do not necessarily translate into similar physical properties. This highlights the importance of caution when extrapolating multiquark predictions across flavor sectors, especially in cases where the underlying dynamics are approximately flavor-independent and dominated by coupled-channel effects.

Exotic hadron spectroscopy remains a powerful testing ground for deepening our understanding of QCD in the non-perturbative regime. Despite the inherent complexity of the subject, this review has outlined several mechanisms that quantitatively account for a variety of compelling experimental observations. While significant challenges persist, continued progress hinges on the development of theoretical frameworks capable of uncovering the dynamics that govern low-energy hadron dynamics. We hope that this work provides a meaningful contribution to that ongoing endeavor.