Review on the Theoretical and Practical Applications of Symmetry in Thermal Sciences, Fluid Dynamics, and Energy
Abstract
1. Introduction
2. Analysis of the Application of Symmetry in Thermal Sciences
2.1. Heat Transfer Modeling
2.2. Nanoscale Thermal Transport
2.3. Thermal Sciences
2.4. Symmetry in Irreversible Processes
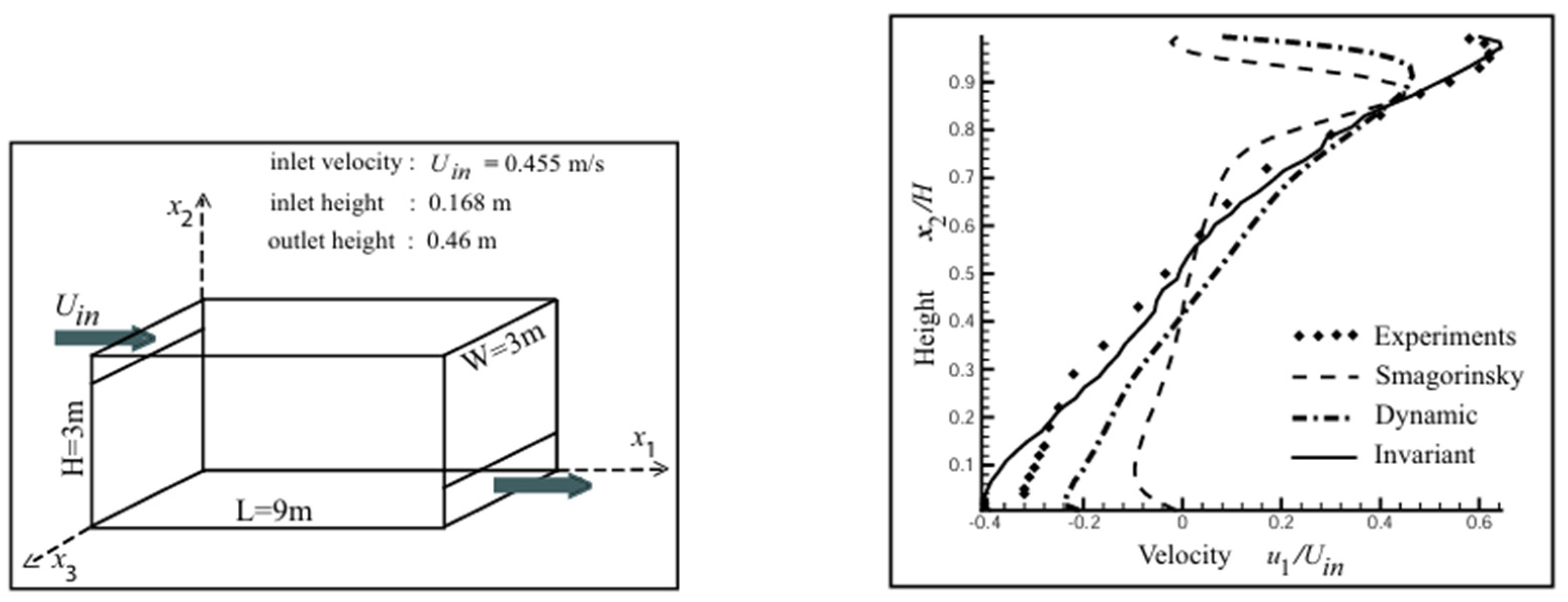
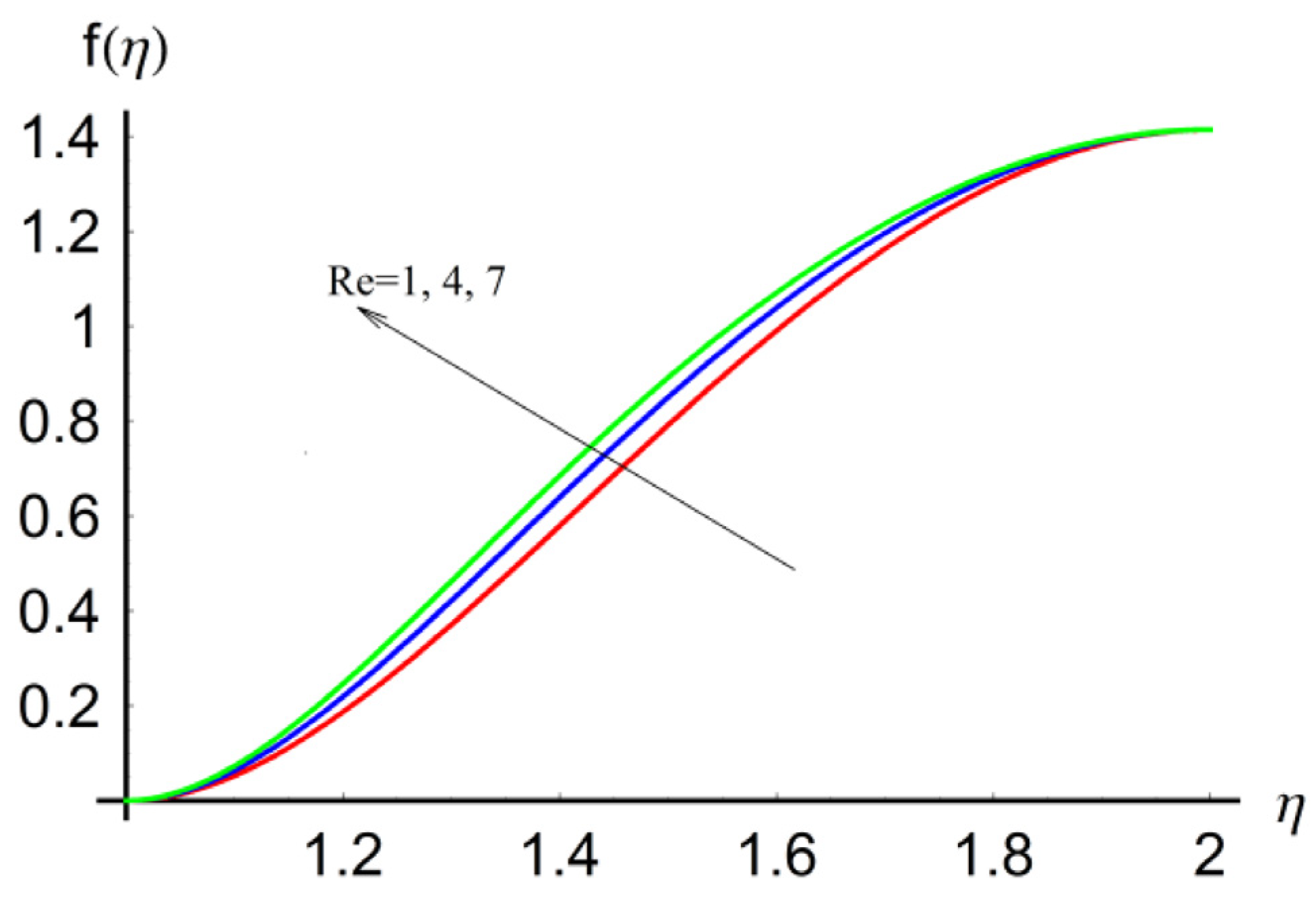
2.5. Thermal Fluid Dynamics
2.6. Symmetry in Renewable Energy Systems
3. Symmetry in Fluid Dynamics
3.1. Noether’s Theorem Links Symmetry to Conservation Laws
3.2. Symmetry Simplifies the Navier–Stokes Equations, Particularly in Axial, Radial, and Translational Flows
- -
- No swirl (uθ = 0);
- -
- All derivatives with respect to θ vanish (∂/∂θ = 0);
- -
- Flow is described in cylindrical coordinates (r,θ,z).
- -
- The θ momentum equation vanishes if uθ = 0.
- -
- The term ur/r2 in the radial momentum equation arises from curvature effects.
- -
- Continuity:
- -
- Momentum Equations:
- -
- Continuity:
- -
- Momentum Equations:
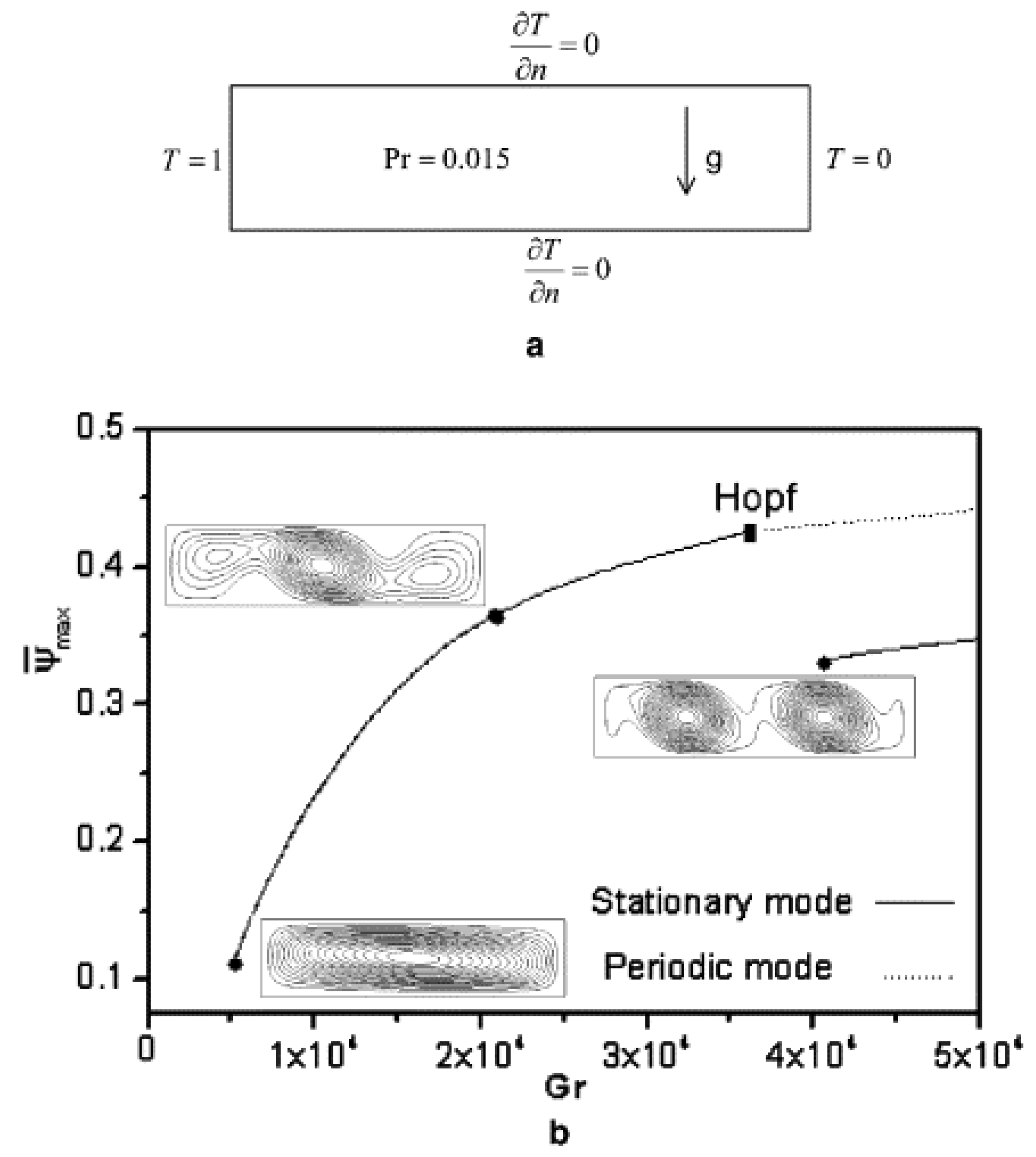
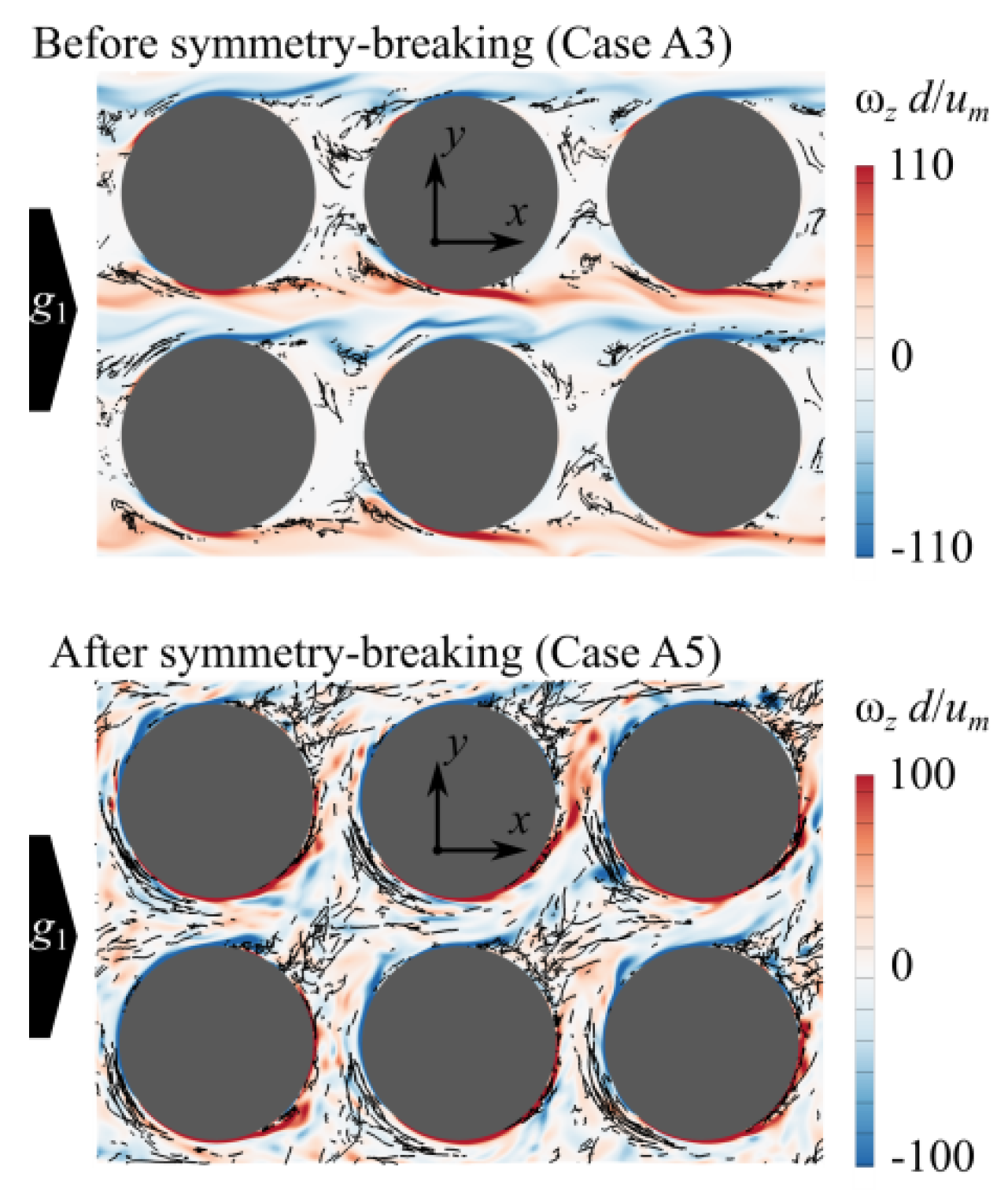
3.3. Symmetry Breaking Explains Transitions
4. Symmetry in Energy Applications
4.1. Heat Exchanger Designs
4.2. Applied Thermal Sciences for Energy
5. Conclusions
Funding
Conflicts of Interest
References
- Tinkham, M. Group Theory and Quantum Mechanics; Dover Publications: New York, NY, USA, 2003; ISBN 9780486432472. [Google Scholar]
- Cotton, F.A. Chemical Applications of Group Theory, 3rd ed.; Wiley: New York, NY, USA, 1990; ISBN 978-0-471-51094-9. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; ISBN 0521833787. [Google Scholar]
- Gatermann, K.; Hohmann, A. Symbolic exploitation of symmetry in numerical pathfollowing. Impact Comput. Sci. Eng. 1991, 3, 330–365. [Google Scholar] [CrossRef]
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2016; pp. 2990–2999. [Google Scholar]
- Bai, Q.; Xu, T.; Huang, J.; Pérez-Sánchez, H. Geometric deep learning methods and applications in 3D structure-based drug design. Drug Discov. Today 2024, 29, 104024. [Google Scholar] [CrossRef] [PubMed]
- Iserles, A.; Hackbusch, W. Elliptic Differential Equations: Theory and Numerical Treatment; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Babai, L. Graph isomorphism in quasipolynomial time. In Proceedings of the Forty-Eighth Annual ACM Symposium on Theory of Computing, Cambridge, MA, USA, 19–21 June 2016; pp. 684–697. [Google Scholar]
- Crawford, J.; Ginsberg, M.; Luks, E.; Roy, A. Symmetry-breaking predicates for search problems. KR 1996, 96, 148–159. [Google Scholar]
- Tu, A.; Ye, J.; Wang, B. Symmetry measures of simplified neutrosophic sets for multiple attribute decision-making problems. Symmetry 2018, 10, 144. [Google Scholar] [CrossRef]
- Ostrowski, J.; Anjos, M.F.; Vannelli, A. Symmetry in Scheduling Problems; GERAD: Montreal, QC, Canada, 2010. [Google Scholar]
- Natapoff, A. How symmetry restricts symmetric choice. J. Math. Psychol. 1970, 7, 444–465. [Google Scholar] [CrossRef]
- Kwapień, J.; Drożdż, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Hutter, K.; Jöhnk, K. Continuum Methods of Physical Modeling: Continuum Mechanics, Dimensional Analysis, Turbulence; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Marsden, J.E.; Wendlandt, J.M. Mechanical systems with symmetry, variational principles, and integration algorithms. In Current and Future Directions in Applied Mathematics; Birkhäuser: Boston, MA, USA, 1997. [Google Scholar]
- Razafindralandy, D.; Hamdouni, A. Consequences of symmetries on the analysis and construction of turbulence models. Symmetry Integr. Geom. Methods Appl. 2006, 2, 20. [Google Scholar] [CrossRef]
- Taranov, V.B. Symmetry extensions and their physical reasons in the kinetic and hydrodynamic plasma models. Symmetry Integr. Geom. Methods Appl. 2008, 4, 006. [Google Scholar] [CrossRef]
- Kuzemsky, A.L. Bogoliubov’s Foresight and Development of the Modern Theoretical Physics. Electron. J. Theor. Phys. 2011, 8, 1–14. [Google Scholar]
- Houle, D.; Pélabon, C.; Wagner, G.P.; Hansen, T.F. Measurement and meaning in biology. Q. Rev. Biol. 2011, 86, 3–34. [Google Scholar] [CrossRef]
- Cahill, D.G.; Braun, P.V.; Chen, G.; Clarke, D.R.; Fan, S.; Goodson, K.E.; Keblinski, P.; King, W.P.; Mahan, G.D.; Majumdar, A.; et al. Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 2014, 1, 011305. [Google Scholar] [CrossRef]
- Thomas, D.M. Symmetry in Scalar Fields. Ph.D. Thesis, Indian Institute of Science Bangalore, Bengaluru, India, 2014. [Google Scholar]
- Frewer, M.; Khujadze, G.; Foysi, H. On the physical inconsistency of a new statistical scaling symmetry in incompressible Navier-Stokes turbulence. arXiv 2014, arXiv:1412.3061. [Google Scholar]
- Stephenson, M.; Clark, A.; Green, R. Novel methods for reflective symmetry detection in scanned 3D models. In Proceedings of the 2015 International Conference on Image and Vision Computing New Zealand (IVCNZ), New York, NY, USA, 23–24 November 2015; pp. 1–6. [Google Scholar]
- Gungor, F. Equivalence and symmetries for linear parabolic equations and applications revisited. arXiv 2015, arXiv:1501.01481. [Google Scholar]
- Kouyialis, G.; Misener, R. Detecting symmetry in designing heat exchanger networks. arXiv 2017. [Google Scholar] [CrossRef]
- Dolbeault, J. Functional inequalities: Nonlinear flows and entropy methods as a tool for obtaining sharp and constructive results. Milan J. Math. 2021, 89, 355–386. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Wang, W.; Li, L.; Qiu, C.-W. Effective medium theory for thermal scattering off rotating structures. Opt. Express 2020, 28, 25894–25907. [Google Scholar] [CrossRef]
- Rashid, F.L.; Hussein, A.K.; Malekshah, E.H.; Abderrahmane, A.; Guedri, K.; Younis, O. Review of heat transfer analysis in different cavity geometries with and without nanofluids. Nanomaterials 2022, 12, 2481. [Google Scholar] [CrossRef]
- Wang, X.; Jacob, Z. Symmetry breaking in thermal photonics. Light. Sci. Appl. 2022, 11, 342. [Google Scholar] [CrossRef]
- Jou, D.; Restuccia, L. Non-equilibrium thermodynamics of heat transport in superlattices, graded systems, and thermal metamaterials with defects. Entropy 2023, 25, 1091. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Construction of analytic solution to axisymmetric flow and heat transfer on a moving cylinder. Symmetry 2020, 12, 1335. [Google Scholar] [CrossRef]
- Latif, A.; Abdel Kader, A.H.; Nour, H.M. Exact implicit solution of nonlinear heat transfer in rectangular straight fin using symmetry reduction methods. Appl. Appl. Math. Int. J. (AAM) 2015, 10, 15. [Google Scholar]
- Verstappen, R.W.C.P.; Van Der Velde, R.M. Symmetry-preserving discretization of heat transfer in a complex turbulent flow. J. Eng. Math. 2006, 54, 299–318. [Google Scholar] [CrossRef][Green Version]
- Nikolaev, P.; Jivkov, A.P.; Margetts, L.; Sedighi, M. Non-local formulation of heat transfer with phase change in domains with spherical and axial symmetries. J. Peridynamics Nonlocal Model. 2023, 6, 231–249. [Google Scholar] [CrossRef]
- Hanc, J.; Tuleja, S.; Hancova, M. Symmetries and conservation laws: Consequences of Noether’s theorem. Am. J. Phys. 2004, 72, 428–435. [Google Scholar] [CrossRef]
- Chavas, J.-P. On the conservation of energy: Noether’s theorem revisited. Heliyon 2024, 10, e27476. [Google Scholar] [CrossRef] [PubMed]
- Voutsas, E.; Magoulas, K.; Tassios, D. Universal mixing rule for cubic equations of state applicable to symmetric and asymmetric systems: Results with the Peng−Robinson equation of state. Ind. Eng. Chem. Res. 2004, 43, 6238–6246. [Google Scholar] [CrossRef]
- Sussman, R.A. On spherically symmetric shear-free perfect fluid configurations (neutral and charged). II. Equation of state and singularities. J. Math. Phys. 1988, 29, 945–970. [Google Scholar] [CrossRef]
- Rodriguez, I.; Campo, A. Numerical investigation of forced convection heat transfer from a sphere at low Prandtl numbers. Int. J. Therm. Sci. 2022, 184, 107970. [Google Scholar] [CrossRef]
- Mehdi Keshtkar, M.; Dadkhodazadeh, M. Thermal simulation of the symmetric and asymmetric arrangement of barriers on heat transfer enhancement in a porous gas heat exchanger. J. Therm. Sci. Eng. Appl. 2018, 10, 051001. [Google Scholar] [CrossRef]
- Lavenda, B.H. Concepts of stability and symmetry in irreversible thermodynamics. I. Found. Phys. 1972, 2, 161–179. [Google Scholar] [CrossRef]
- Lurie, S.A.; Belov, P.A.; Matevossian, H.A. Symmetry Properties of Models for Reversible and Irreversible Thermodynamic Processes. Symmetry 2023, 15, 2173. [Google Scholar] [CrossRef]
- Ellison, C.J.; Mahoney, J.R.; James, R.G.; Crutchfield, J.P.; Reichardt, J. Information symmetries in irreversible processes. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037107. [Google Scholar] [CrossRef] [PubMed]
- Gibb, C.J.; Hobbs, J.; Nikolova, D.I.; Raistrick, T.; Berrow, S.R.; Mertelj, A.; Osterman, N.; Sebastián, N.; Gleeson, H.F.; Mandle, R.J. Spontaneous symmetry breaking in polar fluids. Nat. Commun. 2024, 15, 5845. [Google Scholar] [CrossRef]
- Lappa, M.; Burel, T. Symmetry breaking phenomena in thermovibrationally driven particle accumulation structures. Phys. Fluids 2020, 32, 053314. [Google Scholar] [CrossRef]
- Gross, D.J. The role of symmetry in fundamental physics. Proc. Natl. Acad. Sci. USA 1996, 93, 14256–14259. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Newnham, R.E. Properties of Materials: Anisotropy, Symmetry, Structure; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Norton, T.; Tiwari, B.; Sun, D.-W. Computational fluid dynamics in the design and analysis of thermal processes: A review of recent advances. Crit. Rev. Food Sci. Nutr. 2013, 53, 251–275. [Google Scholar] [CrossRef]
- Semma, E.; Timchenko, V.; El Ganaoui, M.; Leonardi, E. The effect of wall temperature fluctuations on the heat transfer and fluid flow occuring in a liquid enclosure. Int. J. Heat Fluid Flow 2005, 26, 547–557. [Google Scholar] [CrossRef]
- Navarro, R.B.; Alcayde, A. (Eds.) Symmetry in Renewable Energy and Power Systems; MDPI: Basel, Switzerland, 2021. [Google Scholar]
- Gajewski, P.; Pieńkowski, K. Control of the hybrid renewable energy system with wind turbine, photovoltaic panels and battery energy storage. Energies 2021, 14, 1595. [Google Scholar] [CrossRef]
- Göksu, Ö.; Teodorescu, R.; Bak-Jensen, B.; Iov, F.; Kjær, P.C. An iterative approach for symmetrical and asymmetrical Short-circuit calculations with converter-based connected renewable energy sources. Application to wind power. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, New York, NY, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Coppitters, D.; Contino, F. Optimizing upside variability and antifragility in renewable energy system design. Sci. Rep. 2023, 13, 9138. [Google Scholar] [CrossRef]
- Trias, F.; Lehmkuhl, O.; Oliva, A.; Pérez-Segarra, C.; Verstappen, R. Symmetry-preserving discretization of Navier–Stokes equations on collocated unstructured grids. J. Comput. Phys. 2014, 258, 246–267. [Google Scholar] [CrossRef]
- Quintard, M.; Whitaker, S. One-and two-equation models for transient diffusion processes in two-phase systems. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1993; pp. 369–464. [Google Scholar]
- Kurdyumov, V.N.; Jiménez, C. Propagation of symmetric and non-symmetric premixed flames in narrow channels: Influence of conductive heat-losses. Combust. Flame 2014, 161, 927–936. [Google Scholar] [CrossRef]
- Kim, D.; Park, J.; Han, D.; Kim, K.T. Symmetry-breaking for the control of combustion instabilities of two interacting swirl-stabilized flames. Combust. Flame 2018, 194, 180–194. [Google Scholar] [CrossRef]
- Tsai, C.-H. The asymmetric behavior of steady laminar flame propagation in ducts. Combust. Sci. Technol. 2008, 180, 533–545. [Google Scholar] [CrossRef]
- Chang, J.-Y.; Chen, R.-Y.; Tsai, C.-C. Symmetric method of approximate particular solutions for solving certain partial differential equations. Eng. Anal. Bound. Elem. 2020, 119, 105–118. [Google Scholar] [CrossRef]
- Holmes, P.J.; Lumley, J.L.; Berkooz, G.; Mattingly, J.C.; Wittenberg, R.W. Low-dimensional models of coherent structures in turbulence. Phys. Rep. 1997, 287, 337–384. [Google Scholar] [CrossRef]
- Padhye, N.S. Topics in Lagrangian and Hamiltonian Fluid Dynamics: Relabeling Symmetry and Ion-Acoustic Wave Stability. Doctoral Dissertation, The University of Texas at Austin, Austin, TX, USA, 1998. [Google Scholar]
- Olver, P.J. Geometric foundations of numerical algorithms and symmetry. Appl. Algebra Eng. Commun. Comput. 2001, 11, 417–436. [Google Scholar] [CrossRef]
- Ait A., H. Two Cases of Symmetry Breaking of Free Surface Flows. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2008. [Google Scholar]
- Bihlo, A.; Staufer, J. Minimal atmospheric finite-mode models preserving symmetry and generalized Hamiltonian structures. Phys. D Nonlinear Phenom. 2011, 240, 599–606. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A.; Al Sayed, N. Lie-symmetry group and modeling in non-isothermal fluid mechanics. Phys. A Stat. Mech. Its Appl. 2012, 391, 4624–4636. [Google Scholar] [CrossRef]
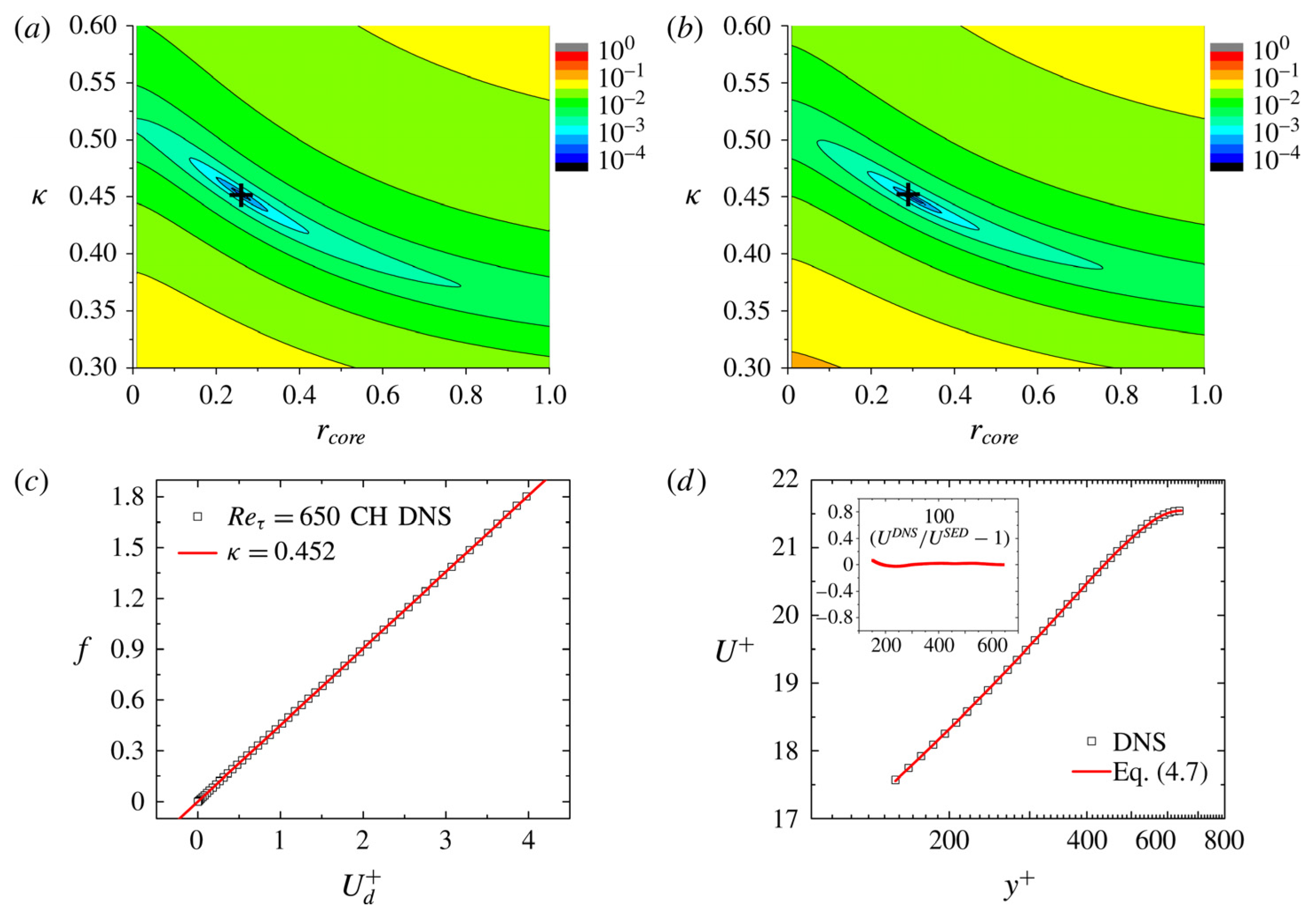
- She, Z.-S.; Chen, X.; Hussain, F. Quantifying wall turbulence via a symmetry approach: A Lie group theory. J. Fluid Mech. 2017, 827, 322–356. [Google Scholar] [CrossRef]
- Cao, N.; Chen, S.; Jin, S.; Martínez, D. Physical symmetry and lattice symmetry in the lattice Boltzmann method. Phys. Rev. E 1997, 55, R21–R24. [Google Scholar] [CrossRef]
- Pal, S.; Lan, C.; Li, Z.; Hirleman, E.D.; Ma, Y. Symmetry boundary condition in dissipative particle dynamics. J. Comput. Phys. 2015, 292, 287–299. [Google Scholar] [CrossRef]
- Srikanth, V.; Huang, C.-W.; Su, T.S.; Kuznetsov, A.V. Symmetry breaking of turbulent flow in porous media composed of periodically arranged solid obstacles. J. Fluid Mech. 2021, 929, A2. [Google Scholar] [CrossRef]
- Sachs, J. Motion, Symmetry & Spectroscopy of Chiral Nanostructures; Springer Nature: Dordrecht, The Netherlands, 2022. [Google Scholar]
- Batchelor, G.K. Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow. Q. J. Mech. Appl. Math. 1951, 4, 29–41. [Google Scholar] [CrossRef]
- Armbruster, D.; Nicolaenko, B.; Smaoui, N.; Chossat, P. Symmetries and dynamics for 2-D Navier-Stokes flow. Phys. D Nonlinear Phenom. 1996, 95, 81–93. [Google Scholar] [CrossRef]
- Crawford, J.D.; Knobloch, E. Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 1991, 23, 341–387. [Google Scholar] [CrossRef]
- Barker, T.; Prange, C.; Tan, J. On Symmetry Breaking for the Navier–Stokes Equations. Commun. Math. Phys. 2024, 405, 25. [Google Scholar] [CrossRef]
- Ukaszewicz, G.; Kalita, P. Navier–Stokes Equations; Advances in Mechanics and Mathematics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 34. [Google Scholar]
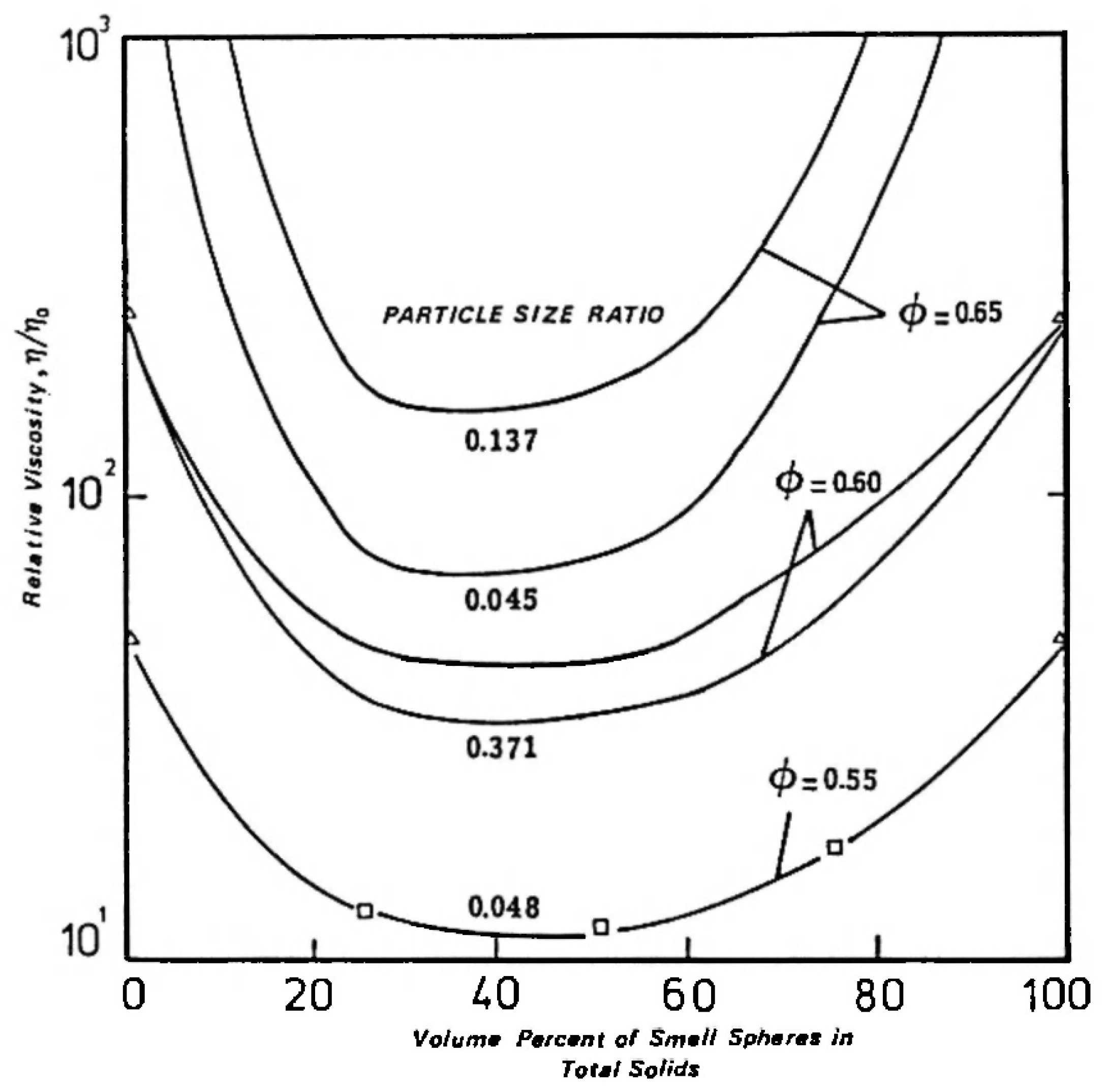
- Kamal, M.; Mutel, A. Rheological properties of suspensions in Newtonian and non-Newtonian fluids. J. Polym. Eng. 1985, 5, 293–382. [Google Scholar] [CrossRef]
- Jung, H.; Park, J.-W.; Park, C.-G. Asymmetric flows of non-Newtonian fluids in symmetric stenosed artery. Korea-Aust. Rheol. J. 2004, 16, 101–108. [Google Scholar]
- Taylor, D.P.; Mathur, P.; Renaud, P.; Kaigala, G.V. Microscale hydrodynamic confinements: Shaping liquids across length scales as a toolbox in life sciences. Lab Chip 2022, 22, 1415–1437. [Google Scholar] [CrossRef]
- Málek, J.; Rajagopal, K.R. Mathematical issues concerning the Navier–Stokes equations and some of its generalizations. In Handbook of Differential Equations: Evolutionary Equations; North-Holland: Amsterdam, The Netherlands, 2005; pp. 371–459. [Google Scholar]
- Mahynski, N.A.; Pretti, E.; Shen, V.K.; Mittal, J. Using symmetry to elucidate the importance of stoichiometry in colloidal crystal assembly. Nat. Commun. 2019, 10, 2028. [Google Scholar] [CrossRef]
- Cheng, M.; Zaletel, M.; Barkeshli, M.; Vishwanath, A.; Bonderson, P. translational symmetry and microscopic constraints on symmetry-enriched topological phases: A view from the surface. Phys. Rev. X 2016, 6, 041068. [Google Scholar] [CrossRef]
- Hanada, M.; Robinson, B. Partial-symmetry-breaking phase transitions. Phys. Rev. D 2020, 102, 096013. [Google Scholar] [CrossRef]
- Gimsa, A. Symmetries in the mathematical and physical description of nature. Int. J. Sci. Res. Manag. 2020, 8, 36–48. [Google Scholar] [CrossRef]
- Mainzer, K. Symmetries of Nature; Walter de Gruyter: Berlin, Germany, 1996. [Google Scholar]
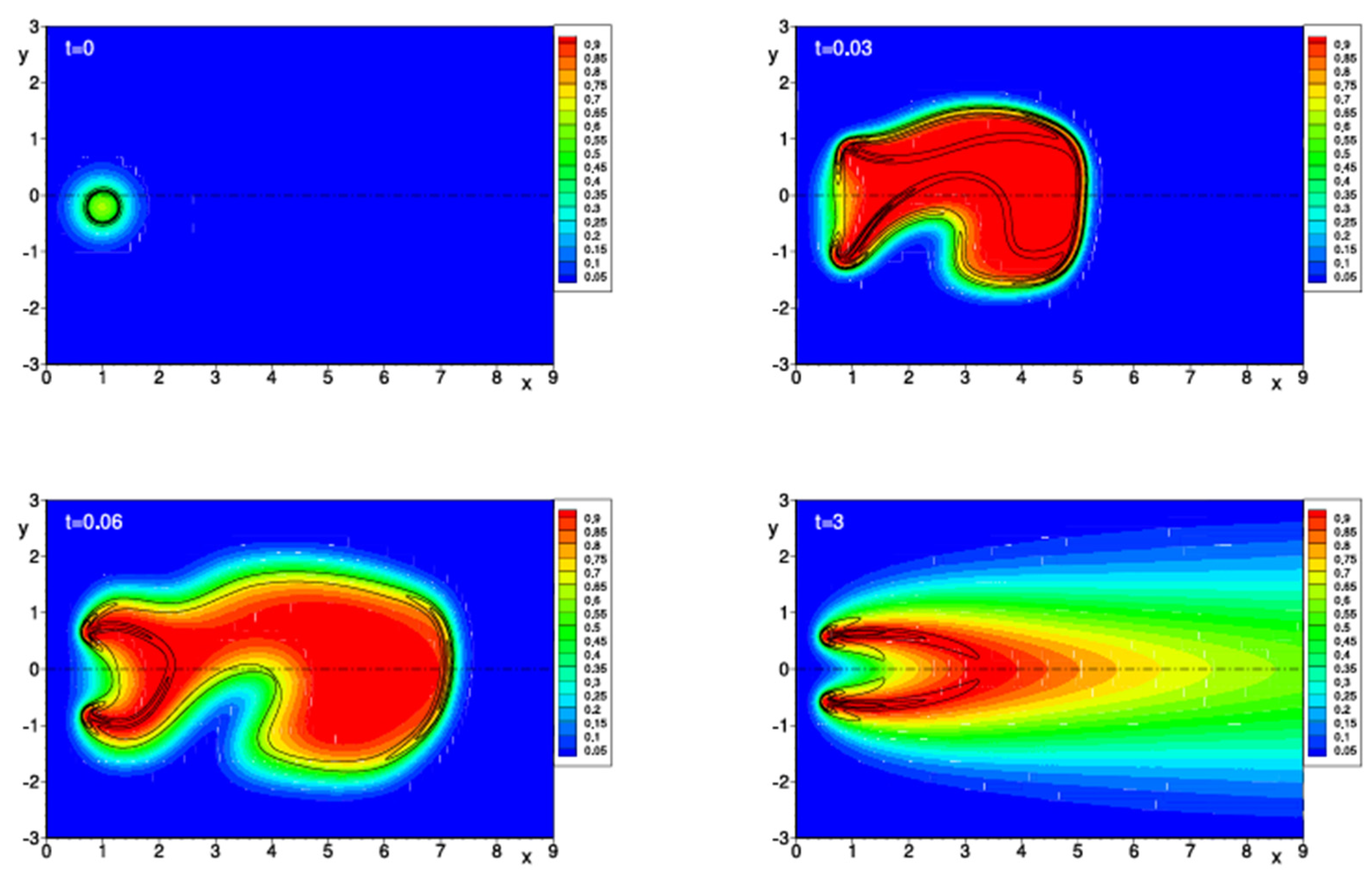
- Hack, M.A.; Vondeling, P.; Cornelissen, M.; Lohse, D.; Snoeijer, J.H.; Diddens, C.; Segers, T. Asymmetric coalescence of two droplets with different surface tensions is caused by capillary waves. Phys. Rev. Fluids 2021, 6, 104002. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, T.; Zhu, C.; Lu, Y.; Ma, Y.; Li, H.Z. Asymmetrical breakup of bubbles at a microfluidic T-junction divergence: Feedback effect of bubble collision. Microfluid. Nanofluidics 2012, 13, 723–733. [Google Scholar] [CrossRef]
- Chu, P.; Finch, J.; Bournival, G.; Ata, S.; Hamlett, C.; Pugh, R.J. A review of bubble break-up. Adv. Colloid Interface Sci. 2019, 270, 108–122. [Google Scholar] [CrossRef]
- Dallas, V.; Seshasayanan, K.; Fauve, S. Transitions between turbulent states in a two-dimensional shear flow. Phys. Rev. Fluids 2020, 5, 084610. [Google Scholar] [CrossRef]
- Cortet, P.-P.; Chiffaudel, A.; Daviaud, F.; Dubrulle, B. Experimental evidence of a phase transition in a closed turbulent flow. Phys. Rev. Lett. 2010, 105, 214501. [Google Scholar] [CrossRef]
- Giulini, D. Recasting Reality: Wolfgang Pauli’s Philosophical Ideas and Contemporary Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 33–82. [Google Scholar]
- Kuzemsky, A.L. Bogoliubov’s vision: Quasiaverages and broken symmetry to quantum protectorate and emergence. Int. J. Mod. Phys. B 2010, 24, 835–935. [Google Scholar] [CrossRef]
- Mouchet, A. Reflections on the four facets of symmetry: How physics exemplifies rational thinking. Eur. Phys. J. H 2013, 38, 661–702. [Google Scholar] [CrossRef]
- Zhang, L.; Dou, S.X.; Liu, H.K.; Huang, Y.; Hu, X. Symmetric electrodes for electrochemical energy-storage devices. Adv. Sci. 2016, 3, 1600115. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F. The nuclear symmetry energy. Prog. Part. Nucl. Phys. 2016, 91, 203–258. [Google Scholar] [CrossRef]
- Dolbeault, J.; Esteban, M.J.; Loss, M. Symmetry and symmetry breaking: Rigidity and flows in elliptic PDEs. In Proceedings of the International Congress of Mathematicians (ICM 2018) (In 4 Volumes) Proceedings of the International Congress of Mathematicians; World Scientific Publishing Co Pte Ltd.: Singapore, 2018; pp. 2261–2285. [Google Scholar]
- Rodríguez-Lara, B.; El-Ganainy, R.; Guerrero, J. Symmetry in optics and photonics: A group theory approach. Sci. Bull. 2018, 63, 244–251. [Google Scholar] [CrossRef] [PubMed]
- Kozic, I. Role of symmetry in irrational choice. arXiv 2018, arXiv:1806.0262. [Google Scholar]
- Siksnelyte-Butkiene, I.; Streimikiene, D.; Agnusdei, G.P.; Balezentis, T. Energy-space concept for the transition to a low-carbon energy society. Environ. Dev. Sustain. 2022, 25, 14953–14973. [Google Scholar] [CrossRef]
- Huynh, B.C.; Wibowo-Teale, M.; Wibowo-Teale, A.M. QSym2: A Quantum Symbolic Symmetry Analysis Program for Electronic Structure. J. Chem. Theory Comput. 2023, 20, 114–133. [Google Scholar] [CrossRef]
- Guo, H.; Xu, Y.; Li, Y.; Huang, L.; Chen, H. A symmetry analysis methodology for general energy conversion systems. Commun. Eng. 2023, 2, 49. [Google Scholar] [CrossRef]
- Andreozzi, A.; Buonomo, B.; Manca, O. Thermal and fluid dynamic behaviors in symmetrical heated channel-chimney systems. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 811–833. [Google Scholar] [CrossRef]
- Fernández, M.; Sanchez-Pérez, J.F.; Del Cerro, F. Study of the Cylindrical Symmetry Materials Dependence with the Temperature in a Nonlinear Heat Transfer by Network Method. In Advances on Mechanics, Design Engineering and Manufacturing II: Proceedings of the International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing (JCM 2018); Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 272–281. [Google Scholar]
- Bailey, J.C.; Intile, J.; Fric, T.F.; Tolpadi, A.K.; Nirmalan, N.V.; Bunker, R.S. Experimental and numerical study of heat transfer in a gas turbine combustor liner. J. Eng. Gas Turbines Power 2003, 125, 994–1002. [Google Scholar] [CrossRef]
- Mueller, C.; Tsvetkov, P. A review of heat-pipe modeling and simulation approaches in nuclear systems design and analysis. Ann. Nucl. Energy 2021, 160, 108393. [Google Scholar] [CrossRef]
- Fayaz, H.; Afzal, A.; Samee, A.D.M.; Soudagar, M.E.M.; Akram, N.; Mujtaba, M.A.; Jilte, R.D.; Islam, T.; Ağbulut, Ü.; Saleel, C.A. Optimization of thermal and structural design in lithium-ion batteries to obtain energy efficient battery thermal management system (BTMS): A critical review. Arch. Comput. Methods Eng. 2021, 29, 129–194. [Google Scholar] [CrossRef]
- Chung, Y.; Kim, M.S. Thermal analysis and pack level design of battery thermal management system with liquid cooling for electric vehicles. Energy Convers. Manag. 2019, 196, 105–116. [Google Scholar] [CrossRef]
- Chen, K.; Chen, Y.; She, Y.; Song, M.; Wang, S.; Chen, L. Construction of effective symmetrical air-cooled system for battery thermal management. Appl. Therm. Eng. 2019, 166, 114679. [Google Scholar] [CrossRef]
- Ellahi, R. Special Issue on symmetry and fluid mechanics. Symmetry 2020, 12, 281. [Google Scholar] [CrossRef]
- Klunk, M.A.; Shah, Z.; Caetano, N.R.; Conceição, R.V.; Wander, P.R.; Dasgupta, S.; Das, M. CO2sequestration by magnesite mineralisation through interaction of Mg-brine and CO2: Integrated laboratory experiments and computerised geochemical modelling. Int. J. Environ. Stud. 2019, 77, 492–509. [Google Scholar] [CrossRef]
- Dasgupta, S.; Das, M.; Klunk, M.A.; Xavier, S.J.S.; Caetano, N.R.; Wander, P.R. Copper and chromium removal from synthetic textile wastewater using clay minerals and zeolite through the effect of pH. J. Iran. Chem. Soc. 2021, 18, 3377–3386. [Google Scholar] [CrossRef]
- Jackson, G.; Avedisian, C. The effect of initial diameter in spherically symmetric droplet combustion of sooting fuels. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1994, 446, 255–276. [Google Scholar]
- Jiménez, C.; Kurdyumov, V.N. Multiplicity of solutions of lifted jet edge flames: Symmetrical and non-symmetrical configurations. Combust. Flame 2023, 256, 112988. [Google Scholar] [CrossRef]
- Caetano, N.R.; Lorenzini, G.; Lhamby, A.R.; Guillet, V.M.M.; Klunk, M.A.; Rocha, L.A.O. Experimental Assessment of Thermal Radiation Behavior Emitted by Solid Porous Material. Int. J. Heat Technol. 2020, 38, 1–8. [Google Scholar] [CrossRef]
- Freschi, A.A.; Caetano, N.R.; Santarine, G.A.; Hessel, R. Laser interferometric characterization of a vibrating speaker system. Am. J. Phys. 2003, 71, 1121–1126. [Google Scholar] [CrossRef]
- Ruoso, A.C.; Bitencourt, L.C.; Sudati, L.U.; Klunk, M.A.; Caetano, N.R. New parameters for the forest biomass waste ecofirewood manufacturing process optimization. Period. Tche Quim. 2019, 16, 560–571. [Google Scholar] [CrossRef]
- da Silva, B.P.; Saccol, F.; Pedrazzi, C.; Caetano, N.R. Technical and economic viability for the briquettes manufacture. Defect Diffus. Forum 2017, 380, 218–226. [Google Scholar] [CrossRef]
- LI, B.; Xu, Z.S.; Zavadskas, E.K.; Antucheviciene, J.; Turskis, Z. A bibliometric analysis of symmetry (2009–2019). Symmetry 2020, 12, 1304. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caetano, N.R. Review on the Theoretical and Practical Applications of Symmetry in Thermal Sciences, Fluid Dynamics, and Energy. Symmetry 2025, 17, 1240. https://doi.org/10.3390/sym17081240
Caetano NR. Review on the Theoretical and Practical Applications of Symmetry in Thermal Sciences, Fluid Dynamics, and Energy. Symmetry. 2025; 17(8):1240. https://doi.org/10.3390/sym17081240
Chicago/Turabian StyleCaetano, Nattan Roberto. 2025. "Review on the Theoretical and Practical Applications of Symmetry in Thermal Sciences, Fluid Dynamics, and Energy" Symmetry 17, no. 8: 1240. https://doi.org/10.3390/sym17081240
APA StyleCaetano, N. R. (2025). Review on the Theoretical and Practical Applications of Symmetry in Thermal Sciences, Fluid Dynamics, and Energy. Symmetry, 17(8), 1240. https://doi.org/10.3390/sym17081240




