Adaptive Switching Surrogate Model for Evolutionary Multi-Objective Community Detection Algorithm

Abstract

Community detection is widely recognized as a crucial area of research in network science. In recent years, multi-objective evolutionary algorithms (MOEAs) have been extensively employed in community detection tasks. Continuous coding is able to transform the discrete problem into a continuous one. However, conventional continuous coding methodologies frequently disregard the relationships between node structures, resulting in low-quality encoded populations that subsequently diminish community detection performance. Furthermore, continuous coding needs to be decoded into to label-based coding during the optimization process to compute objective functions. To alleviate this, we design the surrogate model adaptive switching strategy that selects the optimal surrogate model for the task. Subsequently, the surrogate-assisted evolutionary multi-objective community detection algorithm with core node learning is proposed. The core node learning method is employed to enhance the connection between nodes in augmented sequential coding, which helps initialize the population using the node similarity matrix. The core nodes of the network are subsequently identified based on node weights, which can be utilized to construct a surrogate model between the continuous coding and the objective function. The surrogate model is updated during the optimization process, which effectively improves both the accuracy and efficiency of community detection tasks. Experimental results obtained from synthetic and real-world networks demonstrate that the proposed algorithm exhibits superior performance compared to seven community detection algorithms.

1. Introduction

Networks are used to describe various types of complex systems, such as social networks, biological networks, and the Internet. In recent years, community detection has emerged as a crucial tool for revealing hidden functional and structural properties in complex networks. It involves the partitioning of networks into distinct communities, wherein nodes within the same community are more densely and closely connected, while connections between nodes in different communities are significantly sparser.

Community detection methods have found wide application across multiple scenarios. For example, in the e-Commerce domain, community-based recommendation systems can effectively identify users’ preferences for products and reviews [1]. In the realm of social networks, relationships among individuals sharing common interests can be discovered through community detection methods [2]. Consequently, many researchers have developed diverse community detection approaches. These include algorithms based on modularity optimization [3], information theory-based algorithms [4], dynamics-based algorithms [5], and spectral clustering-based algorithms [6]. Fortunato et al. [7] provide a comprehensive review of these methods for community detection.

In recent years, scientists have proposed numerous metrics and methods for evaluating community detection. In 2004, Newman [8] introduced the concept of modularity to model the community detection problem as an NP-hard optimization problem. In 2009, Andrea Lancichinetti et al. [9] proposed community fitness to assess community detection quality, while Pizzuti [10] introduced the community score for similar assessment purposes. Community detection methods can be categorized into three main groups according to their approach. The first category comprises traditional methods, including graph partitioning, hierarchical clustering, partitional clustering, and spectral clustering [11]. The second category encompasses split-based approaches, which remove edges connecting nodes from different communities. The third category consists of optimization algorithms. Pizzuti et al. [12] proposed the first multi-objective community detection algorithm, called MOGA-Net. Pizzuti et al. [10] proposed a genetic algorithm for community detection through optimization of the community score objective function. Li et al. [13] attempted to apply extended compact genetic algorithms to explore community structures in complex networks. Gong et al. [14] proposed a modal tone algorithm called Meme-Net to optimize the density of the modules. Li et al. [15] designed a multi-objective adaptive fast evolutionary algorithm for extracting communities from networks. Chen [16] proposed a MODTLBO/D community detection algorithm based on multi-objective teaching–learning optimization combined with a decomposition mechanism. DYN-MODPSO [17] modified and enhanced the traditional evolutionary clustering framework and particle swarm algorithm, rendering dynamic detection more effective and efficient. Gong et al. [18] proposed a multi-objective discrete particle swarm optimization algorithm (MODPSO) to address network clustering problems. Yang et al. [19] proposed a multi-objective optimization algorithm based on node classification, NCMOEA, which employs a hybrid representation of different node types and performs effectively.

Single-objective optimization methods have achieved considerable success in community detection. However, as described in [20], several limitations exist when addressing this type of community detection problem. Single-objective optimization typically seeks larger communities within networks while overlooking smaller communities that actually exist. Moreover, the definition of community commonly exhibits characteristics of high cohesion and low coupling; thus, community detection inherently requires multiple objectives to compete simultaneously, which necessitates multi-objective optimization methods to achieve superior performance. Furthermore, multi-objective evolutionary algorithms (MOEAs) [21,22] can provide a set of Pareto-optimal solutions rather than merely a single solution obtained through traditional methods. Consequently, multi-objective optimization has been adopted to overcome the resolution limitation of modularity. Hence, a community detection algorithm based on multi-objective optimization is investigated in this study.

MOEA-based community detection algorithms require encoding and decoding processes. Two of the most extensively utilized encoding methods are locus-based encoding [23,24] and label-based encoding [25]. However, when utilizing discrete variables, minor changes in genotype can lead to substantial changes in phenotype [26]. To address these challenges, Sun et al. [27] proposed a novel continuous coding method employing a neural network approach, wherein each individual is represented as a continuous random vector and the population space is transformed from discrete to continuous. Nevertheless, this approach overlooks the structural relationships between nodes, and the randomly generated initial populations are characterized by poor quality. Since initial population quality typically impacts optimization performance, this paper proposes a novel encoding scheme that integrates similarity between nodes and continuous coding to enhance community detection performance. Moreover, an adaptive multi-objective optimization framework based on surrogate model adaptive switching strategy has been adopted, which establishes the surrogate model between continuous coding and objective functions through the core node learning method.

In summary, the main contributions of this paper are summarized as follows:

(1) A continuous encoding scheme that effectively utilizes similarity between community network nodes has been developed. Through this encoding scheme, the discrete space of the original problem is transformed into a continuous space, which can better assume a certain level of symmetry where similar solutions have similar fitness values.

(2) A simple yet effective strategy capable of acquiring core nodes to compress the sample space of surrogate models has been designed. This approach effectively ensures the quality of initial populations and reduces the impact of randomness on the structure of nodes during the iteration process.

(3) A community detection algorithm framework based on adaptive selection of surrogate models is proposed. For different networks, the framework can adaptively select appropriate surrogate models to establish the relationship between continuous coding and objective functions. Meanwhile, during the iterative process, elite individuals from the population are selected to update the surrogate model, thereby ensuring precision throughout the optimization process.

Together, these contributions form an integrated framework for community detection that combines continuous encoding, surrogate modeling, and multi-objective evolutionary optimization. The proposed method addresses three core challenges: (1) enhancing the quality of the initial population through similarity-guided continuous encoding; (2) improving optimization efficiency via adaptive surrogate model selection; and (3) effectively balancing conflicting structural objectives using a Pareto-based multi-objective strategy. These components are seamlessly integrated into a unified algorithmic pipeline, as detailed in Section 3.

2. Related Work

2.1. Community Detection

The definition of a community is not clearly defined [28]. A widely accepted definition of a community is that it is a set of different nodes in a network where the nodes within the set are tightly connected, and the nodes between different sets are sparsely connected. The goal of community detection is to partition the nodes in a network into different sets (called communities), where the nodes within the same community are tightly connected, and the nodes between different communities are sparsely connected [29]. A complex network can be defined as an undirected graph:

$$\mathit{G}=(V,E)$$

(1)

$V=(v_1,v_2,\dots ,v_n)$ is the set of nodes, and $E=\left\{(v_i,v_j)\right|v_i,v_j\in V,i\ne j\}$ is the set of edges. From a mathematical perspective, a network can be represented by an adjacency matrix $\mathit{A}=\left[a_{ij}\right]$, where $a_{ij}$ denotes the connection between node $v_i$ and node $v_j$, and $i,j=1,2,3,\dots ,n$, and n represents the number of nodes in the network. The value of $a_{ij}$ is typically 1 if there is an edge between $v_i$ and node $v_j$, and 0 otherwise. Community detection is equivalent to finding a partition $\phi =\{C_1,C_2,\dots ,C_k\}$, such that the connections within each community $C_i$ are as dense as possible, and the connections between different communities $C_i$ and $C_j$ are sparse, where $i,j\in \{1,2,\dots ,k\}$ and $i\ne j$. Here, $C_i\subset V$ and $C_i$ represents a community, while k denotes the number of communities in the graph $\mathit{G}$.

2.2. Multi-Objective Optimization

Multi-objective optimization works by optimizing a set of conflicting objective functions and then returning a set of solutions [30]. Taking minimization as an example, the multi-objective optimization problem can be described as

$$\mathrm{minimize}\mathit{F}\left(\mathit{x}\right)={[f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_m\left(\mathit{x}\right)]}^T$$

(2)

where $f_i\left(\mathit{x}\right)$ denotes the ith objective function; $\mathit{x}$ is the decision variable; m denotes the number of objective functions. Solution ${\mathit{x}}_1$ is preferable to solution ${\mathit{x}}_2$, or solution ${\mathit{x}}_1$ dominates ${\mathit{x}}_2$ if it satisfies

$$\forall i,f_i\left({\mathit{x}}_1\right)\le f_i\left({\mathit{x}}_2\right)\mathrm{and}\exists i,f_i\left({\mathit{x}}_1\right)<f_i\left({\mathit{x}}_2\right)$$

(3)

Multi-objective optimization returns a set of such non-dominated solutions instead of a single optimal solution. Such a set of non-dominated solutions is called a Pareto-optimal solution to a multi-objective optimization problem. If there exists no solution $\mathit{x}$ dominating the solution ${\mathit{x}}^{*}$, then ${\mathit{x}}^{*}$ is called a Pareto-optimal solution or a non-dominated solution. The Pareto-optimal solution set or non-dominated solution set is defined as

$${\mathit{P}}^{*}=\{{\mathit{x}}^{*}\in \mathit{X}\mid \nexists \mathit{x}\in \mathit{X},\mathit{x}\mathrm{dominates}{\mathit{x}}^{*}\}$$

(4)

Reference [31] illustrates that the set of Pareto-optimal solutions corresponds to different partitions of a network consisting of different numbers of communities, which provides a better opportunity to analyze multiple communities at different levels. The Pareto-optimal frontier (POF) [32] is obtained by mapping these non-dominated solutions in the multi-objective solution space.

$$POF=\{(f_1\left({\mathit{x}}^{*}\right),f_2\left({\mathit{x}}^{*}\right),\dots ,f_m\left({\mathit{x}}^{*}\right))\mid {\mathit{x}}^{*}\in {\mathit{P}}^{*}\}$$

(5)

Due to the general applicability of multi-objective optimization, community detection inevitably involves various objective functions that need to be balanced. In recent years, numerous high-quality multi-objective optimization-based community detection methods have been developed. Leung [33] proposed a collaborative neuro-dynamics method for multi-objective optimization, wherein a weighted Chebyshev function was employed to scalarize multiple objectives. With the assistance of particle swarm optimization, a multi-projection neural network was utilized to search for Pareto-optimal solutions, thereby achieving satisfactory results. Yang et al. [19] introduced a node classification-based multi-objective optimization algorithm (NCMOEA), which employs a hybrid representation of different types of nodes and demonstrates robust performance. Shao et al. [34] presented a decomposition-based multi-objective meme algorithm (MDMCD), combined with a two-level local search, which yielded effective results across multiple networks. Although EA algorithms exhibit satisfactory performance in community detection, as noted by Pizzuti in [35], evolutionary algorithms are computationally intensive; thus, despite being competitive with non-evolutionary methods in terms of solution quality, they are unsuitable for processing large networks. As the network size increases, the search space for EA expands exponentially; consequently, most existing EA-based community detection algorithms are primarily applied to networks with relatively few nodes. To address this limitation, several approaches have been proposed by researchers. Shi et al. [36] developed a genetic algorithm for community detection in large-scale networks, wherein a site-based neighbor coding scheme was implemented for community delineation to reduce the search space; the effectiveness of this algorithm was subsequently verified in a network comprising a maximum of 22,963 nodes. Liu et al. [37] incorporated network embedding into the multi-objective particle swarm algorithm and mapped the nodes to a low-dimensional space, thereby effectively reducing the search space while enhancing search efficiency through the consistency propagation strategy. Experimental results indicate that this strategy demonstrates significant advantages in handling large-scale multi-objective optimization problems of 1000–10,000 dimensions. Xu [38] designed a fuzzy decision variable framework for large-scale multi-objective optimization to mitigate the issue of excessive decision variables impeding the convergence speed of evolutionary algorithms. This framework improves both the performance and computational efficiency of the algorithm in large-scale multi-objective optimization through a two-step process comprising fuzzy evolution and exact evolution.

In community detection scenarios with conflicting structural objectives, evolutionary algorithms are commonly employed to explore the Pareto-optimal solution set. However, evaluating structural objective functions can be computationally expensive. To address this, surrogate models are often used to approximate objective function values and reduce computational overhead. The next section introduces the role and mechanisms of surrogate modeling within the proposed framework.

2.3. Surrogate Model

A surrogate model is generally defined as an approximate mathematical model used to replace complex and time-consuming numerical analyses in design optimization processes [39]. It is also referred to as a response surface model, approximate model, or meta-model [40,41]. The adoption of surrogate models can significantly enhance optimization efficiency and reduce procedural complexity. The polynomial response surface method, introduced in the 1970s for structural optimization and design [42], is considered the prototype of surrogate modeling.

In most evolutionary algorithms, the fitness values of all individuals in a population are typically evaluated using a fitness function, computational simulation, or experimentation. However, in practical applications, fitness evaluation is often challenging due to high computational cost or the absence of an explicit fitness function. In such cases, approximate models are constructed to estimate the fitness function.

When addressing computationally intensive optimization problems, evolutionary algorithms require numerous fitness evaluations before identifying acceptable solutions. In certain scenarios, computationally efficient approximations of the fitness function are essential. Surrogate-assisted evolutionary computation reduces the computational time by approximating the fitness function and has been successfully applied in domains such as aerodynamic design optimization [43] and drug discovery [44], which often involve expensive simulations.

Various models have been employed for surrogate-based approximation in evolutionary algorithms, including kriging models, multilayer perceptrons, radial basis functions, and support vector machines. However, achieving accurate global approximations of the true fitness function remains difficult due to limited data and the high dimensionality of the input space [45]. Surrogate modeling in evolutionary computation is especially useful in three scenarios: (1) when fitness evaluations are extremely time-consuming; (2) when the fitness function is not explicitly defined; and (3) when the optimization environment is noisy.

The strategies for effectively utilizing surrogate models are generally referred to as model management or evolutionary control [39]. Developing robust model management strategies remains a significant challenge, particularly for high-dimensional and computationally expensive problems.

The first workshop dedicated to surrogate modeling in evolutionary optimization was held at the 2002 Genetic and Evolutionary Computation Conference (GECCO) [46]. Later, in a comprehensive review paper [45], the importance of managing surrogates was emphasized to prevent evolutionary algorithms from converging to incorrect optima produced by inaccurate surrogate models.

3. The Proposed Algorithm

This section presents the proposed multi-objective community detection algorithm based on adaptive surrogate model selection. The method integrates similarity-guided continuous encoding, core node identification, surrogate-assisted optimization, and evolutionary operators into a unified framework. The key components include core node search, solution representation and initialization, objective function design, adaptive surrogate model selection, and the overall evolutionary process.

To address the multi-objective nature of community detection, the algorithm employs a similarity-aware encoding strategy. Specifically, node similarity is quantified using a diffusion kernel similarity matrix, from which similarity vectors are constructed to capture local structural proximity. These vectors are combined with randomly initialized continuous variables via Hadamard product operations, resulting in structure-informed individuals that populate the initial solution set.

The optimization is conducted within a multi-objective evolutionary framework, where surrogate models are adaptively selected to approximate the objective functions and guide the search process. Elite individuals are periodically used to update the surrogate model, ensuring prediction accuracy throughout iterations.

3.1. Core Node Search Strategy

The core node search strategy has been designed to efficiently identify nodes that exhibit high potential as community centers. Prior to determining the core nodes, an evaluation of each network node’s weight must be conducted. Node weights are assigned based on the underlying graph structure and are quantified by the node’s degree. The weight value attributed to each node corresponds to the cardinality of its respective neighborhood set.

$$\mathrm{weight}\left(v\right)=\mathrm{deg}\left(v\right)$$

(6)

The degree of node v, denoted as $\mathrm{deg}\left(v\right)$, is quantified by the cardinality of its neighborhood set.

The construction of the core node set is carried out through a two-step process, as described in Algorithm 1. First, candidate nodes are identified by selecting those whose weights exceed the average weight of all nodes in the network, forming the candidate core node set. Then, the core node set is iteratively built from these candidates. In each iteration, the node with the highest weight in the current candidate set is selected and added to the core node set. This node, together with all its incident edges, is removed from the network. After removal, only the weights of the remaining candidate nodes are updated, reflecting the structural changes caused by the deletion. The process repeats: the updated candidate set is examined, and the next node with the highest weight is selected as a new core node. This selection–removal–update cycle continues until no candidate nodes remain, at which point the construction of the core node set is complete.

Algorithm 1 coreNode

Require: $weight$: weight of all nodes;

Ensure: $corenode$: the core node set;

1: $Avg\leftarrow \mathrm{avg}\left(weight\right)$;

2: Select the nodes with weights greater than the average weight as candidate core nodes;

% % Establishing the candidate core node set

3: Select the node with the largest weight and add it to the core node set;

4: Remove the selected node and its edges from the network;

5: Update the weights of the remaining candidate core nodes;

6: Repeat steps 3, 4, and 5 until the candidate core node set is empty;

7: Return $corenode$;

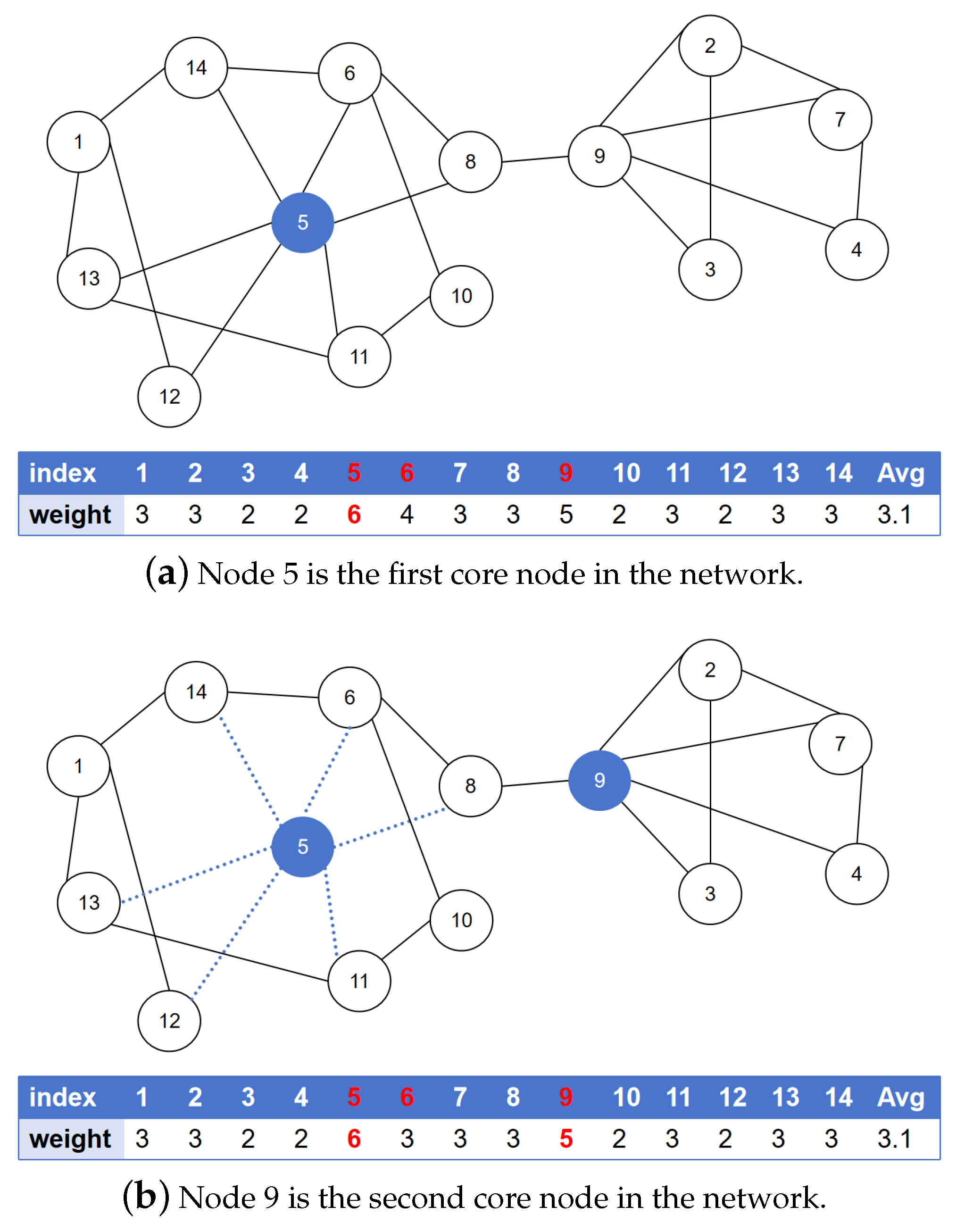
As illustrated in Figure 1, the procedure commences with the calculation of each node’s weight based on its degree, resulting in $weight=\{3,3,2,2,6,4,3,3,5,2,3,2,3,3\}$ with a mean weight value of $av{g}_w=3.1$. Based on these calculated weights, candidate core nodes are identified as those whose weights exceed the mean value of 3.1; consequently, the candidate core node set is established as $P=\{5,6,9\}$. In the subsequent step, node 5, which demonstrates the maximum weight among all candidates, is selected and incorporated into the core node set. Subsequently, this particular node and its associated edges are removed from the network, whereupon the weights of the remaining candidate core nodes undergo recalculation. Through systematic iteration of these procedural steps, the definitive core node set is determined as $corenode=\{5,9,6\}$.

3.2. Solution Representation and Initialization

Existing classical representation methods for network community detection are typically adapted from encodings utilized in evolutionary methodologies to address classical data clustering problems. These include label-based representation, locus-based representation, media-based representation, and permutation representation specifically designed for overlapping communities. Among these, label-based representation and locus-based representation [35] are two commonly employed encoding methodologies.

In locus-based representation, the genotype of a node is considered as one of the nodes to which it is connected. For instance, in the sample network illustrated in Figure 2, node 5 is connected to nodes 6, 7, and 8. Consequently, the genotype of node 5 could be represented as one of the following: 6, 7, or 8. In Figure 2a, the individual genotype is given as $\{2,9,2,1,6,7,5,6,3\}$, which is derived by associating each node with one of its connected nodes. From the graphical representation, it can be observed that this genotype decodes the individual into two distinct communities: $\{1,2,3,4,9\}$ and $\{5,6,7,8\}$.

In label-based representation, the individual genotype can be expressed as $\{1,2,\dots ,r\}$, wherein each value represents the community to which a node belongs. As demonstrated in Figure 2b, each node is assigned a community identifier as its genotype. The decoding process entails placing nodes with identical genotypes into the same community. It can be noted that both encoding methodologies ultimately result in discrete vectors.

Locus-based representation presents difficulties in designing evolutionary operators, whereas label-based representation encounters challenges in initializing high-quality individuals due to its inability to utilize similarity information between nodes. Furthermore, considering that continuous data is extensively employed in surrogate models to substitute the computation of the objective function in evolutionary algorithms, we have designed an improved continuous encoding strategy based on similarity matrices. This strategy aims to enhance the quality of both continuous encoding and the initial population. Algorithm 2 summarizes the pseudo code of the continuous encoding.

Algorithm 2 Continuous encoding

Require: $\mathit{X}=[{\mathit{X}}_1,{\mathit{X}}_2,\dots ,{\mathit{X}}_r]\in {\mathbb{R}}^b$,$\mathit{s}=[{\mathit{s}}_1,{\mathit{s}}_2,\dots ,{\mathit{s}}_r]$;

Ensure: A community partition $\mathcal{G}$;

1: Set $\mathcal{E}=\varnothing$;

2: for i = 1 to r do

3:      ${\mathit{z}}_i\leftarrow \mathrm{hadamard}({\mathit{x}}_i,{\mathit{s}}_i)$;

4:      ${\mathit{h}}_i\leftarrow \sigma \left({\mathit{z}}_i\right)$;

5:      ${\mathit{p}}_i\leftarrow \mathrm{softmax}\left({\mathit{h}}_i\right)$;

6:      $s\leftarrow argmax\left({\mathit{p}}_i\right)$;

7:      $\mathcal{E}\leftarrow \mathcal{E}\cup (V_i,V_s)$;

8: end for

9: $\mathcal{G}\leftarrow \mathrm{Decode}\left(\mathcal{E}\right)$;

10: Return $\mathcal{G}$;

In Algorithm 2, a continuous-valued vector $\mathit{X}\in {\mathbb{R}}^b$, where $b={\sum }_{i,j}{a}_{ij}$ denotes the number of edges in the network, is taken as input. The vector $\mathit{X}$ is constructed by concatenation of r subvectors, where ${\mathit{X}}_i$ is a continuous vector that encodes the connections of node $V_i$ to its neighbors, with $1\le i\le r$. Here, r denotes the number of nodes in the network. The length of each subvector ${\mathit{X}}_i$ is defined as $d_i={\sum }_j{a}_{ij}$, i.e., the degree of node $V_i$. Each element in ${\mathit{X}}_i$ assigns a continuous value to the link connecting node $V_i$ to one of its neighbors. Let ${\mathrm{Nei}}_i$ denote the set of neighboring nodes of $V_i$. Meanwhile, the similarity between node $V_i$ and its neighbors is computed by extracting the corresponding entries from the diffusion kernel similarity matrix, and is represented as a vector ${\mathit{s}}_i$.

During the initialization process, the influence of structurally related neighbors on node $V_i$ is amplified by computing the Hadamard product of ${\mathit{s}}_i$ and ${\mathit{X}}_i$. The objective is to establish connections between node $V_i$ and its more influential neighbors at the initial stage. A detailed description of this improved continuous encoding approach is provided as follows.

For node $V_i$, the corresponding vector ${\mathit{X}}_i=[X_{i1},X_{i2},\dots ,X_{i{d}_i}]$, and the similarity matrix vector ${\mathit{s}}_i=[s_{i1},s_{i2},\dots ,s_{i{d}_i}]$. The Hadamard operator is initially applied to node $V_i$ (line 1), resulting in a continuous vector ${\mathit{z}}_i$:

$${\mathit{z}}_i={\mathit{X}}_i\odot {\mathit{s}}_i$$

(7)

where ⊙ denotes the Hadamard product (element-wise multiplication).

Subsequently, a sigmoid function $\sigma$ is applied, which is defined as follows:

$$\sigma \left(x\right)={\displaystyle \frac{1}{1+exp(-x)}}$$

(8)

Each element of ${\mathit{X}}_i$ is subjected to the sigmoid operation to obtain ${\mathit{h}}_i\in {(0,1)}^{d_i}$ (line 3). Thereafter, a softmax operation is performed on ${\mathit{h}}_i$ to derive ${\mathit{p}}_i=[{\mathit{p}}_{i1},{\mathit{p}}_{i2},\dots ,{\mathit{p}}_{ir}]$ (line 4), whereby softmax is expressed as

$${\mathit{p}}_{ij}={\displaystyle \frac{exp\left({\mathit{h}}_{ij}\right)}{{\sum }_{k=1}^{d_i}exp\left({\mathit{h}}_{ik}\right)}},1\le j\le d_i$$

(9)

Based on ${\mathit{p}}_i$, the index s is selected from the set of $V_i$ neighbor nodes ${\mathrm{Nei}}_i$:

$$s=arg\underset{1\le j\le d_i}{max}{\mathit{p}}_{ij}$$

(10)

The node $V_s$ constitutes the genotype of node $V_i$. The node and its genotype $(V_s,V_i)$ are stored in $\mathcal{E}$. Decoding is then performed using a locus-based decoding method: by tracing links from each node $V_i$ to its selected neighbor $V_s$, communities are formed by grouping nodes that are connected through mutual or transitive links. This process results in a discrete community partition $\mathcal{G}$ by decoding $\mathcal{E}$.

Figure 3 illustrates the encoding process of a single node $V_i$. As observed in the figure, for each node $V_i$, a continuous value is associated with its neighbors. A node $V_s$ is selected to be connected to node $V_i$ through the Hadamard, sigmoid, softmax, argmax operations.

3.3. Objective Functions

In the multi-objective optimization process, two of the objectives are designated as negative ratio association (NRA) and ratio cut (RC) minimization. These particular objectives are capable of breaking the modularity constraints. Given an undirected network $G=(V,E)$, where $\left|V\right|=n$ and $\left|E\right|=m$, let the network be partitioned into k communities, denoted as $\mathsf{\Omega }=\{c_1,c_2,\dots ,c_k\}$, where each $c_i\subset V$. For $c_1,c_2\in \mathsf{\Omega }$, define $L(c_1,c_2)={\sum }_{i\in c_1,j\in c_2}{a}_{ij}$ and $L(c_1,\overline{c_2})={\sum }_{i\in c_1,j\in \overline{c_2}}{a}_{ij}$, where $\overline{c_2}=V\setminus c_2$. Consequently, the optimization problem can be formulated as

In the multi-objective optimization process, two of the objectives are designated as negative ratio association (NRA) and ratio cut (RC) minimization. These particular objectives are capable of breaking the modularity constraints. Given an undirected network $G=(V,E)$, where $\left|V\right|=n$ and $\left|E\right|=m$, let the network be partitioned into k communities, denoted as $\mathsf{\Omega }=\{c_1,c_2,\dots ,c_k\}$, where each $c_i\subset V$ and $c_i\cap c_j=\varnothing$ for $i\ne j$.

For $c_1,c_2\in \mathsf{\Omega }$, define $L(c_1,c_2)={\sum }_{i\in c_1,j\in c_2}{a}_{ij}$, and let $\overline{c_2}=V\setminus c_2$ denote the complement of $c_2$ with respect to the node set V. Consequently, the optimization problem can be formulated as

$$min\left\{\begin{array}{cc}\hfill \mathrm{NRA}& =-\sum _{i=1}^k{\displaystyle \frac{L(c_i,c_i)}{|c_i|}}\hfill \\ \hfill \mathrm{RC}& =\sum _{i=1}^k{\displaystyle \frac{L(c_i,\overline{c_i})}{|c_i|}}\hfill \end{array}\right.$$

(11)

In this paper, NRA is modified to kernel K-means (KKM) as introduced in [47]. Thus, the community detection problem is defined as

$$min\left\{\begin{array}{c}\hfill \mathrm{KKM}=2(n-k)-\sum _{i=1}^k{\displaystyle \frac{L(c_i,c_i)}{|c_i|}}\\ \hfill \mathrm{RC}=\sum _{i=1}^k{\displaystyle \frac{L(c_i,\overline{c_i})}{|\overline{c_i}|}}\end{array}\right.$$

(12)

The rationale for defining the aforementioned objectives stems from the observation, as pointed out by [47], that KKM represents a decreasing function of the number of communities, whereas RC exhibits the opposite behavior. In essence, these objectives constitute two conflicting criteria, considering that the right operand of KKM and RC can be interpreted as the sum of the density of connections within a community. Furthermore, RC can be conceptualized as the sum of the density of connections between distinct communities. The minimization of both KKM and RC ensures that intra-community connections are dense while inter-community connections remain sparse, which aligns with the fundamental characteristics of community structures in networks.

In the context of community detection, intra-community density and inter-community sparsity often exhibit conflicting tendencies. The proposed objective functions, KKM and RC, explicitly capture these two aspects. By optimizing both objectives simultaneously under the multi-objective paradigm, Pareto optimality provides a principled way to balance these structural trade-offs. Each Pareto-optimal solution corresponds to a network partition that represents a distinct trade-off between intra- and inter-community connections, enabling a comprehensive exploration of the solution space and uncovering community structures at different granularity levels.

3.4. Adaptive Selection of Surrogate Models

In the optimization process, continuous coding must first be decoded, followed by the calculation of the objective functions KKM and RC. To enhance computational efficiency, a surrogate model is constructed to establish the relationship between the continuous coding and the objective functions. In order to ensure the predictive accuracy of the constructed surrogate model, its performance is evaluated using Spearman and Kendall correlation coefficients.

Five distinct surrogate models have been collected from the literature, like Carts, SVR, Ridge, Knn, and Bayesian. Through ablation experiments, it has been observed that no single surrogate model consistently outperforms the others in terms of the aforementioned criteria across all datasets. Therefore, we propose a selection mechanism, termed adaptive selection (AC) of surrogate model, as described in Algorithm 3. It constructs all five types of surrogate models in each iteration and adaptively selects the optimal model through cross-validation.  

Algorithm 3 Adaptive selection of surrogate model

Require:  $sample$: a sample space;

Ensure: $model$: surrogate models;

1: Constructing 5 surrogate models;

2: Calculate kendall and spearman coefficients for each surrogate model;

3: Cross-validation to select the optimal surrogate model;

4: Return $model$;

The AC-selected surrogate model is utilized in conjunction with NSGA-II to optimize both KKM and RC (prediction), resulting in a set of solutions as well as a Pareto frontier upon completion of an NSGA-II search round. Due to the variations in accuracy of the objective function values predicted by the surrogate model, the individuals positioned on the Pareto frontier are computed with precision; that is, subsequent to decoding the individuals, the original value is computed using the original function of the objective function to ensure evolutionary accuracy. These individuals are subsequently incorporated into the sample space to enhance the predictive accuracy of the surrogate model.

3.5. Overall Procedure of ACMOEA

For a given network G, the proposed algorithmic framework is partitioned into four distinct components. In the initial component, the primary objective is to determine the core node set and the sample space dimension for the surrogate model (lines 1–2). The core node set $C_1,C_2,\dots ,C_c$ is identified based on the topological structure of network G, where c represents the cardinality of the core node set. The parameter $SaSize$ denotes the number of samples required for constructing the surrogate model, is determined by c.

In the second component, population initialization is conducted using an improved continuous encoding strategy that integrates structural similarity information, as described in Algorithm 2. Specifically, a similarity matrix $\mathbf{SM}$ is first computed to quantify inter-nodal relationships within the network G. By combining $\mathbf{SM}$ with the continuous encoding process, each individual in the initial population is generated with enhanced guidance toward structurally meaningful neighbors. This results in higher-quality initial solutions for subsequent evolutionary optimization. Finally, the evaluation function values of all individuals in the population are calculated. The genotypes corresponding to the core nodes in the initial population are used as features, while their associated evaluation function values serve as labels. Together, these features and labels form the initial training dataset used for surrogate model construction.

The third component involves the training and updating of the surrogate model. The surrogate model training process necessitates a substantial number of samples to achieve superior predictive accuracy; therefore, the initial generations of evolution are utilized to accumulate the requisite samples for training. Once the sample count attains the target threshold, the first generation surrogate model is trained.

In the fourth component (lines 10–35), the optimization process is initiated. The algorithmic framework exhibits similarities with the NSGA-II framework [21], wherein SELECT, NDS, and CD denote binary tournament selection, non-dominated sorting, and crowding distance, respectively.

During the evolutionary process, the crossover mutation operator of differential evolution is utilized to generate novel individuals. Three individuals, ${\mathit{x}}_1$, ${\mathit{x}}_2$, and ${\mathit{x}}_3$, are randomly selected from the mating pool for crossover operations. ${\mathit{x}}_1$, ${\mathit{x}}_2$, and ${\mathit{x}}_3$ are continuous encodings of individuals in the population, each corresponding to a network partition candidate. The formula for differential operation is expressed as follows:

$${\mathit{y}}_i=\left\{\begin{array}{cc}\hfill {\mathit{x}}_1+F·({\mathit{x}}_2-{\mathit{x}}_3),& \mathrm{if}\mathrm{rand}\left(\right)<CR\hfill \\ \hfill {\mathit{x}}_1,& \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

where $\mathrm{rand}\left(\right)$ represents a random number within the interval $(0,1)$, and F and $CR$ denote the scaling factor and crossover probability, respectively. Differential evolution (DE) plays a central role in the optimization component of the algorithm. As shown in Equation (13), DE generates new individuals by performing vector operations on continuous encodings of network partitions. This mechanism is particularly effective in exploring the high-dimensional Pareto front formed by KKM and RC. Through its mutation and crossover strategies, DE promotes diversity while guiding the population toward non-dominated solutions, making it well-suited for discovering multiple structurally distinct yet high-quality community partitions.

Each generational population undergoes sampling and integration into the training set. Upon accumulation of a sufficient number of samples, corresponding surrogate models are trained for the objective functions KKM and RC, respectively. Following the acquisition of the surrogate model, in subsequent optimization iterations, a subset of individuals employs the surrogate model for objective function prediction, while a smaller subset utilizes the original function for precise computation. Concurrently, these individuals are incorporated into the training set, and the surrogate model undergoes real-time updates to ensure predictive accuracy. Ultimately, the definitive community segmentation results are derived from the individuals situated on the Pareto frontier. Algorithm 4 presents the pseudo-code of ACMOEA, and the offspring generation operator is shown in Algorithm 5.

Algorithm 4 Community detection algorithm based on adaptive selection of surrogate models

Require: $\mathit{A}$: the adjacency matrix of the graph; w: the weights of all nodes; $Popsize$:

Population size; $maxAss$: maximum number of assessments; parameters of DE and PM:

F, $CR$, $pm$, $nm$;

Ensure: $PF$: A set of Pareto front solutions;

1: Get the core node and the size of the sample space: $C,SaSize\leftarrow \mathrm{coreNode}\left(w\right)$;

2: $\mathcal{P}\leftarrow$ Initialize the population of size $Popsize$ using the improved continuous encoding strategy described in Algorithm 2;

3: $\mathbf{SM}\leftarrow$ Compute the node similarity matrix using the diffusion kernel method;

4: $\mathit{F}\leftarrow$ Calculate the objective function of the population $\mathcal{P}$;

5: Undominated ordering of populations $\mathcal{P}$ and calculation of crowding distances $L,C_d\leftarrow \mathrm{NDS}\left(\mathcal{P}\right),\mathrm{CD}(\mathcal{P},\mathit{F})$;

6: Get the features in the initial sample space as well as the labels $\mathcal{S}\leftarrow \mathcal{P}[:,C]$;

7: while Number of real evaluations less than $maxAss$ do

8:      $\mathcal{Y}\leftarrow$ Conduct crossover and mutation on $\mathcal{P}$ by Algorithm 5;

9:      if the sample size is insufficient then

10:            ${\mathit{F}}_o\leftarrow$ Calculate the $\mathcal{Y}$ objective function;

11:            Merge samples into sample space $\mathcal{S}\leftarrow \mathcal{S}\cup \mathcal{Y}[:,C]$;

12:      else if $\mathrm{size}\left(\mathcal{S}\right)=SaSize$ then

13:            Perform Algorithm 3 to obtain the appropriate surrogate model;

14:            Calculate the value of the objective function of $\mathcal{Y}$ by means of the surrogate modeling;

15:      else

16:            ${\mathit{F}}_o\leftarrow$ Calculate the value of the objective function of $\mathcal{Y}$ by surrogate model;

17:            ${\mathcal{Y}}_a\leftarrow$ Select quality individuals from $\mathcal{Y}$;

18:            ${\mathit{F}}_a\leftarrow$ Compute the objective function for the population ${\mathcal{Y}}_a$;

19:            Update the sample space and surrogate model $model\leftarrow \mathrm{Train}\left(\mathcal{S}\right)$;

20:      end if

21:      $\mathcal{P},\mathit{F}\leftarrow \mathcal{P}\cup \mathcal{Y},\mathit{F}\cup {\mathit{F}}_o$;

22:      Undominated ordering of population $\mathcal{P}$ and computation of crowding distance: $L,C_d\leftarrow \mathrm{NDS}\left(\mathcal{P}\right),\mathrm{CD}(\mathcal{P},\mathit{F})$;

23:      Environmental selection yields new populations ${\mathcal{P}}_{new}$;

24: end while

25: Return the Pareto frontier and its corresponding individual;

Algorithm 5 Crossover and mutation

Require: $\mathcal{P}$: population;

Ensure: $\mathcal{Y}$: offspring;

1: $\mathcal{Y}\leftarrow \varnothing$;

2: for $1\le j\le Popsize$ do

3:      Creating mating pools through binary tournaments: $M_p\leftarrow \mathrm{Select}\left(\mathcal{P}\right)$;

4:      ${\mathit{x}}_2,{\mathit{x}}_3\leftarrow$ Randomly select from $M_p\setminus \left\{{\mathit{x}}_1\right\}$;

5:      $\mathit{y}\leftarrow$ DE and PM operations;

6:      $\mathcal{Y}\leftarrow \mathcal{Y}\cup \left\{\mathit{y}\right\}$;

7: end for

8: Return offspring $\mathcal{Y}$;

4. Experimental Results

In this section, the performance of the proposed ACMOEA is validated through experimental evaluation on five real networks and compared with nine representative baseline algorithms.

4.1. Experimental Settings

4.1.1. Experimental Networks

Five real-world networks with distinct characteristics were utilized to evaluate the performance of the proposed algorithm. These networks comprise Zachary’s Karate Club network, the Dolphin social network, the Books network about U.S. politics, the American College Football network, and the Net-Science network.

Table 1. Characteristicsof five real-world networks.

Real Networks	Nodes	Links	AD	Density
Karate	34	78	4.59	0.1390
Dolphins	62	159	5.13	0.0841
Polbook	105	441	8.4	0.0808
Football	115	613	10.66	0.0935
Net-Science	1589	2742	3.45	0.0026

presents the detailed characteristics of the five real-world networks. In this table, “AD” denotes the average degree of nodes in the network, whereas “Density” represents the density of the community. It should be noted that three of these networks, namely Karate, Dolphins, and Football, possess established ground-truth community divisions.

The Net-Science network constitutes a collaborative network of scientists comprising 1589 nodes, which represent researchers working in the field of network science, connected by 2742 edges that signify collaborations between them. The Karate network, established in 1977, primarily documented the social interactions among 34 karate club members over a two-year period. The Bottlenose Dolphin network, constructed by David Rousseau in 2003, was developed based on the frequency of associations between Bottlenose Dolphins observed in New Zealand waters. The American College Football network represents the regular season schedules of NCAA Division I teams during the 2000 season. The ground-truth community divisions for these three networks are illustrated in Figure 4.

4.1.2. Comparison Algorithms

The proposed algorithm ACMOEA was compared with several representative evolutionary algorithm-based methods, including a non-evolutionary algorithm (i.e., Community Enhancement-Based Algorithm (CSE [48])), as well as six EA-based algorithms for community detection, namely GA-net [10], SOSFCD [49], MODPSO [18], MOGA-net [31], RMOEA [50], and NSGA-III-KRM [51]. Within this set of comparison algorithms, GA-net and SOSFCD represent single-objective optimization approaches, whereas the remaining algorithms employ multi-objective optimization frameworks.

The parameter settings for the comparison algorithms were maintained consistent with those recommended in their respective references. The implementation of ACMOEA was conducted in Python 3.11, wherein the following parameter configurations were utilized: population size $Popsize$ = 100, number of true evaluations $maxAss$ = 10,000 (equivalent to the number of iterations in the other comparison algorithms, corresponding to 100 generations), $F=0.5$, $CR=0.5$, $pm=0.1$, and $nm=20$. In the subsequent result tables, the optimal values are highlighted in bold typeface.

4.1.3. Evaluation Metrics

In this study, two widely recognized metrics were adopted to evaluate the quality of solutions: modularity (Q) and normalized mutual information (NMI).

For the multi-objective evolutionary algorithms (MOEAs), the metric values (Q and NMI) were calculated for each solution in the final obtained non-dominated solution set; subsequently, the solution with the optimal value was selected for comparison as the representative result of the algorithm on the respective metric. This methodological approach has been extensively utilized in existing MOEA-based community detection algorithms.

The first metric, modularity Q, serves as a quantitative measure for assessing the quality of detected communities in the absence of ground-truth community labels for the network. Specifically, Q is calculated according to the following equation:

$$Q=\sum _{s=1}^c\left[{\displaystyle \frac{l_s}{M}}-{\left({\displaystyle \frac{d_s}{2M}}\right)}^2\right]$$

(14)

where c represents the number of communities, M denotes the number of edges in the network, $l_s$ signifies the total number of edges connecting nodes within community s, and $d_s$ corresponds to the sum of degrees of nodes in community s. A higher Q value indicates superior quality of the detected community structure.

The second metric, NMI, functions as a measure of similarity between the algorithmically detected communities and the ground-truth community labels. The calculation of NMI is performed as follows:

$$NMI={\displaystyle \frac{-2{\sum }_{i=1}^{C_A}{\sum }_{j=1}^{C_B}{C}_{ij}log\left(\frac{C_{ij}N}{C_{i.}{C}_{.j}}\right)}{{\sum }_{i=1}^{C_A}{C}_{i.}log\left(\frac{C_{i.}}{N}\right)+{\sum }_{j=1}^{C_B}{C}_{.j}log\left(\frac{C_{.j}}{N}\right)}}$$

(15)

where $C_A$ and $C_B$ denote the number of community divisions in partitions A and B, respectively; $C_{ij}$ represents the number of nodes shared by community i in partition A and community j in partition B; $C_{.j}$ indicates the sum of all elements in column j; and $C_{i.}$ signifies the sum of all elements in row i. A higher NMI value demonstrates greater similarity between the detected community structure and the ground-truth community organization.

4.2. Continuous Coding Performance

The improved continuous coding approach based on similarity matrix (i.e., SM-CE) has been implemented in ACMOEA. This approach exploits the similarity between nodes to bias the initial population toward a more promising direction.

To verify the effectiveness of the improved continuous coding approach based on similarity matrix, a comparison was conducted with the original continuous coding approach (i.e., CE). Figure 5 illustrates the average Q value of the initial population for the Karate, Football, and Net-Science networks with a population size N of 100. It can be observed that the modularity value of the initial population generated by SM-CE is higher than that of the population generated by CE, indicating that the performance of SM-CE is superior to that of CE.

4.3. Surrogate Model

In order to verify the validity of the surrogate model, the Spearman correlation coefficient was employed to assess the strength of the linear relationship between the surrogate model and the objective function. When the Spearman correlation coefficient approaches 1, it indicates a stronger monotonically positive correlation between the two functions. For two sets of variables X and Y, the Spearman correlation coefficient is calculated as follows:

$$\rho =1-{\displaystyle \frac{6{\sum }_{i=1}^N{d}_i^2}{N(N^2-1)}}$$

(16)

where N denotes the number of elements in X and Y; $x_i$ and $y_i$ represent the ranking of the ith element in X and Y, respectively; and the set of differences d is defined as $d_i=x_i-y_i,1\le i\le N$.

Based on the aforementioned correlation coefficients, various networks were tested. Each network was trained using 500 samples for the surrogate models, and the corresponding Spearman correlation coefficients were calculated for each model as presented in

Table 2. Training results of different web surrogate models.

Network	Carts	Svr	Ridge	Knn	Bayesian	AC
Karate	0.817234	0.798074	0.495903	0.852558	0.496359	0.875546
Dolphins	0.816896	0.872535	0.454046	0.851300	0.452984	0.878931
Football	0.839062	0.791417	0.730501	0.887254	0.730021	0.888103
Polbooks	0.911520	0.831105	0.705444	0.876485	0.703808	0.922999
Net-Science	0.916622	0.827722	0.923409	0.828695	0.898320	0.929131

. The experimental results demonstrate that the objective function predicted by the surrogate model trained using the core nodes is valid.

As observed in Table 2, the adaptive switching method successfully selects a better surrogate model with optimal Spearman results, thereby indicating the effectiveness of the adaptive switching method.

Figure 6 illustrates the performance of the surrogate model for two networks, Polbooks and Net-Science, across different size sample spaces. The horizontal coordinate x indicates that the sample space size is x times that of the core nodes. Although the performance of the surrogate models for both Polbooks and Net-Science varies with different sample space sizes, the performance of adaptive switching consistently exhibits optimal results for both networks.

Figure 7 depicts the true objective function values for five different networks plotted against the values predicted by the surrogate model. The data is uniformly distributed on both sides of the line $y=x$, indicating that the surrogate model performs well across the different networks with good prediction accuracy. Furthermore, the data points do not exhibit a nonlinear trend, and the error remains relatively stable. It is noteworthy that the node distribution of the Football network is relatively uniform, and the generation of the core nodes correlates with the degree of the nodes, which consequently results in less centralized prediction accuracy for the Football network.

4.4. Comparison Results Between ACMOEA and Baselines

4.4.1. Experimental Results in Terms of Modularity Q

Table 3. Comparison of Q results between ACMOEA and baselines, and the best result in each case is shown in bold type.

Network	Measure	CSE	GA-Net	MODPSO	MOGA-Net	RMOEA	NSGA-III-KRM	SOSFCD	ACMOEA
Karate	Qmax	0.3826	0.4059	0.4124	0.4163	0.3857	0.4198	0.4198	0.4198
	Qavg	0.3826	0.4059	0.4121	0.4161	0.3830	0.4194	0.4165	0.4194
	std	0.0000	0.0000	0.0083	0.0033	0.0068	0.0012	0.0060	0.0008
Dolphin	Qmax	0.3476	0.5014	0.5160	0.5115	0.5268	0.5277	0.5268	0.5246
	Qavg	0.3476	0.4946	0.5187	0.4915	0.5262	0.5246	0.5239	0.5222
	std	0.0000	0.0355	0.0064	0.0191	0.0008	0.0031	0.0033	0.0058
Polbooks	Qmax	0.5000	0.4125	0.5237	0.5173	0.5255	0.5269	0.5267	0.5269
	Qavg	0.5001	0.4125	0.5220	0.5073	0.5254	0.5258	0.5168	0.5268
	std	0.0000	0.0000	0.0014	0.0091	0.0008	0.0016	0.0060	0.0054
Football	Qmax	0.5989	0.5940	0.6019	0.4805	0.6046	0.5681	0.5964	0.6046
	Qavg	0.5989	0.5830	0.6011	0.4426	0.6042	0.5462	0.5762	0.5993
	std	0.0045	0.0148	0.0030	0.0258	0.0000	0.0131	0.0091	0.0065
Net-Science	Qmax	0.9152	0.8581	0.9325	0.8768	0.9513	0.9050	0.8754	0.9226
	Qavg	0.9148	0.8473	0.9313	0.8723	0.9512	0.9006	0.8713	0.9174
	std	0.0002	0.0384	0.0063	0.0054	0.0021	0.0024	0.0025	0.0116
+/−/≈		0/5/0	0/5/0	1/4/0	0/5/0	2/2/1	1/2/2	1/3/1

presents the modularity results obtained by the proposed algorithm (ACMOEA) and other comparative algorithms on five benchmark networks. In Table 3, the symbols ‘+’, ‘−’, and ‘≈’ denote that the benchmark algorithm performs better than, worse than, or statistically similar to ACMOEA, respectively.

As demonstrated in Table 3, ACMOEA achieves the highest modularity values on the Karate, Polbooks, and Football networks. The superior performance of multi-objective optimization approaches over single-objective optimization methods can be attributed to their ability to generate solutions that effectively balance conflicting objectives, thereby aligning more closely with the inherent characteristics of community structures. With respect to modularity values, ACMOEA significantly outperforms single-objective optimization algorithms such as MODPSO, MOGA-net, and SOSFCD, whereas ACMOEA exhibits performance comparable to that of the NSGA-III-KRM algorithm, which simultaneously optimizes three objectives (modularity, KKM, and RC).

The non-evolutionary algorithm CSE demonstrates considerably lower modularity optimization compared to evolutionary algorithm-based approaches. This performance discrepancy arises from the fact that CSE does not directly optimize modularity, but rather obtains the final community partitions through community enhancement techniques. Similarly, GA-net, which employs single-objective optimization, focuses on optimizing a single objective; consequently, its modularity optimization results are inferior to those achieved through multi-objective optimization approaches.

The superior performance of RMOEA over ACMOEA in the Dolphin, Football, and Net-Science networks can be attributed to their distinct optimization strategies. RMOEA employs a network reduction approach that recursively identifies local communities using elite individuals and progressively reduces search space, which is particularly effective for networks with well-defined community boundaries. In contrast, ACMOEA relies on surrogate model optimization with adaptive switching strategies that prioritize computational efficiency through objective function approximation. RMOEA’s local community repairing mechanism further enhances performance by correcting misidentified nodes during reduction, proving especially beneficial for networks with moderate density and clear topological separation between communities.

4.4.2. Experimental Results in Terms of NMI

Table 4. Comparisonof NMI results between ACMOEA and baselines, and the best result in each case is shown in bold type.

Network	Measure	CSE	GA-Net	MODPSO	MOGA-Net	RMOEA	NSGA-III-KRM	SOSFCD	ACMOEA
Karate	NMImax	0.8155	0.6369	0.8965	0.8573	0.95	1.0000	0.8041	1.0000
Dolphin	NMImax	0.7244	0.4304	0.8877	0.7869	0.9962	1.0000	0.6169	1.0000
Football	NMImax	0.9079	0.9194	0.9251	0.8011	0.9303	0.8610	0.8860	0.9328
+/−/≈		0/3/0	0/3/0	0/3/0	0/3/0	0/3/0	0/1/2	0/3/0

presents the normalized mutual information (NMI) values obtained from the community detection results of each algorithm when applied to real-world networks. Figure 8 illustrates the optimal community partitioning results achieved by ACMOEA on three networks with known ground-truth community structures. During the detection process, the community structures identified in the Karate and Dolphin networks demonstrate perfect consistency with the actual network divisions, while the Football network exhibits a maximum NMI value of 0.9328.

Furthermore, the statistical results of the normalized mutual information (NMI) obtained by the proposed algorithm and other comparative algorithms when applied to a set of Lancichinetti–Fortunato–Radicchi (LFR) benchmark networks are presented in Figure 9. The mixing parameter $\mu$ of the LFR networks was varied from 0.1 to 0.5 with an increment of 0.1. When $\mu =0.1$, the NMI values of nearly all algorithms approach 1, which indicates that the community structure is well-defined and readily distinguishable under these conditions. At $\mu =0.2$, ACMOEA achieves the optimal NMI value among all the compared algorithms. As the value of $\mu$ increases, the community structure becomes progressively more ambiguous; consequently, the NMI values of all algorithms exhibit a gradual decrease. Nevertheless, ACMOEA consistently maintains either the optimal or second-best performance and demonstrates excellent effectiveness in community detection across the synthetic networks.

5. Conclusions

In this paper, we have proposed a community detection algorithm based on an adaptive switching surrogate model, termed ACMOEA-Net. The proposed approach employs a multi-objective optimization strategy to address the complex challenge of community detection in network structures. Our method simultaneously minimizes two conflicting objective functions, namely KKM and RC, thereby obtaining a partitioned structure characterized by dense intra-community connectivity and sparse inter-community connections.

To enhance computational efficiency, continuous coding has been implemented for community detection, wherein the KKM and RC objectives are predicted using a surrogate model, thus significantly reducing the computational resources required for the decoding process. Furthermore, the continuous coding mechanism has been improved through the initialization of populations based on a similarity matrix, which facilitates more effective exploration of the solution space.

The performance of the ACMOEA-Net algorithm has been extensively validated through comprehensive experiments conducted on both synthetic networks and five real-world network datasets. The experimental results have been systematically compared with seven state-of-the-art community detection algorithms, demonstrating the efficacy of our proposed approach.