Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane
Abstract
1. Introduction
2. The Main Result
3. Numerical Simulation
3.1. Example 1
3.2. Example 2
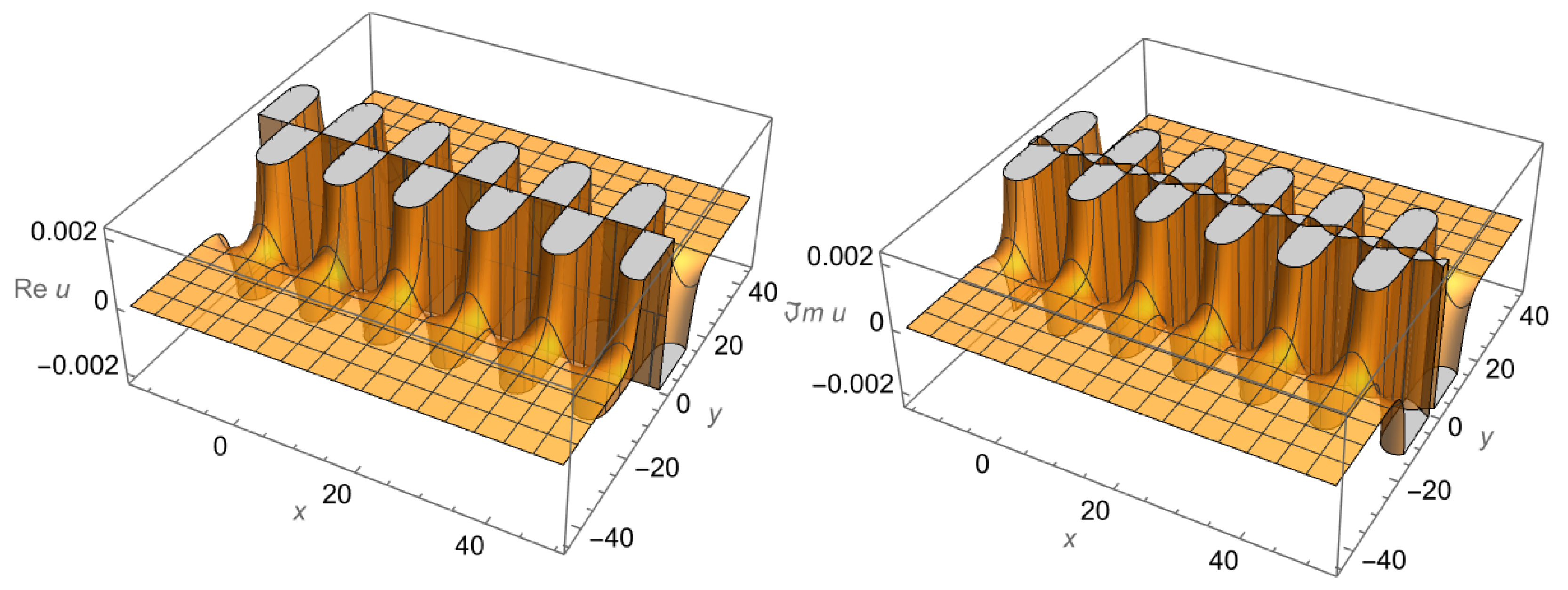
3.3. Example 3
4. Exact Complex Solutions of the EFK
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peletier, L.; Troy, W. Spatial Patterns: Higher Order Models in Physics and Mechanics; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Coullet, P.; Elphick, C.; Repaux, D. Nature of spatial chaos. Phys. Rev. Lett. 1987, 58, 431. [Google Scholar] [CrossRef] [PubMed]
- Dee, G.T.; Van Saarloos, W. Bistable systems with propagating fronts leading to pattern formation. Phys. Rev. Lett. 1988, 60, 2641–2644. [Google Scholar] [CrossRef] [PubMed]
- Swift, J.; Hohenberg, P. Hydrodynamic fluctuations at the convective instability. Phys. Rev. A. 1977, 15, 319–328. [Google Scholar] [CrossRef]
- Aronson, D.G.; Weinberger, H. Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 1978, 30, 33–76. [Google Scholar] [CrossRef]
- Fife, P.C. Mathematical Aspects of Reacting and Diffusing Systems; Springer: New York, NY, USA, 1979. [Google Scholar]
- Bonheure, D. Multitransition kinks and pulses for fourth order equations with a bistable nonlinearity. Ann. I. H. Poincaré–AN 2004, 21, 319–340. [Google Scholar] [CrossRef]
- Korpusov, M.O.; Ovchinnikov, A.V.; Sveshnikov, A.G. On blow up of generalized Kolmogorov–Petrovskii–Piskunov equation. Nonlinear Anal. Theory, Methods Appl. 2009, 71, 5724–5732. [Google Scholar] [CrossRef]
- Smyrnelis, P. Double layered solutions to the extended Fisher–Kolmogorov P.D.E. Nonlinear Differ. Equ. Appl. 2021, 28, 48. [Google Scholar] [CrossRef]
- Peletier, L.A.; Troy, W.C. A topological shooting method and the existence of kinks of the extended Fisher–Kolmogorov equation. J. Juliusz Schauder Cent. Top. Meth. Nonlinear Anal. 1995, 6, 331–355. [Google Scholar] [CrossRef]
- Peletier, L.A.; Troy, W.C.; Van der Vorst, R. Stationary solutions of a fourth-order nonlinear diffusion equation. Differ. Equ. 1995, 31, 301–314. [Google Scholar]
- Peletier, L.A.; Troy, W.C. Chaotic spatial patterns described by the EFK equation. J. Differ. Equ. 1996, 129, 458–508. [Google Scholar] [CrossRef]
- Kalies, W.D.; Van der Vorst, R. Multitransition homoclinic and heteroclinic solutions of extended Fisher–Kolmogorov equation. J. Differ. Equ. 1996, 131, 209–228. [Google Scholar] [CrossRef]
- Van den Berg, G.B.J.; Peletier, L.; Troy, W. Global branches of multi-bump periodic solutions of the Swift–Hohenberg equation. Arch. Ration. Mech. Anal. 2001, 158, 91–153. [Google Scholar] [CrossRef]
- Chaparova, J.V. Existence and numerical approximations of periodic solutions of semilinear fourth-order differential equations. J. Math. Anal. Appl. 2002, 273, 121–136. [Google Scholar] [CrossRef]
- Amster, P.; Mariani, M.C. Oscillating solutions of a nonlinear fourth order ordinary differential equation. J. Math. Anal. Appl. 2007, 325, 1133–1141. [Google Scholar] [CrossRef]
- Carrião, P.C.; Faria, L.F.O.; Miyagaki, O.H. Periodic solutions for extended Fisher–Kolmogorov and Swift–Hohenberg equations by truncature techniques. Nonlinear Anal. Theory Methods Appl. 2007, 67, 3076–3083. [Google Scholar] [CrossRef]
- Samoilenko, A.M.; Nizhnik, I.L. Differential Equations with bistable nonlinearity. Ukr. Math. J. 2015, 67, 584–624. [Google Scholar] [CrossRef]
- Jebelean, P.; Şerban, C. Fisher-Kolmogorov type perturbations of the relativistic operator: Differential vs. difference. Proc. Am. Math. Soc. USA 2018, 146, 2005–2014. [Google Scholar] [CrossRef]
- Nisar, K.S.; Alsallami, S.A.M.; Inc, M.; Baber, M.Z.; Tarar, M.A. On the exact solutions of nonlinear extended Fisher-Kolmogorov equation by using the He’s variational approach. AIMS Math. 2022, 7, 13874–13886. [Google Scholar] [CrossRef]
- Danumjaya, P.; Pani, A.K. Numerical methods for the extended Fisher-Kolmogorov (EFK) equation. Int. J. Numer. Anal. Model. 2006, 3, 186–210. [Google Scholar]
- Thottoli, S.R.; Tamsir, M.; Meetei, M.Z.; Msmali, A.H. Numerical investigation of nonlinear extended Fisher-Kolmogorov equation via quintic trigonometric B-spline collocation technique. AIMS Math. 2024, 9, 17339–17358. [Google Scholar] [CrossRef]
- Al-Musawi, G.A.; Harfash, A. Finite element analysis of extended Fisher-Kolmogorov equation with Neumann boundary conditions. Appl. Numer. Math. 2024, 201, 41–71. [Google Scholar] [CrossRef]
- Van den Berg, J.B. The Phase-plane Picture for a Class of Fourth-order Conservative Differential Equations. J. Differ. Equ. 2000, 161, 110–153. [Google Scholar] [CrossRef][Green Version]
- Orlov, V.; Chichurin, A. Extended Fisher-Kolmogorov equation with singularities in the complex domain. 2025, submitted.
- Kudryashov, N.A. Exact solitary waves of the Fisher equations. Phys. Lett. A 2005, 342, 99–106. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Stationary solitons of the generalized nonlinear Schrödinger equation with nonlinear dispersion and arbitrary refractive index. Appl. Math. Lett. 2022, 128, 107888. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding optical solitons of generalized nonlinear Schrödinger equations. Optik 2022, 261, 169163. [Google Scholar] [CrossRef]
- Orlov, V. Moving Singular Points and the Van der Pol Equation, as Well as the Uniqueness of Its Solution. Mathematics 2023, 11, 873. [Google Scholar] [CrossRef]
- Orlov, V. Dependence of the Analytical Approximate Solution to the Van der Pol Equation on the Perturbation of a Moving Singular Point in the Complex Domain. Axioms 2023, 12, 465. [Google Scholar] [CrossRef]
- Orlov, V.; Chichurin, A. The Influence of the Perturbation of the Initial Data on the Analytic Approximate Solution of the Van der Pol Equation in the Complex Domain. Symmetry 2023, 15, 1200. [Google Scholar] [CrossRef]
- Hille, E. Ordinary Differential Equations in the Complex Domain; Dover Publications: New York, NY, USA, 1997. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orlov, V.; Chichurin, A. Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane. Symmetry 2025, 17, 1156. https://doi.org/10.3390/sym17071156
Orlov V, Chichurin A. Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane. Symmetry. 2025; 17(7):1156. https://doi.org/10.3390/sym17071156
Chicago/Turabian StyleOrlov, Victor, and Alexander Chichurin. 2025. "Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane" Symmetry 17, no. 7: 1156. https://doi.org/10.3390/sym17071156
APA StyleOrlov, V., & Chichurin, A. (2025). Approximate Solutions of the Fisher–Kolmogorov Equation in an Analytic Domain of the Complex Plane. Symmetry, 17(7), 1156. https://doi.org/10.3390/sym17071156









