A Neural Network Training Method Based on Distributed PID Control

Abstract

In the previous article, we introduced a neural network framework based on symmetric differential equations. This novel framework exhibits complete symmetry, endowing it with perfect mathematical properties. While we have examined some of the system’s mathematical characteristics, a detailed discussion of the network training methodology has not yet been presented. Drawing on the principles of the traditional backpropagation algorithm, this study proposes an alternative training approach that utilizes differential equation signal propagation instead of chain rule derivation. This approach not only preserves the effectiveness of training but also offers enhanced biological interpretability. The foundation of this methodology lies in the system’s reversibility, which stems from its inherent symmetry—a key aspect of our research. However, this method alone is insufficient for effective neural network training. To address this, we further introduce a distributed Proportional–Integral–Derivative (PID) control approach, emphasizing its implementation within a closed system. By incorporating this method, we achieved both faster training speeds and improved accuracy. This approach not only offers novel insights into neural network training but also extends the scope of research into control methodologies. To validate its effectiveness, we apply this method to the MNIST (Modified National Institute of Standards and Technology database) and Fashion-MNIST, demonstrating its practical utility.

1. Introduction

1.1. The Tortuous History of Artificial Neural Networks

Artificial neural networks originated from the simulation of biological nerve cells. In early studies, people could only observe the simplest activation behavior of neurons. As the research deepened, people realized that the signals in nerve cells were transmitted through changes in potential and established corresponding differential equations [1]. Since then, differential equations have become the core of describing the dynamics of nerve cells. In the early 20th century, people had been trying to realize artificial neural networks by simulating the signal transmission of differential equations, but they had not been successful due to the complexity of the equations.

To overcome the complexity of biophysical models and explore computational feasibility, researchers turned to more abstract and manageable discrete models, starting with the simplest models, as early studies of biological nerve cells did. This shift directly led to the birth of the perceptron in the late 1950s [2]. The perceptron explicitly introduced the concept of learning: its weights could be automatically adjusted from labeled data through an iterative, error-correction-based rule (the perceptron learning rule). The perceptron, a single-layer neural network (containing only input and output layers), was capable of solving linear separable problems, and demonstrated potential in simple image recognition tasks, sparking the first wave of neural network research.

However, the fundamental limitations of the perceptron were sharply revealed in 1969 by Marvin Minsky and Seymour Papert in their book Perceptrons [3]. They rigorously proved that single-layer perceptrons could not solve linearly inseparable problems—the classic example being the XOR (exclusive OR) logic function. This critical flaw, compounded by the limited computing power of the time and the absence of effective training methods for multilayer networks, led to a withdrawal of research funding and a steep decline in academic interest. Neural network research consequently entered a prolonged “AI Winter” that lasted more than a decade.

A turning point arrived in the 1980s, when several key breakthroughs collectively revived interest in neural networks. In 1982, physicist John Hopfield proposed the Hopfield network—a fully connected, recurrent neural network [4]. He introduced the novel concept of an “energy function” and proved that the network evolves toward a state of lower energy, eventually stabilizing at a local minimum (called an attractor or fixed point). The Hopfield network demonstrates that complex problems can be effectively simulated by building a system containing attractors, and that the network can be effectively trained by adjusting the attractors of the system.

Nevertheless, the true catalyst for modern neural networks was the (re)discovery and widespread adoption of the backpropagation algorithm (BP). Although the core idea of the algorithm appeared earlier, it was not until 1986 that a paper published in Nature magazine—which made the algorithm widely recognized and applied—proved its ability to train multilayer neural networks (MLPs) to solve nonlinear problems [5]. The BP algorithm uses the chain rule to compute the gradient of the loss function with respect to all network weights, then propagates this gradient information backward from the output layer to the input layer, guiding the adjustment of weights to minimize prediction error. It elegantly solved the challenge of training MLPs, enabling them to learn complex nonlinear mappings. The emergence of the BP algorithm, coupled with gradually increasing computational power, made it feasible to train networks with one or more hidden layers, ushering neural network research into a new phase of rapid development.

In the 21st century—especially after the 2010s—neural network development has experienced an unprecedented boom and has fundamentally reshaped the landscape of artificial intelligence. Today, artificial neural networks have long transcended academic research and achieved large-scale, full-spectrum industrial application. They have become deeply integrated into nearly every corner of modern society, including computer vision [6], natural language processing [7], recommendation systems [8], scientific research [9,10,11], and beyond.

Although artificial neural networks have experienced a long period of twists and turns and will be prosperous in the foreseeable future, we should not forget that the training of artificial neural networks has always been closely related to the architecture of neural networks. In the previous paper, we proposed a new neural network framework, so it is natural to provide the corresponding neural network training method.

1.2. Biological Neural Networks and Biological Interpretability

While artificial neural networks based on digital computing are developing rapidly, researchers have not given up on biological neural network models based on differential equations. This is mainly because such models are directly derived from the simulation of biological neuron behavior, which is the origin of artificial neural networks. Therefore, biological neural networks have higher biological rationality in terms of structure and dynamic characteristics.

On the other hand, biological neural systems show extremely high energy utilization efficiency and can complete complex perception and computing tasks with much less energy than current artificial neural networks. Although modern GPU clusters can achieve large-scale deep learning training, their energy efficiency is still far less than that of the human brain. This gap has also prompted researchers to continue to pay attention to biologically inspired neural models with higher energy efficiency.

Since the 1980s, cellular neural networks, chaotic neural networks, and spiking neural networks have been proposed one after another [12,13,14]. Their core goal is to simulate the behavioral mechanism of biological neurons from the perspective of dynamic systems and strive to strike a balance between computational efficiency and biological rationality.

At the same time, although the backpropagation algorithm has made great contributions to the development of deep learning, its biological interpretability has also been increasingly questioned. In the early days, the algorithm faced mathematical challenges such as gradient vanishing and gradient exploding in its applications [15]. Although these problems have been significantly alleviated with the improvement of network structure and activation function, for some of its basic assumptions—such as the availability of global error signals, the precise symmetry of forward and backward propagation weights, and the synchronous update mechanism—it is difficult to find corresponding biological bases in real neural systems [16,17,18].

As early as 1989, Crick expressed caution toward the craze for neural networks, pointing out that backpropagation lacked consistency with biological neural mechanisms [19]. In the same year, Stork pointed out more clearly that “backpropagation is biologically irrational” [20].

In recent years, discussions on this issue have continued [17]. In a systematic review in 2020, it was pointed out that although there is no conclusive evidence that biological neurons can directly implement backpropagation, under certain conditions, the nervous system may achieve functionally similar learning effects through simplified or alternative mechanisms [21]. This has further promoted the exploration of learning mechanisms with stronger biological plausibility, such as forward-forward, feedback alignment, equilibrium propagation, and other methods [16,22,23]. These methods do not fundamentally change the structure of the neural network but try to make partial corrections to the training mechanism to alleviate the biological irrationality of backpropagation. Based on this understanding, even Hinton has publicly called for abandoning the current neural network architecture and finding a new neural network framework with better biological interpretability.

1.3. Neural Network Framework and Training Methods

In this paper, our main contribution is to propose an effective training method for the Wuxing neural network. A review of the development of artificial neural networks reveals that each significant breakthrough in training methodology has substantially advanced the field. This observation suggests that network architecture and training algorithms are deeply intertwined, with their alternating progress jointly driving the success of modern neural networks.

Although differential equations are widely regarded as the fundamental tool for modeling biological neurons, neural networks based on such equations have developed slowly. The primary reason lies in the lack of efficient training methods. Moreover, the difficulty in designing effective training strategies is often rooted in the network architecture itself—when the structure is inherently ill-suited for learning, it becomes exceedingly difficult to devise suitable training algorithms.

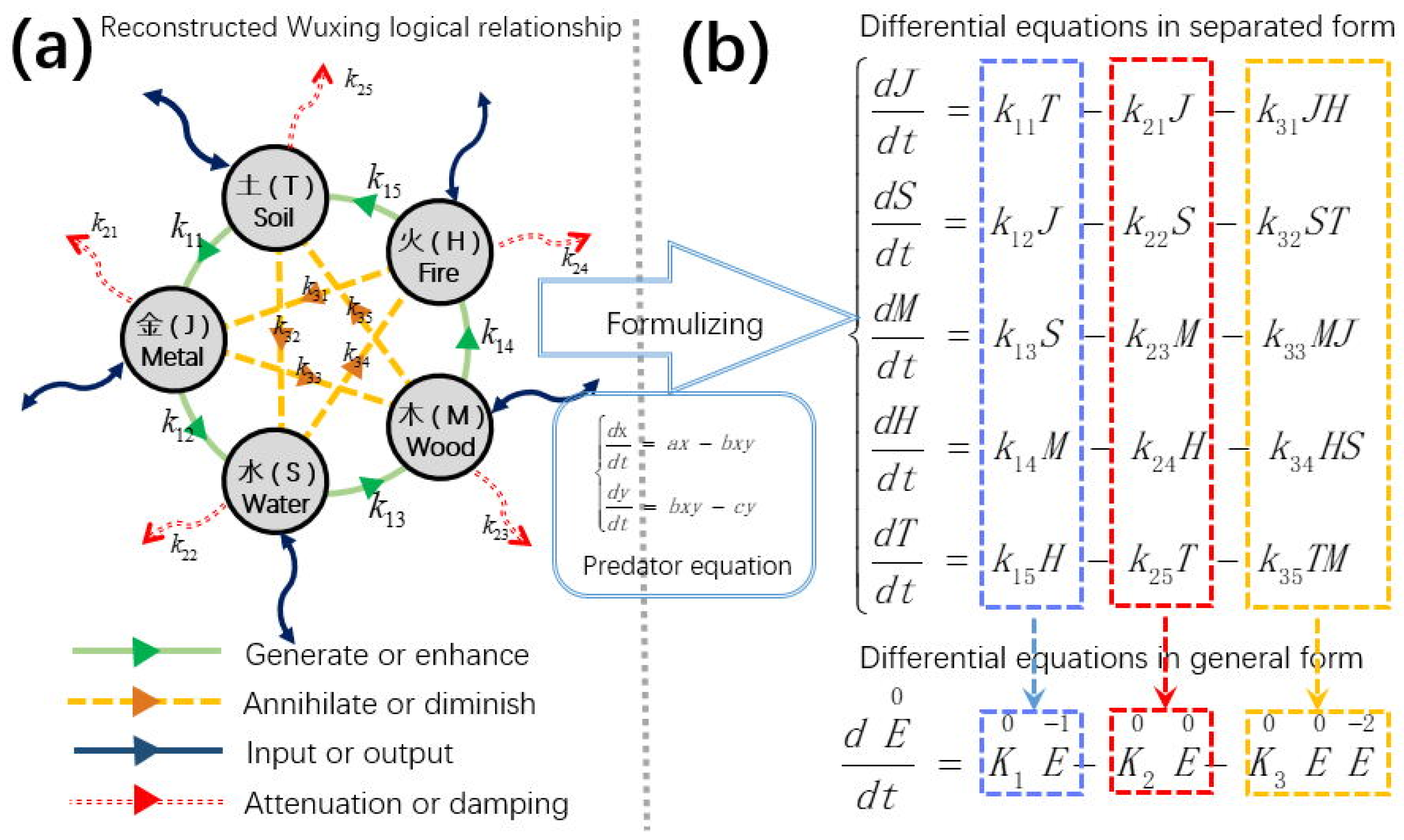
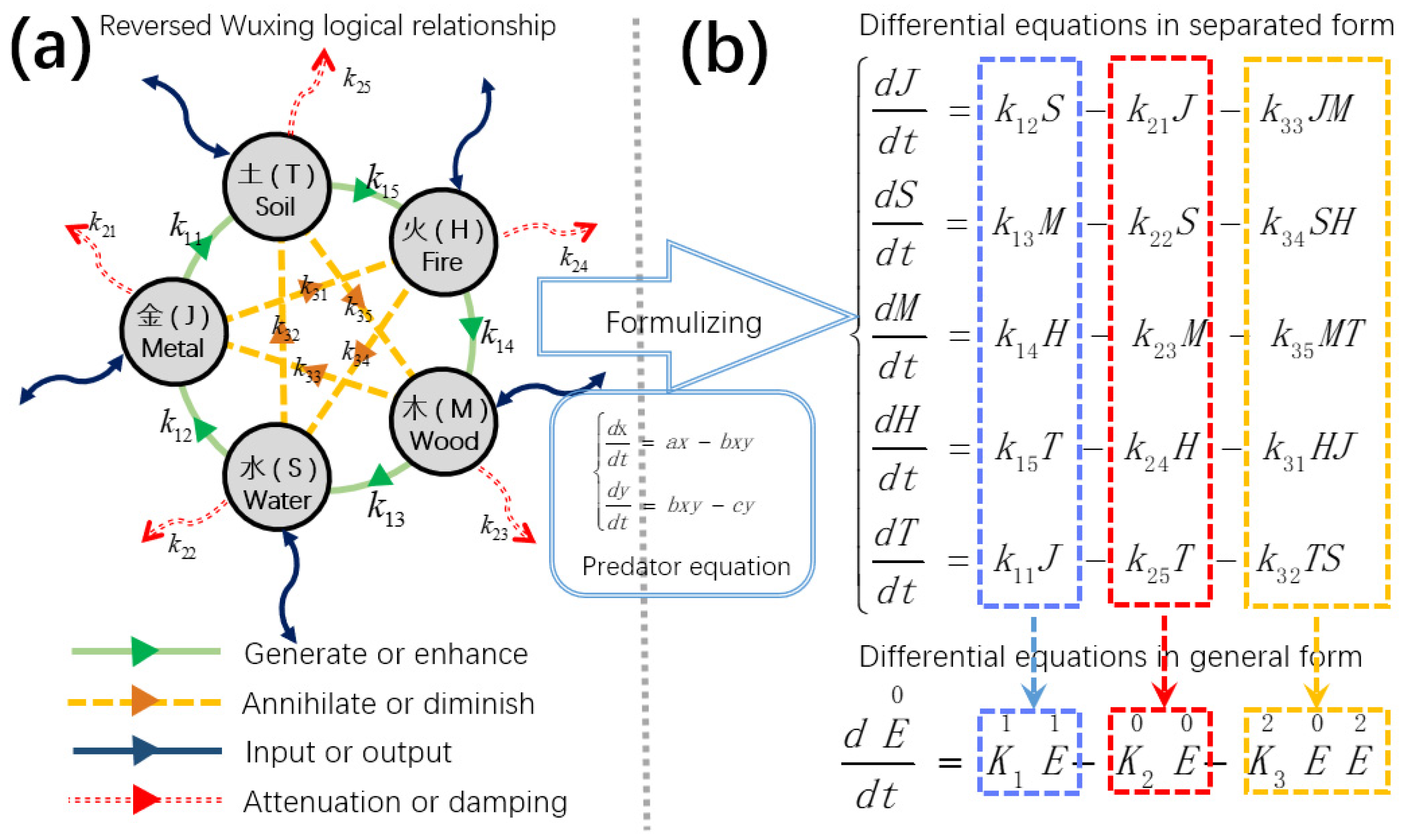
In the previous article, we proposed a neural network framework based on symmetric differential equations [24]. Compared with other biological neural network frameworks, the new framework starts from group theory and constructs symmetric differential equations based on the five-element logic and predator–prey equations. Because the equation has good symmetry, the reversibility of the system becomes a natural property, without the need for additional methods to find a reversible system [25].

From a biological perspective, it is generally believed that individual neurons cannot access global information. Therefore, a training method is considered biologically plausible if neurons can be trained using only local information. Hebbian learning is a classic example of such a local rule; however, its expressive capacity is limited, and it cannot scale to large networks effectively.

In summary, the choice of neural network architecture is closely linked to the design of feasible training methods. In the context of the Wuxing neural network, conventional training approaches prove to be either ineffective or inefficient. Consequently, it is necessary to develop a novel training strategy tailored to this new architecture.

To develop an effective alternative to the backpropagation algorithm, it is essential to first understand the fundamental strengths of backpropagation. In our view, the key advantage of the backpropagation method lies in its point-to-point, precise adjustment capability, which contributes to both training efficiency and robustness. By using backpropagation, we can quantitatively assess the impact of each parameter on the final outcome, enabling targeted adjustments—a feature that many alternative algorithms fail to provide. Therefore, despite criticisms regarding its biological plausibility, the backpropagation algorithm remains indispensable and cannot easily be replaced by other methods.

In our effort to propose an efficient alternative, we have approached the problem from both mathematical and biological perspectives.

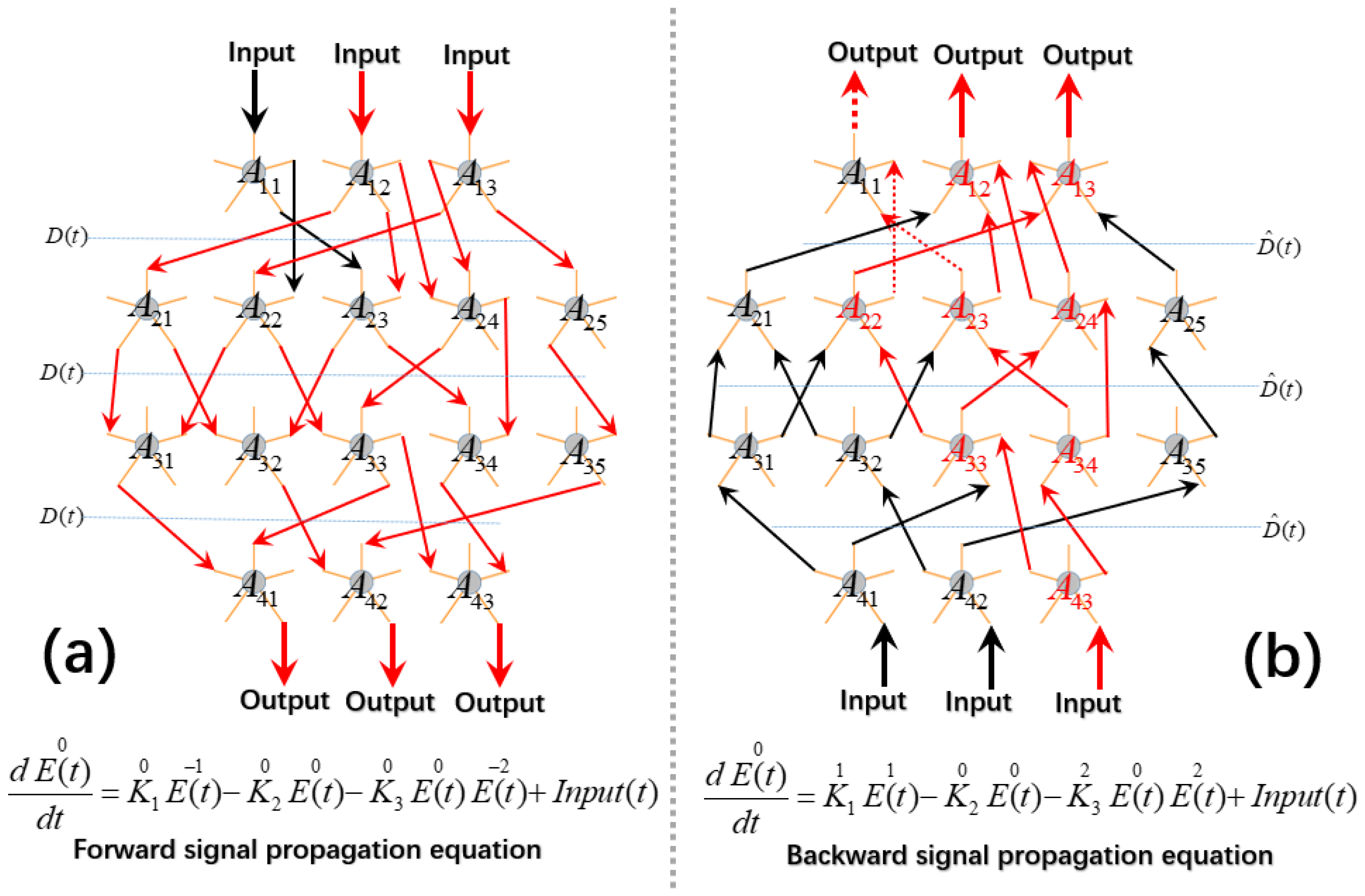
From a mathematical perspective, we propose using signal propagation in differential equations as a replacement for chain rule derivation, a method we refer to as differential equation propagation. This approach maintains a one-to-one correspondence, ensuring high efficiency. The key prerequisite for this method is that the system must be reversible. As established in our earlier design, the system exhibits complete symmetry, which makes reversibility straightforward to achieve. Reversibility implies that we can trace the causal relationships within the system in reverse, analogous to the point-to-point mechanism in the backpropagation algorithm.

From a biological standpoint, we introduce the concept of instinctive design. In this design, each neuron operates autonomously and retains full functionality, meaning that individual neurons can independently execute signal propagation and feedback training without the need for global information. Neurons interact with the external environment through synapses, without requiring any specialized structural design. This approach provides both strong biological interpretability and efficient training capabilities. Within this training framework, each neuron adjusts system parameters by comparing forward and reverse signals passing through it, thereby facilitating neural network training without the need for global coordination.

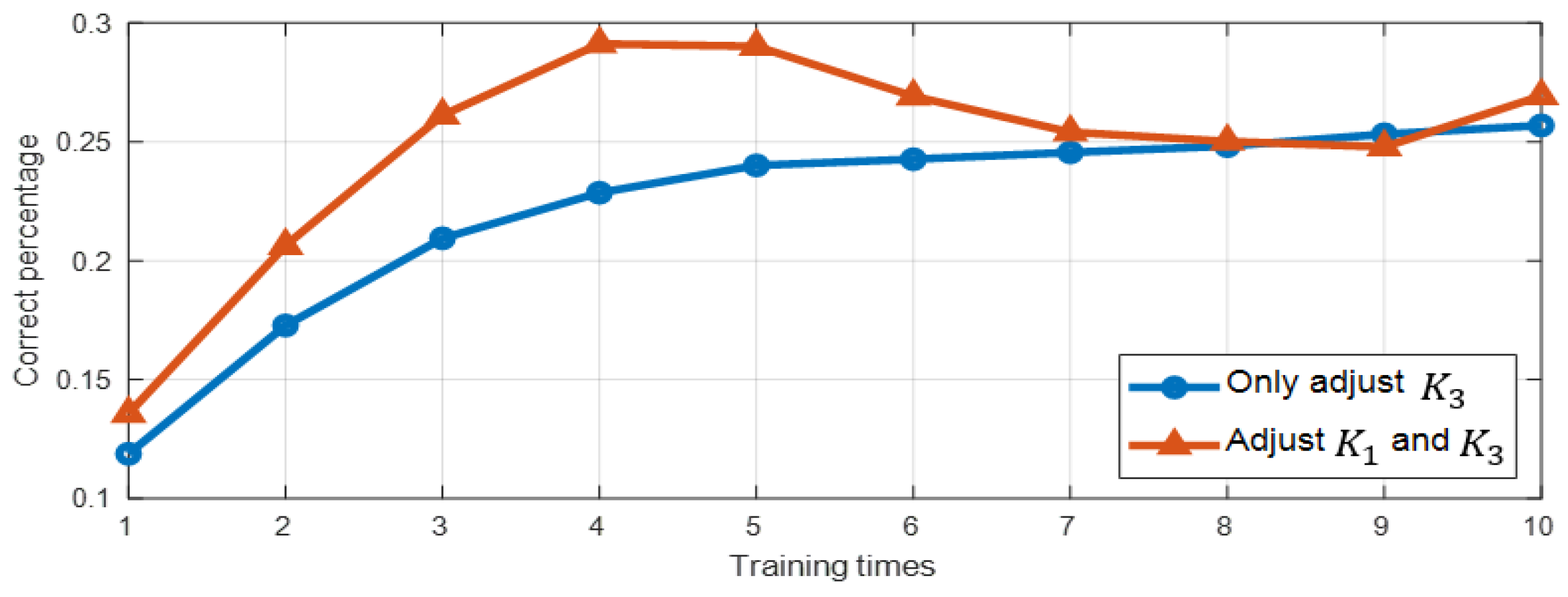
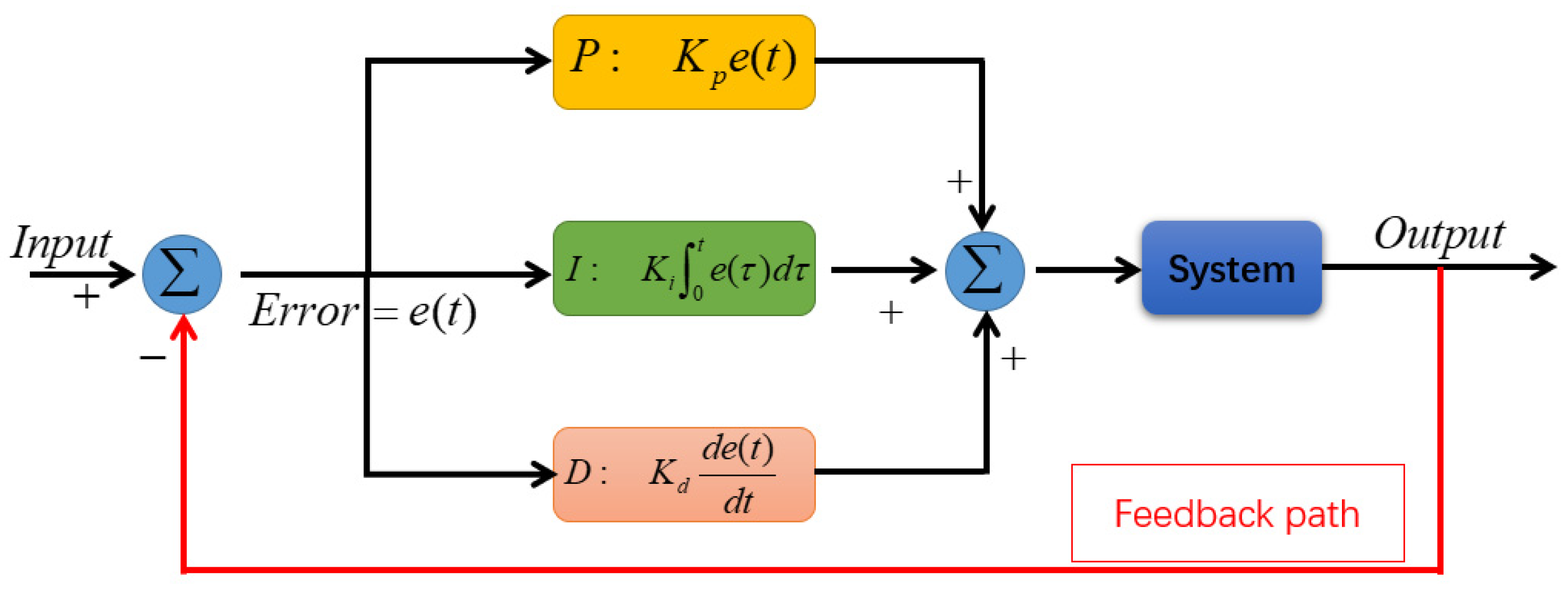
However, adopting this strategy alone is insufficient. The system composed of differential equations contains three distinct sets of parameters. If the same adjustment strategy were applied to all three parameter sets during training, it would be ineffective in enhancing neural network performance. To address this issue, we introduce a distributed Proportional–Integral–Derivative (PID) control method. PID control holds a dominant position in traditional control systems, whether in academic teachings or industrial applications, and remains a critical tool [26]. However, our approach deviates from the conventional PID method. In alignment with the principle of instinctive design, we focus on implementing the PID control logic within a single closed system. Building on the fundamental concepts of PID control, we have developed a novel control method that not only adheres to the instincts of design but also effectively incorporates PID functionality.

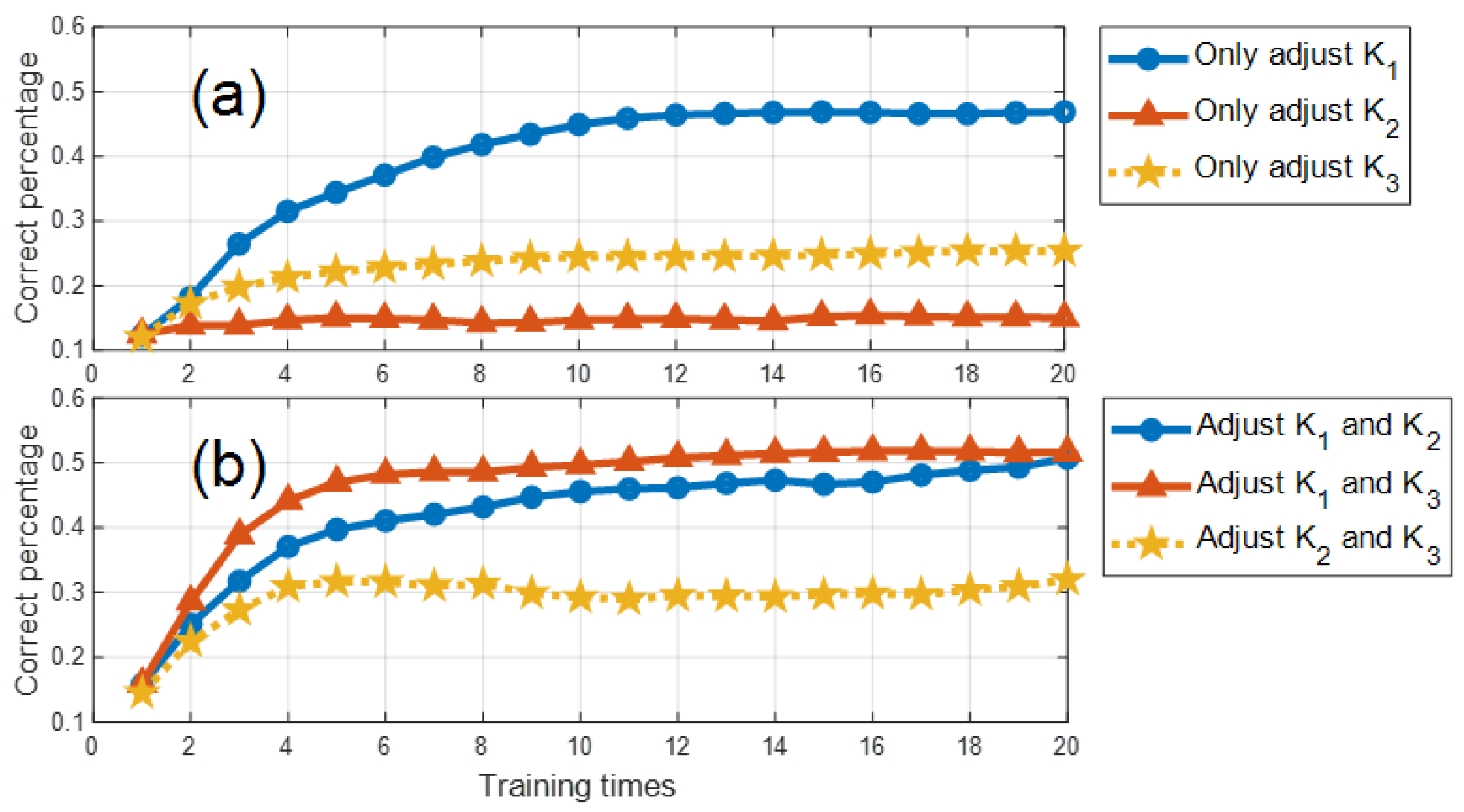
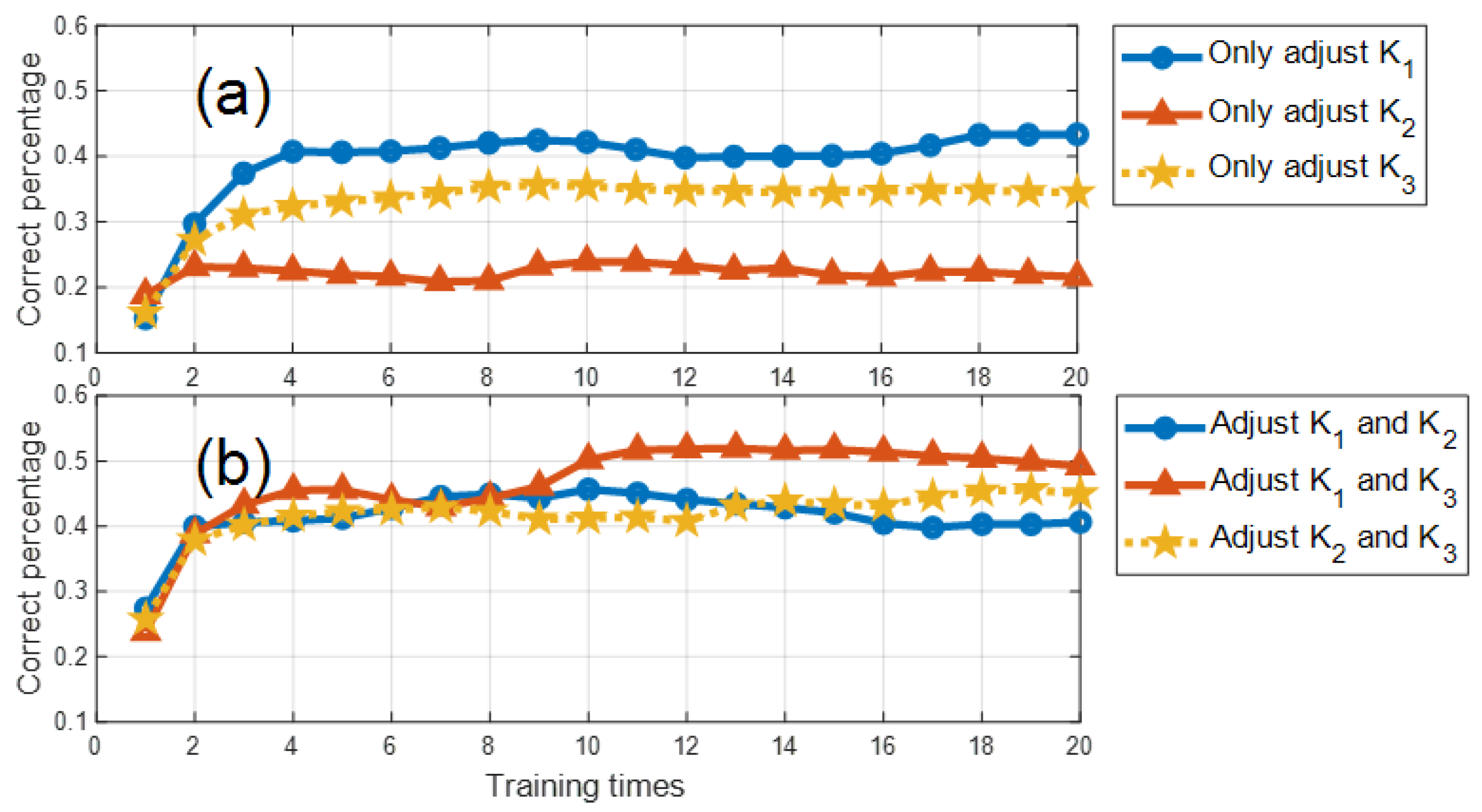
To validate our approach, we conducted experiments on the MNIST (Modified National Institute of Standards and Technology database) and Fashion-MNIST. The results demonstrate that the distributed PID control method effectively enhances the system’s accuracy and training speed.

The remainder of this article is organized as follows: Section 2 provides a brief introduction to the Wuxing neural network, offering a foundational understanding of its core concepts. Section 3 details the training methodology for the Wuxing neural network, emphasizing the use of differential equation signal propagation as a replacement for chain rule derivation. Section 4 explores PID control theory and its application to neural network training, with a particular focus on implementing distributed PID methods in closed systems. Section 5 concludes with a summary of our work and prospects for future research.

2. Wuxing Neural Network

In this section, we will briefly introduce the Wuxing neural network structure, fixed point calculation, and signal propagation method. For more details, please refer to our previous article [24].

2.1. Wuxing Neural Network Differential Equations

Traditional neural networks can generally be divided into two categories: those based on mathematical principles, such as multilayer perceptron (MLPs) and Hopfield networks [4], and those inspired by biological systems, such as chaotic neural networks and cell neural networks [12,13]. Mathematically driven neural networks have given rise to models like convolutional neural networks (CNNs) and recurrent neural networks (RNNs), which serve as the foundation for many large-scale, widely deployed models today. In contrast, while biologically inspired neural networks offer strong biological interpretability, they lack scalability for practical deployment. This limitation stems from their reliance on differential equations, for which suitable mathematical formulations to accurately describe neural activity are still lacking.

In the Wuxing neural network, neurons are modeled as systems composed of a series of symmetrical differential equations. The primary objective of introducing this structure is to address the challenge of manipulating differential equations effectively. Traditional biological neural networks often employ differential equations derived from experimental observations. However, this approach can introduce detailed inconsistencies that undermine the equations’ mathematical properties. To address this issue, our research adopts symmetrical logic based on the Five Elements (Wuxing) theory as its foundation. By incorporating elements of the predator–prey equation, we develop a set of fully symmetrical differential equations to model neural activities, replacing conventional neurons with systems governed by these equations.

Figure 1a illustrates the logical structure underpinning the differential equations, while Figure 1b presents their mathematical formulation. According to the Wuxing theory, the world is composed of five distinct elements that interact through generative and inhibitory relationships, forming a completely symmetrical logical framework. Building on this conceptual basis and incorporating the predator–prey equation, we derived the equations represented in Figure 1b.

In order to better describe similar equations, we use the following general formula to describe the original system of equations:

$${\displaystyle \frac{dE}{dt}}=K_{1}E-K_{2}E-K_{3}EE$$

(1)

In order to represent elements in different orders, we define $E=\{J,S,M,H,T\}$, $K_1=\{k_{11},k_{12},k_{13},k_{14},k_{15}\}$, $K_2=\{k_{21},k_{22},k_{23},k_{24},k_{25}\}$, and $K_3=\{k_{31},k_{32},k_{33},k_{34},k_{35}\}$, so the Wuxing differential equation above can be expressed as

$${\displaystyle \frac{d\stackrel{0}{E}}{dt}}=\stackrel{0}{K_1}\stackrel{-1}{E}-\stackrel{0}{K_2}\stackrel{0}{E}-\stackrel{0}{K_3}\stackrel{0}{E}\stackrel{-2}{E}$$

(2)

The number above the variable indicates the offset of the loop: $\stackrel{-1}{E}=\{T,J,M,S,H\}$.

2.2. Fixed Points of Differential Equations

In chaos theory, the fixed point of a differential equation is a critical property, as it determines the equilibrium state of the system. In Equation (2), three distinct sets of parameters are involved. To analytically determine the fixed point of the equation, it is necessary to simplify the parameters. We assume that the parameters within each of the three sets—denoted as $K_1$, $K_2$, and $K_3$—are equal, allowing for us to analytically derive the fixed point $B_0$ of the equation.

$$B_0={\displaystyle \frac{K_1-K_2}{K_3}}$$

(3)

Equation (3) plays a central role in adjusting the differential equation. Through this equation, we can modify the fixed point of the system. Even when the parameters in $K_1$, $K_2$ and $K_3$ no longer satisfy the condition of equality, the adjustment method remains effective. Furthermore, Equation (3) establishes the relationship between the system’s parameters and the fixed point. For instance, increasing $K_1$ and decreasing $K_3$ produces the same effect on the fixed point.

2.3. Signal Propagation and Network Structure

In our study, we regard the state where the differential equation is at a fixed point as the zero state of the system. Therefore, we can derive the input equation of the system:

$${\displaystyle \frac{d\stackrel{0}{E(t)}}{dt}}=\stackrel{0}{K_1}\stackrel{-1}{E(t)}-\stackrel{0}{K_2}\stackrel{0}{E(t)}-\stackrel{0}{K_3}\stackrel{0}{E(t)}\stackrel{-2}{E(t)}+Input(t)$$

(4)

In Equation (4), $Input\left(t\right)$ is the input signal. When the input is not zero, the system will deviate from its original fixed point. We consider this offset as the output signal caused by the input signal, and the relevant calculation method is as follows:

$$D(t)=E(t)-B_0$$

(5)

In Equation (5), $D\left(t\right)$ is the output signal, which reflects the magnitude of the system’s deviation from the fixed point. $E\left(t\right)$ is the real-time value of the Wuxing element, $B_0$ is the fixed point of the system. When we have both input and output signals, we can further define the network links of the system.

As seen in Figure 2, we built a four-layer network with three inputs and three outputs. The connections between neurons in the figure are uniformly random. The signal propagated in the forward network is marked as $D\left(t\right)$, and the signal propagated in the backward network is marked as $\widehat{D}(t)$. Similar to the previous example, $\widehat{D}(t)$ is determined by the backpropagation element value $\widehat{E}(t)$ and the backpropagation fixed point ${\widehat{B}}_0$.

$$\widehat{D}(t)=\widehat{E}(t)-{\widehat{B}}_0$$

(6)

3. Training Wuxing Neural Network

In this section, we will introduce how to use differential equations for signal propagation and achieve point-to-point parameter adjustment.

3.1. Training Theory

In neural network training, the traditional backpropagation algorithm has been highly successful. Despite ongoing doubts regarding its biological plausibility, no alternative methods have yet been able to match the accuracy achieved by backpropagation. The key advantage of the backpropagation algorithm lies in its point-to-point training approach, which establishes a one-to-one relationship between each parameter and the output. Therefore, when considering the development of a new training method, it is crucial to preserve this point-to-point relationship. From a mathematical perspective, this relationship embodies a form of symmetry, but maintaining this symmetry in practice is not straightforward.

Due to various practical constraints, the equations we derive often lose this symmetry. To address this, we begin with the principle of symmetry and construct symmetric differential equations, which ensure that the system remains symmetric and, consequently, reversible. This reversibility allows for us to trace the cause-and-effect relationships in the system by reversing the signal propagation, enabling us to study the influence of parameters through signal flow. In essence, we replace the reverse differentiation process with the use of differential equations. For example, consider the differential system dX = aY. To study the effect of the parameter a on the outcome, we can establish an inverse differential system dY = aX and compare the results between the two systems to analyze the impact of a on the output.

3.2. Training Method

In Figure 1a, we show the logical relationship of the five elements. For example, water can generate wood because plants can grow with water, and metal can restrain wood because an axe made of metal can cut down trees. Based on this logical relationship, we derive the third equation $dM/dt=k_{13}S-k_{23}M-k_{33}MJ$ in Figure 1b. If we reverse this causal relationship, it becomes such that wood can generate water and wood can restrain metal; similarly, fire can generate wood, and soil restrains wood. When all causal relationships are totally reversed, we can derive the logical structure in Figure 3a. Although this structure is the result of reversing Figure 1a, their topological link relationship has not changed. All the equations obtained in Figure 3b are consistent with the equations in Figure 1b in mathematical structure, and only the order of elements has changed.

According to our definition, the system’s signals can propagate in both directions. Based on the system’s topological structure, we define the inverse equation containing signal propagation term:

$${\displaystyle \frac{d\stackrel{0}{E(t)}}{dt}}=\stackrel{1}{K_1}\stackrel{1}{E(t)}-\stackrel{0}{K_2}\stackrel{0}{E(t)}-\stackrel{2}{K_3}\stackrel{0}{E(t)}\stackrel{2}{E(t)}+Input(t)$$

(7)

Equations (4) and (7) are symmetrical to each other. In Equation (7), the orders of $K_1$, $K_2$, and $K_3$ parameters are also adjusted. This is because $K_1$, $K_2$, and $K_3$ parameters are actually parameters located between two elements (see Figure 1a and Figure 3a). Therefore, when the signal propagation direction changes, the order of parameters must also change.

Equations (4) and (7) seem to be very different, but they have one thing invariant, that is, the connection between the two elements. This is the core method of training in this paper, which leads to a strong correlation between the forward propagation signal and the reverse propagation signal. This correlation is the core of adjusting the system parameters. In the traditional backpropagation training method, people use the chain rule to find the partial derivative of the parameter to the error to adjust the system, and this derivation process is used to find the correlation between the parameter and the signal. Therefore, if we do not use the backpropagation method of derivation, then we must first explain how our method preserves the correlation of the system, and secondly how to apply this correlation to the system and achieve the desired results by changing the parameters.

More generally speaking, finding partial derivatives also involves looking for a reversible causal relationship. If the forward input signal and the reverse input signal are located at the two ends of the system, then according to the propagation of the two signals, the signal connection can be established at different nodes. Depending on the way the coefficients are adjusted, different types of connections can be established within the system.

Through this reversible causal relationship, we can achieve many functions. The following is an example: As seen in Figure 2, we built a four-layer network with three inputs and three outputs. The signal transmitted in the forward network is marked as $D\left(t\right)$, and the signal transmitted in the reverse network is marked as $\widehat{D}(t)$. Therefore, we can define an output variable $Leb$ within time $T$ and take the largest $Leb$ component as the output result.

$$Leb={\displaystyle \frac{1}{T}}{\displaystyle {\int }_0^{T}D(t)dt}$$

(8)

Assuming that the $P_{th}$ component of $Leb$ should be the largest, according to our previous research, the input signal for backpropagation can be defined as follows [24]:

For the $P_{th}$ component, the adjustment error is

$$Erro{r}_p=\left\{\begin{array}{l}targtet1-Le{b}_p(ifLe{b}_p<target1)\\ 0(ifLe{b}_p>target1)\end{array}\right.$$

(9)

For other component, the adjustment error is

$$Erro{r}_{other}=\left\{\begin{array}{l}targtet2-Le{b}_{other}(ifLe{b}_{other}>target2)\\ 0(ifLe{b}_{other}<target2)\end{array}\right.$$

(10)

In these equations, $target1$ and $target2$ represent two predefined target values, where $target1$ is the larger value and $target2$ is the smaller one. This method will make the value of the $P_{th}$ component larger after training, while the others will be smaller, allowing for the system to achieve a higher accuracy rate.

Similar to before, $\widehat{D}(t)$ is determined by the backpropagated element value $\widehat{E}(t)$ and the backpropagated fixed point ${\widehat{B}}_0$.

$$\widehat{D}(t)=\widehat{E}(t)-{\widehat{B}}_0$$

(11)

Assuming that in the forward network of Figure 2, only $A_{12}$ and $A_{13}$ have input signals, then the signal propagation diagram is shown in Figure 2a, where only the paths marked in red have signal propagation. When the signal reaches the output end, it can be compared with the set target. If the comparison is successful, no error signal is returned. If the comparison is unsuccessful, the corresponding error signal is returned. In Figure 2a, we assume that only the result of $A_{43}$ does not meet the requirements, so in Figure 2b, only $A_{43}$ has an input error signal. Based on the forward and reverse signals propagated within time $T$, we can define a correlation variable $G_1$.

$$G_1={\displaystyle {\int }_0^{T}D(t)dt}•{\displaystyle {\int }_0^T\widehat{D}(t)dt}$$

(12)

In Equation (12), $G_1$ is the product of the forward signal integral and the backward signal integral, which reflects the difference between the forward and backward signals. If two signals have opposite signs, it indicates that the parameters at the corresponding position should be reduced. If the signs are the same, it indicates that the parameters at the corresponding position should be increased.

Since $G_1$ may exceed a certain limit, we use the inverse tangent function (other similar functions are also possible) to limit it and obtain $G_2$.

$$G_2=atan(G_1*kt)/kt$$

(13)

$kt$ is the adjustment parameter, and $G_2$ is the adjusted correlation value. The parameter can be adjusted based on $G_2$.

$$K_{3\_new}=K_{3\_old}•exp(-G_2)$$

(14)

4. Distributed PID Control

In this section, we will discuss how to implement distributed PID control in closed systems to address parameter redundancy issues encountered in neural network training.

4.1. Redundant Parameter Adjustment

In the Wuxing neural network, there are three sets of parameters $K_1$, $K_2$, and $K_3$; in previous studies, we only gave the method to adjust $K_3$ because the method is not reusable. The following is an example trained on the MNIST dataset: The model has 784 inputs, 10 outputs, and a total of 6 layers. The number of neurons in each layer is {784, 839, 283, 96, 32, 10}, of which the first and last layers are fully connected, and all interfaces have inputs or outputs. The initial parameters of the model are $K_1$ = {1, 1, 1, 1, 1}; $K_2$ = {0.5, 0.5, 0.5, 0.5, 0.5}; and $K_3$ = {0.5, 0.5, 0.5, 0.5, 0.5}. We use the training method in Section 3. One is to adjust only $K_3$, and the other is to adjust $K_1$ and $K_3$ at the same time. The method of adjusting K₁ can refer to Formula (11). Combined with the relationship in Equation (1), we can get:

$$K_{1\_new}=K_{1\_old}•exp(G_2)$$

(15)

In Figure 4, Case 1 only adjusts $K_3$, and Case 2 adjusts $K_1$ and $K_3$ at the same time. The accuracy of Case 1 improves more slowly, but is also more stable, while the improvement of Case 2 is rapid, but has greater volatility. In this case, simply relying on the same method to adjust two different parameters will not produce the ideal results imagined. This is because the system is strongly coupled. According to Equation (3), adjusting two parameters at the same time actually has a similar effect to adjusting only one parameter, and cannot achieve the ideal purpose. At this time, we need to look at the adjustment problem from the perspective of the system.

4.2. Typical PID Control Method

In the automatic control system, PID control is the absolute leader. PID control adjusts the input by feeding back the error signal and finally achieves the ideal control result.

Figure 4 illustrates a typical PID control process. Assuming the input signal represents the target value we set, the corresponding error signal is derived by comparing the output signal with the input signal. The error signal is then processed through proportional, integral, and derivative control, before being re-input into the system. This results in an adjusted signal. After several iterations of parameter adjustments, the desired outcome is typically achieved.

In automatic control systems, the PID algorithm has achieved great success. Currently, more than 80% of industrial systems use PID control, and all university courses on control theory must also involve PID control. The idea of PID control is so simple and so effective that the development and application of other control theories seem weak. Some people even think that control theory has withered because we cannot find a new theory to challenge the absolute dominance of PID control. However, if we study PID control theory carefully, we will find that the PID method is not perfect. So, let us start with a simple but profound question: why do we need a feedback process?

The traditional perspective is that the original system is an open-loop system, requiring a feedback loop to form a closed-loop system. According to this view, any system, regardless of its initial configuration, is considered open-loop. This contradicts the definition of a closed-loop system. The underlying issue, however, is that the original system is irreversible, preventing us from obtaining the appropriate adjustment signal through backpropagation based on the system’s causal logic. As a result, an additional feedback loop is needed to complete the reverse process.

Nevertheless, Figure 5 provides a valuable insight: to effectively adjust the parameters within a closed system, adjustments must be made simultaneously along three different directions to achieve optimal results. This explains why, in Figure 3, even though two parameters were adjusted simultaneously, satisfactory results were not obtained. Therefore, the key to resolving the system training challenge lies in implementing a distributed PID control strategy within a distributed system.

4.3. Distributed PID Control Strategy

Traditional PID control is based on modeling the overall system, which allows for system control without the need to analyze its intricate details. Instead, it suffices to recognize the system as causal, thus bypassing the need for complex analysis. However, this approach has its limitations. When PID control is applied to the entire system, it sacrifices strong generalization capabilities. Moreover, a closed system implies that any external input is merely a projection of an external state within the system. From a mathematical standpoint, a closed system is considered complete, yet this does not imply that the system’s output fully captures all relevant information. As a result, additional systems must be integrated to expand the system’s state space. This concept is central to our approach of replacing digital neurons with systems in this study.

To implement PID control within a group of differential equations, we must adapt the PID method accordingly. This differs from traditional PID control because we are working within a closed system, necessitating an approach that accounts for the specific characteristics of such systems rather than simply applying open-loop system principles [27]. In this closed system, the parameters of all groups are strongly coupled (see Equation (3)). Adjusting one set of parameters is effectively equivalent to modifying the others. Therefore, to break this strong coupling structure, different strategies must be applied to different parameter groups.

Moreover, applying distributed PID control strategies in neural network training differs significantly from their use in traditional control systems. In neural networks, PID strategies are primarily employed to enhance accuracy and training speed, rather than to reduce oscillations or overshooting. Additionally, unlike in conventional control systems, PID strategies in neural networks cannot monitor system states in real time. This is because the forward and backward propagation processes are separated, making it impossible to obtain real-time feedback. Instead, training effectiveness must be evaluated indirectly through accuracy curves rather than direct real-time monitoring.

Given that we have three distinct sets of parameters, we assign different control strategies to each. Specifically, we apply the integral control method to $K_1$, the differential control method to $K_2$, and the proportional control method to $K_3$.

For $K_1$, an integral control method is adopted

$$G_{1\_k1}={\displaystyle \sum _{i=1}^{kn}{\displaystyle {\int }_0^T{D}_i(t)dt}}•{\displaystyle \sum _{i=1}^{kn}{\displaystyle {\int }_0^T{\widehat{D}}_i(t)dt}}$$

(16)

$$G_{2\_\_k1}=atan(G_{1\_k1}*kt)/kt$$

(17)

$$K_{1\_new}=K_{1\_old}•exp(G_{2\_k1})$$

(18)

As we can see, a similar method is adopted to adjust $K_1$. The difference is that the calculation method of $G_1$ is different. In the integration strategy, we add all the signals in a single neuron together. $kn$ is the number of elements in a single neuron. This is how the integration strategy is implemented in a closed system.

For $K_2$, a differential control method is adopted:

$$G_{1\_k2}={\displaystyle {\int }_0^{T}D(t)dt}•{\displaystyle {\int }_0^T\widehat{D}(t)dt}•inputnode$$

(19)

$$G_{2\_\_k2}=atan(G_{1\_k2}*kt)/kt$$

(20)

$$K_{2\_new}=K_{2\_old}•exp(-G_{2\_k2})$$

(21)

In Equation (19), $inputnode$ is a variable. If this node is an input node in the forward propagation process, then this variable is equal to 1; otherwise, it is equal to 0. Because in the system, the generation of the signal is always caused by the input node, from the causal logic, the input node is in front of other nodes, which is similar to the differential control method.

For $K_3$, a proportional control method is adopted:

$$G_{1\_k3}={\displaystyle {\int }_0^{T}D(t)dt}•{\displaystyle {\int }_0^T\widehat{D}(t)dt}$$

(22)

$$G_{2\_\_k3}=atan(G_{1\_k3}*kt)/kt$$

(23)

$$K_{3\_new}=K_{3\_old}•exp(-G_{2\_k3})$$

(24)

The proportional control method is the easiest to understand. According to Equation (3), changing $K_3$ has the most direct impact on the fixed point. Therefore, we use the method of changing $K_3$ as the proportional control strategy. Although we designed three different control strategies, their efficiencies are different due to the network structure and system structure, and this design method is not the only one. More research is needed to determine their adjustment methods.

4.4. Results

Figure 6 presents the accuracy curves under different training strategies. In Figure 6a, we apply single-strategy training, where each time only one parameter ($K_1$, $K_2$, or $K_3$) is adjusted using one of the three control methods: integral, derivative, or proportional. The results show that the best performance is achieved when using the integral method to adjust $K_1$. According to Equation (16), the integral strategy provides the largest adjustment amplitude for $K_1$, which accelerates convergence. In contrast, the derivative method yields the poorest performance due to two main reasons: it adjusts only a subset of parameters (as seen in Equation (22)) and suffers from inherent instability, leading to slower and less stable training [28].

Figure 6b shows the results when two strategies are combined simultaneously, including $K_1$ with $K_2$, $K_1$ with $K_3$, and $K_2$ with $K_3$. Compared with the single-strategy training in Figure 6a, these combined strategies significantly improve both accuracy and convergence speed. For example, while the single-strategy approach requires about 12 iterations to reach 50% accuracy, the combined strategy achieves the same result in approximately 6 iterations. This demonstrates the effectiveness of the mixed-strategy approach in accelerating training.

It is worth noting that the system’s maximum accuracy in all cases stabilizes around 50%. Our analysis indicates that this limitation is more likely due to the structure and connectivity of the neural network rather than the training strategy itself. In terms of computing speed, biological neural networks are far inferior to mathematical neural networks, as mathematical neural networks can complete calculations in minutes, while biological neural networks take hours. Therefore, in our future work, we will optimize the network structure and accelerate the computing speed.

Importantly, traditional PID control is a dynamic method operating in a closed-loop system. In contrast, the “distributed PID control” employed in this study draws on PID concepts theoretically. Neural network training is an intermittent process, consisting of forward and backward propagation phases. To reduce potential oscillations, conservative learning rates are used. As a result, the training process does not exhibit the oscillatory behavior typical of classical PID-controlled systems, which is also not desired in our case.

The experiments were conducted on a computing platform equipped with two Intel Xeon P8124 processors (18 cores @ 3.0 GHz each), 96 GB of RAM, and running MATLAB 2024a on Ubuntu.

To enhance the comparison and validate the robustness of our conclusions, we additionally employed the Fashion-MNIST dataset as another test set, using exactly the same parameters as those used for MNIST. The results in Figure 7 show that similar conclusions can be drawn: among the single-strategy approaches, the integral strategy achieved the best training performance; among the dual-strategy combinations, the use of both integral and proportional strategies yielded the best results. This outcome is consistent with the results observed on the MNIST dataset.

Moreover, this finding aligns with many other studies that tested both MNIST and Fashion-MNIST, where consistent performance across datasets was also reported—indicating that our training method, like those used in other research, exhibits generalizability. However, unlike the results on MNIST, the training curves on Fashion-MNIST showed slight oscillations, suggesting that the learning rate may need to be adjusted according to the characteristics of the dataset.

5. Summary

In this paper, we present a novel training method for the Wuxing neural network, incorporating innovations in both mathematics and biology. At the mathematical level, we replace the traditional chain derivation with differential equations to solve the one-to-one correspondence between parameters and outputs; at the biological level, we introduce the concept of “instinctive design” to limit the adjustment range during training to only act on a single neuron, thereby enhancing the biological interpretability of the model.

On this basis, this paper further introduces a distributed PID control strategy to apply the classical PID control theory to the individual neuron level. Experimental results show that this method not only provides a new path for neural network training but also provides a new perspective for the development of automatic control theory.

We further expand the theoretical basis of this method and advocate replacing the function of a single neuron in the traditional sense with a “system as a whole”. We believe that a closed system is self-consistent, and its internal integrity enables it to fully respond to the characteristics of external signals; however, this response is often not directly observable from the outside. Therefore, it is necessary to interconnect multiple systems and improve the generalization ability of the system through distributed PID control. This idea constitutes our core understanding of the neural network structure and training mechanism.

The goal of this study is to establish a new set of neural network structures with corresponding training methods and strive to bridge the gap between biological neural networks and mathematical neural networks. The strategy we proposed effectively solves the problem of parameter setting and training method selection in a closed system. Specifically, by using different PID control strategies for different parameter groups, the inefficiency of training caused by a unified strategy can be avoided. Computational experiments show that using two PID strategies for training at the same time improves both accuracy and training speed compared to a single strategy. Although the accuracy of the current model has not yet reached the ideal state, we have prepared a number of improvement plans, and the relevant content will be further explored in subsequent research.