Abstract
Multilevel thresholding image segmentation plays a crucial role in various image processing applications. However, achieving optimal segmentation results often poses challenges due to the intricate nature of images. In this study, a novel metaheuristic search algorithm named Weighted Chimp Optimization Algorithm with Fitness–Distance Balance (WChOA-FDB) is developed. The algorithm integrates the concept of Fitness–Distance Balance (FDB) to ensure balanced exploration and exploitation of the solution space, thus enhancing convergence speed and solution quality. Moreover, WChOA-FDB incorporates weighted Chimp Optimization Algorithm techniques to further improve its performance in handling multilevel thresholding challenges. Experimental studies were conducted to test and verify the developed method. The algorithm’s performance was evaluated using 10 benchmark functions (IEEE_CEC_2020) of different types and complexity levels. The search performance of the algorithm was analyzed using the Friedman and Wilcoxon statistical test methods. According to the analysis results, the WChOA-FDB variants consistently outperform the base algorithm across all tested dimensions, with Friedman score improvements ranging from 17.3% (Case-6) to 25.2% (Case-4), indicating that the FDB methodology provides significant optimization enhancement regardless of problem complexity. Additionally, experimental evaluations conducted on color image segmentation tasks demonstrate the effectiveness of the proposed algorithm in achieving accurate and efficient segmentation results. The WChOA-FDB method demonstrates significant improvements in Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Feature Similarity Index (FSIM) metrics with average enhancements of 0.121348 dB, 0.012688, and 0.003676, respectively, across different threshold levels (m = 2 to 12), objective functions, and termination criteria.
1. Introduction
Image segmentation is a fundamental process in computer vision and image processing that aims to partition an image into distinct and meaningful regions or objects. This division enables a computer to understand and analyze the visual content within an image by identifying and categorizing different entities. Essentially, image segmentation breaks down an image into its constituent parts, allowing for more detailed analysis and interpretation. The significance of image segmentation lies in its ability to provide a more detailed understanding of visual data. By identifying individual objects or regions within an image, segmentation facilitates various applications, including object recognition, scene understanding, and image editing. In an image recognition system, segmentation is an important stage that helps to extract the object of interest from an image. In this context, segmentation is extensively used in medical imaging. For example, in tumor/lesion detection, segmentation helps to isolate tumors/lesions from surrounding healthy tissue, facilitating accurate diagnosis and tailored treatment planning [1,2]. In autonomous driving, image segmentation is critical for scene understanding and safe navigation [3]. Also, segmentation is essential for monitoring crop health in agriculture and managing resources more effectively [4]. By segmenting fields into different categories based on vegetation index or soil moisture levels, farmers can optimize irrigation, fertilization, and harvesting strategies.
Despite its importance, image segmentation poses several challenges. Variability in illumination, complex object boundaries, and the presence of noise make the segmentation process more complex. Additionally, scalability to handle diverse types of images and adaptability to different contexts are ongoing challenges in the field. Researchers are exploring innovative approaches and algorithms to address these issues and enhance the precision and efficiency of image segmentation. For example, symmetry is an important cue for machine perception that involves high-level knowledge of image components, so it was used to improve region-based image segmentation performance [5]. For clustering-based image segmentation, the membership values of points to different clusters were computed based on point symmetry-based distance [6]. By adding symmetric masks in several layers, deep convolutional symmetric neural networks were designed for image segmentation [7].
In the context of multilevel image analysis, segmentation becomes even more critical. Multilevel segmentation involves the identification and categorization of objects at multiple levels of granularity within an image. This is essential for applications such as medical image analysis, satellite imagery interpretation, and industrial inspection. Achieving accurate multilevel segmentation often requires sophisticated algorithms that can handle the complexities associated with diverse image datasets. Accurate image segmentation plays a pivotal role in various domains, contributing significantly to the advancement of computer vision and image processing. The precision and reliability of segmentation techniques have far-reaching implications across different applications.
Image thresholding techniques are widely used in image segmentation due to their simplicity and effectiveness. These methods utilize predefined threshold values to segment specific objects, features, or information within an image. There are two methods for thresholding-based image segmentation [8]. Bilevel thresholding is the process of partitioning an image into two classes using a predetermined threshold value: the gray levels below the threshold value are categorized into one class, while the gray levels greater than the threshold value are categorized into another class. In multilevel thresholding, the image is subdivided into multiple classes using a set of predefined threshold values. That is, these thresholds are used to identify discrete clusters within the image. For color images, segmentation could be achieved via the utilization of a separate threshold value for each color channel (red, green, and blue). The employment of multilevel thresholding for each channel tends to yield improved outcomes in terms of image segmentation accuracy. However, this approach significantly increases computational complexity. Due to this computational complexity, metaheuristic optimization algorithms are used to solve the multilevel thresholding image segmentation problem.
Several approaches have been proposed to determine the optimum threshold values from image histograms. The most frequently used methods are Kapur’s entropy [9] and Otsu’s criterion (between class variance) [10]. Among the thresholding algorithms, Kapur’s entropy outperforms other functions [11]. Kapur’s entropy determines the threshold values that maximize the histogram entropies of segmented classes using the probability distribution of gray levels. Otsu’s method; on the other hand, selects the threshold values that maximize the variance among the gray-level classes. In color image segmentation, threshold values must be determined for all color channels (red, green, and blue) separately.
Thresholding approaches successfully and effectively solve bilevel segmentation problems, but the calculation complexity and computational cost increase exponentially for multilevel segmentation problems. Therefore, in recent years, researchers have proposed the use of metaheuristic search (MHS) algorithms to reduce computational complexity and increase segmentation performance [12,13,14]. Metaheuristic optimization algorithms can perform efficient search in a solution space without having difficulty with local optimums. However, multilevel thresholding image segmentation becomes a complex operation due to the multimodality of the histogram. Additionally, each image histogram and the number of threshold levels are considered as separate problems. Because it is difficult to find an algorithm suitable for many optimization problems, several metaheuristic algorithms have been developed in the literature.
This study introduces a novel approach to multilevel thresholding image segmentation: Weighted Chimp Optimization Algorithm based on Fitness–Distance Balance (WChOA-FDB). Drawing inspiration from the intelligent group hunting behavior of chimps, this metaheuristic optimization algorithm directly overcomes the challenges. WChOA-FDB operates by delicately balancing fitness and distance within the search space, enabling it to navigate effectively and avoid traps of local optima. Furthermore, through the incorporation of a novel weighting scheme, WChOA-FDB further enhances its ability to find optimal solutions. The performance of the proposed algorithm was evaluated using 10 benchmark functions (IEEE CEC 2020) of different types and complexity levels. The search performance of the algorithm was analyzed using the Friedman and Wilcoxon statistical test methods.
This research also investigates the complexities of multilevel segmentation and meticulously details the theoretical foundations, implementation specifics, and evaluation of WChOA-FDB on benchmark datasets. In this paper, we applied WChOA-FDB to perform Multilevel Thresholding Image Segmentation. To evaluate WChOA-FDB’s performance, we employed Kapur’s entropy and Otsu’s between-class variance methods. The performance of WChOA-FDB has been compared with other well-known metaheuristic algorithms, namely Artificial Bee Colony (ABC) [15], Cuckoo Search (CS) [16], Grey Wolf Optimizer (GWO) [17], Harris Hawks Optimization (HHO) [18], Moth Flame Optimization (MFO) [19], Sine Cosine Algorithm (SCA) [20] and Salp Swarm Algorithm (SSA) [21].
Various problems are encountered when studies in the field of multilevel thresholding image segmentation with MHS algorithms are examined. In multilevel image segmentation studies, the number of iterations is generally used as the termination criterion, and these iteration numbers vary. For example, one study can use 100 iterations while the other 300 iterations as termination criteria. So, it is unknown whether the method is still successful for more iterations. In summary, the termination criterion has a significant effect on the results of the optimization process. The value of this parameter can change the quality of the solutions and the algorithms that find the best solutions. Therefore, in this study, the performance of the proposed algorithm was evaluated for two different termination criteria. To compare the algorithms fairly, the maximum number of objective function evaluations, maxFEs = 500 × m (m: number of threshold levels), and maxFEs = 1000 × m were used as termination criteria. Another problem in multilevel thresholding image segmentation literature is the number of threshold levels used in the segmentation of images. In most of the studies, a low number of threshold levels (2, 3, 4, 5) were used. Therefore, it is not known how the algorithm will perform when a medium or high number of threshold levels is used. In this study, segmentation of 10 images with m = 2, 4, 6, 8, 10, 12 levels were performed with the proposed and competitor algorithms.
The results showcase the algorithm’s higher performance compared to existing methods, demonstrating its potential in multilevel image segmentation across a wide range of applications. By harnessing the power of WChOA-FDB, we pave the way for a future where machines can extract deeper insights and unlock greater understanding from the vast realm of visual information. The main contributions of this study are given below.
- Methodological Innovation: This research presents the first application of the Weighted Chimp Optimization Algorithm (WChOA) to multilevel image segmentation, enhanced through integration with the Fitness–Distance Balance (FDB) method to develop WChOA-FDB, a novel hybrid metaheuristic optimization approach.
- Comprehensive Experimental Framework: The proposed WChOA-FDB algorithm was systematically evaluated through rigorous experimentation encompassing ten IEEE CEC 2020 benchmark functions of varying complexity, multilevel segmentation scenarios ranging from low to high threshold levels (m = 2, 4, 6, 8, 10, 12), comparative analysis against seven established metaheuristic algorithms, and assessment under different computational constraints (500 × m and 1000 × m maximum function evaluations).
- Empirical Validation and Performance Assessment: The efficacy of the proposed approach was thoroughly validated through multi-dimensional evaluation criteria, incorporating both optimization performance metrics (fitness function values) and established image quality assessment measures (Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Feature Similarity Index (FSIM)), demonstrating superior performance across diverse segmentation complexity levels.
The rest of the paper is organized as follows. In Section 2, a comprehensive literature review on metaheuristic-based multilevel thresholding image segmentation is presented. The multilevel thresholding problem is clarified, and the proposed method is explained in Section 3. The experimental studies and findings are given in Section 4, and the results are discussed in Section 5.
2. Related Work
Image segmentation, particularly multilevel thresholding, has attracted significant attention in recent years due to its wide range of applications in various fields such as medical imaging, remote sensing, and object recognition. Numerous metaheuristic algorithms have been employed to address the challenges associated with multilevel thresholding, aiming to improve segmentation accuracy and computational efficiency. In this section, we review some of the prominent works in the literature that have explored the application of metaheuristic algorithms in multilevel thresholding image segmentation.
Multilevel image thresholding studies based on meta-heuristic optimization can be divided into two groups. The studies in the first group include the application of an existing MSA to the solution of the problem and its comparison with the competing algorithms. The studies in the second group aim to develop a new algorithm by modifying an existing MSA or hybrid MSA and thus increase the image segmentation performance. However, each algorithm has its limitations. Therefore, researchers try to increase the performance and reduce the complexity by modifying the method by changing the search process strategy in the algorithm or by developing hybrid methods by using the algorithms together.
Su et al. [22] conducted a study on the application of the Artificial Bee Colony algorithm (ABC) and its improved version (CCABC) for the segmentation of COVID-19 X-ray images. They introduced an enhanced ABC algorithm, CCABC, which incorporates horizontal and vertical search mechanisms to improve the optimization performance. Additionally, they proposed a multilevel thresholding image segmentation method based on CCABC to enhance the effectiveness of the segmentation process. The study compared CCABC with 15 algorithms using 30 benchmark functions to demonstrate its performance, showing that CCABC outperforms ABC and other similar algorithms, indicating its ability to find optimal solutions and improve image segmentation accuracy. Liu et al. [23] employed a chimp-inspired remora optimization algorithm to determine optimal threshold values, thereby reducing computational costs and enhancing segmentation accuracy. They used the cross-entropy method for image segmentation. Sharma et al. [24] introduced a modified firefly algorithm with Kapur’s, Tsalli’s, and Fuzzy entropy methods and between-class variance for optimal thresholding. The authors also employed an opposition-based learning method for initializing the candidate solution population and incorporated Levy flight and local search techniques to determine optimal threshold values for multilevel image segmentation. H. Houssein et al. [25] introduced a new optimization algorithm called Improved Gray Wolf Optimization (IGJO) for tumor identification in medical images. The robustness and accuracy of IGJO were tested on different engineering and real-world problems with unknown search spaces. Gharehchopogh et al. [26] introduced an improved African Vultures Optimization Algorithm (AVOA) for multilevel thresholding image segmentation. They utilized Quantum Rotation Gate (QRG) and Association Strategy (AS) mechanisms to enhance the performance of AVOA by increasing diversity and optimizing local trap escapes. Kumar et al. [27] combined the Cuckoo Search Algorithm (CSA) with Recursive Minimum Cross Entropy (R-MCE) to obtain the best threshold values for crop image segmentation. The proposed technique was tested on 20 crop images and demonstrated improved accuracy and segmented image quality compared to other algorithms. Agrawal et al. [28] proposed a Dominant Color Component and Adaptive Whale Optimization Algorithm (DCC-AWOA) method for multilevel thresholding color image segmentation. They compared their proposed technique with existing approaches. They utilized entropic and non-entropic objective functions, such as Kapur’s entropy and edge magnitude-based thresholding. Tan et al. [29] proposed an Improved Cuckoo Search algorithm (ICS) for multilevel color image thresholding based on modified fuzzy entropy. They addressed the time-consuming nature of traditional exhaustive search methods for optimal multilevel thresholds in color images. The ICS incorporates two modifications to enhance the performance of the standard Cuckoo Search Algorithm: an adaptive control parameter mechanism and a hybrid search strategy. The study compared the ICS with six other optimization algorithms and demonstrated its high performance in terms of objective function value, convergence speed, and parametric statistical tests.
Houssein et al. [30] integrated the Improved Heap-Based Optimizer (IHBO) with opposition-based learning to improve the convergence rate and local search efficiency for multilevel thresholding image segmentation. The study evaluates the IHBO-based method on the CEC’2020 test suite and compares it against seven well-known metaheuristic algorithms, demonstrating its effectiveness in solving complex multilevel thresholding problems. The authors provide a comprehensive analysis of the IHBO algorithm’s performance using the Otsu method as the objective function, presenting graphical and statistical results for benchmark images. Wang et al. [31] proposed an improved Golden Jackal Optimization (HGJO) for multilevel thresholding image segmentation. They conducted experiments using the CEC2022 test suite to measure the performance of their algorithm, comparing it with other existing algorithms. The results showed that the proposed HGJO algorithm outperformed the other algorithms in terms of overall performance, demonstrating its effectiveness in reducing image complexity while preserving original features. Abualigah et al. [32] proposed a hybrid Marine Predators Algorithm (MPA) with the Salp Swarm Algorithm (SSA) (MPASSA) to determine the optimal multilevel threshold image segmentation. They employed various benchmark images to validate the proposed algorithm’s performance. The results showed that the proposed MPASSA outperformed other well-known optimization algorithms published in the literature. Eisham et al. [8] proposed a hybrid algorithm named the Spotted Hyena-based Chimp Optimization Algorithm (SSC), which combines the sine-cosine function and the attacking strategy of Spotted Hyena Optimizer (SHO) for solving engineering problems. This algorithm was designed to address the challenges of sluggish convergence speed and entrapment in local optima in high-dimensional problem-solving. Swain et al. [33] introduced a novel objective function named Differential Exponential Entropy (DEE) and a new method called the Equilibrium-Cuckoo Search Optimizer (ECSO) for multilevel threshold selection in color satellite images. They compared the performance of their proposed technique with traditional methods such as Otsu’s between-class variance and Kapur’s entropy. The results showed that the proposed technique outperformed the traditional methods in terms of image segmentation quality. Thomas et al. [34] proposed a novel segmentation model, Harris Hawks Optimizer (HHO) for MR brain images, particularly for Alzheimer’s disease. The model integrates multilevel thresholding with an optimization algorithm to select optimal threshold values for segmentation. They tested the model on MR brain images of patients with Alzheimer’s disease and found that they achieved satisfactory results in terms of performance metrics. Additionally, they discussed various segmentation approaches and machine learning models for Alzheimer’s disease detection, emphasizing the significance of accurate segmentation in healthcare applications.
Renugambal et al. [35] proposed a hybrid Sine-Cosine Crow Search Algorithm (SCCSA) to improve multilevel image segmentation efficiency. They evaluated the hybrid algorithm on 12 standard image sets and compared its performance with other state-of-the-art algorithms such as SCA, CSA, and ABC. The experimental results showed that the proposed SCCSA consistently outperformed the other algorithms in terms of various metrics. Additionally, they conducted a Wilcoxon test to detect significant differences between the proposed algorithm and the other algorithms, and the findings indicated that the SCCSA succeeded in outperforming the other well-known algorithms. Akay et al. [36] conducted a study on nature-inspired optimization algorithms for multilevel thresholding image segmentation. They introduced modifications to the Teaching–Learning-Based Optimization Algorithm (TLBO) to improve its performance, including the use of Levy flight equations and adding an indicator of the fertile area to the framework strategy. A modified version of the Teaching–Learning-Based Artificial Bee Colony (MTLABC) was proposed in this work. The Friedman test and the Wilcoxon signed-rank test were used to determine whether there was a significant difference between the proposed algorithm and other optimization algorithms. Akan et al. [37] proposed a multilevel image thresholding approach using the Battle Royal Optimization (BRO) algorithm. The authors compare the performance of the BRO algorithm with four other optimization algorithms (AMO, PSO, BFO, and GA) on ten benchmark images. The results show that the BRO algorithm is stable and provides satisfactory results, ranking first in terms of the standard deviation (SD) metric. Zhang et al. [38] proposed a hybrid Golden Jackal Optimization with a Sine Cosine Algorithm (SCGJO) for tackling multilevel thresholding image segmentation problems. They compared the SCGJO with other evolutionary algorithms and demonstrated its high segmentation quality and overall optimal value. Additionally, they conducted Wilcoxon’s rank-sum test to confirm the effectiveness and disparity between SCGJO and other algorithms. Kang et al. [39] proposed a multilevel thresholding image segmentation algorithm based on the Mumford–Shah (MSh) model. They used the segmentation method to solve the multitarget segmentation problem and improve the processing accuracy of the algorithm. The algorithm utilizes the MSh model to determine the optimum thresholds and convert the problem into a multi-objective function optimization problem. The results showed that the proposed algorithm had the best objective function value and performed well in terms of segmentation quality and convergence time. Wang et al. [40] introduced the Mixed-Strategy-Based Improved Whale Optimization Algorithm (MSWOA) for multilevel thresholding image segmentation. This innovative algorithm combines the principles of the Whale Optimization Algorithm (WOA) with mixed strategies to enhance the quality and efficiency of image segmentation, with a specific focus on color image segmentation applications. The MSWOA method incorporates several key features to optimize the segmentation process, including k-point initialization, a non-linear convergence factor, and an adaptive weight coefficient.
3. Materials and Methods
3.1. Multilevel Thresholding Problem
Image thresholding problem involves determining the optimal threshold values to effectively segment the image into distinct classes. In other words, the goal is to find a set of thresholds that divides the image into regions, each representing a distinct intensity level or class. If m threshold values are used in the segmentation process, the image will be divided into m + 1 regions. When equals 1, the thresholding problem is referred to as bilevel thresholding. In bilevel thresholding, the image is partitioned into two regions: foreground and background, based on a single threshold value. Conversely, when is greater than one, the problem transforms into multilevel thresholding. Multilevel thresholding extends the concept by segmenting the image into multiple intensity levels or classes using multiple threshold values. This enables a finer segmentation of images with complex intensity distributions or multiple regions of interest. Multilevel thresholding is an optimization problem trying to find the best set of threshold values, represented as , to split an image into regions. Each region corresponds to a specific range of pixel intensities. The intensity at the location in image I is segmented into sub-images as follows:
Equation (1), which is typically used for gray-level images, can also be extended to apply to the red, green, and blue channels of RGB color images. In this case, each channel of the RGB image is considered as a separate individual image.
Various methods have been proposed to determine the threshold values that will make a good distinction between the objects and the background in the image. Kapur’s entropy [9] and Otsu’s method [10] are the most frequently used non-parametric thresholding functions. These methods are briefly described in the next sub-sections.
3.1.1. Kapur’s Entropy-Based Thresholding
The Kapur function [9], also known as the Maximum Entropy Thresholding, aims to find the threshold that maximizes the entropy or uncertainty between the foreground and background regions. By maximizing entropy, the Kapur function effectively captures the overall information content in the image and selects the threshold that maximizes the discriminative power between classes. Kapur’s entropy is calculated based on the probability distributions of the gray levels in the image histogram. Assuming are the threshold values to be used to classify the image, the objective function is defined as,
where
In Equations (3) and (4), are the class entropies and, are the class probabilities. The optimal threshold values are obtained by maximizing the objective function in Equation (3). The complexity of solving this problem increases exponentially depending on the number of thresholds. For this reason, determining the threshold values that will maximize the objective function given in Equation (4) can be considered as an n-dimensional optimization problem and expressed as follows:
3.1.2. Between-Class Variance-Based Thresholding (Otsu’s Method)
Otsu’s method [10] is a non-parametric segmentation method based on minimizing the intra-class variance while maximizing the between-class variance. It calculates the optimal threshold by maximizing the ratio of between-class variance to within-class variance. The method defines the between-class variance as the sum of sigma functions calculated as:
where
In Equation (6), is the average brightness value of the input image, is the average of the i-th class and is calculated using Equation (8).
Here, are the threshold values. The optimal threshold values are obtained by maximizing the objective function in Equation (8) given below:
3.2. Proposed Method
Thresholding image segmentation is a fundamental technique used in image processing to partition an image into foreground and background regions based on intensity levels. The principle behind thresholding is straightforward and is defined as follows: pixels with intensities above a certain threshold value are assigned to one class (often considered as foreground), while pixels with intensities below the threshold belong to the other class (typically background). However, traditional thresholding methods face challenges when dealing with images affected by varying illumination conditions, noise, or complex background structures. In such cases, simple thresholding techniques may lead to sub-optimal segmentation results, with regions of interest being incorrectly classified or merged with background noise. Also, the computational cost of traditional thresholding methods significantly increases for multilevel thresholding problems. Metaheuristic algorithms offer a promising approach to address the limitations of traditional thresholding methods. These algorithms are heuristic search techniques inspired by natural phenomena or social behavior. Unlike exact optimization methods, metaheuristic algorithms do not guarantee finding the global optimum but are capable of efficiently exploring large solution spaces and finding near-optimal solutions. Each type of metaheuristic algorithm has its own set of rules for generating new solutions and deciding which solutions to use [33]. For example, in a genetic algorithm, new solutions are created by combining parts of existing solutions, mimicking the process of natural selection and evolution. Because of these differences in how solutions are generated and updated, each metaheuristic algorithm may produce different results when applied to the same problem. This diversity can be beneficial because it allows researchers and practitioners to explore various approaches and find the most suitable one for their specific problem. In this section, we will present a thorough introduction to a novel metaheuristic algorithm called the WChOA-FDB. We will explore its principles, mechanisms, and characteristics, providing a comprehensive understanding of how it operates and its applications in optimization tasks. This section first introduces the ChOA and WChOA algorithms. Then, the proposed algorithm, a mixed-strategy-based Fitness–Distance Balance and WChOA optimization algorithm (WChOA-FDB) is explained in detail.
3.2.1. WChOA Algorithm
Khishe et al. [41] proposed the Weighted Chimp Optimization Algorithm (WChOA), which is a modified version of ChOA [42], developed in 2021. ChOA is a standard algorithm inspired by the hunting mechanism of chimps in nature. Compared with other nature-inspired methods, ChOA requires the adjustment of only a few operators and can be easily implemented. There are four kinds of chimps—driver, barrier, chaser, and attacker—in a chimp colony. Each role is assigned the responsibility of guiding and coordinating the other chimpanzees toward the prey, aiming for an optimal solution. Achieving the best solution to the optimization problem requires maintaining a balanced equilibrium between exploring and exploiting the search space.
In conventional ChOA, only the initial four solutions—driver, chaser, attacker, and barrier—are employed to update the positions of the remaining chimps. In essence, the remaining chimps are drawn toward these four best solutions. Despite the inherent ability of attackers to forecast prey movement, it is not guaranteed that the solution provided by attackers is always the best. This uncertainty arises because chimps may deviate from their assigned tasks during the hunting process or persist with the same duties throughout. Consequently, updating the positions of other chimps based solely on attackers may lead them into local optima, hindering the exploration of new areas within the search space, given the significant concentration of their solution space around attacker-derived solutions. Similar concerns apply to the other primary solutions (driver, chaser, and barrier).
To address this challenge, the WChOA method was developed. WChOA addresses the limitations of the ChOA by introducing a position-weighted equation based on weights to improve exploration and exploitation. Equations (9)–(11) are employed to update the positions of the remaining chimps. Essentially, this forces the other chimps to adjust their positions based on those of the driver, chaser, attacker, and barrier. Recognizing the limitations mentioned previously opens avenues for novel approaches to update the positions of other chimps. The proposed solution involves a corresponding weighting method based on the Euclidean distance of the step size, as follows:
, , and vectors indicate the current positions of the attacker, barrier, chaser, and driver, respectively. vector is the current position of other chimps. Also, , , and vectors contribute greatly to ChOA. These vectors are calculated by Equations (11)–(13):
where and are random vectors that can vary in the range [0, 1], and f represents a control value that decreases non-linearly from 2.5 to 0. The chaotic vector is used to model the sexual motivation in ChOA and is calculated based on a chaotic map [42]. This chaotic behavior helps chimps alleviate the problems of entrapment in local optima and slow convergence rate in solving high-dimensional problems. Six chaotic maps (Chebyshev map, Circle map, Gauss/mouse map, Iterative map, Logistic map, and Piecewise map) have been used in the study. These chaotic maps are deterministic processes that also have random behavior.
where , , , and are the learning rates of other chimps from the attacker, barrier, chaser, and driver, respectively. Also, |.| indicates the Euclidean distance. In ChOA the relationship between positions was calculated as follows:
However, in WChOA the position-weighted relationship is calculated using Equation (19):
In WChOA, the position-weighted relationship Equation (19) can be utilized instead of Equation (18) in the standard ChOA. The main difference between Equation (19) and the traditional position-weighted relationship Equation (18) is the application of the corresponding learning rate. As mentioned previously, since there is a possibility that some chimps do not have any sexual motivation in the process of hunting, a probability of 50% can be considered to indicate whether the position-weighted strategy of chimps will be normal (Equation (19)) or not (chaotic model). Thus, the following relationship is applied:
where t denotes the current iteration and denotes the probability value in range [0,1] which indicates the position-weighted strategy of chimps.
It is noteworthy that the learning rates in the position-weighted relationship change dynamically. This means that these parameters are not constant during every iteration of WChOA. It enhances the convergence speed and avoidance of local optima where attackers, barriers, chasers, and drivers are less likely to be knowledgeable about the position of the prey.
3.2.2. Fitness–Distance Balance Selection
The Fitness–Distance Balance (FDB) selection method [43] is a fundamental approach employed in population-based and evolutionary-based MHS algorithms. It serves as a mechanism to guide the selection process by evaluating solution candidates based on both their fitness values and distances from the optimal solution. By calculating FDB scores for each candidate using normalized fitness and distance values, the method effectively strikes a balance between selecting high-quality solutions and maintaining diversity within the population. This balance ensures that the algorithm explores various regions of the solution space, thereby enhancing its ability to locate multiple optima. Ultimately, the FDB selection method contributes to the efficiency and effectiveness of MHS algorithms by enabling them to efficiently navigate complex search landscapes. This selection method achieves a balance between fitness and distance by considering candidates with high scores as suitable alternatives for the population to converge towards [44]. In the initial stage of FDB, the distance of the population from the best individual is calculated following Equation (21).
In Equation (21), is the set of solutions, is the number of vectors in , and D represents the distance vector, with and denoting the solution vectors of the best and solutions, respectively. represents the problem dimension (number of variables). To evaluate the scores of solution candidates, the normalized fitness values () and the normalized distance values () of these candidates were utilized. To avoid dominance between two parameters, their normalized values are used. Finally, fitness values and distance values vectors were used to calculate the FDB score using Equation (22) [43].
The vector is the normalized value of the distance of the solution candidate in P to , which has the best fitness value in . When computing the scores of the vectors, a weight coefficient (w) is employed, which determines the impact of fitness and distance values. Based on these descriptions and the explanations 0 < w < 1, the score of each candidate in the P-population is determined. For more information on the FDB method, please review the study referenced in [43].
3.2.3. Proposed WChOA-FDB Scheme
The search capabilities of metaheuristic search algorithms mainly depend on the design of convergence equations. Convergence equations are used to determine the positions of solution candidates in the search space. The positions of solution candidates change depending on the guides used in the convergence equations. Guides determine the direction and behavior of the population in the search space. The guides selected randomly from the population create a diversity effect, while guides selected using the greedy method create an exploitation effect. The FDB selection method considers the fitness values of the solution candidates and their distance values to the best individual in the population. Of these two values, the fitness value reflects the exploitation effect, while the distance value reflects the diversity effect. In this way, the FDB selection method is quite effective in determining the guides that provide the exploitation–exploration balance. According to the studies in the literature, significant improvements have been achieved in the search capabilities of many MHS algorithms whose guidance mechanisms are designed using the FDB selection method [44,45,46,47]. So, in this study, we applied the FDB selection method to improve the design of the guidance mechanism of the WChOA algorithm. Thus, we ensured that the solution candidates that provide the exploitation–exploration balance in the search process are used as guides in the convergence equations of WChOA.
WChOA-FDB represents an evolution of WChOA. While WChOA demonstrated effectiveness in optimization tasks, the integration of Fitness–Distance Balance (FDB) introduces a novel dimension to further enhance its capabilities. The novel aspect of WChOA-FDB lies in the incorporation of FDB principles. FDB is a mechanism designed to balance exploration and exploitation dynamically, ensuring that the algorithm maintains diversity in the solution space while converging toward optimal solutions.
FDB is seamlessly integrated into WChOA to address the subtle challenges of balancing exploration and exploitation. This integration ensures that the algorithm adapts its strategies to explore diverse regions of the solution space while exploiting promising solutions for optimization. FDB introduces a mechanism to measure the fitness of solutions in relation to their distances within the solution space. This measurement guides the algorithm in prioritizing solutions that contribute to both exploration and exploitation goals. The integration of FDB with WChOA adds a layer of dynamic adaptation. As the algorithm progresses, FDB influences the exploration–exploitation trade-off, allowing WChOA-FDB to respond effectively to changes in the optimization landscape.
The WChOA-FDB algorithm works in three main stages: Select, Search, and Update. In the Select phase, the entire search space is explored to find a potential solution. The Search phase focuses on exploiting the selected area, while the Update phase focuses on targeting the best solution. The formulation of the three phases is given in Equations (9)–(19). All these steps together provide the WChOA-FDB. The algorithmic steps and processes of the proposed algorithm are given below:
- Initialization with FDB Parameters: WChOA-FDB begins by initializing a population of potential solutions, incorporating parameters specific to FDB.
- Evaluation and Fitness Assignment: Each solution is evaluated based on the objective function, and the fitness is assigned. FDB principles contribute to fitness assessment by considering the distances between solutions.
- Weighted Solution Evaluation with FDB: The weighted evaluation mechanism, enriched by FDB, assigns weights to solutions based on both their fitness and distances. This weighted approach guides subsequent decision-making processes.
- Collaborative Decision-Making Enhanced by FDB: Solutions engage in collaborative decision-making, now with added guidance from FDB. The algorithm prioritizes solutions not only based on their fitness but also considering their contribution to maintaining diversity within the population.
- Dynamic Adaptation with FDB: WChOA-FDB dynamically adapts its parameters throughout the optimization process, influenced by FDB. This ensures a continuous and adaptive exploration–exploitation balance.
- Iterative Optimization Enhanced by FDB: The algorithm iteratively optimizes solutions, leveraging the integrated FDB principles to achieve a balance between exploration and exploitation. Iterations continue until the termination criterion is met.
- Termination and Solution Retrieval: WChOA-FDB concludes when the termination criterion is satisfied. The best solutions, considering both fitness and distances, are retrieved as the final optimized outcomes.
In this study, multiple WChOA-FDB variants (Case-1 through Case-72) were created by applying the FDB method to different components of the original WChOA algorithm’s equations. Then approximately 10% of the most successful cases (8 cases) were selected and their details are given below. The FDB-based WChOA variants (Case-1, Case-2, Case-3, Case-4, Case-5, Case-6, Case-7, and Case-8) were created to improve the exploration and balanced search ability of the WChOA algorithm. The equations where the FDB method is applied and the mathematical models of the WChOA-FDB variants are given in Table 1. Case-1 replaces the component in the equation with the FDB method (). This modifies how the distance for the driver chimp is calculated. Case-2 replaces the component in the equation with the FDB method (). This changes how the current position of other chimps affects the driver-distance calculation. Case-3 applies FDB to both the and equations simultaneously. It replaces both and with . This modifies how both the attacker and driver guide other chimps. Case-4 applies FDB to the attacker and driver equations, but differently from Case-3. It replaces in the attacker equation and in the driver equation with . This creates a different balance between exploration and exploitation. Case-5 uses FDB to modify the current position component in the attacker equation and the component in the driver equation. Case-6 uses FDB to replace the current position component in both the attacker and driver equations. This creates a consistent modification of how current chimp positions influence both equations. Case-7 applies FDB to the barrier and driver roles by replacing and in the barrier and driver equations, respectively. And finally, Case-8 applies FDB to modify the current position component in the barrier equation and the component in the driver equation. The general framework of the proposed WChOA-FDB algorithm and the equations where the FDB selection method was applied are explained step by step in Algorithm 1. Also, the flowchart of the WChOA-FDB algorithm is given in Figure 1.

Table 1.
Mathematical model of the WChOA-FDB variants (proposed).
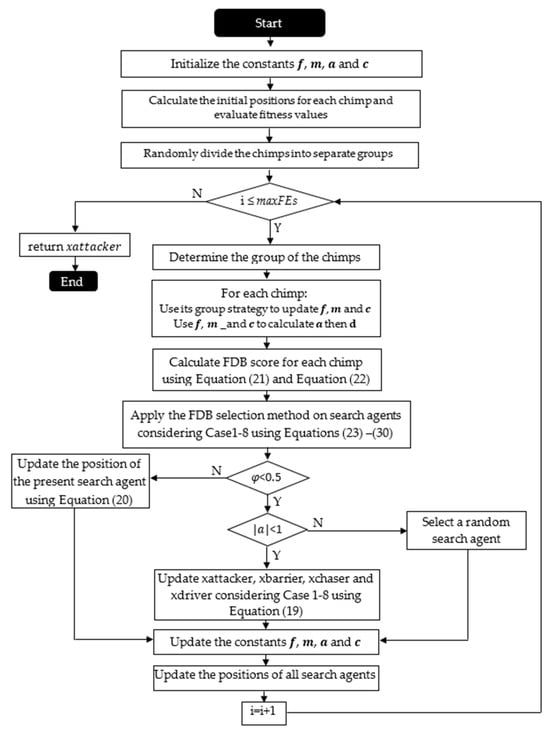
Figure 1.
Flowchart of the proposed WChOA-FDB algorithm.
| Algorithm 1. Pseudo-code of proposed WChOA-FDB algorithm |
| 1. Input: Chimp population (p), Number of iteration (Max_iter), |
| Problem dimension (number of variables) (d) |
| 2. Output: X_Attacker |
| 3. Begin: |
| 4. Initialize the constants f, m, a and c |
| 5. Calculate the initial position (population) for each chimp and evaluate fitness |
| 6. Randomly divide the chimps into separate groups |
| 7. for i = 1:p do |
| 8. Evaluate the fitness of each chimp |
| 9. end for |
| 10. xattacker = the best search agent |
| 11. xbarrier = the second best search agent |
| 12. xchaser = the third best search agent |
| 13. xdriver = the fourth best search agent |
| 14. //Meta-heuristic search process// |
| 15. while (l < Max_iter) //Number of iteration is not achieved |
| 16. for i = 1: p do |
| 17. for each chimp: |
| 18. Extract the chimp’s group |
| 19. Use its group strategy to update f, m and c |
| 20. Use f, m _and c to calculate a then d |
| 21. end for |
| 22. //Implementation of FDB selection method// |
| 23. for i = 1:p do |
| 24. Calculate Euclidean distance for each chimp using Equation (21) |
| 25. Calculate FDB score for each chimp using Equation (22) |
| 26. end for |
| 27. Create D and S as vectors using Equation (21) and Equation (22), respectively |
| 28. Determine x_FDB based on FDB philosophy by using Equation (9) |
| 29. Calculate d_Driver using Equation (23)//Case-1// |
| 30. Calculate d_Driver using Equation (24)//Case-2// |
| 31. Calculate d_Attacker and d_Driver using Equation (25)//Case-3// |
| 32. Calculate d_Attacker and d_Driver using Equation (26)//Case-4// |
| 33. Calculate d_Attacker and d_Driver using Equation (27)//Case-5// |
| 34. Calculate d_Attacker and d_Driver using Equation (28)//Case-6// |
| 35. Calculate d_Barrier and d_Driver using Equation (29)//Case-7// |
| 36. Calculate d_Barrier and d_Driver using Equation (30)//Case-8// |
| 37. Calculate d_Chaser using Equation (9) |
| 38. end for |
| 39. for i = 1: p do |
| 40. if (φ < 0.5) |
| 41. if (|a| < 1) |
| 42. Update the position of the driver by Equation (19)//Case-1// |
| 43. Update the position of the driver by Equation (19)//Case-2// |
| 44. Update the position of the attacker and driver by Equation (19)//Case-3// |
| 45. Update the position of the attacker and driver by Equation (19)//Case-4// |
| 46. Update the position of the attacker and driver by Equation (19)//Case-5// |
| 47. Update the position of the attacker and driver by Equation (19)//Case-6// |
| 48. Update the position of the barrier and driver by Equation (19)//Case-7// |
| 49. Update the position of the barrier and driver by Equation (19)//Case-8// |
| 50. Update the position of the chaser by Equation (19) |
| 51. else if (|a| > 1) |
| 52. Select a random search agent |
| 53. end if |
| 54. else if (φ > 0.5) |
| 55. Update the position of the present search agent by Equation (20) |
| 56. end if |
| 57. end for |
| 58. Update the constants f, m, a and c |
| 59. Update xattacker, xbarrier, xchaser and xdriver |
| 60. end while |
| 61. return xattacker |
The most significant theoretical contribution of WChOA-FDB is the dynamic improvement of the exploration and exploitation balance, which is one of the most critical challenges in metaheuristic algorithms. The FDB approach considers both the fitness values of candidate solutions and their distribution in the solution space. It enables candidate solutions to be evaluated not only based on their fitness values but also according to their distances from each other. This helps maintain diversity during the search process while also supporting convergence toward good solutions. Modifying the behaviors of different guide chimps in various variants (Cases 1–8) enables more effective exploration of different regions of the solution space.
The complexity of WChOA relies on the number of chimps (n), the number of iterations (maxFEs), and the sorting method for each iteration [41]. In each iteration, the first four best solutions were found and assigned as driver, chaser, attacker, and barrier. Quick sort employed by this method means that, in the best and worst cases, complexity is and , respectively. The computational complexity of WChOA is defined as follows:
For the proposed algorithm, WChOA-FDB, the Euclidean distances and FDB scores for each chimp are calculated using Equations (21) and (22). So, the computational complexity of WChOA-FDB is defined as:
4. Experimental Results
4.1. Experimental Settings
A brief description of the experimental working environment and settings is given below.
- The IEEE CEC 2020 suite [48], which has four different types of benchmark problems, was used to investigate the performance of the proposed algorithm.
- The optimization process termination criterion is determined by the maximum number of objective function evaluations, denoted as maxFEs. This criterion is set as maxFEs = 1000 × D, where D represents the problem dimension.
- The experiments were conducted independently for four varying problem dimensions (D = 10, D = 30, D = 50, and D = 100) to analyze and evaluate the performance of the proposed algorithm in low, medium, and high-dimensional optimization scenarios.
- The experiments were repeated 25 times for the optimization of each problem.
- Statistical test methods were employed to analyze the data obtained from experimental studies.
- Pairwise comparisons were conducted using the Wilcoxon test, while multiple comparisons were performed using the Friedman test.
- Experiments were conducted utilizing MATLAB R2018b on a Core i7 1065G7 1.30 GHz CPU with 12 GB of RAM and running Windows 11.
4.2. Testing and Analyzing the Performance of the Proposed WChOA-FDB Algorithm
The experimental results of the WChOA-FDB are provided, wherein several cases of the proposed WChOA-FDB algorithm are compared with the base algorithm. The performance of the developed WChOA-FDB algorithm is tested on IEEE CEC 2020 [48] benchmark problems. Ten different problems taken from CEC 2020 presented in Table 2 were analyzed in dimensions of 10, 30, 50, and 100 using the Friedman and Wilcoxon pairwise comparison tests.

Table 2.
Summary of the CEC’2020 test suite.
Table 2 presents the function types, search range, and the problem sizes of the test functions used in the study. These functions are designed to test the exploration, exploitation, and balanced search capability of meta-heuristic search algorithms. Unimodal and multimodal test functions aim to determine the exploitation and exploration capabilities of an algorithm, respectively. Hybrid and composition test functions are more complex. Hybrid functions are used to investigate the algorithm’s ability to balance between exploration and exploitation. Composition functions are the same as real-world optimization problems because they have many local minima.
Statistical Analyses on CEC’2020 Test Suite
The Friedman test is a non-parametric statistical test used to detect differences in treatments across multiple test attempts. This test is particularly useful in situations where multiple measurements are taken from different methods, algorithms, or conditions on the same subjects. Our statistical analyses included 10 test functions, 25 runs, and 9 algorithms. Table 3 displays the Friedman test results of the experimental data. The results indicated that the WChOA-FDB variants demonstrated better search performance compared to the base WChOA algorithm in all experiments. According to the mean rank index, the Case-4 variant was identified as the most successful among the WChOA-FDB variants. The dimensional scalability analysis reveals that Case-4 achieves the best overall performance with a mean rank of 4.690, demonstrating good optimization capability across varying problem dimensions, particularly excelling in high-dimensional scenarios (D = 100) where it attains the lowest mean rank of 4.492. Case-3 emerges as the second-best performer (mean rank = 4.708) with notably strong performance in higher dimensions (D = 50 and D = 100), suggesting enhanced scalability characteristics compared to other variants. Case-2 maintains consistent performance across all dimensional levels with minimal variance (4.678–4.804), indicating robust stability regardless of problem complexity, while Case-8 shows dimension-dependent behavior with exceptional performance at moderate dimensions (4.478 at D = 30) but degraded performance at higher scales. The analysis demonstrates a clear performance hierarchy where Cases 1–4 significantly outperform Cases 5–8, with the original WChOA exhibiting the poorest scalability (mean rank = 6.272), particularly deteriorating at higher dimensions (6.709 at D = 100). Case 5 and Case 6 consistently rank among the worst performers across all dimensions, suggesting that their specific algorithmic modifications may introduce computational overhead without corresponding optimization benefits. The dimensional analysis indicates that problem complexity significantly influences algorithmic ranking, with high-dimensional scenarios (D ≥ 50) favoring Case 3 and Case 4, while lower dimensions show more balanced performance distribution among the top-performing variants.

Table 3.
Friedman test rankings for WChOA and WChOA-FDB variants.
The Wilcoxon method is a non-parametric statistical test used to compare two related samples to assess whether their population mean ranks differ. It serves as a robust alternative to the paired t-test, especially when the data does not meet the normality assumptions. This makes it particularly useful for evaluating the performance of various algorithms or their variants across multiple data items. In the context of MHS algorithms, the Wilcoxon signed-rank test can be used to determine the best algorithm by comparing their performance metrics pairwise. Table 4 presents the results of the Wilcoxon pairwise comparison of the base algorithm and its FDB variants. In Table 4, the sum of the items in every cell represents the total number of test functions, which is 10 in this study. For example, “Case-1 vs. WChOA” represents the pairwise comparison between a WChOA-FDB variant and the base algorithm WChOA. The pairwise (+/=/−) in each cell indicates the test problem number in which the associated WChOA-FDB variant showed better, similar, or worse performance, respectively, when compared to the original WChOA algorithm. For example, the pairwise (7_3_0) in the last column (D = 100) of Case-4 means that the Case-4 variant performed better than the base algorithm WChOA in seven problems, showed similar performance in three problems, and performed worse in zero problems. In Table 4, the information about the performance of all WChOA-FDB variants for 10, 30, 50, and 100 dimensions was presented. In D = 10 dimensions, Case-1, Case-2, and Case-5 achieved the best score (5-5-0) in all pairwise comparisons. For D = 30 dimensions, Case-1 and Case-2 obtained the best score as (6-4-0). Also, Case-3, Case-4, Case-7, and Case-8 performed better than the base algorithm with a score of (5-5-0). In D = 50 dimensions, Case-8 achieved the best score (7-3-0) among all cases. Besides Case-4, Case-6 outperformed the base algorithm with score (5-5-0), while Case-1, Case-3, and Case-7 performed better with score of (6-4-0). Finally, we can conclude that the experimental results for all WChOA-FDB variants in D = 100 dimensions performed better than the original algorithm.

Table 4.
Wilcoxon pairwise comparison results between WChOA-FDB variants and WChOA.
4.3. Image Segmentation Performance of the Proposed WChOA-FDB Method
In this section, the multilevel image segmentation performance of the proposed WChOA-FDB algorithm is analyzed. Experimental studies were carried out on 10 color images taken from the Berkeley image segmentation database [49]. The test images and their histograms are presented in Figure 2. The images with complex histograms were chosen to investigate the solution of complex problems. When the histograms were examined, it can be seen that the test images have various brightness and color distributions.

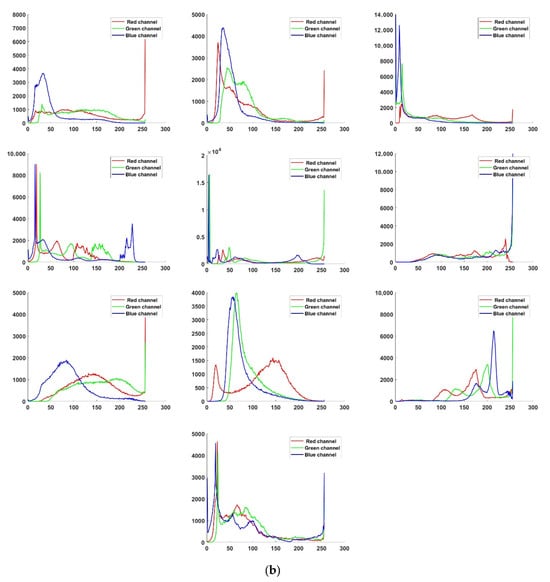
Figure 2.
Test images (a) and their histograms (b) (The image names are from left to right and top to bottom: 12003.jpg, 108073.jpg, 124084.jpg, 232038.jpg, 323016.jpg, 106024.jpg, 291000.jpg, 12084.jpg, 61060.jpg, 65010.jpg).
To evaluate WChOA-FDB’s multilevel thresholding image segmentation performance, we employed Kapur’s entropy and Otsu’s between-class variance methods. The performance of WChOA-FDB has been compared with other well-known metaheuristic algorithms, namely ABC, CS, GWO, HHO, MFO, SCA, and SSA. Experimental studies were carried out using 10 color images, 2 thresholding functions (Kapur’s entropy and Otsu’s method), 16 MHS algorithms (WChOA, 8 WChOA variants, and 7 well-known competitor algorithms), 6 different threshold levels (m = 2, 4, 6, 8, 10, 12), and two different search process termination criterion (maxFEs = 500 × m and maxFEs = 1000 × m, m is the number of threshold levels, maxFEs is the search process termination criterion). As a result, a total of 11,520 = 10 image × 3 channel (RGB) × 2 thresholding functions × 16 MHS algorithms × 6 threshold levels × 2 search process termination criteria (500 × m, 1000 × m) experiments were conducted to evaluate multilevel thresholding image segmentation performance of the proposed WChOA-FDB method. The algorithms execute 25 runs for each segmentation task. The original settings of the algorithms were used in the experiments. These settings are presented in Table 5.

Table 5.
Algorithm settings.
4.3.1. Statistical Analysis on Test Images
In this sub-section, the analysis results of the segmentation process using Kapur’s entropy and Otsu’s method as objective functions were given. The fitness values of 16 MHS algorithms for 10 test images, 6 different threshold levels, and R-G-B channels were analyzed. The Friedman test was used for statistical comparisons. Analysis results obtained using Otsu’s method and Kapur’s entropy as objective functions for 2 different maxFEs values were presented in Table 6 and Table 7, respectively. The performance analysis reveals distinct algorithmic behavior patterns across varying experimental conditions, with Case-8 demonstrating the most robust performance by achieving first rank in 7 out of 24 scenarios, particularly excelling at higher threshold levels (m ≥ 8), regardless of fitness function or computational cost. Case-2 emerges as the second most successful variant with 7 first-place rankings, showing particular strength in lower threshold scenarios (m = 2.4) and maintaining competitive performance across both Otsu and Kapur fitness functions. The data indicates a clear threshold-dependent performance hierarchy where simpler segmentation tasks (m = 2.4) favor Case-2’s approach, while complex multilevel scenarios (m ≥ 8) consistently benefit from Case-8’s enhanced optimization mechanism. Computational cost allocation significantly influences algorithmic ranking, as increased function evaluations (1000 × m vs. 500 × m) enable previously underperforming cases like Case-1 and Case-4 to achieve better results, suggesting that these variants require extended exploration phases to reach optimal solutions. The fitness function selection also demonstrates notable impact on case performance, with Kapur’s entropy optimization exhibiting more diverse case rankings compared to Otsu’s method, indicating that the entropy-based objective landscape provides different optimization challenges that favor varied algorithmic strategies across different cases.

Table 6.
Friedman rankings of algorithms at different threshold levels for maxFEs = 500 × m and maxFEs = 1000 × m (Otsu’s method).

Table 7.
Friedman rankings of algorithms at different threshold levels for maxFEs = 500 × m and maxFEs = 1000 × m (Kapur’s entropy).
In multilevel image segmentation, the increase in the number of threshold levels increases the complexity of the problem. The Friedman rankings in Table 6 and Table 7 indicate that the increase in the complexity of the search space has made distinctive differences between the top-ranking algorithms and their competitors. The change in the threshold level value changes the boundaries and geometric structure of the search space. The success of different algorithms at different threshold levels is related to the algorithms’ exploitation and exploration capabilities. However, the results show that the WChOA-FDB method proposed in the study is more successful than the base algorithm and other competitive algorithms for two thresholding functions, in all threshold levels and maxFEs values, except m = 2 and maxFEs = 1000 × m for Otsu’s thresholding function. This means that the proposed method exhibits a more balanced search capability compared to its competitors for all segmentation problems with different complexities used in the experiments. In addition, the WChOA algorithm, which was used for the first time in the field of multilevel image segmentation, was generally the second most successful algorithm for both objective functions, according to the Friedman scores.
4.3.2. Performance Metrics
Fitness function, PSNR (Peak Signal-to-Noise ratio), SSIM (Structural Similarity Index Measure), and FSIM (Feature Similarity Index) criteria were used as evaluation metrics in the study for image segmentation. Otsu’s method and Kapur’s entropy functions were used as fitness functions. Algorithms were trying to maximize these fitness functions. Therefore, the highest fitness value shows the success of that algorithm. PSNR, SSIM, and FSIM criteria were used to evaluate the quality of segmented images.
PSNR is defined as the ratio between the maximum possible power of signal and noise introduced. It is used to measure the reconstruction quality of an image. Mean Square Error (MSE) measures the error at each pixel location and generates the mean value which is further utilized to generate the PSNR of the image. MSE is defined as the difference between the intensity of the original image and the segmented image. A higher value of PSNR denotes good segmentation. PSNR value was calculated with Equation (33). In the equation, x is the original image, y is the segmented image, and (m, n) is the number of rows and columns of images.
SSIM is a perception-based model that considers image degradation as a perceived change in structural information. SSIM is generally used to find out the inter-dependencies between original and segmented images. The SSIM is calculated as in Equation (34):
In the equation, μx and μy represent mean value, σx and σy show standard deviation, σxy refers to the correlation between x and y images, respectively. C1 and C2 are constants chosen to avoid division by zero error. It can be concluded that higher quality thresholding is made at large values of the SSIM.
FSIM is the metric that is used to estimate the structural similarity of the original and segmented image. It is defined as:
where Ω represents the entire image and indicates the similarity between the segmented images obtained through multilevel thresholding task and the input image. The FSIM parameter of an RGB color image is calculated as the mean of the FSIM parameter of each color channel.
4.3.3. Performance Evaluation Using the Fitness Function
During the optimization process, Otsu’s method and Kapur’s entropy are used as the objective functions in the study. Algorithms were trying to maximize these fitness functions. Therefore, the highest fitness value shows the success of that algorithm. The average fitness function values of each algorithm using Otsu’s method for maxFEs = 500 × m and maxFEs = 1000 × m are presented in Table 8 and Table 9, respectively. It is seen that the WChOA and the proposed WChOA-FDB variants are the most outstanding in almost all experiments. In Table 8 and Table 9, WChOA and the proposed WChOA-FDB variants give higher fitness function values in 53 out of 60 experiments for maxFEs = 500 × m and in 49 out of 60 experiments for maxFEs = 1000 × m. Of these successful experiments, WChOA-FDB algorithm gave better fitness value results in 39 experiments for maxFEs = 500 × m and in 35 experiments for maxFEs = 1000 × m.

Table 8.
The average fitness values of Otsu’s method in comparison with other algorithms (maxFEs = 500 × m).

Table 9.
The average fitness values of Otsu’s method in comparison with other algorithms (maxFEs = 1000 × m).
The average fitness function values of each algorithm using Kapur’s entropy for maxFEs = 500 × m and maxFEs = 1000 × m are presented in Table 10 and Table 11, respectively. It is seen that the WChOA and the proposed WChOA-FDB variants give better results in almost all experiments. In Table 10 and Table 11, WChOA and the proposed WChOA-FDB variants give higher fitness function values in 46 out of 60 experiments for maxFEs = 500 × m and 48 out of 60 experiments for maxFEs = 1000 × m. Of these successful experiments, the proposed WChOA-FDB algorithm gave better fitness value results in 38 and 37 experiments for maxFEs = 500 × m and maxFEs = 1000 × m, respectively.

Table 10.
The average fitness values of Kapur’ entropy in comparison with other algorithms (maxFEs = 500 × m).

Table 11.
The average fitness values of Kapur’ entropy in comparison with other algorithms (maxFEs = 1000 × m).
This experimental analysis demonstrates the superior performance of the proposed WChOA-FDB algorithm in multilevel image segmentation optimization. The results show that WChOA and WChOA-FDB variants consistently outperform competing algorithms across both objective functions (Otsu’s method and Kapur’s entropy) and maximum number of fitness evaluations. Specifically, the WChOA family achieves success rates of 88% (53/60) and 82% (49/60) for Otsu’s method at maxFEs = 500 × m and 1000 × m, respectively, and 77% (46/60) and 80% (48/60) for Kapur’s entropy under the same conditions. Notably, within these successful experiments, the proposed WChOA-FDB algorithm demonstrates improved optimization capability, achieving the highest fitness values in approximately 73% of successful cases for Otsu’s method and 80% for Kapur’s entropy across both maxFEs values. These findings indicate that WChOA-FDB exhibits enhanced search balance and convergence characteristics, making it particularly effective for complex multilevel thresholding problems with varying difficulty levels, thereby establishing its strong practical applicability in color image segmentation tasks.
4.3.4. Performance Evaluation Using PSNR, SSIM and FSIM
In this section, the PSNR, SSIM, and FSIM metrics were used to evaluate the multilevel image segmentation performances of the proposed and competitor algorithms. The average PSNR, SSIM, and FSIM results obtained by each algorithm for each number of threshold levels, thresholding functions, and termination criteria on 10 images are shown graphically.
The average PSNR values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and a number of threshold levels are presented in Figure 3. The figure shows the graphs of the average PSNR values of the Otsu and Kapur functions on 10 test images for the maxFEs = 500 × m and maxFEs = 1000 × m for each number of threshold levels. As can be seen from the figure, the WChOA algorithm, which was first applied to the image segmentation problem and its proposed variants, gives higher PSNR results at all number of threshold levels compared to the competing algorithms. By using the PSNR metric, the image distortion degree can be compared. This is also used to evaluate the image quality. The smaller image distortions result in a higher PSNR value. According to the results, the proposed method shows higher performance in image segmentation when compared to other algorithms.
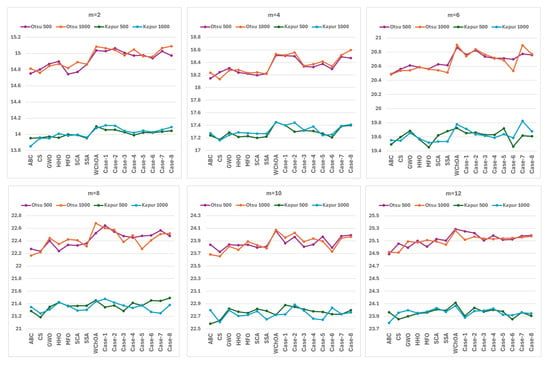
Figure 3.
The average PSNR values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and number of threshold levels (m). (Otsu 500: Otsu’s method for maxFEs = 500 × m, Otsu 1000: Otsu’s method for maxFEs = 1000 × m, Kapur 500: Kapur’s entropy for maxFEs = 500 × m, Kapur 1000: Kapur’s entropy for maxFEs = 1000 × m).
When the PSNR values, including 16 algorithms, 10 images, and 6 threshold levels, 2 termination criteria for Otsu’s method are examined, the WChOA and WChOA variants give higher PSNR values in 49 of 60 experiments. For maxFEs = 1000 × m the number of higher PSNR values is 48. When Kapur’s entropy is used as an objective function, the number of experiments in which the PSNR values are higher than other algorithms for the proposed method are 45 for maxFEs = 500 × m and 44 for maxFEs = 1000 × m. These results establish the proposed method’s consistent success in producing higher quality segmented images, with an overall success rate of approximately 78% across both objective functions and maxFEs values, confirming its robust performance in practical image segmentation applications.
The SSIM is an important metric that is used to evaluate the similarity of the original image and the segmented image visually. It is based on contrast, brightness, and structural information of the images. If the segmented image and the original image are more similar, the SSIM value is higher. Also, the value of SSIM increases as the number of thresholds increases, which means that the segmented images are more similar to the original images and the interested objects can be extracted more accurately.
The average SSIM values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and the number of threshold levels are presented in Figure 4. The figure shows the graphs of the average SSIM values of the Otsu and Kapur functions on 10 test images for the maxFEs = 500 × m and maxFEs = 1000 × m for each number of threshold levels. As can be seen from the figure, the WChOA algorithm and the proposed WChOA-FDB variants give higher SSIM results at almost all threshold levels.
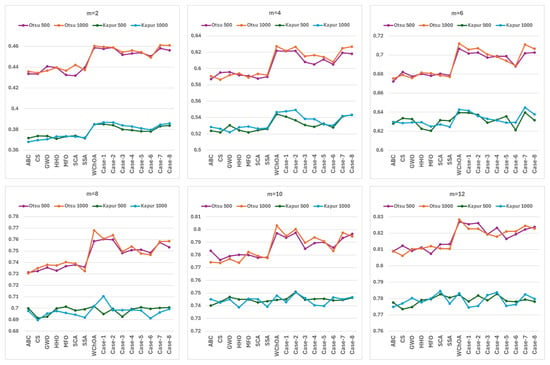
Figure 4.
The average SSIM values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and number of threshold levels (m). (Otsu 500: Otsu’s method for maxFEs = 500 × m, Otsu 1000: Otsu’s method for maxFEs = 1000 × m, Kapur 500: Kapur’s entropy for maxFEs = 500 × m, Kapur 1000: Kapur’s entropy for maxFEs = 1000 × m).
The experimental results indicate that the SSIM of the proposed method has the highest values for the majority of experiments and outperforms all the other algorithms. When maxFEs = 500 × m, the number of experiments in which WChOA and the proposed WChOA-FDB method achieved higher SSIM values were 55 and 43 (out of 60 experiments) for Otsu’s method and Kapur’s entropy, respectively. The number of successful experiments for Otsu’s method and Kapur’s entropy are 56 and 49 when maxFEs = 1000 × m. The consistently high success rates across both objective functions and maxFEs values, with an average of 84.6% better performance, demonstrate the proposed algorithm’s remarkable capability in preserving structural information during image segmentation, indicating excellent correlation between optimized thresholds and perceptual image quality.
FSIM is based on the fact that the human visual system understands an image mainly according to its low-level features. Specifically, phase congruency, which is a dimensionless measure of the significance of a local structure, is used as the primary feature in FSIM. Considering that PC is contrast invariant while the contrast information does affect the human visual system’s perception of image quality, the image gradient magnitude is employed as the secondary feature in FSIM. Therefore, the FSIM is an important metric that is used to evaluate the feature similarity of the original image and the segmented image. If the segmented image and the original image are more similar, the FSIM value is higher. Also, the value of FSIM increases as the number of thresholds increases.
The average FSIM values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and the number of threshold levels are presented in Figure 5. The figure shows the graphs of the average FSIM values of the Otsu and Kapur functions on 10 test images for the maxFEs = 500 × m and maxFEs = 1000 × m for each number of threshold levels. As can be seen from the figure, the WChOA algorithm and the proposed WChOA-FDB variants also give higher FSIM results at almost all number of threshold levels.
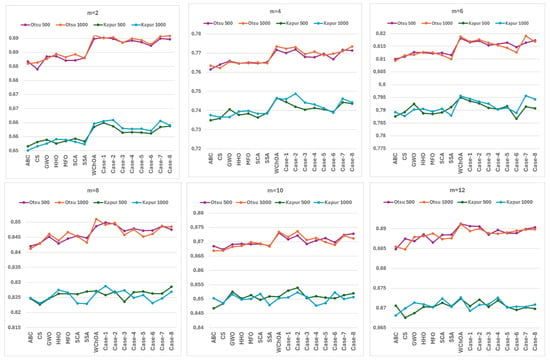
Figure 5.
The average FSIM values of the MHS algorithms for Otsu’s method and Kapur’s entropy for both termination criteria (maxFEs = 500 × m and maxFEs = 1000 × m) and number of threshold levels (m). (Otsu 500: Otsu’s method for maxFEs = 500 × m, Otsu 1000: Otsu’s method for maxFEs = 1000 × m, Kapur 500: Kapur’s entropy for maxFEs = 500 × m, Kapur 1000: Kapur’s entropy for maxFEs = 1000 × m).
The experimental results indicate that the FSIM index of the proposed method has the highest values for the majority of experiments and outperforms all the other algorithms. When maxFEs = 500 × m, the number of experiments in which WChOA and the proposed WChOA-FDB method achieved higher FSIM values were 54 and 48 (out of 60 experiments) for Otsu’s method and Kapur’s entropy, respectively. The number of successful experiments for Otsu’s method and Kapur’s entropy are 51 and 48 when maxFEs = 1000 × m. The high success rates across both objective functions, with an overall average of 83.8% higher performance, confirm the proposed algorithm’s remarkable capability in preserving critical image features during segmentation.
In the study, a huge number of segmented images, 3840 in total, were obtained for 10 images, 6 threshold levels, 16 algorithms, 2 thresholding functions, and 2 maxFEs values. The top-ranking algorithms according to the Friedman scores given in Section 4.3.1. are presented in Table 12. This table shows the success of the proposed method in image segmentation at different threshold levels, thresholding functions, and termination criteria. Images segmented with the algorithms in Table 12 are given in Figure 6, Figure 7, Figure 8 and Figure 9.

Table 12.
Top ranking algorithms according to the Friedman scores.

Figure 6.
Segmentation results of the best algorithms for Otsu’s method and maxFEs = 500 × m.

Figure 7.
Segmentation results of the best algorithms for Otsu’s method and maxFEs = 1000 × m.

Figure 8.
Segmentation results of the best algorithms for Kapur’s method and maxFEs = 500 × m.

Figure 9.
Segmentation results of the best algorithms for Kapur’s method and maxFEs = 1000 × m.
Based on the computational performance analysis, Table 13 presents the execution times in seconds for the base WChOA algorithm and its eight FDB variants across different problem dimensions (m = 2, 6, 12) with maxFEs = 500 × m. The computational performance analysis reveals that all FDB variants demonstrate comparable efficiency to the base WChOA algorithm, with execution times exhibiting predictable scaling characteristics as problem dimensionality increases from m = 2 to m = 12. The algorithms show sub-exponential computational complexity, with approximately 4-fold and 2.8-fold increases in execution time for m = 6 and m = 12, respectively, indicating favorable scalability properties. Among the variants, Case-6 consistently demonstrates the most efficient performance across all tested dimensions (0.723 s, 2.986 s, 8.817 s), while Case-4 and Case-5 exhibit marginally higher computational overhead.

Table 13.
Computation times (in seconds) of the base algorithm and FDB variants for m = 2, 6, 12 and maxFEs = 500d (1 image/1 run).
The tight clustering of execution times within approximately 3.5–6.3% variance across all variants suggests that the FDB enhancements introduce negligible computational penalty while potentially offering distinct algorithmic advantages, thereby positioning computational efficiency as a secondary consideration in variant selection compared to optimization effectiveness and convergence characteristics.
5. Discussion and Conclusions
In this study, a novel MHS algorithm named WChOA-FDB is developed. The algorithm’s performance was evaluated using 10 benchmark functions (IEEE CEC 2020) of different types and complexity levels. The search performance of the algorithm was analyzed using the Friedman and Wilcoxon statistical test methods. The results indicated that the WChOA-FDB variants demonstrated higher search performance when compared to the base WChOA algorithm in all experiments on benchmark functions. In the study, many FDB variants were produced, the eight most successful cases were selected, and their results were given. Then, the performance of these algorithms in the image segmentation problem was evaluated.
Experiments conducted on color image segmentation tasks demonstrate the effectiveness of WChOA-FDB in achieving accurate and efficient segmentation results. The results of image segmentation experiments show that the WChOA-FDB method proposed in the study is more successful than the base algorithm and other competitive algorithms for two thresholding functions, in all threshold levels and maxFEs values. This means that the proposed method exhibits a more balanced search capability compared to its competitors for all segmentation problems with different complexities. This shows the proposed algorithm’s considerably strong practicability in color image segmentation. Also, according to the PSNR, SSIM, and FSIM results, the proposed method demonstrated enhanced performance in image segmentation when compared to other algorithms. It has been observed that among the proposed FDB variants, Case-1, Case-2, Case-4, Case-7, and Case-8 are more successful in the segmentation problem. The synergy between WChOA-FDB and WChOA enhances the algorithm’s robustness, adaptability, and overall performance. The algorithm’s convergence speed, solution quality, and resilience in diverse and dynamic optimization landscapes are notably improved with the integration of FDB.
The comprehensive analysis of both performance results (Table 3, Table 6 and Table 7) reveals a complex algorithmic behavior pattern where Case-8’s dominance in multilevel image segmentation tasks (achieving first rank in 7 out of 24 scenarios) contrasts sharply with its moderate performance in benchmark function optimization (4th place with mean rank 4.752), indicating that algorithm effectiveness is highly task-dependent and cannot be generalized across different optimization domains. Case-4 demonstrates the most robust scalability characteristics by achieving the best overall performance in dimensional analysis (mean rank 4.690) and showing particular strength in high-dimensional problems (rank 4.492 at D = 100), yet it only achieves top performance in two specific image segmentation scenarios, primarily at higher threshold levels with increased computational cost (m = 10,12 with 1000 × m evaluations). Case-2 exhibits remarkable consistency across both evaluation frameworks, maintaining competitive performance in image segmentation tasks (7 first-place rankings) while achieving third place in dimensional scalability (mean rank 4.722), suggesting it represents the most balanced and reliable algorithmic variant for diverse optimization challenges. The stark performance degradation of the original WChOA (worst performer in dimensional analysis with mean rank 6.272, and only one first-place ranking in segmentation tasks) validates the necessity of the proposed hybrid modifications, while Cases 5–8 generally underperform in benchmark optimization despite Case-8’s segmentation success, highlighting the critical importance of algorithm-problem matching in metaheuristic optimization design.
It is observed that the methods proposed in image segmentation studies are generally tested on a small number of images. This is a general limitation of these studies. A larger and more diverse set of test images would provide stronger evidence of the algorithm’s effectiveness. In this study, 10 test images are used for the image segmentation experiments. In future studies, it is aimed to increase the number of images and evaluate the method performance on images with different characteristics such as medical and satellite images. In this study, the performance of the proposed method was compared with seven well-known MHS methods. It aims to compare the proposed method with different MHS algorithms in future studies. Also, parameter optimization for the proposed algorithm can be performed.
Author Contributions
Conceptualization, A.G.Y.; methodology, A.G.Y.; software, S.A.; validation, A.G.Y. and S.A.; writing—original draft preparation, A.G.Y. and S.A.; writing—review and editing, A.G.Y.; supervision, A.G.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare that no funds, grants, or other support was received during the preparation of this manuscript.
Data Availability Statement
The original data presented in the study are openly available in https://doi.org/10.5281/zenodo.15590550 (accessed on 3 July 2025).
Conflicts of Interest
The authors have declared no conflicts of interest.
References
- Biratu, E.S.; Schwenker, F.; Ayano, Y.M.; Debelee, T.G. A Survey of Brain Tumor Segmentation and Classification Algorithms. J. Imaging 2021, 7, 179. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Yuan, D.; Li, L.; Shu, X. MFPNet: Mixed Feature Perception Network for Automated Skin Lesion Segmentation. In Pattern Recognition and Computer Vision. PRCV 2024. Lecture Notes in Computer Science; Lin, Z., Cheng, M.-M., He, R., Ubul, K., Silamu, W., Zha, H., Zhou, J., Liu, C.-L., Eds.; Springer: Singapore, 2025; Volume 15044. [Google Scholar] [CrossRef]
- Muhammad, K.; Hussain, T.; Ullah, H.; Del Ser, J.; Rezaei, M.; Kumar, N.; Hijji, M.; Bellavista, P.; de Albuquerque, V.H.C. Vision-Based Semantic Segmentation in Scene Understanding for Autonomous Driving: Recent Achievements, Challenges, and Outlooks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22694–22715. [Google Scholar] [CrossRef]
- Singh, V.; Misra, A. Detection of plant leaf diseases using image segmentation and soft computing techniques. Inf. Process. Agric. 2017, 4, 41–49. [Google Scholar] [CrossRef]
- Sun, Y.; Bhanu, B. Symmetry integrated region-based image segmentation. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 826–831. [Google Scholar] [CrossRef]
- Saha, S.; Bandyopadhyay, S. MRI brain image segmentation by fuzzy symmetry based genetic clustering technique. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4417–4424. [Google Scholar] [CrossRef]
- Chen, H.; Qin, Z.; Ding, Y.; Tian, L.; Qin, Z. Brain tumor segmentation with deep convolutional symmetric neural network. Neurocomputing 2020, 392, 305–313. [Google Scholar] [CrossRef]
- Eisham, Z.K.; Haque, M.; Rahman, S.; Nishat, M.M.; Faisal, F.; Islam, M.R. Chimp optimization algorithm in multilevel image thresholding and image clustering. Evol. Syst. 2022, 14, 605–648. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B.L. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–168. [Google Scholar]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Suresh, S.; Lal, S. An efficient cuckoo search algorithm based multilevel thresholding for segmentation of satellite images using different objective functions. Expert Syst. Appl. 2016, 58, 184–209. [Google Scholar] [CrossRef]
- Pare, S.; Kumar, A.; Bajaj, V.; Singh, G.K. An efficient method for multilevel color image thresholding using cuckoo search algorithm based on minimum cross entropy. Appl. Soft Comput. 2017, 61, 570–592. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Futur. Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Su, H.; Zhao, D.; Yu, F.; Heidari, A.A.; Zhang, Y.; Chen, H.; Li, C.; Pan, J.; Quan, S. Horizontal and vertical search artificial bee colony for image segmentation of COVID-19 X-ray images. Comput. Biol. Med. 2022, 142, 105181. [Google Scholar] [CrossRef]
- Liu, Q.; Li, N.; Jia, H.; Qi, Q.; Abualigah, L. A chimp-inspired remora optimization algorithm for multilevel thresholding image segmentation using cross entropy. Artif. Intell. Rev. 2023, 56, 159–216. [Google Scholar] [CrossRef]
- Sharma, A.; Chaturvedi, R.; Bhargava, A. A novel opposition based improved firefly algorithm for multilevel image segmentation. Multimed. Tools Appl. 2022, 81, 15521–15544. [Google Scholar] [CrossRef]
- Houssein, E.H.; Abdelkareem, D.A.; Emam, M.M.; Hameed, M.A.; Younan, M. An efficient image segmentation method for skin cancer imaging using improved golden jackal optimization algorithm. Comput. Biol. Med. 2022, 149, 106075. [Google Scholar] [CrossRef] [PubMed]
- Gharehchopogh, F.S.; Ibrikci, T. An improved African vultures optimization algorithm using different fitness functions for multi-level thresholding image segmentation. Multimed. Tools Appl. 2023, 83, 16929–16975. [Google Scholar] [CrossRef]
- Kumar, A.; Vishwakarma, A.; Singh, G.K. Multilevel thresholding for crop image segmentation based on recursive minimum cross entropy using a swarm-based technique. Comput. Electron. Agric. 2022, 203, 107488. [Google Scholar] [CrossRef]
- Agrawal, S.; Panda, R.; Choudhury, P.; Abraham, A. Dominant color component and adaptive whale optimization algorithm for multilevel thresholding of color images. Knowl.-Based Syst. 2022, 240, 108172. [Google Scholar] [CrossRef]
- Tan, Z.; Li, K.; Wang, Y. An improved cuckoo search algorithm for multilevel color image thresholding based on modified fuzzy entropy. J. Ambient. Intell. Humaniz. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Houssein, E.H.; Mohamed, G.M.; Ibrahim, I.A.; Wazery, Y.M. An efficient multilevel image thresholding method based on improved heap-based optimizer. Sci. Rep. 2023, 13, 9094. [Google Scholar] [CrossRef]
- Wang, Z.; Mo, Y.; Cui, M.; Hu, J.; Lyu, Y.; Oliva, D. An improved golden jackal optimization for multilevel thresholding image segmentation. PLoS ONE 2023, 18, e0285211. [Google Scholar] [CrossRef]
- Abualigah, L.; Al-Okbi, N.K.; Elaziz, M.A.; Houssein, E.H. Boosting Marine Predators Algorithm by Salp Swarm Algorithm for Multilevel Thresholding Image Segmentation. Multimed. Tools Appl. 2022, 81, 16707–16742. [Google Scholar] [CrossRef]
- Swain, M.; Tripathy, T.T.; Panda, R.; Agrawal, S.; Abraham, A. Differential exponential entropy-based multilevel threshold selection methodology for colour satellite images using equilibrium-cuckoo search optimizer. Eng. Appl. Artif. Intell. 2022, 109, 104599. [Google Scholar] [CrossRef]
- Thomas, E.; Kumar, S.N. Harris Hawks Optimization-Based Multilevel Thresholding Segmentation of Magnetic Resonance Brain Images. In International Conference on Communication, Devices and Computing; Springer Nature: Singapore, 2023. [Google Scholar]
- Renugambal, A.; Bhuvaneswari, K.S.; Tamilarasan, A. Hybrid SCCSA: An efficient multilevel thresholding for enhanced image segmentation. Multimed. Tools Appl. 2023, 82, 32711–32753. [Google Scholar] [CrossRef]
- Akay, R.; Saleh, R.A.A.; Farea, S.M.O.; Kanaan, M. Multilevel thresholding segmentation of color plant disease images using metaheuristic optimization algorithms. Neural Comput. Appl. 2021, 34, 1161–1179. [Google Scholar] [CrossRef]
- Akan, T.; Oliva, D.; Feizi-Derakhshi, A.R.; Feizi-Derakhshi, A.R.; Pérez-Cisneros, M.; Bhuiyan, M.A.N. Battle royale optimizer for multi-level image thresholding. J. Supercomput. 2023, 80, 5298–5340. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Kong, M.; Zhang, T. SCGJO: A hybrid golden jackal optimization with a sine cosine algorithm for tackling multilevel thresholding image segmentation. Multimed. Tools Appl. 2023, 83, 7681–7719. [Google Scholar] [CrossRef]
- Kang, X.; Hua, C. Multilevel thresholding image segmentation algorithm based on Mumford–Shah model. J. Intell. Syst. 2023, 32, 20220290. [Google Scholar] [CrossRef]
- Wang, C.; Tu, C.; Wei, S.; Yan, L.; Wei, F. MSWOA: A Mixed-Strategy-Based Improved Whale Optimization Algorithm for Multilevel Thresholding Image Segmentation. Electronics 2023, 12, 2698. [Google Scholar] [CrossRef]
- Khishe, M.; Nezhadshahbodaghi, M.; Mosavi, M.R.; Martin, D. A Weighted Chimp Optimization Algorithm. IEEE Access 2021, 9, 158508–158539. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Orujpour, M.; Feizi-Derakhshi, M.-R.; Akan, T. A multimodal butterfly optimization using fitness-distance balance. Soft Comput. 2023, 27, 17909–17922. [Google Scholar] [CrossRef]
- Ozkaya, B.; Guvenc, U.; Bingol, O. Fitness Distance Balance Based LSHADE Algorithm for Energy Hub Economic Dispatch Problem. IEEE Access 2022, 10, 66770–66796. [Google Scholar] [CrossRef]
- Zheng, K.; Yuan, X.; Xu, Q.; Dong, L.; Yan, B.; Chen, K. Hybrid particle swarm optimizer with fitness-distance balance and individual self-exploitation strategies for numerical optimization problems. Inf. Sci. 2022, 608, 424–452. [Google Scholar] [CrossRef]
- Tang, Z.; Tao, S.; Wang, K.; Lu, B.; Todo, Y.; Gao, S. Chaotic Wind Driven Optimization with Fitness Distance Balance Strategy. Int. J. Comput. Intell. Syst. 2022, 15, 46. [Google Scholar] [CrossRef]
- Liang, J.J.; Suganthan, P.N.; Qu, B.Y.; Gong, D.W.; Yue, C.T. Problem Definitions and Evaluation Criteria for the CEC 2020 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization, Technical Report 201911; Nanyang Technological University: Singapore, 2020.
- The Berkeley Segmentation Dataset: Images. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/BSDS300/html/dataset/images.html (accessed on 3 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).