Symmetries, Conservation Laws, and Exact Solutions of a Potential Kadomtsev–Petviashvili Equation with Power-Law Nonlinearity
Abstract
1. Introduction
2. Conservation Laws Associated with Equation (2)
- Case 1: p is arbitrary but
- Case 2:
- Case 3:
- Case 4:
3. Symmetry Reduction of Equation (2)
3.1. Case
3.2. Case
4. Exact Solution of (2) Using the Kudryashov Method and Direct Integration
- Step 1. The transformation , where k and are constants, reduces Equation (64) to the ordinary differential equation (ODE)
- Step 2. It is assumed that the exact solution of Equation (65) can be expressed by a polynomial in Q as follows:where the coefficients () are constants to be determined, such that , and is the solution of the first-order nonlinear ODEWe note that Equation (67) has the solution given byThe positive integer N is determined by taking the pole order of general solution for Equation (65). Substituting into monomials of Equation (65) and comparing the two or more terms with smallest powers in the equation, we find the value for
- Step 3. We substitute the derivatives of with respect to z and the expression for into Equation (65), and as a result, we obtain the equation that has the function Q, coefficients , and parameters of Equation (65).
- Step 4. The KM effectively reduces the task of finding an exact solution to the ordinary differential equation (ODE) (65) to solve a corresponding system of algebraic equations. By substituting the assumed solution form into the ODE and collecting like powers of the function one obtains a polynomial expression in Setting the coefficients of each power of Q to zero yields a system of algebraic equations, which can then be solved to determine the parameters of the exact solution. The resulting system takes the form
- Step 5. Solving the system of algebraic equations, we obtain values of coefficients and relations for the parameters of Equation (65). As a result of the solution, we obtain exact solutions of Equation (65) in the form (66).
- Step 6. We present the solution of Equation (65) in a more convenient form and verify the solutions.
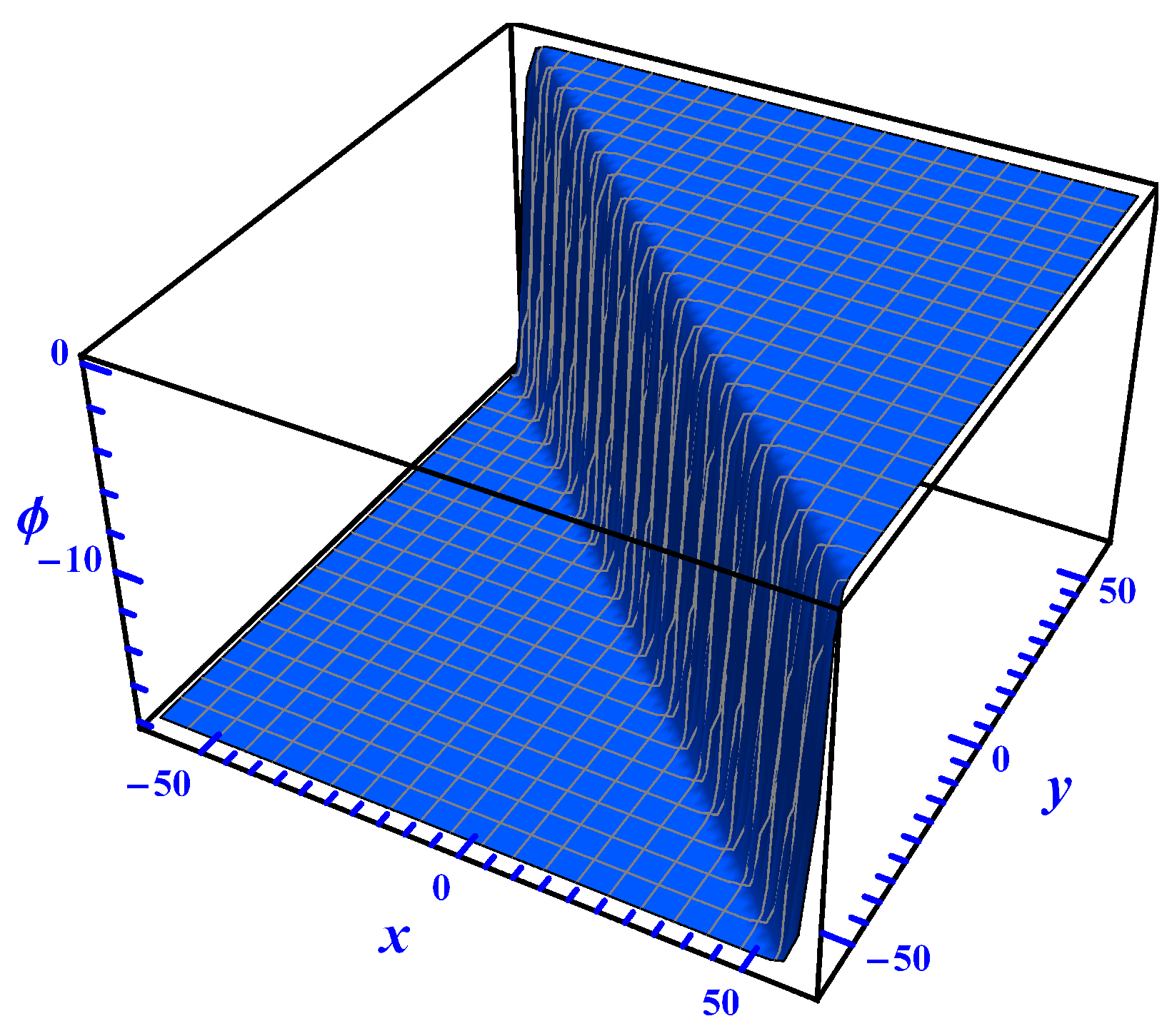
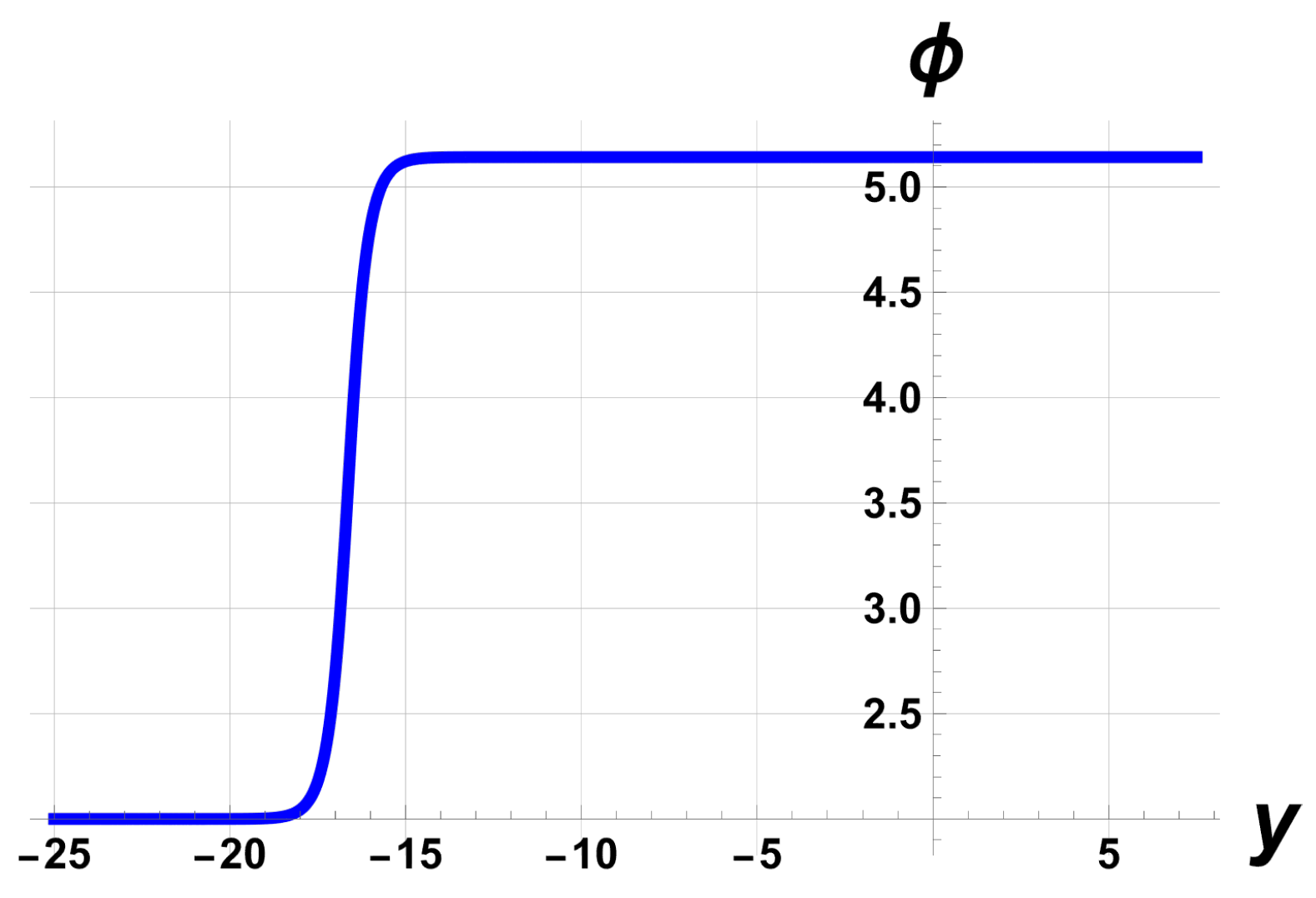
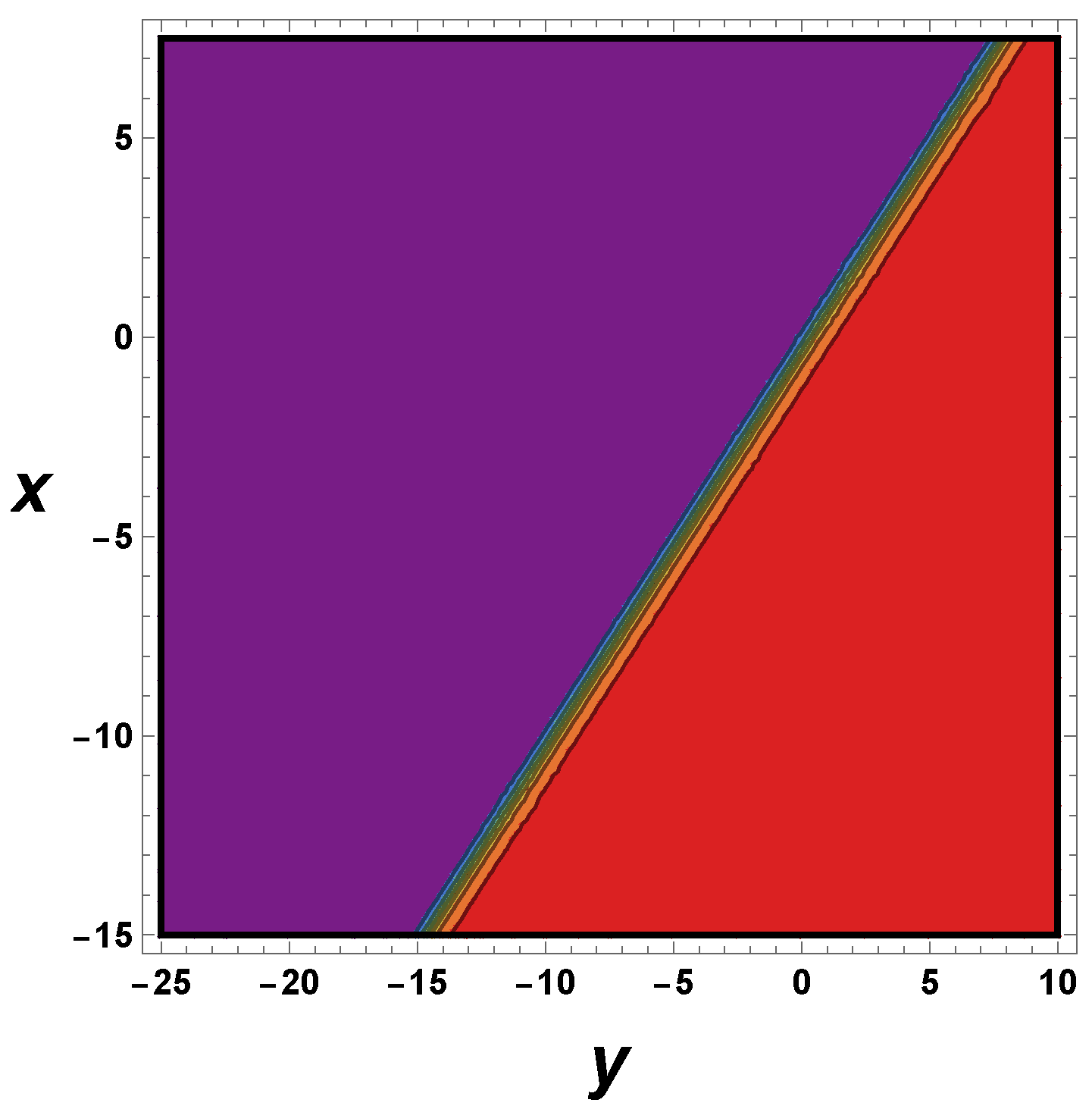
4.1. Solutions of (2) with Using the Kudryashov Method
4.2. Solutions of (2) with Using Direct Integration
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NLPDE | Nonlinear Partial Differential Equation |
| NLPDEs | Nonlinear Partial Differential Equations |
| PDEs | Partial Differential Equations |
| PDE | Partial Differential Equation |
| ODEs | Ordinary Differential Equations |
| ODE | Ordinary Differential Equation |
| KDV | Korteweg–de Vries |
| KP | Kadomtsev–Petviashvili |
| PKP | Potential Kadomtsev–Petviashvili |
| PKPp | Potential Kadomtsev–Petviashvili with Power-Law Nonlinearity |
| VCPKP | Variable Coefficient Potential Kadomtsev–Petviashvili |
| KM | Kudryashov Method |
References
- Chatziafratis, A.; Ozawa, T.; Tian, S.F. Rigorous analysis of the unified transform method and long-range instabilities for the inhomogeneous time-dependent Schrödinger equation on the quarter-plane. Math. Ann. 2024, 389, 3535–3602. [Google Scholar] [CrossRef]
- Wu, Z.; Tian, S. Nonlinear stability of smooth multi-solitons for the Dullin-Gottwald-Holm equation. J. Differ. Equ. 2024, 412, 408–446. [Google Scholar] [CrossRef]
- Wu, Z.; Tian, S.; Liu, Y.; Wang, Z. Stability of smooth multisolitons for the two-component Camassa–Holm system. J. Lond. Math. Soc. 2025, 111, e70158. [Google Scholar] [CrossRef]
- Sherawat, A.; Jiwari, R. New multiple analytic solitonary solutions and simulation of (2+1)-dimensional generalized Benjamin-Bona-Mahony-Burgers model. Nonlinear Dyn. 2023, 111, 13297–13325. [Google Scholar]
- Kumar, V.; Gupta, R.K.; Jiwari, R. Painlevé analysis, Lie symmetries and exact solutions for variable coefficients Benjamin—Bona—Mahony—Burger (BBMB) equation. Commun. Theor. Phys. 2013, 2, 175. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai sur la théorie des Eaux Courantes; Imprimerie Nationale: Flers en Escrebieux, France, 1877; pp. 1–680. [Google Scholar]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 1970, 15, 539–541. [Google Scholar]
- Xu, P.; Huang, H.; Wang, K. Dynamics of real and complex multi-soliton solutions, novel soliton molecules, asymmetric solitons and diverse wave solutions to the Kadomtsev-Petviashvili equation. Alex. Eng. J. 2025, 125, 537–544. [Google Scholar] [CrossRef]
- Liu, H.; Shen, J.; Geng, X. Higher-order pole solutions of Kadomtsev-Petviashvili I equation. J. Math. Anal. Appl. 2025, 125, 129718. [Google Scholar] [CrossRef]
- Asadullah, M.; Javid, A.; Raza, N.; Chahlaoui, Y.; Bekir, A. Envelope solitons and wave structures in the (2+1)-dimensional KP equation. Mod. Phys. Lett. B 2025, 2550174. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Alrashedi, Y.; Ahmad, H. Discovery of exact solitons to the fractional KP-MEW equation with stability analysis. Eur. Phys. J. Plus 2025, 140, 316. [Google Scholar] [CrossRef]
- Bhan, C.; Karwasra, R.; Malik, S.; Kumar, S.; Arnous, A.H.; Sha, N.A.; Chung, J. Bifurcation, chaotic behavior and soliton solutions to the KP-BBM equation through new Kudryashov and generalized Arnous methods. AIMS Math. 2024, 9, 8749–8767. [Google Scholar] [CrossRef]
- Humbu, I.; Muatjetjeja, B.; Motsumi, T.G.; Adem, A.R. Multiple solitons, periodic solutions and other exact solutions of a generalized extended (2+1)-dimensional Kadomstev–Petviashvili equation. J. Appl. Anal. 2024, 30, 197–208. [Google Scholar] [CrossRef]
- Senthilvelan, M. On the extended applications of homogenous balance method. Appl. Math. Comput. 2001, 123, 381–388. [Google Scholar] [CrossRef]
- Kaya, D.; El-Sayed, S.M. Numerical soliton-like solutions of the potential Kadomtsev-Petviashvili equation by the decomposition method. Phys. Lett. A 2003, 320, 192–199. [Google Scholar] [CrossRef]
- Li, D.; Zhang, H. Symbolic computation and various exact solutions of potential Kadomtsev-Petviashvili equation. Appl. Math. Comput. 2003, 145, 351–359. [Google Scholar]
- Xian, D.; Dai, Z. Application of Exp-function method to potential Kadomtsev-Petviashvili equation. Chaos Soliton Fract. 2009, 42, 2653–2659. [Google Scholar]
- Inan, I.E.; Kaya, D. Some exact solutions to the potential Kadomtsev-Petviashvili equation and to a system of shallow water wave equations. Phys. Lett. A 2006, 355, 314–318. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Wang, M.; Chen, X. Exact solutions for nonlinear evolution equations modified by power-law terms. Appl. Math. Comput. 2015, 269, 632–641. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Ibragimov, N.H. A new conservation theorems. Appl. Math. Comput. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G.W. Direct construction method for conservation laws of partial differential equations. Part I: Examples of conservation law classifications. Eur. J. Appl. Math. 1997, 13, 545–566. [Google Scholar] [CrossRef]
- Xian, D.; Chen, H. Symmetry reductions and new exact non-traveling wave solutions of potential Kadomtsev–Petviashvili equation with p-power. Appl. Math. Comput. 2010, 216, 70–79. [Google Scholar] [CrossRef]
- Gupta, R.K.; Bansal, A. Painleve analysis, Lie symmetries and invariant solutions of potential Kadomtsev-Petviashvili equation with time dependent coefficients. Appl. Math. Comput. 2013, 219, 5290–5302. [Google Scholar]
- Xian, D.; Chen, H. Symmetry reduced and new exact non-traveling wave solutions of potential Kadomtsev-Petviashvili equation with p-power. Appl. Math. Comput. 2010, 217, 1340–1349. [Google Scholar] [CrossRef]
- Sebogodi, M.C.; Muatjetjeja, B.; Adem, A.R. Exact solutions and conservation laws of a (2+1)-dimensional combined potential kadomtsev-petviashvili-b-type kadomtsev-petviashvili equation. Int. J. Theor. Phys. 2023, 62, 165. [Google Scholar] [CrossRef]
- Afolabi, O.A.; Johnpillai, A.G. Exact solutions of generalized KP equations using Kudryashov and Lie symmetry methods. Results Phys. 2021, 25, 104311. [Google Scholar]
- Alquran, M.; Mohd, N.A. Wave structures and solutions of KP-type equations via analytical techniques. J. Math. 2022, 12, 2042. [Google Scholar]
- Umaru, M.A.; Mahgoub, A. Noether symmetries and conservation laws of nonlinear evolution equations in 2D. Symmetry 2023, 15, 870. [Google Scholar]
- Muatjetjeja, B.; Khalique, C.M. Symmetry analysis and conservation laws for a coupled (2+1)-dimensional hyperbolic system. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 1252–1262. [Google Scholar] [CrossRef]
- Noether, E. Invariante variationsprobleme. Math. Phys. Kl. Heft 1918, 2, 235–257. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, Graduate Texts in Mathematics, 2nd ed.; Springer: Berlin, Germany, 1993. [Google Scholar]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Solitons of the complex modified Korteweg–de Vries hierarchy. Chaos Solitons Fractals 2024, 184, 115010. [Google Scholar] [CrossRef]
- Ege, S.M.; Misirli, E. The modified Kudryashov method for solving some fractional-order nonlinear equations. Adv. Differ. Equ. 2014, 135, 1–13. [Google Scholar] [CrossRef]
- Hubert, M.B.; Betchewe, G.; Doka, S.Y.; Crepin, K.T. Soliton wave solutions for the nonlinear transmission line using the Kudryashov method and the (G′/G)-expansion method. Appl. Math. Comput. 2014, 239, 299–309. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Moatimid, G.M.; Al-Nowehy, A. The generalized Kudryashov method and its applications for solving nonlinear PDEs in mathematical physics. Sci. J. Math. Res. 2015, 5, 19–39. [Google Scholar]
- Islam, M.S.; Khan, K.; Arnous, A.H. Generalized Kudryashov method for solving some (3+1)-dimensional nonlinear evolution equations. New Trends Math. Sci. 2015, 3, 46–57. [Google Scholar]
- Cheviakov, A.F. GeM software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 2007, 176, 48–61. [Google Scholar] [CrossRef]
- Adem, A.R.; Khalique, C.M.; Biswas, A. Solutions of Kadomtsev–Petviashvili equation with power law nonlinearity in 1+3 dimensions. Math. Method Appl. Sci. 2011, 34, 532–543. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mothibi, D.M. Symmetries, Conservation Laws, and Exact Solutions of a Potential Kadomtsev–Petviashvili Equation with Power-Law Nonlinearity. Symmetry 2025, 17, 1053. https://doi.org/10.3390/sym17071053
Mothibi DM. Symmetries, Conservation Laws, and Exact Solutions of a Potential Kadomtsev–Petviashvili Equation with Power-Law Nonlinearity. Symmetry. 2025; 17(7):1053. https://doi.org/10.3390/sym17071053
Chicago/Turabian StyleMothibi, Dimpho Millicent. 2025. "Symmetries, Conservation Laws, and Exact Solutions of a Potential Kadomtsev–Petviashvili Equation with Power-Law Nonlinearity" Symmetry 17, no. 7: 1053. https://doi.org/10.3390/sym17071053
APA StyleMothibi, D. M. (2025). Symmetries, Conservation Laws, and Exact Solutions of a Potential Kadomtsev–Petviashvili Equation with Power-Law Nonlinearity. Symmetry, 17(7), 1053. https://doi.org/10.3390/sym17071053





