Ferromagnet-Type System: Integrable Flows of Curves/Surfaces, Soliton Solutions, and Equivalence
Abstract
1. Introduction
2. The Myrzakulov-XIII Equation
3. Integrable Flows of Space Curves Induced by the M-XIII Equation
4. Gauge Equivalent Counterpart
5. Integrable Surfaces Related to the M-XIII Equation
5.1. Case 1:
5.2. Case 2:
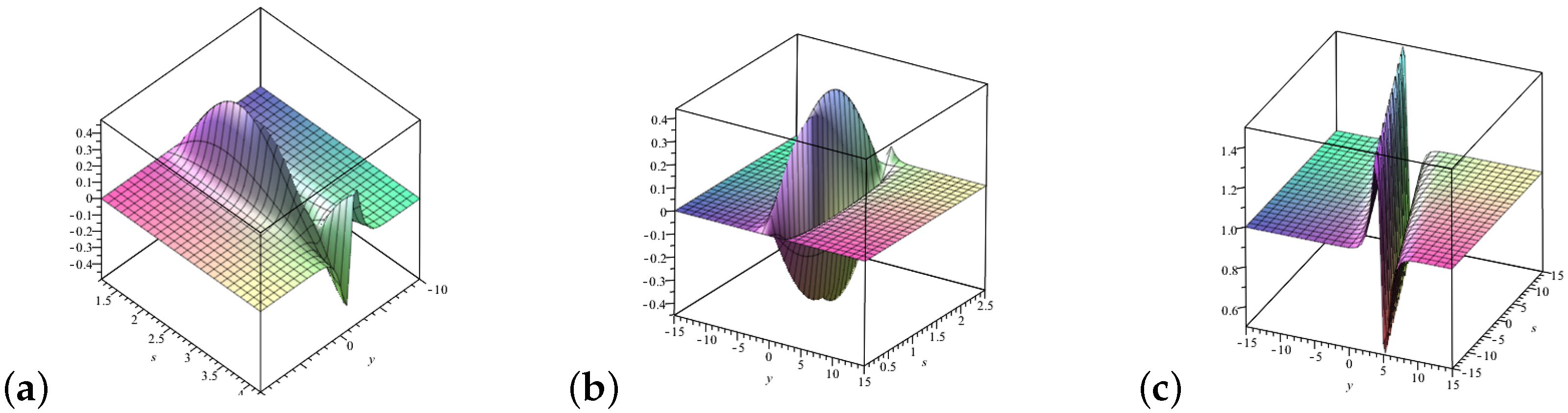
6. Soliton Solutions of the M-XIII Equation
7. Fractional CCD Equation
7.1. Description of the Kudryashov Method
7.2. Solutions of the Fractional Nonlinear Schrödinger Equation
- Real part:
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Lakshmanan, M. The Fascinating World of the Landau-Lifshitz-Gilbert Equation: An Overview. Phil. Trans. R. Soc. A 2011, 369, 1280–1300. [Google Scholar] [CrossRef] [PubMed]
- Myrzakulov, R.; Vijayalakshmi, S.; Nugmanova, G.; Lakshmanan, M. A (2+1)-Dimensional Integrable Spin Model: Geometrical and Gauge Equivalent Counterpart, Solitons and Localized Coherent Structures. Phys. Lett. A 1997, 233, 391–396. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Takhtadzhyan, L.A. Equivalence of the nonlinear Schrödinger equation and the equation of a Heisenberg ferromagnet. Theor. Math. Phys. 1979, 38, 17–23. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Gautam, S.; Adhikari, S.K. Solitons in a Spin-Orbit-Coupled Spin-1 Bose-Einstein Condensate. Braz. J. Phys. 2021, 51, 297–307. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Bullough, R.K. Geometry of generalised nonlinear Schrödinger and Heisenberg ferromagnetic spin equations with linearly x-dependent coefficients. Phys. Lett. A 1980, 80, 287–292. [Google Scholar] [CrossRef]
- Ma, L.-Y.; Shen, S.-F.; Zhu, Z.-N. Soliton solution and gauge equivalence for an integrable nonlocal complex modified Korteweg-de Vries equation. J. Math. Phys. 2017, 58, 103501. [Google Scholar] [CrossRef]
- Mikeska, H.-J.; Steiner, M. Solitary excitations in one-dimensional magnets. Adv. Phys. 1991, 40, 191–356. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Nugmanova, G.; Syzdykova, R. Gauge Equivalence Between (2+1)-Dimensional Continuous Heisenberg Ferromagnetic Models and Nonlinear Schrödinger-Type Equations. J. Phys. A Math. Theor. 1998, 31, 9535–9545. [Google Scholar] [CrossRef]
- Porsezian, K.; Tamizhmani, K.M.; Lakshmanan, M. Geometrical equivalence of a deformed Heisenberg spin equation and the generalized nonlinear Schrödinger equation. Phys. Lett. A 1987, 124, 159–160. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Terng, C.L.; Uhlenbeck, K. Geometry of solitons. Not. AMS 2000, 47, 17–25. [Google Scholar]
- Sasaki, R. Soliton equations and pseudospherical surfaces. Nucl. Phys. B 1979, 154, 343–357. [Google Scholar] [CrossRef]
- Takhtajan, L.A. Integration of the continuous Heisenberg spin chain through the inverse scattering method. Phys. Lett. A 1977, 64, 235–238. [Google Scholar] [CrossRef]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Jiao, W.; Xianguo, G.; Xin, W. An integrable generalization of the Fokas–Lenells equation: Darboux transformation, reduction and explicit soliton solutions. Chin. Phys. B 2024, 33, 070202. [Google Scholar]
- Batool, N.; Masood, W.; Siddiq, M.; Alhejaili, W.; El-Sherif, L.S.; El-Tantawy, S.A. Interaction of Gardner dust ion-acoustic multiple solitons in a dusty plasma: Insights from Cassini observations. Braz. J. Phys. 2025, 55, 112. [Google Scholar] [CrossRef]
- Lakshmanan, M. Continuum spin system as an exactly solvable dynamical system. Phys. Lett. A 1977, 61, 53–54. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Daniel, M.; Amuda, R. Nonlinear spin-phonon excitations in an inhomogeneous compressible biquadratic Heisenberg spin chain. Physica A 1997, 234, 715–724. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Pashaev, O.; Kholmurodov, K. Particle-like excitations in many-component magnon-phonon systems. Phys. Scr. 1986, 33, 378–384. [Google Scholar] [CrossRef]
- Yan, Z.-W.; Chen, M.-R.; Wu, K.; Zhao, W.-Z. (2+1)-Dimensional integrable Heisenberg supermagnet model. J. Phys. Soc. Jpn. 2012, 81, 094006. [Google Scholar] [CrossRef]
- Yan, Z.-W.; Chen, M.-R.; Wu, K.; Zhao, W.-Z. Integrable deformations of the (2+1)-dimensional Heisenberg ferromagnetic model. Commun. Theor. Phys. 2012, 58, 463–468. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Lakshmanan, M.; Vijayalakshmi, S.; Danlybaeva, A. Motion of curves and surfaces and nonlinear evolution equations in (2+1) dimensions. J. Math. Phys. 1998, 39, 3765–3771. [Google Scholar]
- Myrzakulov, R.; Makhankov, V.G.; Pashaev, O. Gauge equivalence, supersymmetry and classical solutions of the ospu(1,1/1) Heisenberg model and the nonlinear Schrödinger equation. Lett. Math. Phys. 1988, 16, 83–92. [Google Scholar]
- Anco, S.C.; Myrzakulov, R. Integrable generalizations of Schrödinger maps and Heisenberg spin models from Hamiltonian flows of curves and surfaces. J. Geom. Phys. 2010, 60, 1576–1603. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Martina, L.; Kozhamkulov, T.A.; Myrzakul, K. Integrable Heisenberg ferromagnets and soliton geometry of curves and surfaces. In Nonlinear Physics: Theory and Experiment. II; World Scientific: London, UK, 2003; pp. 248–253. [Google Scholar]
- Martina, L.; Myrzakul, K.; Myrzakulov, R.; Soliani, G. Deformation of surfaces, integrable systems, and Chern–Simons theory. J. Math. Phys. 2001, 42, 1397–1417. [Google Scholar] [CrossRef]
- Feng, B.-F.; Maruno, K.; Ohta, Y. Geometric formulation and multi-dark soliton solution to the defocusing complex short pulse equation. Stud. Appl. Math. 2017, 138, 343–367. [Google Scholar] [CrossRef]
- Novikov, S. The Hamiltonian formalism and a multivalued analogue of Morse theory. Russ. Math. Surv. 1982, 37, 1–56. [Google Scholar] [CrossRef]
- Balakrishnan, R. Geometry and nonlinear evolution equations. Pramana J. Phys. 1997, 48, 189–204. [Google Scholar] [CrossRef]
- Hussien, R.A.; Mohamed, S.G. Generated surfaces via inextensible flows of curves in R3. J. Appl. Math. 2016, 6178961. [Google Scholar]
- Dullin, H.R.; Gottwald, G.A.; Holm, D.D. Camassa–Holm, Korteweg–de Vries-5 and other asymptotically equivalent equations for shallow water waves. Fluid Dyn. Res. 2003, 33, 73–95. [Google Scholar] [CrossRef]
- Barman, H.K.; Roy, R.; Mahmud, F.; Akbar, M.A.; Osman, M.S. Harmonizing wave solutions to the Fokas–Lenells model through the generalized Kudryashov method. Optik 2021, 229, 166294. [Google Scholar] [CrossRef]
- Sulaiman, T.; Abdulkadir, T.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota–Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of optical solitons of dimensionless Fokas–Lenells equation with perturbation term using Sardar sub-equation method. Opt. Quant. Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Xie, X.-Y.; Bo, T.; Sun, W.-R.; Sun, Y.; Liu, D.-Y. Soliton collisions for a generalized variable-coefficient coupled Hirota–Maxwell–Bloch system for an erbium-doped optical fiber. J. Mod. Opt. 2015, 62, 1374–1380. [Google Scholar] [CrossRef]
- Feng, B.-F. Complex short pulse and coupled complex short pulse equations. Physica D 2015, 297, 62–75. [Google Scholar] [CrossRef]
- Shen, S.; Feng, B.-F.; Ohta, Y. From the real and complex coupled dispersionless equations to the real and complex short pulse equations. Stud. Appl. Math. 2016, 136, 64–88. [Google Scholar] [CrossRef]
- Matsuno, Y. Integrable multi-component generalization of a modified short pulse equation. J. Math. Phys. 2016, 57, 111507. [Google Scholar] [CrossRef]
- Ghosh, U.N.; Abdikian, A.; Chatterjee, P. Study of multi-solitons, breather soliton structures with (r,q) distributed ions and electrons. Braz. J. Phys. 2024, 54, 218. [Google Scholar] [CrossRef]
- Zhassybayeva, M.; Bekova, G.; Yesmakhanova, K.; Myrzakulov, R. Integrable motions of curves of the induced Fokas–Lenells equation. Optik 2023, 286, 170979. [Google Scholar] [CrossRef]
- Yesmakhanova, K.; Zhassybayeva, M.; Myrzakulov, R. Soliton surfaces induced by the Fokas–Lenells equation. J. Phys. Conf. Ser. 2019, 1416, 012042. [Google Scholar] [CrossRef]
- Myrzakul, A.; Myrzakulov, R. Integrable motion of two interacting curves, spin systems and the Manakov system. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1550134. [Google Scholar] [CrossRef]
- Awadalla, M.; Taishiyeva, A.; Myrzakulov, R.; Alahmadi, J.; Zaagan, A.A.; Bekir, A. Exact analytical soliton solutions of the M-fractional Akbota equation. Sci. Rep. 2024, 14, 13360. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nugmanova, G.; Bekova, G.; Zhassybayeva, M.; Taishiyeva, A.; Yesmakhanova, K.; Myrzakulova, Z. Ferromagnet-Type System: Integrable Flows of Curves/Surfaces, Soliton Solutions, and Equivalence. Symmetry 2025, 17, 1041. https://doi.org/10.3390/sym17071041
Nugmanova G, Bekova G, Zhassybayeva M, Taishiyeva A, Yesmakhanova K, Myrzakulova Z. Ferromagnet-Type System: Integrable Flows of Curves/Surfaces, Soliton Solutions, and Equivalence. Symmetry. 2025; 17(7):1041. https://doi.org/10.3390/sym17071041
Chicago/Turabian StyleNugmanova, Gulgassyl, Guldana Bekova, Meruyert Zhassybayeva, Aigul Taishiyeva, Kuralay Yesmakhanova, and Zhaidary Myrzakulova. 2025. "Ferromagnet-Type System: Integrable Flows of Curves/Surfaces, Soliton Solutions, and Equivalence" Symmetry 17, no. 7: 1041. https://doi.org/10.3390/sym17071041
APA StyleNugmanova, G., Bekova, G., Zhassybayeva, M., Taishiyeva, A., Yesmakhanova, K., & Myrzakulova, Z. (2025). Ferromagnet-Type System: Integrable Flows of Curves/Surfaces, Soliton Solutions, and Equivalence. Symmetry, 17(7), 1041. https://doi.org/10.3390/sym17071041





