On the Symmetry and Domination Integrity of Some Bidegreed Graphs
Abstract
1. Introduction
1.1. Scientific Motivation
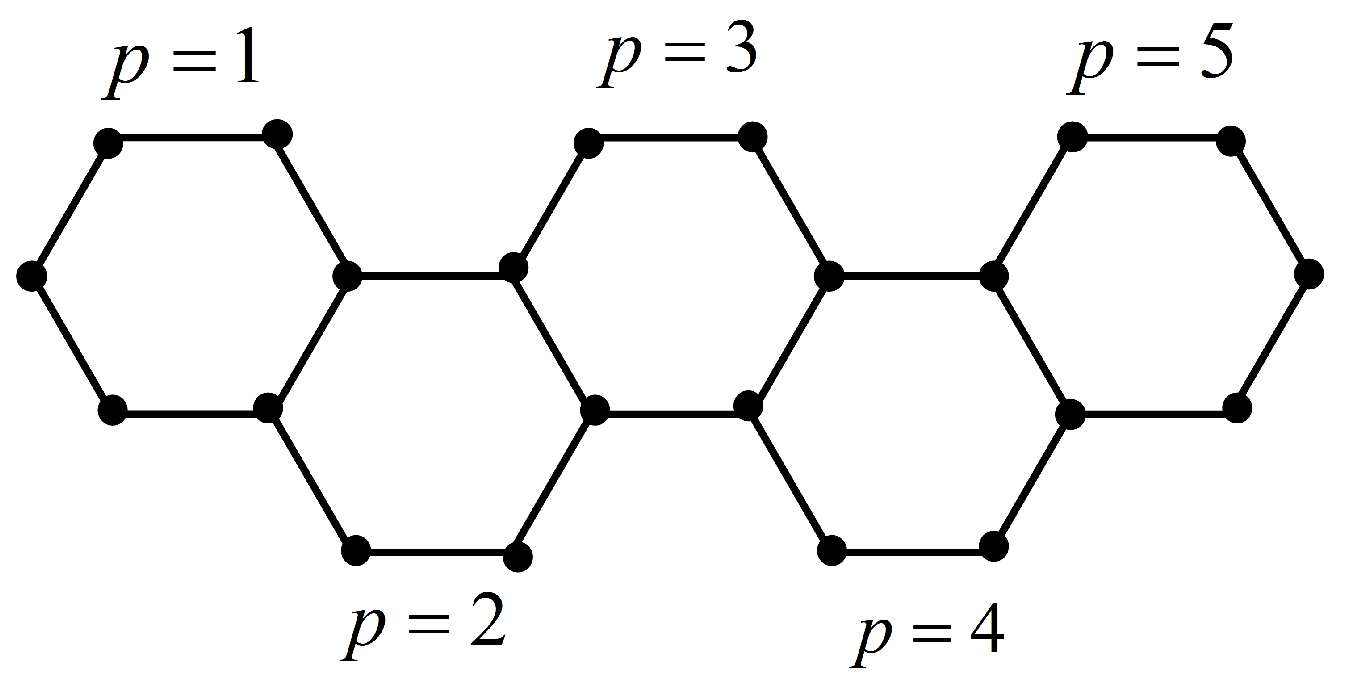
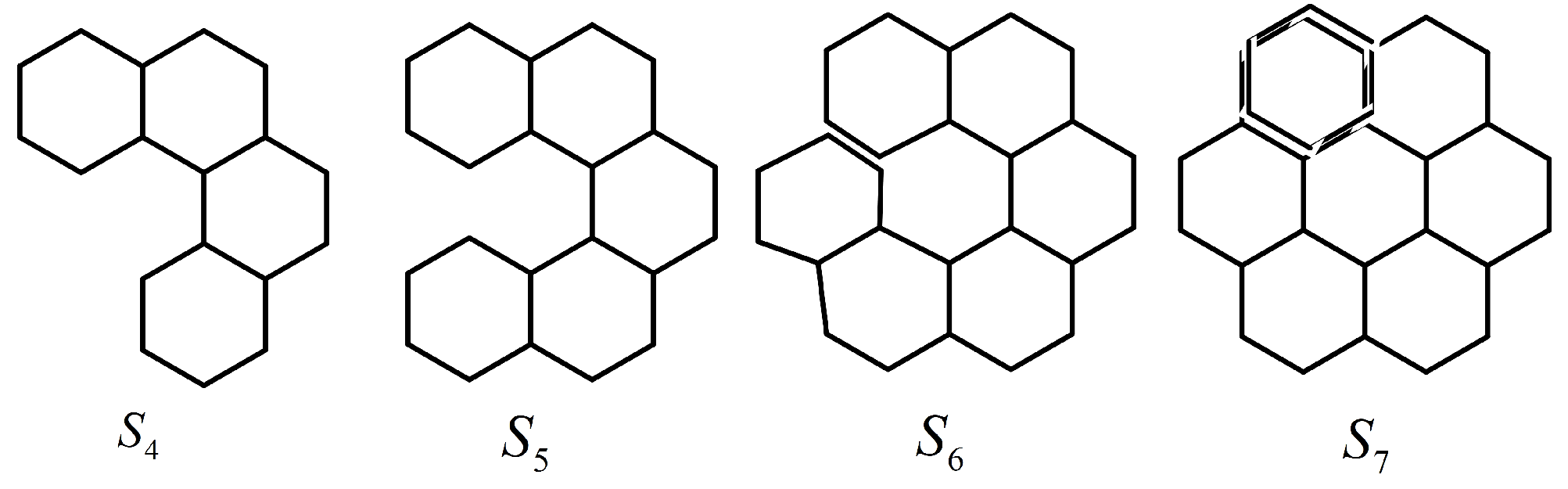
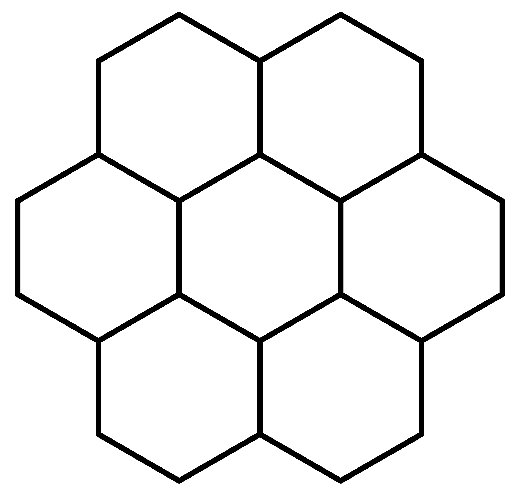
1.2. Hexagonal Systems
1.3. Silicate Networks
2. Measures of Vulnerability in Graph Structures
- 1.
- , where Ω is a graph of order p
- 2.
- iff
- 3.
- iff
- 4.
- If T is a subgraph of Ω then
- 1.
- If is a path graph, then
- 2.
- If is a cycle graph, then
- 3.
- If be a Complete Bipartite graph, then
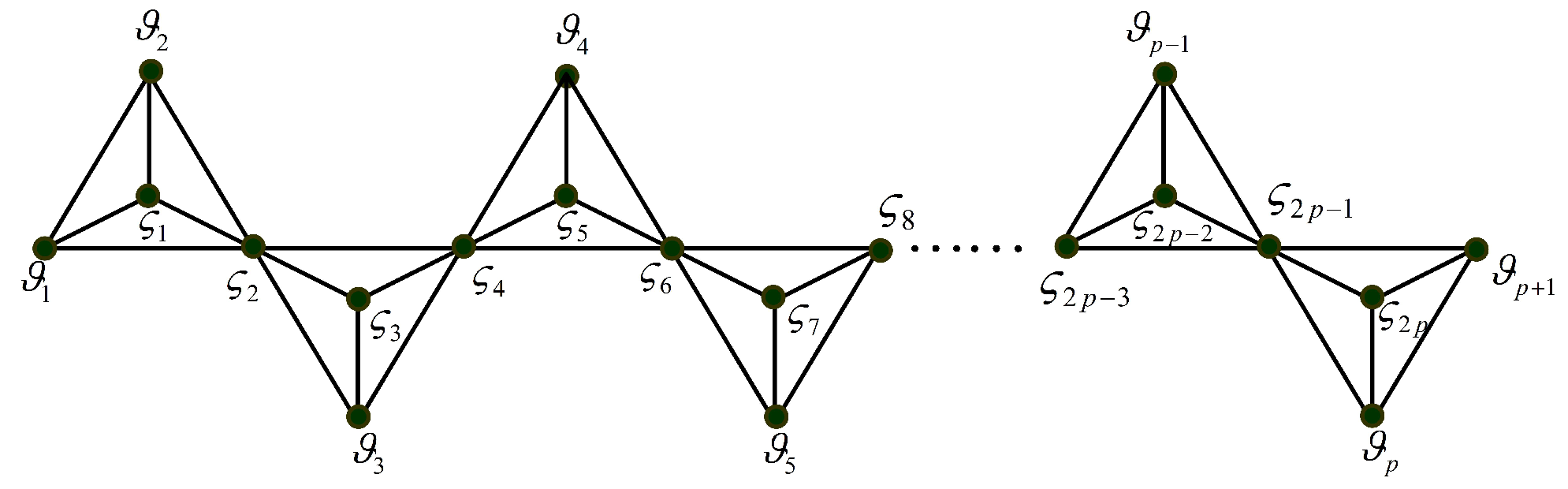
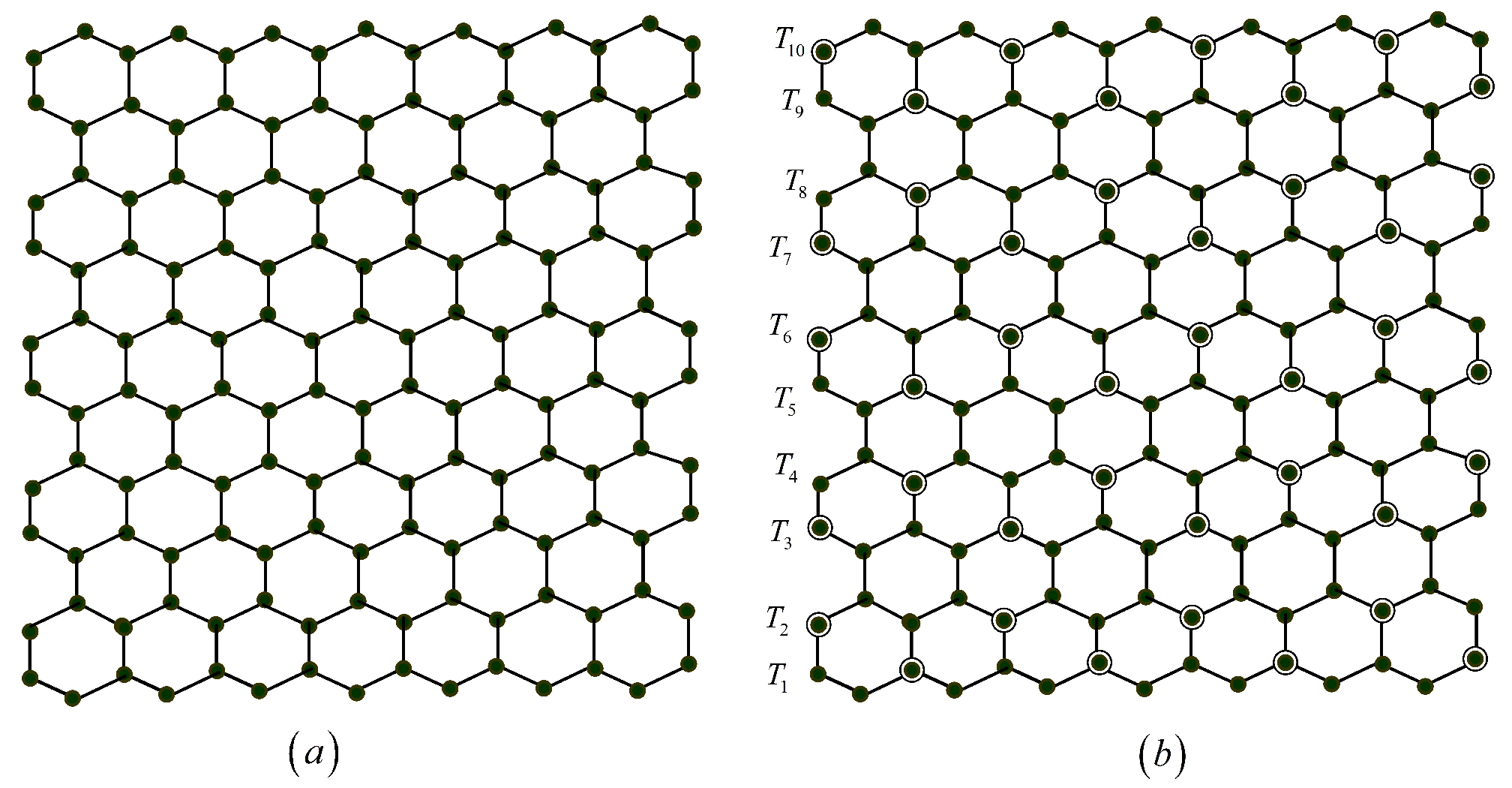
3. Domination Integrity in Hexagonal Graph Structures
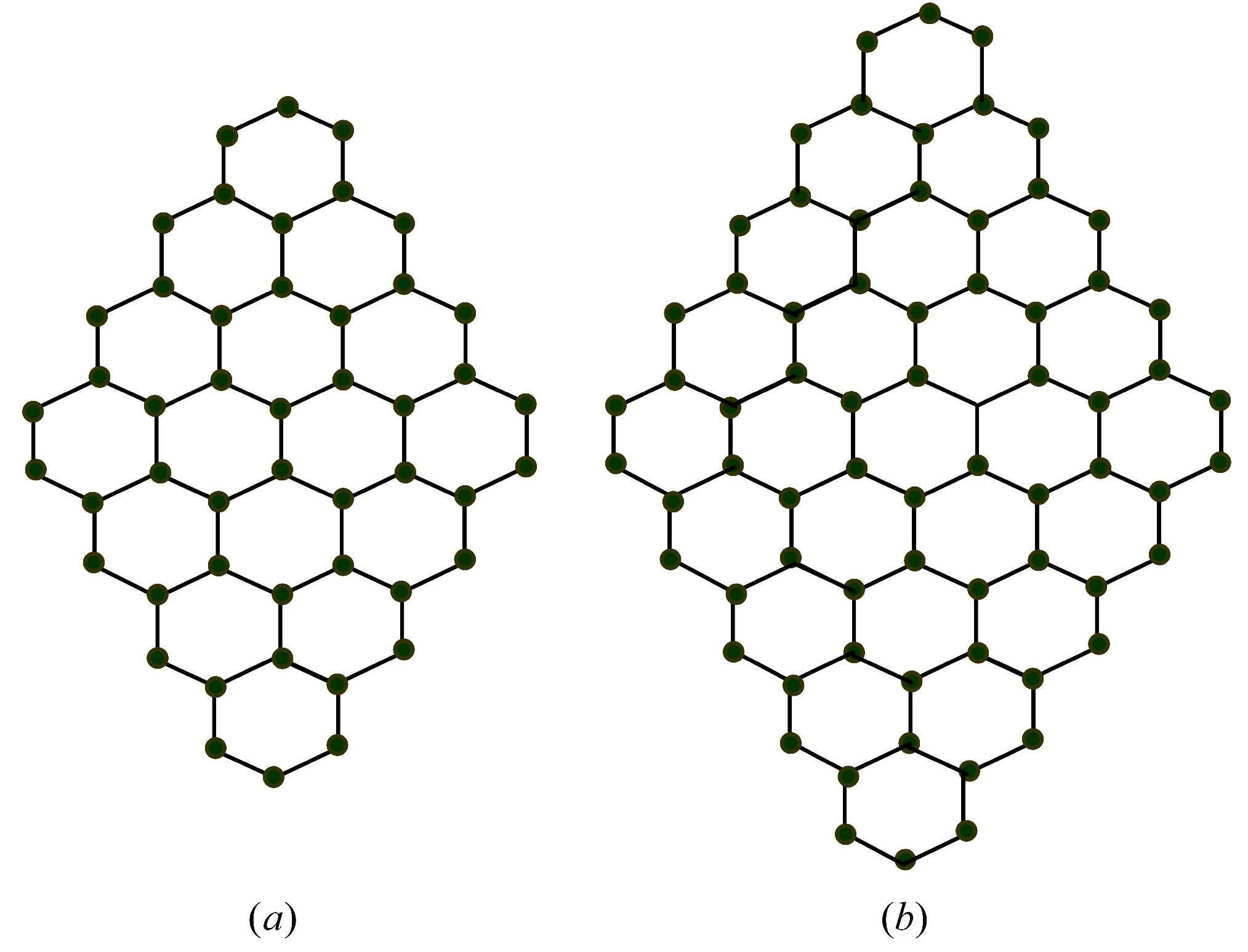
- Case (i): If , then , we have .
- Case (ii): Let . Construct a dominating set which consists of elements in the row and elements in the row (Figure 11). We get and . Therefore .

- Case (i): If , then , we have .
- Case (ii): If , choose a minimum dominating set K such that , we have .
- Case (iii): If , choose a minimum dominating set K such that , we have .
- Case (iv): Let be an odd integer. Formulate a minimal dominating set denoted as K:Let for allfor allfor allfor allNow, . We get . Removal of these vertices gives . Therefore
- Case (v): Let be an even integer. Formulate a minimal dominating set denoted as K:Let for allfor allfor allfor allNow, 1. We get . Removal of these vertices gives . Therefore
- Case (i) Let p = odd, q = odd. Formulate a minimal dominating set denoted as K:for everyfor everyfor everyfor everyNow, forms a dominating set such that . Removing the above vertices gives . The dominating set K defined above gives least values of . Thus, .
- Case (ii): Let p = odd, q = even. Formulate a minimal dominating set denoted as K:for everyfor everyfor everyfor everyNow, forms a dominating set such that . Removing the above vertices gives . The dominating set K defined above gives least values of . Thus .
- Case (iii): Let p = even, q = odd. Formulate a minimal dominating set denoted as K:, for everyfor everyfor everyfor everyWe note that forms a minimum dominating set such that . Removing the above defined set K gives . The dominating set K defined above gives least values of . Thus .
- Case (iv): Let p = even, q = even. Formulate a minimal dominating set denoted as K:for everyfor everyfor everyfor everyWe note that forms a minimum dominating set such that . Removing the above defined set K gives . The dominating set K defined above gives minimum values of . Thus .
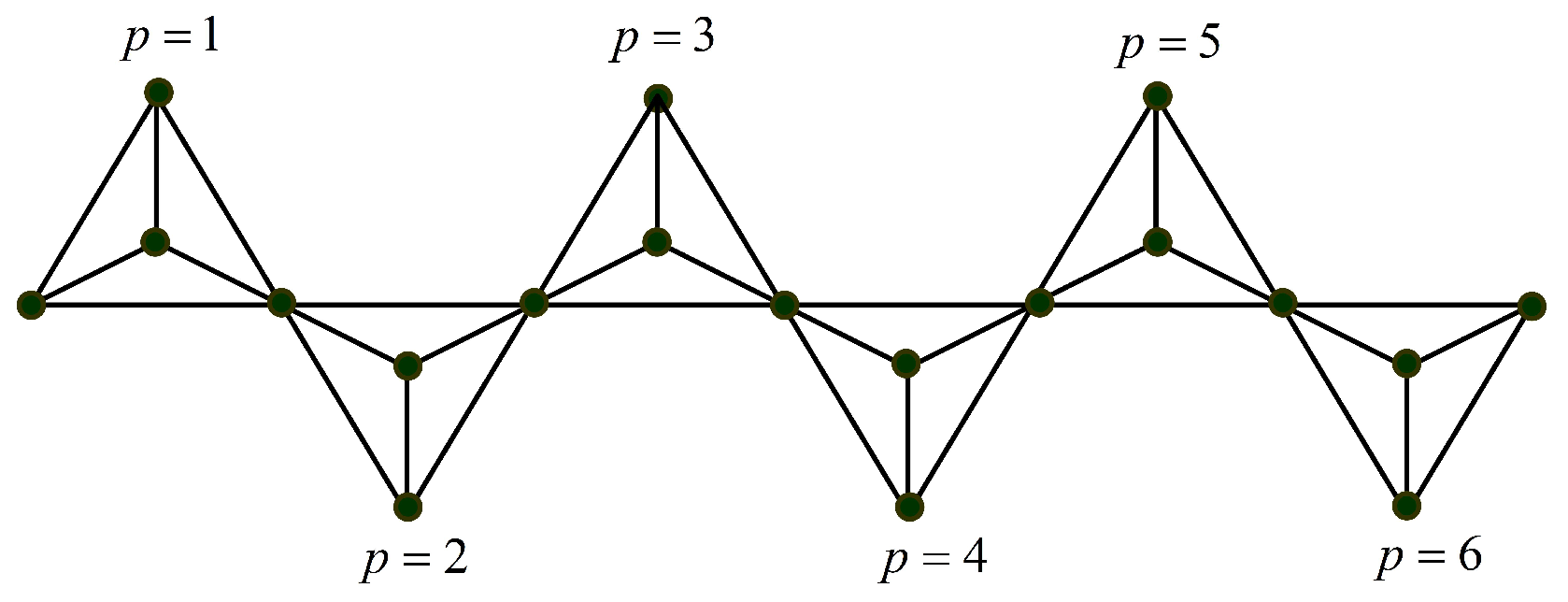
- Case (i) Let . . Since , we have .If then easily we can get .
- Case (ii) Let be even integers. Formulate a minimal dominating set denoted as K:for everyfor everyfor everyfor everyNow, . The above defined set K constitutes a minimum dominating set, resulting in . Consequently, we have . An illustration of the Honeycomb structure along with its dominating set is presented in Figure 15.

4. Domination Integrity Measures in Silicate Network Structures
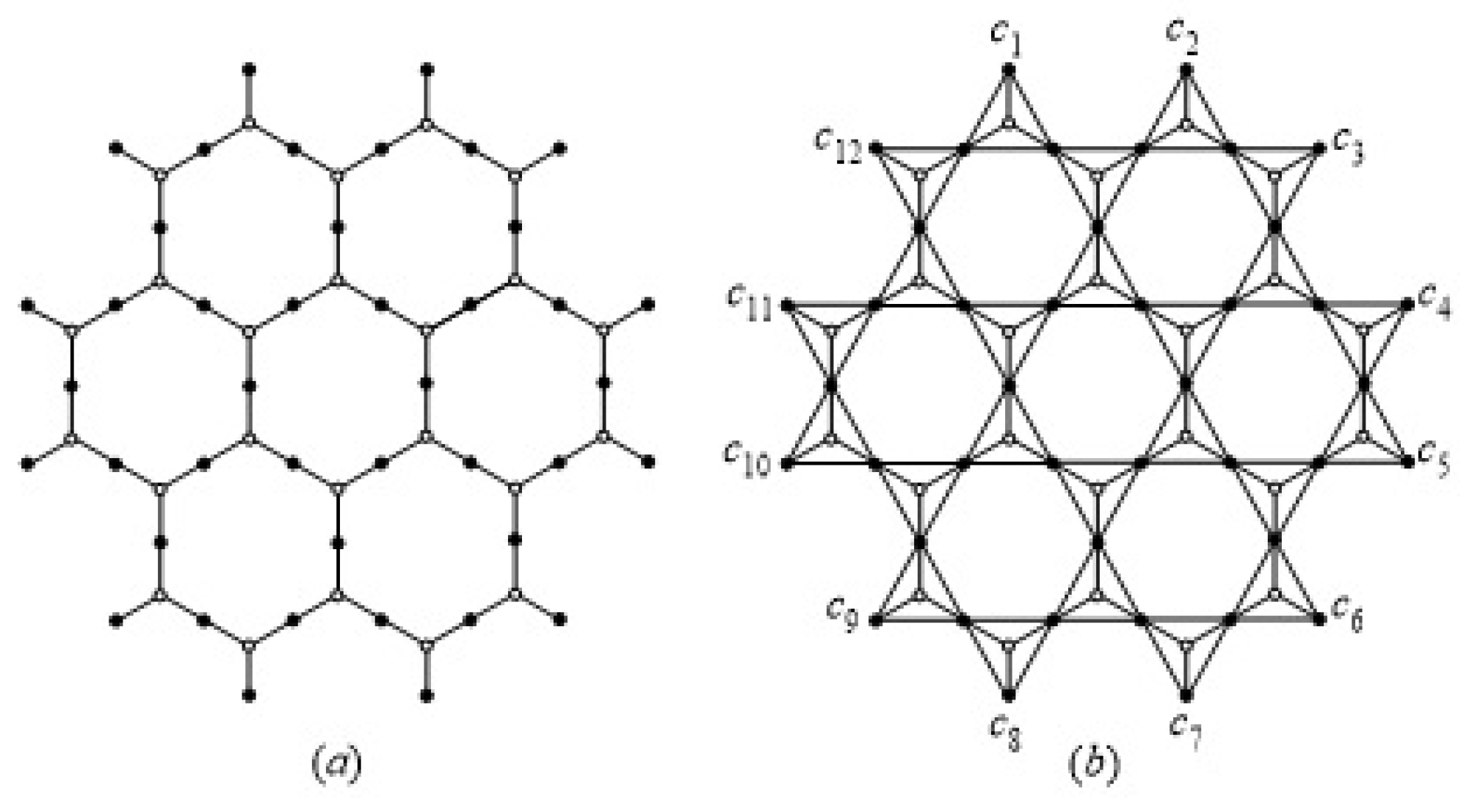
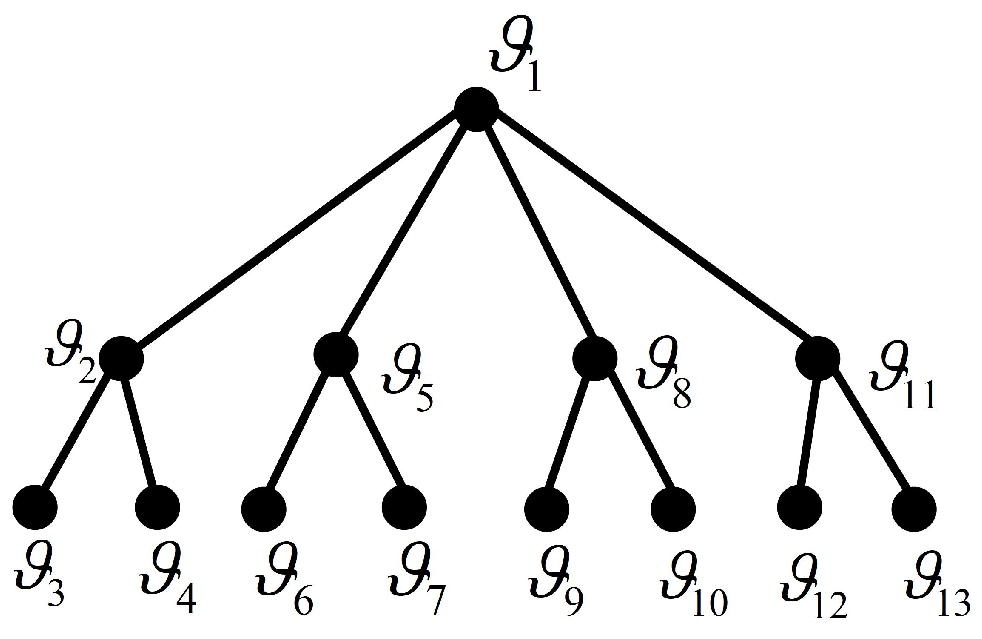
- Case (i): If then . Since , we have .If then is twin structure, by Proposition 4, .If , then is a dominating set such that . We have .If then is a minimal dominating set such that . We have .If , then form a dominating set , . We have
- Case (ii): Let be an even. Define the minimum dominating set which consists of elements. Exclusion of this set K results in , leading to the conclusion that Suppose K is any other dominating set other than minimal dominating set gives Therefore
- Case (iii): Let be an odd. Define the minimum dominating set which consists of elements. Exclusion of this set K results in , leading to the conclusion that Suppose K is any other dominating set other than minimal dominating set gives Therefore, .
5. Results and Discussion
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hedetniemi, S.T.; Laskar, R.C. Bibliography on domination in graphs and some basic definitions of domination parameters. Discret. Math. 1990, 86, 257–277. [Google Scholar] [CrossRef]
- Sampathkumar, E.; Pushpa Latha, L. Strong weak domination and domination balance in a graph. Discret. Math. 1996, 161, 235–242. [Google Scholar] [CrossRef]
- Quadras, J.; Mahizl, A.S.M.; Rajasingh, I.; Rajan, R.S. Domination in certain chemical graphs. J. Math. Chem. 2015, 53, 207–219. [Google Scholar] [CrossRef]
- Mojdeh, D.A.; Habibi, M.; Badakhshian, L. Total and connected domination in chemical graphs. Ital. J. Pure Appl. Math. 2018, 39, 393–401. [Google Scholar]
- Suganya, V.; Anitha, J. Independent domination in chain silicate networks. J. Int. Pharm. Res. 2019, 46, 384–387. [Google Scholar]
- Chithra, M.R.; Menon, M.K. Secure domination of honeycomb networks. J. Comb. Optim. 2020, 40, 98–109. [Google Scholar] [CrossRef]
- Shukur, A.A.; Shelash, H.B.; Ashrafi, A.R. Resolvent energy and pseudospectrum energy of fullerenes. Fuller. Nanotub. Carbon Nanostructures 2021, 30, 512–515. [Google Scholar] [CrossRef]
- Ante, G.; Ali, R.A.; Ottorino, O. Chapter 1—Topological Efficiency Approach to Fullerene Stability—Case Study with C50. In Advances in Mathematical Chemistry and Applications; Subhash, C.B., Guillermo, R., José, L.V., Eds.; Bentham Science Publishers: Sharjah, United Arab Emirates, 2015; pp. 3–23. [Google Scholar]
- Shukur, A.A.; Jahanbani, A.; Shelash, H. The Behavior of Weighted Graph’s Orbit and Its Energy. Math. Probl. Eng. 2021, 1–6. [Google Scholar] [CrossRef]
- Almalki, N.; Kaemawichanurat, P. Domination and independent domination in hexagonal systems. Mathematics 2022, 10, 67. [Google Scholar] [CrossRef]
- Takahashi, Y.; Ichishima, R.; Muntaner-Batle, F.A. On the strength and domination number of graphs. Contrib. Math. 2023, 8, 11–15. [Google Scholar] [CrossRef]
- Manuel, P.; Rajasingh, I. Topological properties of silicate networks. In Proceedings of the 5th IEEE GCC Conference and Exhibition, Kuwait City, Kuwait, 17–19 March 2009; pp. 16–19. [Google Scholar]
- Chvatal, V. Tough graphs and hamiltonian circuits. Discret. Math. 1973, 5, 215–228. [Google Scholar] [CrossRef]
- Jung, H.A. On a class of posets and the corresponding comparability graphs. J. Comb. Theory Ser. B 1978, 24, 125–133. [Google Scholar] [CrossRef]
- Cozzens, M.B.; Moazzami, D.; Stueckle, S. The tenacity of a graph. Graph Theory. In Combinatorics, and Algorithms; Alavi, Y., Schwenk, A., Eds.; Wiley: New York, NY, USA, 1995; pp. 1111–1112. [Google Scholar]
- Cozzens, M.B.; Moazzami, D.; Stueckle, S. The tenacity of the harary graphs. J. Comb. Math. Comb. Comput. 1994, 16, 33–56. [Google Scholar]
- Zhang, S.; Li, Y.; Li, X. Rupture degree of graphs. Int. J. Comput. Math. 2005, 82, 793–803. [Google Scholar]
- Li, F.; Li, X. Computing the rupture degrees of graphs. In Proceedings of the 7th International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN04), Hong Kong SAR, China, 10–12 May 2004. [Google Scholar]
- Barefoot, C.A.; Entringer, R.; Swart, H.C. Vulnerability in graphs a comparative survey. J. Combin. Math. Combin. Comput. 1987, 1, 13–22. [Google Scholar]
- Goddard, W.; Swart, H.C. Integrity in graphs: Bounds and basics. J. Combin. Math. Combin. Comput. 1990, 7, 139–151. [Google Scholar]
- Sundareswaran, R.; Swaminathan, V. Domination integrity in graphs. In Proceedings of the International Conference on Mathematical and Experimental Physics, Prague, Czech Republic, 3–8 August 2009; pp. 46–57. [Google Scholar]
- Vaidya, S.K.; Kothari, N.J. Some new results on domination integrity of graphs. Open J. Discret. Math. 2012, 2, 96–98. [Google Scholar] [CrossRef]
- Vaidya, S.K.; Kothari, N.J. Domination integrity of splitting graph of path and cycle. ISRN Comb. 2013, 795427. [Google Scholar] [CrossRef]
- Vaidya, S.K.; Shah, N.H. Domination integrity of total graphs. TWMS J. App. Eng. Math. 2014, 4, 117–126. [Google Scholar]
- Vaidya, S.K.; Shah, N.H. Domination integrity of some path related graphs. Appl. Appl. Math. 2014, 9, 780–794. [Google Scholar]
- Sundareswaran, R.; Swaminathan, V. Computational complexity of domination integrity in graphs. TWMS J. App. Eng. Math. 2015, 5, 214–218. [Google Scholar]
- Mahde, S.S.; Mathad, V. Global domination integrity of graphs. Math. Sci. Lett. 2017, 6, 263–269. [Google Scholar] [CrossRef]
- Besirik, A. Total domination integrity of graphs. J. Mod. Technol. Eng. 2019, 4, 11–19. [Google Scholar]
- Harisaran, G.; Shiva, G.; Sundareswaran, R.; Shanmugapriya, M. Connected domination integrity in graphs. Indian J. Nat. Sci. 2021, 12, 30271–30276. [Google Scholar]
- Balaraman, G.; Sampath Kumar, S.; Sundareswaran, R. Geodetic domination integrity in graphs. TWMS J. App. Eng. Math. 2021, 11, 258–267. [Google Scholar]
- Onur, Ş.; Turan, G.B. Geodetic domination integrity of thorny graphs. J. New Theory 2024, 46, 99–109. [Google Scholar] [CrossRef]
- Gutman, I.; Cyvin, S. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: New York, NY, USA, 1989. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganesan, B.; Raman, S. On the Symmetry and Domination Integrity of Some Bidegreed Graphs. Symmetry 2025, 17, 953. https://doi.org/10.3390/sym17060953
Ganesan B, Raman S. On the Symmetry and Domination Integrity of Some Bidegreed Graphs. Symmetry. 2025; 17(6):953. https://doi.org/10.3390/sym17060953
Chicago/Turabian StyleGanesan, Balaraman, and Sundareswaran Raman. 2025. "On the Symmetry and Domination Integrity of Some Bidegreed Graphs" Symmetry 17, no. 6: 953. https://doi.org/10.3390/sym17060953
APA StyleGanesan, B., & Raman, S. (2025). On the Symmetry and Domination Integrity of Some Bidegreed Graphs. Symmetry, 17(6), 953. https://doi.org/10.3390/sym17060953





