Symmetry-Driven Modeling of Electron Multiple Scattering: A Random Walk Approach on the Unit Sphere

Abstract

Lewis’ theory of multiple scattering has been modeled as a random walk on a unit sphere for calculating the multiple scattering angular distribution of charged particles, which is more intuitive and mathematically simpler. This formalism can lead to the Goudsmit–Saunderson theory and the Lewis theory of multiple scattering angular distribution, thus providing an easier-to-understand framework to unify both the Goudsmit–Saunderson and the Lewis theories. This new random walk method eliminates the need for integro-differential expansions in Lewis theory and is faster at calculating multiple scattering angular distributions, reducing the required Legendre series terms by 80% at small step (path) length (<20) and providing much greater calculation efficiency. Crucially, the random walk formalism explicitly preserves spherical symmetry by treating angular deflections as steps on a unit sphere, enabling the efficient sampling of scattering events while maintaining accuracy. Further, a robust algorithm for numerically calculating multiple scattering angular distributions of electrons based on the Goudsmit–Saunderson and Lewis theories has been developed. Partial wave elastic scattering differential cross-sections, generated with the program ELSEPA, have been used in the calculations. A two-point Gauss–Legendre quadrature method is used to calculate the Legendre coefficients (multiple scattering moments).

1. Introduction

Electrons undergo a very large number of elastic scatterings during transport simulation, so the multiple scattering method is used to calculate its cumulative effects of electron angular deflection in the Monte Carlo electron transport simulation [1]. However, previously developed multiple scattering theories, such as in the work of Williams [2], Moliere [3,4], and Snyder & Scott [5], include several approximations, especially small-angle or Born approximations, which limited their accuracy [6].

Some modifications have been performed to partially correct these flaws [6]. Goudsmit and Saunderson (GS) [7,8] exploited the persistence property of the Legendre polynomials to derive a more or less exact method to calculate the angular distribution of multiple scattering without any approximation; however, energy loss was neglected in this theory, hence it is only more or less exact. Lewis [9] studied the integro-differential diffusion equation of the multiple scattering problem in an infinite, homogeneous medium and obtained an exact expression of the multiple scattering angular distribution. Both the Goudsmit–Saunderson and Lewis theories prove to be more accurate than conventional approximate methods [10,11].

The Lewis theory, since it is exact, is mathematically very complex to derive, involving the expansion of the integro-differential equation in spherical harmonics. The purpose of this study is to develop a more intuitive and mathematically simpler method that can unify both GS and Lewis’s multiple scattering angular distribution theory.

Traditional methods such as Goudsmit–Saunderson theory and Lewis theory are accurate but have some limitations. Firstly, they assume that the elastic scattering differential cross-section (ecDCS) depends only on the polar scattering angle, not the azimuthal angle. This only applies to materials with spherically symmetrical atoms or amorphous and polycrystalline materials in which atoms are isotropically oriented. Secondly, its Legendre series converges very slowly, making multiple scattering simulation a computationally intensive process. The slow convergence of both methods has hindered their application in radiation transport simulation, and small-angle approximate theories have to be used [12]. With the development of computer technology and highly accurate Monte Carlo simulation methodology, the GS and Lewis theories are used more often [13,14,15,16,17,18,19,20,21,22,23,24]. But still, calculation time can be extremely long at small step length [20], so simplification has to be made [21] or a very large pre-calculated database has to be stored [22]. Therefore, the main objective of this work is to improve the convergence significantly at small step length.

Therefore, we proposed to model multiple scattering as a random walk on a unit sphere, since any unit vector can correspond to a point on a sphere. The random walk method, able to be applied to crystalline materials as long as accurate ecDCS with respect to azimuthal angle, is provided, and gives a more generalized formula for electron multiple scattering simulation. The proposed method is equivalent to Lewis theory [9] when isotropic orientation is assumed, and the spherical harmonics degenerate into Legendre functions. But the proposed method usually converges much faster, usually requiring 10 times less order in the summation of the Legendre series. The reason is that slow convergence is usually due to the small number of scatterings, which leads the angular distribution to be heavily forward-peaked. The proposed method samples the number of elastic scattering first, and thus the small-angle approximation method can be used when the number of scatterings is small.

2. Multiple Scattering Theories

This section briefly describes the multiple scattering angular distributions of electrons provided by the Goudsmit–Saunderson theory and the Lewis theory of multiple scattering. Further, a random walk method, developed by Wasaye et al. [25] and Roberts et al. [26], is applied to the Lewis theory, and it is evident that the random walk formula reduces to the Lewis theory of multiple scattering.

2.1. Goudsmit–Saunderson Theory of Multiple Scattering

Consider an electron of kinetic energy E that is moving along the z-axis in our frame of reference. We assume that the energy of the electron remains the same along its path. Let $F_{GS}\left(\theta ;t\right)$ denote the probability density (per unit solid angle) of finding the electron moving in the direction $\theta$ after traveling a path length t. The angular distribution after a path length t can then be expressed as [7,8].

$$F_{GS}\left(\theta ;t\right)=\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{4\pi }}\times \left[e^{-t/\lambda }\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(t/\lambda \right)}^n}{n!}}{\left(F_l\right)}^n\right]P_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)$$

(1)

Introducing the coefficients

$$F_l=2\pi \underset{-1}{\overset{1}{\int }}{P}_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)f_l\left(\theta \right)d\left(\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)$$

(2)

The quantities $g_l=1-F_l=2\pi {\displaystyle \underset{-1}{\overset{1}{\int }}\left[1-P_l\left(\cos \theta \right)\right]f_1\left(\theta \right)d\left(\cos \theta \right)}$ will be referred to as transport coefficients. Where $f_1\left(\theta \right)={\displaystyle \frac{1}{\sigma }}{\displaystyle \frac{d\sigma \left(\theta \right)}{d\Omega }}$: angular distribution after a single scattering event. $P_l\left(cos\theta \right)$ represents Legendre polynomials. $\lambda$ is a mean free path (mfp) between two scattering events. The multiple scattering distribution can be finally written in the form

$$F_{GS}\left(\theta ;t\right)=\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{4\pi }}\times e^{-t{G}_l} P_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)$$

(3)

which is the expansion derived by Goudsmit and Saunderson. The convergence of expression in Equation (3) requires a larger number of terms as the path length decreases. For short distances, the series’ convergence may be improved by isolating the contribution made by unscattered electrons [27].

$$F_{GS}\left(\theta ;t\right)=e^{-t/\lambda }{\displaystyle \frac{\delta \left(\mathrm{c}\mathrm{o}\mathrm{s}\theta -1\right)}{\pi }}+\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{4\pi }}\times \left[e^{-t{G}_l}-e^{-t/\lambda }\right] P_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)$$

(4)

The lth transport mean free path, ${\lambda }_l$, is defined as ${\lambda }_l=G_l^{-1}$. The first term of Equation (4) represents unscattered electrons. The first inverse transport mean free path

$${\lambda }_1^{-1}=G_1={\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \underset{-1}{\overset{1}{\int }}\left[1-\cos \theta \right]}{f}_1\left(\theta \right)d\left(\cos \theta \right)={\displaystyle \frac{{〈1-\cos \theta 〉}_1}{\lambda }}$$

(5)

gives a measure of the average angular deflection per unit path length. Let us define

$$\mu =\cos \theta$$

(6)

Using a change of variable, Equations (2) and (4) become

$$F_l=2\pi {\displaystyle \underset{-1}{\overset{+1}{\int }}\frac{1}{\sigma }\frac{d\sigma }{d\Omega }}{P}_l\left(\mu \right)d\mu \mathrm{and} g_l=2\pi {\displaystyle \underset{-1}{\overset{+1}{\int }}\frac{1}{\sigma }\frac{d\sigma }{d\Omega }\left[1-P_l\left(\mu \right)\right]}d\mu$$

(7)

$$F_{GS}\left(\theta ;t\right)=e^{-t/\lambda }{\displaystyle \frac{\delta \left(\mu -1\right)}{\pi }}+\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{4\pi }}\times \left[e^{-t{G}_l}-e^{-t/\lambda }\right] P_l\left(\mu \right)$$

(8)

2.2. Lewis Theory of Multiple Scattering

Lewis has established a more comprehensive theory of multiple scattering that primarily encompasses angular distributions and energy losses [9]. The energy losses in this theory are managed using the continuous slow-down approximation (CSDA). In this approximation, the projectile is assumed to experience a continual loss of energy as it travels, resulting in its stopping power $S\left(E\right)$, i.e., the average energy loss per unit path length by the electron as it travels through the medium.

$$S\left(E\right)=-{\displaystyle \frac{\mathrm{d}E}{\mathrm{d}S}}$$

(9)

The CSDA range of an electron of energy E is given as

$$R\left(\mathrm{E}\right)={\int }_{{\mathrm{E}}_{\mathrm{a}\mathrm{b}\mathrm{s}}}^{\mathrm{E}}{\displaystyle \frac{\mathrm{d}E’}{\mathrm{S}\left(E’\right)}}$$

(10)

In this equation, E_abs represents the absorption energy. The angular distribution function that Lewis provides, which may be derived by solving the diffusion equation, is

$$F_L\left(S;\theta \right)=\sum _{l=0}^{\infty }{\displaystyle \frac{2l+1}{4\pi }}{e}^{-k_l\left(s\right)}{P}_l\left(\mathrm{c}\mathrm{o}\mathrm{s} \theta \right)$$

(11)

where all definitions of the parameters are the same as discussed in GS theory of multiple scattering, except the transport coefficient, which is now a function of path length and can be calculated by integrating the Legendre coefficients over the path length, and is given as

$$G_{lewis}\left(l\right)={\int }_o^s{G}_{l}ds’$$

(12)

Evidently, the results of Equation (11) reduce to the GS distribution when energy losses are neglected.

2.3. Random Walk Method and Extension to Lewis Theory

Multiple scattering can be modeled as a random walk, especially in optically thick media where the mean free path between scatterings is short compared to the dimensions of the medium. As a result, the distribution of scattering angles can sometimes approach a diffusion-like process, where the direction of the outgoing particles becomes increasingly isotropic the more scatterings they undergo.

We consider each scattering event to be equivalent to one step in the random walk sequence, with the scattering angle characterized by the step length of each random walk step and scattering azimuthal angle corresponding to step direction. The elastic scattering DCS determines the distribution function of the random walk step length and direction. Given the distribution function of step length and step direction, the distribution function of a point’s position on the sphere going through N steps of a random walk can be derived as a series of spherical harmonics. This distribution function also gives the angular distribution function of an electron undergoing N elastic scatterings. Since the number of elastic scattering an electron undergoes in a given track length is governed by the Poisson distribution, combining these two formulas, the angular distribution of electron multiple scattering angular distribution in a given track length is formulated.

In the research of wasaye et al. [25], it is found that the random walk method gives the same formula for multiple scattering angular distribution with Goudsmit–Saunderson theory, assuming the elastic scattering DCS is invariant during a transport step. However, electrons gradually lose energy during a step, causing DCS to change as well. Lewis’ theory proposes to take this energy loss effect into account. In this section, it is proven that with varying DCS effects taken into consideration, the Lewis theory can also be derived from the random walk method.

As mentioned in wasaye et al. [25], the eigenvalue of the kth random walk step (i.e., kth scattering event) is

$${\lambda }_{l,k}=\underset{0}{\overset{\pi }{\int }}{P}_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }\right)p_k\left(\alpha \right) d\alpha$$

(13a)

Here, $p_k\left(\alpha \right)={\displaystyle \frac{1}{\sigma }}{\displaystyle \frac{d{\sigma }_k}{d\alpha }}$ represents the normalized angular distribution for the kth scattering event.

$${\lambda }_{l,k}=2\pi \underset{0}{\overset{\pi }{\int }}{P}_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\alpha \right){\displaystyle \frac{1}{\sigma }}{\displaystyle \frac{d{\sigma }_k}{d\alpha }}\mathrm{s}\mathrm{i}\mathrm{n}\alpha d\alpha$$

(13b)

The number of collisions an electron undergoes in a given step with step length t complies with Poisson distribution $P_n$. Assuming that the scattering mean free path is λ, the probability that an electron undergoes n multiple scattering is $P_n=e^{-t/\lambda }{\displaystyle \frac{{\left(t/\lambda \right)}^n}{n!, }}$ and the multiple scattering angular distribution after step length t is

$$F_{MS}{\left(\alpha \right)}_{\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{y}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=\sum _{n=0}^{\infty }{P}_n{f}_n\left(\alpha \right)=\sum _{n=0}^{\infty }\mathrm{e}\mathrm{x}\mathrm{p}\left(-t/\lambda \right){\displaystyle \frac{{\left(t/\lambda \right)}^n}{n!}}\left[\sum _{l=0}^{\mathrm{\infty }}{\displaystyle \frac{2l+1}{4\pi }}\prod _{k=1}^n{ɑ}_{l,k}{P}_l\left(\mathrm{c}\mathrm{o}\mathrm{s}\alpha \right)\right]$$

(14)

With scaled path length $t/\lambda ={\displaystyle {\int }_0^{t}1/\lambda \left(s\right)\mathrm{d}s}$ and λ(s) defined as $\lambda (s)={\displaystyle \frac{1}{n\sigma (s)}}$. It is unnecessary to obtain the exact value of each transport (Legendre) coefficient ${ɑ}_{l,k}$, which rely on the exact location (and hence electron energy) of each scattering event on the step length, because we are interested in deriving the cumulative angular distribution of n scattering events which is an average effect of all these n scattering events happening at all possible locations along the step. As a result, the expected value of $\prod _{k=1}^n{ɑ}_{l,k}$ is used in Formula (14).

It is worth noting that since the number of scattering events follows a Poisson distribution, each event occurs as evenly as possible in the step length (in the mean free path length to be exact). So, all the ${ɑ}_{l,k}$ have the same distribution.

$$〈{\displaystyle \prod _{k=1}^n{a}_{l,k}}〉={〈a_l〉}^n$$

(15)

Since scattering DCS, which determines ${ɑ}_{l,k}$, depends on electron energy, and thus the scattering locations along the step length, ${ɑ}_{l,k}$ should be calculated using an average DCS along the step length.

$$〈a_l〉={\displaystyle \frac{{\displaystyle {\int }_0^t{a}_l(s)/\lambda (s)\mathrm{d}s}}{{\displaystyle {\int }_0^{t}1/\lambda (s)\mathrm{d}s}}}={\displaystyle \frac{{\displaystyle {\int }_0^t{a}_l(s)/\lambda (s)\mathrm{d}s}}{t/\lambda }}$$

(16)

Combining Equations (14)–(16)

$$F_{\mathrm{MS}}{(\alpha )}_{\mathrm{energyloss}}={\displaystyle \sum _{n=0}^{\infty }\exp (-t/\lambda )\frac{{(t/\lambda )}^n}{n!}\cdot \left[{\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }{〈a_l〉}^n\cdot P_l(\cos \alpha )}\right]}={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\left[\exp (-t/\lambda ){\displaystyle \sum _{n=0}^{\infty }\frac{{(t/\lambda )}^n}{n!}{〈a_l〉}^n}\right]}\cdot P_l(\cos \alpha )$$

(17)

Using Taylor expansion as well, we can derive

$$\begin{array}{l}{F}_{\mathrm{MS}}{(\alpha )}_{\mathrm{energyloss}}={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\exp (-t/\lambda )\cdot \exp \left[t/\lambda \cdot 〈a_l〉\right]\cdot }{P}_l(\cos \alpha )={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\exp \left[-t/\lambda +{\displaystyle {\int }_0^t{a}_l(s)/\lambda (s)\mathrm{d}s}\right]}{P}_l(\cos \alpha )\\ ={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\exp \left[-{\displaystyle {\int }_0^{t}1/\lambda \left(s\right)\mathrm{d}s}+{\displaystyle {\int }_0^t{a}_l(s)/\lambda (s)\mathrm{d}s}\right]}{P}_l(\cos \alpha )={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\exp \left[-{\displaystyle {\int }_0^t\left[1-a_l(s)\right]/\lambda (s)\mathrm{d}s}\right]}{P}_l(\cos \alpha )\end{array}$$

(18)

Defining $g_l(s)\equiv 1-a_l(s)$, the following equation is derived

$$F_{\mathrm{MS}}{(\alpha )}_{\mathrm{energyloss}}={\displaystyle \sum _{l=0}^{\infty }\frac{2l+1}{4\pi }\exp \left[-{\displaystyle {\int }_0^t{g}_l(s)/\lambda (s)\mathrm{d}s}\right]\cdot P_l(\cos \alpha )}$$

(19)

This formula is exactly the same as the Lewis theory, derived without using the expansion of the integro-differential equation in spherical harmonics.

3. Numerical Methods

A complete numerical method, along with the algorithm for the calculation of Legendre series expansion coefficients and angular distribution of multiple scattering, is presented in this section.

3.1. Differential Cross-Sections

Elastic and inelastic scattering differential cross-sections are calculated by the highly accurate code ELSEPA [28]. A table of numerical values of scattering differential cross-sections (DCSs) is constructed, which includes DCS for energies 100 eV to 100 MeV for given elements from Z = 1–105. DCSs are defined in an unevenly spaced fine angular grid of 606 grid points so as to ensure that even the most peaked scattering DCS varies by less than a factor of 2 in any sub-interval, which allows accurate Log cubic spline interpolation, even for the highest energies considered.

3.2. Numerical Calculation of Legendre Coefficients and Angular Distribution

In order to accurately calculate the angular distributions of electrons by multiple elastic scattering, the first step is the evaluation of Legendre coefficients, which are also called the transport coefficients. The transport coefficients $G_l$ can be obtained by means of Gauss–Legendre quadrature, with the angular range split into a number of sub-intervals to improve accuracy.

Let Equation (2) become

$$G_l={\displaystyle \frac{2\pi }{\lambda }}{\displaystyle \underset{-1}{\overset{1}{\int }}\left[1-P_l\left(\mu \right)\right]\frac{1}{\sigma }\frac{\mathrm{d}\sigma }{\mathrm{d}\Omega }d\mu }$$

(20)

Integrals in Equation (5) can be evaluated to very high accuracy with the Gauss–Legendre quadrature formula. The n-point Gauss–Legendre quadrature has the form

$$\begin{array}{l}{\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx\approx \frac{b-a}{2}{\displaystyle \sum _{i=1}^n{w}_{i}f\left(\frac{b-a}{2}{\xi }_i+\frac{b+a}{2}\right)}}\\ w_i={\displaystyle \frac{2}{(1-{\xi }_i^2){\left[P_N^{’}\left({\xi }_i\right)\right]}^2}}\end{array}$$

(21)

where ${\xi }_i$ represents the n-zeros of the nth order Legendre polynomial. We have used a two-point Gauss–Legendre quadrature to evaluate the integral in Equation (21) with ${\xi }_{1,2}=\pm {\displaystyle \frac{1}{\sqrt{3}}}$ and $w_1=w_2=1$. There are two points in each sub-interval, and there are 605 sub-intervals in [−1, 1]. The maximum number of coefficients that can be obtained from our code is 20,000. Convergence was determined when the relative difference between successive Legendre coefficients met the condition $\left|G_{l+1}-G_l\right|/G_l<{10}^{-6}$.

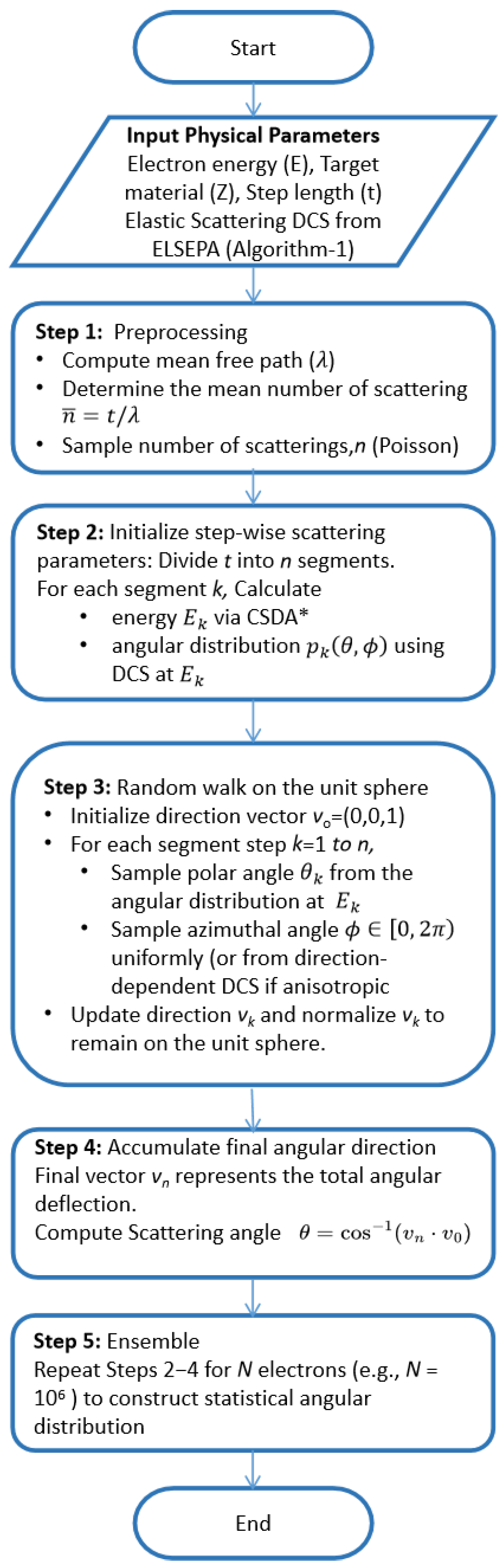
3.3. Numerical Simulation

Figure 1 illustrates the random walk process on the unit sphere, linking geometric steps to angular deflection distributions.

4. Results and Discussion

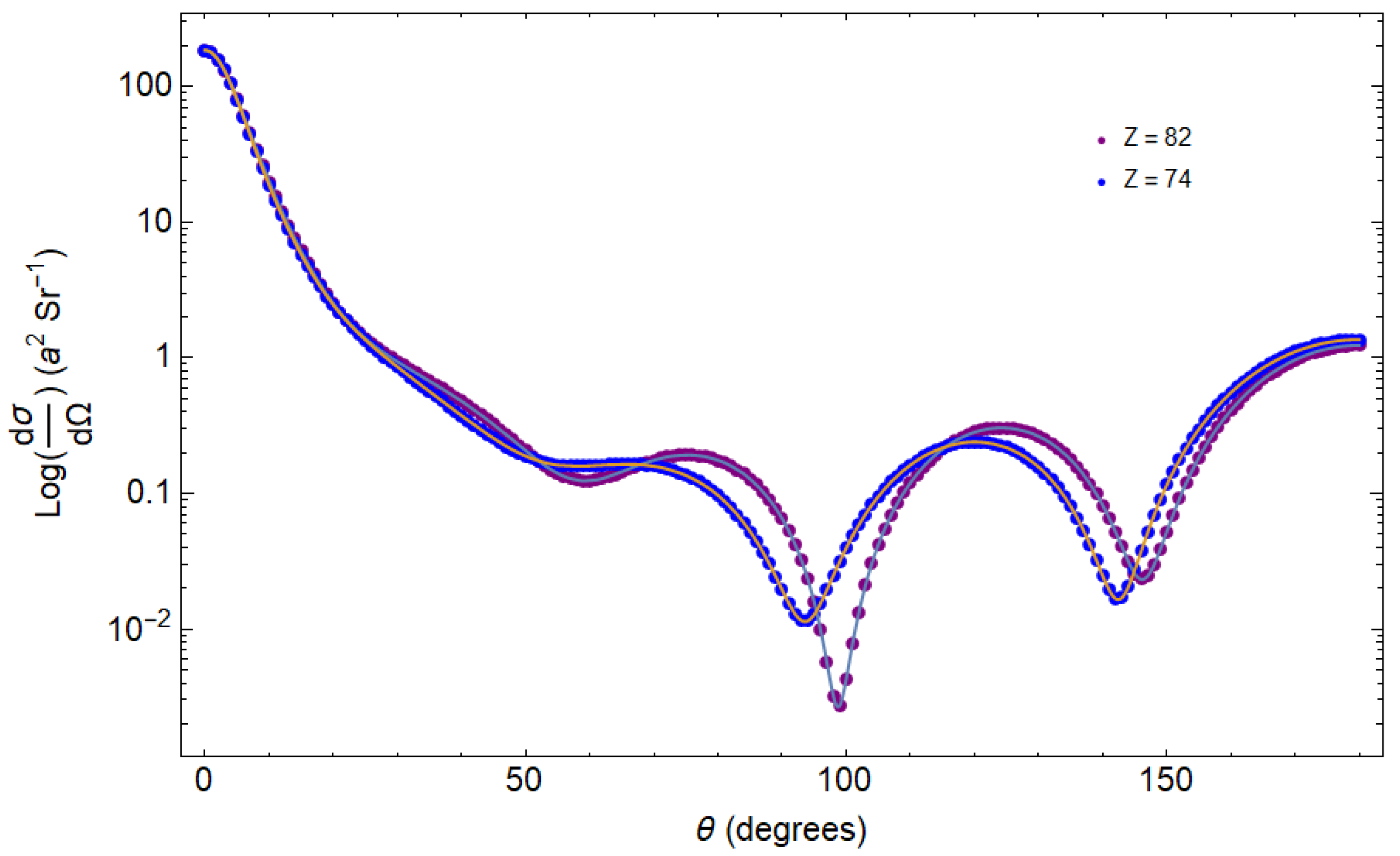
4.1. Interpolated Differential Cross-Sections

Interpolated elastic differential cross-sections of 1 keV electrons incidents on Lead (Pb) and Tungsten (W) are plotted in Figure 2 along with the numerical values of elastic DCSs, which are calculated through the ELSEPA code systems [28]. Log cubic spline interpolation is used up to a higher order of accuracy to account for the highly oscillating behavior of the DCSs at large angles. In order to make differential cross-sections representable, their values are expressed in the units of Bohar radius ($a_0=5.2917\times {10}^{-11} \mathrm{m}$).

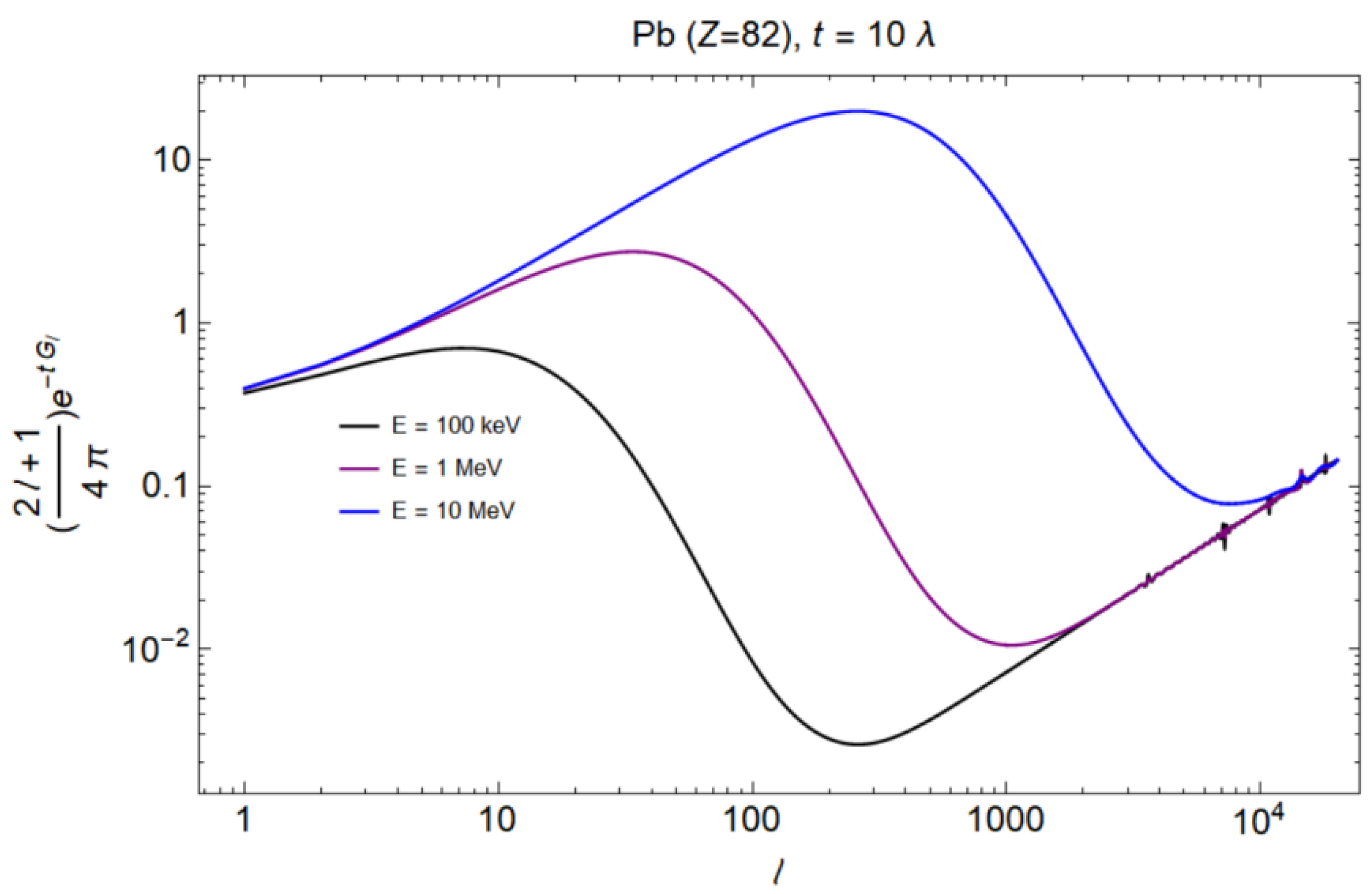
4.2. Legendre Expansion Coefficients

Legendre expansion coefficients (transport coefficients or multiple scattering moments) are calculated through Algorithm 1 and are plotted in Figure 3 and Figure 4.

Algorithm 1. Calculation of Legendre Coefficients (Multiple Scattering Moments): Multiple Scattering Moments ($\sigma G_l$) from the 1st to the 20,000th order.
Calculation Method: 2 points Gauss–Legendre quadrature.
Interpolation Method: Log Cubic Spline.
	INPUT:T (KE of incident electron in MeV), Z (atomic number Z = 1–95)
	OUTPUT: Interpolated Values of elastic differential cross-section. Multiple Scattering Moments (σ $G_l$). Angular distribution of Multiple scattering.
1	START
2	INTERPdcs (Z, T, $\theta$) gives interpolated values of elastic differential cross-sections which are calculated by the Log-Cubic Spline method.
3	function MSdistribution (Z, T)
4	define
5	${\xi }_{1,2}=\pm {\displaystyle \frac{1}{\sqrt{3}}}$;
6	$w_1=w_2=1$;
7	$t=$in terms of mean free path (mfp)
8	$f_l\left(\mu \right)=1-{\mathrm{P}}_l\left(\mu \right)\times \mathbf{I}\mathbf{N}\mathbf{T}\mathbf{E}\mathbf{R}\mathbf{P}\mathbf{d}\mathbf{c}\mathbf{s}\left(Z,T,\mu \right)$;
9	$\mathbf{f}\mathbf{o}\mathbf{r} l=\mathrm{0,1},..,\mathrm{20,000}$
10	→$\mathbf{f}\mathbf{o}\mathbf{r} i=\mathrm{1,2},..,605$
11	${\mu }_1=-1<{\mu }_2...<{\mu }_n=1$ (* 606 angles points*)
12	$\sigma G_l={\displaystyle \sum _{i=1}^{605}}{w}_1\times f_l\left({\displaystyle \frac{{\mu }_{i+1}-{\mu }_i}{2}}{\mathsf{\xi }}_1+{\displaystyle \frac{{\mu }_{i+1}+{\mu }_i}{2}}\right)+w_2\times f_l\left({\displaystyle \frac{{\mu }_{i+1}-{\mu }_i}{2}}{\mathsf{\xi }}_2+{\displaystyle \frac{{\mu }_{i+1}+{\mu }_i}{2}}\right)$
13	→end
14	$F_{GS}\left(l\right)=\sum _{l=0}^{\mathrm{20,000}}{\displaystyle \frac{2l+1}{4\pi }}\times e^{-t{G}_l} P_l\left(\mu \right)$
15	end
16	End

Figure 3 shows the Legendre coefficients for the 100 keV, 1 MeV, and 10 MeV electrons interacting with Aluminum (Al) with a path length of 100 mfp. A similar scenario is shown in Figure 4 where electrons are incident on Lead (Pb) and scattered with even smaller path lengths of 10 mfp. It is evident from Figure 3 and Figure 4 that 20,000 terms are enough for the convergence of the Legendre series.

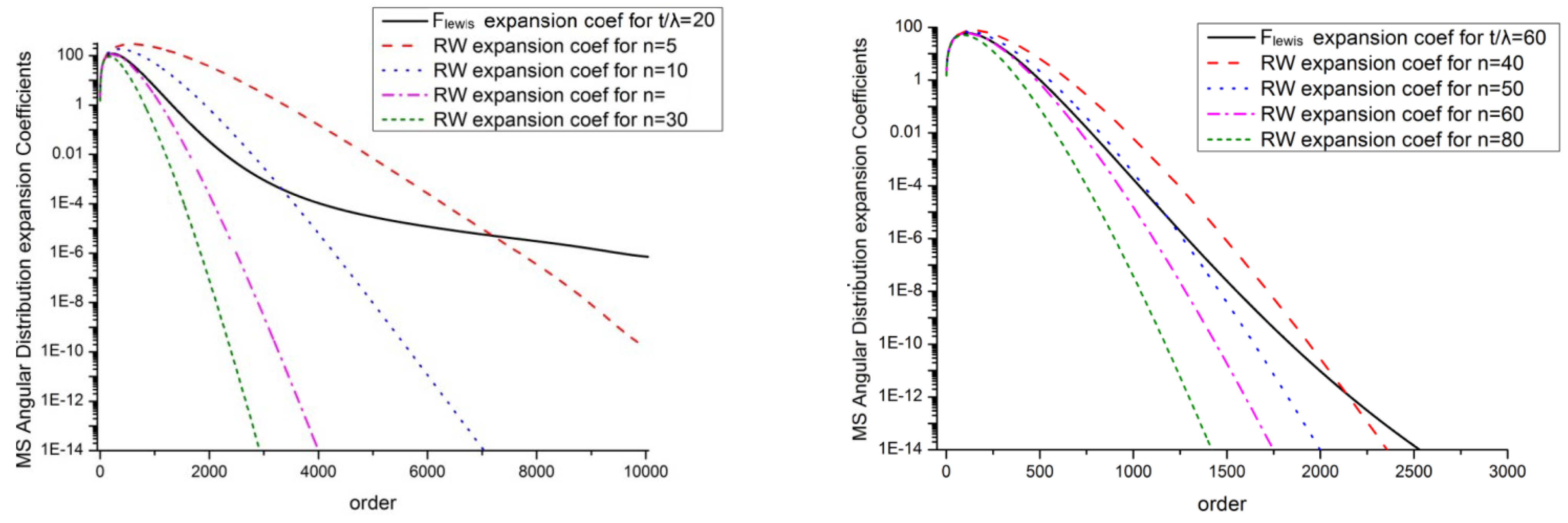
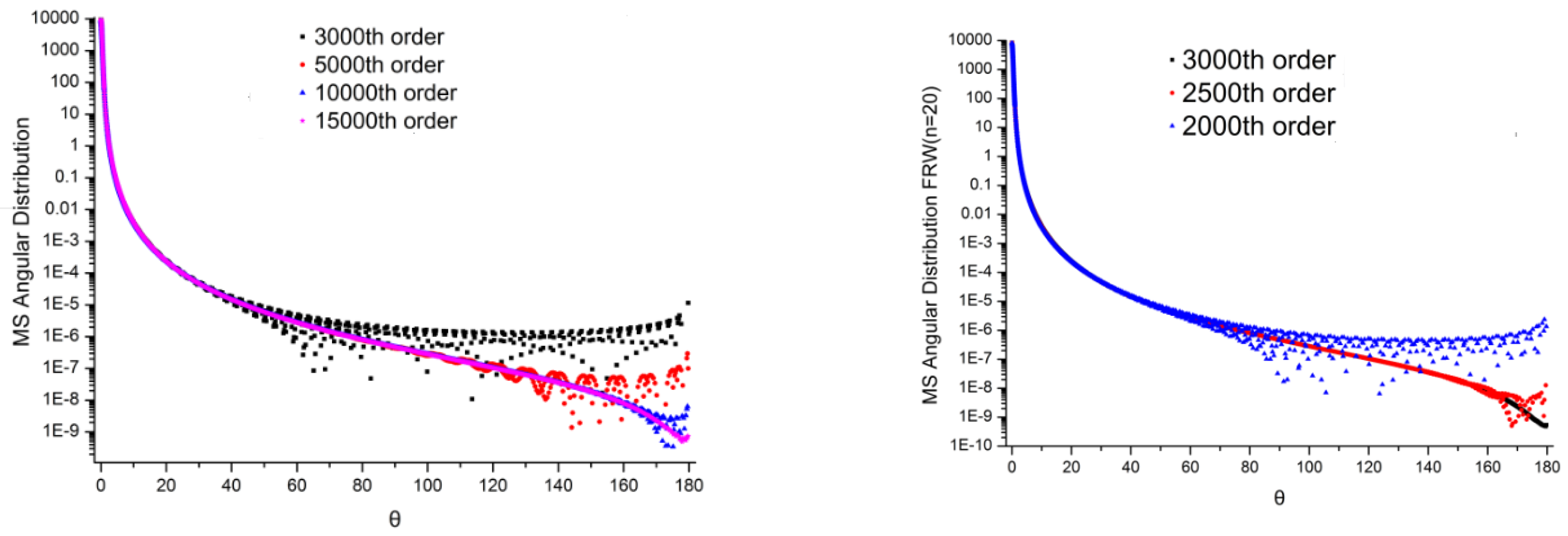
4.3. Multiple Scattering Angular Distributions; Comparison with Random Walk Method

Here is a comparison of Legendre coefficients calculated from the Lewis theory $G_{lewis}\left(l\right)$ of multiple scattering equation and random walk method (rw_l) 10MeV electron multiple scattering in oxygen. As shown in Figure 5, rw_l decreases rapidly, which leads to F_MS(α) being much easier to calculate than for n > 10. And it should be noted that for a step length of t/λ = 20, the probability of having at least 10 scattering event is about 99.5%.

One can note that at higher step lengths, the Legendre coefficients expansion converges faster. Therefore, there is no significant difference with the random walk method at longer step lengths.

In order to investigate the effect of expansion coefficients on multiple scattering angular distributions, we calculated angular distributions for 10 MeV electrons interacting through oxygen using Lewis theory and random walk theory. For comparison, the angular distribution of electrons going through a step length of about 20 m.f.p (t/λ = 20) and 20 scattering events F_RW(n = 20) are calculated, and the results are shown in Figure 6.

As shown in both figures, the summation of inadequate expansion terms leads to highly oscillated distribution behavior and negative values of the distribution function (not fully shown in the figure due to its logarithmic scale). For Lewis theory (t/λ = 20), summation up to the 15,000th order is required to obtain a convergence, while for F_RW (n = 20), expansion up to only 3000th order is enough for a convergent result. In other words, calculating F_RW (n = 20) requires 80% less time than calculating $G_{lewis}\left(l\right)$ (t/λ = 20).

4.4. Validation Metrics

In order to quantitatively evaluate the accuracy and computational efficiency of the proposed random walk method, we employed validation metrics such as 1/e width of the distribution and the computation time.

(1)

1/e width of the angular distribution:

The 1/e width is the angular separation where the distribution falls to 1/e (≈0.3679) of its peak value and thus quantifies the core broadening of the scattering distribution. The 1/e widths (θ_1/e) of the angular distributions of 10 MeV electrons for Oxygen from Lewis theory (t/λ = 20) and the random walk method F_RW(n = 3000) are given in

Table 1. Comparison of the values of 1/e width of the distribution θ_1/e (degrees) and computational time for Lewis theory and random walk method for 10 MeV electrons in oxygen (t/λ = 20).

Parameter	Lewis Theory	Random Walk	% Difference
θ1/e (Degrees)	9.605	9.654	0.52%
Computation Time (ms)	1850	320	82.7%

. The difference between the random walk method and the Lewis distribution is 0.52%. The random walk method accounts for small-angle scattering events leading to marginally broader core broadening.

(2)

Computational efficiency:

The computational efficiency of the random walk method was benchmarked against the traditional Lewis theory. All simulations were performed on AMD Ryzen-7 (4700 U) 2.00 GHz (8 CPUs) with Radeon(^TM) Graphics and 8GB memory to ensure reproducibility. The time to compute 15,000 Legendre terms, including the integration of transport coefficients (G_l), was recorded. Similarly, the time to compute 3000 Legendre terms, along with the overhead for Poisson sampling, was measured. Each calculation was repeated 10 times, and the median time is recorded to minimize the impact of system noise. The results demonstrate an 80% reduction in computation time for the random walk method while maintaining comparable accuracy to the Lewis theory.

5. Conclusions

A robust numerical algorithm for calculation multiple scattering angular distributions is developed. Goudsmit–Saunderson and Lewis theories of multiple scattering are implemented in this algorithm. Elastic and inelastic differential cross-sections which are used to calculate multiple scattering angular distributions are generated through partial wave analysis code ELSEPA [28] and interpolation of these differential cross-sections is performed in our algorithm. The robustness of the algorithm allows the generation of a large number of Legendre expansion coefficients up to the order of 20,000, rapidly and accurately. Furthermore, using the random walk method, a new formula for calculating the multiple scattering angular distribution of charged particles was derived, which is more intuitive and mathematically simpler. The formula can lead to the Lewis theory of multiple scattering angular distribution, thus providing an easier-to-understand framework to unify both GS and Lewis theory. This new method is faster to calculate at a small step length, providing much greater calculation efficiency.

Another assumption made by previous theories is that each scattering is azimuthally symmetric, which is not valid, but it is not a problem as long as the atoms in the medium are isotropically oriented (amorphous assumption), which cancels out the azimuthal dependence. Apparently, this assumption is not valid in materials such as crystals. The random walk method has the potential to include azimuthal dependence in multiple scattering. The random walk framework inherently supports an azimuthal angle-dependent DCS for crystalline materials by generalizing the scattering kernel to spherical harmonics ${\mathrm{Y}}_{l,m}\left(\theta ,\varphi \right)$. For example, in a cubic crystal, a DCS would depend on $\left(\theta ,\varphi \right)$, and transport coefficients G_l would include sums over m. The algorithm’s existing Gauss–Legendre quadrature can be extended to 2D angular grids, and directional scattering probabilities can be sampled using crystal symmetry-adapted basis functions.