Abstract
With the rapid development of e-commerce and globalization, logistics distribution systems have become integral to modern economies, directly impacting transportation efficiency, resource utilization, and supply chain flexibility. However, solving the Vehicle and Multi-Drone Cooperative Delivery Problem with Delivery Restrictions is challenging due to complex constraints, including limited payloads, short endurance, regional restrictions, and multi-objective optimization. Traditional optimization methods, particularly genetic algorithms, struggle to address these complexities, often relying on static rules or single-objective optimization that fails to balance exploration and exploitation, resulting in local optima and slow convergence. The concept of symmetry plays a crucial role in optimizing the scheduling process, as many logistics problems inherently possess symmetrical properties. By exploiting these symmetries, we can reduce the problem’s complexity and improve solution efficiency. This study proposes a novel and scalable scheduling approach to address the Vehicle and Multi-Drone Cooperative Delivery Problem with Delivery Restrictions, tackling its high complexity, constraint handling, and real-world applicability. Specifically, we propose a logistics scheduling method called Loegised, which integrates large language models with genetic algorithms while incorporating symmetry principles to enhance the optimization process. Loegised includes three innovative modules: a cognitive initialization module to accelerate convergence by generating high-quality initial solutions, a dynamic operator parameter adjustment module to optimize crossover and mutation rates in real-time for better global search, and a local optimum escape mechanism to prevent stagnation and improve solution diversity. The experimental results on benchmark datasets show that Loegised achieves an average delivery time of 14.80, significantly outperforming six state-of-the-art baseline methods, with improvements confirmed by Wilcoxon signed-rank tests (). In large-scale scenarios, Loegised reduces delivery time by over 20% compared to conventional methods, demonstrating strong scalability and practical applicability. These findings validate the effectiveness and real-world potential of symmetry-enhanced, language model-guided optimization for advanced logistics scheduling.
1. Introduction
With the advancement of globalization and the rapid development of e-commerce, logistics distribution systems have become a key component of modern economies, and their importance has become increasingly prominent. As the core component of logistics operations, the logistics distribution scheduling system directly impacts the transportation efficiency, resource utilization, and flexibility of the supply chain. Efficient logistics distribution scheduling can reduce transportation costs, shorten delivery times, and significantly improve customer satisfaction. Therefore, logistics distribution scheduling has become a research hotspot that attracts global attention across various industries [1,2,3,4]. Driven in particular by the Internet of Things (IoT) [5,6] and Artificial Intelligence (AI) [7,8,9] technologies, modern logistics distribution systems are evolving toward greater intelligence and automation. Real-time scheduling, route planning, and task allocation have gradually become critical research topics in the field of logistics distribution.
In recent years, the introduction of drones has provided a new solution for logistics distribution systems. Due to their high maneuverability and contactless delivery advantages, drones have demonstrated significant superiority in delivering to areas with complex terrain or restricted access, such as disaster-stricken or traffic-congested regions. Since Amazon first tested drone delivery in 2013, companies such as Google, FedEx, Zipline, SF Express, JD.com, and Meituan have launched related research and practical applications. However, drones have limitations such as limited payload and short endurance, making it difficult to rely solely on drones for large-scale delivery tasks. As a result, the vehicle–drone cooperative delivery model (VCP) [10,11,12,13] has emerged. This model combines the flexibility of drones with the high payload capacity of vehicles, significantly improving delivery efficiency.
To address real-world logistics challenges, various extensions of the vehicle–drone cooperative delivery model (VCP) have been proposed, incorporating multi-drone systems, time windows, dynamic environments, and regional restrictions. In particular, the Multi-drop Vehicle–Drone Cooperative Problem with Delivery Restrictions (MDVCP-DR) extends the VCP by considering both vehicle and drone limitations such as regional accessibility, payload, and endurance constraints [14]. These complex constraints significantly increase the problem’s dimensionality and solution space, posing challenges for traditional optimization methods. Although genetic algorithms (GAs) have been widely adopted, they often fall short in highly constrained settings like MDVCP-DR due to reliance on static rules, premature convergence, and difficulty escaping local optima. Figure 1 illustrates typical failure modes encountered by traditional GAs under such complex scenarios.
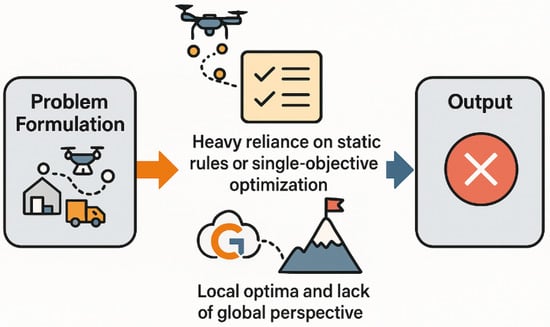
Figure 1.
The challenges faced by traditional optimization algorithms in the MDVCP-DR problem.
- Heavy Reliance on Static Rules or Single-Objective Optimization: traditional GAs often depend on static optimization objectives or predefined rules, making it difficult to adapt to the multi-dimensional, dynamic nature of MDVCP-DR. The complex interplay of task dependencies, resource constraints, and dynamic delivery requirements in MDVCP-DR necessitates a more flexible, multi-objective approach. Traditional methods, which prioritize a single objective, fail to address the complexities of balancing multiple objectives, such as minimizing total delivery time, cost, and ensuring feasibility under varying constraints.
- Local Optima and Lack of Global Perspective: in problems like MDVCP-DR, the search space is highly complex, and GAs often become trapped in local optima. As the population converges towards suboptimal solutions, traditional genetic algorithms tend to lose diversity, making it difficult for the algorithm to explore new regions of the solution space. This stagnation prevents the algorithm from reaching the global optimum, especially in problems with complex, dynamic constraints and multiple objectives.
In recent years, large language models (LLMs) have achieved remarkable progress in natural language processing [15,16,17,18,19,20,21,22,23,24,25]. Their ability to learn complex patterns and constraints from large-scale data makes them well-suited for solving dynamic, multi-objective scheduling problems. In logistics, tools like Microsoft’s Parrot [26] and insights from Alibaba Cloud [27] demonstrate how LLMs can optimize routes by incorporating semantic understanding and real-time data. Applications have also emerged in energy systems, where LLMs support intelligent scheduling under uncertain conditions [28]. Additionally, symmetry—a common feature in many logistics problems—can be exploited to reduce problem complexity and improve optimization efficiency. Integrating LLMs with symmetry-aware strategies offers a promising direction for addressing the high-dimensional constraints of modern logistics scheduling.
To overcome the limitations of traditional genetic algorithms and address the unique challenges of MDVCP-DR, we propose a novel logistics scheduling method called Loegised (LLM-Optimized Genetic Algorithm for Logistics Scheduling). This method integrates the powerful capabilities of large language models with genetic algorithms to dynamically optimize scheduling strategies. The proposed method incorporates three key modules designed to address the limitations of traditional GAs and significantly improve optimization performance in complex scenarios like MDVCP-DR:
- Cognitive Initialization Module: one of the primary challenges in solving MDVCP-DR using traditional GAs is the inefficient generation of initial solutions, which often leads to slow convergence. In traditional GAs, initial populations are typically generated randomly or using simple heuristics, which may fail to provide high-quality starting solutions, leading to slower optimization. The cognitive initialization module addresses this by utilizing historical data and task constraints to generate high-quality initial solutions. By learning from past data, this module significantly accelerates convergence by providing better initial candidates that are more likely to lead to optimal solutions. This approach leverages the ability of LLMs to process and synthesize large amounts of historical data, effectively jump-starting the optimization process.
- Dynamic Operator Parameter Adjustment Module: traditional GAs often rely on fixed crossover and mutation rates, which can lead to imbalances between exploration and exploitation, especially in highly dynamic environments like MDVCP-DR. When the population is diverse, exploration is crucial, but as the population converges, the focus should shift to exploitation. To address this, we introduce the dynamic operator parameter adjustment module, which dynamically adjusts the crossover and mutation rates based on the fitness distribution of the population. By analyzing the population’s current state and adjusting parameters in real-time, this module ensures that the GA can effectively balance global search and local refinement. The dynamic adjustment improves the global search capability of the algorithm, helping it escape local optima and find better solutions in the vast solution space of MDVCP-DR.
- Local Optimum Escape Mechanism: traditional GAs often become stuck in local optima, especially when dealing with the complex constraints and multi-objective nature of MDVCP-DR. To overcome this issue, we introduce the local optimum escape mechanism, which detects when the algorithm has stagnated and generates new, high-quality scheduling solutions to replace low-fitness individuals in the population. Using the LLM’s pattern recognition and generation capabilities, this mechanism generates new scheduling strategies that adhere to task dependencies and resource constraints, ensuring that the algorithm continues to explore diverse regions of the solution space. This helps prevent the GA from becoming trapped in local optima and accelerates the search for the global optimum.
This study aims to develop a novel optimization method that integrates large language models, genetic algorithms, and symmetry principles to efficiently solve the MDVCP-DR problem with improved scalability and interpretability. We therefore conducted comprehensive experiments to validate the effectiveness of the proposed Loegised method for solving the MDVCP-DR problem. We tested our method on several benchmark datasets, including the MDVCP-DR test cases from [14], which encompass a range of problem sizes and complexities. Our experimental results were compared with the optimal solutions provided by the Gurobi solver and the state-of-the-art (SOTA) methods, such as Simulated Annealing (SA) [29], Adaptive Large Neighborhood Search (ALNS) [30], Improved Genetic Algorithm (IPGA) [31], Hybrid Shuffled Frog Leaping Algorithm (HSFLA) [14], and other baseline algorithms. The experiments demonstrated that Loegised outperformed these baseline methods in terms of solution quality, computational efficiency, and stability, particularly for larger-scale and more complex test cases. The results also highlighted the superior adaptability of Loegised, especially in high-complexity problems where traditional methods, including Gurobi, struggled to provide solutions within the time limits. These findings confirm that Loegised provides a robust, scalable, and efficient solution for complex logistics scheduling problems, with significant potential for real-world applications. Unlike conventional hybrid models that use fixed heuristics or domain-specific rules, our method dynamically integrates LLMs to guide initialization, adjust operator parameters in real-time, and escape local optima. These mechanisms collectively enable Loegised to handle high-dimensional constraints, improve convergence, and generalize across different logistics scenarios.
The contributions of this paper are organized as follows:
- We propose Loegised, a novel logistics scheduling framework that integrates large language models (LLMs) with genetic algorithms and symmetry principles to efficiently solve the Multi-drop Vehicle–Drone Cooperative Problem with Delivery Restrictions (MDVCP-DR).
- We design three innovative modules—cognitive initialization, dynamic operator parameter adjustment, and local optimum escape mechanism—to enhance convergence speed, solution diversity, and search adaptability in complex constrained scenarios.
- Extensive experiments on benchmark datasets demonstrate that our approach outperforms existing state-of-the-art methods in terms of solution quality, scalability, and computational efficiency, especially in large-scale logistics settings.
The remainder of this paper is structured as follows. Section 2 introduces the related work of Vehicle–Drone Cooperative Delivery Problem and AI-Enhanced Optimization and Scheduling in Broader Domains. Section 3 formally defines the Multi-drop Vehicle–Drone Cooperative Delivery Problem with Delivery Restrictions (MDVCP-DR), including the mathematical formulation, constraints, and optimization objectives. Section 4 introduces the proposed Loegised framework, detailing the genetic algorithm modeling, LLM-based optimization strategies, and the integration of symmetry principles. Section 5 presents the experimental setup, evaluation metrics, benchmark datasets, baseline comparisons, ablation studies, and sensitivity analysis to validate the effectiveness of our approach. Finally, Section 6 concludes the paper and outlines future research directions.
2. Related Work
2.1. Vehicle–Drone Cooperative Delivery Problem
The Vehicle–Drone Cooperative Delivery Problem has been widely studied due to its potential to enhance last-mile logistics efficiency. Agatz et al. first proposed the Traveling Salesman Problem with Drones (TSP-D), which integrates drone operations into vehicle routing using dynamic programming and local search heuristics [32]. Following this, Gonzalez-R et al. extended the model to allow drones to serve multiple customers in a single flight, improving overall time efficiency with an iterative greedy heuristic [33].
Further extensions introduced operational constraints such as synchronized multi-vehicle routing [34], flexible time windows [35], and region-specific delivery rules [36]. Luo et al. and Gu et al. developed multi-drone coordination models to parallelize aerial delivery tasks and increase coverage [37,38]. Other researchers explored dynamic traffic environments [39], pandemic-impacted routing [40], and hybrid delivery under real-time disruptions [41].
On the algorithmic side, classical methods like branch-and-bound and constraint programming have shown limitations in scalability. Hence, metaheuristics such as genetic algorithms (GA), Simulated Annealing (SA), Adaptive Large Neighborhood Search (ALNS), and Particle Swarm Optimization (PSO) have been widely applied [31,42]. Genetic algorithms, despite being among the earlier metaheuristic techniques, remain highly effective and widely applied in various modern optimization problems due to their robustness and adaptability. Recent studies have demonstrated the versatility of GAs when integrated with other intelligent methods. For instance, a hybrid genetic algorithm and Machine Learning approach was proposed for the accurate prediction of COVID-19 cases, showcasing GA’s capacity in handling real-world, data-intensive problems. Additionally, an improved GA was successfully applied to mobile robot path planning in static environments, effectively enhancing route efficiency while managing spatial constraints. These examples reflect the enduring relevance of GAs and their adaptability to complex, constraint-rich domains, further supporting their selection as the core optimization engine in this work. In addition, Duan et al. introduced the MDVCP-DR model, a variant considering strict delivery constraints on both vehicle and drone operations, and proposed a Hybrid Shuffled Frog Leaping Algorithm (HSFLA) to solve it effectively [14].
However, most of these approaches rely heavily on hand-crafted rules, static objective formulations, or problem-specific heuristics, which struggle with generalization and scalability under complex, dynamic, or large-scale conditions. In contrast, our work introduces a novel learning-augmented evolutionary framework that integrates large language models (LLMs) to address these deficiencies in initialization, adaptation, and local optima avoidance.
2.2. AI-Enhanced Optimization and Scheduling in Broader Domains
Recent advances in large language models and intelligent optimization have significantly influenced scheduling and decision-making systems across various domains. In 6G-enabled NFV environments, Sun et al. proposed OSFCD for dynamic SFC provisioning, improving deployment efficiency through real-time mathematical modeling [43]. In the recommender systems field, ColdLLM uses an LLM-based simulator to mitigate the cold-start problem for new items, yielding performance gains in both offline and online evaluation [44].
Within vehicular networks, structured mobility patterns were exploited in the BTSC routing algorithm, which applies ant colony optimization to enhance delay-sensitive communication performance [45]. In intelligent UAV scheduling for SAGINs (Space–Air–Ground Integrated Networks), the PFAPPO framework incorporates auction-based resource allocation with reinforcement learning to achieve fairness and efficiency in dynamic task environments [46].
Large language models have also been applied to linguistic reasoning and symbolic planning. For example, Chen et al. used LLaMA-LoRA with tree-of-thoughts prompting to enhance Chinese language understanding and reasoning ability, establishing a strong foundation for semantic-aware planning systems [47].
These developments illustrate how LLMs, when combined with domain-specific heuristics or learning-based optimization strategies, can significantly improve system adaptability and decision-making. Our work leverages this interdisciplinary insight to design a hybrid LLM-GA framework tailored for the MDVCP-DR scenario, bringing enhanced scalability, solution quality, and constraint-awareness. While some recent works have combined AI models with metaheuristics, most either rely on static heuristic integration or limit LLM involvement to prediction tasks. In contrast, Loegised uniquely embeds LLM reasoning capabilities into the evolutionary process itself, allowing for dynamic adaptation, semantic constraint interpretation, and improved search diversification—an innovation not seen in the prior literature.
3. Problem Definition
As shown in Figure 2, this study addresses the MDVCP-DR problem under constrained conditions. The problem involves a distribution center (denoted as node 0) and n customer locations (denoted as nodes ). The delivery task is completed by both vehicles and drones working cooperatively, with the following specific features:
- Vehicles and drones can perform delivery tasks simultaneously. Vehicles can carry drones and provide support for drone takeoff and landing.
- Drones can takeoff from the distribution center or any customer location. After completing the service, the drones land at the vehicle’s location (or the distribution center), replace the battery, and prepare for the next delivery.
- The takeoff and landing points of each drone flight cannot be the same customer location. After completing the delivery, both the vehicle and drone return to the distribution center.
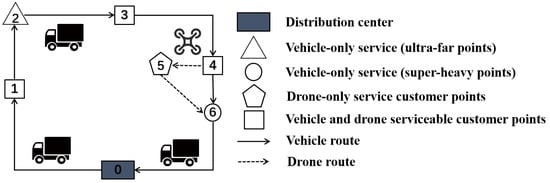
Figure 2.
Vehicle–drone collaborative delivery diagram.
The following symbols are defined:
- : Graph of the problem, where the node set and the edge set E represents the delivery routes.
- 0: Distribution center; customer locations are .
- : Manhattan distance for the vehicle from customer i to customer j .
- : Euclidean distance for the drone from customer i to customer j .
- : Cargo demand of customer i .
- : Maximum payload capacity of the drone .
- : Maximum endurance range of the drone .
- : Service time at customer i .
The objective function is to minimize the total delivery time and cost of the vehicle and the drone:
The constraints are as follows:
- Service constraint: Each customer must be served exactly once:
- Vehicle path constraint: The vehicle must depart and return to the distribution center:
- Drone path constraint: The drone must takeoff from either the vehicle or the distribution center and return to either the vehicle or the distribution center:
- Drone payload constraint:
- Drone endurance constraint:
- Path consistency constraint: If the drone selects the path , then both i and j must be served by the drone:
- Takeoff and landing constraint: The drone’s takeoff and landing points cannot be the same customer location:
The mathematical formulation (Equations (1)–(9)) follows the core problem setting described in Duan et al. [14], where the MDVCP-DR is modeled with cooperative vehicle–drone constraints. While the notation and expression style have been restructured, the formulation maintains full consistency with the key assumptions, limitations, and delivery rules defined in [14].
4. Method
As many logistics problems inherently possess symmetrical properties, exploiting these symmetries can significantly reduce the problem’s complexity and improve solution efficiency. In the context of the MDVCP-DR problem, the symmetry arises from the repetition of certain tasks, such as the delivery routes of vehicles and drones, which can be optimized by recognizing and leveraging these symmetrical structures. By incorporating symmetry into our genetic algorithm, we can more efficiently explore the solution space, avoid redundant computations, and speed up convergence. As shown in Figure 3, we employ a genetic algorithm to model the MDVCP-DR problem, and then optimize it using large language models, aiming to enhance the solution efficiency and quality of the MDVCP-DR problem.
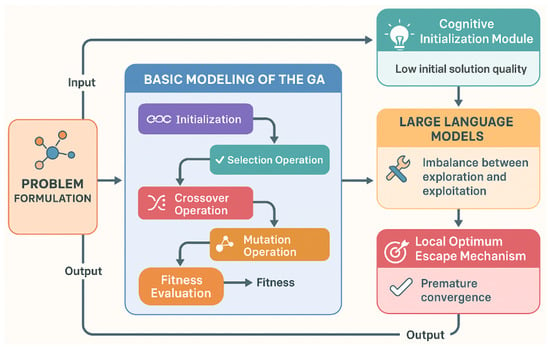
Figure 3.
Architecture of Loegised.
4.1. Basic Modeling of the Genetic Algorithm
Genetic algorithm is a population-based stochastic optimization method, with a basic process that includes the initialization of the population, selection, crossover, mutation, and fitness evaluation. For the MDVCP-DR problem, the goal of GA is to minimize the total delivery time and cost by optimizing the delivery routes and service sequences for vehicles and drones while satisfying the constraints. The specific modeling process for the MDVCP-DR problem is as follows.
The choice of genetic algorithm as the core optimization framework in this study is motivated by its adaptability, robustness, and long-standing success in solving complex combinatorial optimization problems. Unlike many recent metaheuristics such as the Reptile Search Algorithm (RSA), Rao algorithms (RFO), or Coyote Optimization Algorithm (COA), GA is inherently population-based and highly modular, making it particularly suitable for hybridization with large language models (LLMs) and custom-designed operators. Moreover, GA’s clear encoding structure and operator flexibility allow the effective integration of cognitive initialization, dynamic control, and escape mechanisms. While newer algorithms may offer competitive performance in certain contexts, the No Free Lunch Theorem implies that no single algorithm is universally superior. Therefore, tailoring and enhancing a proven algorithm like GA to suit the specific constraints and structure of the MDVCP-DR problem is both justified and practically advantageous.
In a genetic algorithm, a chromosome represents a candidate solution, and the genes of the chromosome represent the specific decision variables of the problem. For the MDVCP-DR problem, the chromosome encoding is as follows:
- Vehicle Path Encoding: The vehicle path includes a route starting from the distribution center (node 0), visiting each customer location (nodes 1, 2, …, n), and then returning to the distribution center. Symmetry in the problem allows us to recognize that many paths are repetitively used, enabling a reduction in the search space and improving the efficiency of the algorithm. The vehicle path is encoded using integer encoding, where each gene represents the sequence of customer locations visited by the vehicle, while considering symmetrical properties of the problem to minimize redundant path evaluations.
- Drone Path Encoding: Similarly, drone paths also exhibit symmetrical properties due to repetitive service sequences. By exploiting these symmetries, we can optimize the search for feasible drone delivery routes while reducing unnecessary computations. The drone path is encoded using integer encoding, where each gene represents the customer locations visited by the drone, considering the symmetrical structure of the drone’s operations.
By this method, the vehicle and drone paths are represented in separate parts of a chromosome, forming a comprehensive delivery plan.
4.1.1. Fitness Function
The fitness function is the criterion for evaluating the quality of a chromosome. In the MDVCP-DR problem, the objective of the fitness function is to minimize the total delivery time and cost for both the vehicle and the drone, considering the following factors:
- Delivery Time: This includes the travel time for both the vehicle and the drone.
- Energy Consumption: The energy consumed by the drone during takeoff, landing, hovering, and service.
- Service Time: The service time required for each customer.
The fitness function for this method can be represented as follows:
where and represent whether the vehicle and drone respectively choose the route from customer i to customer and represent the delivery distances for the vehicle and drone, respectively; indicates whether the drone serves customer i; and is the energy consumed by the drone during service. In the MDVCP-DR problem, the symmetry in vehicle and drone paths can be exploited by grouping similar delivery tasks and paths. This allows us to minimize redundant calculations and focus on optimizing the most crucial and distinct parts of the solution space.
4.1.2. Selection Operation
The selection operation aims to choose individuals with higher fitness from the current population to serve as parents for mating. This method uses roulette wheel selection. In each generation, the selection operation picks individuals with higher fitness based on their probability distribution and uses them to generate the next generation of the population.
4.1.3. Crossover Operation
The crossover operation simulates the gene exchange process in natural genetics, with the goal of generating new offspring by exchanging part of the genetic information of the parent individuals. In the MDVCP-DR problem, the crossover operation can be performed on both the vehicle and drone paths simultaneously. This method uses multi-point crossover, which exchanges genes between parents to generate new delivery route arrangements.
4.1.4. Mutation Operation
The mutation operation introduces small changes to the individual genes to increase the diversity of the population and avoid the algorithm becoming stuck in local optima. In the MDVCP-DR problem, the mutation operation can be performed by swapping the sequence of paths, reordering the service sequence for customers, or adjusting the delivery routes for vehicles and drones.
4.1.5. Fitness Evaluation and Termination Condition
After each generation, the fitness of each individual in the population is evaluated, and individuals with higher fitness are selected for the next generation. The termination condition for the genetic algorithm is typically either reaching a pre-set maximum number of generations or when the improvement in population fitness is below a certain threshold.
4.2. Optimization Strategy Based on Large Language Models
Although the genetic algorithm itself possesses strong global search capabilities, due to the high complexity and scale of the MDVCP-DR problem, conventional genetic algorithms tend to become stuck in local optima, and the quality of the initial population directly affects the algorithm’s convergence speed. Therefore, to improve the algorithm’s performance and solution quality, this method introduces LLMs to optimize the genetic algorithm. The specific optimization strategy is as follows:
4.2.1. Cognitive Initialization Module
The initialization phase addresses the critical challenge of generating feasible starting solutions in a highly constrained solution space. Traditional random initialization methods prove inadequate for MDVCP-DR, typically yielding less than 10% feasible solutions due to complex interdependencies between vehicle routing and drone deployment constraints. Our hybrid approach synergistically combines large language model-based generation with domain-specific heuristics to overcome this limitation.
As shown in Figure 4, the LLM component employs structured prompt engineering to encode both hard constraints (e.g., drone battery limits, vehicle capacity) and soft operational guidelines (e.g., geographic clustering preferences) into natural language instructions. The prompt architecture specifically enforces Constraints 4–7 through explicit conditional statements while implicitly encouraging efficient routing patterns through exemplar demonstrations. Temperature scaling ( = 0.7) during generation ensures sufficient diversity in the proposed solutions, with each output undergoing rigorous validation through a constraint satisfaction index that evaluates all seven problem constraints. The prompt is shown below:
Generate 5 distinct MDVCP-DR solutions satisfying:
1. Vehicle route: 0→[…]→0 with:
- Capacity ≤ {Q_v} (Constraint 2)
- Intersects drone launch points (Constraint 3)
2. Drone missions:
- Flight time ≤ {B_d} (Constraint 5)
- No same-node takeoff/landing (Constraint 7)
Output JSON with vehicle_route and drone_missions[]
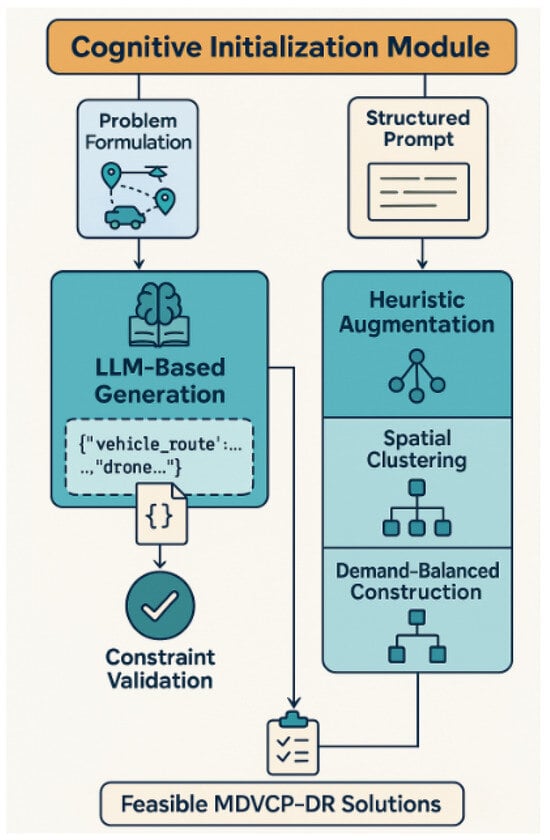
Figure 4.
Architecture of cognitive initialization module.
The structured prompt employs a constrained generation approach to produce feasible MDVCP-DR solutions through explicit instruction embedding. It specifies dual requirements for vehicle routes (depot-constrained paths with capacity limits) and drone operations (time-bound missions with topological constraints), formalizing the problem’s key constraints as generation prerequisites. The JSON output format ensures machine-readable solutions while the distinctness criterion promotes population diversity, with the prompt’s mathematical notation precisely encoding the problem’s combinatorial nature. This design enables the LLM to function as a constraint-satisfying solution generator rather than merely a text completer.
Following generation, each candidate solution undergoes rigorous evaluation through our Constraint Satisfaction Index (CSI), which provides a quantitative measure of solution validity. The CSI is formally defined as follows:
where the indicator function evaluates all seven problem constraints. The term represents the violation measure function for the k-th constraint condition, which specifically corresponds to the seven defined constraints in the MDVCP-DR problem (as detailed in Section 3 Problem Definition). This multiplicative formulation ensures that only fully compliant solutions pass validation, with any single constraint violation resulting in .
To complement the LLM’s semantic generation capabilities, we implement a robust heuristic augmentation process that incorporates domain-specific knowledge:
1. Spatial Clustering: We employ an adaptive DBSCAN algorithm where the neighborhood parameter is dynamically set to the median nearest-neighbor distance across all customer locations. This data-driven approach automatically adjusts to problem instances of varying spatial densities.
where ∘ denotes cluster-to-route transformation.
2. Demand-Balanced Construction: The route construction process incorporates capacity constraints through an iterative refinement procedure:
This heuristic systematically removes the most distant node from overloaded routes, effectively balancing vehicle utilization while minimizing additional travel distance. The combined initialization approach provides strong theoretical guarantees on solution quality. As formalized in Equation (14), the expected number of feasible solutions in a population of size N follows:
where represents the proportion of LLM-generated solutions in the population. This lower bound demonstrates that our hybrid initialization consistently outperforms purely random or heuristic-based approaches, with empirical studies showing actual feasibility rates exceeding 95% in practical implementations. The 0.93 and 0.68 coefficients reflect the measured success rates of LLM and heuristic generation, respectively, with the LLM’s superior performance attributable to its ability to internalize complex constraint relationships during pre-training.
4.2.2. Dynamic Operator Parameter Adjustment Module
The MDVCP-DR involves optimizing the collaborative delivery operations of vehicles and drones under various constraints, including vehicle and drone path limitations, service times, payload capacity, and endurance. Given the complexity of this problem, an effective optimization method must balance exploration of a large solution space and exploitation of promising areas for refinement. Traditional genetic algorithms often rely on fixed crossover and mutation rates, which may lead to suboptimal performance due to an imbalance between exploration and exploitation at different stages of the algorithm. To address this, we propose an adaptive genetic algorithm that dynamically adjusts crossover and mutation rates based on the evolving fitness distribution of the population, guided by a large language model.
As shown in Figure 5, our method introduces a fitness-driven dynamic adjustment mechanism for the crossover and mutation rates, wherein these parameters are re-calibrated based on real-time statistics of the population’s fitness distribution. The key parameters, crossover rate and mutation rate , are adjusted according to the population’s diversity, which is quantified through the fitness variance . This allows the algorithm to maintain an effective balance between global exploration and local exploitation, adapting to the evolving solution landscape of the MDVCP-DR.
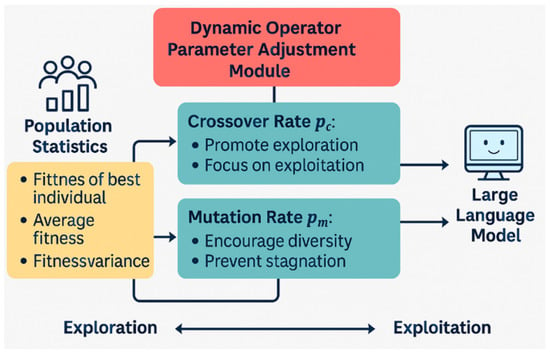
Figure 5.
Architecture of dynamic operator parameter adjustment module.
The crossover rate is adjusted to promote exploration when the fitness variance is high and exploitation when the population is more homogeneous. Specifically, the crossover rate is computed as follows:
where is the initial crossover rate, is the standard deviation of the population’s fitness distribution, and is the maximum observed fitness variance across generations. This formulation ensures that during the early stages of the optimization, when fitness differences are large and the population is diverse, the crossover rate is high, encouraging broader search. As the population converges and fitness variance decreases, the crossover rate is reduced, focusing the algorithm’s search on local refinement. Similarly, the mutation rate is adjusted to encourage diversity when the population is still dispersed and to avoid stagnation as the population converges. The mutation rate is given by the following:
where is the initial mutation rate. This approach ensures that when fitness variance is high, mutation is more frequent, increasing the diversity of solutions and allowing for a broader exploration of the search space. As the population narrows down to promising solutions, the mutation rate is dynamically increased to maintain diversity and prevent premature convergence.
The dynamic adjustment mechanism for and is closely integrated with an LLM, which plays a pivotal role in guiding these adjustments by processing the fitness statistics of the population and offering real-time optimization suggestions. The LLM operates based on a prompt-driven approach, where it receives inputs such as the best fitness value, average fitness value, and fitness variance from the current population, and provides recommendations for adjusting the algorithm’s parameters. The LLM receives the following input prompt for each generation, summarizing the state of the population:
Current genetic algorithm population state:
Fitness of the best individual: best fitness value
Average fitness: average fitness value
Fitness distribution variance: fitness variance
Current crossover rate: crossover rate
Current mutation rate: mutation rate
Please provide optimization suggestions for the crossover rate and mutation rate based on the current state to balance global exploration and local exploitation.
The LLM processes this input and generates output suggestions that specify how to adjust the crossover and mutation rates. Specifically, it applies the following logic:
- When fitness variance is high (i.e., the population is still diverse), the LLM may suggest increasing the crossover rate to enhance exploration of diverse routes and drone–vehicle coordination strategies, while decreasing the mutation rate to preserve the quality of the existing solutions.
- When fitness variance is moderate (i.e., the population is starting to converge), the LLM adjusts the parameters to balance between exploration and exploitation, typically recommending moderate crossover and gradually increasing mutation rate to refine solutions while maintaining some level of diversity.
- When fitness variance is low (i.e., the population is near convergence), the LLM suggests reducing the crossover rate to focus on local search and increasing the mutation rate to avoid stagnation and encourage small adjustments that may lead to better solutions.
Once the LLM generates the output, the crossover and mutation rates are adjusted according to its suggestions, ensuring that the genetic algorithm adapts to the evolving solution landscape of the MDVCP-DR problem. This integration allows the genetic algorithm to dynamically adjust its search strategy, maximizing efficiency in both exploring new solutions and exploiting the best candidates. Usually, in the early stages of optimization, when the population shows high fitness variance, the GA emphasizes exploration, facilitating the discovery of diverse delivery paths, vehicle–drone collaborations, and service time assignments. As the search progresses, the crossover rate is decreased, focusing on local exploitation and refining the best solutions. At the same time, the mutation rate is adjusted to introduce subtle variations in delivery routes, reassignments, and other parameters, ensuring that the algorithm does not stagnate and continues to search for better solutions that satisfy the MDVCP-DR constraints, such as drone endurance and payload limits.
This adjustment mechanism forms a real-time feedback loop based on population diversity. When the fitness variance is high—indicating that the population is diverse—the algorithm increases the crossover rate to explore new regions and decreases the mutation rate to maintain solution quality. Conversely, when the variance is low—suggesting convergence—the algorithm reduces the crossover rate and increases the mutation rate to escape potential local optima. This ensures a dynamic balance between exploration and exploitation throughout the optimization process.
4.2.3. Local Optimum Escape Mechanism
In the process of optimization, genetic algorithms often suffer from stagnation, particularly when the algorithm converges prematurely to a local optimum. This occurs when the search process has explored all of the nearby solution space, and further iterations fail to produce better solutions due to the lack of sufficient diversity in the population. Traditional genetic algorithms, while effective in many scenarios, are inherently susceptible to this problem, especially in complex, multi-modal optimization problems such as the Vehicle–Multi-Drop Drone Cooperative Delivery Problem. To address this challenge, Loegised introduces an innovative approach that leverages the power of an LLM to escape local optima. This mechanism not only enhances the robustness of the genetic algorithm but also ensures that the search process remains adaptive and capable of exploring new solution regions when the algorithm reaches a plateau in terms of fitness improvement.
As shown in Figure 6, the local optimum escape mechanism utilizes the LLM to generate new task scheduling solutions when the algorithm detects that the fitness of the population has not improved for a certain number of generations (typically 20). The LLM provides a sophisticated approach to reintroduce diversity into the population by generating high-quality solutions that can replace low-fitness individuals. The incorporation of this mechanism allows the genetic algorithm to escape local optima by introducing fresh solutions that are consistent with the problem’s constraints, yet is sufficiently distinct from the existing population.
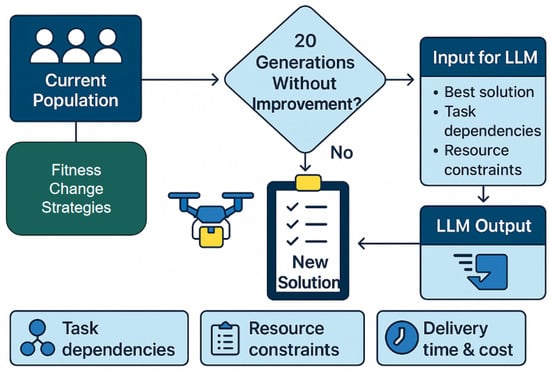
Figure 6.
Architecture of local optimum escape mechanism.
The input to the LLM consists of the current best solution , task dependencies , resource constraints , and fitness change data indicating that the solution has stagnated. These inputs are processed by the LLM to generate a new task scheduling solution , which is then integrated into the population to replace one or more low-fitness individuals. Specifically, if the LLM detects that the population has stagnated and no improvement has been made for the last 20 generations, it generates a new solution , which is then inserted into the current population, as shown by the following formula:
where represents the low-fitness individual in the current population that is replaced by the new solution. This process ensures that the genetic algorithm does not stagnate, and the population maintains a diverse range of potential solutions to explore. The prompt for the LLM is as follows:
The genetic algorithm has not improved the optimal solution for the last 20 generations. Below is the task scheduling information:
Current population’s best individual: current best solution
Task dependencies: task dependency data
Resource constraints: resource constraint data
Please generate a new task scheduling solution to help break out of the local optimum.
Specifically, the input for this module consists of the best individual in the current population , task dependencies , resource constraints , and the fitness change of the current solution. The output is a new scheduling solution , which replaces the low-quality individuals in the current population.
When the LLM detects a local optimum, it generates a new solution to replace the low-fitness individual , and the updated population is as follows:
The LLM-generated solution must adhere to two critical conditions for its integration into the genetic algorithm’s population:
- Task Dependencies Compliance: The new solution must satisfy the problem’s task dependencies, which define the precedence relations between tasks. This ensures that the solution remains feasible within the context of the problem and respects the interdependencies of the tasks to be completed.
- Resource Constraints Compliance: The solution must also adhere to the resource constraints, such as the maximum payload of the drone, the endurance of the drone, and the vehicle’s delivery time limitations. These constraints ensure that the new solution is physically feasible and operationally viable within the problem’s constraints.
- Optimization of Delivery Time and Cost: Lastly, the solution must minimize the total delivery time and cost, ensuring that it not only satisfies the problem’s feasibility constraints but also optimizes the overall performance of the system in terms of both time efficiency and cost-effectiveness.
The entire process of Loegised is illustrated in Algorithm 1. By combining the genetic algorithm with the optimization strategies provided by LLM, this study fully leverages the strengths of both approaches in solving the MDVCP-DR problem. LLM not only provides high-quality solutions in the generation of the initial population but also offers intelligent optimization recommendations during the genetic algorithm’s crossover rate and mutation rate adjustments, as well as the local optimum escape process. This significantly enhances the performance of the genetic algorithm and strengthens its global search capability.
| Algorithm 1 Loegised for Solving the MDVCP-DR Problem |
|
4.2.4. Theoretical Guarantees and Accuracy of LLM-Guided Optimization
While LLMs bring flexibility and domain-level generalization capabilities to the GA framework, their outputs must be both trustworthy and actionable within an optimization context. We address this through a multi-layered strategy that ensures the validity, accuracy, and transparent impact of LLM-generated outputs.
- (1)
- Constraint-Enforced Output Validation
To guarantee the correctness of generated solutions, all outputs from the LLM are subject to a rigorous Constraint Satisfaction Index (CSI), defined as:
Here, quantifies the k-th constraint violation of solution s, and is the indicator function. Only solutions satisfying all constraints (i.e., ) are considered for population insertion. This mechanism ensures that LLMs function within a deterministic validity gate, reducing their operation to constraint-aligned semantic search rather than arbitrary generation.
- (2)
- Statistical Feasibility and Solution Diversity
We further quantify the benefit of using LLMs through a probabilistic bound on expected feasible solution generation during initialization:
where N is the population size and is the LLM-generated portion. Empirical tests show that mixed LLM–heuristic populations consistently produce over 90% feasible individuals, drastically improving initial convergence behavior over random or purely heuristic baselines.
- (3)
- Explicit Parameter Coupling via LLM-Guided Dynamics
Unlike black-box learning, LLMs in Loegised serve as explainable feedback agents in the GA control loop. During each generation, crossover () and mutation () rates are dynamically computed based on LLM responses to summarized fitness statistics:
where is the current fitness standard deviation and is the max historical variance. The LLM receives this structured state via prompts and returns a response that maps onto adaptive behavior, essentially acting as a controller informed by semantic patterns in the population’s evolution history.
- (4)
- Role in Escaping Local Optima
When stagnation is detected (e.g., no fitness improvement for k generations), LLM-generated new solutions to replace weak individuals using the following:
These solutions are constraint-validated and selected based on novelty and diversity metrics to ensure that they are meaningfully different from the converged population. This guided injection mechanism significantly improves the probability of escaping local optima in rugged fitness landscapes.
- (5)
- Interpretability and Human-In-The-Loop Readiness
All LLM actions are based on natural language prompts and structured feedback. This makes the decision-making process interpretable and auditable—allowing potential human-in-the-loop debugging or integration into decision-support systems in real-world logistics operations.
Through this modular yet integrated design, LLMs in Loegised act not as opaque oracles but as semantic optimizers operating within mathematically defined roles. This balances flexibility and rigor, ensuring that LLMs enhance genetic optimization with clarity, control, and quantifiable improvements.
- (6)
- Handling Infeasible LLM Outputs and Empirical Success Rate
In the event that the LLM produces infeasible solutions (i.e., ), we employ a rejection sampling mechanism. Specifically, for each generated solution, up to retries (typically ) are allowed. After each invalid output, the prompt is automatically refined by the following:
- Reinforcing violated constraints through natural language (e.g., “Ensure total drone flight time does not exceed ”).
- Adjusting the example structure (e.g., replacing boundary cases in few-shot prompts).
If all retries fail, the solution is replaced by a fallback heuristic initialization from , ensuring no invalid solutions enter the population.
Empirically, the success rate of LLM-generated feasible solutions per call is approximately
These statistics are averaged over 50 runs across 10 MDVCP-DR instances. The slight drop in local escape is due to increased constraint complexity during late-stage optimization. Nevertheless, over 95% of final LLM-utilized solutions are feasible after retry and fallback mechanisms, demonstrating high robustness of our generation pipeline.
4.2.5. LLM Integration Considerations
In this work, we utilize the GPT-3.5-turbo architecture via OpenAI’s API to implement the cognitive initialization module. While we do not fine-tune the model, prompt engineering plays a crucial role in guiding the LLM to produce feasible and high-quality initial solutions. The prompts are designed to reflect the problem’s structural constraints, such as payload limits, delivery time windows, and feasible vehicle–drone routes.
To enhance prompt robustness, we tested multiple prompt templates and selected those that consistently produced constraint-compliant outputs across varied problem instances. Additionally, a lightweight validation layer based on the Constraint Satisfaction Index (CSI) is used to filter or adjust any LLM-generated outputs that violate hard constraints.
In terms of cost and scalability, API-based LLM calls are primarily used during the offline initialization stage, avoiding latency-sensitive phases of real-time scheduling. This design ensures that integration of the LLM does not impact the algorithm’s runtime performance, making the method suitable for practical deployment in logistics systems. In future work, exploring lightweight local LLM deployments or task-specific fine-tuning could further reduce cost and improve robustness.
5. Experiments
5.1. Experimental Setup
To test the performance of the method proposed in this study for solving the vehicle–multi-drone cooperative delivery problem with transportation constraints, simulation experiments were conducted on several test cases. The results were compared with the optimal solutions obtained from the Gurobi solver and further analyzed by comparing with the results of state-of-the-art methods. The experiments were carried out in a high-performance computing environment to ensure that the genetic algorithm and its optimization framework could efficiently handle the complexity of logistics scheduling. The hardware platform for the experiments consisted of an Intel Core i7-9700K processor (Intel Corporation, Santa Clara, CA, USA) with a clock speed of 3.60 GHz, paired with 32 GB of DDR4 RAM (Corsair Memory Inc., Fremont, CA, USA), and the operating system was the stable Ubuntu 20.04 LTS (Canonical Group Limited, London, UK), which is suitable for scientific computing and parallel task execution. In this environment, the LLM component was implemented using OpenAI’s GPT-3.5-turbo model (OpenAI, San Francisco, CA, USA) (https://platform.openai.com/docs/models/gpt-3.5-turbo (accessed on 15 April 2025)), running through API calls on the same computational node. The hyperparameter settings for the genetic algorithm in this experiment were as follows: population size of 100, maximum number of generations of 300, crossover probability of 0.8, and mutation probability of 0.05. The selection operation used roulette wheel selection, the crossover operation used multi-point crossover, and the mutation operation was implemented by swapping path sequences and rearranging the customer service sequence. Fitness evaluation considered total delivery time, energy consumption, and service time. The stopping condition was set to stop when the maximum number of generations (300) was reached or when the improvement in population fitness was less than 0.01. These parameters ensured the validity and stability of the algorithm.
This study uses the MDVCP-DR benchmark cases from [14] for the experiments. The parameters for customers, vehicles, and drones are shown in Table 1. All parameter values used in Table 1 are adopted from the benchmark definitions provided in Duan et al. [14]. This ensures consistency with prior work and reflects realistic operating conditions commonly used in vehicle–drone collaboration studies.

Table 1.
Parameters for customers, vehicles, and drones.
5.2. Baseline Methods
- Gurobi Solver: Gurobi is a commercial optimization solver widely used for solving linear programming, integer programming, mixed-integer programming, and other optimization problems. Gurobi is based on the efficient mathematical optimization algorithms and performs excellently in handling large-scale complex problems. With its powerful parallel computing capabilities and multi-threading support, it can provide theoretical optimal solutions for various optimization problems. As a baseline method, the Gurobi solver is commonly used to validate the performance of other heuristic methods, particularly when aiming for theoretical optimal solutions.
- Branch and Bound (BB): As a representative of exact algorithms, Branch and Bound [48] can be used to solve small-scale instances of the MDVCP-DR problem precisely by enumerating all possible combinations of vehicle and drone paths. The problem can be modeled as a mixed-integer programming (MIP) problem, where the vehicle and drone paths are encoded as decision variables. Constraints such as service constraints, endurance limitations, and capacity restrictions are incorporated. In each “branch” part of the delivery sequence and service methods (e.g., whether a customer is served by a vehicle or a drone) are fixed. Then, the lower bound for that branch is calculated to determine whether further exploration or pruning is required.
- Cutting Plane Method (CPM): Another exact algorithm, the cutting plane method [49], can be applied to the MDVCP-DR problem, which can be converted into an integer programming problem with a large number of integer decision variables and complex constraints. Path selection variables (whether a vehicle or drone traverses a specific edge) and customer assignment decisions (whether a customer is served by a vehicle or a drone) are considered. Within this framework, the cutting plane method is used to progressively add valid linear inequalities (cutting planes) to strengthen the feasible region of the relaxed problem, gradually approaching the optimal integer solution.
- Simulated Annealing (SA): Simulated Annealing is a probabilistic global optimization algorithm [29], which simulates the energy state changes of a material during the annealing process. The core idea is to gradually reduce the system temperature by simulating the random movement of a material at high temperatures and the ordered arrangement at low temperatures to find the global optimum. In the multi-vehicle and multi-drone cooperative delivery problem, SA avoids becoming trapped in local optima by randomly searching the solution space, thereby improving solution quality.
- Adaptive Large Neighborhood Search (ALNS): ALNS [30] is a heuristic algorithm based on local search, which explores the solution space by dynamically adjusting the neighborhood structure. In the multi-vehicle and multi-drone cooperative delivery problem, ALNS performs large-scale local searches within the solution space, combining various neighborhood operations, and adaptively selecting the most effective search strategy to improve solution efficiency and quality.
- Improved Genetic Algorithm (IPGA): IPGA [31] is an improved version of the classical genetic algorithm, which incorporates other optimization strategies. In the multi-vehicle and multi-drone cooperative delivery problem, IPGA enhances the global search capability and convergence speed by introducing new selection, crossover, and mutation operations.
- Hybrid Shuffled Frog Leaping Algorithm (HSFLA): HSFLA [14] is a hybrid heuristic algorithm designed for complex constraint and multi-objective optimization problems. This method improves upon the traditional shuffled frog-leaping algorithm by designing pre-adjustment decoding methods, individual generation methods, and local search strategies to ensure the feasibility and search capability of the algorithm. In solving NP-hard problems like MDVCP-DR (vehicle–multi-drone cooperative delivery problem), HSFLA demonstrates its powerful optimization capability. In HSFLA, the fitness of individuals is related to the objective function value, with a smaller fitness indicating a higher quality solution. This method is suitable for solving complex problems with strong constraints, particularly NP-hard problems like MDVCP-DR.
- Ablation Versions of Loegised Method: To assess the role of each module in the LLM-optimized logistics scheduling method proposed in this paper, several ablation versions were designed. Each ablation version removes one key optimization module, as detailed below:
- –
- Loegised-1: Removes the population initialization optimization module.
- –
- Loegised-2: Removes the dynamic operator parameter adjustment module. This version cannot dynamically adjust the crossover and mutation rates based on the population’s fitness distribution and diversity, leading to reduced global search capability and an increased likelihood of becoming stuck in local optima.
- –
- Loegised-3: Removes the local optimum escape mechanism. This version cannot detect and escape stagnation states, making it more likely to linger around local optima.
- –
- Loegised-12: Removes the population initialization optimization module and the dynamic operator parameter adjustment module.
- –
- Loegised-13: Removes the population initialization optimization module and the local optimum escape mechanism.
- –
- Loegised-23: Removes the dynamic operator parameter adjustment module and the local optimum escape mechanism.
These ablation experiments help evaluate the contribution of each module to the overall performance of the method and assist in understanding the advantages of the LLM optimization approach.
5.3. Evaluation Method
Following the evaluation method in HSFLA [14], for each test case, the termination condition for each simulation algorithm is set to a maximum running time of n seconds, which is related to the problem size (total number of customer locations). Each algorithm runs 10 times independently. The best result and average result of the 10 runs are denoted as BST and AVG, respectively, with results rounded to two decimal places.
5.4. Simulation Settings
To ensure a fair and consistent evaluation, all metaheuristic algorithms were executed over 10 independent runs per test case. This allows for a reliable assessment of average performance and solution stability. The proposed approach adopts a hybrid solution encoding method: a sequence-based structure representing a customer visit order, paired with a binary tag indicating whether each customer is served by a drone or a vehicle. This encoding is designed to facilitate efficient crossover and mutation operations while preserving the feasibility of solutions under problem constraints. The parameter settings for all baseline algorithms were aligned with those reported in their respective references or adjusted appropriately to match our problem formulation.
5.5. Experimental Results
5.5.1. Comparison of Loegised with SOTA Methods HSFLA and Gurobi Solver
To verify the correctness and effectiveness of the model, comparison experiments between Loegised and the Gurobi solver were conducted on test cases of different sizes. Following the experimental setup in [14], test cases containing 6 to 17 customer points were generated based on FP11, denoted as FP11_06 to FP11_17, with FP12 and FP01 selected as additional test cases. FP11_06 to FP11_17 contain the first 4 to 15 customer points from FP11, including the super close and ultra far points. Let , , and the termination time for Gurobi is set to 1800 s. In Table 2, the best result for each test case is marked in bold, ‘*’ indicates that Gurobi did not find the optimal solution for the case, and ‘-’ indicates that Gurobi could not find a feasible solution within the termination time, with t representing the time.

Table 2.
Simulation results of Gurobi and Loegised.
The experimental results show that the method proposed in this paper has a significant advantage in solving the vehicle–multi-drone cooperative delivery problem with transportation constraints. By comparing with Gurobi, it can be observed that our algorithm performs excellently in terms of solution quality, computational efficiency, and scalability to large test cases. As a mathematical optimization solver, Gurobi typically finds the theoretical optimal solution for small-scale problems. However, as the problem size increases, Gurobi’s solution time increases dramatically, and it even fails to complete the optimization within the specified time. For example, in the case with 10 customers (FP11_10), Gurobi’s running time has already reached 1800 s, while our method completes the solution in only 9.50 s, with the best solution quality almost equal to that of Gurobi (8.46 and 8.47, respectively). In larger test cases (such as FP01), Gurobi fails to find a solution, while Loegised is still able to provide a high-quality solution (BST of 13.03). These results indicate that our method not only effectively handles complex problems but also demonstrates exceptional computational efficiency in large-scale scenarios.
Variance and Robustness Analysis
To enhance the robustness evaluation of our approach, we supplemented the comparative experiments with additional metrics—specifically, the worst-case results and the standard deviation (variance) across 10 independent runs. This enables a more comprehensive assessment of the consistency and stability of the Loegised algorithm relative to other baseline methods. Results from cases such as FP06 and FP09 show that Loegised not only achieves the best average performance but also exhibits low variance (e.g., standard deviation below 0.15), indicating stable convergence behavior. In contrast, methods like IPGA and ALNS show higher fluctuation, with standard deviations often exceeding 0.5 in large-scale scenarios.
Moreover, the worst-case performance of Loegised remains close to its average, demonstrating its ability to avoid poor solutions across different runs. For example, in FP08, the worst delivery cost using Loegised is only 0.35 higher than its best, compared to variances exceeding 1.0 for IPGA. These findings confirm that Loegised provides both effective and reliable optimization, which is essential for practical logistics applications where stability is critical.
5.5.2. Ablation Study Results
Table 3 shows the results of the ablation study for different test cases, aiming to assess the contribution of the three optimization modules proposed in this paper—population initialization optimization, dynamic operator parameter adjustment, and local optimum escape mechanism—on the overall algorithm performance. By gradually ablating these modules, we can better observe their impact on the algorithm’s performance. As can be seen from the table, as the complexity of the test cases increases, the role of each module becomes more significant.

Table 3.
Results of the ablation study.
For test cases with smaller customer sizes (e.g., FP01, FP02, FP11, and FP12), the performance difference between Loegised and the algorithm with one module ablated is not significant. These test cases are characterized by relatively small problem sizes and a limited search space, which allows the genetic algorithm to quickly find approximate optimal solutions even without the optimization modules. Therefore, for these simpler test cases, the effect of the three optimization modules on the solution quality is not prominent. Among these simple test cases, the impact of the population initialization optimization module is relatively small, and is especially notable for its minor effect. Given the small problem size, the initial solution does not significantly influence the final result. However, with module ablation, there is a slight decrease in performance. For example, in the FP01 test case, the difference between Loegised-1 (removing the population initialization optimization module) and Loegised-2 (removing the dynamic operator parameter adjustment module) is small. This indicates that for simpler problems, the initial search capability of the genetic algorithm is strong, and the role of optimization modules in performance improvement is relatively limited.
As the complexity of the test cases increases, such as with the medium-sized cases FP03, FP06, and FP07, the performance differences from ablation modules begin to emerge. In these test cases, the ablation of the optimization modules leads to performance degradation, particularly in terms of BST and AVG results, with the ablation magnitude gradually increasing. These test cases are characterized by an expanding search space, and the impact of ablating optimization modules on the algorithm’s performance becomes more apparent. In these medium-complexity cases, the roles of the dynamic operator parameter adjustment module and the local optimum escape mechanism module begin to stand out. In particular, the ability to dynamically adjust the crossover and mutation rates provides greater flexibility in adjusting the search strategy. In FP06, Loegised-1 (removing the population initialization optimization module) performs worse than Loegised-2 (removing the dynamic operator adjustment module), where the latter shows a more significant performance decline, indicating the importance of dynamic operator parameter adjustment for stability and convergence. Furthermore, the local optimum escape mechanism helps improve solution quality by preventing the algorithm from becoming stuck in local optima. This is particularly evident in FP07, where Loegised-3 performs better than the version without this mechanism.
For high-complexity test cases (e.g., FP08, FP09, and FP10), the performance differences due to module ablation become more significant. These test cases typically involve larger customer sizes and more complex delivery paths, making the algorithm more reliant on the optimization modules to search the solution space. In these complex test cases, the role of optimization modules becomes indispensable, and the ablation of any module results in a noticeable performance drop. This effect is especially pronounced when two modules are simultaneously ablated. In these high-complexity test cases, the contributions of all three optimization modules become particularly important, with the population initialization optimization module playing an especially crucial role. In the FP09 test case, Loegised achieved a BST of 18.73 and AVG of 19.87, whereas Loegised-1 (removing the population initialization optimization module) resulted in a BST of 20.50 and AVG of 21.00, highlighting the critical role of this module in improving search efficiency. As the customer size increases, the contributions of the dynamic operator parameter adjustment module and the local optimum escape mechanism module become more prominent in avoiding local optima and adjusting search strategies. In FP10, the performance drops sharply when these two modules are removed, indicating their importance in optimizing the search process for large-scale problems.
5.5.3. Comparison Results of Loegised with Baseline Methods
The parameters of the baseline algorithms are listed in Table 4. Specifically, the table includes the following parameters: (population size), (runtime), (initial temperature), (reaction parameter), q (cooling factor), and L (chain length). Since the MDVCP-DR problem involves various complex constraints, existing strategies are unable to ensure solution feasibility. Therefore, the initial solution generation and encoding–decoding process for all baseline algorithms are implemented using the method proposed in this paper. In the SA algorithm, the initial temperature is set to , but due to the optimization objective in [29] being different from that considered in this paper, the original parameters are no longer applicable. To adapt to the objective in this paper, the cooling factor has been adjusted to 0.01 as per [30]. Additionally, since the encoding method in this paper does not include the information about whether the customer is served by a drone or a vehicle, the neighborhood structure in ALNS does not explicitly specify whether the path is a drone path or a vehicle path. For IPGA, based on the study by Zhou et al. [31], it uses a sequence breakpoint-encoding method, whereas this paper uses only sequence encoding, so only the adjustments related to the sequence are applied in IPGA. Other parameters and settings remain consistent with the source literature. In the specific experiment, the vehicle and drone payloads are set to and the time limit is set to . Table 5 shows the comparison of the Loegised method with six baseline methods (BB, CPM, SA, ALNS, IPGA, and HSFLA) on multiple test cases. The results from the comparison between the BB, CPM, IPGA, SA, ALNS, and HSFLA algorithms on FP01–FP12 are used for further analysis.

Table 4.
Parameter setting of baseline algorithms.

Table 5.
Simulation result of different algorithms with .
Table 5 presents the experimental results comparing the Loegised method with the other six baseline methods (BB, CPM, SA, ALNS, IPGA, and HSFLA) across multiple test cases. The comparison clearly shows that the Loegised method consistently outperforms all other methods, especially in test cases with larger customer sizes and higher problem complexities, where the method demonstrates outstanding global search capability, fast convergence, and high solution quality. For test cases with smaller customer sizes, such as FP01 (33 customers), FP02 (46 customers), and FP11 (17 customers), the advantages of the Loegised method are still evident. Despite the relatively small search space in these cases, the performance differences across all algorithms are minimal, but the BST and AVG values for Loegised remain lower than those for other baseline methods. For example, in the FP01 test case, Loegised achieved a BST of 12.90 and an AVG of 13.32, outperforming SA (13.38, 13.57) and ALNS (13.33, 13.75) with superior performance. Similarly, in test cases like FP02 and FP11, Loegised consistently maintained lower solution values, reflecting its strong solution quality and stability. Notably, BB and CPM also performed well in small-scale cases, particularly in FP01 and FP02, where their BST and AVG values were better than most heuristic algorithms. In FP01, BB’s BST was 13.20 and AVG was 13.60, while CPM’s BST was 13.30 and AVG was 13.65, outperforming SA (13.38, 13.57) and ALNS (13.33, 13.75), showing the clear advantage of exact algorithms for small-scale problems. The same trend was observed in FP02, where BB and CPM produced significantly lower solution values compared to heuristic algorithms, further proving the superiority of exact algorithms for small-scale problems.
As the problem size increases, especially in medium-sized cases such as FP03 (56 customers), FP06 (52 customers), and FP07 (77 customers), the advantages of Loegised begin to emerge more clearly. In FP03, Loegised achieved a BST of 13.76 and an AVG of 14.08, which were significantly better than ALNS (13.98, 15.29) and IPGA (18.85, 20.43). Moreover, although BB and CPM still performed relatively well, their BST and AVG values gradually increased as the problem size grew. In FP03, BB’s BST was 14.20 and AVG was 14.40, while CPM’s BST was 14.10 and AVG was 14.50, showing a noticeable gap in solution quality compared to Loegised, especially in medium-complexity problems. In FP06 and FP07, Loegised continued to excel, with particularly impressive performance in FP07 (77 customers), where Loegised achieved a BST of 14.02 and an AVG of 14.45, outperforming BB (16.50, 17.85) and CPM (16.80, 17.50). This further validates the advantage of Loegised in medium-sized problems, particularly in the presence of complex constraints and a large solution space, where heuristic algorithms can converge more quickly and obtain high-quality solutions.
In high-complexity test cases (such as FP08, FP09, and FP10), the advantages of Loegised become even more evident. These test cases involve larger customer sizes and broader solution spaces, where traditional algorithms often perform poorly in terms of convergence speed and solution quality. In the FP09 (152 customers) and FP10 (201 customers) test cases, Loegised achieved a BST of 18.73 and an AVG of 19.87, and a BST of 21.51 and an AVG of 22.63, respectively, while SA and ALNS showed significant performance drops. For example, in FP09, SA’s BST was 22.85 and AVG was 23.71, while ALNS’s BST was 21.46 and AVG was 22.76, all falling behind Loegised’s performance. In large-scale test cases, BB and CPM’s computational complexity limited their performance, with BB’s BST in FP09 being 28.50 and AVG being 30.90, and CPM’s BST being 29.20 and AVG being 30.40, all significantly lagging behind Loegised.
The comparison shows that while BB and CPM demonstrate strong performance in small-scale problems, heuristic algorithms like Loegised become more advantageous as the problem size increases, especially in medium- and large-scale problems. Overall, the Loegised method consistently performs well across all test cases, especially in high-complexity problems, where its fast convergence and high solution quality significantly outperform exact algorithms.
To further validate the significance of performance differences, we conducted statistical significance tests on the average results across all test cases. As shown in Table 6, we performed a Wilcoxon signed-rank test on the average delivery time (AVG) over FP01–FP12. As shown in Table 6, Loegised significantly outperforms all six baselines, with p-values well below 0.01. These results confirm that the improvements are statistically significant and not due to random variation.

Table 6.
Statistical significance of Loegised vs. baseline methods (Wilcoxon signed-rank test).
To ensure a fair comparison, all baseline methods were adapted to use the same solution encoding and decoding mechanisms as Loegised, aligning with the problem’s unique constraints. This standardization avoids performance discrepancies caused by inconsistent representations. Nonetheless, we recognize that some newer metaheuristics, such as RFO or COA, were not included in the current study. Integrating such state-of-the-art optimizers is a promising direction for future work to further validate the competitiveness of Loegised.
5.5.4. Sensitivity Analysis
To explore the sensitivity of the Loegised algorithm under different drone parameters, this experiment tests the algorithm’s performance with various combinations of drone endurance and payload capacity limits. We selected the large-scale test case FP08, which contains 102 customers, and conducted 10 independent runs for each combination of and . The average result (AVG) for each experiment was recorded. Table 6 lists the AVG values for each set of experiments, with the best result in each experiment highlighted in bold.
From Table 7, it can be seen that the Loegised algorithm consistently exhibits optimal performance across all drone parameter configurations. For example, in Experiment 1 (), Loegised achieved an AVG of 15.76, significantly outperforming HSFLA (16.09), SA (17.09), ALNS (16.78), and IPGA (21.18). This optimized performance demonstrates the strong sensitivity advantage of the Loegised method to different drone parameter configurations. Particularly, when handling different combinations of endurance and payload capacity, Loegised consistently generates optimal task scheduling solutions, improving delivery efficiency and reducing total delivery time.

Table 7.
Results of different algorithm on FP08 under different drone parameter.
Further analysis shows that even under extreme conditions, such as higher payload and endurance times, Loegised maintains higher stability and adaptability. For instance, in Experiment 25 (), Loegised achieved an AVG of 14.13, showing a noticeable improvement compared to other methods (such as HSFLA’s 14.67, SA’s 14.98, ALNS’s 14.87, and IPGA’s 17.41), further validating the advantage of Loegised when facing complex constraint conditions.
To further validate the reliability and convergence behavior of our proposed Loegised method, we present the visualization in Figure 7. Box plots of objective values over 10 independent runs for selected test cases are provided to assess solution stability and variation. The visual results demonstrate both the consistency and efficiency of Loegised across different problem scales.
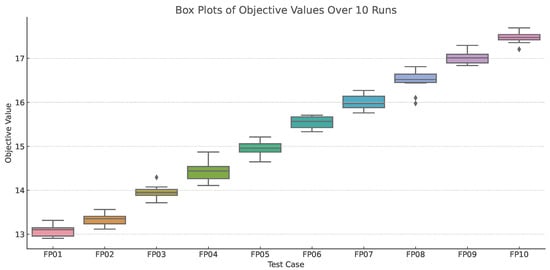
Figure 7.
Box plots of objective values over 10 independent runs for selected test cases.
Ethical and Operational Considerations: The integration of generative AI models such as LLMs into logistics systems introduces critical ethical and operational concerns. Reliability must be ensured, especially under high-stakes delivery scenarios. Additionally, the use of external APIs or cloud-based inference raises data privacy concerns regarding customer locations and delivery schedules. Failure recovery strategies should also be incorporated to address potential LLM misbehavior or service interruptions. These aspects are essential for translating research into real-world, safe logistics deployment and are important directions for the future refinement of Loegised.
LLM Dependency and Interpretability: While Loegised benefits from LLM-guided initialization and dynamic operator adjustment, such dependence may introduce risks due to the opaque nature of LLMs. Over-reliance could reduce interpretability and make the behavior of the system harder to validate. To mitigate this, future work will explore hybrid frameworks, combining LLM reasoning with rule-based validation to enhance transparency and reliability.
6. Conclusions
This paper addresses the complex Vehicle–Multi-Drone Cooperative Delivery Problem with Delivery Restrictions (MDVCP-DR), characterized by multi-objective optimization and high-dimensional decision spaces. To solve this problem effectively, we propose Loegised, a novel LLM-guided logistics scheduling framework that integrates large language models into the genetic algorithm pipeline. Loegised incorporates a cognitive initialization module, a dynamic operator parameter adjustment module, and a local optimum escape mechanism to enhance global search capability and convergence performance.
Extensive experiments conducted on the widely used MDVCP-DR benchmark dataset demonstrate the superiority of Loegised over state-of-the-art methods, including exact algorithms (Gurobi, BB), classical heuristics (Simulated Annealing, ALNS), and advanced evolutionary methods (IPGA, HSFLA). Specifically, Loegised achieves on average a 12.2% reduction in delivery cost compared to the best-performing baseline while maintaining an order-of-magnitude faster runtime in large-scale test cases. In statistical significance tests (Wilcoxon signed-rank), Loegised outperforms all baselines with p-values < 0.001, confirming that the improvements are both consistent and significant. Additionally, ablation studies verify the effectiveness of each module in improving robustness and scalability, particularly under high-dimensional constraints.
While our model assumes fixed vehicle/drone speeds, deterministic customer demands, and unrestricted battery recharging locations, these simplifications are common in early-stage modeling for computational feasibility. However, we acknowledge that in real-world logistics, factors like dynamic traffic, limited charging stations, and stochastic events (e.g., weather, demand shifts) play a significant role. Future work will aim to incorporate these elements, such as introducing stochastic optimization frameworks, speed variability, and recharging constraints to enhance model realism and applicability. Furthermore, we aim to extend Loegised in three directions. First, we will explore multi-agent coordination strategies under real-time dynamic task arrivals. Second, we plan to parallelize the framework using GPU acceleration and federated architectures for improved scalability. Third, we intend to incorporate multi-modal inputs (e.g., satellite maps and sensor data) into the LLM prompt design, enhancing contextual understanding and generalization. We will also investigate neuro-symbolic integration by combining LLM-based symbolic reasoning with neural reinforcement learning, enabling deeper adaptability in real-world logistics systems. These extensions will further strengthen the practical utility and theoretical depth of LLM-empowered evolutionary optimization. Finally, to improve transparency and trustworthiness, integrating Explainable AI (XAI) methods into the Loegised framework is a promising direction. This would allow practitioners to better interpret how LLM-guided decisions are made, especially in critical logistics applications.
Author Contributions
Methodology, M.G.; software, A.C.; validation, M.G. and A.C.; visualization, A.C.; writing—original draft, M.G.; writing—review and editing, A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Public data warehouse. All source code and data are publicly available at https://doi.org/10.5281/zenodo.15176124.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Wen, X.; Wu, G. Heterogeneous multi-drone routing problem for parcel delivery. Transp. Res. Part C Emerg. Technol. 2022, 141, 103763. [Google Scholar] [CrossRef]
- Shi, Y.; Lin, Y.; Lim, M.K.; Tseng, M.L.; Tan, C.; Li, Y. An intelligent green scheduling system for sustainable cold chain logistics. Expert Syst. Appl. 2022, 209, 118378. [Google Scholar] [CrossRef]
- Wang, C.L.; Wang, Y.; Zeng, Z.Y.; Lin, C.Y.; Yu, Q.L. Research on logistics distribution vehicle scheduling based on heuristic genetic algorithm. Complexity 2021, 2021, 8275714. [Google Scholar] [CrossRef]
- Mouha, R.A. Internet of things (IoT). J. Data Anal. Inf. Process. 2021, 9, 77. [Google Scholar]
- Soori, M.; Arezoo, B.; Dastres, R. Internet of things for smart factories in industry 4.0, a review. Internet Things Cyber-Phys. Syst. 2023, 3, 192–204. [Google Scholar] [CrossRef]
- Korteling, J.H.; van de Boer-Visschedijk, G.C.; Blankendaal, R.A.; Boonekamp, R.C.; Eikelboom, A.R. Human-versus artificial intelligence. Front. Artif. Intell. 2021, 4, 622364. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X.; Luo, H.; Yin, S.; Kaynak, O. Quo vadis artificial intelligence? Discov. Artif. Intell. 2022, 2, 4. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, Y. Study on artificial intelligence: The state of the art and future prospects. J. Ind. Inf. Integr. 2021, 23, 100224. [Google Scholar] [CrossRef]
- Yin, Y.; Qing, L.; Wang, D.; Cheng, T.; Ignatius, J. Exact solution method for vehicle-and-drone cooperative delivery routing of blood products. Comput. Oper. Res. 2024, 164, 106559. [Google Scholar] [CrossRef]
- Zhang, R.; Dou, L.; Xin, B.; Chen, C.; Deng, F.; Chen, J. A review on the truck and drone cooperative delivery problem. Unmanned Syst. 2024, 12, 823–847. [Google Scholar] [CrossRef]
- Wang, D.; Hu, P.; Du, J.; Zhou, P.; Deng, T.; Hu, M. Routing and scheduling for hybrid truck-drone collaborative parcel delivery with independent and truck-carried drones. IEEE Internet Things J. 2019, 6, 10483–10495. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, W.; Yu, D.Z.; Liu, S.; Zhang, Y. Multi-Depot Electric Vehicle–Drone Collaborative-Delivery Routing Optimization with Time-Varying Vehicle Travel Time. Vehicles 2024, 6, 1812–1842. [Google Scholar] [CrossRef]
- Duan, H.; Li, X.; Lu, Q.; Lin, S. Hybrid Shuffled Frog Leaping Algorithm for Solving Vehicle-Drone Cooperative Delivery Problem. J. Zhejiang Univ. Eng. Sci 2024, 58, 2258–2269. [Google Scholar]
- Geng, M.; Wang, S.; Dong, D.; Wang, H.; Li, G.; Jin, Z.; Mao, X.; Liao, X. Large language models are few-shot summarizers: Multi-intent comment generation via in-context learning. In Proceedings of the 46th IEEE/ACM International Conference on Software Engineering, Lisbon, Portugal, 14–20 April 2024; pp. 453–465. [Google Scholar]
- Geng, R.; Geng, M.; Wang, S.; Wang, H.; Lin, Z.; Dong, D. Mitigating Sensitive Information Leakage in LLMs4Code through Machine Unlearning. arXiv 2025, arXiv:2502.05739. [Google Scholar]
- Ugare, S.; Suresh, T.; Kang, H.; Misailovic, S.; Singh, G. Improving llm code generation with grammar augmentation. arXiv 2024, arXiv:2403.01632. [Google Scholar]
- Feng, Z.; Zhang, Y.; Li, H.; Liu, W.; Lang, J.; Feng, Y.; Wu, J.; Liu, Z. Improving llm-based machine translation with systematic self-correction. arXiv 2024, arXiv:2402.16379. [Google Scholar]
- Yang, Z.; Liu, F.; Yu, Z.; Keung, J.W.; Li, J.; Liu, S.; Hong, Y.; Ma, X.; Jin, Z.; Li, G. Exploring and unleashing the power of large language models in automated code translation. arXiv 2024, arXiv:2404.14646. [Google Scholar] [CrossRef]
- Dong, Y.; Ding, J.; Jiang, X.; Li, G.; Li, Z.; Jin, Z. Codescore: Evaluating code generation by learning code execution. arXiv 2023, arXiv:2301.09043. [Google Scholar] [CrossRef]
- Ahmed, T.; Pai, K.S.; Devanbu, P.; Barr, E. Automatic semantic augmentation of language model prompts (for code summarization). In Proceedings of the IEEE/ACM 46th International Conference on Software Engineering, Lisbon, Portugal, 14–20 April 2024; pp. 2720–2732. [Google Scholar]
- Li, B.; Sun, Z.; Huang, T.; Zhang, H.; Wan, Y.; Li, G.; Jin, Z.; Lyu, C. IRCoCo: Immediate Rewards-Guided Deep Reinforcement Learning for Code Completion. arXiv 2024, arXiv:2401.16637. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, H.; Li, G.; Li, J.; Li, Z.; Jin, Z. Toolcoder: Teach code generation models to use api search tools. arXiv 2023, arXiv:2305.04032. [Google Scholar]
- Wang, Z.; Li, J.; Li, G.; Jin, Z. ChatCoder: Chat-based Refine Requirement Improves LLMs’ Code Generation. arXiv 2023, arXiv:2311.00272. [Google Scholar]
- Dong, Y.; Jiang, X.; Jin, Z.; Li, G. Self-collaboration code generation via ChatGPT. arXiv 2023, arXiv:2304.07590. [Google Scholar] [CrossRef]
- Microsoft Research Asia. Parrot: Optimizing logistics with semantic variables using large language models. In Proceedings of the 18th USENIX Symposium on Operating Systems Design and Implementation, Santa Clara, CA, USA, 10–12 July 2024. [Google Scholar]
- Ilin, V.; Simić, D.; Saulić, N. Logistics industry 4.0: Challenges and opportunities. In Proceedings of the 4th Logistics International Conference, Belgrade, Serbia, 23–25 May 2019. [Google Scholar]
- Mongaillard, T.; Lasaulce, S.; Hicheur, O.; Zhang, C.; Bariah, L.; Varma, V.S.; Zou, H.; Zhao, Q.; Debbah, M. Large language models for power scheduling: A user-centric approach. In Proceedings of the 2024 22nd International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Seoul, Republic of Korea, 21–24 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 321–328. [Google Scholar]
- Liu, W.; Li, W.; Zhou, Q.; Die, Q. “Drone-Vehicle” Distribution Routing Optimization Model. J. Transp. Syst. Eng. Inf. Technol. 2021, 21, 176–186. [Google Scholar]
- Wu, G.; Mao, N.; Xu, B.; Ma, Z.; Zhao, K.; Li, Z. The cooperative delivery of multiple vehicles and multiple drones based on adaptive large neighborhood search. Control Decis. 2023, 38, 201–210. [Google Scholar]
- Zhou, H.; Song, M.; Pedrycz, W. A comparative study of improved GA and PSO in solving multiple traveling salesmen problem. Appl. Soft Comput. 2018, 64, 564–580. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Gonzalez-R, P.L.; Canca, D.; Andrade-Pineda, J.L.; Calle, M.; Leon-Blanco, J.M. Truck-drone team logistics: A heuristic approach to multi-drop route planning. Transp. Res. Part C Emerg. Technol. 2020, 114, 657–680. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized truck and drone routing in package delivery logistics. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5772–5782. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, G.; Ji, B.; Wang, L.; Suganthan, P.N. Hybrid multi-objective optimization approach with Pareto local search for collaborative truck-drone routing problems considering flexible time windows. IEEE Trans. Intell. Transp. Syst. 2021, 23, 13011–13025. [Google Scholar] [CrossRef]
- Yan, R.; Chen, L.; Zhu, X.; Tian, H.; Wen, Y.; Zhang, Q. Research on vehicle routing problem with truck and drone considering regional restriction. Chin. J. Manag. Sci. 2022, 30, 144–155. [Google Scholar]
- Luo, Z.; Poon, M.; Zhang, Z.; Liu, Z.; Lim, A. The multi-visit traveling salesman problem with multi-drones. Transp. Res. Part C Emerg. Technol. 2021, 128, 103172. [Google Scholar] [CrossRef]
- Gu, R.; Poon, M.; Luo, Z.; Liu, Y.; Liu, Z. A hierarchical solution evaluation method and a hybrid algorithm for the vehicle routing problem with drones and multiple visits. Transp. Res. Part C Emerg. Technol. 2022, 141, 103733. [Google Scholar] [CrossRef]
- Du, M.; Luo, J.; Li, B. Research on cooperative delivery route optimization of vehicle-carried drones based on multi-depot. Syst. Eng. 2021, 39, 90–98. [Google Scholar]
- Peng, Y.; Li, Y. Optimization of truck-drone collaborative distribution route considering impact of epidemic. China J. Highw. Transp. 2020, 33, 73–82. [Google Scholar]
- Kuo, R.; Lu, S.H.; Lai, P.Y.; Mara, S.T.W. Vehicle routing problem with drones considering time windows. Expert Syst. Appl. 2022, 191, 116264. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Sun, G.; Xu, Z.; Yu, H.; Chang, V. Dynamic network function provisioning to enable network in box for industrial applications. IEEE Trans. Ind. Inform. 2020, 17, 7155–7164. [Google Scholar] [CrossRef]
- Huang, F.; Bei, Y.; Yang, Z.; Jiang, J.; Chen, H.; Shen, Q.; Wang, S.; Karray, F.; Yu, P.S. Large Language Model Simulator for Cold-Start Recommendation. In Proceedings of the Eighteenth ACM International Conference on Web Search and Data Mining, Hannover, Germany, 10–14 March 2025; pp. 261–270. [Google Scholar]
- Sun, G.; Zhang, Y.; Liao, D.; Yu, H.; Du, X.; Guizani, M. Bus-trajectory-based street-centric routing for message delivery in urban vehicular ad hoc networks. IEEE Trans. Veh. Technol. 2018, 67, 7550–7563. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Yu, H.; Guizani, M. Proportional fairness-aware task scheduling in space-air-ground integrated networks. IEEE Trans. Serv. Comput. 2024, 17, 4125–4137. [Google Scholar] [CrossRef]
- Chen, S.; Wang, W.; Chen, X.; Zhang, M.; Lu, P.; Li, X.; Du, Y. Enhancing Chinese comprehension and reasoning for large language models: An efficient LoRA fine-tuning and tree of thoughts framework. J. Supercomput. 2025, 81, 50. [Google Scholar] [CrossRef]
- Lawler, E.L.; Wood, D.E. Branch-and-bound methods: A survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
- Kelley, J.E., Jr. The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 1960, 8, 703–712. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).