1. Introduction
Biological materials often achieve remarkable functional performance, not through chemical diversity but through the spatial organization of compositionally simple building blocks. Studies have shown that natural structural materials gain exceptional strength and toughness through hierarchical architectures and functional synergy, even when composed of simple components [
1,
2]. The hierarchical design of biological composites—such as wood, bone, and nacre—enables them to exhibit outstanding mechanical performance for multifunctional applications [
3,
4]. Among these biological composites and polymers, keratin stands out for its exceptional versatility, displaying superior mechanical, thermal, and optical properties, making it a valuable model for bioinspired designs [
5,
6].
Unlike engineered systems that rely on a wide array of specialized materials, living organisms frequently repurpose a limited set of molecular components into structurally diverse and functionally adapted forms. For example, collagen in the musculoskeletal system supports both tensile tendons and rigid bone [
3], while keratin in skin and its appendages gives rise to soft epidermis, rigid scales, flexible claws, and load-bearing feathers [
5,
7,
8]. The role of keratin in skin regeneration—particularly its expression during wound healing—further underscores its importance in maintaining the structural and functional integrity of skin appendages [
9]. This capacity to generate functional diversity from a conserved molecular toolkit highlights the significance of spatial organization and symmetry-related design principles in biological materials.
Among keratin-based structures, the avian feather rachis stands out as a lightweight, anisotropic, and resilient shaft capable of withstanding repetitive aerodynamic loads. With its high specific strength and structural economy, the rachis has attracted interest as a model in both biomechanics and biomimetic materials research. Its compositionally simple yet hierarchically integrated architecture has been the subject of intensive empirical work [
4,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22], highlighting how keratin organization contributes to remarkable energy absorption, flexural stiffness, and direction-dependent stability. The rachis achieves its mechanical robustness through a hierarchical design, where complex arrangements of keratin fibers and elements across scales provide an optimized balance of strength, flexibility, and lightweight performance [
10,
12,
13]. Species-specific adaptations further enhance these properties, with variations in laminar composition, cross-sectional geometry, and fiber orientation optimizing mechanical performance for different flight styles [
11,
16,
17,
18,
19]. The mechanical anisotropy, driven by the hierarchical organization of keratin fibers, governs tensile strength, fracture behavior, and load distribution [
20,
21]. Recent autofluorescence microscopy revealed how keratin density and assembly influence regional mechanical strength along with branching feather growth [
14,
19,
20,
21]. In the rachis core, the presence of foam-filled medullary regions provides damping properties that improve energy absorption and vibration control, maintaining flight stability even under dynamic loading [
22]. This combination of hierarchical design, species-specific adaptation, anisotropic behavior, and damping capacity makes the feather rachis an exceptional example of nature’s ability to achieve mechanical efficiency through spatial organization rather than material complexity.
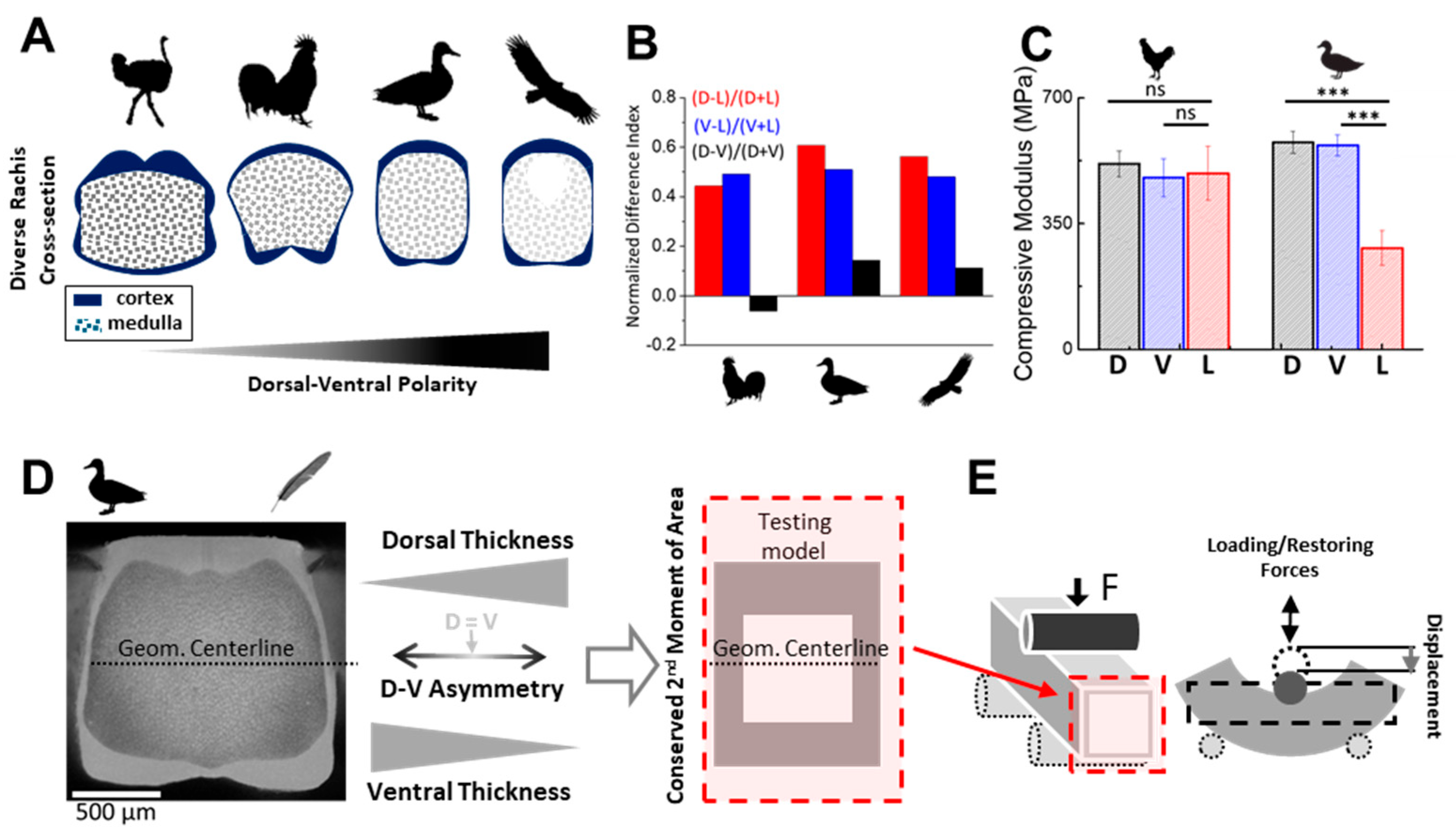
This asymmetry-driven mechanical performance has motivated a range of studies aimed at characterizing keratin integration in the rachis cortex. Traditional material tests have reported bulk stiffness and flexural properties along the rachis [
16,
17,
19,
20,
21,
22]. However, while several studies have noted cross-sectional asymmetries in feather rachises [
13,
16,
19,
20,
23], systematic investigation of these features—particularly along the dorsal–ventral (D–V) and lateral axes—remains limited. To resolve these subtleties, we previously developed a morphometric pipeline to quantitatively analyze rachis cross-sections [
13,
24]. Applying this to multiple avian lineages [
13,
25], we revealed that flight-specialized birds tend to exhibit subtle but consistent D–V polarization of cortical geometry. More recently, we used autofluorescence microscopy to map keratin density distributions with high spatial fidelity [
14], showing that mechanical heterogeneity is shaped not only by morphology but also by regional material content—further supporting the presence of spatially patterned keratin allocation within the cortex. These findings suggest that keratin polarization—in both geometric and compositional terms—plays a role in tailoring the rachis to species-specific flight demands. However, while the anatomical and developmental basis of these patterns is increasingly well-characterized [
13,
25], their mechanical consequences remain less well understood. In particular, it is unclear how variations in material distribution across the cortex affect local stress routing, strain accumulation, and overall shaft performance. The lack of studies directly addressing this gap limits our ability to interpret morphological adaptations in mechanical terms or to translate these symmetry-informed design principles into engineered structures.
To address this gap, we applied finite element modeling (FEM) to test how D–V asymmetry in cortex allocation influences mechanical behavior under bending. FEM has become a widely adopted tool in the study of avian feather rachises, enabling researchers to simulate and analyze their complex mechanical behaviors under various loading conditions [
16,
17,
18,
19,
20,
21,
22]. Rather than reproducing the full morphological variety observed across birds, we focused on square and rectangular cross-sections—an empirically supported shaft shape among flight-specialized birds [
13,
19,
23]—to isolate the role of material placement. This modeling framework was selected to capture broadly applicable biomechanical principles, allowing for the isolation of geometric effects without confounding influences from species-specific shape variation.
In this study, the emphasis is on how the spatial distribution of a single material—rather than its composition—determines mechanical performance. Our FEM approach standardizes material properties across all models, ensuring that observed differences arise solely from spatial variation. This approach highlights a core principle in biological design: optimization often emerges from the strategic spatial placement of simple materials rather than from the use of complex or exotic substances. We aim to demonstrate that, even with identical material properties, dorsal reinforcement significantly improves strain distribution, delays yield onset, and enhances elastic recovery—indicating that spatial asymmetry contributes substantially to mechanical performance, even when compositional variation is absent. While simplified, this approach allows for us to disentangle the effects of keratin distribution from those of shape-related mechanics, providing a controlled framework to evaluate how spatial asymmetry modulates strain dynamics, yield onset, and post-deformation recovery. This strategy is supported by our recent biological findings in frizzling feathers, where dorsoventral disruption in cortex development led to mechanical dysfunction, illustrating the role of spatial material asymmetry in rachis performance [
26], as further discussed in the Discussion section. The feather rachis thus provides a compelling example of how functionally adaptive mechanics can emerge from compositionally simple but spatially asymmetric architectures—offering insight into the broader relationship between structural asymmetry and mechanical function in natural systems.
2. Materials and Methods
2.1. Model Construction and Geometric Framework
To evaluate the mechanical effects of symmetry breaking via dorsoventral (D–V) keratin distribution in the feather rachis cross-section, a series of simplified two-dimensional finite element models were constructed. Each model was composed of four rectangular cortical blocks—dorsal, ventral, and two lateral segments—assembled into a hollow square or rectangular tube to simulate a feather shaft cross-section. This modular design mimics the typical organization of the cortex in flight feather rachises, allowing for precise geometric control over both baseline symmetry and directional asymmetry while maintaining generalizability and minimizing confounding effects from species-specific shape differences.
To account for natural variation in rachis size across bird species, all models were scaled relative to the cortex-to-total cross-sectional area ratio measured in the duck feather shaft (Anas platyrhynchos domesticus). The baseline model featured a geometrically symmetric square cross-section with a side length of 16.23 mm, approximately 10 times the actual width of a duck feather shaft at the mid-proximal region. The cortical shell occupied 27.9% of the total cross-sectional area. The overall shaft length was set to 120 mm, with a 100 mm span between the two supports in the three-point bending setup, ensuring consistent aspect ratios across all simulations. Geometries were created in SolidWorks (v2014) and exported as Parasolid (.x_b) files to ANSYS Workbench (R17.2) for further analysis.
Each model was discretized using hexahedron elements, appropriate for simulating mid-span deformation in long beams. The average element size was approximately 0.4 mm, with a total of ~160,000–185,000 elements, depending on model geometry. Mesh sensitivity analysis was conducted to ensure that the stress and displacement results were independent of mesh density, with convergence defined as a change of less than 1% in maximum stress values between successive mesh refinements. To conserve simulation resources, the presented results were generated without element refinement near interfaces and curved regions. This decision followed a thorough evaluation confirming that the accuracy and consistency of key reported features were not significantly affected by the absence of local refinement.
2.2. Material Properties and Assignment Strategy
All simulations employed the same material definition across all regions of the cortex to isolate the effects of geometry-induced symmetry variation. Each model used a bilinear elastic–plastic material model. Young’s modulus was set to 5 GPa, representing the material property of feather rachis keratin, which typically ranges from 3 to 7 GPa [
16,
19]. Poisson’s ratio was fixed at 0.3, a commonly used value for keratinous materials [
19,
23]. The yield strength—defined as the onset of bilinear isotropic hardening in ANSYS—was set to 138 MPa, based on prior experimental data reporting the tensile strength of keratin fibers reconstituted from feather shafts [
27]. Beyond yield, the material response was modeled as perfectly plastic, with a tangent modulus of 50 MPa, consistent with the brittle behavior of keratin materials [
5].
This uniform material assignment ensured that all observed differences in mechanical response among model variants were attributed solely to geometry-based symmetry breaking—including the spatial distribution and relative thickness of cortex regions—rather than to differences in intrinsic material properties.
2.3. Medulla Exclusion and Geometric Justification
The medullary core of the rachis was excluded from all models. This decision was based on prior empirical observations showing that the medulla exhibits a porous, foam-like morphology and has significantly lower stiffness than the surrounding cortex—by orders of magnitude—and, therefore, contributes minimally to the shaft’s bending resistance [
21,
28]. By excluding the medulla, we focused computational resources on the cortical shell, which dominates load-bearing mechanics and asymmetry-driven strain distribution under bending conditions.
2.4. Boundary Conditions and Loading Scheme
All simulations were conducted under quasi-static, three-point bending conditions using ANSYS’s static structural solver. The shaft was supported laterally by two 2 mm-wide virtual contact plates positioned symmetrically 100 mm apart. These supports constrained vertical motion but allowed for longitudinal sliding to avoid reaction force artifacts. A rigid structural-steel cylindrical indenter (6 mm radius, 24 mm length) was used to apply vertical displacement at the dorsal midline of the shaft, simulating the compressive load experienced during the downstroke phase of flapping flight. The displacement ranged from 0 to 5 mm. The finite contact area of the indenter minimized stress concentration effects and ensured stable convergence during loading.
The simulations assumed plane-strain conditions and were run with enabled large deformation settings to accommodate geometric nonlinearities where applicable. Output variables included equivalent von Mises stress, total strain, and overall deformation profile. Key structural performance indicators were extracted at three displacement stages: pre-yield, yield onset, and post-yield plateau. This symmetrically controlled loading setup provided a consistent baseline for evaluating how dorsoventral asymmetry in cortex structure influences mechanical outcomes.
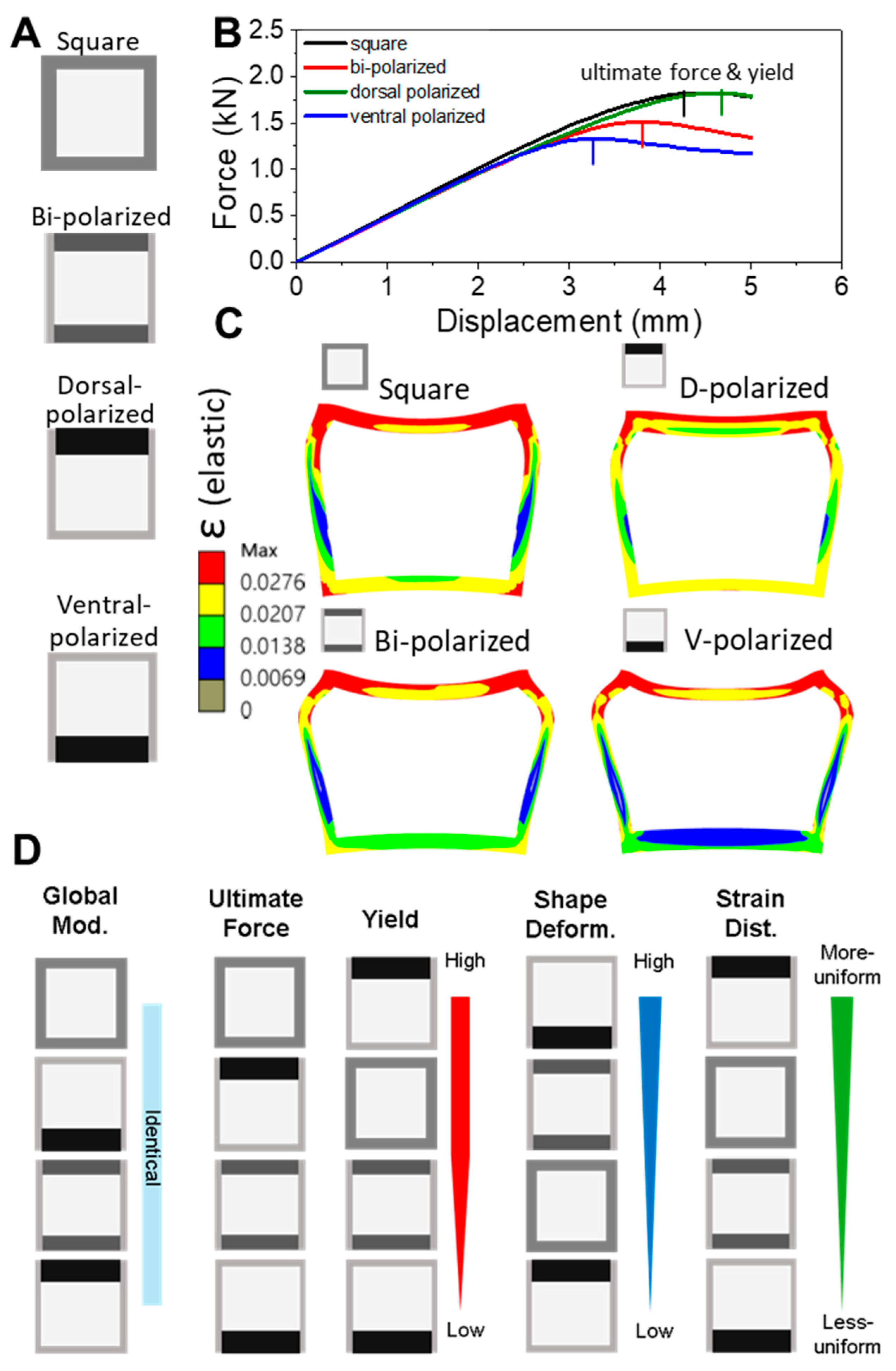
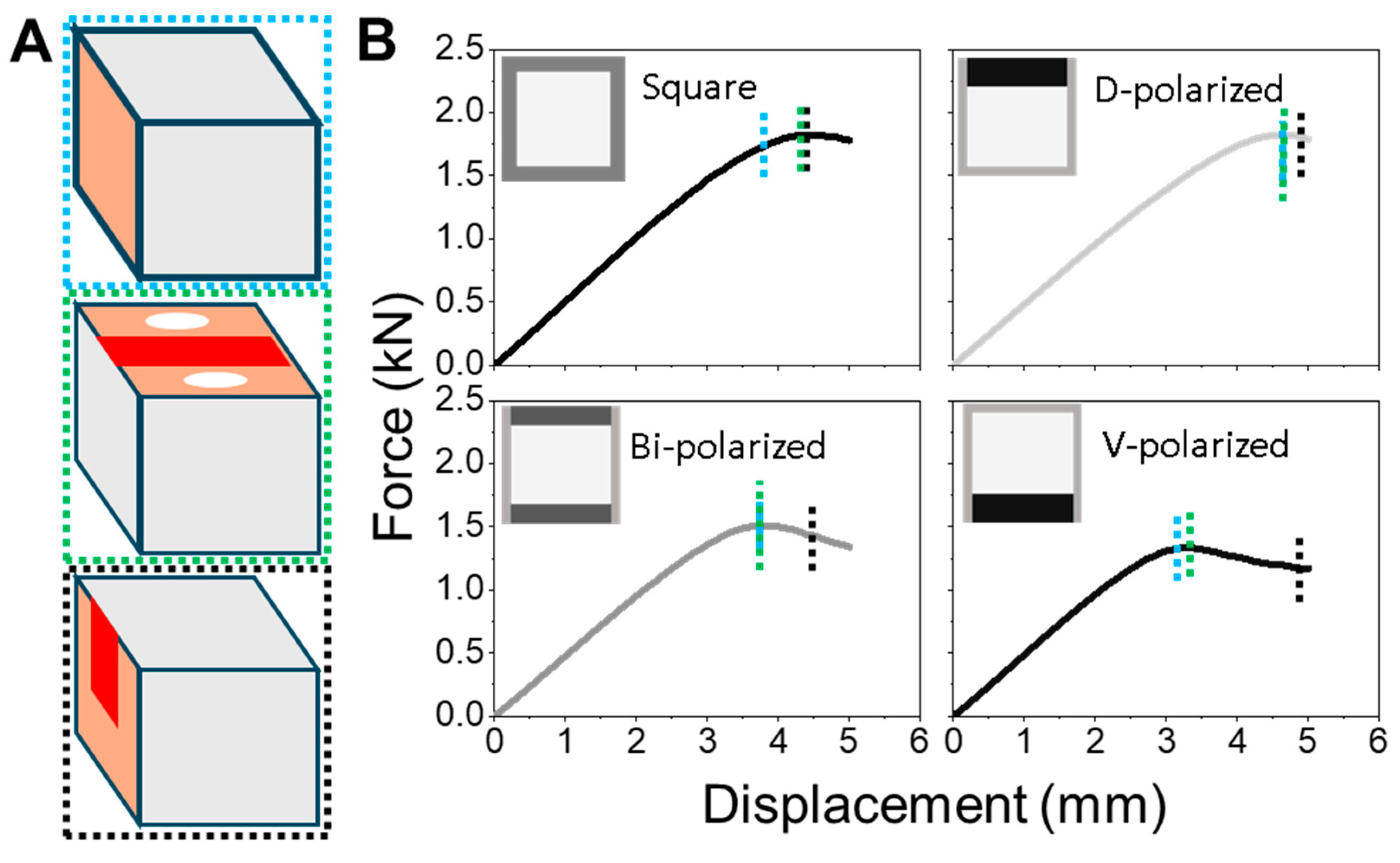
2.5. Model Variants and Comparative Design
Two classes of models were constructed for comparative analysis:
All models shared identical material parameters, meshing resolution, and boundary conditions. Comparative metrics included effective stiffness, yield displacement, strain localization, and plastic deformation recovery. This contrast between geometrically symmetric and biologically informed asymmetric configurations enabled a targeted investigation of symmetry breaking in structural performance. Our models isolate the mechanical effects of dorsoventral (D–V) polarization while intentionally excluding factors such as medullary porosity, laminar microstructure, and dynamic loading to maintain computational efficiency.
A key design constraint was the conservation of the second moment of area (I), which governs bending resistance. By keeping I constant across all configurations and varying only the spatial distribution of cortical material, we ensured that differences in mechanical response arose purely from internal asymmetry rather than global stiffness. This design reflects the biological principle that keratin allocation can be spatially optimized without altering overall shaft geometry.
2.6. Compressive Testing of Real Feather Rachises
To support our FEM-based findings, we performed simplified compressive tests on proximal rachis segments (~2 cm in length and ~2 mm in thickness) from adult chicken and duck feathers. Each specimen was tested along three directions—dorsal (D), ventral (V), and lateral (L)—using a flat steel probe mounted on a vertical depth gauge. Compressive modulus was estimated by normalizing the indentation depth to local rachis thickness. Measurements were repeated five times at three locations per direction and averaged. Statistical comparisons were performed using two-tailed
t-tests. The results are shown in
Figure 1C.
4. Discussion
This study demonstrates that even modest shifts in cortical keratin distribution can significantly influence the mechanical performance of hollow biological beams such as feather shafts. By manipulating dorsoventral (D–V) polarization in simplified square cross-sections, we show that dorsal-biased reinforcement improves resistance to bending, delays yield onset, and promotes more uniform strain distribution. In contrast, ventral polarization compromises these features, resulting in early strain localization, plasticity-dominated deformation, and poor structural recovery.
Our findings demonstrate that dorsal reinforcement delays strain localization, promotes elastic recovery, and aligns with natural adaptations in flight feather rachises. This pattern reflects the adaptive strategy of the thickened dorsal cortex in birds, optimizing mechanical resilience under asymmetric aerodynamic loading. These results underscore the role of spatial asymmetry—not simply material composition—in governing performance, even when volume and stiffness are globally conserved.
Central to our modeling framework is the conservation of I, a geometric property that governs resistance to bending about a given axis. All FEM variants in this study were designed to maintain the same I, ensuring that differences in performance arose solely from spatial redistribution of cortical material—not from changes in global stiffness. By repositioning material dorsally or ventrally while preserving external dimensions, we could isolate how internal asymmetry affects strain behavior and mechanical resilience. This design principle reflects a biologically inspired strategy, where directional mechanical performance is tuned without significantly altering bulk shape or composition.
The superior performance of the dorsal-polarized models is tightly linked to the dominant mechanical environment of the feather rachis during flight. In the downstroke phase of flapping—a key moment for lift generation—the shaft bends upward, placing the dorsal cortex in compression and the ventral cortex in tension. Our FEM simulations reproduce this regime by applying displacement to the dorsal surface, effectively mimicking this loading condition. Reinforcing the dorsal side thus aligns with the aerodynamic stress pattern, providing targeted resistance where strain accumulates most. Additionally, the feather vane is anchored dorso-laterally, transmitting aerodynamic loads directly into the dorsal cortex. This anatomical configuration further concentrates mechanical demand on the dorsal surface, reinforcing the structural logic behind dorsal-side thickening in flight feathers.
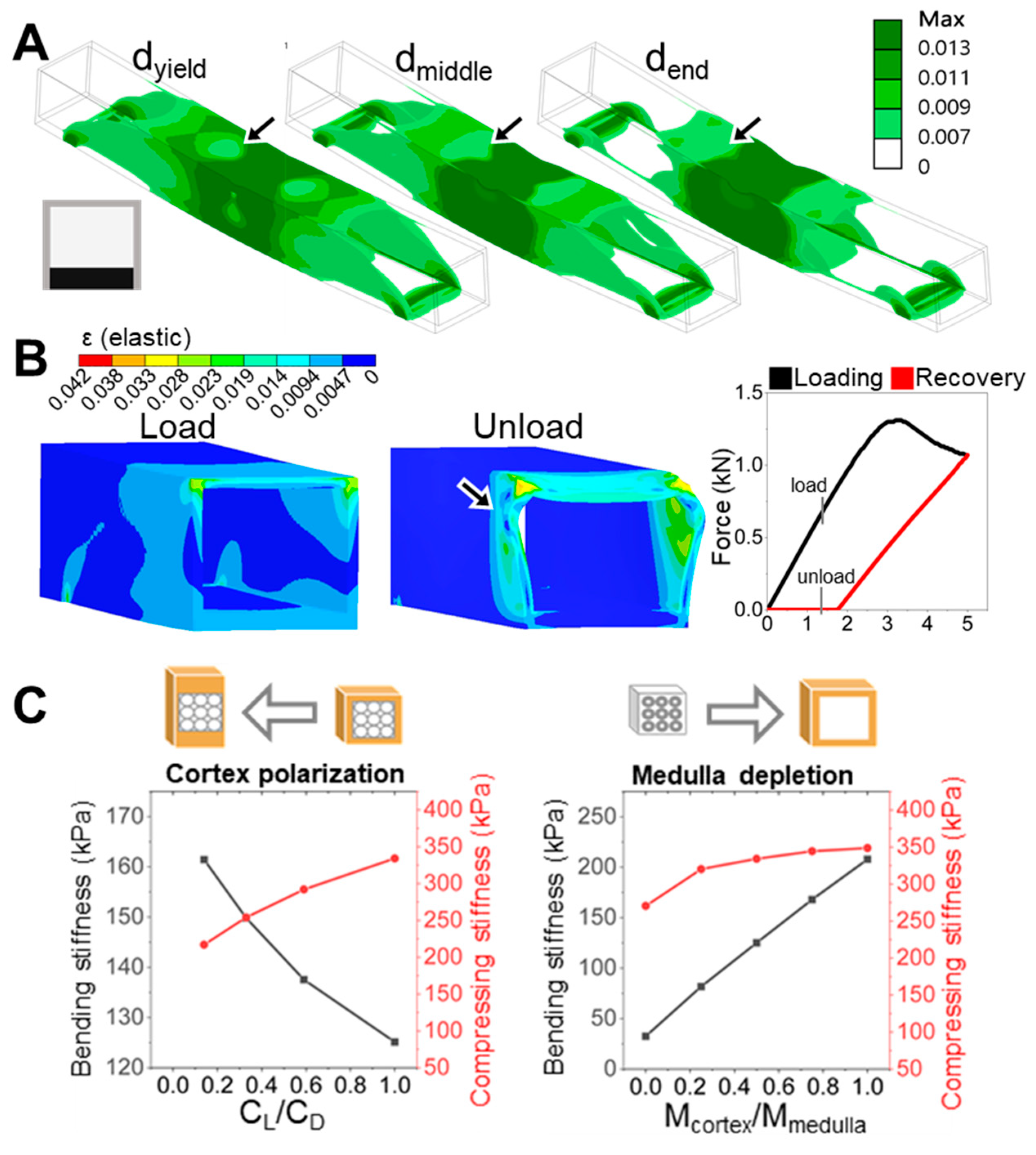
In contrast, a ventral-thickened rachis would misalign with the dominant aerodynamic loading pattern, placing the dorsal side at risk of early strain localization and mechanical failure. Our simulations (
Figure 5A,B) confirm that ventral reinforcement accelerates strain localization and yield onset, undermining structural resilience. Notably, such ventral-thickened rachises are more common in flightless birds like ostriches, where reduced flight demands relax the need for directional mechanical optimization [
13]. This evolutionary comparison highlights that D–V polarization is an adaptive trait, providing load-specific mechanical optimization for active fliers.
These insights align with comparative morphological studies of flight feathers, where dorsal cortical thickening is a recurring pattern in birds exposed to high bending loads [
13]. Our modeling results provide a structural and mechanical rationale for this evolutionary trend: asymmetric material placement—especially in the dorsal–ventral direction—emerges as an efficient strategy for tuning local stiffness and failure tolerance under directional aerodynamic loading. In this way, biological shafts such as the feather rachis demonstrate how internal symmetry breaking at the material level can yield adaptive advantages at the structural scale.
The alignment between our FEM simulation results and experimental measurements (
Figure 1C) supports the central hypothesis that spatial redistribution of cortical material—while conserving
I with similar volume—governs the directional mechanical performance of the feather rachis. Specifically, the higher stiffness along the D–V axis observed in duck rachises with dorsoventral cortical polarization, compared to the near-isotropic stiffness in chicken rachises with symmetric geometry, underscores the critical role of D–V asymmetry in enhancing directional stiffness and mechanical resilience.
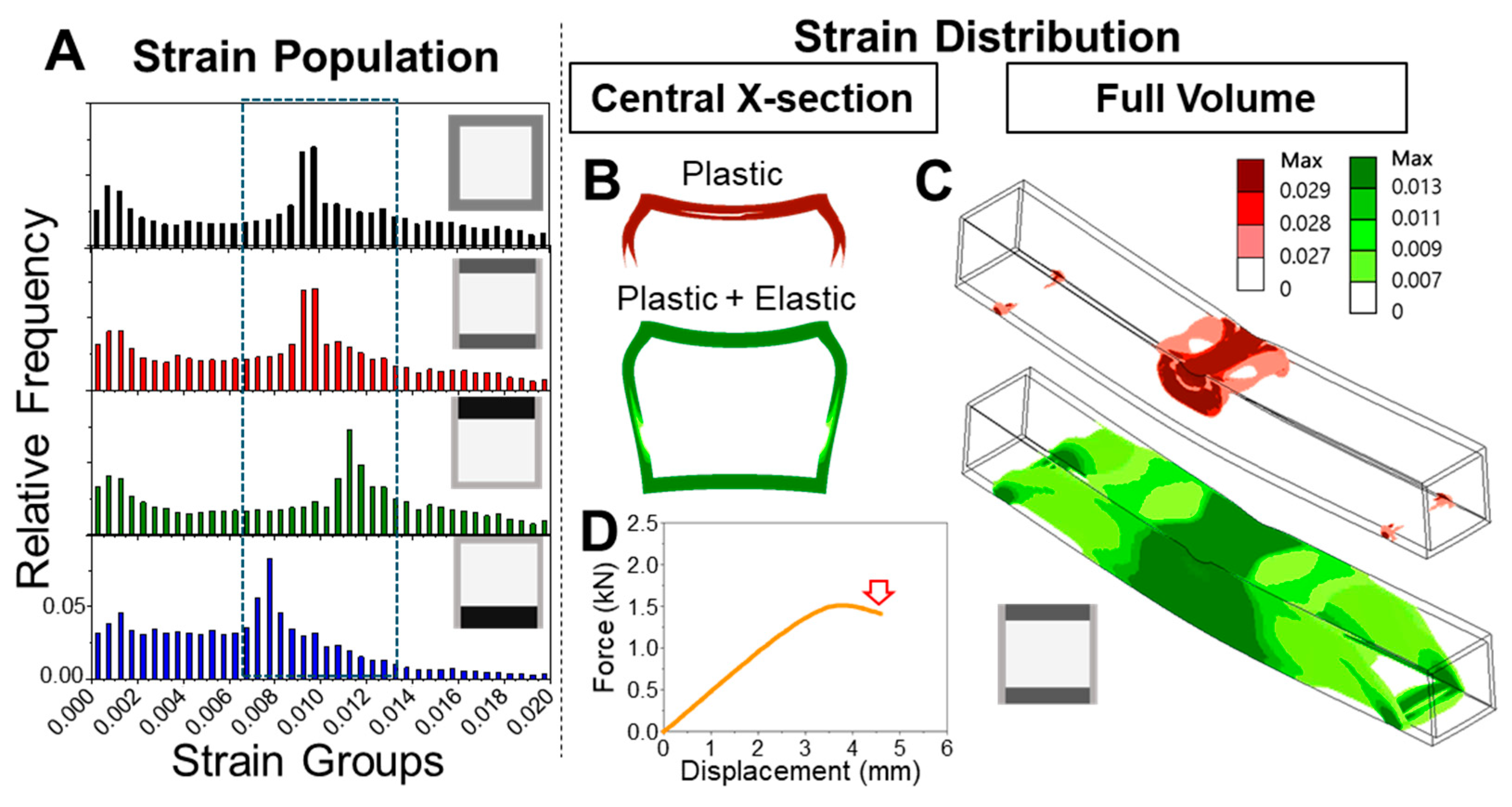
The progression of strain localization in each model further clarifies how these shaft architectures either fail or resist failure. Using the ventral-polarized configuration as an example, strain zones initially concentrate near the dorsal midline and then extend laterally and even ventrally under continued displacement. These zones emerge early, remain spatially fixed (
Figure 5A), and persist throughout the deformation cycle. Simulation of a full loading–unloading cycle revealed significant residual deformation (
Figure 5B), consistent with a broad population of plastic elements and confirmed by a pronounced hysteresis loop in the force–displacement curve. These effects highlight a cascade mechanism: initial strain localization impedes redistribution, amplifying deformation and energy loss. In contrast, the dorsal-polarized models distribute strain more broadly and recover more elastically, suggesting a more resilient and dissipative deformation pathway. The ability—or failure—to redirect strain appears to be a critical determinant of post-yield mechanical behavior.
In this work, we focused on square and rectangular cross-sections—shapes frequently observed in the rachis of strong flyers [
13]—to isolate the role of dorsoventral material asymmetry while minimizing confounding effects from geometry. This simplification allowed for us to decouple keratin distribution from shape-driven influences, such as dorsal curvature or moment-arm variation. While real feather shafts display more elaborate cross-sectional profiles (
Figure 1), incorporating such complexity may obscure the effects of internal symmetry breaking. Nonetheless, features such as dorsoventral curvature or lateral ridges may further modulate strain pathways, potentially redistributing stress and delaying local failure. Given the asymmetrical aerodynamic forces during flapping, structural symmetry is not always mechanically optimal. Future studies integrating morphotype-specific geometry with material asymmetry may better resolve how natural shafts achieve performance tuning through multiscale symmetry modulation.
To conceptually extend our findings beyond dorsoventral (D–V) polarization, we explored an orthogonal form of symmetry breaking: radial material redistribution between the cortex and medulla. While structurally weaker, the medulla functions as a potential keratin reservoir that can be reallocated to reinforce specific regions of the shaft. Our FEM simulations showed that cortex-biased redistribution—effectively representing medulla depletion—increases both bending and compressive stiffness. In contrast, D–V polarization improved bending resistance at the expense of compressive strength (
Figure 5C). These results indicate that radial and dorsoventral asymmetries can be leveraged as distinct yet complementary strategies for mechanical tuning. This radial shift—from a medulla-centered to cortex-dominant structure—not only increases
I but also enhances stiffness routing, strain confinement, and directional resilience through internal symmetry modulation.
These computational findings are supported by our previous developmental study of frizzling chicken feathers [
26], where we showed that the medulla, although mechanically soft, is crucial during rachis formation. In that work, defective integration between the ventral medulla and cortex disrupted dorsoventral patterning, resulting in incomplete ventral cortex development and a mechanically compromised shaft. This biological scenario demonstrates how internal material asymmetry—if mis-regulated—can lead to global structural failure. Here, by extending that insight into a mechanical modeling framework, we show that both internal (radial) and external (D–V) keratin allocations are central to how feather shafts achieve mechanical resilience through multiscale symmetry modulation.
Although our FEM models were simplified, their predictions are consistent with real feather shaft mechanics. In complementary compression tests on chicken and duck flight feathers, we observed dorsoventral differences in stiffness that parallel our simulations. The duck, which exhibits stronger D–V cortex polarization, showed significantly higher compressive stiffness in the dorsal and ventral cortex compared to the lateral regions. In contrast, the chicken—whose rachis morphology is more laterally reinforced—displayed a more uniform stiffness profile. While medullary structure and curvature may also influence these patterns, the alignment between empirical and modeled trends reinforces the importance of spatial keratin allocation in governing real-world mechanical anisotropy.
Taken together, this study bridges biological form, mechanical function, and design abstraction. By showing how directional keratin allocation governs performance in a geometrically constrained model, we highlight a fundamental principle: it is not just the material itself but its spatial deployment that enable resilience in lightweight biological beams. This strategy—mirroring the keratin polarization observed in feather rachises—suggests broader implications for structural design. Asymmetric reinforcement targeted toward zones of directional loading can enhance yield resistance and strain moderation without adding bulk. Such principles could be translated into engineered systems where localized reinforcement and energy dissipation are critical, such as bioinspired actuators, fatigue-resistant aerospace components, or morphing shell structures. In resource- or mass-constrained environments, like deployable shelters or planetary habitats, this geometry-driven material deployment—using a single material with spatially varied thickness—could offer modular, resilient performance without added complexity or diverse materials.
To contextualize our findings and guide future research, we acknowledge several limitations in the present study, particularly regarding model simplifications and biological generalizations.
While our FEM models captured macrostructural effects of cortex asymmetry, several technical limitations remain. For example, integrating real medullary porosity or laminar microstructures would require significantly finer meshing, leading to greater computational demand without proportionate gain in interpretability. Additionally, modeling dynamic or fatigue loading over flapping cycles would necessitate time-dependent boundary conditions and constitutive models that are beyond the scope of the current framework. Nevertheless, our simplified approach offers valuable insights into how geometric polarization influences bending resistance. We anticipate that future work incorporating realistic morphotypes and multiscale heterogeneity will refine these insights under more biologically complex scenarios.
Keratin is a hierarchically structured material, with regional variation in fibril alignment, density, and composition [
6]. While our FEM models assumed homogeneous, bilinear elastic–plastic properties to isolate geometric effects, real feather rachises may exhibit localized material heterogeneity—especially at dorsal and ventral contact zones. Such internal heterogeneity, including porosity, lamination, and differential cross-linking, likely contributes to strain modulation and yield behavior. We acknowledge this limitation in our current modeling framework and suggest that future simulations incorporate position-dependent material properties derived from imaging or microscale testing to better capture the full spectrum of keratin’s mechanical sophistication.
While this study focuses on dorsoventral (D–V) polarization, feather rachises exhibit asymmetries across multiple axes and scales. Beyond D–V distribution, features such as proximal–distal shaft tapering, dorsal ridges, and ventral invaginations can introduce localized reinforcements that further tailor mechanical performance. Although our FEM models abstracted these complexities to isolate D–V effects, such multiaxial asymmetries represent important directions for our future research. These higher-order geometric features may contribute to load redirection, strain redistribution, or torsional resistance, allowing for feather shafts to adapt to diverse flight regimes.