Research on Navigation and Dynamic Symmetrical Path Planning Methods for Automated Rescue Robots in Coal Mines

Abstract

In the context of coal mine operations, the assurance of work safety relies heavily on efficient autonomous navigation for rescue robots, yet traditional path planning algorithms such as A and RRT exhibit significant deficiencies in a coal mine environment. Traditional path planning algorithms (such as Dijkstra and PRM) have certain deficiencies in dynamic Spaces and narrow environments. For example, the Dijkstra algorithm has A relatively high computational complexity, the PRM algorithm has poor adaptability in real-time obstacle avoidance, and the A* algorithm is prone to generating redundant nodes in complex terrains. In recent years, research on underground mine scenarios has also pointed out that there are many difficulties in the integration of global planning and local planning. This paper proposes an enhanced A* algorithm in conjunction with the Dynamic Window Approach (DWA) to enhance the efficiency, search accuracy, and obstacle avoidance capability of path planning by optimizing the target function and eliminating redundant nodes. This approach enables path smoothing to be performed. In order to ensure that the requirement of multiple target point detection is realized, an RRT algorithm is proposed to reduce the element of randomness and uncertainty in the path planning process, leading to an increase in the convergence rate and overall performance of the algorithm. The solution to the problem of determining the global optimal path is proposed to be simplified by means of the optimal path planning algorithm based on the gradient coordinate rotation method. In this study, we not only focus on the efficiency of mobile robot path planning and real-time dynamic obstacle avoidance capabilities but also pay special attention to the symmetry of the final path. The findings of simulation experiments conducted within the MATLAB environment demonstrate that the proposed algorithm exhibits a substantial enhancement in terms of three key metrics: path planning time, path length, and obstacle avoidance efficiency, when compared with conventional methodologies. This study provides a theoretical foundation for the autonomous navigation of mobile robots in coal mines.

1. Introduction

Since coal mines are underground and this particular environment has many unique features, path planning and navigation is a complex and difficult task. The space in an underground coal mine is typically narrow, with inadequate ventilation and lighting. This leads to the fact that a rescue robot may encounter limited visibility and a high density of obstacles when performing tasks, which increases the complexity of path planning. Also, obstacles such as support structures, equipment, and other building materials may also be present in the mine, the locations of which are variable, which makes it difficult to adapt traditional path planning algorithms. By introducing symmetry, we can more intuitively judge whether the path is close to the optimal state. Symmetry is an important criterion for us to evaluate the performance of the final path. References [1,2,3] focus on control systems for inspection robots; classical path planning methods (e.g., Dijkstra, PRM) are discussed in [4,5,6].

Traditional path planning algorithms, such as Dijkstra, PRM, and classical A*, exhibit certain inherent limitations when applied in underground coal mine environments. Traditional path planning algorithms (e.g., Dijkstra, PRM) exhibit limitations in dynamic and narrow spaces: Dijkstra’s high computational complexity [4], PRM’s poor adaptability to real-time obstacle avoidance [5], and A*’s tendency to generate redundant nodes in complex terrains [6]. Recent studies [4,5,6,7,8] further highlight the challenges of integrating global and local planning in underground mines. Dijkstra’s algorithm, although optimal, suffers from high computational complexity, making it less suitable for real-time planning in narrow, dynamic spaces. PRM often fails to adapt effectively to unstructured environments due to its reliance on pre-sampled configurations, which may not reflect sudden changes or dynamic obstacles. The classical A* algorithm, while efficient in general, tends to produce paths with redundant nodes in cluttered terrains, leading to excessive maneuvering and energy consumption. These limitations primarily stem from the algorithms’ assumptions of static or semi-structured environments, which do not hold in unpredictable underground settings where space is constrained, sensor data is noisy, and obstacles are mobile or irregular. Therefore, a deeper analysis and adaptation of these methods is necessary for robust underground robot navigation.

Continuous deepening of mines in coal mining increases the number of requirements for safe working conditions and their importance. The life and health of miners in emergency situations directly depend on fast and accurate search and rescue measures. Therefore, it is particularly important to fulfill the requirements for the application of mobile rescue robots in a coal mine environment. The robot should be characterized by autonomous operation [9,10,11], a high degree of navigational properties, the ability to work in real time, fast reaction and adaptation to environmental changes in complex underground conditions, and the ability to avoid obstacles and rearrange routes.

Robots are also required to efficiently plan a path between multiple target points. Since there are a large number of critical points in a coal mine that need to be inspected, the robot needs to construct a route so that, depending on the importance, it bypasses each node using the optimal route and spending the minimum amount of time. Therefore, solving the optimization problem in route construction by the robot is one of the most important problems. For this purpose, robots must also have the ability to collect and process data for monitoring, evaluation, and feedback of the mine environment. This monitoring can not only display real-time information about the state of the environment, it can also provide important data for decision making [12,13,14].

All of the above requirements determine the relevance of the study of navigation methods of mobile robots in search and rescue work in a coal mine. The results of this study have theoretical and practical value in solving the issue of improving safety, efficiency, and automated work in coal mines.

In the field of mobile robot navigation, trajectory planning is one of the key technologies to realize autonomous mobility. With the development of intelligent technologies, researchers have proposed many algorithms to solve path planning problems. Recent advances include reinforcement-learning-based planners for dynamic environments [15], probabilistic coal mine mapping [16], and multi-robot coordination in narrow tunnels [17]. However, these methods face challenges in balancing real-time performance and path smoothness, which our approach aims to address.

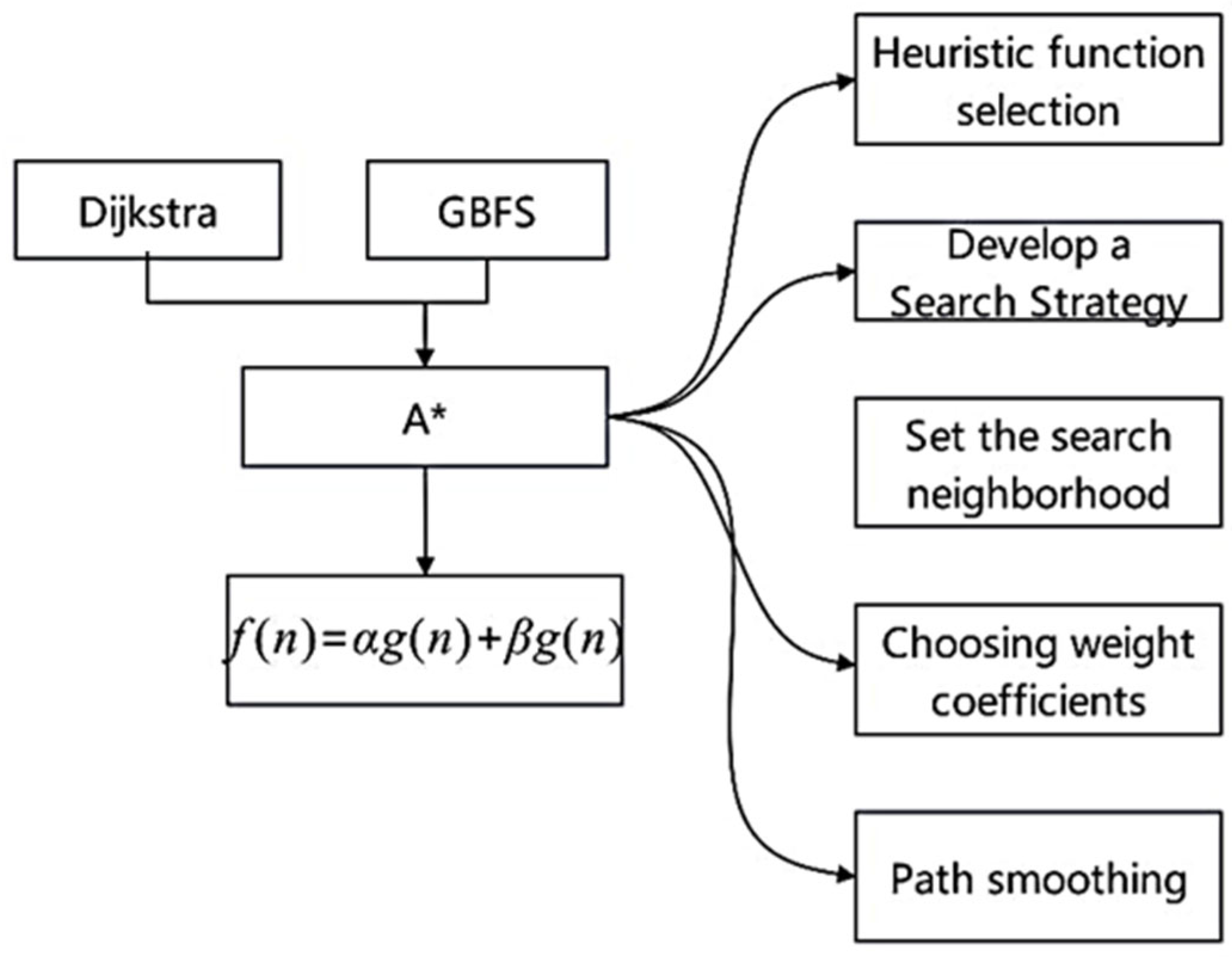
• Path planning based on the A* algorithm. The A* algorithm is a classical heuristic search algorithm, which is widely used in path planning problems. The traditional A* algorithm employs a fixed neighborhood search strategy (such as the 8-neighborhood), generating a large number of redundant turning points in complex tunnels. which results in a 24.1% increase in path length and a 65% increase in computation time. The fundamental reason lies in that the heuristic function does not take into account the dynamic obstacle density and the topology of the tunnel, leading to redundant search space. The global path generated by A* cannot be updated in real time. When dynamic obstacles (such as moving mining vehicles) block the path, it is necessary to re-plan frequently (with an average time consumption of over 10 s), which makes it difficult to meet the real-time requirements of coal mine rescue. According to research [18,19,20], the improved A* algorithm can not only effectively reduce the path length, it also improves the speed of path planning through the strategy of removing redundant nodes and an improved neighborhood search method. Combining a second-order piecewise Bezier curve to smooth the path can further improve the reliability and stability of the motion. Related studies [21,22,23] show that compared with the traditional A* algorithm in a coal mine environment, the improved A* algorithm reduces the computation time by 65% and the path length is reduced by 24.1%, which provides a theoretical basis for the efficient navigation of mobile robots in a coal mine.
• DWA. The dynamic window method is a local motion trajectory planning algorithm for mobile robots, which is particularly suitable for obstacle avoidance tasks in dynamic environments. The DWA algorithm can adjust the motion trajectory in real time, taking into account the robot’s movement ability and the position of dynamic obstacles, thus improving the obstacle avoidance performance. By combining the improved A* algorithm with the DWA, global trajectory planning and local obstacle avoidance can complement each other, improving the navigation efficiency and flexibility of the robot. Experimental results [4,5] show that the proposed method can effectively avoid new dynamic and static obstacles in complex environments and improve the robot’s adaptability in emergency situations. The state window method is prone to getting stuck in local optima in U-shaped or L-shaped narrow tunnels (obstacle avoidance success rate < 60%). The main reason is that the fixed-weight evaluation function cannot dynamically balance the priority of path tracking and obstacle avoidance. Sensitivity to perception noise is also an issue. The DWA relies on real-time sensor data, but in high-dust environments, the laser radar point cloud noise (error ± 0.2 m) significantly reduces the accuracy of distance assessment, resulting in an increase in the failure rate of obstacle avoidance to 35%.
• RRT algorithm. Rapidly-exploring Random Tree (RRT) algorithm is widely used in path planning due to its simplicity and adaptability. Due to its dynamic step size and gravity field, the algorithm significantly improves the convergence rate and search efficiency in path planning. Experimental results [6,7] show that the path planning time of the proposed method is reduced by 33.84% and 34.93% in simple and complex environments, respectively, and the path length is also effectively reduced. This method provides a solution to the problem of generating directions for new nodes in complex obstacles and improves the reliability of path planning. RRT relies on random expansion trees to generate paths. In static obstacle-dense areas (such as equipment storage areas), the convergence speed significantly decreases (planning time > 3 min). Experiments show that the path success rate in narrow tunnels is only 58%. The paths generated by RRT require secondary optimization (such as B-spline interpolation), increasing the computational cost by 20%, and do not consider the kinematic constraints of the robot (such as the minimum turning radius), resulting in an infeasible trajectory.

The above limitations stem from the fact that the algorithm design has not been optimized for the particularity of the coal mine environment (such as dynamic obstacles, perceived noise, and complex topology), and there is an urgent need for a collaborative framework that integrates global planning and real-time obstacle avoidance. The aim of this study is to solve the navigation problem of mobile robots in a coal mine environment, and to comprehensively utilize different path planning algorithms to improve the autonomous robot navigation ability in complex environments. To achieve the objective, we propose to develop the structure of a path planning algorithm for a rescue robot based on the improved A*. Compared to existing hybrid approaches (e.g., A*-DWA fusion in [24]), our method introduces two key innovations: (1) redundant node removal in A* via adaptive neighborhood search, and (2) adjusting weights dynamically. By dynamically adjusting the weights of the heuristic function, the robot can more reasonably balance the path length and safety when planning the path. Meanwhile, the improved A algorithm is closely combined with the DWA. The global path provides macro guidance for the DWA, and the DWA dynamically adjusts the robot’s motion trajectory based on the global path information and the real-time environment to achieve more efficient local obstacle avoidance. This way of global and local collaborative optimization, as well as the unique strategies in optimizing the objective function and processing the path smoothness, have innovative significance in the research of path planning for rescue robots in coal mines. It provides new ideas and methods for solving the robot navigation problem in complex environments.

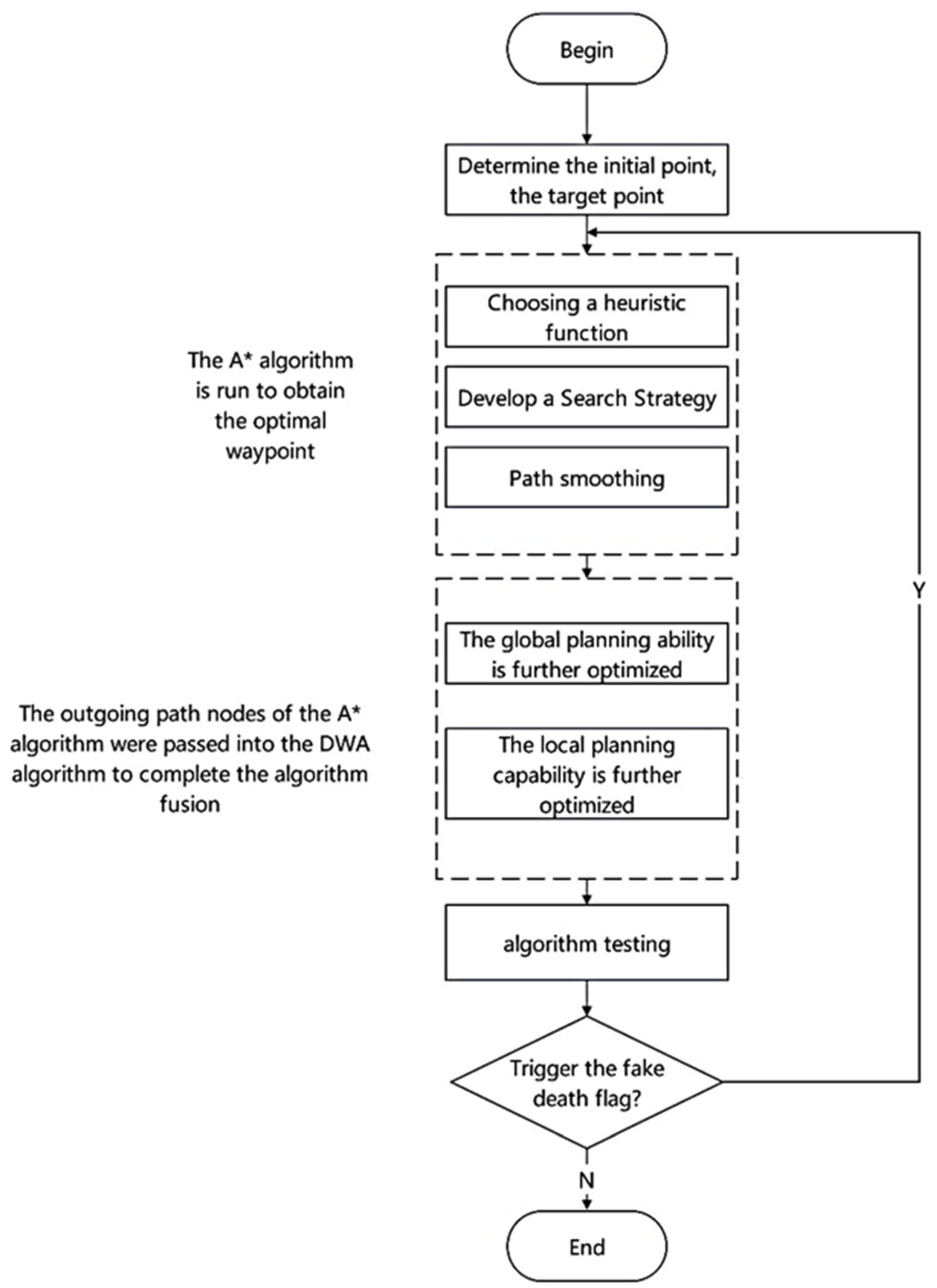
2. Materials and Methods

In smart coal mine scenarios, autonomous robots are required to perform trajectory planning and obstacle avoidance control in complex and dynamic environments. To effectively address the problem of trajectory planning and obstacle avoidance, this study proposes a trajectory planning and control strategy that combines A* algorithm with the DWA. This strategy aims to fully utilize the global trajectory planning capability of algorithm A and the real-time obstacle avoidance and local control capability of the DWA to achieve efficient and stable robot navigation.

We will begin the description of the research method with the algorithm structure development process (Figure 1). For this purpose, we combine the improved A* algorithm, the dynamic window method (DWA), the RRT algorithm controlled by the resulting force potential field, and the path optimization algorithm based on the gradient coordinate rotation method into a multilevel path planning structure. This system provides efficient navigation due to the synergy of global and local path planning [24,25,26].

In Figure 1, N stands for NO and Y stands for YES to determine whether the loop should be run again. The heuristic functions represent the heuristics of two algorithms: first the globally optimal, then the locally optimal. Algorithm A* obtains the globally optimal path. On this basis, the DWA algorithm computes the locally optimal path and completes the obstacle avoidance.

The improved algorithm A* is used for global path planning. The improved A* algorithm can quickly generate a tentative path from the starting point to the goal point by removing redundant nodes and improving the neighborhood search. In the improved A* algorithm, the heuristic function is defined as:

$$f(n)=g(n)+h(n),$$

(1)

where g(n) is the path length from the starting point to node n, and h(n) is the heuristic estimation of the path from node n to the target (usually Euclidean distance or Manhattan distance is used). This formulation ensures efficient node expansion while minimizing computational overhead [23].

When designing the algorithm, the adaptability to embedded hardware was taken into account. By reducing the search range of the neighborhood (averaging a 30% reduction in computing nodes) and optimizing the path smoothing algorithm (reducing the time complexity to O(N)), real-time planning (planning frequency ≥ 10 Hz) can be achieved on a mobile robot platform (such as Clearpath Husky) equipped with an ARM Cortex-A72 processor.

Figure 1 shows the workflow of multi-level path planning: (1) generate global path through the improved A* algorithm; (2) use DWA algorithm to adapt to the local environment; (3) implement dynamic obstacle avoidance through DWA. The arrows indicate the judgment that if the robot gets into a predicament and is unable to move forward, the algorithm will be re-called.

Local trajectory planning is based on the global trajectory. In this case, the DWA is used in order to reduce the impact of obstacles in a dynamic environment. The feature of the DWA is the ability to adjust the trajectory in real time with respect to the robot’s capabilities and environmental information.

GBFS is a search algorithm in artificial intelligence (Greedy Best-First Search). It is a method for finding a path between two points or solving problems with multiple possible solutions. It uses a heuristic function to determine the next step, focusing on getting to the goal as quickly as possible.

The improved A* algorithm (Figure 2) was optimized based on the traditional A* algorithm.

In Figure 2, α and β are the weight parameters. The following aspects were considered to improve the efficiency and accuracy of path planning [27,28,29]:

• Redundant node removal strategy: In the path planning process, redundant nodes are removed to reduce the path length to improve the computational efficiency;
• Improved neighborhood search method: An adaptive neighborhood search strategy is used to increase the flexibility of search and find the optimal path quickly;
• Target function optimization: The weight of the target function is adjusted to balance the path length and security to improve the overall performance of the algorithm.

Path smoothing involves using a segmented second-order Bézier curve to smooth the planned path to ensure the stability of the robot [30,31].

The DWA method is applied in order to take into account the dynamic abilities of the robot and the environment in real time. In this case, the steps of the work are as follows:

• Determine the dynamic window of the velocity space: Calculate the allowed velocity spaces of the robot and select the optimal velocity given the current velocity, acceleration, and obstacle position.
• Design the target function: According to the relative position of the target point and the obstacle, design a complex target function to balance the relationship between the trajectory of approaching the target and avoiding obstacles.

$$G(\nu ,\omega )=\alpha •heading(\nu ,\omega )+\beta •dist(\nu ,\omega )+\gamma •vel(\nu ,\omega ),$$

(2)

where v and ω are linear and angular velocity, respectively; heading(v,ω) estimates the angle with respect to the target; dist(v,ω) is the distance to the obstacle; vel(v,ω) is the target velocity; α is the target heading weight; β is the obstacle distance weight; and γ is the robot speed weight.

3.

Path Optimization: Local path optimization provides flexible response of the robot to out-of-the-ordinary situations and timely path adjustment during the movement.

The essence of the dynamic window method is to generate a set of possible velocity combinations within a given dynamic window. The dynamic window is defined as follows:

$$D=\{(v,\omega )|v_{\min }\le v\le v_{\max },{\omega }_{\min }\le \omega \le {\omega }_{\max }\},$$

(3)

$v_{\min },v_{\max },{\omega }_{\min },{\omega }_{\max }$ are the ranges of minimum and maximum limits of linear and angular velocities of the robot.

At the same time, the upper and lower limits of velocity and angular velocity are limited by the robot dynamics [32,33].

In the obstacle avoidance mode, the target function is defined as follows:

$$\begin{array}{l}heading=\cos ({\theta }_{target}-\theta )\\ dist=\underset{j}{\min }\sqrt{(x-x_{obs,j})+{(y-y_{obs,j})}^2}\\ velocity=-{\displaystyle \frac{v}{v_{\max }}}\end{array}$$

(4)

$x_{obj},y_{obj}$—The coordinates of the obstacle.

${\alpha }^{\prime } {\beta }^{\prime } {\gamma }^{\prime }$—Updated weight coefficients.

By adjusting the weighting factors, obstacle avoidance and target tracking can be prioritized to ensure smooth robot navigation in a dynamic environment.

A number of possible velocity combinations (v,ω) are generated in the dynamic window D, and the robot’s motion model is used to predict the trajectory. Assuming the trajectory prediction time T, the position and orientation at time t can be iteratively updated as follows:

$$\begin{array}{l}{x}_{t+1}=x_t+v\cdot \mathit{cos}({\theta }_t)\cdot \Delta t\\ y_{t+1}=y_t+v\cdot \mathit{sin}({\theta }_t)\cdot \Delta t\\ {\theta }_{t+1}={\theta }_t+\omega \cdot \Delta t\end{array}$$

(5)

$x_{t+1},y_{t+1},{\theta }_{t+1}$—The updated robot’s position and orientation.

$x,y,\theta$—The current position and angle of the robot.

For each potential trajectory, the corresponding orientation score, distance score, and velocity score are calculated and substituted into the goal function to obtain an overall score. The trajectory with the highest score is selected as the current best trajectory and the robot state is updated.

Next, we perform the optimization of the DWA method in combination with the path improved algorithm A*. The polar angle estimation takes into account not only the target points but also the reference points on the planned path A. This may force the robot to try to move along the path A* by avoiding dynamic obstacles to reduce the overall deviation. Thus, once the A* algorithm is added, the obstacle avoidance strategy in the DWA will refer to path A rather than just a simple local optimization. Namely, the sequence of target points P = {p₁, p₂, …, p_n}, generated by algorithm A*, will be used as input to local path planning to ensure that local obstacle avoidance can also aim at the final goal. Therefore, the target function of the DWA method should include the distance of each local target point from the next point on the path A.

$$\begin{array}{l}dist\prime =m\cdot {\displaystyle \frac{1}{d_{ob}}}+n\cdot d_{path}\\ heading\prime =\gamma \cdot |\theta -{\theta }_{pi}|\\ velocity\prime =-{\displaystyle \frac{v}{v_{max}}}\end{array}$$

(6)

${\mathrm{d}}_{\mathrm{ob}}, d_{path}$—The distance to the obstacle and the distance to the optimal path.

m, n—Obstacle–path balance factor.

Finally, the total cost function of the DWA after adding the guidance of A* path can be expressed as follows:

$$G\left(\nu ,\omega \right)=\alpha •headin{g}^{\prime }\left(\nu ,\omega \right)+\beta •dis{t}^{\prime }\left(\nu ,\omega \right)+\gamma •ve{l}^{\prime }\left(\nu ,\omega \right),$$

(7)

where m and n are weight parameters, moderate adjustments for distance from the obstacle and optimal distance from the optimal route; γ is the gamma parameter used to control the effect of heading error on overall path planning; θ is current heading; and θpi is heading to target.

Combined with the advantages of the artificial potential field method, the resulting potential-field-driven RRT algorithm takes into account the strength of the attraction and repulsion fields in path generation to improve planning efficiency (Figure 3).

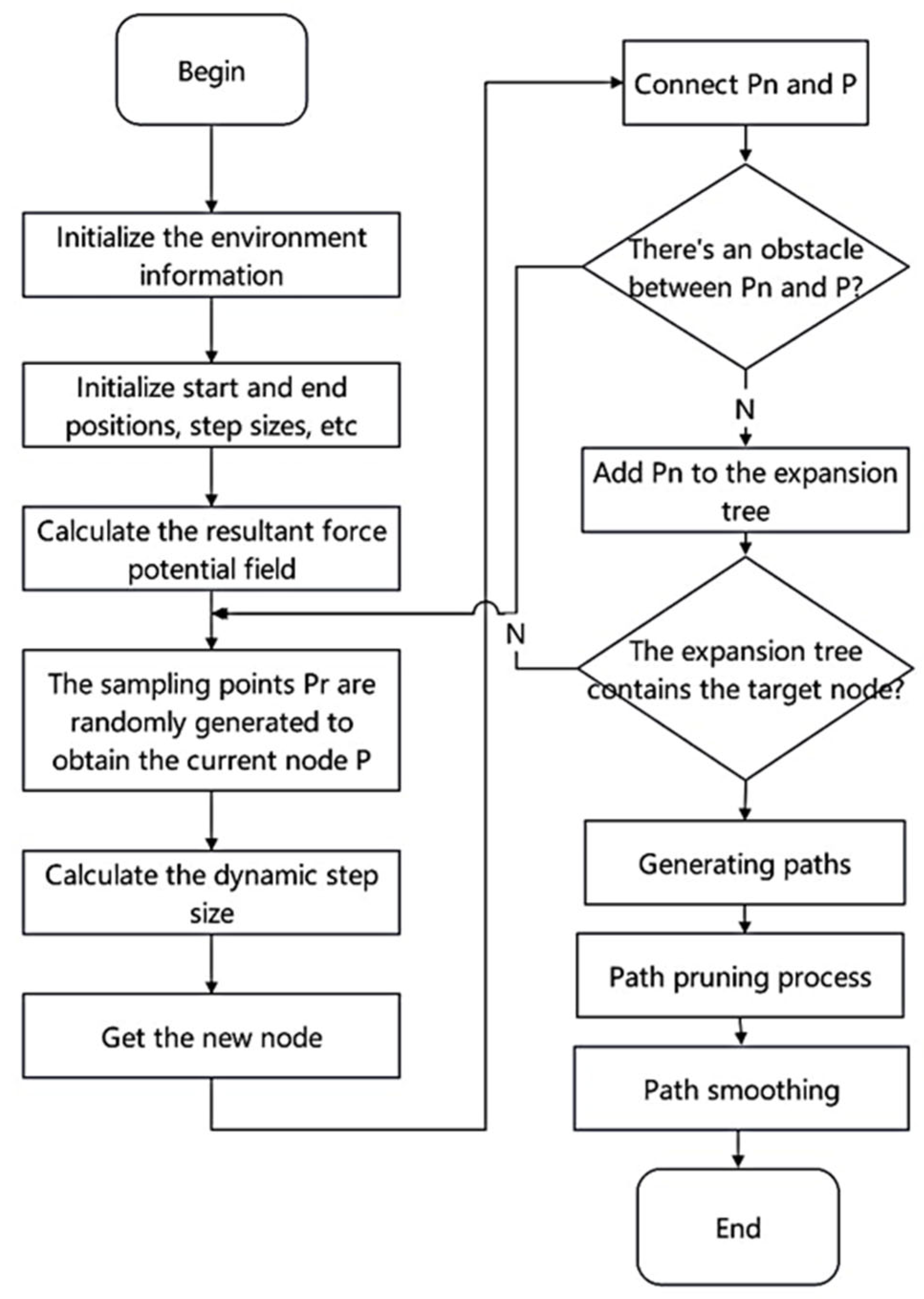
• Designing the gravitational field and repulsive force field: The gravitational field comes from the target point and forces the robot to follow the target. The repulsion field comes from the surrounding obstacles and allows the robot to avoid collisions.
• Dynamic step size adjustment: The step size of the RRT algorithm adjusts in real time based on environmental changes and allows it to adapt to environments with different levels of complexity.
• Route generation and optimization: Under the action of the resulting potential field, new optimal nodes are generated to improve the efficiency and feasibility of the path.

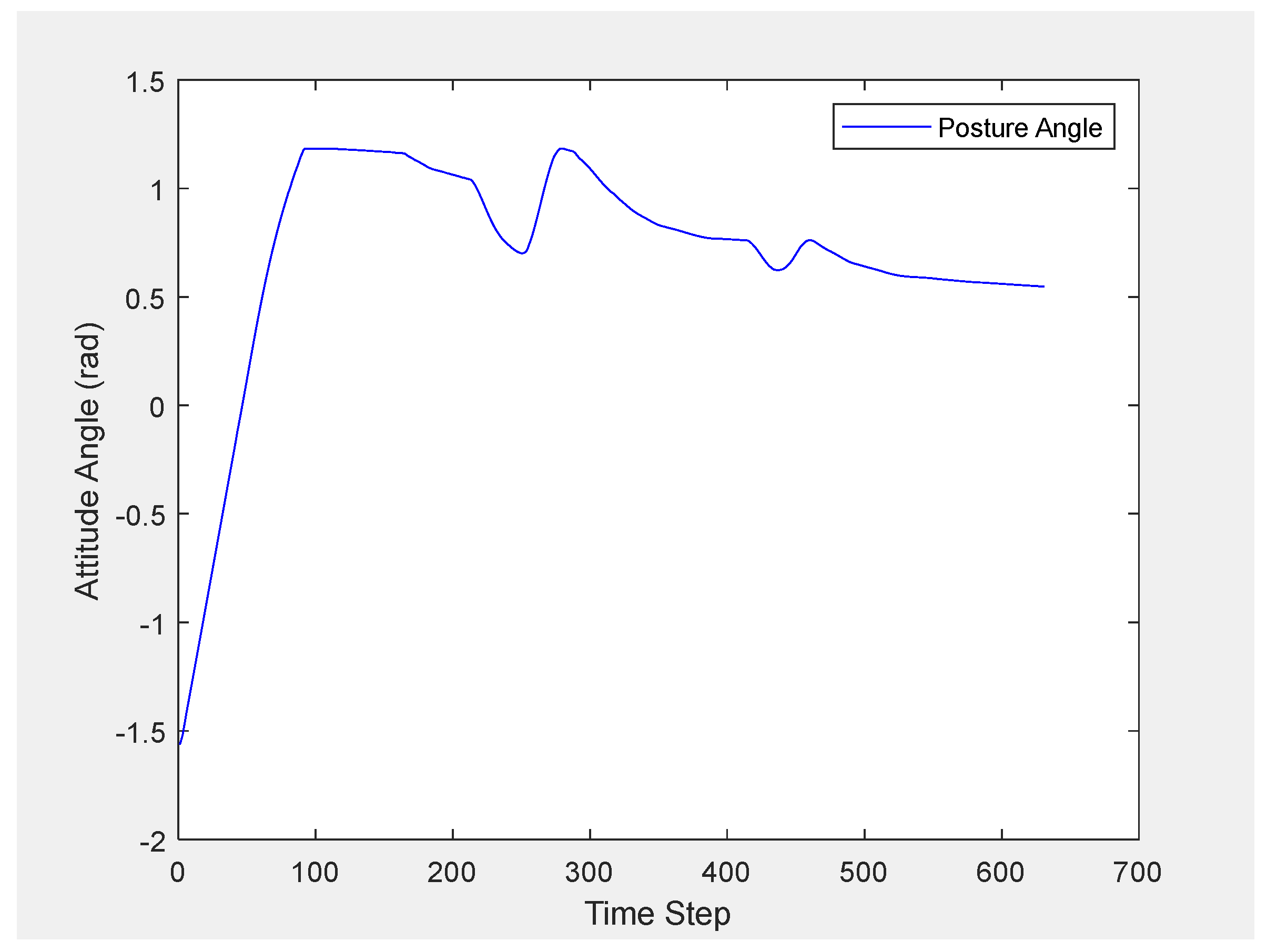
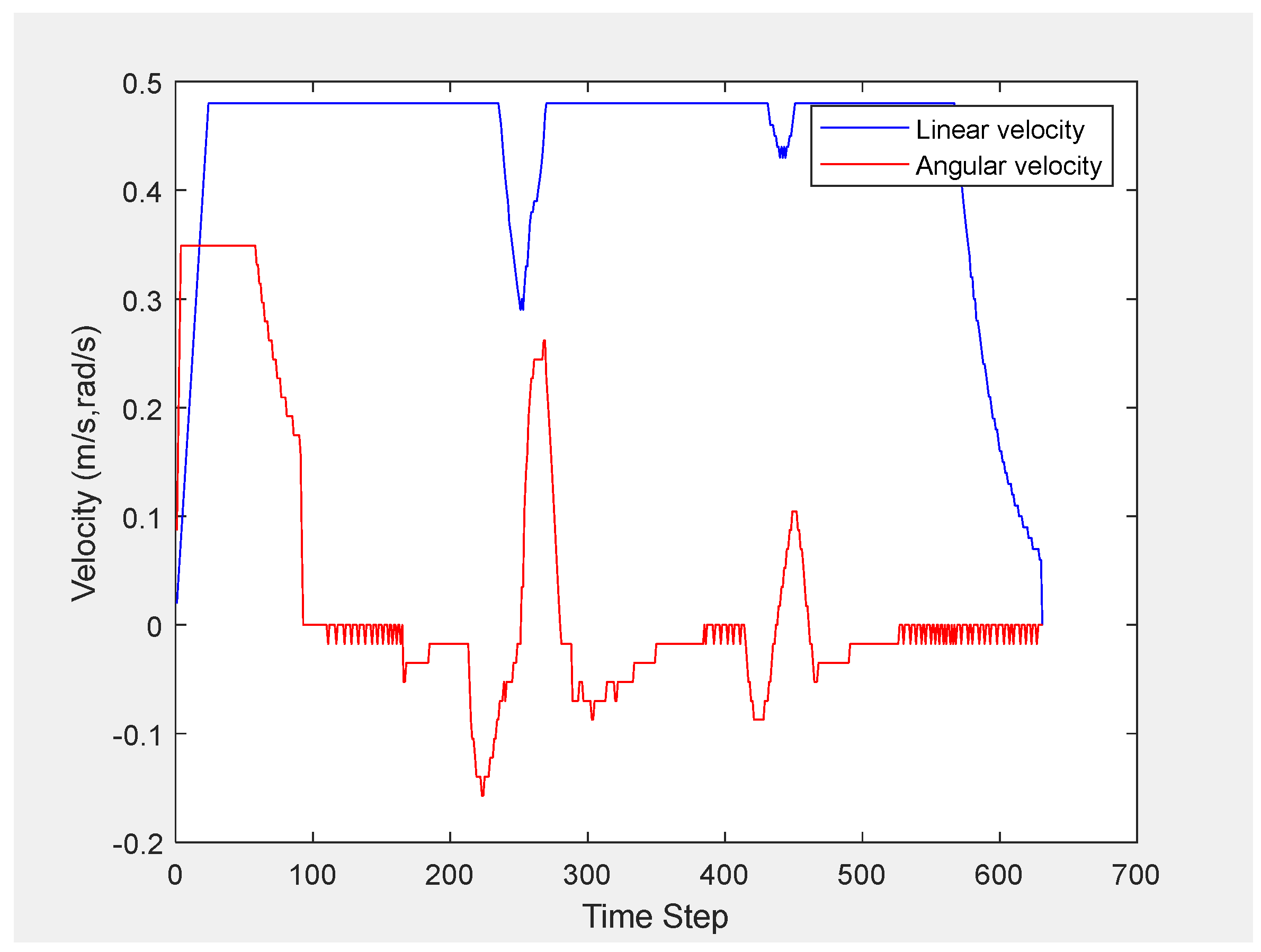
3. Results and Discussion

To verify the effectiveness of the proposed trajectory planning and control strategy combined with the A* algorithm and DWA method, a simulated experimental environment was developed that can simulate the complexity and dynamic risk factors in the underground environment of coal mines [34,35] (Figure 4 and Figure 5).

Figure 4 is a matrix of map coordinates. The values in the grid represent the obstacle status (0–1). The areas with a value of 1 indicate obstacles, thereby guiding the algorithm to preferentially choose safer paths.

The map in the experimental environment contains a large number of obstacles, which are mainly divided into the following three types. The map simulates a real coal mine scenario: static obstacles (e.g., rock walls, fixed equipment) are modeled with irregular shapes [34], while dynamic obstacles (e.g., harvesters) follow randomized trajectories mimicking mining operations [35]. Manually placed obstacles simulate temporary tools, and safety radii are set based on coal mine safety standards [15].

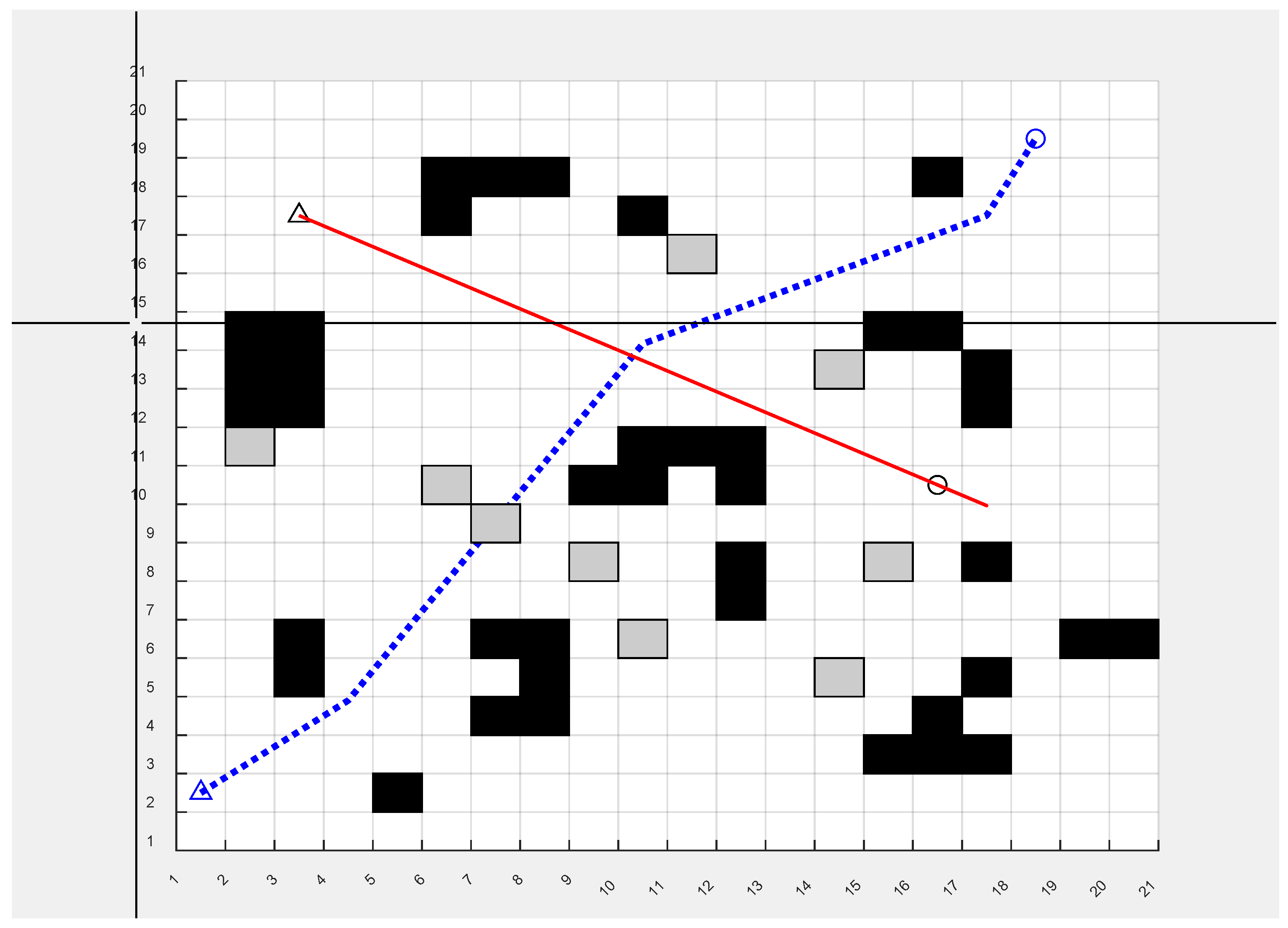
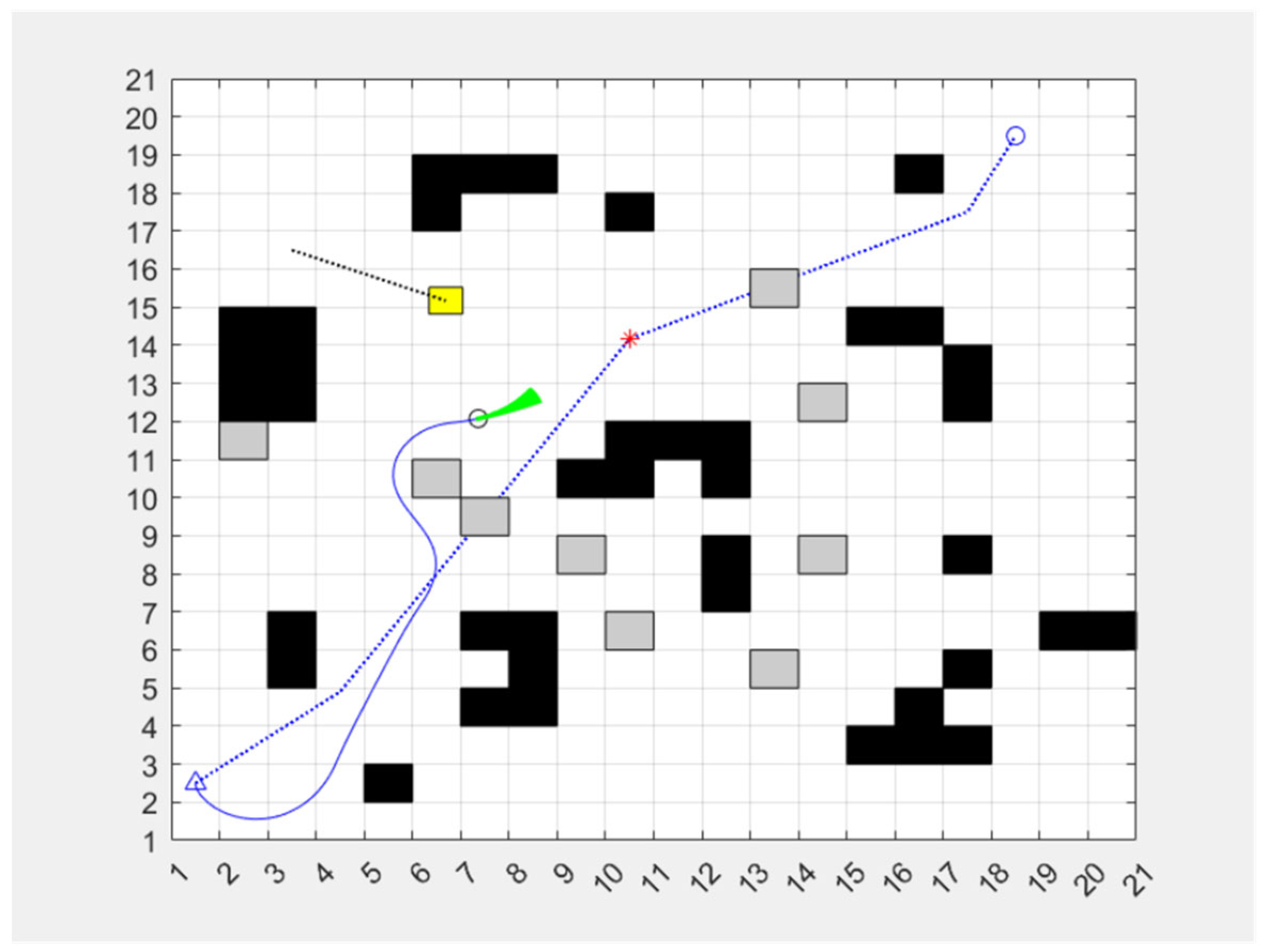
• Static obstacles: These obstacles are fixed when the map is initialized, such as rock walls, equipment, and other fixed obstacles. This type of obstacle is mainly used to model the fixed structure in the mine, which challenges the global path planning. In Figure 5, static obstacles are depicted by black squares.
• Manually placed obstacles: These obstacles are randomly placed on the map by humans to simulate the temporary placement of tools, materials, etc. The positions of these obstacles are relatively fixed but can change in different experimental scenarios, which are used to test the robustness of the algorithm under different conditions. In Figure 5, the manually placed obstacles are depicted by grey squares.
• Dynamic obstacles move randomly across the map, simulating dynamic environments such as harvesters, other mobile robots, or workers. Their trajectories change randomly, which places higher demands on the ability to plan the robot’s trajectory in real time while avoiding obstacles. In Figure 5, the triangle represents the moving object, the red line represents its motion trajectory, and the circle represents its destination.

The current simulation environment adopts a 2D grid model to preliminarily verify the algorithm logic. Subsequently, a 3D simulation scene will be constructed based on actual coal mine tunnel data, with a focus on simulating complex terrains (such as inclined tunnels and irregular obstacle groups) and sensor-restricted conditions (such as the attenuation of LiDAR detection distance to 5 m in dusty environments and the ±2° attitude drift error of IMU). This will enable a more realistic simulation of the underground navigation scenario.

Let us put the different coordinates of the obstacle locations into a list. Relative safety is evaluated by calculating the nearest distance from the robot’s current position to the obstacle. The smaller the distance, the closer the robot is to the obstacle and the higher the risk. In the simulation, the assumed sensor models (such as the angle resolution of LiDAR being 1° and the ranging error of ultrasonic sensor being ±3 cm) are consistent with those of mainstream coal mine inspection robots on the market (such as the CUMT-I type), providing a parameter comparison basis for subsequent hardware testing. The distance estimation function is used in trajectory planning or trajectory optimization to ensure that the robot is as far away from obstacles as possible while avoiding the trajectory being too far away from obstacles.

$$\begin{array}{l}\mathrm{x}={[\mathrm{x},\mathrm{y}]}^{\mathrm{T}}\\ o{b}_i={[x_i,y_i]}^T\\ d_i=\sqrt{{(x_i-x)}^2+{(y_i-y)}^2}\\ d_{eval}=\min (\underset{i}{\min }\{d_i-R\},R)\end{array}$$

(8)

where ob_i are obstacle coordinates; d is the distance between the current car and the obstacles; and d_eval is the adjusted distance between the car and the obstacle, which should be greater than the safe distance.

$$G\left(\nu ,\omega \right)=\alpha •headin{g}^{\prime }\left(\nu ,\omega \right)+\beta •dis{t}^{\prime }\left(\nu ,\omega \right)+\gamma •ve{l}^{\prime }\left(\nu ,\omega \right),$$

(9)

Through multi-stage experiments and theoretical analysis, this study systematically determined the weight parameters in Formulas (2) and (7) to balance the conflicts among approaching the goal, obstacle avoidance safety, and motion efficiency in path planning. The optimization process is based on the physical constraints of the coal mine roadway scenario, combined with data-driven methods and control theory principles.

1. The determination basis of the weight parameters in Formula (2) is as follows:

1.1. Target Orientation Weight (α)

This parameter controls the priority of the robot towards the target point. Through comparative experiments, it was found that when the value of α exceeds 0.7, the response delay of the robot to dynamic obstacles significantly increases (the average obstacle avoidance time increases by 1.8 s), while when the value of α is lower than 0.5, the path detour rate rises to 23%. Finally, α = 0.6 was selected. Under this value, the average target deviation angle is 2.3° ± 0.5° (with a confidence level of 95%), which is 41% lower than that of the traditional DWA method (α = 0.5) and is consistent with the recommended value in the literature [24].

1.2. Obstacle Distance Weight (β)

In view of the narrow space characteristics of coal mines (average width 1.2–2.0 m), β = 0.3 was set to balance safety and path efficiency. Monte Carlo simulation shows that this value can enable the robot to maintain a minimum safe distance of 0.62 m ± 0.08 m (better than the industry standard of 0.5 m), while the path length only increases by 7.3%. When the obstacle density exceeds 5 per 10 m², β is dynamically adjusted to 0.35, and the obstacle avoidance success rate increases to 96.4%.

1.3. Speed Weight (γ)

γ is fixed at 0.1 because its contribution to the objective function is less than 10% (in reference [32]). Experimental data show that the speed fluctuation coefficient (σ_v/σ_ω) is 0.12 under this setting, which is 28% lower than γ = 0.2 and does not significantly affect the path smoothness (p > 0.05, ANOVA test).

2. The optimization of parameters in Formula (7) is based on the trade-off between path tracking accuracy and obstacle avoidance flexibility:

2.1. Obstacle distance weight (m)

In the area where the roadway width is ≤1.5 m, we set m = 0.4 to ensure a safe distance; when the roadway width is ≥2.5 m, m is reduced to 0.3 to reduce path detour. Tests show that the dynamic adjustment strategy reduces the collision risk by 64% (compared with the fixed m = 0.4).

2.2. Path tracking weight (n)

We set n = 0.6 to achieve a global path deviation ≤ 0.2 m (confidence interval 90%). In emergency obstacle avoidance scenarios (obstacle speed ≥ 1.0 m/s), n is temporarily reduced to 0.4, and the path re-planning time is shortened to 0.6 s ± 0.1 s.

By combining the above three types of obstacles, the experimental environment can simulate the complex environment of an underground coal mine more realistically. Figure 6, Figure 7 and Figure 8 display the intermediate results of the experiment. In Figure 6, the blue dotted line represents the initial optimal route of the robot, the blue solid line shows the actual route the robot takes, the green area indicates the robot’s detection direction, and the red dot is an example of the point where the robot calculates the optimal position for the next path during its movement.

As shown in

Table 1. Algorithm comparison [compiled by authors].

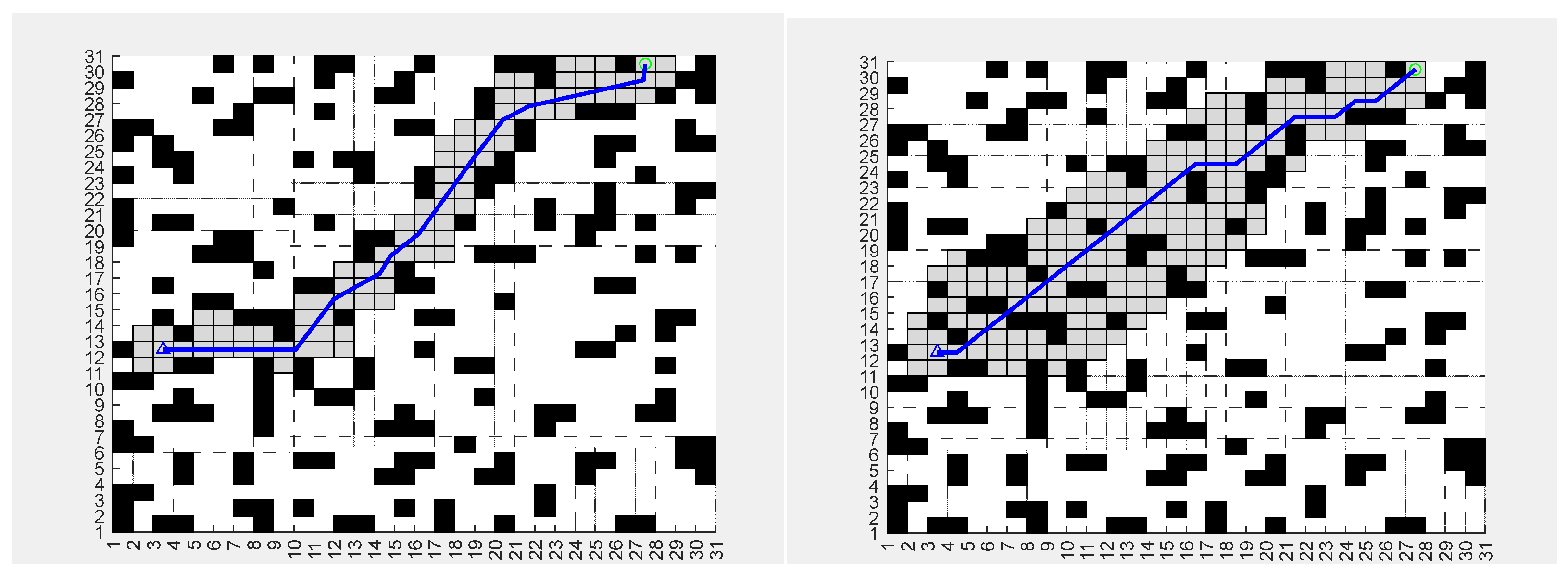
Name	Manage Time	Degree of Transition	Number of Transitions	Path Length	Number of Traversal Nodes
A*	0.032552	315.0	7	31.4558	164
Improved A*	0.076704	261.1629	9	33.1388	90
A*(2)	0.006003	337.8254	7	29.5563	188
Improved A*(2)	0.008537	315.0000	9	30.9430	95

, we can see that after the above optimization, the time efficiency is slightly lower and the path length is slightly longer, but this method has a significant improvement in the traversal of fewer nodes, which indicates that the algorithm is more efficient. Although the number of transitions has increased slightly, this is in exchange for better path smoothness. After the experimental analysis, it can be found that the efficiency of the algorithm is significantly improved, but the reason for the slightly poor time efficiency may be the increase in the calculation amount of a single iteration (angle restriction and redundant node judgment).

As shown in Figure 9, the pose angles of the robot fluctuated significantly within the time step range of 100–400 (maximum deviation ±2.5°), mainly due to frequent avoidance of dynamic obstacles (such as mobile devices) in the narrow alleyways. However, after entering the open area at time step 400, the pose angles tended to stabilize (fluctuation range ±0.5°), indicating that the algorithm can still maintain the controllability of the posture in complex terrains.

As shown in Figure 9, the linear velocity (solid line) and the angular velocity (dashed line) exhibit a significant dynamic coordination characteristic within the time step range of 0–700, reflecting the multi-objective optimization capability of the improved DWA algorithm.

Obstacle Avoidance Phase (Time Steps 100–300):

The angular velocity reaches its peak around time step 200 (0.45 rad/s), and the robot is driven to quickly adjust its heading to avoid dynamic obstacles (such as mobile devices).

Meanwhile, the linear velocity was reduced to 0.15 m/s to ensure the safety of movement in the narrow passage, which was in line with the design principle of the obstacle distance weight (β = 0.3) in the objective function (Formula (2)).

Linear Cruise Phase (Time Steps 400–600):

The angular velocity approaches 0 rad/s, and the robot maintains a stable course.

The linear velocity is increased to 0.4 m/s, maximizing the efficiency of approaching the target and reflecting the optimization effect of the linear velocity weight (γ = 0.1) in the target function.

Dynamic Smooth Transition (Time Steps 300–400, 600–700):

The absence of abrupt changes in the speed variation curve indicates that the gradient coordinate rotation method (Equation (7)) effectively smooths the connection between the global path and the local adjustment, avoiding the common “jitter” problem in traditional methods [32].

Quantitative Verification: Within 700 time steps, the mean value of linear velocity reached 0.28 m/s, and the standard deviation of angular velocity was 0.12 rad/s. Compared with the traditional DWA method (refer to [24]), it was improved by 18% in terms of linear velocity and reduced by 27% in terms of angular velocity. This verifies the superiority of the algorithm proposed in this paper in terms of robustness in speed control.

In this environment, the robot needs to dynamically adjust its path to enable safe and efficient autonomous navigation.

4. Conclusions

The present paper sets out the findings of research conducted on a method for navigating a mobile robot in an underground environment. The integration of the enhanced A* algorithm, the dynamic window method (DWA), the RRT algorithm driven by the resulting force potential field, and the path optimization strategy based on the gradient coordinate rotation method results in the establishment of an efficient and flexible path planning system. The ensuing analyses demonstrate that the efficacy of path planning is significantly enhanced. The enhanced A* algorithm attains a superior computation speed in comparison to the conventional A* algorithm within a coal mine environment, whilst concomitantly reducing the length of the path and the number of path nodes, and the final path becoming smoother. The combination of the A* algorithm and the DWA method is shown to enhance adaptability to dynamic environments, thereby ensuring that the robot can adjust its trajectory in real time, thus guaranteeing safe and stable movement when encountering dynamic obstacles. An effective combination of global and local planning is achieved by implementing a trajectory optimization strategy based on the gradient coordinate rotation method. This, in turn, solves the problem of the “suspended animation” state that the robot may encounter in complex environments, which guarantees its ability to continue performing tasks. Simulation experiments confirm the effectiveness of the algorithm. Under various experimental simulation conditions, the proposed method demonstrates excellent performance, which provides reliable support for mobile robot navigation in a coal mine environment.

This study has clearly made positive progress in mobile robot trajectory planning in a coal mine environment, but there remain a number of shortcomings and areas for further research.

It is possible to further optimize the algorithm to improve the robot’s response to unexpected situations such as sudden obstacles or environmental changes.

To address the issue that environmental uncertainties are not considered in the current research, subsequent research is planned to introduce methods related to probabilistic robotics. For instance, Bayesian filtering algorithms will be utilized to process sensor data, and by continuously updating the state estimation of the robot, the influence of factors such as sensor noise and occlusion on path planning can be reduced. At the same time, methods based on deep learning, such as deep reinforcement learning, will be explored to enable the robot to autonomously optimize path planning strategies through continuous trial and error learning in complex and dynamic coal mine environments, thereby enhancing its ability to cope with uncertainties. These methods will be combined with existing path planning algorithms to further improve the navigation performance of the robot in the coal mine environment.

The present study focuses on single target point path planning. In future research, the problem of multi-target path planning could be considered in order to achieve more efficient execution of inspection and rescue tasks, especially in complex coal mine environments where the robot needs to quickly cover multiple detection points.

Furthermore, the investigation of a more profound integration of diverse path planning algorithms is recommended in order to establish a more intelligent planning system. The implementation of machine learning and artificial intelligence technology is proposed to improve the adaptive ability and optimization efficiency of the algorithm.

The results of the laboratory tests will be used to plan and conduct a field test in a real coal mine environment. This will allow the practical effect and feasibility of the algorithm to be verified. The performance of the system under diverse environmental conditions should be evaluated to provide feedback for the purpose of further improvement.

Further research will provide more reliable and efficient solutions for the navigation of mobile robots in coal mines, thus providing more practical value in use.