Divergence Measures for Globular T-Spherical Fuzzy Sets with Application in Selecting Solar Energy Systems
Abstract
1. Introduction
- Development of novel Div-Ms based on Chi-square, Canberra, and exponential functions for both weighted and un-weighted G-TSF information.
- The proposed measures are rigorously analyzed to verify essential axiomatic properties and other supporting mathematical characteristics, thereby reinforcing their theoretical soundness.
- New distance measures (DMs) and similarity measures (SMs) are formulated based on the proposed Div-Ms, applicable to both weighted and un-weighted G-TSF environments, where DMs and SMs are symmetry-based.
- A comprehensive G-TSF-TOPSIS framework is developed by integrating the proposed measures into a G-TSF-based TOPSIS model, capable of effectively handling complex MCGDM scenarios.
- The practicality and effectiveness of the proposed approach are demonstrated through its application to the selection of optimal solar energy systems. Detailed illustrative examples are provided to validate the applicability and robustness of the method.
2. Preliminaries
- When setting , G-TSFSs transform into C-SFSs.
- When setting , G-TSFSs transform into TSFSs.
- When setting , G-TSFSs transform into C-qROFSs.
- When setting and , G-TSFSs transform into C-PFSs.
- When setting and , G-TSFSs transform into C-IFSs.
- (i)
- iff and , and
- (ii)
- iff and , and
- (iii)
- (iv)
- (v)
- (vi)
- (vii)
Limitations of Existing Frameworks
- (a)
- Fuzzy Sets (FSs): FSs fall short in modeling non-membership grades, as they solely rely on membership degrees, limiting their effectiveness in scenarios that require a fuller representation of uncertainty.
- (b)
- Intuitionistic Fuzzy Sets (IFSs): Although IFSs consider both degrees of membership (DoM) and non-membership (DNM), they are inadequate in situations requiring explicit modeling of neutrality or refusal.
- (c)
- Pythagorean Fuzzy Sets (PFSs): While PFSs can accommodate indeterminacy and refusal to some extent, their strict characteristic function constraints limit flexibility and restrict decision-making to a narrow domain.
- (d)
- Spherical and T-Spherical Fuzzy Sets (SFSs and TSFSs): Although SFSs overcome the limitations of PFSs, and TSFSs further generalize SFSs, both frameworks still face limitations, especially when the parameter t > 2, or when membership grades must be expressed using spherical geometry.
- (e)
- Globular T-Spherical Fuzzy Sets (G-TSFSs): The cumulative limitations of FSs, IFSs, PFSs, SFSs, and TSFSs render their associated divergence measures (Div-Ms) insufficient for effectively handling uncertainty within the broader and more flexible G-TSFS framework.
3. The Proposed Divergence Measures
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If .
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
Proposed Measures for Weighted Information
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (iv)
- and .
- (i)
- .
- (ii)
- If
- (iii)
- and .
- (Iv)
- and .
- (i)
- .
- (ii)
- If .
- (iii)
- and .
- (iv)
- and .
Advantages of the Proposed Work
- 1.
- Comprehensive Representation of Uncertainty: Unlike FSs and IFSs, the proposed model captures membership, non-membership, hesitancy, and neutrality explicitly, offering a more complete and realistic representation of expert opinions under uncertainty.
- 2.
- Enhanced Flexibility Through Generalization: By extending the capabilities of TSFSs, the proposed G-TSFS-based approach accommodates a broader range of values for the tunable parameter “t”, including cases where t > 2, thus allowing greater modeling flexibility across various decision contexts.
- 3.
- Geometric Expressiveness: The model supports the expression of membership grades in spherical form, overcoming the geometric limitations of PFSs and SFSs, enabling more nuanced interpretations of vague or overlapping criteria.
- 4.
- Overcoming Functional Constraints: Unlike PFSs, which are constrained by rigid characteristic functions, the proposed approach provides a relaxed and adaptable structure that facilitates decision-making in wider and more complex domains.
- 5.
- Effective Divergence Measurement: The proposed divergence measures (Div-Ms) are specifically tailored to the G-TSFS environment, ensuring more accurate and meaningful differentiation between alternatives, even in highly uncertain and imprecise scenarios.
- 6.
- Improved Decision-Making Capability: By integrating a richer informational structure with robust divergence computation, the proposed framework enhances decision quality and interpretability, especially in multi-criteria group decision-making (MCGDM) problems.
4. Globular T-Spherical Fuzzy TOPSIS
- Step 1. Construction of decision matrix (DM): Suppose that the decision-makers give their expert opinion as an evaluation of each alternative on the basis of each attribute in the form of G-TSFVs . Using these evaluation values, we construct a DM known as G-TSFDM, and it is symbolized as .
- Step 2. Normalization of DM: We transform the G-TSFDM to the normalized G-TSFDM as follows:where is the complement of .
- Step 3. Determining the PIS and NIS: We determine the G-TSF PIS and G-TSF NIS as:
- Step 4. Compute the weighted Distance Measures (Dis-Ms): We compute the weighted Dis-Ms between the alternatives and both the G-TSF PIS as well as with the G-TSF NIS by using the following formulae:
- Step 5. Calculation of closeness index: We determine the relative closeness degree of each alternative to the G-TSF ideal solution as follows:
- Step 6. Rank the alternatives: We rank the alternatives in descending order based on their relative closeness degrees (RCD) to identify the most desirable option. We select the alternative with the highest degree as the optimal choice.
5. Application in the Selection of Solar Energy Systems
- Efficiency: The ability of the solar panels to convert sunlight into usable electricity efficiently.
- Durability and Longevity: The lifespan of the solar panels and their ability to withstand various environmental conditions.
- Cost-effectiveness: The overall cost of installation, maintenance, and operation, including return on investment.
- Scalability: The flexibility of the system to expand and adapt to increasing energy demands over time.
- Environmental Impact: The ecological footprint of the solar panels, including production, installation, and disposal processes.
- Step 1. Construction of decision matrix (DM)
- Step 2. Normalization of DM: Since all of the attributes are of the benefit type, there is no need to normalize the G-TSFDM.
- Step 3. Determining PIS and NIS: We compute G-TSF PIS and G-TSF NIS using Equations (45) and (46), respectively, as shown below:
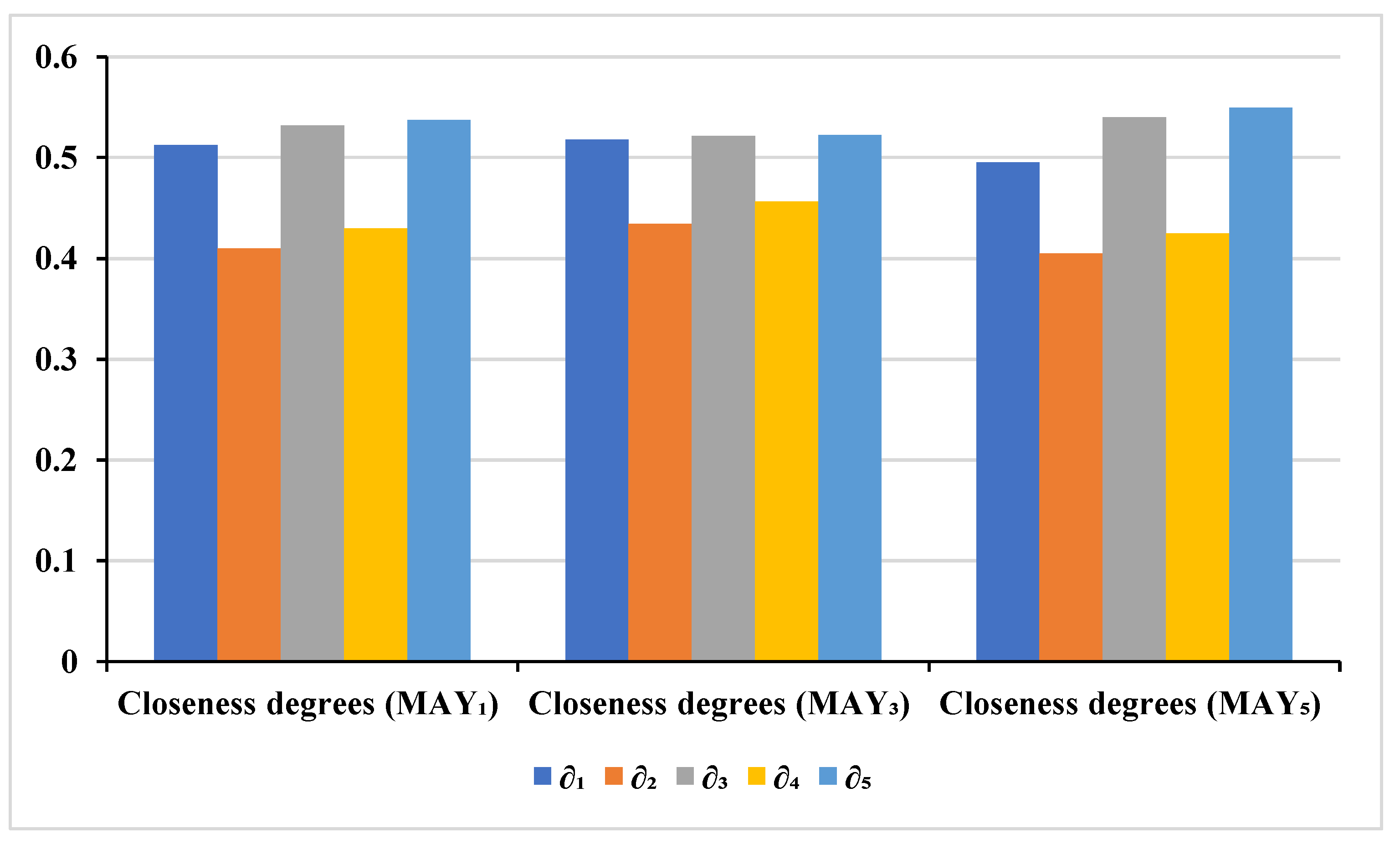
- Step 5. Calculating RCDs and ranking of : We calculated the RCD of each alternative to the G-TSF PIS using Equation (49). Finally, we rank the alternatives in decreasing order of their RCD as shown in Table 12, and select the alternative having the highest RCD as the most desirable alternative. Figure 5 below presents the order of ranking closeness degrees for , , and .
| Algorithm 1: Core 3-Step Div-M Computation |
| Input: Fuzzy decision matrix from multiple experts. Criteria weights. Parameter t (sensitivity control). Step 1: Experts selection
Step 2: Aggregate expert assessments Aggregate expert assessments by using G-TSFs via: and . Step 3: Compute distance measures and closeness indices
and and
. Step 4: Rank alternatives Rank the alternatives in descending order of their closeness coefficients. Output: Final ranking of alternatives |
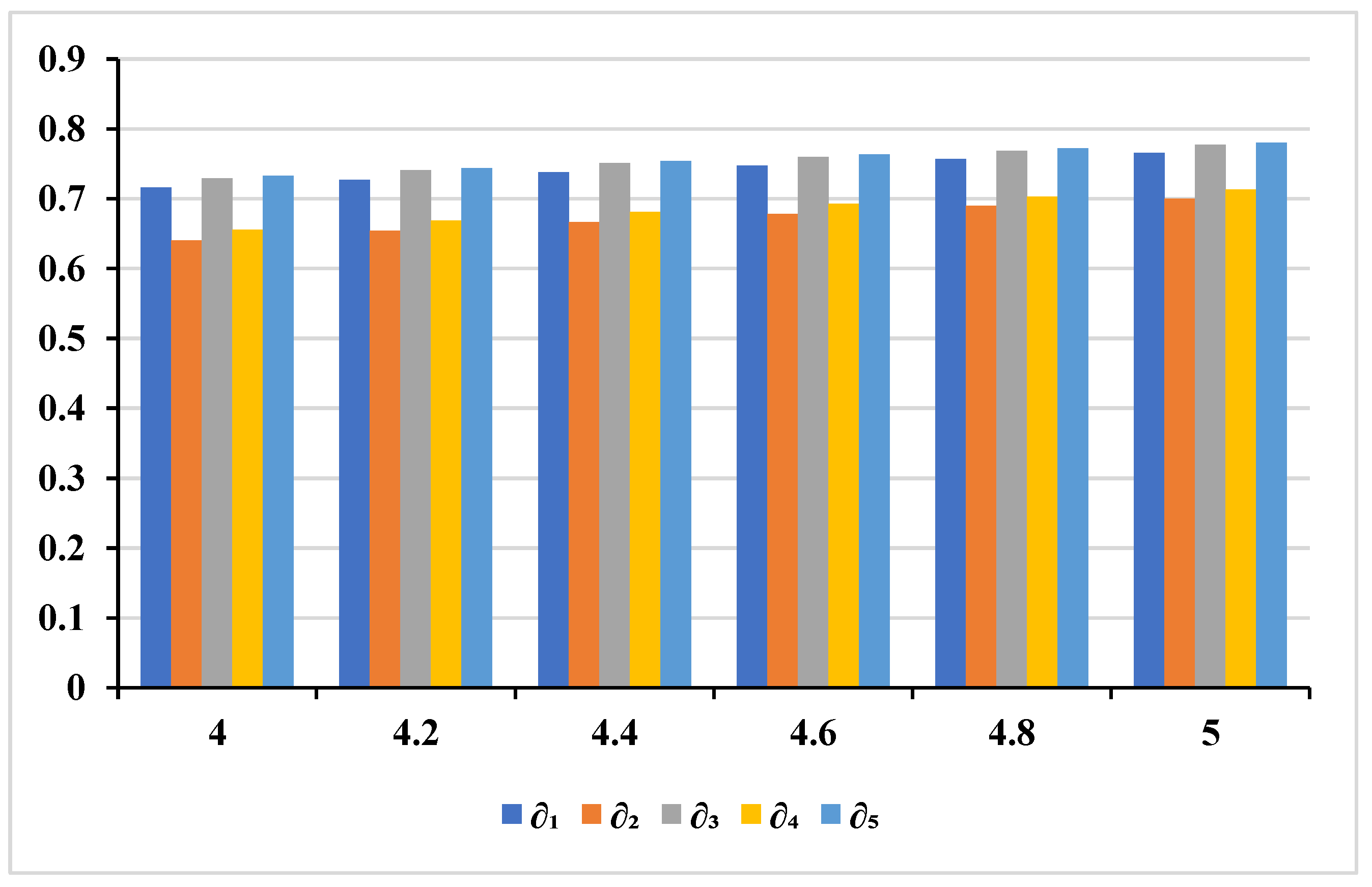
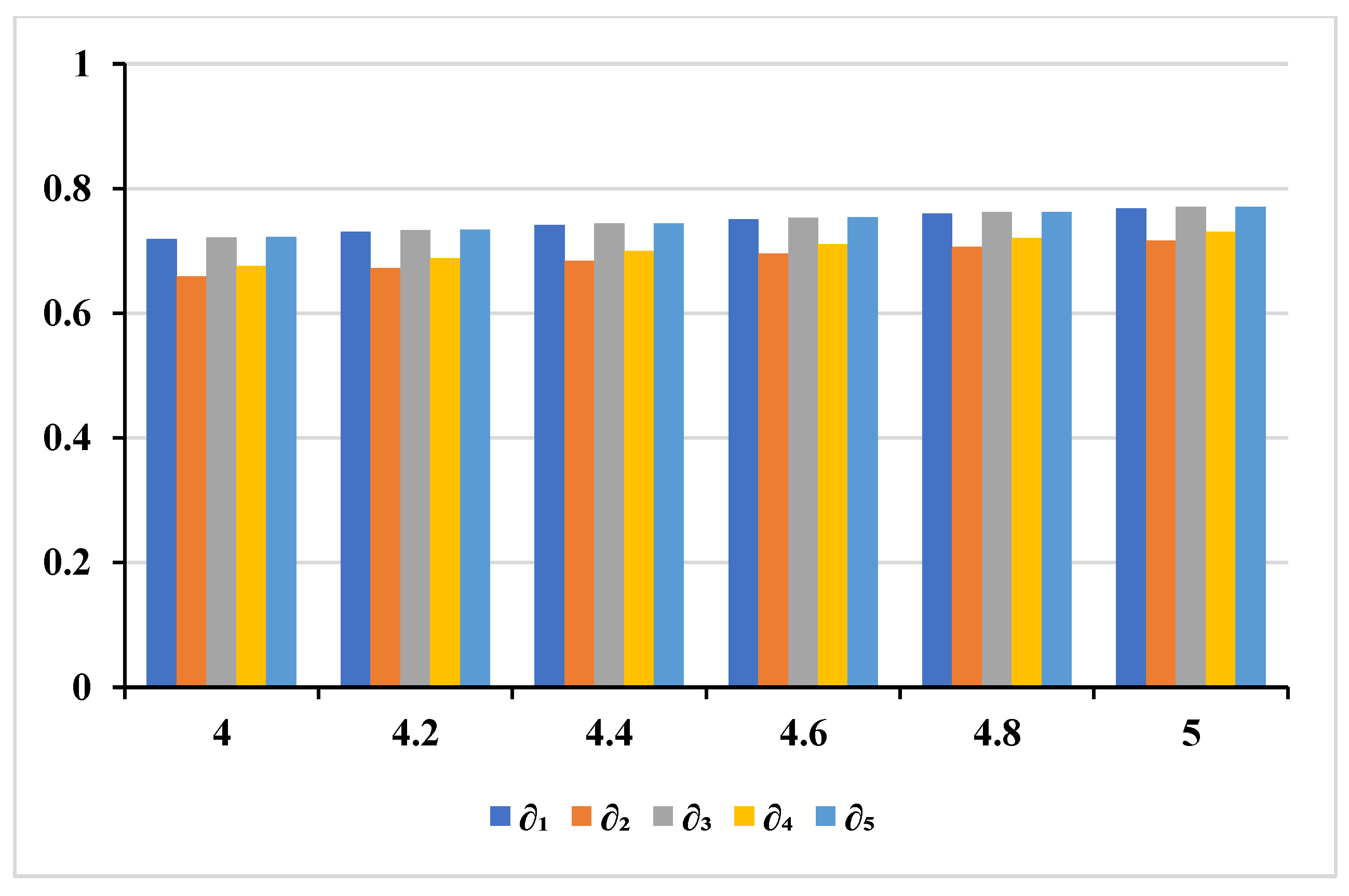
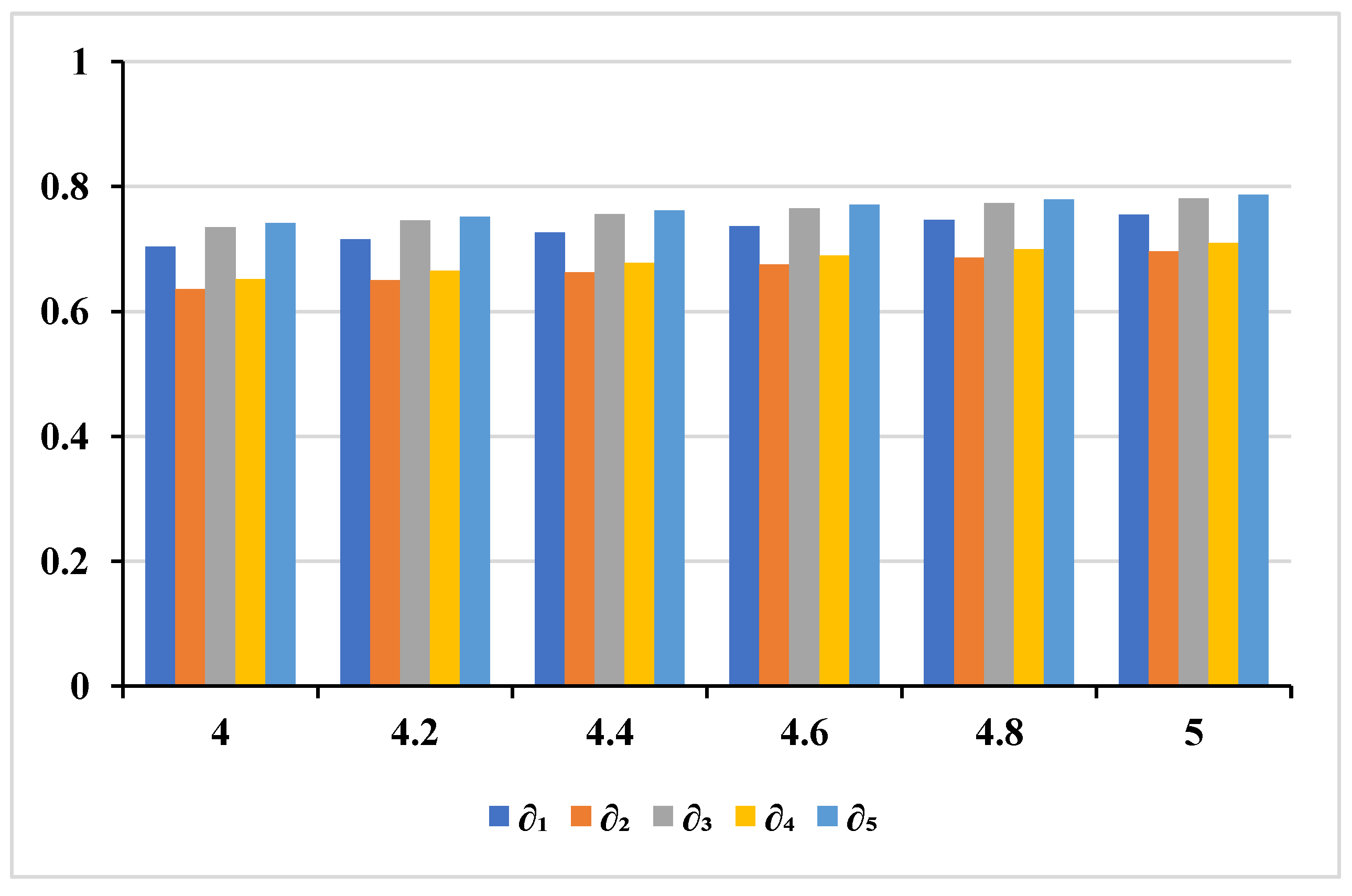
6. Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Pozna, C.; Precup, R.E.; Horvath, E. Hybrid particle filter–particle swarm optimization algorithm and application to fuzzy controlled servo systems. IEEE Trans. Fuzzy Syst. 2022, 30, 4286–4297. [Google Scholar] [CrossRef]
- Azeem, M.; Anwar, S.; Jamil, M.K.; Saeed, M.; Deveci, M. Topological numbers of fuzzy soft graphs and their application. Inf. Sci. 2024, 667, 120468. [Google Scholar] [CrossRef]
- Chen, H.; Gao, X.; Wu, Q. An enhanced fuzzy time series forecasting model integrating fuzzy c-means clustering, the principle of justifiable granularity, and particle swarm optimization. Symmetry 2025, 17, 753. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Hwang, C.M.; Yang, M.S. New construction for similarity measures between intuitionistic fuzzy sets based on lower, upper and middle fuzzy sets. Int. J. Fuzzy Syst. 2013, 15, 359–366. [Google Scholar]
- Garg, H.; Kumar, K. Linguistic interval-valued Atanassov intuitionistic fuzzy sets and their applications to group decision making problems. IEEE Trans. Fuzzy Syst. 2019, 27, 2302–2311. [Google Scholar] [CrossRef]
- Joshi, R.; Kumar, S. An intuitionistic fuzzy (δ, γ)-norm entropy with its application in supplier selection problem. Comput. Appl. Math. 2018, 37, 5624–5649. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Wei, G. Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.Y.; Wang, J.Q.; Li, L. Picture fuzzy normalized projection-based VIKOR method for the risk evaluation of construction project. Appl. Soft Comput. 2018, 64, 216–226. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef]
- Smarandache, F. Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst. 2018, 22, 168–170. [Google Scholar]
- Saqlain, M.; Riaz, M.; Saleem, M.A.; Yang, M.S. Distance and similarity measures for neutrosophic hypersoft set (NHSS) with construction of NHSS-TOPSIS and applications. IEEE Access 2021, 9, 30803–30816. [Google Scholar] [CrossRef]
- Jafar, M.N.; Saeed, M.; Saqlain, M.; Yang, M.S. Trigonometric similarity measures for neutrosophic hypersoft sets with application to renewable energy source selection. IEEE Access 2021, 9, 129178–129187. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N. Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 2018, 10, 193. [Google Scholar] [CrossRef]
- Abid, M.N.; Yang, M.S.; Karamti, H.; Ullah, K.; Pamucar, D. Similarity measures based on T-spherical fuzzy information with applications to pattern recognition and decision making. Symmetry 2022, 14, 410. [Google Scholar] [CrossRef]
- Tran, T.H.; Nguyen, P.H.; Nguyen, L.A.T.; Nguyen, T.H.T. Understanding the complexities: Interrelationships of critical barriers to university technology transfer in Vietnam using T-spherical fuzzy MCDM Approach. IEEE Access 2024, 12, 169683–169719. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Štreimikienė, D.; Khan, S.A.R. Pythagorean fuzzy SWARA–VIKOR framework for performance evaluation of solar panel selection. Sustainability 2020, 12, 4278. [Google Scholar] [CrossRef]
- Kumar, N.; Mahanta, J. A matrix norm-based Pythagorean fuzzy metric and its application in MEREC-SWARA-VIKOR framework for solar panel selection. Appl. Soft Comput. 2024, 158, 111592. [Google Scholar] [CrossRef]
- Hamdy, M.; Ibrahim, A.; Abozalam, B.; Helmy, S. Design and implementation of Type-3 intuitionistic fuzzy logic MPPT controller for PV solar system: Comparative study. ISA Trans. 2024, 154, 488–511. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, S.; Jana, C.; Sohail, M.; Choudhary, R.; Ahmad, S.; Deveci, M. Multi-criteria decision-making model based on picture hesitant fuzzy soft set approach: An application of sustainable solar energy management. Inf. Sci. 2025, 686, 121334. [Google Scholar] [CrossRef]
- Atanassov, K.T. Circular intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
- Atanassov, K.; Marinov, E. Four distances for circular intuitionistic fuzzy sets. Mathematics 2021, 9, 1121. [Google Scholar] [CrossRef]
- Garg, H.; Ünver, M.; Olgun, M.; Türkarslan, E. An extended EDAS method with circular intuitionistic fuzzy value features and its application to multi-criteria decision-making process. Artif. Intell. Rev. 2023, 56 (Suppl. S3), 3173–3204. [Google Scholar] [CrossRef]
- Alreshidi, N.A.; Shah, Z.; Khan, M.J. Similarity and entropy measures for circular intuitionistic fuzzy sets. Eng. Appl. Artif. Intell. 2024, 131, 107786. [Google Scholar] [CrossRef]
- Bozyiğit, M.C.; Olgun, M.; Ünver, M. Circular Pythagorean fuzzy sets and applications to multi-criteria decision making. Informatica 2023, 34, 713–742. [Google Scholar] [CrossRef]
- Yusoff, B.; Kilicman, A.; Pratama, D.; Hasni, R. Circular q-rung orthopair fuzzy set and its algebraic properties. Malays. J. Math. Sci. 2023, 17, 363–378. [Google Scholar] [CrossRef]
- Ying, G. Mental health assessment model for college students using circular q-rung orthopair fuzzy Muirhead means and MULTIMOORA method. IEEE Access 2025, 13, 35433–35451. [Google Scholar] [CrossRef]
- Ashraf, S.; Iqbal, W.; Ahmad, S.; Khan, F. Circular spherical fuzzy Sugeno Weber aggregation operators: A novel uncertain approach for adaption a programming language for social media platform. IEEE Access 2023, 11, 124920–124941. [Google Scholar] [CrossRef]
- Ashraf, S.; Jana, C.; Iqbal, W.; Deveci, M. Regret-based domination three-way decision-making model with circular spherical fuzzy Mahalanobis distance. Inf. Sci. 2025, 691, 121616. [Google Scholar] [CrossRef]
- Ashraf, S.; Chohan, M.S. Circular spherical fuzzy aggregation operators: A case study of risk assessments on industry expansion. Eng. Appl. Artif. Intell. 2025, 145, 110202. [Google Scholar] [CrossRef]
- Yang, M.S.; Akhtar, Y.; Ali, M. On globular T-spherical fuzzy (G-TSF) sets with application to G-TSF multi-criteria group decision-making. arXiv 2024, arXiv:2403.07010. [Google Scholar]
- Bhandari, D.; Pal, N.R.; Majumder, D.D. Fuzzy divergence, probability measure of fuzzy events and image thresholding. Pattern Recognit. Lett. 1992, 13, 857–867. [Google Scholar] [CrossRef]
- Chaira, T.; Ray, A.K. Segmentation using fuzzy divergence. Pattern Recognit. Lett. 2003, 24, 1837–1844. [Google Scholar] [CrossRef]
- Wu, M.Q.; Chen, T.Y.; Fan, J.P. Divergence measure of T-spherical fuzzy sets and its applications in pattern recognition. IEEE Access 2019, 8, 10208–10221. [Google Scholar] [CrossRef]
- Khan, M.J.; Kumam, W.; Alreshidi, N.A. Divergence measures for circular intuitionistic fuzzy sets and their applications. Eng. Appl. Artif. Intell. 2022, 116, 105455. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, Z.; Ulutagay, G.; Deveci, M.; Pamucar, D. Novel α-divergence measures on picture fuzzy sets and interval-valued picture fuzzy sets with diverse applications. Eng. Appl. Artif. Intell. 2024, 136, 109041. [Google Scholar] [CrossRef]
- Khan, F.M.; Munir, A.; Albaity, M.; Nadeem, M.; Mahmood, T. Software reliability growth model selection by using VIKOR method based on q-rung orthopair fuzzy entropy and divergence measures. IEEE Access 2024, 12, 86572–86582. [Google Scholar] [CrossRef]
- Riaz, M.; Habib, A.; Saqlain, M.; Yang, M.S. Cubic bipolar fuzzy VIKOR method using new distance and entropy measures and Einstein averaging aggregation operators with application to renewable energy. Int. J. Fuzzy Syst. 2023, 25, 510–543. [Google Scholar] [CrossRef]




| Div-Ms (Framework) | Features | |||||
|---|---|---|---|---|---|---|
| t | Radius | |||||
| 1 | FSs | Yes | No | No | No | No |
| 2 | IFSs | Yes | No | Yes | No | No |
| 3 | C-IFSs | Yes | No | Yes | No | Yes |
| 4 | PyFSs | Yes | No | Yes | No | No |
| 5 | C-PyFSs | Yes | No | Yes | No | Yes |
| 6 | q-ROFSs | Yes | No | Yes | Yes | No |
| 7 | C-qROFSs | Yes | No | Yes | Yes | Yes |
| 8 | PFSs | Yes | Yes | Yes | No | No |
| 9 | SFSs | Yes | Yes | Yes | No | No |
| 10 | C-SFSs | Yes | Yes | Yes | No | Yes |
| 11 | TSFSs | Yes | Yes | Yes | Yes | No |
| 12 | G-TSFSs (Proposed) | Yes | Yes | Yes | Yes | Yes |
| Assumption | Description and Rationale |
|---|---|
| Independence of Criteria | All decision criteria are assumed mutually independent to streamline aggregation and divergence calculations, an approach commonly adopted in MCGDM when inter-criteria correlations are minimal or modeled separately. |
| Expert Rationality | Experts are assumed to provide consistent and transitive judgments under uncertainty, enabling meaningful aggregation of their fuzzy evaluations. |
| Parameter Range | The tunable parameter is assumed to have a minimum effective value of 3. For sensitivity analysis, values from 4 to 5 are considered in increments (e.g., 4, 4.2, …, 5), ensuring bounded divergence and controlled variability. |
| Static Decision Environment | All input data and expert evaluations are treated as static for analysis purposes. |
| Complete Membership Information | Each alternative is assigned complete G-TSFS membership, non-membership, and indeterminacy values, ensuring well-defined behavior in all divergence computations. |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| <0.55, 0.35, 0.4> | <0.6, 0.45, 0.33> | <0.45, 0.3, 0.4> | <0.5, 0.34, 0.42> | <0.56, 0.35, 0.45> | |
| <0.6, 0.3, 0.4> | <0.42, 0.29, 0.42> | <0.72, 0.35, 0.41> | <0.52, 0.4, 0.45> | <0.65, 0.47, 0.35> | |
| <0.75, 0.44, 0.35> | <0.62, 0.5, 0.35> | <0.59, 0.28, 0.36> | <0.41, 0.52, 0.66> | <0.71, 0.25, 0.6> | |
| <0.34, 0.3, 0.45> | <0.47, 0.32, 0.45> | <0.62, 0.35, 0.41> | <0.54, 0.34, 0.51> | <0.29, 0.39, 0.49> | |
| <0.49, 0.36, 0.43> | <0.58, 0.51, 0.47> | <0.44, 0.53, 0.54> | <0.63, 0.35, 0.6> | <0.5, 0.3, 0.42> | |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| <0.65, 0.41, 052> | <0.58, 0.3, 0.34> | <0.52, 0.51, 0.48> | <0.63, 0.28, 0.37> | <0.48, 0.41, 0.34> | |
| <032, 0.35, 056> | <0.45, 0.41, 0.53> | <0.35, 0.42, 0.54> | <0.44, 0.54, 0.64> | <0.45, 0.51, 0.44> | |
| <0.62, 0.26, 0.53> | <0.59, 0.31, 0.42> | <0.32, 0.4, 0.55> | <0.56, 0.34, 0.29> | <0.62, 0.32, 0.43> | |
| <0.54, 0.34, 0.44> | <0.56, 0.33, 0.47> | <0.69, 0.56, 0.28> | <0.63, 0.52, 0.48> | <0.68, 0.35, 0.45> | |
| <0.63, 0.27, 0.56> | <0.45, 0.48, 0.52> | <0.65, 0.46, 0.38> | <0.71, 0.32, 0.54> | <0.66, 0.34, 0.41> | |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| <0.48, 0.32, 0.42> | <0.42, 0.26, 0.56> | <0.37, 041, 0.52> | <0.45, 0.22, 0.32> | <0.39, 0.23, 0.39> | |
| <0.43, 0.29, 0.48> | <0.49, 0.26, 0.38> | <0.61, 0.37, 0.51> | <0.56, 0.24, 0.36> | <0.53, 0.19, 0.49> | |
| <0.36, 0.41, 0.44> | <0.48, 0.35, 0.46> | <0.63, 0.38, 0.45> | <0.47, 0.41, 0.38> | <0.35, 0.43, 052> | |
| <0.46, 0.42, 0.35> | <0.45, 0.4, 0.38> | <0.41, 0.32, 0.38> | <0.45, 0.38, 0.36> | <0.27, 0.4, 0.51> | |
| <0.36, 0.47, 0.34> | <0.61, 0.34, 0.35> | <0.5, 0.38, 0.29> | <0.31, 0.43, 0.39> | <0.57, 045, 0.39> | |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| <0.56, 0.36, 0.44> | <0.53, 0.33, 0.41> | <0.44, 0.40, 0.46> | <0.52, 0.28, 0.37> | <0.47, 0.33, 0.39> | |
| <0.45, 0.31, 0.48> | <0.5, 0.32, 0.44> | <0.56, 0.38, 0.48> | <0.50, 0.39, 0.48> | <0.54, 0.39, 0.42> | |
| <0.57, 0.37, 0.44> | <0.56, 0.38, 0.41> | <0.51, 0.35, 0.45> | <0.48, 0.42, 0.44> | <0.56, 0.33, 0.51> | |
| <0.44, 0.35, 0.41> | <0.49, 035, 0.43> | <0.57, 0.41, 0.35> | <0.54, 0.41, 0.45> | <0.41, 0.38, 0.48> | |
| <0.49, 0.36, 0.44> | <0.54, 0.44, 0.44> | <0.53, 0.45, 0.40> | <0.55, 0.36, 0.51> | <0.57, 0.36, 0.40> | |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| 0.498034 | 0.457265 | 0.503924 | 0.47993 | 0.490226 | |
| 0.430263 | 0.469697 | 0.52049 | 0.524518 | 0.47846 | |
| 0.548949 | 0.469032 | 0.478534 | 0.501435 | 0.523532 | |
| 0.472652 | 0.451848 | 0.551261 | 0.537483 | 0.468503 | |
| 0.510841 | 0.492917 | 0.527087 | 0.605935 | 0.484195 | |
| Features | Alternative | ||||
|---|---|---|---|---|---|
| <0.56, 0.36, 0.44;0.49> | <0.53, 0.33, 0.41;0.45> | <0.44, 0.40, 0.46;0.50> | <0.52, 0.28, 0.37;0.47> | <0.47, 0.33, 0.39;0.49> | |
| <0.45, 0.31, 0.48;0.43> | <0.5, 0.32, 0.44;0.46> | <0.56, 0.38, 0.48;0.52> | <0.50, 0.39, 0.48;0.52> | <0.54, 0.39, 0.42;0.47> | |
| <0.57, 0.37, 0.44;0.54> | <0.56, 0.38, 0.41;0.46> | <0.51, 0.35, 0.45;0.47> | <0.48, 0.42, 0.44;0.50> | <0.56, 0.33, 0.51;0.52> | |
| <0.44, 0.35, 0.41;0.47> | <0.49, 035, 0.43;0.45> | <0.57, 0.41, 0.35;0.55> | <0.54, 0.41, 0.45;0.53> | <0.41, 0.38, 0.48;0.46> | |
| <0.49, 0.36, 0.44;0.51> | <0.54, 0.44, 0.44;0.49> | <0.53, 0.45, 0.40;0.52> | <0.55, 0.36, 0.51;0.60> | <0.57, 0.36, 0.40;48> | |
| Measures | Alternative | ||||
|---|---|---|---|---|---|
| 0.002038 | 0.002973 | 0.002009 | 0.002711 | 0.001814 | |
| 0.002246 | 0.001431 | 0.002595 | 0.001537 | 0.002446 | |
| 0.04515 | 0.054522 | 0.044821 | 0.052068 | 0.042588 | |
| 0.047397 | 0.037827 | 0.050944 | 0.039198 | 0.049458 | |
| Measures | Alternative | ||||
|---|---|---|---|---|---|
| 0.024043 | 0.032561 | 0.023671 | 0.030376 | 0.023562 | |
| 0.02771 | 0.019192 | 0.028078 | 0.021382 | 0.02814 | |
| 0.155059 | 0.180447 | 0.153853 | 0.174286 | 0.1535 | |
| 0.166463 | 0.138535 | 0.167566 | 0.146226 | 0.16775 | |
| Measures | Alternative | ||||
|---|---|---|---|---|---|
| 0.053204 | 0.073172 | 0.04757 | 0.067578 | 0.041995 | |
| 0.051229 | 0.033811 | 0.065423 | 0.036844 | 0.062492 | |
| 0.230661 | 0.270503 | 0.218107 | 0.259958 | 0.204926 | |
| 0.226338 | 0.183878 | 0.255779 | 0.191948 | 0.249984 | |
| Measures | Alternative | ||||
|---|---|---|---|---|---|
| Closeness degrees () | 0.512141 | 0.409612 | 0.531965 | 0.429494 | 0.537314 |
| Ranking | |||||
| Closeness degrees () | 0.517733 | 0.434305 | 0.521333 | 0.456226 | 0.522179 |
| Ranking | |||||
| Closeness degrees () | 0.495271 | 0.404678 | 0.539749 | 0.424753 | 0.549525 |
| Ranking | |||||
| Relative Closeness Degrees (RCD) | Ranking | |||||
|---|---|---|---|---|---|---|
| 4.0 | 0.71564 | 0.64001 | 0.72936 | 0.655358 | 0.733017 | |
| 4.2 | 0.727133 | 0.653756 | 0.740403 | 0.668679 | 0.743939 | |
| 4.4 | 0.737742 | 0.666509 | 0.750588 | 0.681024 | 0.754009 | |
| 4.6 | 0.747563 | 0.67837 | 0.760009 | 0.692494 | 0.763322 | |
| 4.8 | 0.75668 | 0.689428 | 0.768749 | 0.703179 | 0.771961 | |
| 5.0 | 0.765166 | 0.69976 | 0.776879 | 0.713153 | 0.779994 | |
| RCD | Ranking | |||||
|---|---|---|---|---|---|---|
| 4.0 | 0.719537 | 0.659018 | 0.722034 | 0.675445 | 0.72262 | |
| 4.2 | 0.730904 | 0.672235 | 0.733319 | 0.688185 | 0.733885 | |
| 4.4 | 0.741393 | 0.684481 | 0.743731 | 0.699974 | 0.74428 | |
| 4.6 | 0.751101 | 0.695856 | 0.753367 | 0.710915 | 0.753898 | |
| 4.8 | 0.760112 | 0.706449 | 0.762309 | 0.721094 | 0.762825 | |
| 5.0 | 0.768498 | 0.716338 | 0.77063 | 0.730587 | 0.77113 | |
| RCD | Ranking | |||||
|---|---|---|---|---|---|---|
| 4.0 | 0.703755 | 0.636143 | 0.734676 | 0.65173 | 0.741299 | |
| 4.2 | 0.715628 | 0.649994 | 0.745542 | 0.665154 | 0.751942 | |
| 4.4 | 0.726595 | 0.662847 | 0.75556 | 0.677596 | 0.76175 | |
| 4.6 | 0.736755 | 0.674805 | 0.764824 | 0.68916 | 0.770817 | |
| 4.8 | 0.746193 | 0.685955 | 0.773416 | 0.699933 | 0.779222 | |
| 5.0 | 0.754983 | 0.696376 | 0.781406 | 0.709994 | 0.787037 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.-S.; Akhtar, Y.; Ali, M. Divergence Measures for Globular T-Spherical Fuzzy Sets with Application in Selecting Solar Energy Systems. Symmetry 2025, 17, 872. https://doi.org/10.3390/sym17060872
Yang M-S, Akhtar Y, Ali M. Divergence Measures for Globular T-Spherical Fuzzy Sets with Application in Selecting Solar Energy Systems. Symmetry. 2025; 17(6):872. https://doi.org/10.3390/sym17060872
Chicago/Turabian StyleYang, Miin-Shen, Yasir Akhtar, and Mehboob Ali. 2025. "Divergence Measures for Globular T-Spherical Fuzzy Sets with Application in Selecting Solar Energy Systems" Symmetry 17, no. 6: 872. https://doi.org/10.3390/sym17060872
APA StyleYang, M.-S., Akhtar, Y., & Ali, M. (2025). Divergence Measures for Globular T-Spherical Fuzzy Sets with Application in Selecting Solar Energy Systems. Symmetry, 17(6), 872. https://doi.org/10.3390/sym17060872






