An Improved Whale Migration Algorithm for Global Optimization of Collaborative Symmetric Balanced Learning and Cloud Task Scheduling

Abstract

In today’s complex and ever-changing fields of science and engineering, intelligent optimization algorithms have become a key tool. However, the complexity of the problem itself often poses a severe challenge to the performance of the algorithm. The whale migration algorithm stands out among numerous optimization algorithms with its simple and efficient implementation and has received extensive attention. However, when confronted with complex issues such as global optimization and task scheduling, it still exposes some deficiencies including low initial population symmetry (i.e., poor distribution uniformity and insufficient balance between exploration and exploitation in iterative processes). The development ability of the algorithm is relatively weak, making it difficult to conduct an effective search and optimization in the complex problem space. The task scheduling strategy is not optimized enough, which affects the application of the algorithm in actual task scheduling scenarios. To overcome these challenges, this paper proposes an improved whale migration algorithm. Based on inheriting the original advantages of the whale migration algorithm, this algorithm effectively solves the above problems by introducing a new mechanism. The CEC2021 test function set was selected, and the effectiveness of the proposed strategy was verified through point-by-point ablation experiments. The algorithm was comprehensively verified through the CEC2022 test problem set, verifying the effectiveness and robustness of the algorithm in global optimization problems. Furthermore, the proposed algorithm was tested for cloud task scheduling problems of different scales. The experimental results show that the proposed algorithm can reduce the total scheduling cost by about 9% or more.

1. Introduction

Through the deep integration of data centers, cloud computing, and big data, the “East Data West Computing” project has built a new computing power network architecture, effectively promoted the integration of data processing, and optimized the supply and demand balance of resource equipment. It promotes the efficient interconnection of the Internet and reduces carbon emissions to a large extent. For example, with the support of the architecture of “counting in the East and counting in the West”, remarkable achievements have been made in task unloading [1], resource integration [2], and data integration [3]. However, with the exponential growth of data volume [4], the problem of unbalanced resource load has gradually become prominent, which can be attributed to the lack of symmetry in task allocation and resource utilization. To solve this problem effectively, it is urgent to scientifically and reasonably allocate the tasks with data to the corresponding computing resources, requiring algorithms to maintain symmetry between exploration and exploitation. At present, common task scheduling methods include the first-come-first-served (FCFS) [5], which treats all tasks as undifferentiated and only takes the arrival time of tasks as a scheduling standard. Although its implementation is simple, it does not consider the task’s performance and specific requirements, which may lead to an unbalanced computer load, resulting in long task blocking and other problems. In round robin (RR) [6], each time slice is assigned to a task and switches to the next task when the time slice of a task is used up, ensuring that each task has an equal opportunity to execute. However, because this method does not consider the priority of tasks, it cannot effectively solve the task method problem with correlation. The highest response ratio next (HRRN) [7] scheduling algorithm determines the execution order of tasks by comprehensively considering the time spent waiting and execution time of tasks, and fully considers the time proportion of tasks, but does not consider the assignment of tasks from the perspective of load, which may cause tasks to be concentrated on a certain computing resource, which affects the system performance. The shortest process first (SPF) [8] algorithm reduces the average system response time by selecting the task with the shortest waiting time. However, tasks of a large scale and high priority cannot be processed for a long time, resulting in task hunger.

Compared with the classical method, intelligent optimization algorithms show an excellent ability in solving optimization problems and make great efforts in various fields, for instance, working on images [9], feature selection problems [10], path planning [11], and natural language processing [12]. In this paper, we categorized intelligent optimization algorithms into four groups: intelligent optimization algorithms based on mathematical theory; intelligent optimization algorithms based on physics; intelligent optimization algorithms based on biology; and intelligent optimization algorithms based on human behavior. Among them, mathematical intelligent optimization algorithms include particle swarm optimization (PSO) [13], arithmetic optimization algorithm (AOA) [14], sine cosine algorithm (SCA) [15], subtraction-average-based optimizer (SABO) [16], and the exponential distribution optimizer (EDO) [17]. In the field of intelligent physics-based optimization algorithms, the gravitational search algorithm (GSA) [18], light spectrum optimizer (LSO) [19], energy valley optimizer (EVO) [20], Kepler optimization algorithm (KOA) [21], transient search optimization (TSO) [22], atom search optimization (ASO) [23], and other algorithms are representative. In biology-based intelligent optimization algorithms, the puma optimizer (PO) [24], ant colony optimization (ACO) [25], grey wolf optimizer (GWO) [26], whale optimization algorithm (WOA) [27], glowworm swarm optimization (GSO) [28], and Harris hawks optimizer (HHO) [29] perform well. Finally, in terms of intelligent optimization algorithms based on human behavior, the football team training algorithm (FTTA) [30], teaching-learning-based optimization (TLBO) [31], student psychology-based optimization (SPBO) [32], group teaching optimization algorithm (GTOA) [33], human memory optimization algorithm (HMO) [34], human evolutionary optimization algorithm (HEOA) [35], and other algorithms show a unique optimization ability.

In the field of agriculture, Chenbo Ding et al. introduced blockchain technology into the agricultural machinery resource scheduling system [36], which not only improved the utilization rate of agricultural machinery resources, but also reduced the production costs. However, this method has not been introduced into the field of heterogeneous type systems so far, and therefore has certain limitations. Yiyuan Pang et al. combined the frequency optimization of traditional motors and established multiple scheduling schemes to improve the energy-saving rate of the system [37]. Yiyuan Pang et al. proposed a new irrigation scheduling scheme [38] that balanced the relationship between system energy conservation and the working frequency of pumps. In the field of task scheduling, Poria Pirozmand et al. proposed multi-adaptive learning for particle swarm optimization (MALPSO) [39]. By introducing adaptive learning strategies, this method effectively reduces the response time of the system and improves the efficiency of task scheduling. However, this method does not fully consider the cost factors in actual task scheduling, which may lead to high costs in practical applications. Zhou Zhou et al. introduced the greedy strategy into the genetic algorithm and proposed a modified genetic algorithm combined with the greedy strategy (MGGS) [40]. MGGS can obtain the optimal solution with fewer iterations, thus shortening the optimization time of task scheduling. However, MGGS does not consider the task load balancing problem. In practical applications, a large number of tasks may be concentrated on resources with strong computing power, resulting in device load imbalance. Ali Al-maamari et al. improved the PSO algorithm by introducing an adaptive strategy and formed a dynamic adaptive particle swarm optimization algorithm (DAPSO) [41]. The algorithm optimizes the task scheduling process by reducing the period of the task and improving resource utilization. However, DAPSO has its limitations when dealing with large-scale task scheduling, which may not solve the load balancing problem effectively, resulting in unequal resource allocation in large-scale task scheduling scenarios. As “no free lunch (NFL)” expresses [42], although the structure of the whale migrating algorithm (WMA) is simple and efficient [43], there are still many problems in the application of task scheduling such as an unbalanced computing resource load, a long system response time, and high computing cost. Fortunately, this paper presents an algorithm that can effectively solve the above problems. The main contributions of this paper are as follows:

(1)

A mixed disturbance strategy was introduced into WMA. Compared with the traditional random initialization method, the mixed disturbance strategy interferes with the position of individuals in the initial community accurately and effectively by the obvious advantages of chaotic function and Cauchy mutation, that is, its high randomness and aperiodicity. This interference mechanism can make individuals evenly distributed in a larger space, significantly improving the diversity.

(2)

A balanced learning strategy was introduced into WMA to reduce the time for the WMA to break free from the local optimum to enhance the accuracy of the final solution. Specifically, individuals make up for their shortcomings by comprehensively learning from intermediate individuals and nearby optimal individuals, thus optimizing individual positions. In addition, through the dynamic change of mutation parameters, the population can still maintain sufficient diversity in the late iterations, which further improves the global search capability.

(3)

An oppositional learning strategy was introduced in the iterative process to enhance the diversity in the iterative process. Individuals explore the direction opposite to their current position by learning their relative knowledge in reverse, thus expanding their position to unknown areas. This strategy can effectively expand the search scope in the iterative process and further promote the WMA’s capability for global exploration.

(4)

By coordinating the above strategies, the improved whale migrating algorithm (IWMA) was obtained and applied to the CEC2017 test problem and cloud computing task scheduling problem.

The rest of this paper is structured as follows. Section 2 describes the related works, Section 3 describes the standard WMA, Section 4 presents the motivation and principle of IWMA, Section 5 completes the experimental analysis, and Section 6 presents the conclusions and outlook.

2. Related Works

In this section, firstly, we briefly introduce the recently proposed improved optimization algorithms for solving global optimization problems, and deeply analyze the advantages and disadvantages of these algorithms. Then, we focus on the newly emerging task scheduling algorithm and analyze its scheduling model as well as the performance and characteristics of the algorithm itself in detail.

2.1. Improved Algorithm Analysis

Ya Shen et al. proposed a multi-population evolution whale optimization algorithm (MEWOA) to solve the problems of the slow convergence speed and low convergence accuracy of WOA [44], and updated the position of individuals through different mechanisms in MEWOA to ensure that the algorithm jumped out of the local optimal trap. Experiments showed that MEWOA had a faster convergence speed and a more accurate global optimal solution in most benchmark functions. Ernest Bonah and others quantified characteristic parameters [45], such as bacteria in food, by combining a meta-heuristic algorithm. Their results showed that the proposed algorithm could effectively monitor the changes of bacterial pathogens. Ernest Bonah and others effectively predicted the classification and differentiation of bacterial food-borne pathogens by combining the PSO algorithm with a support vector machine (SVM) [46]. Experiments showed that the prediction rate of pathogens could be effectively improved by adding an SVM model to the PSO algorithm. Ningqiu Tang and others put forward a rapid detection method based on hyperspectral imaging technology by cooperating SVM with WOA [47]. Through the cooperation of SVM and WOA to improve the prediction accuracy, the experiment showed that WOA-SVM had an 88% prediction accuracy for the datasets and training sets. Hui Jiang et al. applied the optimization algorithm to the sensor [48], back-propagated the collaborative neural network, and proposed a rapid detection method of the fatty acid content. By optimizing the sensor characteristics with different optimization algorithms, the sensing efficiency was improved, and then the detection accuracy of the fatty acid content was improved. Zhiming Guo et al. proposed an efficient method to determine the components of the bioactive substance in green tea and its antioxidant capacity [49], and further suggested the potential application of near infrared spectroscopy combined with SA-PLS through a collaborative partial least squares method and simulated annealing algorithm (SA-PLS).

2.2. Analysis of Task Scheduling Status

Sumit Bansal and others proposed a PSO-WOA scheduling method to solve the problems of non-optimal solutions of PSO and the fast convergence speed of WOA [50]. In addition, a workflow task scheduling model was constructed to verify the effectiveness of the proposed algorithm. The performance of the proposed algorithm was evaluated by the period and total execution cost. Experiments showed that PSO-WOA could effectively reduce the total scheduling cost of the task workflow and reduce the scheduling time. However, in this model, the load journals of tasks are not taken into account, which may lead to a system crash because computing resources cannot handle a task. In addition, although PSO and WOA were combined, their algorithm characteristics were not changed essentially, so the PSO-WOA may be incomplete due to the limitations of the algorithm itself. Nebojsa Bacanin and others combined the original firefly metaheuristics with genetic operators and a learning process based on quasi-reflection [51] and proposed an improved firefly algorithm. A workload scheduling problem model was established, then the proposed algorithm and other algorithms were applied to this model, and the performance of the algorithm was characterized by the total cost and completion time. Experiments showed that the proposed algorithm could effectively improve the total cost of workflow scheduling and save the scheduling completion time. However, because the constructed workflow scheduling does not consider the priority between tasks, this method is not appropriate if there are links between workflows. Ipsita Behera cooperated a GWO and genetic algorithm to overcome their respective shortcomings [52], established a multi-objective task scheduling model in a cloud environment, and evaluated the effectiveness of the proposed algorithm through the completion time, execution cost, and energy consumption. Experiments showed that the proposed algorithm is an efficient and low-loss multi-objective task scheduling method. However, because the task needs to be transmitted in computing resources, and the transmission has a certain cost, this model still has some shortcomings. Sundas Iftikhar and others put forward a new algorithm called HunterPlus [53] and studied the application of a convolutional neural network to task scheduling in cloud and fog systems. Experiments showed that the proposed method could effectively improve the system scheduling performance and reduce the system scheduling energy consumption.

3. Original Whale Migrating Algorithm

By simulating whale migration behavior to the tropics, the WMA guides the information of each member to the optimal member. By dynamically merging the location information of the leaders and followers, the algorithm cleverly balances the relationship between exploration and development, thus significantly improving its convergence performance.

3.1. Algorithmic Process

Initially, the original community of WMA is obtained based on the scale of solving the problem. Under the characteristics of a random function, each individual is arbitrarily dispersed in the solution space, and the specific generation mode is obtained in Equation (1).

$$W{h}_i=Lb+rand\left(1,Dim\right)\cdot \left(Ub-Lb\right)$$

(1)

In Equation (1), $W{h}_i$ stands for the $i$ whale in the initial population, $Lb$ is the minimum vector for solving the question, $rand\left(\cdot \right)$ is a random value function, $rand\left(1,Dim\right)$ is a stochastic value that randomly lies between $\left[1,Dim\right]$, and $Ub$ is the maximum for solving the question.

In whale migration, each group of whales has an experienced leader who can guide the other whales toward their destination with their vast experience. In the WMA, other whales are guided toward their destination by the average leader. The position of the average leader is calculated from Equation (2).

$$W{h}_{lead}={\displaystyle \frac{1}{NLe}}\cdot {\displaystyle \sum _{i=1}^{NLe}W{h}_i}$$

(2)

where $W{h}_{lead}$ indicates the location of the average leader and $NLe$ symbolizes the count of leader whales.

Then, depending on the whale’s characteristics, its position or the leader’s position is updated. Less experienced whales will be guided toward their destination by experienced leaders, the leader, on the other hand, is primarily responsible for identifying and choosing the best path to the destination, which is expressed by Equation (3):

$$W{h}_i^{new}=\left\{\begin{array}{l}W{h}_{lead}+\alpha \cdot \left(W{h}_{i-1}-W{h}_i\right)+\alpha \cdot \left(W{h}_{best}-W{h}_{lead}\right) if i > NLe\\ W{h}_i+\beta \cdot Lb+\beta \cdot \delta \cdot \left(Ub-Lb\right) otherwise\end{array}\right.$$

(3)

where $W{h}_i^{new}$ represents the individual after the iteration of individual $W{h}_i$, and $\alpha$ is randomly situated between 0 and 1. $W{h}_{i-1}$ represents the $\left(i-1\right)$ whale, $W{h}_{best}$ is the destination (the best position at present), and $i$ represents the individual’s serial number. $\beta$ represents random numbers that are different from $\alpha$ and have values between 0 and 1, and $\delta$ represents random numbers that are different from $\alpha$ and $\beta$ and have values between 0 and 1.

Individual $W{h}_i$ and $W{h}_i^{new}$ are selected, which is expressed in Equation (4).

$$W{h}_i=W{h}_i^{new} if fi{t}_{inew} < fi{t}_i$$

(4)

where $fi{t}_i$ expresses the fitness of $W{h}_i$, and $fi{t}_{inew}$ is the fitness of individual $W{h}_i^{new}$.

Then, the optimal individual in the current population is updated, which is specifically expressed as Equation (5).

$$W{h}_{best}=W{h}_i if fi{t}_i < fi{t}_{best}$$

(5)

where $fi{t}_{best}$ represents the fitness of $W{h}_{best}$.

3.2. Concrete Implementation Operation of WMA

The pseudo-code of WMA is expressed in Algorithm 1, and the procedure of WMA is described below.

Step 1: Initialization arguments: population magnitude $\left(N\right)$, dimension of solving question $\left(Dim\right)$, and the lower bound and upper bound of solving problems $\left[Lb,Ub\right]$.

Step 2: Using Equation (1) and the arguments initialized in Step 1, the initial population $PW$ is generated, and $PW$ represents a matrix of $N\cdot Dim$.

Step 3: Entering the cycle, the average leader $W{h}_{lead}$ in $PW$ is obtained by Equation (2).

Step 4: The $W{h}_i^{new}$ individual is obtained according to Equation (3).

Step 5: Select individual $W{h}_i$ and individual $W{h}_i^{new}$ through Equation (4) in the population $PW$.

Step 6: Select individual $W{h}_{best}$ and individual $W{h}_i$ through Equation (4) in the population $PW$.

Step 7: If the iteration is complete, the optimal $W{h}_{best}$ is returned, otherwise, proceed to Step 3.

Algorithm 1: Pseudo-code of WMA

Input: Objective function: $Fun$, Solve the upper and lower bounds of the problem: $[Lb,Ub]$, Population size: $N$, Problem dimension: $Dim$, Maximum iterations: $MaxIters$, and set the iteration number: $Iters=1$. Output: Globally optimal individual: $W{h}_{best}$

1: Input: $N$$, Dim$$, MaxIters$$, \left[Lb,Ub\right]$.

2: The population $PW$ is initialized by Equation (1).

3: while $Iters \le MaxIters$ do

4:    The position of the average leader $W{h}_{lead}$ is calculated by Equation (2).

5:    The individual was obtained by updating the $W{h}_i$ individual by Equation (3).

6:     if $fi{t}_{inew} < fi{t}_i$

7:         $W{h}_i=W{h}_i^{new}$.

8:     end if

9:     if $fi{t}_i<fi{t}_{best}$

10:        $W{h}_{best}=W{h}_i$.

11:    end if

12: end while

13: Output: $W{h}_{best}$.

4. An Improved Whale Migrating Algorithm

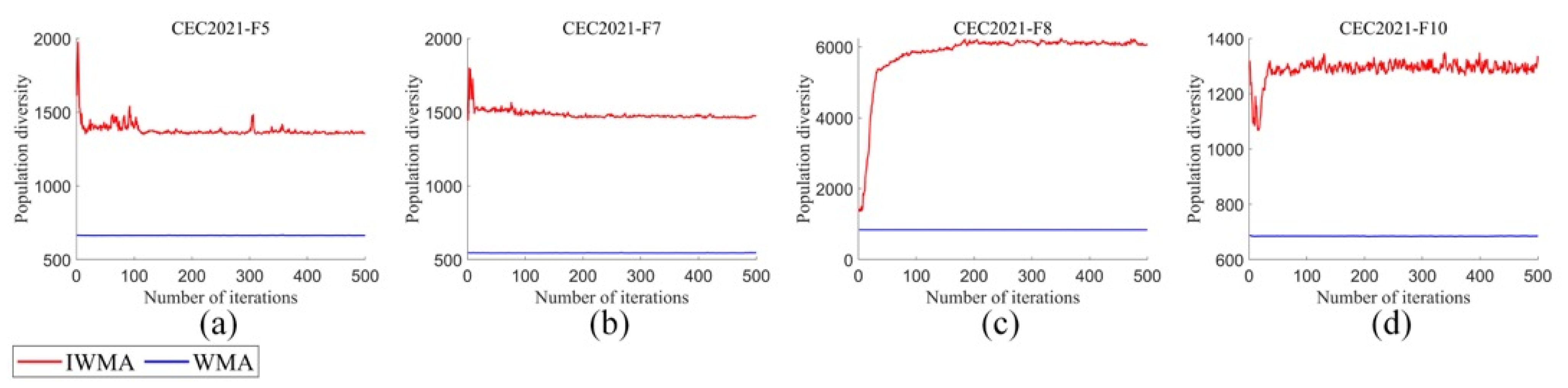
When applying the WMA to task scheduling problems, some limitations are exposed. For example, after the completion of iteration, WMA often only receives the current suboptimal scheduling policy, and the performance of time cost optimization in the optimization process is not ideal. The main reason is that in the process of iteration, the WMA finally obtains a non-optimal solution, which may be due to the poor quality of the initial population or the gradual approach of individuals to the destination, as the iteration progresses, thus reducing the population diversity. Therefore, this paper introduces a mixed disturbance initialization strategy, a balanced learning strategy, and an oppositional learning strategy into the WMA to form the IWMA.

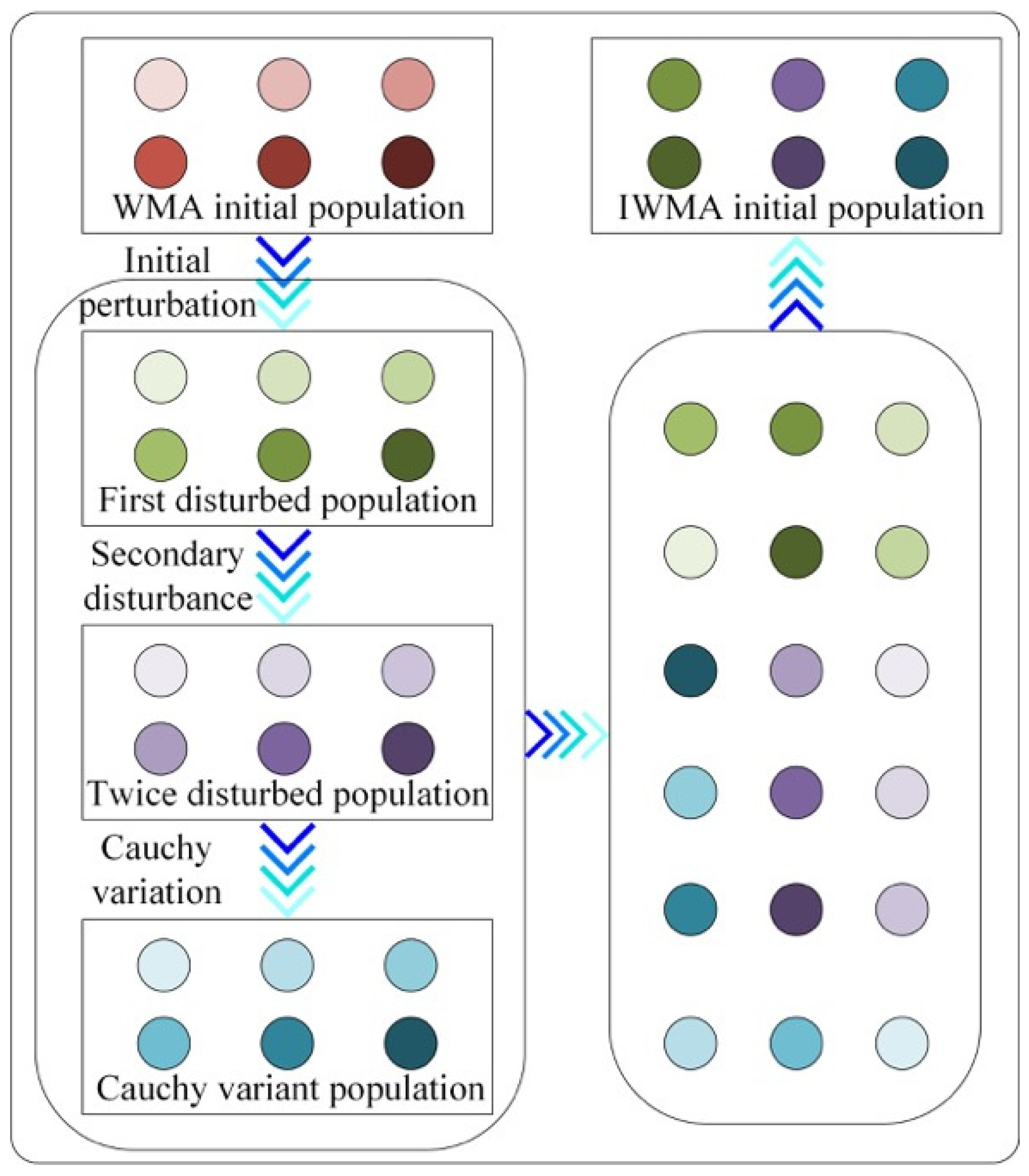
4.1. Mixed Disturbance Initialization Strategy

The more dispersed the individual location distribution, the higher the diversity, and the variety directly determines the final convergence accuracy of the WMA. Reference [54] pointed out that in the optimization algorithm, the chaos strategy can greatly enhance the quality of the initial population. Therefore, two-dimensional chaotic mapping was introduced into WMA in this paper. However, perturbation of the initial population using only two-dimensional chaotic mapping can only make the initial population individuals change slightly near the original location. Given this, this paper proposed the introduction of the Cauchy variation strategy based on two-dimensional chaotic mapping to further perturb individual positions to enhance diversity. The resulting initial population of the IWMA is described below, and the methodology is presented in Figure 1.

The initial population $PW$ obtained from Equation (1) is initially disturbed by Equation (6) to obtain a one-dimensional chaotic population $PC$.

$$W{h}_{pci}=mod\left(W{h}_i+\epsilon -\left({\displaystyle \frac{\phi }{2\cdot \pi }}\right)\cdot sin\left(2\cdot \pi \cdot W{h}_i\right),1\right)$$

(6)

where $W{h}_{pci}$ represents the $i$ individual in the population $PC$ after one-dimensional chaos mapping and $mod\left(\cdot \right)$ represents the modular division function. $\epsilon$ and $\phi$ represent the one-dimensional chaos parameters and specifies $\epsilon =0.2$, $\phi =0.4$, and $sin\left(\cdot \right)$ represents the sinusoidal value function.

After the initial disturbance of one-dimensional chaotic function, the obtained population $PC$ is further subjected to two-dimensional chaotic disturbance to obtain a two-dimensional chaotic disturbance population $PCH$. The specific disturbance process is calculated by Equation (7).

$$W{h}_{pchi}=cos\left(\gamma \cdot {\displaystyle \frac{1}{cos\left(W{h}_{pci}\right)}}\right)$$

(7)

where $W{h}_{pchi}$ represents the $i$ entity in $PCH$, $cos\left(\cdot \right)$ represents the cosine value function, and $\gamma$ represents the two-dimensional chaos parameter and specifies $\gamma =4$.

After the completion of two-dimensional chaotic perturbation, the obtained population $PCH$ is further disturbed by Cauchy variation, thus the $PK$ is obtained. The specific perturbation process is shown in Equation (8).

$$W{h}_{pki}=W{h}_{pchi}+{\displaystyle \frac{\nu \cdot \sigma }{abs\left(\sigma \right)}}$$

(8)

where $\nu$ represents the Cauchy variation parameter and specifies $\nu =0.5$. $\sigma$ is a random value that follows a normal distribution, and $abs\left(\cdot \right)$ is an absolute value function.

After the three populations ($PC$, $PCH$, and $PK$) are obtained, they are combined. Then, following the individual fitness, the merged population was sorted in ascending order. Finally, individuals with the top $N$ fitness values were selected from the sorted populations to form the initial population $P$ of the IWMA.

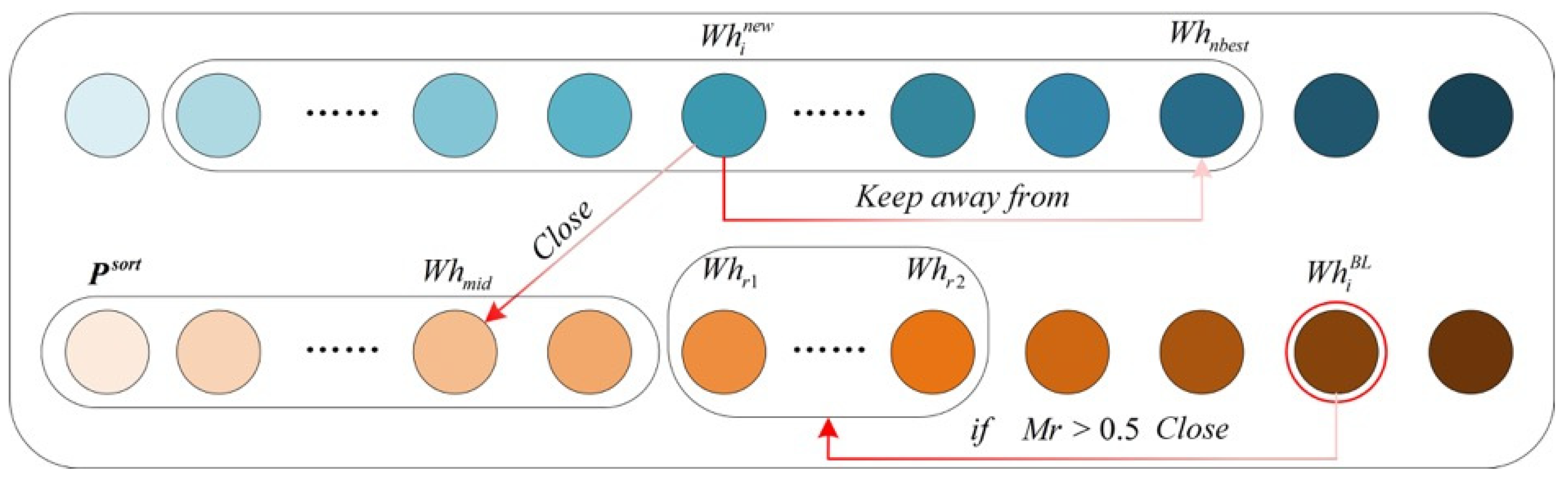
4.2. Balanced Learning Strategy

In the iterative process, WMA tends to fall into local optimization, which leads to load imbalance and cost optimization problems in task scheduling. The cause is that the operation process of the WMA only takes the individual with the best performance as the reference base, and through its guiding role, other individuals gradually approach the local optimal solution and eventually converge to the local optimality. To this end, the IWMA introduces a balanced learning strategy to assist individuals in updating their positions by learning from intermediate individuals and neighborhood optimal individuals. Meanwhile, to maintain the diversity in the iterative process, variation factors are introduced to participate in individual renewal. The process is expressed in Figure 2, and the individual updating process is listed below.

The intermediate individual $W{h}_{mid}$ is calculated by Equation (9).

$$W{h}_{mid}=P_{\tau }^{sort}$$

(9)

where $P^{sort}$ represents the population after the $P$ in order of fitness values arranged in increasing order, and $\tau$ is calculated by Equation (10).

$$\tau =⌈i\cdot rand/2⌉$$

(10)

where $i$ means the sequence number of an individual in population $P$, and $rand$ is a real number randomly generated in the range of 0 to 1.

Then, the first 5 and last 5 individuals of the $i$ individual are selected to form the neighborhood population, and the optimal individual $W{h}_{nbest}$ is selected.

Then, the value of the variation parameter $Mr$ is calculated by Equation (11).

$$Mr={\displaystyle \frac{1}{1+{\mathrm{e}}^{\left(-Iters+MaxIters/3\right)}}}$$

(11)

In Equation (11), ${\mathrm{e}}^{\left(\cdot \right)}$ represents the exponential function with $\mathrm{e}$ as the base. Finally, the individual $W{h}_i^{new}$ is updated according to the value of the variation parameter, and the specific updating is Equation (12).

$$W{h}_i^{BL}=\left\{\begin{array}{ll}\left(W{h}_i^{new}+W{h}_{mid}\right)/2-\left(W{h}_i^{new}-W{h}_{nbest}\right)/2& if Mr < 0.5\\ \left(W{h}_i^{new}+W{h}_{mid}\right)/2-\left(W{h}_i^{new}-W{h}_{nbest}\right)/2+\left(W{h}_{r1}-Mr\cdot W{h}_{r2}\right)& otherwise\end{array}\right.$$

(12)

where $W{h}_i^{BL}$ represents the individual updated by the balanced learning strategy, $r1$ and $r2$ are two distinct positive integers that are not equal to $i$ and have values ranging from $1$ to $N$, $W{h}_{r1}$ is said population $P$ in the first $r1$ individuals, and $W{h}_{r2}$ is said population $P$ in the first $r2$ individuals.

Finally, individual $W{h}_i^{new}$ and individual $W{h}_i^{BL}$ are selected by the greedy strategy, and the specific expression is shown in Equation (13).

$$W{h}_i^{new}=W{h}_i^{BL} if fi{t}_{iBL} < fi{t}_{inew}$$

(13)

In Equation (13), $fi{t}_{iBL}$ is the fitness of the individual $W{h}_i^{BL}$.

4.3. Oppositional Learning Strategy

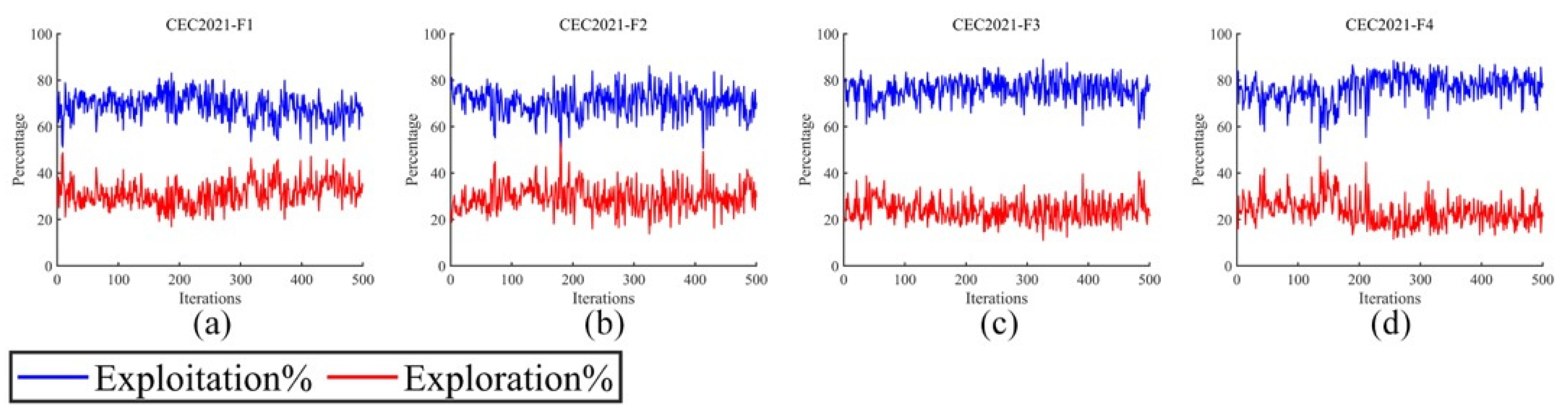
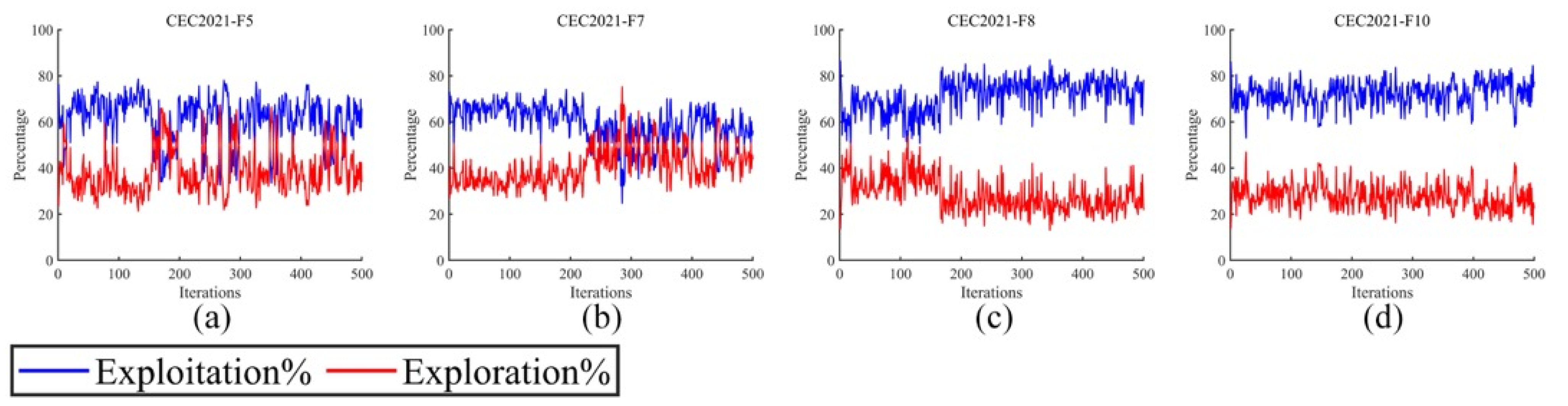
In the WMA, the main purpose of the development stage is to prevent it from finally obtaining a non-optimal solution. However, when the WMA is solving multi-task scheduling, the computer’s response time is too long, which may cause task blocking, which in turn affects the service life of the computer. Therefore, an oppositional learning way is cooperated in the IWMA to improve the development process in the iterative process.

Opposites are learned from individuals $W{h}_i$ using Equation (14) to generate opposites $W{h}_i^{OL}$.

$$W{h}_{iOL}^j=W{h}_i^{max}+W{h}_i^{min}-W{h}_i^j$$

(14)

where $W{h}_{iOL}^j$ is the value of the $W{h}_i^{OL}$ of the $i$ entity in the $j$ dimension, $W{h}_i^{max}$ represents the maximum value in all dimensions of the $i$ entity, $W{h}_i^{min}$ is the smallest information of the $i$ individual in all dimensions, and $W{h}_i^j$ is the value of the $i$ entity in the $j$ dimension.

Then, the individual $W{h}_i^{OL}$ and individual $W{h}_i^{new}$ are selected according to the greedy strategy, and the specific expression is shown in Equation (15).

$$W{h}_i^{new}=W{h}_i^{OL} if fi{t}_{iOL} < fi{t}_{inew}$$

(15)

where $fi{t}_{iOL}$ represents the fitness of the entity $W{h}_i^{OL}$.

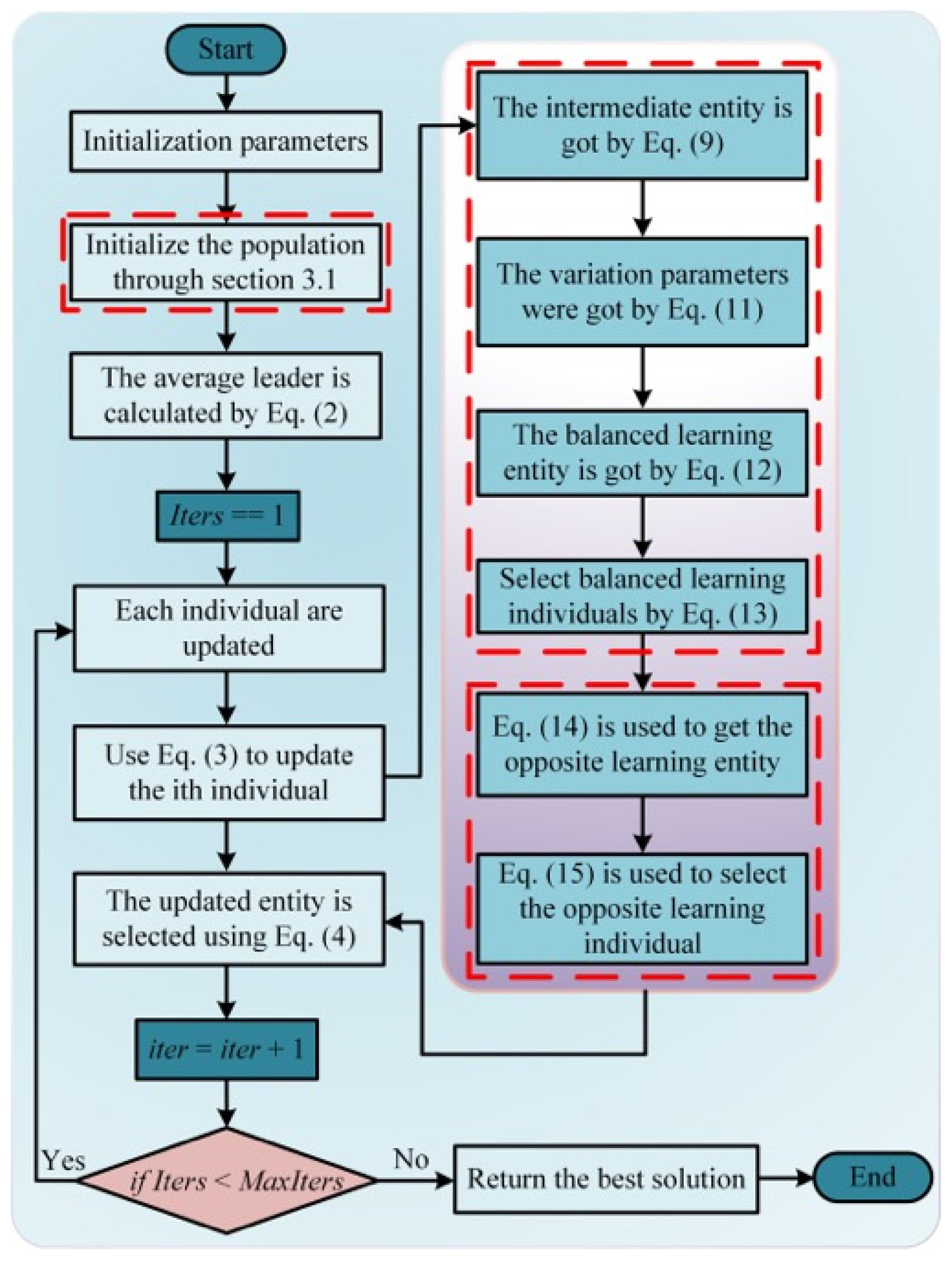
4.4. The Concrete Implementation Process of IWMA

The pseudo-code of the IWMA is shown in Algorithm 2, and its specific flow is shown in Figure 3. The following is a detailed description of the IWMA implementation details.

Step 1: Set parameters: Initial population number $\left(N\right)$, dimension of solving problem $\left(Dim\right)$, lower bound and upper bound of the solved problem $\left[Lb,Ub\right]$, chaotic parameter $\epsilon$, $\phi$, and $\gamma$.

Step 2: Initialize population $P$ by Section 3.1, $P$ represents a matrix of $N\cdot Dim$.

Step 3: Entering the cycle, the position of the average leader $W{h}_{lead}$ in the population $P$ is calculated by Equation (2).

Step 4: The $W{h}_i^{new}$ individual is obtained according to Equation (3).

Step 5: Individual $W{h}_i^{BL}$ is calculated by Equation (12).

Step 6: The individual $W{h}_i^{new}$ is updated by Equation (13).

Step 7: The opposite individual $W{h}_i^{OL}$ is calculated by Equation (14).

Step 8: The individual $W{h}_i^{new}$ is updated by Equation (15).

Step 9: Individuals in the population $P$ are selected by Equation (4).

Step 10: The current optimal individual $W{h}_{best}$ is updated by Equation (5).

Step 11: If the iteration is complete, the optimal entity $W{h}_{best}$ is returned, otherwise, go to Step 3 to continue the execution.

Algorithm 2: Pseudo-code of the IWMA

Input: Objective function: $Fun$, the upper and lower bounds of the solve problem: $[Lb,Ub]$, Initial population size: $N$, Problem dimension: $Dim$, Maximum iterations: $MaxIters$, chaotic parameter $\epsilon$$, \phi$ and $\gamma$. And set the current iteration number: $Iters=1$. Output: Globally optimal individual:

1: Input: $N$$, Dim$$, MaxIters$$, \epsilon$$, \phi$$, \gamma$$, \left[Lb,Ub\right]$.

2: The population $P$ is initialized by the Section 3.1.

3: while $Iters \le MaxIters$ do

4:    The position of the average leader $W{h}_{lead}$ is calculated by Equation (2).

5:    The individual $W{h}_i^{new}$ was obtained in population $P$ according to Equation (3).

6:    The balanced learning entity $W{h}_i^{BL}$ is obtained by Equation (12).

7:    Individual $W{h}_i^{new}$ is updated by Equation (13).

8:    if $fi{t}_{inew} < fi{t}_i$$W{h}_i=W{h}_i^{new}$.

9:    The opposite learning entity $W{h}_i^{OL}$ is obtained by Equation (14).

10:    Individual $W{h}_i^{new}$ is updated by Equation (15).

11:    if $fi{t}_i<fi{t}_{best}$$W{h}_{best}=W{h}_i$.

12: end while.

13: Output: $W{h}_{best}$.

4.5. Complexity Assessment

In this section, we focus on discussing the time complexity and the complexity of function evaluation times of the proposed IWMA. To present its performance characteristics more clearly, we first reviewed the time complexity characteristics of the standard WMA. In the standard WMA, the time complexity of the initialization stage is $O\left(N\cdot Dim\right)$, where $N$ represents the population size and $Dim$ indicates the dimension of the problem to be optimized. During the iterative process, each individual in the population updates its position under the guidance of the leader whale. Therefore, the time complexity of the WMA throughout the entire iteration process is $O\left(N\cdot Dim\cdot Iters\right)$, where $Iters$ is the number of iterations. Compared with the WMA, the IWMA introduces a mixed perturbation strategy in the initialization stage, aiming to enhance the diversity of the population. In the update stage, the IWMA incorporates balanced learning strategies and adversarial learning strategies to enhance the global search ability and convergence speed of the algorithm. Although the IWMA introduces these improvement strategies, its core computing logic has not changed. Therefore, the time complexity of the IWMA remains $O\left(N\cdot Dim\cdot Iters\right)$. This result indicates that the IWMA significantly improves the performance of the algorithm through strategy optimization while maintaining the same time complexity as the WMA. In terms of function evaluation, the proposed IWMA evaluates three populations in the initialization stage. Therefore, in the initialization stage, the number of function evaluations of the IWMA is three times that of the WMA. In the iterative process, IWMA introduces two learning strategies, and each learning strategy has a function evaluation. Therefore, in an iterative process, the IWMA’s function evaluation times are three times that of the WMA.

5. Experimental Results and Discussion

In this particular section, the performance of the IWMA in resolving global optimization problems and cloud task scheduling problems is tested. The CEC2021 and CEC2022 test functions and a cloud scheduling problem were introduced to prove the strength of the IWMA. To ensure the experiment’s fairness, all experiments were restricted to the Windows 11 operating system, and the programming environment was MATLAB 2024b.

5.1. Test of the Proposed Method

This section tests the mixed disturbance initialization strategy, balanced learning strategy, and oppositional learning strategy. The mixed disturbance initialization strategy was designed to address the WMA’s insufficient initial population diversity, so it was tested separately. However, the equilibrium learning method and the opposition learning method are committed to improving the problem of insufficient diversity in the iterative process, so strategies were combined for testing.

5.1.1. Effects of Mixed Disturbance Initialization Strategies on Population Diversity

In optimization algorithms, diversity describes the differences between individuals and has an important impact on the global search, which is given by Equation (16).

$$PD\left(Iters\right)=\sqrt{{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^{Dim}{\left(W{h}_i^j-CM\left(Iters\right)\right)}^2}}}$$

(16)

Here, $PD\left(Iters\right)$ represents the diversity value at the $Iters$ iteration, and $CM\left(Iters\right)$ represents the centroid value at the $Iters$ iteration, which is obtained by Equation (17).

$$CM\left(Iters\right)={\displaystyle \frac{1}{Dim}}\cdot {\displaystyle \sum _{i=1}^{N}W{h}_i^j}$$

(17)

In order to verify the effectiveness of the mixed disturbance initialization strategy in improving the diversity of initial population, this section applied the WMA and IWMA to the CEC2017 problem, and the latter only introduced the mixed disturbance initialization strategy. The results are shown in Figure 4 and Figure 5. See

Table 1. CEC2021 test function information.

Index	Types	Name	Optimum
CEC2021_F1	Unimodal function	Shifted and Rotated Bent Cigar Function (CEC 2017 F1)	100
CEC2021_F2	Basic functions	Shifted and Rotated Schwefel’s Function (CEC 2014 F11)	1100
CEC2021_F3		Shifted and Rotated Lunacek bi-Rastrigin Function (CEC 2017 F7)	700
CEC2021_F4		Expanded Rosenbrock’s plus Griewangk’s Function (CEC 2017 f19)	1900
CEC2021_F5	Hybrid functions	Hybrid Function 1 $(N=3)$(CEC 2014 F17)	1700
CEC2021_F6		Hybrid Function 2 $(N=4)$(CEC 2017 F16)	1600
CEC2021_F7		Hybrid Function 3 $(N=5)$(CEC 2014 F21)	2100
CEC2021_F8	Composition functions	Composition Function 1 $(N=3)$(CEC 2017 F22)	2200
CEC2021_F9		Composition Function 2 $(N=4)$(CEC 2017 F24)	2400
CEC2021_F10		Composition Function 3 $(N=5)$(CEC 2017 F25)	2500
Search range: [−100, 100]

for detailed information about the CEC2021 test function. In the experimental setup in this section, the problem dimension was 20, the population size was 30, and the total number of iterations was 500.

To avoid unnecessary experiments, in this section, we carefully selected the following test functions: F1 in unimodal function, F2, F3, and F4 in basic function, F5 and F7 in mixed function, and F8 and F10 in combined function. The test results are shown in Figure 4 and Figure 5, respectively. As can be seen from Figure 4a, when dealing with unimodal function F1, the starting point of the IWMA using only the mixed disturbance initialization strategy was higher than that of the traditional WMA. This shows that this strategy can effectively improve the diversity of the initial population of the algorithm when dealing with unimodal function problems. Figure 4b, c further shows that this strategy can also significantly improve the diversity of the initial WMA population when dealing with the basic function problem. In addition, it can be seen from Figure 5a–c that the hybrid perturbation initialization strategy can significantly improve the diversity of the algorithm population, even in the face of complex mixed function and composite-function problems. Although the initial population diversity of the IWMA was slightly improved when solving the function F8 problem, the population diversity of IWMA was significantly improved when dealing with the combined function F10, which once again confirmed the effectiveness of the proposed strategy.

5.1.2. Effects of Balanced Learning Strategy and Oppositional Learning Strategy

During the WMA, the exploration phase mainly relies on experienced leaders to explore new areas, while the exploitation phase is when the average leader leads other whales to move. The percentages of exploration and exploitation were obtained by Equation (18).

$$\left\{\begin{array}{l}Exploration\left(\%\right)={\displaystyle \frac{Ddiv\left(Iters\right)}{Ddi{v}_{max}}}\cdot 100\\ Exploitation\left(\%\right)={\displaystyle \frac{\left|Ddiv\left(Iters\right)-Ddi{v}_{max}\right|}{Ddi{v}_{max}}}\cdot 100\end{array}\right.$$

(18)

where $Ddiv\left(Iters\right)$ represents the dimensional diversity, $Ddi{v}_{max}$ represents the maximum dimensional diversity during the whole iteration, and $Ddiv\left(Iters\right)$ is obtained by Equation (19).

$$Ddiv\left(Iters\right)={\displaystyle \frac{1}{Dim}}\cdot {\displaystyle \sum _{j=1}^{Dim}\frac{1}{N}}\cdot {\displaystyle \sum _{i=1}^N\left|median\left(W{h}_j\right)-W{h}_i^j\right|}$$

(19)

where $median\left(\cdot \right)$ represents the function of taking an intermediate value.

Because the ability of development and exploration has a great influence on the WMA, this section tested the exploration and development percentage of the IWMA, while the IWMA only included balanced and opposing learning strategies. CEC2021 Test Function Verification IWMA, the Table 1 describes the details of the CEC2021 test problems. The total population was set to 30, the dimension of problem solving was set to 20, and the iteration count was 500. The results are included in Figure 6 and Figure 7.

When dealing with unimodal function problems and basic function problems, the IWMA can ensure a high proportion in the development stage at the beginning of the iteration, so that its population individuals can explore different positions extensively at the beginning of the iteration. As shown in Figure 6a–d, with the advancement of the iteration, the proportion of the IWMA in the development phase remains high when dealing with simple problems. This shows that the introduction of two strategies in the WMA can encourage individuals to explore the unknown space and then help them get rid of the local optimal dilemma. When the IWMA is faced with complex and combinatorial function problems, its development ability is still strong. It can be seen from Figure 7c,d that when the scale of the problem increases, the proportion of IWMA development not only did not decrease, but increased. This fully proves that the IWMA has remarkable potential in dealing with complex problems.

5.2. Global Optimization Ability Test

In this section, to verify the IWMA’s ability to handle global optimization problems, the IWMA and other algorithms were compared including classical algorithms ACO, PSO, WOA, novel algorithms such as the hiking optimization algorithm (HOA) [55], remora optimization algorithm (ROA) [56], and WMA as well as the red-billed blue magpie optimizer (RBMO) [57] and differential squirrel search algorithm (DSSA) [58]. These algorithms were applied to the CEC2022 test problem, the specifics of which are presented in

Table 2. CEC2022 test function information.

Index	Types	Name	Optimum
CEC2022_F1	Unimodal function	Shifted and full Rotated Zakharov Function	300
CEC2022_F2	Basic functions	Shifted and full Rotated Rosenbrock’s Function	400
CEC2022_F3		Shifted and full Rotated Expanded Schaffer’s f6 Function	600
CEC2022_F4		Shifted and full Rotated Non-Continuous Rastrigin’s Function	800
CEC2022_F5		Shifted and full Rotated Levy Function	900
CEC2022_F6	Hybrid functions	Hybrid Function 1 $(N=3)$	1800
CEC2022_F7		Hybrid Function 2 $(N=6)$	2000
CEC2022_F8		Hybrid Function 3 $(N=5)$	2200
CEC2022_F9	Composition functions	Composition Function 1 $(N=5)$	2300
CEC2022_F10		Composition Function 2 $(N=4)$	2400
CEC2022_F11		Composition Function 3 $(N=5)$	2600
CEC2022_F12		Composition Function 4 $(N=6)$	2700
Search range: [−100, 100]

.

Firstly, the number of iterations was set to 50, the population size was 30, and the problem dimension was 20. The IWMA and other algorithms were verified on the CEC2022 test function, and all the algorithms are independently run 30 times. The experimental results are shown in Figure 8. As can be seen from Figure 8, the stability of the IWMA was better than the other comparison algorithms, especially when the CEC2022 tested functions F1, F5, and F6, the IWMA was ahead of the other algorithms. Then, the total number of iterations was increased to 500, and the other parameters were changed. Then, the IWMA and other algorithms were applied to the CEC2022 test function problem, and the results are shown in Figure 9. When solving the CEC2022 function problems, the IWMA algorithm showed an excellent optimization performance, and it was almost the best in unimodal, complex, and combinatorial problems. As shown in Figure 9, when faced with simple problems, the IWMA, like most excellent algorithms, can quickly converge to the optimal solution at the initial stage of iteration. Particularly when dealing with F2 and F3 functions in CEC2022, many algorithms fell into a local optimal dilemma in the iterative process, and only the HOA, DSSA, and IWMA could successfully jump out of this trap. After about 200 iterations, the IWMA was always in the leading position and always maintained its advantage in subsequent iterations. In the face of complex mixed problems, the IWMA still showed strong optimization ability. Especially when dealing with the F6 function in the CEC2022 test function, the IWMA could quickly avoid the local optimal trap almost at the beginning of the iteration and accurately found the global optimal solution in about 150 iterations. Although the IWMA failed to achieve the optimal optimization effect when dealing with the F7 function in the CEC2022 test function, its performance was only slightly inferior to that of DSSA, which ranked first. When dealing with combinatorial problems, although the IWMA failed to find the global optimal solution immediately at the beginning of the iteration, with the continuation of iterations, the IWMA finally succeeded in converging to the global optimal solution. This shows that the IWMA has good adaptability and strong optimization ability when dealing with different types of optimization problems.

5.3. Cloud Task Scheduling Test

To verify the performance of the IWMA in dealing with cloud task scheduling, a scheduling model was introduced to observe the ability of the IWMA in dealing with its problems. The scheduling ability of the IWMA was evaluated by a series of evaluation indices. Because this section only discusses the performance of the proposed algorithm in cloud task scheduling, in this section of the experiment, all of the algorithms were only run once independently, and we ensured that the other conditions were the same.

5.3.1. Scheduling Model Between Tasks and Computing Resources

Let the number of tasks be $O$ and the total number of computing resources (virtual machines) be $K$, then the relationship between them can be described by matrix $M$.

$$\mathit{M}={\left[\begin{array}{lllll}{m}_1^1& \cdots & m_1^j& \cdots & m_1^K\\ ⋮& & ⋮& & ⋮\\ m_i^1& \cdots & m_i^j& \cdots & m_i^K\\ ⋮& & ⋮& & ⋮\\ m_O^1& \cdots & m_O^j& \cdots & m_O^K\end{array}\right]}_{O\cdot K}$$

(20)

where $m_i^j$ represents a binary number; when $m_i^j=1$, this indicates that the $i$ task is computed on the $j$ VM, otherwise, vice versa. It is stipulated that a task can only be calculated on one virtual machine at a time, so ${\displaystyle {\sum }_{j=1}^K{m}_i^j=1}$ for $i\in \left[1,O\right]$.

In this experiment, we assumed that all tasks were scheduled serially. This means that when the virtual machine receives a batch of tasks, these tasks will be executed one after another in a certain order. In the actual cloud computing environment, virtual machines may experience overload due to an excessive task volume. However, in this experiment, we assumed that the computing resources of the virtual machine were sufficient and that there would be no overload phenomenon. This assumption enabled us to ignore the resource limitations of virtual machines and focus on the impact of the scheduling strategies on the task execution time.

5.3.2. Cloud Computing Task Scheduling Evaluation Indicators

To evaluate the performance of the algorithm in task scheduling, combined with the actual scheduling scenario, this experiment adopted the three indices of time expenditure, price cost, and load expenditure to measure the performance of the algorithms in solving scheduling problems. The total cost was calculated by adding the time expenditure, price expenditure, and load expenditure. However, since the units of these three costs were different, direct summing can lead to unreasonable results. Therefore, the minimum-maximization method was used to normalize the above three cost data to ensure that they were comparable in the total cost calculation. The total expenditure rule is displayed in Equation (21).

$$TotalCost=\omega 1\cdot TimeCost+\omega 2\cdot PriceCost+\omega 3\cdot LoadCost$$

(21)

where $\omega 1$, $\omega 2$, and $\omega 3$ represent the weight in terms of the time consumption, price consumption, and load consumption, respectively. Since this experiment only discusses the advantages and disadvantages of the algorithm, $\omega 1=\omega 2=\omega 3=1/3$ was specified this time. $TimeCost$ represents the time cost and is calculated by Equation (22).

$$TimeCost={\displaystyle \frac{1}{O}}\cdot {\displaystyle \sum _{i=1}^O{\displaystyle \sum _{j=1}^K{m}_i^j\cdot \frac{C_t^i/C_n^j}{\underset{\forall i,j}{max}\left\{C_t^i/C_n^j\right\}}}}$$

(22)

where $C_t^i$ is the handling ability demanded by the $i$ task, and $C_n^j$ is the computing power possessed by the $j$ VM. The load cost of the computer is associated with the storage size of the task and the storage size of the virtual machine, which is obtained by Equation (23).

$$LoadCost={\displaystyle \frac{1}{O}}\cdot {\displaystyle \sum _{i=1}^O{\displaystyle \sum _{j=1}^K{m}_i^j\cdot \frac{M{e}_t^i/M{e}_n^j}{\underset{\forall i,j}{max}\left\{M{e}_t^i/M{e}_n^j\right\}}}}$$

(23)

where $M{e}_t^i$ represents the amount of storage needed for the $i$ task, and $M{e}_n^j$ represents the storage size belonging to the $j$ computing resource. The price cost of cloud computing scheduling is related to both the scheduling time and scheduling transmission cost. The cost of scheduling transfers depends on the resource bandwidth required by the task and the resource bandwidth capacity that can be handled by computing resources. The specific calculation method of the price cost is given by Equation (24).

$$PriceCost={\displaystyle \frac{1}{O}}\cdot {\displaystyle \sum _{i=1}^O{\displaystyle \sum _{j=1}^K{m}_i^j\cdot \frac{\left(unit\cdot C_t^i\cdot R{b}_t^i\right)/\left(C_n^j\cdot R{b}_n^j\right)}{\underset{\forall i,j}{max}\left\{\left(unit\cdot C_t^i\cdot R{b}_t^i\right)/\left(C_n^j\cdot R{b}_n^j\right)\right\}}}}$$

(24)

where $R{b}_t^i$ represents the resource bandwidth specified by the $i$ task, $R{b}_n^j$ represents the resource bandwidth possessed by the $j$ VM, and $unit$ represents the price cost unit and stipulates $unit=8$.

5.3.3. Small-Scale Task Scheduling Application Test

To verify the effectiveness of the IWMA in dealing with small-scale task assignment problems, this section carried out an experimental design. In the experiment, the total number of tasks was set to 100 while the total number of virtual machines was 30. In addition, the total number of iterations of the algorithm was set to 100, and the population size was 30 individuals.

Table 3. Task and computing resource-related variables.

Parameters	Range (VM)	Range (Task)
$C$	[200, 500]	[10, 50]
$Me$	[100, 500]	[50, 100]
$Rb$	[100, 250]	[20, 50]

details the variable values related to tasks and computing resources. Based on these parameters, we applied the IWMA and other algorithms for task scheduling. Finally, the optimal scheduling result is shown in Figure 10, and the dataset generated in the scheduling process is recorded in

Table 4. Small-scale task scheduling data result set.

Metric	ACO	PSO	WOA	HOA	RBMO	ROA	DSSA	WMA	IWMA
Best	0.3138	0.2940	0.2838	0.2788	0.2766	0.2857	0.2611	0.2516	0.2434
Mean	0.3332	0.3225	0.2838	0.3003	0.2766	0.3136	0.2789	0.2563	0.2444
Worst	0.3124	0.2962	0.2838	0.2895	0.2766	0.2990	0.2706	0.2517	0.2437
Std	0.0165	0.0063	0	0.0053	2.2584	0.0085	0.0050	0.0008	0.0002
Running time	4.45 s	4.32 s	3.98 s	4.19 s	3.72 s	4.65 s	5.16 s	4.43 s	4.27 s

in detail. The cost reduction rate mentioned in this section was calculated by subtracting the optimized cost from the original cost and then dividing the original cost. The following cost reduction rates were all the same.

It can be observed from Figure 10a that almost all curves showed a downward trend, which fully shows that the optimization algorithm could effectively improve the task scheduling process of cloud computing. As shown in Figure 10a, the total cost of IWMA optimal scheduling was the lowest after the iteration was completed. Compared with the original WMA, the total cost of the IWMA after optimization was significantly reduced by about 8%. In addition, Figure 10c, d further reveals the significant advantages of the IWMA compared with the WMA in load cost optimization and time cost optimization. From the aspect of price and cost optimization, when the iteration reached about the 55th generation, the optimization effect of the WMA gradually tended to be stable, while the IWMA successfully broke through the dilemma of the non-optimal solution, making the price and cost continue to decrease. According to the data in Table 4, during the scheduling process, the individuals in the population optimized by the IWMA gradually moved closer to the optimal scheduling strategy when scheduling small-scale tasks, which strongly proved the effectiveness of the IWMA in dealing with small-scale task scheduling problems. In addition, when conducting small-scale task scheduling, the IWMA also stood out with third place in terms of time consumption.

5.3.4. Medium-Scale Task Scheduling Application Test

This section further expands the scale of the experiment, increasing the number of tasks to 500 while maintaining the number of virtual machines to 30 and the number of iterations to 100. In addition, the total population was adjusted to 40. See

Table 5. Task and computing resource-related variables.

Parameters	Range (VM)	Range (Task)
$C$	[400, 1000]	[1860, 2660]
$Me$	[50, 100]	[2048, 4096]
$Rb$	[20, 50]	[400, 500]

for the specific parameter configurations of tasks and virtual machines. The IWMA and other algorithms were retested. The optimal task scheduling results are shown in Figure 11, and the datasets generated during the scheduling process are recorded in

Table 6. Medium-scale task scheduling results dataset.

Metric	ACO	PSO	WOA	HOA	RBMO	ROA	DSSA	WMA	IWMA
Best	0.4806	0.4647	0.4616	0.4510	0.4503	0.4773	0.4417	0.4335	0.3861
Mean	0.5024	0.4969	0.4616	0.4763	0.4503	0.4951	0.4706	0.4335	0.3861
Worst	0.4911	0.4662	0.4616	0.4598	0.4503	0.4851	0.4573	0.4335	0.3861
Std	0.0057	0.0053	5.62183 × 10−17	0.0055	5.05965 × 10−16	0.0054	0.0050	1.68655 × 10−16	5.62183 × 10−17
Running time	23.45 s	21.32 s	24.98 s	21.19 s	22.72 s	25.65 s	24.16 s	21.43 s	22.27 s

in detail.

When tacking the medium-sized task assignment problem, the IWMA demonstrated excellent optimization ability. As can be seen from Figure 11a, the optimization effect of the WMA tended to be stable and common, while the optimization effect of the IWMA was excellent. Compared with the optimization results of other algorithms, the IWMA achieved a significant reduction of more than 14% in total cost. Especially when compared with the optimization results of the ant colony algorithm, the cost of the IWMA was reduced by about 21%. Most algorithms deal with multi-task scheduling problems, although they showed some performance in load and cost optimization, the optimization effect of the IWMA was more significant. This fully proves that the IWMA has a stronger ability in cloud computing task scheduling optimization. According to the data in Table 6, the worst and best values obtained by the IWMA were better than the other algorithms. Especially when compared with the initial WMA, the lowest cost and the highest cost in the scheduling process decreased by about 10%, respectively. This result further verifies the effectiveness of introducing the proposed strategy in dealing with medium-scale task scheduling problems. When dealing with medium-sized scheduling problems, the IWMA performed well in finding the optimal scheduling time and ranked fourth in terms of performance. More importantly, the scheduling loss values obtained by the IWMA were all lower than the corresponding results of the other algorithms. This indicates that the IWMA not only has a high efficiency in optimizing the scheduling time, but also shows significant advantages in reducing scheduling losses, giving it high application value and competitiveness in solving medium-scale scheduling problems.

5.3.5. Large-Scale Task Scheduling Application Test

To simulate the possible data explosion in the actual scheduling scenario, this section increased the number of tasks to 1000, set the number of resource nodes to 50, and kept the total number of iterations to 100 and the population count to 40. Refer to Table 5 for the related variable parameters of the tasks and virtual machines. Based on these parameter settings, algorithms such as IWMA were verified again. The verification result is shown in Figure 12, and the detailed dataset in the scheduling process is recorded in Table 6.

As can be seen from Figure 12a, the performance of ACO and ROA in total cost optimization was very limited, and it almost stagnated when the number of tasks reached 1000. Although the WMA still had a certain optimization ability, the IWMA had a better optimization effect and stronger optimization potential. Looking further at Figure 12b, in terms of load cost optimization, the WMA’s optimization progress was relatively slow, while the IWMA quickly found the optimal scheduling strategy around the eighth iteration and maintained a leading position in subsequent iterations. This once again proves the remarkable advantages of the IWMA in optimization ability. The IWMA also performed well in terms of price, cost, and time cost optimization. Compared with other algorithms, the IWMA achieved the best optimization effect in the eighth iteration, and kept ahead in subsequent iterations. This shows that IWMA not only has a fast optimization speed, but also a stable optimization benefit when dealing with a large number of task assignment problems, which can greatly reduce the total cost and enhance the scheduling ability.

Table 7. Large-scale task scheduling result dataset.

Metric	ACO	PSO	WOA	HOA	RBMO	ROA	DSSA	WMA	IWMA
Best	0.4944	0.4695	0.4798	0.4772	0.4728	0.4794	0.4633	0.4540	0.3844
Mean	0.5124	0.4942	0.4878	0.4887	0.4728	0.5060	0.4862	0.4555	0.3844
Worst	0.5008	0.4822	0.4878	0.4831	0.4728	0.4936	0.4778	0.4550	0.3844
Std	0.0035	0.00235	3.3731 × 10−16	0.0032	0	0.0063	0.0026	0.0002	5.62183 × 10−17
Running time	62.45 s	73.32 s	69.98 s	67.19 s	71.72 s	73.65 s	65.16 s	78.43 s	75.27 s

once again shows the effectiveness of the IWMA in executing large-scale task scheduling. Even in the face of a large number of large-scale task scheduling scenarios, it could stably and quickly search for the optimal scheduling strategy. When dealing with large-scale scheduling problems, in the process of finding the optimal scheduling strategy, the optimization time performance of IWMA does have certain deficiencies.

6. Conclusions and Prospects

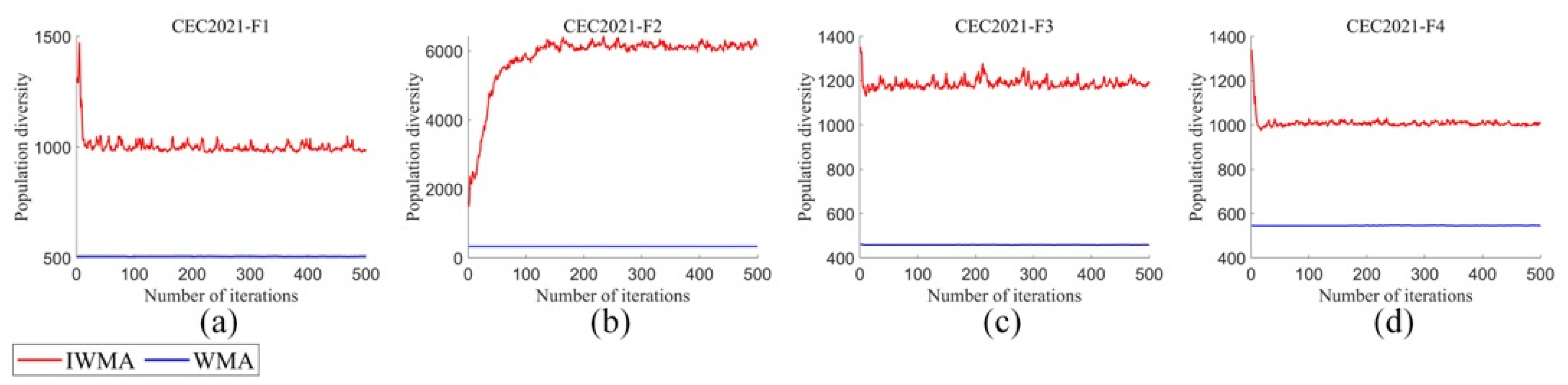
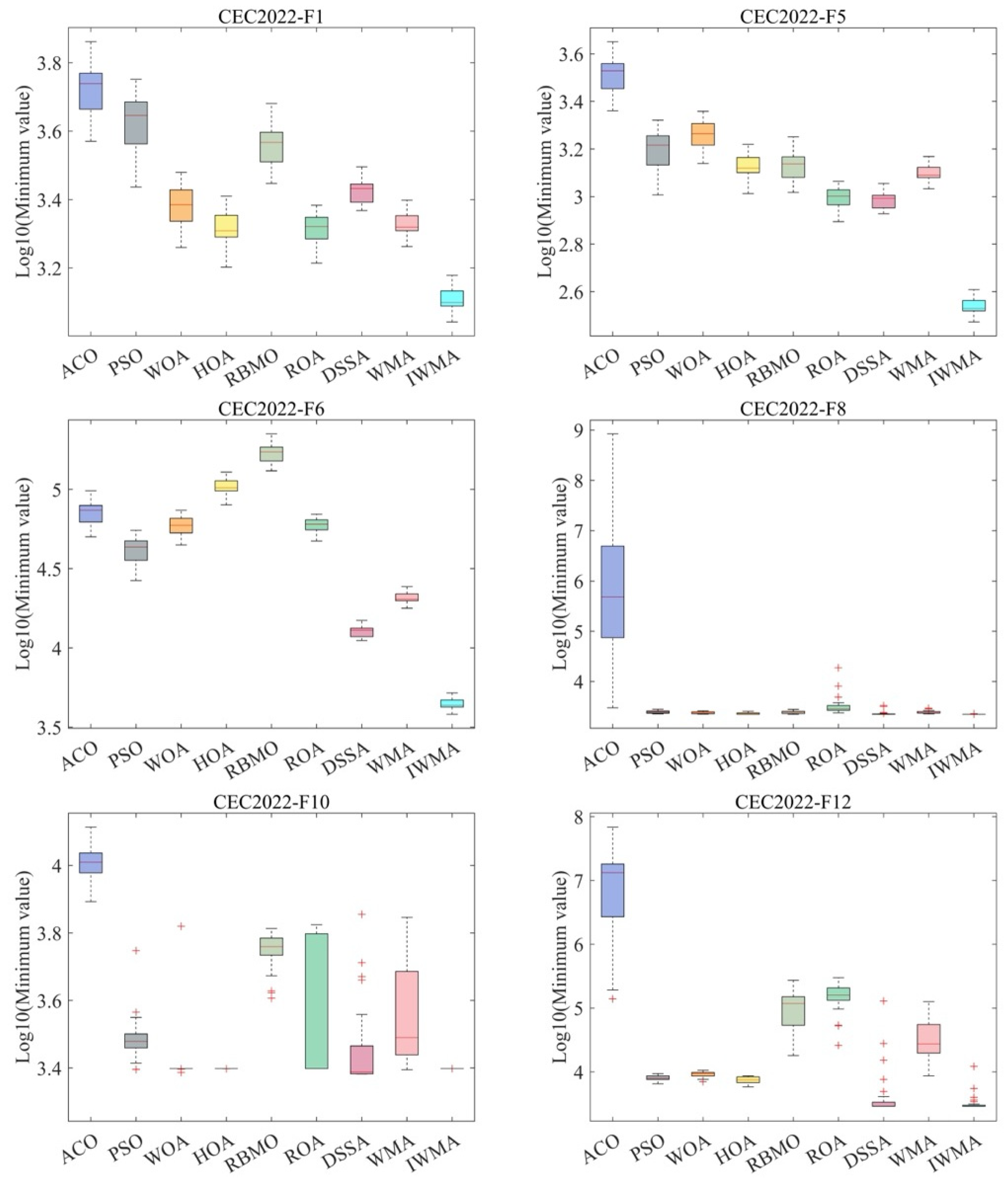
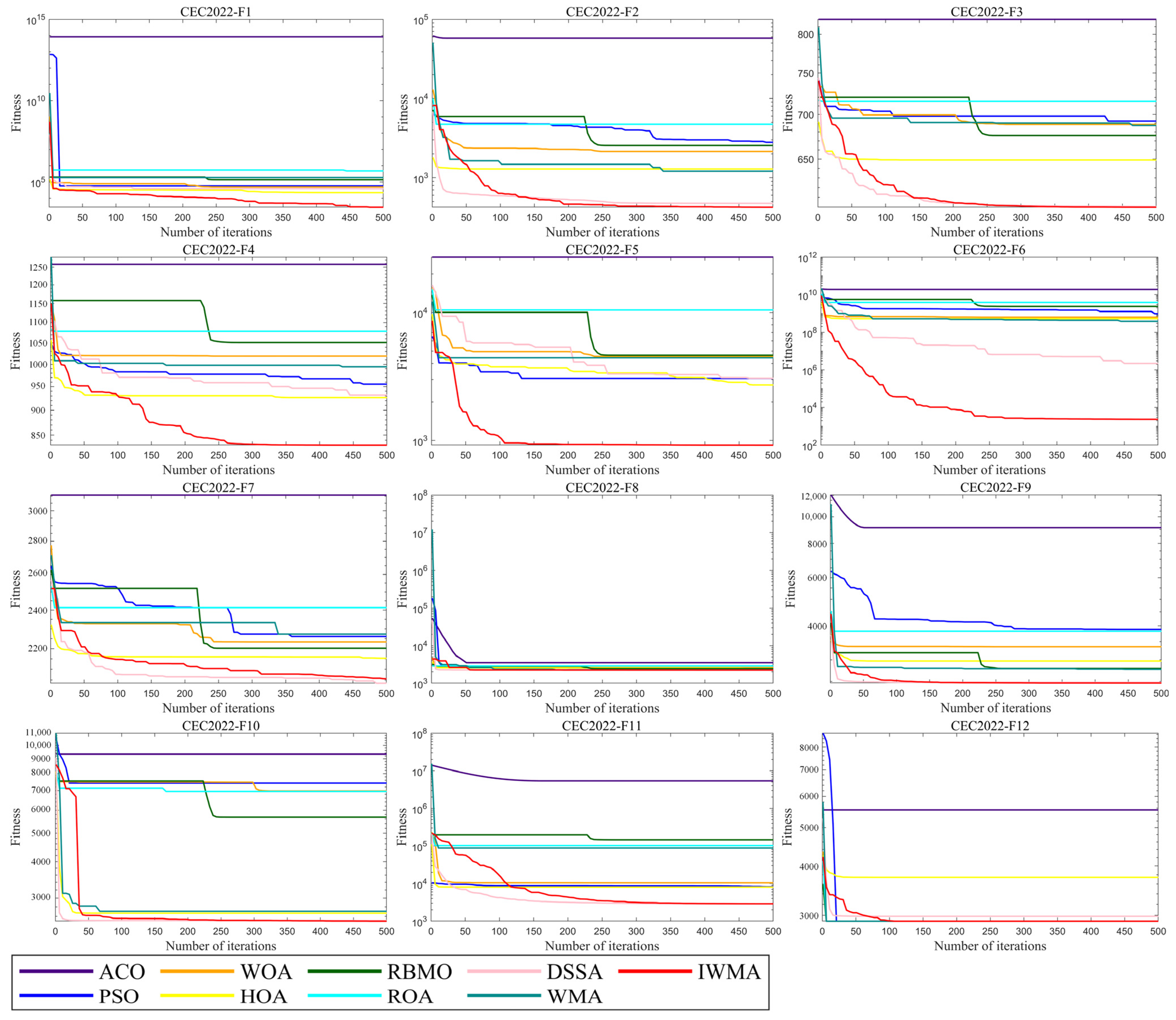
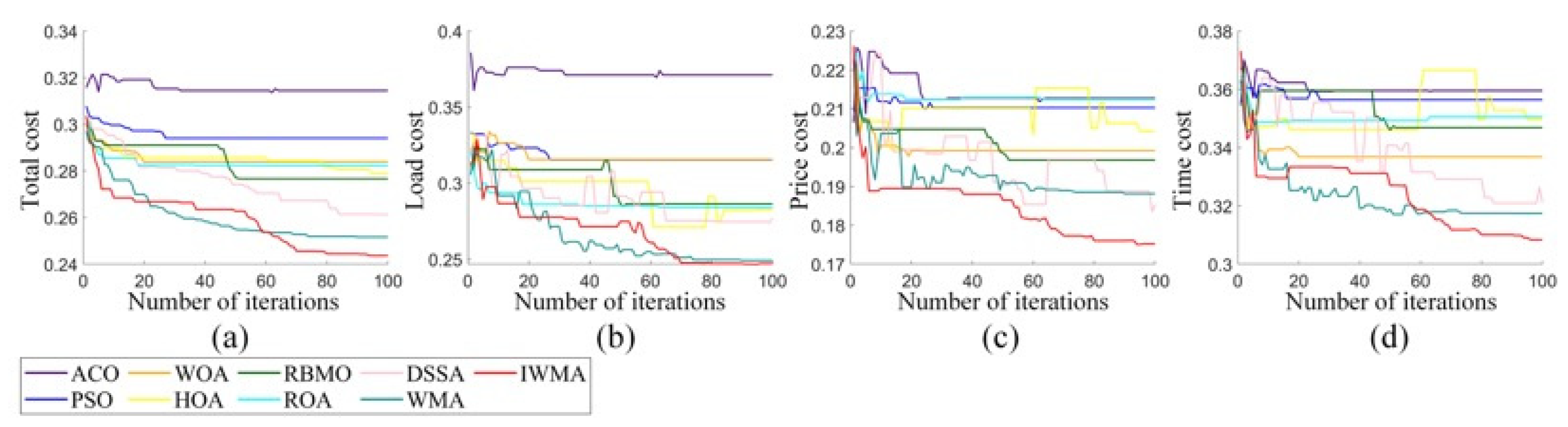
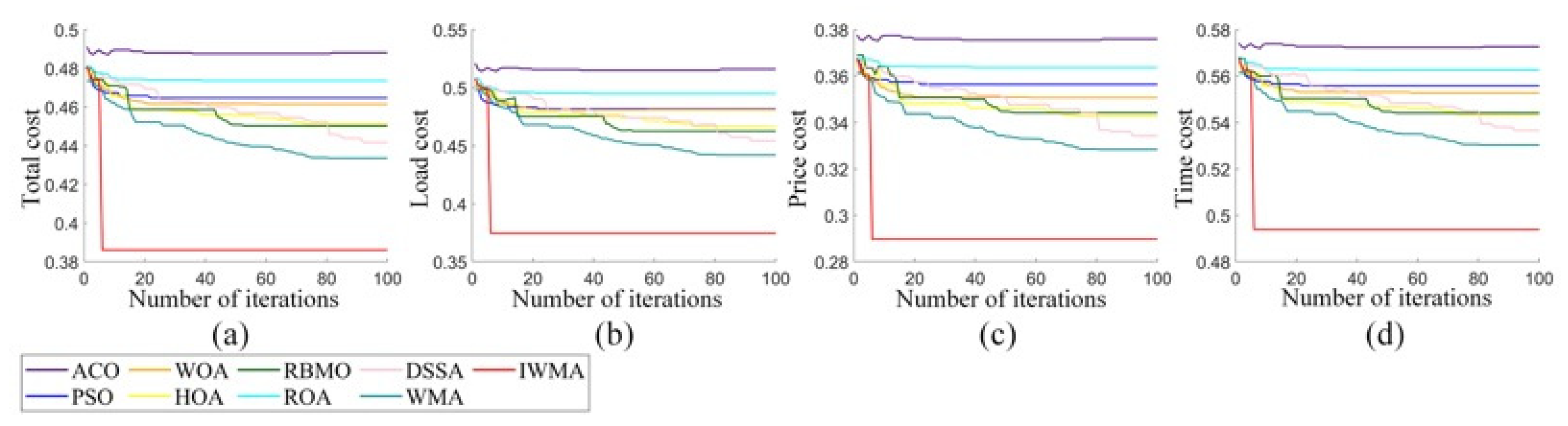
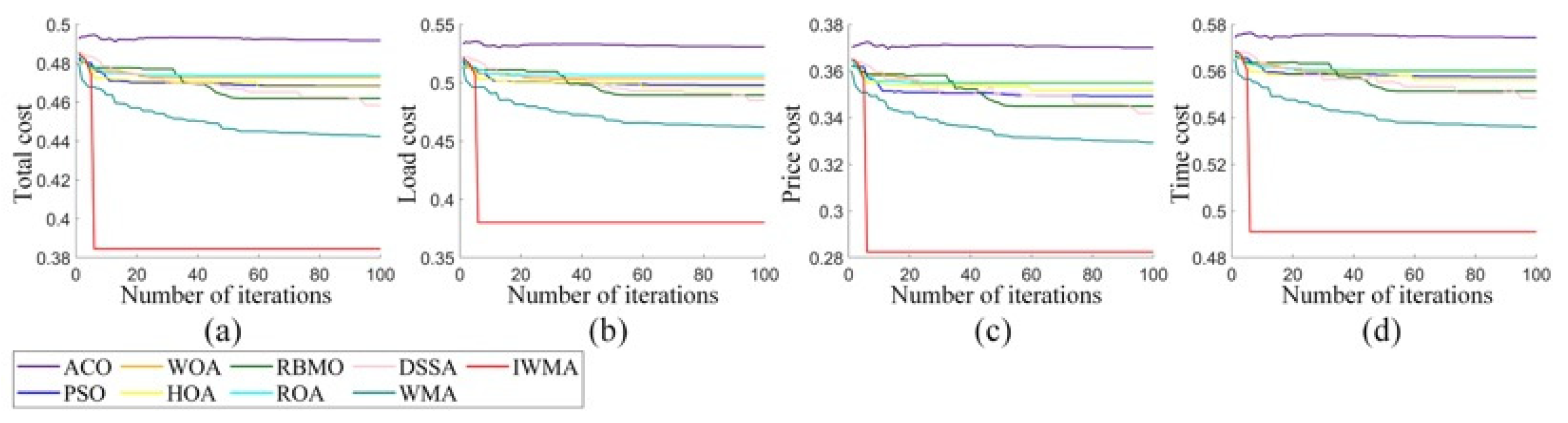
Aiming at the shortcomings of solving global optimization and scheduling problems, this paper proposed the IWMA. Firstly, by introducing the mixed disturbance initialization strategy, the diversity of the initial population as improved, thus improving the accuracy of the final optimal solution. Secondly, the balanced learning method and the opposition learning strategy were combined into the WMA, which effectively improved the development ability in the iterative process and further improved the population diversity in later iterations. The IWMA could effectively avoid falling into the global optimization trap. Through the verification of the CEC2021 test function, it was proven that these strategies significantly improved the diversity and development ability of IWMA. To comprehensively evaluate the global optimization ability of the IWMA, this paper applied it to the CEC2022 test problem together with several classical algorithms, new algorithms, and mutation algorithms. The results showed that the IWMA has an excellent optimization performance and strong global optimization ability. In addition, the IWMA was applied to the task scheduling problem of cloud computing to further verify the performance of the IWMA in dealing with complex scheduling problems. The results showed that the IWMA is an efficient and robust algorithm.

In future research work, we are committed to constructing solutions to complex scheduling problems that are more suitable for practical applications. On the one hand, given that the IWMA is currently mainly applied to single-objective task scheduling problems, future work will focus on the improvement and expansion of the IWMA to enable it to handle multi-objective problems more effectively. On the other hand, considering that when the IWMA is applied to cloud task scheduling, as the number of tasks increases, the optimization time of IWMA also increases. Therefore, future research will also focus on improving the running time of the IWMA to enhance its efficiency and applicability in large-scale task scheduling.