An Improved Dark Channel Prior Method for Video Defogging and Its FPGA Implementation

Abstract

In fog, rain, snow, haze, and other complex environments, environmental objects photographed by imaging equipment are prone to image blurring, contrast degradation, and other problems. The decline in image quality fails to satisfy the requirements of application scenarios such as video surveillance, satellite reconnaissance, and target tracking. Aiming at the shortcomings of the traditional dark channel prior algorithm in video defogging, this paper proposes a method to improve the guided filtering algorithm to refine the transmittance image and reduce the halo effect in the traditional algorithm. Meanwhile, a gamma correction method is proposed to recover the defogged image and enhance the image details in a low-light environment. The parallel symmetric pipeline design of the FPGA is used to improve the system’s overall stability. The improved dark channel prior algorithm is realized through the hardware–software co-design of ARM and the FPGA. Experiments show that this algorithm improves the Underwater Image Quality Measure (UIQM), Average Gradient (AG), and Information Entropy (IE) of the image, while the system is capable of stably processing video images with a resolution of 1280 × 720 @ 60 fps. By numerically analyzing the power consumption and resource usage at the board level, the power consumption on the FPGA is only 2.242 W, which puts the hardware circuit design in the category of low power consumption.

1. Introduction

Computer vision has been more widely used with the addition of artificial intelligence. However, in environments such as fog, haze, smoke, snow, etc., the scattering effect of fine particles in the air will contribute to a notable reduction in the quality of the acquired images, resulting in degradation phenomena such as image blurring, color distortion, etc. [1]. The serious deterioration in image quality will lead to its inability to meet automatic driving, satellite reconnaissance, target tracking, and other application scenarios. Defogging can significantly improve image visibility and correct the color deviation produced by the refraction of suspended particles. Image defogging algorithms are mainly classified into three categories [2,3]: physical model-based image restoration [4,5,6,7,8], non-physical model-based image enhancement [9,10,11], and deep learning model-based [12,13,14]. Currently, the dark channel prior (DCP) proposed by Kaiming He et al. [4] is still the dominant defogging algorithm, and the traditional algorithms using the dark channel prior are less effective on hardware. Therefore, the process of dark channel image, transmittance image, and image restoration needs to be continuously optimized, including the use of mean filtering, soft keying strategy, Gaussian filtering [15,16], guided filtering [10,12,17], and bilateral filtering [18]. In addition, in order to realize the real-time video image defogging algorithm, the traditional graphics processor (GPU) finds it difficult to meet the demand in real time, and the GPU has problems such as a “power wall” and “memory wall”. More and more researchers use the FPGA’s high parallelism, low power consumption, and other characteristics to realize the defogging of video images, as it contains rich logic resources, independent IP cores, and powerful programmability [5,6,7,9,11].

Optimizing video image defogging algorithms is gaining more attention as the requirements for edge deployment performance and defogging quality increase. Zhang et al. [5] used a low-pass filter to smooth the transmitted image and further reduce the computational complexity of the dark-channel prior algorithms. Li et al. [6] realized the defogging of the video image from the perspective of the traditional dark channel. Liu et al. [7], from the perspective of the sky region segmentation, reduced sky color distortion and estimated atmospheric light values and transmittance more accurately. Young et al. [9] implemented real-time image defogging by deploying a Contrast-Limited Adaptive Histogram Equalization Algorithm (CLAHE) on FPGAs. Munaf et al. [11] implemented image enhancement under low light intensity using the Retinex algorithm and Verilog HDL language implementation deployed on Xilinx FPGAs. Lv et al. [12] enhanced the speed of hardware defogging by differential guided filtering and parallel grayscale linear stretch fusion defogging hardware architecture. Teng et al. [13] optimized the convolutional neural network structure from the point of view of a lightweight neural network and achieved 105 frames per second of video processing.

Given the need for video image defogging to be deployed at the edge, we conducted experiments to improve the dark channel prior algorithm video defogging. The contributions of this paper are as follows:

(1)

The refinement of transmittance images by an improved guided filtering algorithm to reduce the halo effect;

(2)

It proposes the gamma correction method to realize image enhancement during the image restoration process;

(3)

Under the premise of improving the quality of defogging, the system can stably realize the video processing speed of 1280 × 720 @ 60 fps.

This paper is organized as follows: Section 2 presents the theory of the dark channel prior algorithm, the guided filtering algorithm, and gamma correction. Section 3 describes the overall flow of the improved dark-channel prior algorithm and analyzes in detail the dark-channel image module, the transmittance image module, and the image restoration module. Section 4 describes the analysis of the ZYNQ-based experimental platform. Section 5 describes the results of this experiment, which are analyzed in detail in terms of image quality, hardware power consumption, and resource usage. Section 6 outlines the summary of this experiment.

2. Principle of Image Defogging Algorithm

2.1. Dark Channel Prior Theory

The atmospheric scattering model [2,3,14] influenced Kaiming He et al. to propose the dark channel prior theory. Through the observation of fog-free pictures, it is found that for inputting an arbitrary pair of images, in the absence of fog, the pixel values of at least one of the three color channels of R, G, and B are low, and its dark channel value tends to zero, which can be formulated as:

$$J^{dark}\left(x\right)=\underset{y\in \Omega \left(x\right)}{min}(\underset{c\in \{r,g,b\}}{min}{J}^c\left(y\right))\approx 0$$

(1)

where $J^c\left(y\right)$ represents the value of the pixel on color channel C (red, green, and blue), $\Omega \left(x\right)$ represents a square field window centered on x pixel with a filter of size $n\times n$, and $J^{dark}\left(x\right)$ represents the dark channel image.

The atmospheric scattering model shows that it realizes the energy attenuation and path-radiation effects of light propagating in the atmosphere through the physical mechanisms of Rayleigh scattering and Mie scattering, as shown in Figure 1. Its mathematical expression is:

$$I\left(x\right)=J\left(x\right)t\left(x\right)+A(1-t(x\left)\right)$$

(2)

where $I\left(x\right)$ represents a foggy image captured by the imaging device; $J\left(x\right)$ represents a fog-free image to be recovered; $t\left(x\right)$ represents the image transmittance, which reflects the strength of the light reaching the imaging device through the particulate medium; and A represents the atmospheric light value. $J\left(x\right)t\left(x\right)$ represents the amount of environmental objects that enter the imaging device after atmospheric scattering attenuation, and $A(1-t(x\left)\right)$ represents the amount of atmospheric light that enters the imaging device after scattering through the particulate medium.

To find the atmospheric transmittance $\tilde{t}\left(x\right)$, it is necessary to refine the image with a split-window refinement, and then two minimum filtering operations of Equation (2) can be obtained:

$$\underset{y\in \Omega \left(x\right)}{min}\left(\underset{c\in (r,g,b)}{min}{\displaystyle \frac{I^c\left(y\right)}{A}}\right)=\tilde{t}\left(x\right)\underset{y\in \Omega \left(x\right)}{min}\left(\underset{c\in (r,g,b)}{min}{\displaystyle \frac{J^c\left(y\right)}{A}}\right)+1-\tilde{t}\left(x\right)$$

(3)

where $\tilde{t}\left(x\right)$ is the transmittance in the local region $\Omega \left(x\right)$; according to the dark channel prior principle, it is known that the dark channel value of the fog-free image tends to zero, and the transmittance can be estimated by bringing together Equations (1)–(3) as:

$$\tilde{t}\left(x\right)=1-\underset{y\notin \Omega \left(x\right)}{min}\left(\underset{c\in \left\{r,g,b\right\}}{min}{\displaystyle \frac{I^c\left(y\right)}{A}}\right)$$

(4)

In the atmospheric environment, the influence of a particulate medium on object imaging exists both day and night. Therefore, a foggy influence factor $w(0<w<1)$ is introduced into Equation (4). Usually, $w=0.95$, to preserve a moderate level of haze, making the image more realistic and reliable after defogging. The transmittance after adding the fog influence factor is calculated as:

$$\tilde{t}\left(x\right)=1-w\underset{y\notin \Omega \left(x\right)}{min}\left(\underset{c\in \left\{r,g,b\right\}}{min}{\displaystyle \frac{I^c\left(y\right)}{A}}\right)$$

(5)

When the transmittance $\tilde{t}\left(x\right)$ tends to zero, the value of $J\left(x\right)$ is large, resulting in an overall white field situation in the image. To avoid this situation, a lower threshold value of $t_0=0.1$ is usually set for $\tilde{t}\left(x\right)$, and the expression of the recovered fog-free image is:

$$J\left(x\right)={\displaystyle \frac{I\left(x\right)-A}{max(\tilde{t}\left(x\right),t_0)}}+A$$

(6)

2.2. Guided Filtering Theory

In a two-dimensional plane, the guided filter [10,12,16,17,19] has a local linear relationship between the guide image and the output image, which is able to preserve the edge information, and belongs to an efficient and information-extracting filtering method, which is defined as:

$$q_i=a_k{I}_i+b_k,\forall i\in w_k$$

(7)

where q represents the value of the output image pixel; a and b represent the fixed coefficients when the center of the current window w is located at k; I represents the value of the input guide image pixel; and i and k represent the pixel positions. In order to determine the linear coefficients, the difference between the minimization and the filter inputs, the minimization cost function is introduced in the window denoted as:

$$E(a_k,b_k)=\sum _{i\in w_k}({(a_k{I}_i+b_k-p_i)}^2+\epsilon a_k^2)$$

(8)

where $\epsilon$ represents the regularization factor that prevents the parameter $a_k$ from being too large, and $p_i$ represents the pixel value at position i in the target image; in this paper, p represents the coarse transmittance image to be filtered, and I represents the gray scale image of the original image as the guide image, with weights derived from the guide image and applied to the image to be filtered, p. The solution in Equation (8) using linear regression is:

$$a_k={\displaystyle \frac{\frac{1}{\left|w\right|}\sum _{i\in w_k}{I}_i{p}_i-{\mu }_k{\overline{p}}_k}{{\sigma }_k^2+\epsilon }}$$

(9)

$$b_k={\overline{p}}_k-a_k{\mu }_k$$

(10)

where ${\mu }_k$ and ${\sigma }_k^2$ represent the mean and variance in the bootstrap image window, respectively; $\left|w\right|$ represents the quantity of pixels in window I; and ${\overline{p}}_k$ represents the mean within the input image p window. The linear model is applied to all the local windows in the whole image and averaged:

$$q_i={\displaystyle \frac{1}{\left|w\right|}}\sum _{k,i\in w_k}(a_k{I}_i+b_k)={\overline{a}}_i{I}_i+{\overline{b}}_i$$

(11)

where ${\overline{a}}_i={\displaystyle \frac{1}{\left|w\right|}}{\sum }_{k\in w_i}{a}_k$ and ${\overline{b}}_i={\displaystyle \frac{1}{\left|w\right|}}{\sum }_{k\in w_i}{b}_k$ are the average values of pixel point i over multiple windows; it follows that ${\overline{a}}_i$ and ${\overline{b}}_i$ are spatially varying.

2.3. Gamma Correction

In order to counteract the nonlinear nature of the display device, gamma correction [3] is a common means of enhancing image contrast, as shown in Figure 2. Performing one gamma transformation, its mapping relation can be expressed as:

$$G\left(I\right)=round(255\times {\left({\displaystyle \frac{I}{255}}\right)}^{\gamma })$$

(12)

where I is the original image; $G\left(I\right)$ is the output image after gamma transformation; and $\gamma$ is the gamma correction coefficient; when $0<\gamma <1$ , the details of the dark areas of the picture are enhanced, and the image as a whole becomes brighter; when $\gamma =1$, there is no change; when $\gamma >1$ , the details of the highlighted areas of the image are enhanced, and the image as a whole becomes darker, and $round\left(\right)$ is a rounding operation. Gamma correction with $\gamma =1/1.3$ is used in this application to improve the contrast of the image after reducing the fog.

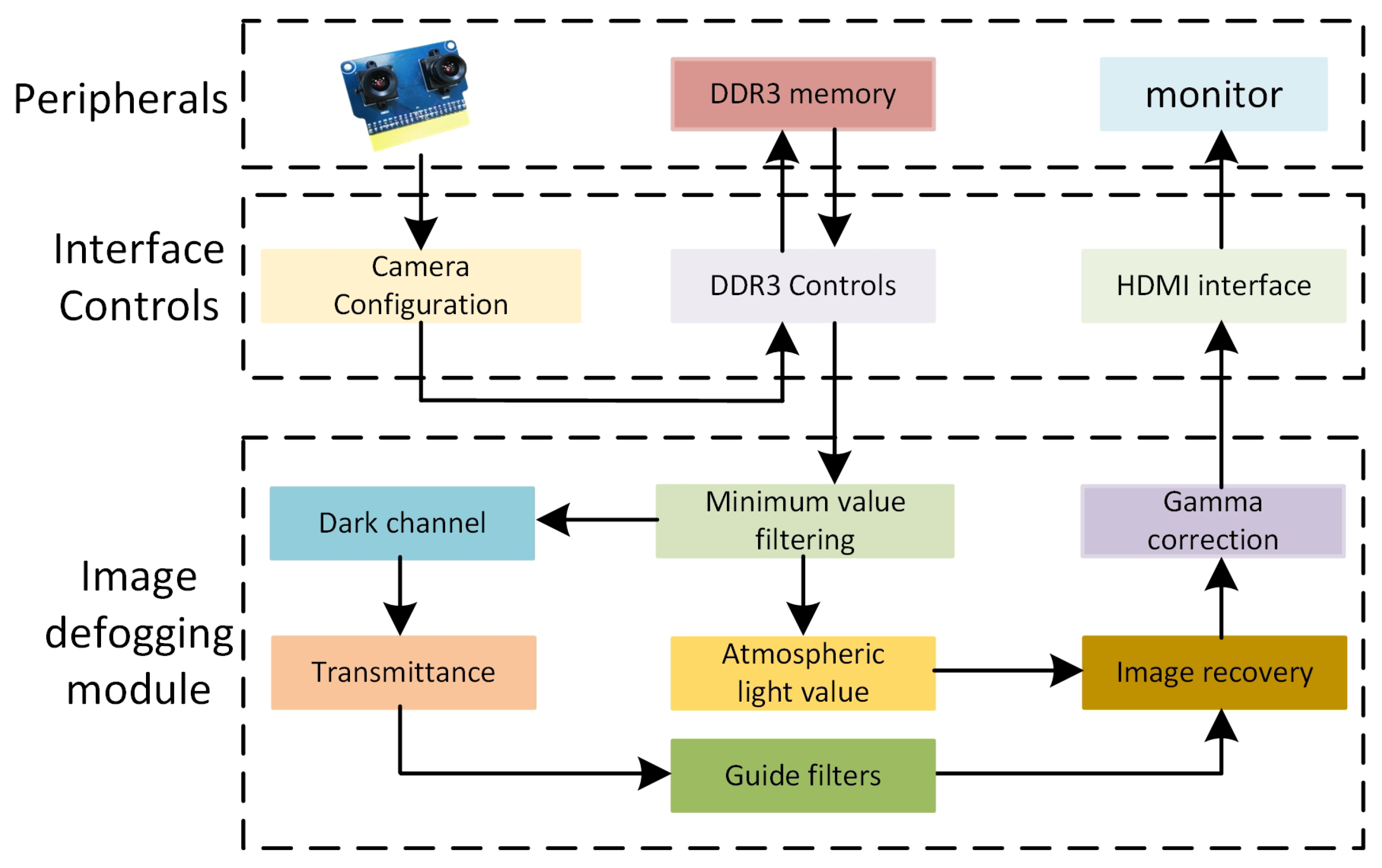
3. Systematic Implementation of Dark Channel Prior Algorithms

Through an in-depth analysis of the traditional dark channel prior defogging algorithm, this paper adopts a guided filtering algorithm for transmittance calculation while using gamma correction to optimize the image effect after defogging; the overall algorithm design structure is shown in Figure 3. The process mainly contains three parts: a dark channel calculation module, atmospheric light value and transmittance module, and image restoration module. Firstly, the minimum value of the RGB channel is calculated for the original image in the dark channel calculation module, and then the minimum value filtering is performed to generate the dark channel image $J^{dark}$. In the atmospheric light value and transmittance calculation module, the maximum value in the RGB corresponding to this pixel is found from the pixel with the maximum dark channel value as the atmospheric light value A. According to Equations (4) and (5), and after repeated comparisons, this paper chooses the fog factor $w=0.9$ as the best, and the refined transmittance $\tilde{t}\left(x\right)$ is obtained by taking the coarse transmittance as the input image and then performing a guided filtering. The guide image is obtained by using the brightness weighted gray scale of the original image: $I=0.299R+0.587G+0.114B$. In the image restoration module, the A and $\tilde{t}\left(x\right)$ calculated in the previous module are substituted into Equation (6) to obtain the restored image. Then, the final defogged image is obtained using gamma correction.

3.1. Dark Channel Image Research

The concentration of haze in the environment shows a linear relationship with the dark channel value; the denser the haze, the larger the value, and conversely, the less haze, the smaller the value. The dark channel images are mainly acquired by minimum value filtering [3,5], Gaussian filtering [3,15], mean value filtering, and other methods. This paper uses the minimum value filtering algorithm [20]; the algorithm acts on the RGB three-channel generated minimum value map of foggy images, and then, the RGB minimum value map is minimally filtered to obtain the dark channel image. This filtering traverses the entire image through a sliding window and replaces the center pixel’s value with the pixel’s minimum value inside the window. In order to save logic resources such as BRAM and DSP, and at the same time enhance the detail retention of the image edges, this paper uses a 3 × 3 filtering window and does not use the traditional 5 × 5 filtering window. Furthermore, to form the 3 × 3 window, it is necessary to buffer two lines of the input image [20]. This is accomplished using the two FIFOs as shown in Figure 4. When working, the first line of data of the fog image is written to FIFO2, and the first line of data is output to FIFO1. The second line of data is written to FIFO2, and when all the data are written to FIFO2, FIFO1 reads out the first line of data, FIFO2 reads out the second line of data, and the third line directly outputs. By utilizing separability, we use a vertical minimum operation on the data output from the delay module and then a comparator matrix on the calculation result to obtain the minimum for that module. The 3 × 3 minimum filtering module we have designed achieves a reduction in the traditional eight minimum operations to four minimum operations while improving the computational efficiency of the module. At each clock signal, the minimum value of the RGB channels and the minimum value after filtering are calculated repeatedly, and finally, the pixels at the frame rate are reconstructed to obtain the final dark channel image.

3.2. Transmittance Image Research

A transmittance image is the proportion of light intensity that is not scattered and absorbed during propagation of light through a medium of suspended particles in the environment, reflecting how much of the image contains a concentration of fog at that pixel point. For the calculation of transmittance, Zhang et al. [5] used a low-pass filter to optimize the transmittance, which may not be good for image restoration due to the inherent shortcomings of the low-pass filter. Rahmawati et al. [21] proposed Laplace filtering to enhance the estimation process of the transmittance image, which makes the edge details of the low-brightness channel image more visible. Xue et al. [22] used a multi-scale approach to optimize and integrate the transmittance images to improve the system robustness from the perspective of image enhancement algorithms. Liu et al. [2] proposed a dark channel-based adaptive defogging algorithm to enhance the estimation efficiency of background light and transmittance according to the optical characteristics of the underwater imaging device. Using a soft keying mechanism in the traditional dark channel principle can better achieve the transmittance optimization, but the overall implementation of the algorithm has problems such as large arithmetic volume and high complexity, and the implementation efficiency is difficult to ensure. Instead, this paper adopts the guided filtering algorithm to refine the transmittance and thus eliminate the block effect of the image and designs a 3 × 3 guided filter to refine the detail retention, as shown in Figure 5. In the implementation process, the data stream and algorithm logic are efficiently processed by the computation unit, and the fixed-point operation and IP core are combined to achieve efficient calculation, which is more suitable for hardware realization. First, in the FIFO row buffer, each column of the coarse transmittance image pixel data matrix P is added and summed, and then the square value of each pixel is obtained and summed. The formula is:

$$\begin{array}{cc}\hfill A_0& =P_{00}+P_{10}+P_{20}\hfill \\ \hfill sum1\_A& =A_0+A_1+A_2\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill B_0& =P_{00}^2+P_{10}^2+P_{10}^2\hfill \\ \hfill sum2\_B& =B_0+B_1+B_2\hfill \end{array}$$

(14)

where $P_{nn}$ represents the pixel value within the current filter window; $P_{nn}^2$ represents the square of each pixel value within the current window; $A_n$ represents the column summation of the pixel values; $B_n$ represents the square summation of the pixel values; and $sum1\_A$ and $sum2\_B$ represent the summation of $A_n$ and $B_n$, respectively. The approximation of fixed-point multiplication is then performed for $sum1\_A$ and $sum2\_B$, and a and a are solved:

$$\begin{array}{cc}\hfill P_m& =(sum1\_A\times 114)\gg 10\hfill \\ \hfill P{P}_m& =(sum2\_B\times 114)\gg 10\hfill \\ \hfill a& ={\displaystyle \frac{(P{P}_m-P_m·P_m)\times 1024}{(P{P}_m-P_m·P_m)+E}}\hfill \\ \hfill b& =(1024-a)·P_m\hfill \end{array}$$

(15)

where $(sum1\_A\ast 114)>>10$ and $(sum2\_B\ast 114)>>10$ are realized by shift register and multiplication to approximate equivalent division $114/1024\approx 1/9$; $P_m$ represents the mean value of pixels in the current filter window; $P{P}_m$ represents the mean value of pixels squared in the current filter window; and a and b are the computational parameters in the current filter window. E is the regularization term in the guide filter formula. In this paper, the value of E is 100 to prevent division by zero and improve stability. Then, repeat the steps of Equations (13) and (15) for the matrices traversed by parameters a and b. Each column is summed, and then the fixed-point multiplication calculation is performed to find the averaged $am$ and $bm$. Finally, $am$ is multiplied by I and summed with $bm$. The final transmittance image data $\tilde{t}$ equation is:

$$\tilde{t}=am\ast I+bm$$

(16)

where P is the input image from the coarse transmittance image, and I is the guide image data from the gray scale image of the original image. The latency of the filters requires delaying the image I by three rows (one row for calculating $J^{dark}$, one row for calculating a and b, and one row for calculating $am$ and $bm$). The process maintains the bit width consistency between the gray scale image and the coarse transmittance image while utilizing separability and stream processing, which means reducing the number of calculations by first calculating the data in the vertical direction and then calculating the data in the horizontal direction. In addition, floating-point operations are converted to fixed-point operations to avoid state overflow and retain sufficient data precision. With the arrival of each clock signal, the filter continuously performs filtering operations and finally reconstructs the data of that pixel to obtain a refined transmittance image.

3.3. Image Restoration Research

Image restoration is the computation of fog-free images using estimated atmospheric light values and transmittance maps to recover the true color and contrast of the scene. In the image restoration process, the loss of details in the low-brightness regions of the image is minimized, and the over-enhancement of the image in the high-brightness regions is avoided. Yu et al. [23] used an adaptive histogram equalization algorithm to achieve contrast enhancement of output images from underwater imaging environments. Zhang et al. [16] used contrast stretching means in the reduction process in order to enhance the overall brightness of the image. What is more, this paper proposes a gamma correction approach to make the recovered image closer to the natural visualization of the human eye. Gamma correction is a nonlinear exponential mapping, acting on grayscale images. Moreover, this paper utilizes the look-up table (LUT) method to realize the Gamma transform, where the $\gamma =1/1.3$ expression is:

$$G\left(I\right)=255\times {\left({\displaystyle \frac{I}{255}}\right)}^{1/1.3}$$

(17)

Then, each of the three RGB color channels are Gamma corrected to obtain new pixel data, as shown in Figure 6. By individually modularizing the correction for each color channel, the details of the low-brightness part are enhanced, and the overall contrast of the image is enhanced. In addition, a data delay register module is designed to ensure the accuracy of the timing logic and prevent image distortion.

4. Analysis of ZYNQ-Based Experimental Platform

4.1. Experimental Platforms

The experimental platform of this paper is I5-12600KF+RTX4060 (Windows 11 system), the MATLAB (version R2023a) software platform, and the Vivado and Vitis (version 2023.2) hardware platforms, and the development board model is ZYNQ-7020 series of Xilinx company. The hardware platform includes a video capture unit, video processing unit, video caching unit, and video display unit; the system’s real-time defogging system block diagram and the experimental development environment are shown in Figure 7 and Figure 8, respectively. Figure 8 in the left display shows the defogged image, and the right shows the foggy image. Video acquisition unit: real-time data acquisition is achieved through the OV5640 camera, capable of realizing 1280 × 720 @ 60fps video images. Video processing unit: the optimized design of the dark channel prior algorithm is encapsulated in the form of a RAM IP core, forming a complete IP Block Design module. Video cache unit: DDR3 is utilized for frame caching for each frame of captured data and processed data. Video display unit: high-speed image data transmission is through the configuration of VDMA IP cores and conversion of the video data in DDR3 to an HDMI display.

4.2. ZYNQ System Architecture

The ZYNQ platform of this experiment uses the chip model XC7Z020CLG400 chip [7,24,25,26], which integrates a dual-core ARM Cortex-A9 processing system (PS) and FPGA programmable logic (PL) based on the Artix-7 architecture. The PS completes the acquiring and storing of images, while the PL realizes the image processing and display. They interconnect the hardware and software through the high-speed AXI bus to realize the high efficiency of the video image defogging system. The core experimental platform is shown in Figure 9. The clock frequency of the development board is usually 100 MHZ, and the clock frequency of this paper’s design is 75 MHZ; the on-chip memory is 256 KB; there are 85,000 logic units; the number of I/O pins is 200; the maximum operating temperature is 100 degrees Celsius; and the external interfaces support USB2.0, DDR3, I²C, UART, and so on.

5. Experimental Results and Data Analysis

5.1. Defogging Effect Analysis

To analyze the defogging influence of this paper’s algorithm, the defogging effects of References [4,27,28] were compared, as shown in Figure 10, with five scene pictures labeled (1), (2), (3), (4), and (5) from top to bottom, respectively. As illustrated in the figure, picture (1) processed by the algorithm of Reference [27] has a more obvious halo effect, the articulation between the distant objects and the near objects in the picture is not natural, and the effect is worse in the low-light environment in picture (5). The algorithm of Reference [4] has an obvious blocky effect in picture (4), and there is a color shift for the distant objects in picture (2). For the algorithm of Reference [28], processed images are darker overall, and there are shortcomings such as sky color aberration in picture (2) and picture (3). In contrast, the defogged pictures processed by the algorithm in this paper have no obvious halo effect and color distortion, the excess between the near-view objects and the far-view objects is more natural, and the picture clarity is higher.

This paper objectively analyzes the defogging effect using four indexes: UIQM, AG, IE, and running time. The defogged images from the proposed algorithm are compared numerically with the algorithms from References [4,27,28]. UIQM is a weighted calculation of the underwater image color measurement (UICM), underwater image sharpness measurement (UISM), and underwater image contrast measurement (UIConM). The higher the value of UIQM, the better the image’s visual quality. AG is an edge detection method based on the Sobel operator, which globally averages the gradient amplitude in the horizontal and vertical directions of the image. The larger the value of AG, the clearer the image edge and the richer the details. IE is a statistical measure of the distribution of pixel values in an image; the larger the IE, the more information the picture expresses. In this paper, the IE is expressed by Shannon entropy. The running time represents the simulation time for each frame in the PC software side and FPGA hardware side. As can be seen in

Table 1. Objective quality analysis of different defogging methods.

Imagery	Algorithm	IE/bit	UIQM	AG	Running Time (PC)/(FPGA)/s
(1)	Original	7.2668	3.8923	21.5147	-/-
	He [4]	7.3827	6.8962	34.0108	4.8684/-
	Ehsan [27]	7.0880	6.9383	33.2866	7.7856/-
	Zhu [28]	7.5437	6.8943	31.9447	2.0293/-
	Proposed	7.5463	7.3546	42.2765	3.1853/0.0138
(2)	Original	7.4554	3.0642	12.6117	-/-
	He [4]	6.9130	6.4483	14.4420	4.3005/-
	Ehsan [27]	6.7227	5.4782	15.8163	7.9553/-
	Zhu [28]	7.5427	5.3679	13.9631	1.8057/-
	Proposed	7.4560	6.5842	27.7230	2.9842/0.0138
(3)	Original	7.2492	4.2847	22.3559	-/-
	He [4]	7.3827	7.4891	36.6422	4.4382/-
	Ehsan [27]	7.2837	8.2204	38.3339	6.9987/-
	Zhu [28]	7.4317	7.7548	31.7208	1.7906/-
	Proposed	7.5903	8.0671	41.9183	3.0853/0.0138
(4)	Original	7.5295	4.7281	23.6353	-/-
	He [4]	6.9065	7.8931	29.8417	4.1062/-
	Ehsan [27]	6.8268	8.0142	30.8351	7.1346/-
	Zhu [28]	7.1068	7.0763	28.7505	2.3571/-
	Proposed	7.1428	7.7149	36.9836	3.0356/0.0138
(5)	Original	7.2107	3.3648	12.2805	-/-
	He [4]	7.0103	6.0671	18.9904	4.7693/-
	Ehsan [27]	6.7471	6.4837	21.4487	7.6148/-
	Zhu [28]	7.3504	5.3301	16.4952	1.9250/-
	Proposed	7.4335	6.6748	27.1644	3.0961/0.0138

, the AG value and IE of images (1)–(5) after processing by the algorithm of this paper are larger than those of the previous three algorithms, while the UIQM value of images (3) and (4) appears to be slightly lower than those of Reference [27], which may be affected by the gamma correction to change the contrast of the images. In addition, the overall running time of this algorithm is shorter and more efficient. On the whole, the algorithm in this paper is implemented better.

5.2. Power Consumption and Resource Utilization Analysis

Based on the ZYNQ-7020 series development board for video image defogging, its power consumption is shown in

Table 2. On-chip power consumption.

Types	Targets								Overall
Dynamic	Clocks	Signals	Logic	BRAM	DSP	MMCM	I/O	PS7
	0.088 W	0.103 W	0.093 W	0.007 W	0.009 W	0.106 W	0.133 W	1.543 W	2.082 W
	4%	5%	4%	1%	1%	5%	6%	74%	93%
Static	-								0.160 W
	-								7%

; according to the figure, it is observed that the dynamic power consumption accounts for 93% of the total power consumption, the value of 2.082 W, while the static power consumption accounts for 7% of the total power consumption, the value of 0.160 W, and the overall value of the power consumption is 2.242 W. Compared with the power consumption of Reference [29], which is 2.283 W, and the power consumption of Reference [30], which is 6.958 W, the power consumption in this paper is lower. The resource utilization of the FPGA platform is shown in

Table 3. Resource utilization.

Reference	Resource	Resource Consumption	Available Resources	Utilization/%
Proposed	LUT	8986	53,200	16.89
	FF	12,192	106,400	11.46
	BRAM	7	140	5.00
	DSP	6	220	2.73
[29]	LUT	7705	53,200	14.48
	FF	10,936	106,400	10.28
	BRAM	12	140	8.57
	DSP	8	220	3.64
[30]	LUT	23,496	53,200	45
	FF	39,875	106,400	39
	BRAM	160	220	76
	DSP	42	140	31

. Compared with Reference [29], this paper has less BRAM and DSP usage but more LUT and FF usage; this phenomenon may be attributed to the design of the guided filter and gamma correction module, which adds a large number of logic operation units. Compared with Reference [30], this paper has less primary resource usage in LUT, FF, BRAM, and DSP, which ensures the overall development and design of the system. Overall, the design of this system falls into the category of low energy consumption and high efficiency.

6. Conclusions

To meet the needs of video image defogging in edge devices, the dark channel prior algorithm is optimized, the guided filtering is improved to refine the transmittance image, and gamma correction is used to restore the fog-free image. The system adopts an FPGA parallel pipeline design, mainly applicable to foggy scenes, reduces computational complexity, and is more suitable for hardware transplantation. The experimental results of the FPGA-based video image defogging algorithm show that the image is improved in terms of UIQM, AG, and IE, and the algorithm can stably process 1280×720@60fps video images, with low power and resource consumption at the board level, which meets the requirements of engineering applications. Further detailed optimization for dense fog scenes will be carried out in the future.