Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling
Abstract
1. Introduction
2. Literature Review
2.1. Introduction to Integrated Process Planning and Scheduling (IPPS)
2.2. Classical Methods for IPPS
2.3. Metaheuristic Approaches for IPPS
2.4. Improvements in ACO for Minimizing Makespan
3. Problem Description
- Each part has several operations, and there is a total of I parts to be processed.
- Once a task started, it cannot be suspended or interrupted. This assumption streamlines the scheduling problem by eliminating intricate preemption logic and concentrating on uninterrupted job execution.
- Among all possible POs of a part, only one (the most suitable) is selected for processing.
- The precedence constraints among the selected processes must be strictly followed.
- Once a PO is allocated to a machine, it remains on that machine for the duration of its processing longevity. The reallocation of processes among machines is prohibited.
- All machines and parts are assumed to be accessible at time zero, and the scheduling procedure begins with all resources prepared for utilization.
- Upon completion of work using a machine, it is promptly conveyed to the subsequent machine in the process, with the transmission delay considered insignificant.
- The duration of every task is predetermined and established beforehand. The algorithm presumes that the processing time for each task is fixed and remains constant throughout execution.
- The cost associated with processing each task on a specific machine is constant and established in advance.
- Each machine is chosen according to a static time window that considers its availability and the processing duration of the preceding task.
3.1. Main Constraints
- , ,
- , ,
3.2. Objective
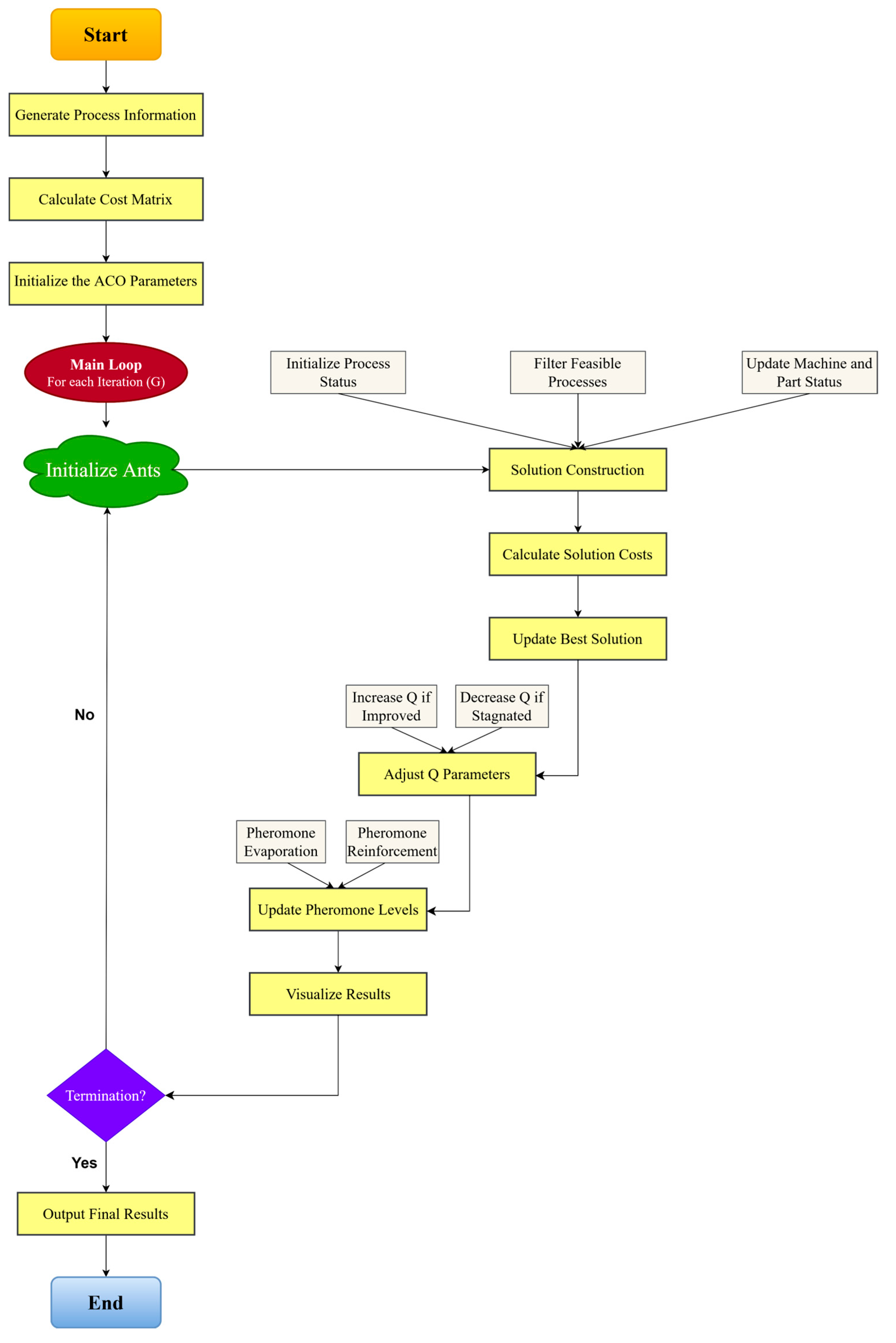
4. Proposed Symmetry-Aware Adaptive Ant Colony Optimization (SA-AACO) Algorithm
4.1. The Framework of Proposed SA-AACO
4.1.1. Heuristic Information
4.1.2. Time Window Mechanism for Machine Selection
4.1.3. Pheromone-Based Learning in SA-AACO Algorithm
- If an improvement is found, Q rises by Qstep_increase, although it is constrained by Qmax.
- 2.
- If no enhancement is observed after a certain number of iterations (monitored by no_improvement_count), Q is reduced by Qstep_decrease, with a lower limit of Qmin.
- is the pheromone magnitude at iteration t;
- is the rate at which Q increases when improvements are found;
- is the rate at which Q decreases when no improvements are found;
- and are the upper and lower bounds for Q, respectively.
- Pheromone Evaporation:
- 2
- Pheromone Reinforcement:
- Evaporation reduces the pheromone by a factor of (1 − ρ);
- Reinforcement increases the pheromone based on the inverse of the solution’s cost;
- τmin and τmax ensure that pheromone values remain bounded, preventing early convergence and maintaining search diversity.
4.1.4. Dynamic Idle Time Penalty Adjustment
4.1.5. Probability for Random Selection of Processes
5. Experiments and Discussions
5.1. Parameter Settings
5.2. Analysis of Experimental Results
5.3. Statistical Validation
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marri, H.B.; Gunasekaran, A.; Grieve, R.J. Computer-aided process planning: A state of art. Int. J. Adv. Manuf. Technol. 1998, 14, 261–268. [Google Scholar] [CrossRef]
- Xia, H.; Li, X.; Gao, L. A hybrid genetic algorithm with variable neighborhood search for dynamic integrated process planning and scheduling. Comput. Ind. Eng. 2016, 102, 99–112. [Google Scholar] [CrossRef]
- Trstenjak, M.; Cosic, P. Process planning in Industry 4.0 environment. Procedia Manuf. 2017, 11, 1744–1750. [Google Scholar] [CrossRef]
- Zhang, Z.; Benyoucef, L.; Sialat, A. Sustainable Integrated Process Planning and Scheduling (IPPS) in RMS: Past, Present and Future. IFAC-PapersOnLine 2022, 55, 791–797. [Google Scholar] [CrossRef]
- Chaudhry, I.A.; Usman, M. Integrated process planning and scheduling using genetic algorithms. Teh. Vjesn. Gaz. 2017, 24, 1401–1409. [Google Scholar]
- Erden, C.; Demir, H.I.; Canpolat, O. A modified integer and categorical PSO algorithm for solving integrated process planning, dynamic scheduling, and due date assignment problem. Sci. Iran. 2023, 30, 738–756. [Google Scholar] [CrossRef]
- Lin, L.; Hao, X.; Gen, M.; Ohno, K. A hybrid evolutionary algorithm for integrated production planning and scheduling problems. Comput. Ind. Eng. 2012, 42. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, C.; Shao, X. An effective hybrid honey bee mating optimization algorithm for integrated process planning and scheduling problems. Int. J. Adv. Manuf. Technol. 2015, 80, 1253–1264. [Google Scholar] [CrossRef]
- Demir, H.İ.; Phanden, R.; Kökçam, A.; Erkayman, B.; Erden, C. Hybrid evolutionary strategy and simulated annealing algorithms for integrated process planning, scheduling and due-date assignment problem. Acad. Platf.-J. Eng. Sci. 2021, 9, 86–91. [Google Scholar] [CrossRef]
- Zhang, L.; Wong, T.N. Solving integrated process planning and scheduling problem with constructive meta-heuristics. Inf. Sci. 2016, 340, 1–16. [Google Scholar] [CrossRef]
- Demir, H.İ.; Erden, C.; Kökçam, A.; Göksu, A. A tabu search and hybrid evolutionary strategies algorithms for the integrated process planning and scheduling with due-date agreement. J. Intell. Syst. Theory Appl. 2021, 4, 24–36. [Google Scholar] [CrossRef]
- Leung, C.W.; Wong, T.N.; Mak, K.-L.; Fung, R.Y.K. Integrated process planning and scheduling by an agent-based ant colony optimization. Comput. Ind. Eng. 2010, 59, 166–180. [Google Scholar] [CrossRef]
- Wang, J.; Fan, X.; Zhang, C.; Wan, S. A graph-based ant colony optimization approach for integrated process planning and scheduling. Chin. J. Chem. Eng. 2014, 22, 748–753. [Google Scholar] [CrossRef]
- Liu, X.; Ni, Z.; Qiu, X. Application of ant colony optimization algorithm in integrated process planning and scheduling. Int. J. Adv. Manuf. Technol. 2016, 84, 393–404. [Google Scholar] [CrossRef]
- Zhang, S.; Wong, T.N. Integrated process planning and scheduling: An enhanced ant colony optimization heuristic with parameter tuning. J. Intell. Manuf. 2018, 29, 585–601. [Google Scholar] [CrossRef]
- Huang, F.; Wang, H.; Gu, J.; Sun, Q. Ant colony optimization approach based on precedence constraint matrix for flexible process planning. J. Eng. Res. 2020, 8, 272–293. [Google Scholar] [CrossRef]
- Demir, H.I.; Erden, C. Dynamic integrated process planning, scheduling and due-date assignment using ant colony optimization. Comput. Ind. Eng. 2020, 149, 106799. [Google Scholar] [CrossRef]
- Nascimento, P.J.; Silva, C.; Antunes, C.H.; Moniz, S. Optimal decomposition approach for solving large nesting and scheduling problems of additive manufacturing systems. Eur. J. Oper. Res. 2024, 317, 92–110. [Google Scholar] [CrossRef]
- Zhang, S.; Campos, J.; Feldmann, C.; Walz, D.; Sandfort, F.; Mathea, M.; Tsay, C.; Misener, R. Optimizing over trained GNNs via symmetry breaking. Adv. Neural Inf. Process. Syst. 2023, 36, 44898–44924. [Google Scholar]
- Yuan, G.; Liu, X.; Zhu, C.; Wang, C.; Zhu, M.; Sun, Y. Multi-objective coupling optimization of electrical cable intelligent production line driven by digital twin. Robot. Comput. Integr. Manuf. 2024, 86, 102682. [Google Scholar] [CrossRef]
- Yuan, G.; Lv, F.; Shi, J.; Tian, G.; Feng, Y.; Li, Z.; Truong Pham, D. Integrated optimisation of human-robot collaborative disassembly planning and adaptive evaluation driven by a digital twin. Int. J. Prod. Res. 2024, 1–19. [Google Scholar] [CrossRef]
- Ausaf, M.F.; Li, X.; Gao, L. Optimization algorithms for integrated process planning and scheduling problem—A survey. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5287–5292. [Google Scholar]
- Jin, L.; Tang, Q.; Zhang, C.; Shao, X.; Tian, G. More MILP models for integrated process planning and scheduling. Int. J. Prod. Res. 2016, 54, 4387–4402. [Google Scholar] [CrossRef]
- Barzanji, R.; Naderi, B.; Begen, M.A. Decomposition algorithms for the integrated process planning and scheduling problem. Omega 2020, 93, 102025. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, C.; Wong, T.N. A graph-based constraint programming approach for the integrated process planning and scheduling problem. Comput. Oper. Res. 2021, 131, 105282. [Google Scholar] [CrossRef]
- Shi, G.; Yang, Z.; Xu, Y.; Quan, Y. Solving the integrated process planning and scheduling problem using an enhanced constraint programming-based approach. Int. J. Prod. Res. 2022, 60, 5505–5522. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.R.; Heydari, M.; Mahdavi Mazdeh, M. New mathematical modeling and a constructive heuristic algorithm for integrated process planning and scheduling. J. Ind. Syst. Eng. 2023, 14, 30–49. [Google Scholar]
- Imsetif, J.; Nezamoddini, N.; Aqlan, F. Job shop planning and scheduling of reconfigurable manufacturing systems. Oper. Manag. Res. 2025, 1–22. [Google Scholar] [CrossRef]
- Wu, X.; Li, J. Two layered approaches integrating harmony search with genetic algorithm for the integrated process planning and scheduling problem. Comput. Ind. Eng. 2021, 155, 107194. [Google Scholar] [CrossRef]
- Cao, Y.; Shi, H. An adaptive multi-strategy artificial bee colony algorithm for integrated process planning and scheduling. IEEE Access 2021, 9, 65622–65637. [Google Scholar] [CrossRef]
- Mahdi, M.A.; Dawood, L.M. A grey wolf optimization algorithm for integrating process planning and scheduling problem. In Proceedings of the 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 9–11 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Mahdi, M.A.; Dawood, L.M. Optimization algorithms for integrated process planning and scheduling: A review. Int. J. Mech. Eng. 2022, 7, 1060–1066. [Google Scholar]
- Wen, X.; Qian, Y.; Lian, X.; Zhang, Y.; Wang, H.; Li, H. Improved genetic algorithm based on multi-layer encoding approach for integrated process planning and scheduling problem. Robot. Comput. Integr. Manuf. 2023, 84, 102593. [Google Scholar] [CrossRef]
- Jokić, A.; Petrović, M.; Miljković, Z. Integrated Process Planning and Scheduling of Production Systems Based on Mountain Gazelle Optimizer. In Proceedings of the 20th International May Conference on Strategic Management (IMCSM24), Smart Miner Section, Bor, Serbia, 30 May 2024; University of Belgrade-Technical Faculty in Bor: Bor, Serbia, 2024; Volume 20, pp. 142–151. [Google Scholar]
- Samhouri, M.; Qareish, S.Z. Hybrid fuzzy genetic algorithm for the integration of process planning and scheduling for distributed flexible job shop. Neural Comput. Appl. 2025, 37, 2775–2798. [Google Scholar] [CrossRef]
- Sun, M.; Cai, Z.; Yang, C.; Zhang, H. Digital twin for energy-efficient integrated process planning and scheduling. Int. J. Adv. Manuf. Technol. 2023, 127, 3819–3837. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Zhuang, C.; Dong, H.; Zhang, F. A hyper-heuristic for dynamic integrated process planning and scheduling problem with reconfigurable manufacturing cells. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 3892–3905. [Google Scholar] [CrossRef]
- Engin, O.; Güçlü, A. A new hybrid ant colony optimization algorithm for solving the no-wait flow shop scheduling problems. Appl. Soft Comput. 2018, 72, 166–176. [Google Scholar] [CrossRef]
- Ha, C. Evolving ant colony system for large-sized integrated process planning and scheduling problem considering sequence-dependent setup times. Flex. Serv. Manuf. J. 2020, 32, 523–560. [Google Scholar] [CrossRef]
- Uslu, M.F.; Uslu, S.; Bulut, F. An adaptive hybrid approach: Combining genetic algorithm and ant colony optimization for integrated process planning and scheduling. Appl. Comput. Inform. 2022, 18, 101–112. [Google Scholar] [CrossRef]
- Brandimarte, P. Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 1993, 41, 157–183. [Google Scholar] [CrossRef]
- Kim, Y.K.; Park, K.; Ko, J. A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling. Comput. Oper. Res. 2003, 30, 1151–1171. [Google Scholar] [CrossRef]
- Wan, L.; Li, X.; Gao, L.; Wen, X.; Wang, W. A novel two-level genetic algorithm for integrated process planning and scheduling. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2790–2795. [Google Scholar]
- Liu, Q.; Li, X.; Gao, L.; Fan, J. A multi-MILP model collaborative optimization method for integrated process planning and scheduling problem. IEEE Trans. Eng. Manag. 2022, 71, 4574–4586. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, C.; Li, X.; Gao, L. Mathematical modeling and a multiswarm collaborative optimization algorithm for fuzzy integrated process planning and scheduling problem. Tsinghua Sci. Technol. 2023, 29, 285–304. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: Abingdon, UK, 2013. [Google Scholar]








| Notation | Description |
|---|---|
| I | Parts set. |
| OSij | Operations set for part i. |
| PO | Potential operation set consisting of potential machines and tools for all the operations. |
| POij | Potential operation set for operation OSij. |
| N | Total number of POs for all parts I. |
| i, i′ | Parts, 1 ≤ i ≤ │I│, where i′ is the next part. |
| j, j′ | Operations, 1 ≤ j ≤ │Ji│, where j′ is the next operation. |
| k, k′ | Potential operations, 1 ≤ k ≤ │Kij│, where k′ is the next PO. |
| im | Index of machine m (1 ≤ m ≤ │10│). |
| POijk | kth PO for operation OSij of the part i. |
| mijk | Index of the machine chosen for kth PO, POijk. |
| tijk | Index of the tool chosen for PO, POijk. |
| mtijk | Machine time of PO, POijk. |
| α | Influence of pheromone information. |
| β | Influence of heuristic information. |
| ρ | Pheromone evaporation rate. |
| Qmax | Upper bound for Q (pheromone deposition constant). |
| Qmin | Lower bound for Q (pheromone deposition constant). |
| τmax | The maximum pheromone level. |
| τmin | The minimum pheromone level. |
| Widle | Weight factor for idle time penalty. |
| λ | Scaling factor that regulates the impact of idle time on the total cost. |
| uijk | If the kth potential operation for jth operation of part i is selected, 1; 0, otherwise; |
| vijkj′k′ | If the kth potential operation for jth operation is machined before the k′ th potential operation for j′th operation selected 1; 0, otherwise. |
| wijki′j′k′ ITidlem | 1, the kth potential operation for jth operation of part i is machined before the k′th potential operation for j′th operation of part i’ and mijk = mi′j′k′; Idle time for machine im for all the parts. |
| MNim | The makespan of the im machine. |
| MNmax | The maximum makespan of all machines. |
| OMS | Overall or cumulative makespan of all machines. |
| Cij | The machine cost for operation j of part i;. |
| Ctool,i | The tool cost for operation j of part i. |
| Csetup,i | The setup cost for operation j of part i. |
| Cidle | Idle time cost. |
| Ctotal | Total cost. |
| ηijki′j′k′ | Heuristic value. |
| Problem | Number of Parts | Index of Parts |
|---|---|---|
| 1 | 6 | 1 4 8 12 15 17 |
| 2 | 6 | 2 6 7 10 14 18 |
| 3 | 6 | 1 4 7 10 13 16 |
| 4 | 9 | 1 4 5 7 8 10 13 14 16 |
| 5 | 12 | 4 5 6 7 8 9 13 14 15 16 17 18 |
| 6 | 12 | 1 2 4 5 7 8 10 11 13 14 16 17 |
| 7 | 12 | 2 3 5 6 8 9 11 12 14 15 17 18 |
| 8 | 15 | 2 3 4 5 6 8 9 10 11 12 13 14 16 17 18 |
| 9 | 15 | 1 4 5 6 7 8 9 11 12 13 14 15 16 17 18 |
| 10 | 18 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
| Prob. | CCGA | SEA | HA | ALGA | TGA | ICA | ACO | GA VNS | MMCO | MSCOA | Proposed Algorithm |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 378 | 372 | 372 | 372 | 372 | 372 | 283 | 372 | 372 | 372 | 268 |
| 2 | 363 | 343 | 343 | 347 | 352 | 343 | 295 | 343 | 343 | 339 | 270 |
| 3 | 312 | 306 | 306 | 306 | 306 | 306 | 293 | 306 | 306 | 306 | 265 |
| 4 | 360 | 328 | 327 | 327 | 321 | 327 | 306 | 319 | 318 | 322 | 268 |
| 5 | 466 | 431 | 423 | 423 | 414 | 443 | 392 | 362 | 344 | 384 | 324 |
| 6 | 396 | 379 | 377 | 377 | 363 | 384 | 380 | 349 | 318 | 349 | 309 |
| 7 | 535 | 490 | 476 | 474 | 468 | 490 | 362 | 427 | 427 | 445 | 338 |
| 8 | 567 | 534 | 518 | 513 | 493 | 529 | 480 | 433 | 427 | 481 | 412 |
| 9 | 531 | 498 | 470 | 470 | 456 | 495 | 461 | 388 | 372 | 440 | 354 |
| 10 | 611 | 587 | 544 | 548 | 523 | 577 | 487 | 446 | 427 | 522 | 483 |
| Problem | Best Makespan Value | Algorithm | CPU Time (minutes) |
|---|---|---|---|
| 1 | 268 | Proposed Algorithm | 7.8 |
| 2 | 270 | Proposed Algorithm | 8.5 |
| 3 | 265 | Proposed Algorithm | 6.2 |
| 4 | 268 | Proposed Algorithm | 12.4 |
| 5 | 324 | Proposed Algorithm | 18.5 |
| 6 | 309 | Proposed Algorithm | 16.1 |
| 7 | 338 | Proposed Algorithm | 21.7 |
| 8 | 412 | Proposed Algorithm | 24.3 |
| 9 | 354 | Proposed Algorithm | 23.5 |
| 10 | 427 | MMCO | 28.6 |
| Algorithm | p-Value | Cohen’s d | Mean Improvement (%) |
|---|---|---|---|
| CCGA | 0.003 | 2.1 | 24.9 |
| SEA | 0.008 | 1.8 | 22.1 |
| HA | 0.005 | 1.7 | 21.3 |
| ALGA | 0.007 | 1.6 | 20.5 |
| TGA | 0.009 | 1.5 | 19.8 |
| ICA | 0.010 | 1.4 | 18.2 |
| ACO | 0.015 | 1.3 | 17.6 |
| GA-VNS | 0.018 | 1.1 | 15.9 |
| MMCO | 0.012 | 1.2 | 13.0 |
| MSCOA | 0.022 | 0.9 | 12.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Yuan, G.; Wang, C.; Liu, X.; Hu, T. Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling. Symmetry 2025, 17, 824. https://doi.org/10.3390/sym17060824
Raza A, Yuan G, Wang C, Liu X, Hu T. Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling. Symmetry. 2025; 17(6):824. https://doi.org/10.3390/sym17060824
Chicago/Turabian StyleRaza, Abbas, Gang Yuan, Chongxin Wang, Xiaojun Liu, and Tianliang Hu. 2025. "Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling" Symmetry 17, no. 6: 824. https://doi.org/10.3390/sym17060824
APA StyleRaza, A., Yuan, G., Wang, C., Liu, X., & Hu, T. (2025). Enhancing Manufacturing Efficiency Through Symmetry-Aware Adaptive Ant Colony Optimization Algorithm for Integrated Process Planning and Scheduling. Symmetry, 17(6), 824. https://doi.org/10.3390/sym17060824






