Threshold Fully Homomorphic Encryption Scheme Based on NGS of Symmetric Encryption

Abstract

Homomorphic encryption is an important means for cloud computing to ensure information security when outsourcing data. Among them, threshold fully homomorphic encryption (ThFHE) is a key enabler for homomorphic encryption and, from a wider perspective, secure distributed computing. However, current ThFHE schemes are unsatisfactory in terms of security and efficiency. In this paper, a novel ThFHE is proposed for the first time based on an NTRU-based GSW-like scheme of symmetric encryption—Th-S-NGS scheme. Additionally, the threshold structure is realized by combining an extended version of the linear integer secret sharing scheme such that the scheme requires a predetermined number of parties to be online, rather than all the parties being online. The Th-S-NGS scheme is not only more attractive in terms of ciphertext size and computation time for homomorphic multiplication, but also does not need re-linearization after homomorphic multiplication, and thus does not require the computing key, which can effectively reduce the communication burden in the scheme and thus simplify the complexity of the scheme.

1. Introduction

Cloud computing technology has been a popular topic in recent years [1,2], as it enables individuals and organizations to outsource large amounts of computation on large databases to third-party servers that may not be reliable. Conventional encryption techniques must decrypt data before any calculation can be performed on it. However, this brings new challenges to data security and privacy, especially when the data contains sensitive information.

In this moment, the study of homomorphic encryption (HE) has attracted wide attention; the concept was first proposed by Rivest et al. [3] in 1978, and is characterized by the fact that arbitrary operations can be performed directly on the ciphertext without decryption and the result of the operation is the same as that of the direct calculation operation on the plaintext. Therefore, homomorphic encryption applied to cloud computing not only realizes the advantages of outsourcing data, but also prevents the leakage of important information when computing data in an untrusted environment. In 2009, Gentry [4,5] proposed the first fully homomorphic encryption (FHE) scheme based on ideal lattice implementation, which can support an arbitrary number of addition and multiplication. Since then, a series of FHE schemes based on different mathematical objects have been proposed successively, such as LWE [6], Ring-LWE [7], NTRU [8], and the solution of the FHE scheme [9]. In recent years, a large quantity of research on FHE has emerged [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], leading to FHE gradually going from theory to practice, and continuously improving in terms of efficiency and security.

Initially, FHE used single-key encryption and only supported operations between data encrypted under the same key. This brings many inconveniences and potential security risks to the application of homomorphic encryption in privacy computation. In many application scenarios, people need to perform collaborative computations on data provided by each party without compromising data privacy. Therefore, driven by this demand, the research on FHE for multi-key approaches has emerged [13,14,15,16,17,18,19,20,21,22,23,24,25,26]. In addition, it is also possible to outsource the computational security of multi-party participation to third-party servers [26,27,28], relieving the computing burden of local clients.

FHE for multi-key approaches has two types of mainstream schemes, namely threshold fully homomorphic encryption (ThFHE) [14,15,16,17,18,19] and Multi-Key Fully Homomorphic Encryption (MKFHE) [20,21,22,23,24,25,26]. For a scenario where the participant set is predetermined, ThFHE is an alternative scheme that can decrypt successfully when the number of private keys involved in the decryption reaches a certain threshold. Due to the joint public key used in the ThFHE scheme, its computational performance is comparable to that of single-key fully homomorphic encryption schemes. ThFHE schemes are generally more efficient in terms of ciphertext size and computational cost than MKFHE schemes.

In 2012, Asharov et al. [17] first proposed a ThFHE scheme based on the BGV scheme—AJL+—the main idea is to utilize the homomorphic nature of the LWE encryption key to sum the public–private key pairs of multiple participants to obtain a new public–private key pair as the joint key. Research progress on ThFHE utilizing joint keys has been stagnant for a long period of time since then. In 2021, Mouchet et al. [18] improved the AJL+ scheme by constructing a ThFHE scheme based on the BFV scheme, which allows for less noise to be introduced. However, these efforts require a multi-round key generation process involving interactions between parties. In the same year, Park [19] designed a ThFHE scheme based on the BFV scheme based on the above work [18] and provided a conversion algorithm between MKFHE and ThFHE. A simple preprocessing step and distribution of the public key to each party involved makes it possible to generate the computational key without interaction between the parties involved, thus reducing the amount of communication in ThFHE, but the re-linearization process is still unavoidable.

Most of the above ThFHE schemes are constructed based on the (R-)LWE problem, while those based on the NTRU problem seem to be the most efficient. The reason is that the NTRU-based ciphertext can be expressed as a single polynomial $c={[hs+2e+m]}_q$ compared to the pair of polynomials $(c_1,c_2)$ in the RLWE-based scheme, where $c_1=⌊q/2⌋\cdot m+b{e}_2+e_3\in {\mathcal{R}}_q$, $c_2=a{e}_2+e_4\in {\mathcal{R}}_q$. Therefore, using the NTRU problem to design FHE schemes is more likely to decrease the memory requirement and runtime by half. In particular, the earlier FHE scheme YASHE [29] based on the NTRU problem proved to be extremely efficient compared to similar schemes. Moreover, the NTRU scheme has natural multi-key homomorphism, a property that is a unique advantage in the design of FHE schemes for multi-key approaches. Specifically, given two ciphertexts $c_1={[h_1{s}_1+e_1+m_1]}_q$, $c_2={[h_2{s}_2+e_2+m_2]}_q$, where $h_1={[2g_1{f}_1^{-1}]}_q$, $h_2={[2g_2{f}_2^{-1}]}_q$, where we let $c_{\mathrm{add}}:={[c_1+c_2]}_q$, $c_{\mathrm{mult}}:={[c_1{c}_2]}_q$, the decryption key is $f_1$, $f_2$.

• Additive homomorphism:

$$\begin{array}{l}{f}_1{f}_2(c_1+c_2)=2(f_1{f}_2{e}_1+f_1{f}_2{e}_2+f_2{g}_1{s}_1+f_1{g}_2{s}_2)+f_1{f}_2(m_1+m_2)\\ =2e_{\mathrm{add}}+f_1{f}_2(m_1+m_2)\end{array}$$

(1)

• Multiplicative homomorphisms:

$$\begin{array}{l}{f}_1{f}_2(c_1{c}_2)=2(2g_1{g}_2{s}_1{s}_2+g_1{s}_1{f}_2(2e_2+m_2)+g_2{s}_2{f}_2(2e_1+m_1)+\\ f_1{f}_2(e_1{m}_2+e_2{m}_1+2e_1{e}_2))+f_1{f}_2(m_1{m}_2)\\ =2e_{\mathrm{mult}}+f_1{f}_2(m_1{m}_2)\end{array}$$

(2)

In 2022, Xu et al. [30] used gadget vectors to encrypt messages into vectors consisting of NTRU ciphertexts (g-NTRU) and designed a new ThFHE. The g-NTRU inherits the advantages of the GSW in that it does not require expensive re-linearization after homomorphic multiplication and accordingly does not need a computing key, and this approach greatly reduces the amount of communication in ThFHE.

However, using the NTRU problem to design FHE schemes does not achieve the expected results for two main reasons. For one reason, almost all NTRU-based FHE schemes are not resistant to “Subfield Lattice Attacks”, which can recover the key in polynomial time, invalidating the difficulty assumption of these schemes [31,32,33,34,35]. Another reason is that the decryption of NTRU-based FHE schemes for multi-key approaches requires multiplying the ciphertext with a series of secret keys, and there is lack of research on secure and effective joint decryption protocols for this decryption structure.

The original attack utilized the sublattice of the NTRU lattice to reduce the lattice dimension of the search key, and subsequently, Kirchner and Fouque [31] proposed a new attack that can be launched as long as there is a dense sublattice in the NTRU lattice. Such an attack stems from the structure of the NTRU’s own lattice and cannot be solved by switching to another polynomial ring. As a result, there is difficulty in estimating the impact of “Subfield Lattice Attacks” on the security of the NTRU, and thus in guaranteeing the security of a scheme constructed on the basis of the NTRU problem. A large number of scholars have made numerous attempts in this area, e.g., LTV [8] and YASHE [29], which were considered as safe NTRU-based FHE schemes until then, and in 2016, Albrecht et al. [32] and Cheon et al. [33], in two independent papers, proposed sub exponential level attacks on the above schemes and found short vectors in the lattice to be more efficient than conventional techniques. In 2019, Gentry et al. proposed a FHE scheme based on the matrix NTRU problem [34], but soon Lee et al. [35] found that the scheme is vulnerable to “Subfield Lattice Attacks”. Therefore, constructing FHE schemes based on the NTRU problem is challenging.

Recently, the breakthrough seen in Ducas and Woerden’s latest research result [36] shows that resisting sublattice attack for NTRU problem can be avoided by setting $q\in O(n^{2.484})$. Based on the above research, in 2022, Bonte et al. first proposed an NTRU-based FHE scheme [37] by using the NTRU problem to construct a GSW-like scheme defined as NGS, demonstrating that adapting the framework of FHEW [38] to the NTRU setting is possible. The GSW-like scheme was constructed to efficiently compute the decryption function of the underlying scheme based on the GSW-like scheme for the RLWE problem when Ducas et al. proposed a bootstrapping framework for FHEW [38] in 2015. The advantage of the GSW-like scheme is that the noise growth is quasi-additive when computing long multiplicative chains, and the final noise in the “refreshed” ciphertext can be as small as $\tilde{O}(n)$, which is in line with the proposal in the work by Ducas and Woerden [36].

As in the GSW-like scheme [38], NGS can encrypt polynomials in two ciphertext formats. Let $m\in \mathcal{R}:=\mathbb{Z}[X]/(X^n+1)$,

• Scalar ciphertext: $c=g/f+\Delta m\in {\mathcal{R}}_{\mathcal{Q}}$;
• Vector ciphertext: $c=g/f+\mathfrak{g}\cdot m\in {\mathcal{R}}_{\mathcal{Q}}^{\mathcal{l}}$,

where $\mathfrak{g}$ is a gadget vector and $\mathcal{l}=⌈\log (Q)⌉$. Bonte et al. showed that constructing FHE schemes using NGS schemes not only results in faster bootstrapping algorithms than TFHE [39], but also requires less key material, which improves the advanced state-of-the-art nature of the FHE framework. Subsequently, in 2023, Zhang et al. [40] proposed a novel blind rotation algorithm for TFHE based on NGS, the performance of which is asymptotically independent of the key distribution, and has benefits in terms of computing key size and computational efficiency when the key distribution is large. This shows that the use of NGS in the design of FHE schemes is very prospective research.

1.1. Our Contribution

In this work, we applied the NGS scheme to threshold fully homomorphic encryption for the first time, and use NGS of symmetric encryption to instantiate our ideas. Before that, in order to realize the threshold structure, the extended version of the Linear Secret Sharing (CS-LISS) [41] scheme proposed by Chowdhury is used for key distribution and distributed decryption. We define it as an CL-LISS scheme in this paper. In other words, only a predefined number of participants are required to be online without the response of all participants. Compared to the traditional version of the LISS scheme [42], the CS-LISS scheme supports the secret in the form of binary polynomials, rather than being restricted to a scalar secret, which provides support for our work. The informal version of the Th-S-NGS below is described as follows.

The NGS key $f$ is used as the public key to encrypt the message and an LWE key $s$ is used as the private key to decrypt the message. Given an access structure $M_t$ and an NGS ciphertext, the secret key $sk$ is shared in $T$ parts $\left\{s{k}_{i{d}_{i\prime }}\right\}$ using the CS-LISS scheme. Then, the homomorphism operation of the NGS scheme is performed on the ciphertext. To realize the conversion between ciphertexts, a novel key-switching procedure [36] is utilized to obtain an LWE ciphertext under the key $ksk$. Finally, the participants use their individual secret keys to restore the message $\mu$.

$$m\stackrel{pk}{\to }\mathrm{NGS}.\mathrm{ciphertext}\stackrel{ksk}{\to }\mathrm{LWE}.\mathrm{ciphertext}\stackrel{sk}{\to }\mu .$$

This scheme does not require re-linearization after homomorphic multiplication and accordingly does not require computing keys. As a consequence, utilizing an NGS of symmetric encryption to construct ThFHE eliminates the interaction required to generate the computation key, which greatly reduces the communication of the scheme.

The flowchart of our scheme is shown in Figure 1. To avoid confusion, we summarize the abbreviations defined in this paper and their meanings in

Table 1. Abbreviations and their meanings.

Abbreviation	Implication
S-NGS	NGS of symmetric encryption
Th-S-NGS	ThFHE based on S-NGS scheme
${\mathrm{SNGS}}_{Q,f}$	scalar ciphertext
$SNG{S}_{Q,f}$	vector ciphertext

.

1.2. Roadmap

The preliminaries are presented in Section 2, which includes the CS-LISS scheme and key-switching technique. In Section 3, the NGS of symmetric encryption is introduced. Then, we propose an NGS-based ThFHE scheme in Section 4. Section 5, Section 6, Section 7 and Section 8 present the correctness analysis, noise analysis, security, and performance of the NGS-based ThFHE scheme, respectively. Finally, a short summary is shown in Section 9.

2. Preliminaries

This section introduces the terminology used in this paper, which include symbolic representations, hard problems, gadget vectors, a CS-LISS scheme, and a necessary technique—key-switching.

2.1. Symbolic Representations

In this paper, $n,N,q,Q$ are positive integers, where $n,N$ are powers of 2. By $\mathcal{R}$ (resp., $\widehat{\mathcal{R}}$) and ${\mathcal{R}}_Q$, we denote the $2N$-th (resp., $2n$-th) cyclotomic ring $\mathcal{R}=\mathbb{Z}[X]/(X^N+1)$ (resp., $\widehat{\mathcal{R}}=\mathbb{Z}[X]/(X^n+1)$) and its quotient ring ${\mathcal{R}}_Q=\mathcal{R}/Q\mathcal{R}$ (resp., $\widehat{\mathcal{R}}=\widehat{\mathcal{R}}/q\widehat{\mathcal{R}})$. Let ${[\cdot ]}_Q$ be the coefficient-wise modulo $Q$ reduction in the set $(-Q/2,Q/2]\cap \mathbb{Z}$, so that any element $f$ in $\mathcal{R}$ can be viewed as a unique polynomial less than $N$. Define $\varphi (f):=(f_0,\dots ,f_{n-1})\in {\mathbb{Z}}^N$ as the coefficient vector of $f$. The infinite norm is defined as $\Vert \cdot {\Vert }_{\infty }$.

Given a matrix $A$, then the $i+1-\mathrm{th}$ column representing $A$ is ${\mathrm{col}}_i(A)$, and the rows are similarly represented as ${\mathrm{row}}_i(A)$. For the vectors $a$ and $b$, their inner product is denoted as $a\cdot b$. Denote $x\leftarrow \chi$ to represent that an element $x$ is sampled uniformly at random from $\chi$.

2.2. Hard Problems and Ciphertexts

The relevant definitions are given in this part, on which this paper is based.

Definition 1

(LWE Ciphertexts [40]). Given positive integers $q$ and $n$, a message $m\in \mathbb{Z}$ and a secret key $s\in {\mathbb{Z}}^n$. An LWE-based encryption can be defined as

$${\mathrm{LWE}}_{q,s}(m):=(a,b=\langle a,s\rangle -\mathrm{noised}(m))\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q,$$

where $a\leftarrow {\mathbb{Z}}_q^n$ is random and $\mathrm{noised}(m)\in {\mathbb{Z}}_q$ is an noised encoding of $m\in \mathbb{Z}$ with some noise selected from the distribution $\chi$ over $\mathbb{Z}$.

Definition 2

(Decisional LWE Problem [43]). Given the LWE parameters $(q,n,m,\chi )$, $a\leftarrow {\mathbb{Z}}_q^n$, $s\leftarrow {\mathbb{Z}}^n$, $e\leftarrow \chi$, $v\leftarrow {\mathbb{Z}}_q$ are randomly selected based on their corresponding distributions. The decisional LWE problem is to distinguish between $(a,b=\langle a,s\rangle -e)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ and $(a,v)\in {\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$.

Definition 3

(Decisional NTRU Problem [44]). Given positive integers $N$, $Q$, denote $\chi$ to be a noise distribution over  $\mathcal{R}$. Let  $f,g\leftarrow \chi$, where  $f$ has an inverse in  ${\mathcal{R}}_Q$, and randomly sample a polynomial  $v$ over  ${\mathcal{R}}_Q$. The decisional NTRU problem is to distinguish between  $g/f\in {\mathcal{R}}_Q$ and  $v\in {\mathcal{R}}_Q$.

2.3. Gadget Decomposition

The technique of “gadget decomposition” is used to solve the ciphertext dimension expansion and noise control problems in fully homomorphic encryption, and is an important tool for optimizing computational efficiency and achieving practicality.

Given integers $q$ and $B$, set $\mathcal{l}:=⌈{\log }_B(Q)⌉$ and define ${\mathfrak{g}}_{q,B}:=(B^0,\dots ,B^{\mathcal{l}-1})$. For any $k\in {\mathbb{Z}}_q$, let the integer in $[-q/2,q/2)$ denote $k$ and define its signed decomposition in the basis $B$ to be ${\mathfrak{g}}^{-1}(k):=(k_0,\dots ,k_{\mathcal{l}-1})$ for each integer $\left|k_i\right|\le B/2$, where $i\in [\mathcal{l}]$. Then, it can be obtained that ${\mathfrak{g}}^{-1}(k)\cdot \mathfrak{g}=k$.

There is ${\mathfrak{g}}^{-1}(f):={\Sigma }_{i=0}^{N-1}{\mathfrak{g}}^{-1}(f_i{X}^i)$ for any $f\in {\mathcal{R}}_Q$. Hence it follows that

$${\mathfrak{g}}^{-1}(f)\cdot \mathfrak{g}={\displaystyle \sum _{l=0}^{N-1}{f}_i}\cdot X^i=f.$$

(3)

2.4. CS-LISS Scheme

In this part, we review some of the preprocessing steps required for the CL-LISS scheme.

Theorem 1

(CS-LISS scheme [41]). Assume $T$ parties are involved, and set  $\mathcal{P}=\{P_1,\dots ,P_T\}$ . Let  ${\mathcal{P}}^{\prime }$ be a  $t$-sized subset of  $\mathcal{P}$ with the  $\mathrm{group}.\mathrm{id}$ value of  $\mathrm{gid}$ that is authorized to threshold decrypt the ciphertext. The membership in  ${\mathcal{P}}^{\prime }$ is denoted as  ${\mathcal{P}}^{\prime }=\{P_{i{d}_{1\prime }},P_{i{d}_{2\prime }},\dots ,P_{i{d}_{t\prime }}\}$, where  $i{d}_{1\prime }<i{d}_{2\prime }<\dots i{d}_{t\prime }$, and  $1^{\prime }\le i^{\prime }\le t^{\prime }$. Each  $P_{i{d}_{i\prime }}$ has a key sharing  $s{k}_{i{d}_{i\prime }}$ , where  $1\le i^{\prime }\le t$. The upper bound on the coefficient value in the  $k$ polynomial of  $s{k}_{i{d}_{i\prime }}$ is  $t$ only. All the rest of the  $k$ polynomials of the key shares have binary coefficients.

According to Theorem 1, let $P_{i{d}_{1\prime }}$ have a non-binary key share $s{k}_{i{d}_{1\prime }}$ of ${\mathcal{P}}^{\prime }$. After all parties have received the key shares, each $P_{i{d}_{i\prime }}\subseteq {\mathcal{P}}^{\prime }$ has exactly one key share $s{k}_{i{d}_{i\prime }}$. Therefore, any group of $t$-sized parties should be able to reconstruct $sk$ using the key shares it owns, and denote these $t$ key shares as $\{s{k}_{i{d}_{1\prime }},s{k}_{i{d}_{2\prime }},\dots ,s{k}_{i{d}_{t\prime }}\}$.

• SS.Share ($s{k}_{i{d}_{i\prime }},M$): Given a distribution matrix $M$ for $(t,T)$-threshold secret sharing, each party $P_{i{d}_{i\prime }}$ runs the $t$-out-of-$T$ secret sharing Alg.1 to create shares on a secret $s{k}_{i{d}_{i\prime }}$.
• SS.Combine ($s{k}_{i{d}_{i\prime }}$): The secret key $sk$ can be reconstructed as

  $$sk=s{k}_{i{d}_{1\prime }}-{\displaystyle \sum _{i\prime =2}^{t}s}{k}_{i{d}_{i\prime }}.$$

  (4)

2.5. Key-Switching

In general, the base scheme constructed based on the NTRU problem requires greater dimensionality to achieve the same level of security as the LWE-based scheme. Therefore, Bonte et al. utilized the idea of LWE-based schemes in FHEW and TFHE to refresh LWE ciphertexts using S-NGS schemes as accumulators [37]. The goal is to convert the form of the ciphertext encrypting the same message from an S-NGS ciphertext to an LWE ciphertext.

Let $L=⌈{\log }_{B_{\mathrm{ksk}}}(q)⌉$ and define $(A,B)$ as an LWE sample with a secret key $s$. The key-switching key is defined as the following LWE sample vector.

$${\mathrm{ksk}}_{\mathrm{SNGS}\to \mathrm{LWE}}:=(A,B:=A\cdot s+e+P\cdot {\mathrm{col}}_0(\Phi (f))),$$

(5)

with $A\in {\mathbb{Z}}_q^{(N\cdot L)\times n},e\leftarrow {\chi }_e^{N\cdot L},{\mathrm{col}}_0(\Phi (f))\in {\mathbb{Z}}^N$, and $P=I_N\otimes {\mathfrak{g}}_{q,B_{\mathrm{ksk}}}$. Then, given a ciphertext ${\mathrm{SNGS}}_{Q,f}=g/f+ϵ+\Delta \cdot m$, where $ϵ$ is the rounding error after modulus switching, the key-switching is defined as follows:

• ${\mathrm{KeySwitch}}_{\mathrm{SNGS}\to \mathrm{LWE}}:{\mathrm{LWE}}_{q,s}:=(a,b)\leftarrow \mathrm{KeySwitch}({\mathrm{SNGS}}_{Q,f},(A,B))$.

Namely, the vector of coefficients of ${\mathrm{SNGS}}_{Q,f}$ are decomposed and multiplied by the two components of ${\mathrm{ksk}}_{\mathrm{SNGS}\to \mathrm{LWE}}$. Define $y:={\mathfrak{g}}^{-1}(\varphi (c))\in {\mathbb{Z}}^{N\cdot L}$ and compute

$${\mathrm{LWE}}_{q,s}:=(a,b)=(y\cdot A,y\cdot B)\in {\mathbb{Z}}_q^{n+1}.$$

(6)

It can be seen that

$$\begin{array}{l}b=a\cdot s+y\cdot e+\varphi (c)\cdot {\mathrm{col}}_0(\Phi (f))\\ =a\cdot s+y\cdot e+g_0+ϵ\cdot ((1,0)+4\cdot \varphi (f^{\prime }))+4\cdot {ϵ}^{\prime }\cdot \varphi (m)\cdot \varphi (f^{\prime })+\Delta \cdot m_0,\end{array}$$

(7)

where $ϵ\in (-1/2,1/2]$ and $m_0$ are the constant terms of $m$. In other words, $(a,b)$ is a valid LWE ciphertext of $m_0$.

3. NGS of Symmetric Encryption

In this section, we review a variant of the NTRU scheme—NGS of symmetric encryption (S-NGS) [37]. The S-NGS scheme has two encryption functions, scalar encryption and vector encryption, where the first encrypts the plaintext $m$ as elements of ${\mathcal{R}}_Q$, and the second encrypts it as vectors over ${\mathcal{R}}_Q$ using “gadget decomposition”. Having defined the two types of scalar encryption and vector encryption, an “external product” between them is given, which is cheaper than NGS homomorphic multiplication.

• S-NGS.ParamGen ($1^{\lambda }$): Receives the security parameter and outputs the tuple $(N,Q,\varsigma ,B,\mathcal{l})$, where $B$ is a base used to decompose the ciphertexts and $\mathcal{l}:=⌈{\log }_B(Q)⌉$.
• S-NGS.KeyGen: Sample $f\prime \leftarrow {\chi }_{\varsigma }^N$ and set $f:=1+4\cdot f\prime$ until $f^{-1}$ exists in ${\mathcal{R}}_Q$. Output $sk=f$.
• S-NGS.EncS ($sk,m$): Let $u\in {\mathcal{R}}_Q$, $g\leftarrow {\chi }_{\varsigma }^N$, define $\Delta :=Q/2$, and output ${\mathrm{SNGS}}_{Q,f}:=g/f+\Delta \cdot m\in {\mathcal{R}}_Q$. The ${\mathrm{SNGS}}_{Q,f}$ is a “scalar encryption” of $m$.
• S-NGS.EncVec ($sk,m$): Given $v\in {\mathcal{R}}_Q$, sample $g_i\leftarrow {\chi }_{\varsigma }^N$ for $0\le i\le \mathcal{l}-1$. Define $g:=(g_0,\dots ,g_{\mathcal{l}-1})$ and $\mathfrak{g}:=(B^0,B^1,\dots ,B^{\mathcal{l}-1})$. Output $SNG{S}_{Q,f}$ is a “vector encryption” of $m$, where $SNG{S}_{Q,f}:=g/f+\mathfrak{g}\cdot m\in {\mathcal{R}}_Q^{\mathcal{l}}$.
• S-NGS.DeS ($sk,c$): Use the secret key $f$ and output the message $\mu ={[f\cdot c]}_Q$.
• S-NGS.Exp ($c,c$): Given a scalar encryption $c\in {\mathcal{R}}_Q$ of a ternary polynomial $u$ and a vector encryption $c\in {\mathcal{R}}_Q^{\mathcal{l}}$ of a message $v\in \mathbb{M}$, the “external product” of $c$ and $c$ is defined as follows:

$$\begin{array}{l}c\odot c={\mathfrak{g}}^{-1}(c)\cdot c\\ \begin{array}{ccc}& & \end{array}=({\mathfrak{g}}^{-1}(c)\cdot g)/f+({\mathfrak{g}}^{-1}(c)\cdot \mathfrak{g}\cdot v)\\ \begin{array}{ccc}& & \end{array}=g\prime /f+\Delta u\cdot v\in {\mathcal{R}}_Q\end{array}$$

(8)

where $g^{\prime }={\mathfrak{g}}^{-1}(c)\cdot g+g\cdot v$. Hence, $c\odot c$ is a valid scalar encryption of the product $u\cdot v$ as long as the noise term $g^{\prime }$ is small enough.

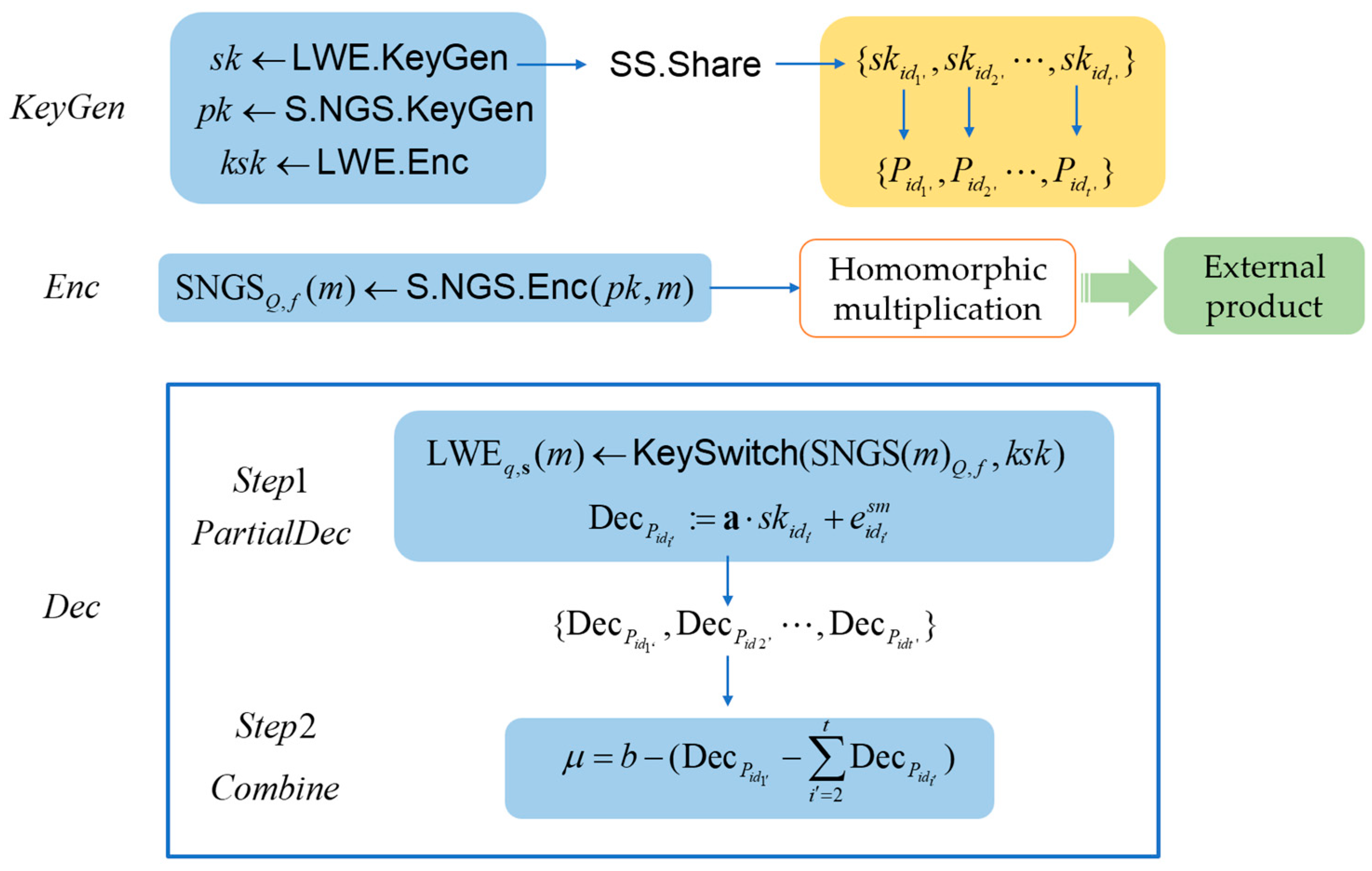
4. NGS-Based ThFHE Scheme

In this section, we design a novel ThFHE using the S-NGS scheme—Th-S-NGS. ThFHE supports homomorphic operations on inputs from multiple data owners without sacrificing user priorities. The constructed ThFHE scheme needs to be combined with the CS-LISS scheme to realize the threshold access structure. For this purpose, all parties encrypt the data using a key issued by a trusted third party, and decryption only requires $t (t\le T)$ participants to agree and cooperate in decrypting any ciphertext, without requiring all participants to join.

In the Th-S-NGS scheme, the secret key $f$ of S-NGS is used as the public key to encrypt the message and the secret key $s$ of LWE is used as the private key to decrypt the message. The formal version is described as follows:

• Th-S-NGS.KeyGen ($pk,sk,ksk$): The number of participants $T$ and the threshold $t$ corresponding to the threshold access structure $M$ entered by a trusted third party of the key authority. Generate a Th-S-NGS instance with

  $$\begin{gathered} pk:f\leftarrow \text{S-NGS.KeyGen}, \\ sk:s\leftarrow \text{LWE.KeyGen}, \\ ksk:(A,B)\leftarrow \mathrm{LWE}.\mathrm{Enc}(s,{\mathrm{col}}_0(\Phi (f)). \end{gathered}$$
  Execute the secret sharing algorithm of CS-LISS scheme to set the secret key shares for parties.

  $$\left\{s{k}_{i{d}_{i\prime }}\right\}\leftarrow \mathrm{SS}.\mathrm{Share}(s,M).$$

• Th-S-NGS.Enc ($sk,m$): A trusted third party runs the encryption algorithm of S-NGS and output the ciphertext.

$${\mathrm{SNGS}}_{Q,f}(m)\leftarrow \mathrm{S}-\mathrm{NGS}.\mathrm{Enc}(pk,m).$$

• Th-S-NGS.Exp ($c,c$): While entering two ciphertexts, execute S-NGS. Exp.
• Th-S-NGS.PartialDec ($\left\{s{k}_{i{d}_{i\prime }}\right\},{\mathrm{SNGS}}_{Q,f}(m),ksk$): Given the key-switching key $ksk$, compute

  $${\mathrm{LWE}}_{q,s}(m)\leftarrow {\mathrm{KeySwitch}}_{\mathrm{SNGS}\to \mathrm{LWE}}(\mathrm{SNGS}{(m)}_{Q,f},ksk).$$
  Upon input of the LWE ciphertext ${\mathrm{LWE}}_{q,s}(m)$ and a key set $\left\{s{k}_{i{d}_{i\prime }}\right\}$, each $P_{i{d}_{i\prime }}$ calculates the following:

  $${\mathrm{Dec}}_{P_{i{d}_{i\prime }}}:=a\cdot s{k}_{i{d}_{i\prime }}+e_{i{d}_{i\prime }}^{sm}.$$

  (9)
  Then, $P_{i{d}_{i\prime }}$ broadcasts ${\mathrm{Dec}}_{P_{i{d}_{i\prime }}}$ to remaining parties.

• Th-S-NGS.Combine ($\{{\mathrm{Dec}}_{P_{i{d}_{i\prime }}}\},{\mathrm{LWE}}_{q,s}(m)$): Inputting the ciphertext ${\mathrm{LWE}}_{q,s}(m)$ and the predetermined $t$ participants, the decryption in this step is computed as

$$\mu =\mathrm{Dec}({\mathrm{LWE}}_{q,s}(m))=b-({\mathrm{Dec}}_{P_{i{d}_{1\prime }}}-{\displaystyle \sum _{i\prime =2}^t{\mathrm{Dec}}_{P_{i{d}_{i\prime }}}}).$$

(10)

5. Correctness

A correct Th-S-NGS ciphertext $c=(a,b)$ is obviously exactly an LWE ciphertext. According to the LWE decryption algorithm, it can be obtained as

$$\mathrm{Dec}(c)=b-a\cdot s=y\cdot e+\varphi (c)\cdot {\mathrm{col}}_0(\Phi (f))$$

(11)

The final ciphertext of the Th-S-NGS scheme is in the form of an LWE ciphertext and the decryption is combined with the CS-LISS scheme, thus the correctness of the decryption is analyzed as follows:

$$\begin{array}{l}\mu =b-({\mathrm{Dec}}_{P_{i{d}_{1\prime }}}-{\displaystyle \sum _{i^{\prime }=2}^t{\mathrm{Dec}}_{P_{i{d}_{i\prime }}}})\\ =b-((a\cdot s{k}_{i{d}_{1\prime }}+e_{i{d}_{1\prime }}^{sm})-{\displaystyle \sum _{i^{\prime }=2}^t(a\cdot s{k}_{i{d}_{i\prime }}+e_{i{d}_{i\prime }}^{sm})})\\ =b-(a\cdot (s{k}_{i{d}_{1\prime }}-{\displaystyle \sum _{i^{\prime }=2}^{t}s}{k}_{i{d}_{i\prime }})+(e_{i{d}_{1\prime }}^{sm}-{\displaystyle \sum _{i^{\prime }=2}^t{e}_{i{d}_{i\prime }}^{sm}}))\\ =b-a\cdot s+e^{sm}=y\cdot e+\varphi (c)\cdot {\mathrm{col}}_0(\Phi (f))+e^{sm}.\end{array}$$

(12)

Given the key $f=1+4\cdot f\prime$, let $\Delta =Q/2+ϵ$ so that $\left|ϵ\right|\le 1/2$, and then perform the S-NGS decryption algorithm. Since these hold in ${\mathcal{R}}_Q$, it follows that

$$c\cdot f=g+4\cdot f\prime \cdot ϵ\cdot m+\Delta \cdot m.$$

(13)

It is possible to discover that $\varphi (c)\cdot \Phi (f)=(g_0,\dots ,g_{\mathcal{l}-1})+4\cdot ϵ\cdot \varphi (f\prime )+\Delta \cdot (m_0,0,\dots ,0)$.

Then, $\varphi (c)\cdot {\mathrm{col}}_0(\Phi (f))=g_0+4\cdot ϵ\cdot f_0^{\prime }+\Delta \cdot m_0$. Therefore, the following can be obtained:

$$\mu =\underset{e}{\underbrace{y\cdot e+g_0+4\cdot ϵ\cdot f_0^{\prime }}}+\Delta \cdot m_0+e^{sm}=\Delta \cdot m_0+e+e^{sm},$$

(14)

where $m_0$ is the constant term of $m$, which has $\mu =\Delta \cdot m_0$ as long as the noise $e+e^{sm}$ is sufficiently small. In other words, $c$ is a valid Th-S-NGS ciphertext of $m_0$.

6. Noise Analysis

In this section, the upper bounds of various noise parameters are discussed to ensure the correctness of our proposed Th-S-NGS schemes. In other words, the noise disturbances are minimized as much as possible without affecting the correctness of the decryption protocol. Therefore, the upper bound of the noise is set to $\Delta /2$. The noise generated by the LWE decryption and smudging noise from the threshold structure are discussed separately for the Th-S-NGS scheme. First of all, a lemma for the noise flooding technique is given.

Lemma 1

(Noise Flooding [17]). For positive integers $B_1=B_1(\lambda )$, $B_2=B_2(\lambda )$ and fixed $e_1\in [-B_1,B_1]\cap \mathbb{Z}$, a uniformly random sample of $e_2\leftarrow [-B_2,B_2]\cap \mathbb{Z}$ is chosen from the interval. Hence, if $B_2/B_1=2^{\omega (\log \lambda )}$, the distributions of $e_2$ and $e_2+e_1$ are statistically indistinguishable.

Given a valid LWE ciphertext $c$, compute $\mathrm{Dec}(c)=b-a\cdot s$, which essentially equals $\Delta \cdot m_0+e+e^{sm}$. The coefficients of $\mu$ are then rounded and approximated in the LWE decryption process as

$$\Delta \cdot m_0+e+e^{sm}\stackrel{round}{\to }\Delta \cdot m_0\stackrel{approximate}{\to }{m}_0,$$

And for correctness, we need $\Vert e+e^{sm}{\Vert }_{\infty }<\Delta /2$.

Here, the $e=y\cdot e+g_0+4\cdot ϵ\cdot f_0^{\prime }$, where $ϵ\in (-1/2,1/2]$. The $e$ is sampled from ${\chi }_e^{N\cdot L}$, bounded by $B_e$, and ${\mathfrak{g}}^{-1}$ is bounded by $B_{\mathfrak{g}}$. The $g_0$ and $f_0$ are bounded by $B_e$ and obtained from ${\chi }_e^N$. As a result, the following can be obtained:

$$\begin{array}{ll}\Vert e{\Vert }_{\infty }& =\Vert y\cdot e+g_0+4\cdot ϵ\cdot f_0^{\prime }{\Vert }_{\infty }\\ & <\Vert y\cdot e{\Vert }_{\infty }+\Vert g_0{\Vert }_{\infty }+\Vert 4\cdot ϵ\cdot f_0^{\prime }{\Vert }_{\infty }\\ & <N^2\cdot B_{\mathfrak{g}}\cdot B_e+3\cdot B_{\varsigma }.\end{array}$$

(15)

Each party $P_{i{d}_{i\prime }}$ computes the partial decryption ${\mathrm{Dec}}_{P_{i{d}_{i\prime }}}$ in conjunction with its own key $s{k}_{i{d}_{i\prime }}$. The computation is as follows:

$$a\cdot (s{k}_{i{d}_{1\prime }}-{\displaystyle \sum _{i^{\prime }=2}^{t}s}{k}_{i{d}_{i\prime }})+(e_{i{d}_{1\prime }}^{sm}-{\displaystyle \sum _{i^{\prime }=2}^t{e}_{i{d}_{i\prime }}^{sm}}).$$

(16)

The information recovery procedure is $b-\left\{{\mathrm{Dec}}_{P_{i{d}_{i\prime }}}\right\}=\Delta \cdot m_0+e+e^{sm}$. In order to decrypt it correctly, it has to satisfy $\Vert e+e^{sm}{\Vert }_{\infty }<\Delta /2$, such that

$$\Vert e+e_{i{d}_{1\prime }}^{sm}-{\displaystyle \sum _{i^{\prime }=2}^t{e}_{i{d}_{i\prime }}^{sm}}{\Vert }_{\infty }<\Vert e{\Vert }_{\infty }+\Vert e_{i{d}_{1\prime }}^{sm}{\Vert }_{\infty }.$$

(17)

Let the smudging noise be $\Vert e^{sm}{\Vert }_{\infty }<2^{\omega (\log \lambda )}{B}_{\sigma }$ according to Lemma 1. After a homomorphic “external product” of depth $d$, for the correctness of $(t,T)$ distributed decryption to hold, the following conditions need to be satisfied:

$$\begin{array}{l}\Vert e{\Vert }_{\infty }+\Vert e^{sm}{\Vert }_{\infty }<d\cdot N^2\cdot B_{\mathfrak{g}}\cdot B_e+3\cdot B_e+N\cdot 2^{\omega (\log \lambda )}{B}_e\\ \begin{array}{cccccc}& & & & & \end{array}\begin{array}{cc}& \end{array}<N^2\cdot B_e(d\cdot B_{\mathfrak{g}}+2^{\omega (\log \lambda )}),\end{array}$$

(18)

which needs to be below $\Delta /2$ for the decryption protocol to be correct, where $\Delta /2\approx Q/4$. Thus, we can obtain $8(N^2\cdot B_e(d\cdot B_{\mathfrak{g}}+2^{\omega (\log \lambda )}))<Q.$ Based on this analysis, the parameters are chosen such that

$$O(N^2\cdot B_e(d\cdot B_{\mathfrak{g}}+2^{\omega (\log \lambda )}))<Q.$$

(19)

7. Security

7.1. IND Security for NGS Ciphertext

It is clear from Section 4 that the Th-S-NGS scheme has more than one form of ciphertexts, as shown in

Table 2. Forms of ciphertexts in different phases.

Phase	Form of Ciphertext
Encrypted ciphertext	${\mathrm{SNGS}}_{Q,f}(m):g/f+\Delta \cdot u$
Decrypted ciphertext	${\mathrm{LWE}}_{q,s}(m):(A,B)$

.

The scalar ciphertext form of the Th-S-NGS scheme is shown in Table 1, which can be simplified as ${\mathrm{SNGS}}_{Q,f}:=t\cdot g/f+u$, where $t$ is an integer and $\Delta$ is a publicly defined constant. Since the standard NTRU encryption has the form $c:=t\cdot g/f+m$ in a symmetric key setting, it is clear that an S-NGS ciphertext is a standard NTRU ciphertext. Therefore, the security of NGS ciphertexts needs to rely on the cyclic security assumption of the standard NTRU scheme [34,37,45].

Th-S-NGS scheme has vector ciphertexts in the form of $c:=g/f+\mathfrak{g}\cdot m\in {\mathcal{R}}_Q^{\mathcal{l}}$. In fact, the NGS vector ciphertexts essentially encrypt different messages using the same key as in Ref [37,45], and their security is essentially guaranteed by the decision vector–NTRU assumption. In conclusion, the IND-CPA security of the S-NGS scheme can be guaranteed by the cyclic security assumption of Definition 3.

7.2. IND Security for NGS-Type ThFHE

In this part, we consider the IND-CPA security of Th-S-NGS, which guarantees that the encryption does not reveal any information to the passive adversary, even if he possesses at most $t-1$ of $k$ keys. The IND-CPA security definition of ThFHE from [14] effectively combined previous definitions [15,16] of simulation and semantic security for ThFHE. Informally, for arbitrarily chosen plaintext messages $m_0$ and $m_1$, a PPT adversary cannot effectively distinguish between them, and thus it can be said that the ThFHE scheme provides semantic security.

Given the security parameters $\lambda$ and the depth $d$ of the Th-S-NGS scheme, and according to Theorem 1, $M_{t,T}$ is a threshold access structure and $\mathcal{P}=\{P_1,\dots ,P_T\}$ is a set of participants. Let $\mathcal{C}$ be a $PPT$ challenger and $\mathcal{A}$ be an adversary, so a game ${\mathrm{Expt}}_{\mathcal{A},\mathrm{Th}-\mathrm{S}-\mathrm{NGS},\mathrm{sem}}(1^{\lambda },1^d)$ is defined as follows:

Initialization phase.

• The challenger $\mathcal{C}$ runs Th-S-NGS.Gen $(1^{\lambda },1^d,M_{t,T})$ to obtain $(pk,sk,\{s{k}_{i{d}_{i\prime }}\})$, and provides the public key $pk$ to the adversary $\mathcal{A}$.
• The adversary $\mathcal{A}$ outputs a set $\mathcal{P}=\{P_1,\dots ,P_T\}$, and receives the set of secret key shares $\left\{s{k}_{i{d}_{i\prime }}\right\}$ from $\mathcal{C}$.

Challenge phase.

• The adversary $\mathcal{A}$ outputs two sets of equal length messages $m_0$, $m_1$.
• $ct$ = Th-S-NGS.Enc $(pk,m^b)$ is provided by the challenger, for $b\leftarrow \{0,1\}$ and $\left\{s{k}_{i{d}_{i\prime }}\right\}$ to $\mathcal{A}$.

Partial decryption query phase.

• The adversary $\mathcal{A}$ issues $(ct,m^b)$.
• $\mathcal{A}$ receives ${\mathrm{Dec}}_{P_{i{d}_{i\prime }}}$= Th-S-NGS.PartialDec $(s{k}_{i{d}_{i\prime }},ct)$.

Output phase.

• The adversary $\mathcal{A}$ eventually outputs a bit $b^{\prime }\in \{0,1\}$.
• If $b^{\prime }=b$, the game outputs 1, otherwise it outputs 0.

Let ${\gamma }_{\beta }=\mathrm{Pr}[{\mathrm{G}}_{\mathrm{ThS}-\mathrm{NGS},\mathcal{A},{\mathbb{M}}_{t,T}}(1^{\lambda },1^d)=\beta ]$ for $\beta \in \{0,1\}$, so the probability is over the random coins used by Th-S-NGS.Gen, Th-S-NGS.Enc, and the adversary $\mathcal{A}$, and we have $|{\gamma }_0-{\gamma }_1|\le \mathrm{negl}(\lambda )$. In summary, the IND-CPA security of the Th-S-NGS scheme is ensured by the IND-CPA security of the NGS scheme and the security of the CS-LISS scheme.

7.3. Discussion of Potential Resistance to Quantum Attacks

The Th-S-NGS scheme proposed in this paper is based on the approximate shortest vector problem on the NTRU lattice and Learning with Error (LWE) problem, both of which are widely recognized to remain difficult under the quantum computing paradigm [46]. Specifically, quantum algorithms targeting the NTRU lattice (e.g., attacks based on Grover’s algorithm) are currently only capable of polynomial speedups, and are not able to efficiently break the scheme with a reasonable set of parameters [47].

The threshold decryption protocol in this paper accomplishes decryption through multi-participant collaboration, and the attackers still need to simultaneously break more than a threshold number of participants even if the quantum computation cracks a single-party key in the future, which significantly improves the system’s tolerance to quantum attacks [48].

8. Performance

8.1. Computation Time

In analyzing the computational overhead of homomorphic operations, it is clear that homomorphic multiplication dominates the total overhead, hence this section focuses on comparing the number of polynomial multiplications that need to be performed in each scheme.

In the case of ignoring the variability in the time-consuming multiplication of polynomial coefficients ($\left[-q/2,q/2\right)$ within the real numbers), the “gadget decomposition” takes $\Delta t$s to perform a polynomial factorization. The schemes designed by Li et al. and Xu et al. using NTRU and its variants—g-NTRU, respectively, where the ciphertexts are realized by tensor products, and ${\mathcal{l}}^2$ multiplications are required to compute one tensor product.

Since an “external product” is computed between the two ciphertext types in the S-NGS scheme, the output is another scalar ciphertext. Note that only $\mathcal{l}$ ring elements of each vector cipher are required. Thus, the external product of Th-S-NGS is computed with $\mathcal{l}$ products in ${\mathcal{R}}_Q$, while the ciphertexts of the GSW scheme used in TFHE are composed of $4\mathcal{l}$ ring elements. Therefore, they need $4\mathcal{l}$ multiplications per external product.

As not all of the comparison schemes are threshold schemes, we compare the time required to perform a homomorphic multiplication, and

Table 3. Comparison of computation time of Th-S-NGS scheme with other schemes.

Scheme	Based	Homomorphic Multiplication	Computation Time
Li [24]	NTRU	Tensor product	${\mathcal{l}}^2\Delta t$
Xu [25]	g-NTRU	Tensor product	${\mathcal{l}}^2\Delta t$
TFHE [38]	GSW	External product	$4\mathcal{l}\Delta t$
Th-S-NGS	S-NGS	External product	$\mathcal{l}\Delta t$

shows that the homomorphic multiplication using the S-NGS scheme has a better running time, both in comparison with the NTRU-based scheme and the TFHE scheme, which is currently the best performing scheme.

8.2. Parameters

The NGS-based ThFHE scheme realizes homomorphic multiplication by means of the “external product” in Equation (8) instead of the traditional homomorphic multiplication. The scalar ciphertext and vector ciphertext are computed by the external product to obtain the scalar ciphertext, which effectively reduces the size of the ciphertext, thus eliminating the complex linearization process.

We summarize the comparison of the Th-S-NGS scheme with previous work in Table 2, where the public key is $f\in {\mathcal{R}}_Q$ obtained from the S-NGS scheme, the private key of the Th-S-NGS is $s$ from the LWE, and the switching key $ksk:=(A,B)$ is a matrix of $(N\cdot L)$-by-$(n+1)$ dimensions.

From Section 4 and Table 2, the final ciphertext of the Th-S-NGS scheme in this paper is in the form of an LWE ciphertext, which is converted from an S-NGS ciphertext to an LWE ciphertext by the key switching technique. Therefore, the ciphertext size in this paper is the LWE ciphertext size.

Since the scheme proposed in this paper does not need a computing key, as an example, the scheme of Li et al. is used to explain the parameters of the scheme in

Table 4. The comparison of the Th-S-NGS scheme with the previous NTRU-based FHE for multi-key approaches.

Scheme	Based	Ciphertext Size	Computing Key Size
L’opez-Alt [8]	NTRU	$O(n\log ⌈q⌉)$	$O(tn{\log }^3⌈q⌉)$
Li [24]	NTRU	$O(tn\log ⌈q⌉)$	$O(t\mathcal{l}n\log ⌈q⌉)$
Che-B [25]	NTRU	$O((2n-1)\log ⌈q⌉)$	$O(N(n-1){\log }^2⌈q⌉)$
Che-M [25]	NTRU	$O((2n-1){(\log ⌈q⌉)}^2)$	\
Xu [30]	g-NTRU	$O(\mathcal{l}n\log ⌈q⌉)$	\
Th-S-NGS	S-NGS	$O((n+1)\log ⌈q⌉)$	\

.

Assuming that there are $t$ participants in the homomorphic operation, a multi-key ciphertext consists of $t$ polynomials; a total of $t$ computational keys are required to perform the homomorphic multiplication, each computational key consists of $2\mathcal{l}$ polynomials. The scheme from Li et al. is a proxy re-encryption scheme, hence $t$ re-encryption keys are also required to perform proxy re-encryption, and each re-encryption key consists of $2\mathcal{l}$ polynomials. As a result, the size of the ciphertext in homomorphic computation is $O(tn\log ⌈q⌉)$, and the size of the computational key generated by a single user is $O(\mathcal{l}n\log ⌈q⌉)$. The size of the computational key generated by A participant is $O(t\mathcal{l}n\log ⌈q⌉)$.

The results in Table 4, comparing the Th-S-NGS scheme and NTRU-based FHE for multi-key approaches, show that the Th-S-NGS scheme, as well as Che-M [25], Xu’s [30] scheme, do not need to be re-linearized after homomorphic multiplication, and accordingly do not need a computing key, which not only effectively reduces the communication burden of the scheme, but also simplifies the complexity of the scheme. Furthermore, the Th-S-NGS scheme is even more attractive in terms of ciphertext size, which is only $O((n+1)\log ⌈q⌉)$.

9. Conclusions

In this paper, we propose for the first time an NGS-type ThFHE based on S-NGS. The threshold structure is achieved by combining the CS-LISS scheme with noise flooding, which allows the scheme to require a predetermined number of parties to be online, rather than all parties being online. The Th-S-NGS scheme in this paper has the advantages of (1) resisting subfield lattice attacks, (2) enabling distributed decryption, (3) reducing key exchange in communication, and (4) the ciphertext size does not increase with the number of participating parties.

Furthermore, compared with previous works, the Th-S-NGS scheme obviously saves the computation time required by homomorphic multiplication, and not only has a significant advantage in terms of ciphertext size, but also does not need re-linearization after homomorphic multiplication, which greatly simplifies the complexity of the scheme. Generally speaking, we demonstrate that it is possible to construct an efficient ThFHE scheme based on NGS, and in the end, we hope that the results of this paper will be useful for research on NGS schemes in other aspects.