Research on the Stability Control of Four-Wheel Steering for Distributed Drive Electric Vehicles

Abstract

To address the challenge of optimizing system adaptability, disturbance rejection, control precision, and convergence speed simultaneously in four-wheel steering (4WS) stability control, a 4WS controller with a variable steering ratio (VSR) strategy and fast adaptive super-twisting (FAST) sliding mode control is proposed to control and output the steering angles of four wheels. The ideal VSR strategy is designed based on the constant yaw rate gain, and a cubic quasi-uniform B-spline curve fitting method is innovatively used to optimize the VSR curve, effectively mitigating steering fluctuations and obtaining precise reference front wheel angles. A controller based on FAST is designed for active rear wheel steering control using a symmetric 4WS vehicle model. Under double-lane change conditions with varying speeds, the simulations show that, compared with the constant steering ratio, the proposed VSR strategy enhances low-speed sensitivity and high-speed stability, improving the system’s adaptability to different operating conditions. Compared with conventional sliding mode control methods, the proposed FAST algorithm reduces chattering while increasing convergence speed and control precision. The VSR-FAST controller achieves optimization levels of more than 7.3% in sideslip angle and over 41% in yaw rate across different speeds, achieving an overall improvement in the stability control performance of the 4WS system.

1. Introduction

1.1. Motivation and Technical Challenge

With the development of the new energy trend in the automotive industry, electric vehicles have attracted widespread attention for their energy-saving and precise control advantages [1]. Distributed drive technology represents a significant developmental direction. Distributed drive electric vehicles (DDEVs) possess a relatively rapid response speed, rendering them an ideal platform for the research of chassis control and optimization techniques [2]. Under complex and variable road conditions, DDEVs are prone to potential hazards such as drifting and slipping [3]. Enhancing vehicle stability is an effective approach to addressing road safety issues; hence, chassis control technologies, including steering systems, have become a focal point of research [4].

In the early stages of research, scholars endeavored to enhance yaw stability by employing active front steering (AFS). However, the impact of AFS on stability was confined to medium- and low-speed ranges [5]. The rear wheels of AFS merely performed a following motion, which could pose certain risks when the vehicle was making emergency turns or traveling on narrow roads. Compared to AFS, the four-wheel steering (4WS) system effectively enhances vehicle handling characteristics by precisely controlling the steering angles of both front and rear wheels, resulting in high sensitivity and rapid response. This has increasingly positioned 4WS as a primary developmental direction for future automotive power steering technology [6,7,8]. Currently, the field of stability control for 4WS systems still faces challenges, including the delay in vehicle dynamic response, the need for enhanced control precision, and improved adaptability. Therefore, to address these challenges, an in-depth study to improve the control algorithm so as to enhance the stability of 4WS system is particularly necessary.

1.2. Literature Review

Scholars worldwide have conducted extensive research on the stability of 4WS systems. Zhu et al. [9] designed a fuzzy PID controller to optimize the dynamic performance of the four-wheel steering system, but the vehicle dynamic response had a delay. Yu et al. [10] proposed a combined feedforward and feedback control strategy based on Ackermann steering and fuzzy PID theory, which, however, requires further enhancement in control precision and disturbance rejection when facing complex conditions and nonlinear characteristics. Luo et al. [11] introduced a time-varying LQR controller based on genetic algorithms to address the coordinated control issue of 4WS and torque, but its adaptability to the nonlinear characteristics of vehicles was relatively weak.

Thus, the stability of 4WS can be enhanced through the following approaches: increasing system control precision and strengthening system adaptability and disturbance rejection. Variable steering ratio (VSR) technology dynamically adjusts the steering ratio according to driving conditions, thereby improving control precision, enhancing adaptability, and elevating stability.

With the rapid development of automotive electronics technology, VSR control methods began to receive widespread attention after 2000. In 2014, Zhou Bing et al. [12] proposed a study on the design of improved variable ratio curves for active front-wheel steering systems based on fuzzy reasoning, which marked a new stage in the research of VSR control methods in both academia and industry. However, fuzzy rules are mainly based on empirical judgments and have a low accuracy. Nogami et al. [13] improved the Pure Pursuit method by dynamically adjusting the ratio of front- and rear-wheel steering angles to optimize path tracking, which can adapt to different steering modes. However, the curve lacks smoothness. To address this issue, Kang et al. [14] used Hermite interpolation near the segment points to smooth the VSR curve, but it could not ensure the continuity of the second-order derivative. Li et al. [15] used a specific fitting function to process the VSR function curve, but the local control capability of this method needs to be improved, and the fitting error of the curve is relatively large. Therefore, Li et al. [16] used the arctan function for the local fitting of the VSR curve, but the steering ratio at low and high speeds needs optimization. Chen et al. [17] proposed a fuzzy control method based on particle swarm optimization, using steering wheel angle and vehicle speed as fuzzy inputs to dynamically optimize the VSR curve. This method can automatically adjust fuzzy rules, avoiding the limitations of traditional fuzzy control that relies on expert experience. However, the output transmission ratio is affected by the discretization of rules. Zhao et al. [18] optimized the variable transmission ratio based on constant weight and constant lateral acceleration gain, which can effectively avoid the problems of under-steering or over-steering during vehicle turns. However, this method has a high design complexity and requires a more accurate vehicle dynamics model. Therefore, Liu et al. [19] optimized the variable transmission ratio curve based on yaw rate gain, combining vehicle speed and steering wheel angle with particle swarm optimization for steering gain. This method has strong global optimization capabilities but is not suitable for fine-tuning specific speed ranges. Based on existing research, studies on 4WS systems with VSR are relatively rare. Moreover, current methods for optimizing VSR curves often fail to balance smoothness, continuity, local control capability, and design complexity. Therefore, the further exploration of VSR curve optimization methods is needed to resolve these contradictions.

In addition, enhancing the system’s disturbance rejection capability can also improve stability. Compared with other methods, the sliding mode control (SMC), proposed by the Soviet scholar Fliigge-Lotz in 1950, achieves the dynamic control of the system by designing sliding surfaces, which has the advantages of fast response speed, insensitivity to parameter changes and disturbances, etc., and can overcome the uncertainty of the system, which is commonly used in the stability control of vehicles [20]. Traditional SMC, however, due to the use of a linear sliding surface, faces the issue of chattering when the state trajectory reaches the sliding mode surface, leading to a slow convergence speed [21]. V. Changoski and Dai P mitigated chattering to a certain extent by modifying the sign function [22,23], yet the robustness and convergence speed still require enhancement. Dang et al. [24] implemented 4WS control based on the exponential reaching law using Fuzzy-SMC, which to some extent improved the convergence speed. However, this method is prone to high-frequency switching, thereby causing chattering. To alleviate chattering, Tushar Khanke et al. [25] combined inertial-delay-SMC with VSR, effectively compensating for the vehicle’s nonlinear dynamics, but the system performance is affected when facing external disturbances and system uncertainties. Zhou et al. [26] considered the parameter uncertainties and disturbances and proposed an adaptive sliding mode control strategy for yaw stability based on the phase plane, which can effectively reduce the error between the actual and ideal values of the control parameters. However, the computational load is increased. Tian et al. [27] employed optimal control and fractional-order-SMC for the state error of 4WS and the system control precision needs improvement. Tan et al. [28] proposed an integral time-varying sliding mode controller to eliminate steady-state errors, but the control precision is limited, failing to adjust the control quantity in time to achieve the desired performance. To enhance the control accuracy, Zhang et al. [29] proposed a robust sliding mode control method based on the Takagi–Sugeno fuzzy model, which addresses the coordination challenge between ride comfort and vehicle stability in the four-wheel steering system. However, this method requires a high degree of precision in the system model.

As a high-order sliding mode control method, the super-twisting (ST) algorithm was firstly proposed by Levant in 1993 [30], which achieves the finite time convergence of the system through the continuous control law and effectively reduces the jitter phenomenon, and has the advantages of reducing the jitter, simple design, strong robustness, and high control accuracy [31]. Dan et al. [32] proposed an SMC method based on rapid state feedback and disturbance observer, which has strong disturbance rejection capability, but requires the upper bound of system uncertainties for finite-time stability. To address this, Tu et al. [33] introduced a novel super-twisting decoupled non-singular fast terminal sliding mode control, while achieving the finite-time convergence of system states. However, the system’s adaptive adjustment capability in the face of parameter changes and complex disturbances needs improvement. Hu et al. [34] proposed an adaptive multivariable super-twisting control algorithm to mitigate the effect of chattering, enhancing the robustness of 4WS system. Yet, when dealing with rapidly changing dynamic systems, the convergence speed requires further optimization. Given the current research on sliding mode control methods, it is known that there is a trade-off between disturbance rejection, convergence speed, computational complexity, and control precision. How to improve the sliding mode control algorithm to enhance these characteristics comprehensively is the focus of this paper.

1.3. Main Contributions

In summary, in the field of 4WS stability control, research that can simultaneously achieve high control precision, strong adaptability, superior disturbance rejection capability, and rapid convergence is relatively limited. Therefore, this paper proposes a 4WS controller based on VSR and FAST sliding mode control to regulate and output the steering angles of all four wheels. Compared with the constant steering ratio and conventional sliding mode control methods, VSR-FAST controller enhances the system’s disturbance rejection capability while improving its adaptability, control precision, and convergence speed, thereby significantly enhancing the handling stability of the 4WS system. The main contributions are as follows:

(1)

Based on the design of constant yaw rate gain VSR strategy, the reference front wheel angle is obtained, which solves the problem that the traditional constant steering ratio cannot dynamically adjust the transmission ratio according to vehicle speed and driver input angle. It achieves the sensitivity of low-speed steering and the stability of high-speed steering, and improves system adaptability;

(2)

To reduce steering fluctuations, the VSR strategy is combined with a cubic quasi-uniform B-spline curve fitting method to achieve the purpose of locally optimizing the VSR curve, thereby improving the steering performance caused by non-smooth curves at critical speeds;

(3)

To solve the problems of chattering and slow convergence speed in traditional SMC, a 4WS controller based on the FAST algorithm is designed to calculate the additional rear wheel angle. This algorithm does not require prior knowledge of the system uncertainty boundary, taking into account system anti-interference, and has relatively fast convergence speed and control accuracy, thereby enhancing the handling stability of four-wheel steering at different speeds.

1.4. Paper Organization

The structure of this paper is as follows: In Section 2, the establishment of 2-DOF reference vehicle model is introduced. In Section 3, the VSR strategy design and curve fitting optimization based on fixed yaw rate gain are introduced. In Section 4, the design of VSR-FAST 4WS controller and the stability proof of FAST algorithm are presented. In Section 5, the co-simulation results using MATLAB/Simulink and Carsim under different speeds are presented. The conclusion of this paper is presented in Section 6.

2. Vehicle Dynamic Model

2.1. Vehicle Lateral Dynamics Model

In order to conduct a more thorough investigation into the lateral dynamics of a 4WS system, and consider the effects of the sideslip angle and yaw rate on the stability of a vehicle, the symmetric 2-DOF 4WS vehicle model was established, as shown in Figure 1 [35], without considering the impact of rolling and assuming a constant speed.

The motion equation of the symmetric vehicle model is obtained from Figure 1 [35]:

$$\left\{\begin{array}{l}m{v}_x\left(\dot{\beta }+\gamma \right)=\left(k_1+k_2\right)\beta +{\displaystyle \frac{\left(a{k}_1-b{k}_2\right)\gamma }{v_x}}-k_1{\delta }_f-k_2{\delta }_r\hfill \\ I_z\dot{\gamma }=\left(a{k}_1-b{k}_2\right)\beta +{\displaystyle \frac{a^2{k}_1+b^2{k}_2}{v_x}}\gamma -a{k}_1{\delta }_f+b{k}_2{\delta }_r\hfill \end{array}\right.$$

(1)

where $\beta$ is the sideslip angle, $\gamma$ is the yaw rate, ${\delta }_f$ is the front wheel angle, ${\delta }_r$ is the rear wheel angle, $k_1$ is the lateral stiffness of front axle, $k_2$ is the lateral stiffness of rear axle, $a$ is the distance from CG to front axle, $b$ is the distance from CG to rear axle, $L$ is the wheelbase and $L=a+b$, $v_x$ is the longitudinal velocity, $m$ is the total mass of the vehicle, $I_z$ is the yaw inertia moment, $F_{yf}$ is the lateral tire force of the front wheel, $F_{yr}$ is the lateral tire force of the front wheel, $v_y$ is the lateral velocity, ${\alpha }_f$ is the front tire slip angle, ${\alpha }_r$ is the rear tire slip angle, $v_f$ is front wheel velocity, and $v_r$ is the rear wheel velocity.

Converted to the state space equation, the symmetric 2-DOF 4WS vehicle model can be written as

$$\left[\begin{array}{c}\dot{\beta }\\ \dot{\gamma }\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \frac{k_1+k_2}{m{v}_x}}& {\displaystyle \frac{a{k}_1-b{k}_2}{m{v}_x^2}}-1\\ {\displaystyle \frac{a{k}_1-b{k}_2}{I_z}}& {\displaystyle \frac{a^2{k}_1+b^2{k}_2}{I_z{v}_x}}\end{array}\right]\left[\begin{array}{c}\beta \\ \gamma \end{array}\right]+\left[\begin{array}{cc}-{\displaystyle \frac{k_1}{m{v}_x}}& -{\displaystyle \frac{k_2}{m{v}_x}}\\ -{\displaystyle \frac{a{k}_1}{I_z}}& {\displaystyle \frac{b{k}_2}{I_z}}\end{array}\right]\left[\begin{array}{c}{\delta }_f\\ {\delta }_r\end{array}\right]$$

(2)

2.2. Ideal Reference Model

Utilizing the steady-state yaw rate based on the 2-DOF front-wheel steering vehicle model ensures that the yaw rate response of a 4WS vehicle closely approximates that of a front-wheel steering vehicle, thereby providing the driver with a satisfactory driving experience. Therefore, this section assumes that the vehicle moves in an ideal circle, ignores the difference between the front and rear wheels of the vehicle and the influence of air resistance, establishes the 2-DOF vehicle model, as shown in Figure 2.

The kinetic differential equation of the 2-DOF vehicle model can be written as

$$m{v}_x\left(\dot{\beta }+\gamma \right)=\left(k_1+k_2\right)\beta +{\displaystyle \frac{\left(a{k}_1-b{k}_2\right)\gamma }{v_x}}-k_1{\delta }_f$$

(3)

$$I_z\dot{\gamma }=\left(a{k}_1-b{k}_2\right)\beta +{\displaystyle \frac{a^2{k}_1+b^2{k}_2}{v_x}}\gamma -a{k}_1{\delta }_f$$

(4)

From Equation (4), it can be deduced:

$$\beta ={\displaystyle \frac{I_z\dot{\gamma }-\frac{a^2{k}_1+b^2{k}_1}{v_x}\gamma +a{k}_1{\delta }_f}{a{k}_1-b{k}_2}}$$

(5)

By substituting the preceding equation into Equation (3) and proceeding with further derivations, the following result can be obtained:

$${\gamma }_{rm}={\displaystyle \frac{v_x/L}{\frac{m}{L^2}\left(\frac{a}{k_2}-\frac{b}{k_1}\right)v_x^2+1}}{\delta }_f$$

(6)

where ${\gamma }_{rm}$ is the ideal yaw rate; let $K={\displaystyle \frac{m}{L^2}}\left({\displaystyle \frac{a}{k_2}}-{\displaystyle \frac{b}{k_1}}\right)$, $K$ is the stability factor.

To ensure the stability of the vehicle driving at a high speed, the limit of road adhesion coefficient on the yaw rate is considered, and 15% road adhesion margin is reserved [36]; so, the yaw rate amplitude constraint is taken as follows:

$$\left|{\gamma }_{max}\right|\le \left|{\displaystyle \frac{0.85 \mathsf{\mu }\mathrm{g}}{v_x}}\right|$$

(7)

where $\mu$ is the road adhesion coefficient and $g$ is the acceleration of gravity.

The ideal yaw rate is determined as follows:

$${\gamma }_d=\min \left(\left|{\displaystyle \frac{v_x/L}{1+K{v}_x^2}}\cdot {\delta }_f\right|,\left|{\displaystyle \frac{0.85 \mathsf{\mu }\mathrm{g}}{v_x}}\right|\right)sgn\left({\delta }_f\right)$$

(8)

3. Variable Steering Ratio Curve Design

The steering ratio of passenger vehicles is generally regarded as a fixed value, ranging from 15:1 to 20:1. This can lead to an excessively high gear ratio at low speeds, resulting in sluggish steering operations that are not conducive to driver control. Conversely, at high speeds, the gear ratio is too low, leading to an overly sensitive response, which can compromise stability and safety. While, during the four-wheel steering process, the steering angle and slip speed of the front and rear wheels will be different. To enhance the stability and balance of four-wheel steering, VSR is employed to ensure that the vehicle remains stable and maintains consistent steering sensitivity across different operating conditions.

3.1. Constant Yaw Rate Gain

An excessively low yaw rate gain can result in sluggish vehicle steering response; an overly high yaw rate can lead to excessively sensitive steering, which may compromise safety. To ensure lateral stability when steering at any speed, the yaw rate gain should be constant.

Based on the constant yaw rate gain, Laplace transform is performed by Equation (4), and the steady yaw rate gain can be expressed as:

$$G_s={\displaystyle \frac{v_x/L}{1+K{v}_x^2}}$$

(9)

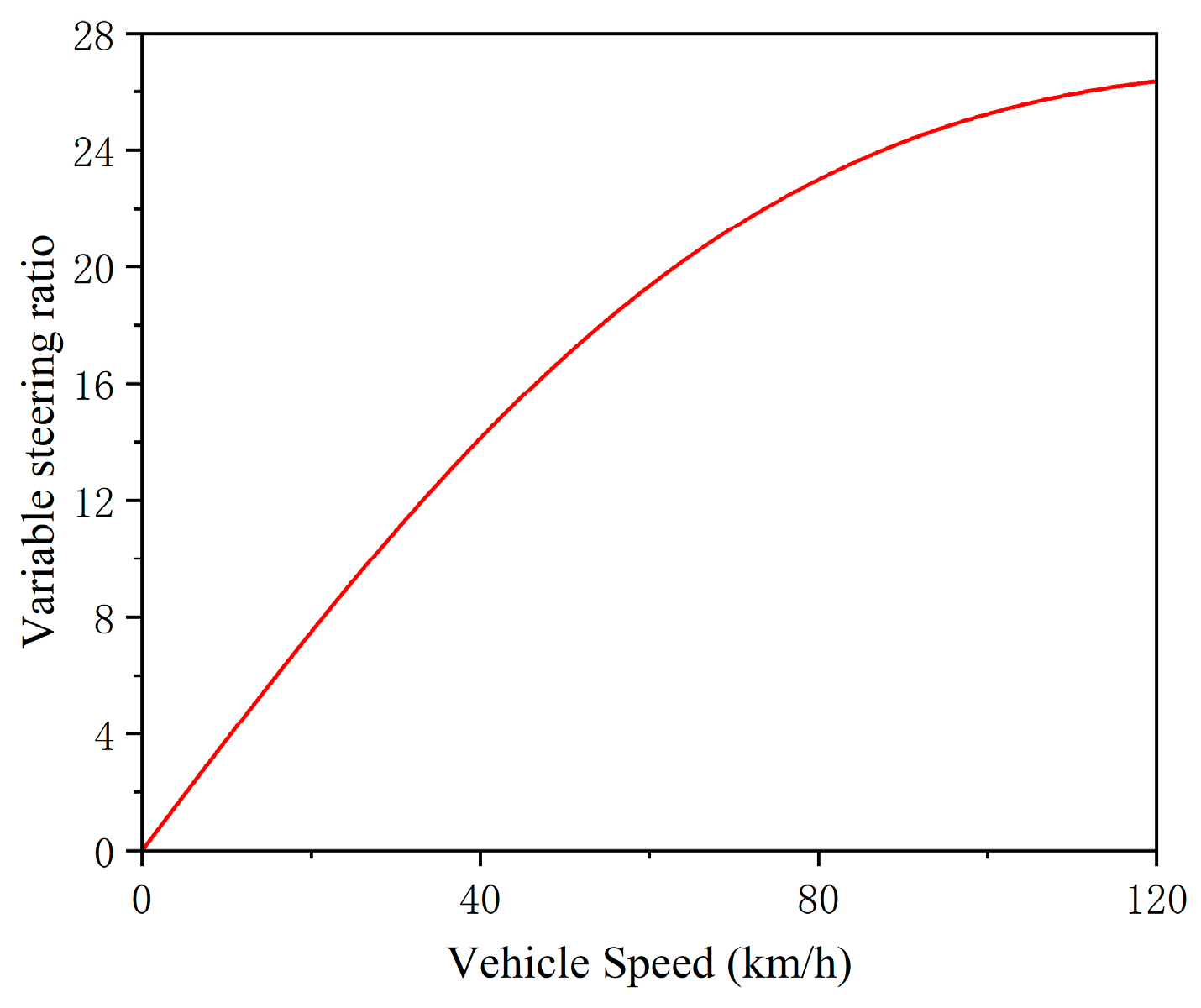
3.2. Ideal VSR Curve

To ensure that the fixed proportional relationship between the steering wheel angle and the heading angle is independent of speed, the steady yaw rate gain should be a constant that does not change with speed; so, the ideal VSR is based on the constant yaw rate gain. The rule of ideal VSR is derived as follows:

$$i_w={\displaystyle \frac{{\delta }_{sw}}{{\delta }_f}}$$

(10)

where $i_w$ is the ideal VSR and ${\delta }_{sw}$ is the steering wheel angle.

The steering sensitivity can be calculated as [14]:

$$G_{\mathrm{h}}={\displaystyle \frac{G_s}{i_w }}={\displaystyle \frac{v_x/L}{\left(1+K{v}_x^2\right)i_w}}$$

(11)

Generally, the value of $G_{\mathrm{h}}$ ranges from 0.22 to 0.37 s⁻¹ [37]. In this paper, $G_{\mathrm{h}}=$ 0.25 ${\mathrm{s}}^{-1}$ was set. The ideal VSR $i_w$ is further expressed as

$$i_w ={\displaystyle \frac{v_x/L}{G_{\mathrm{h}}\left(1+K{v}_x^2\right)}}$$

(12)

The ideal VSR curve within 0–120 km/h can be obtained as:

From Figure 3, the value of steering ratio increases from 0 to 32.79 with the increase in the speed. At a low speed, an excessively small steering ratio can lead to overly sensitive steering operations, which may impact stability and safety. At high speed, an excessively large steering ratio can result in sluggish steering, which is not conducive to lane changes and obstacle avoidance, thereby increasing driver fatigue.

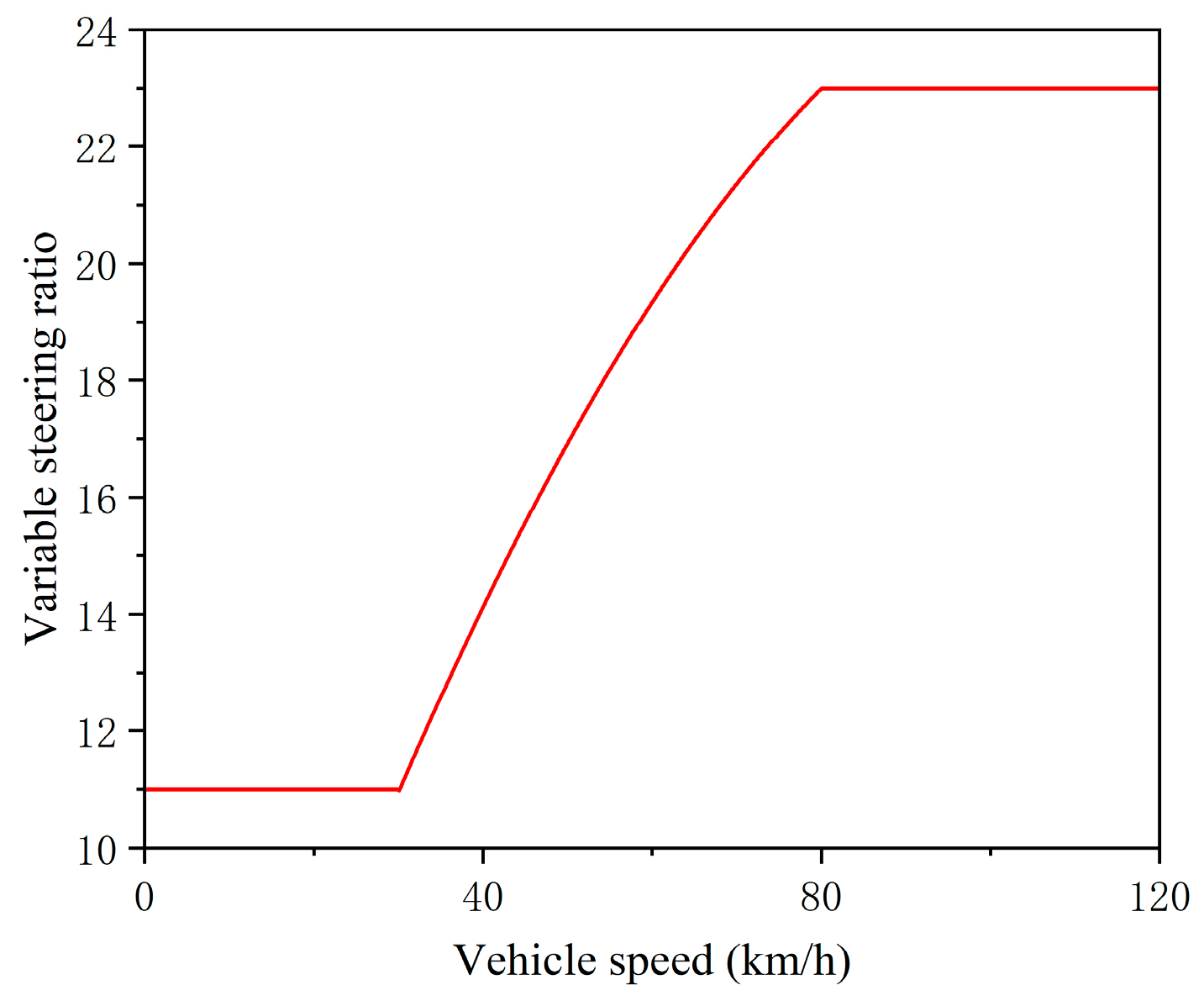
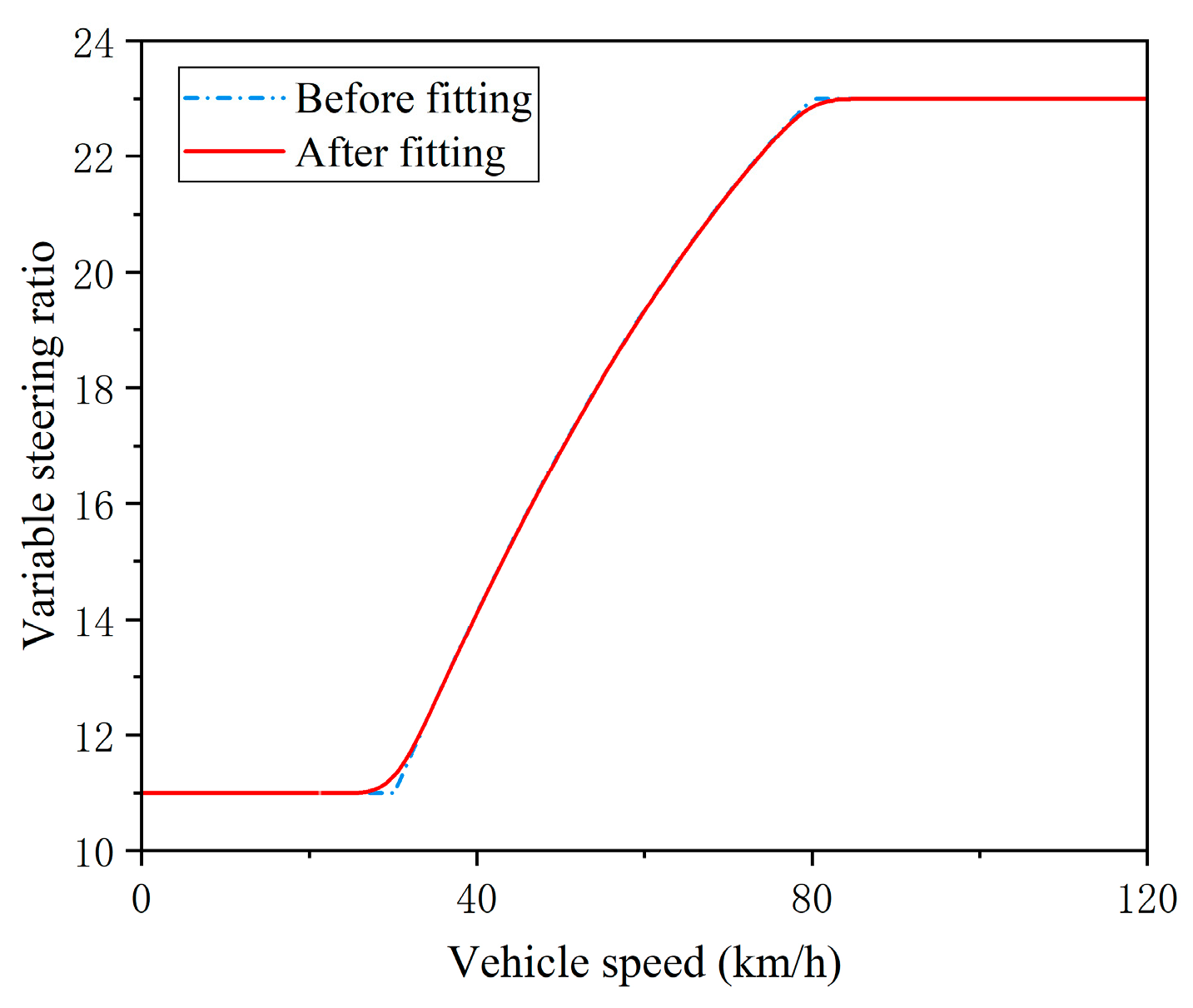
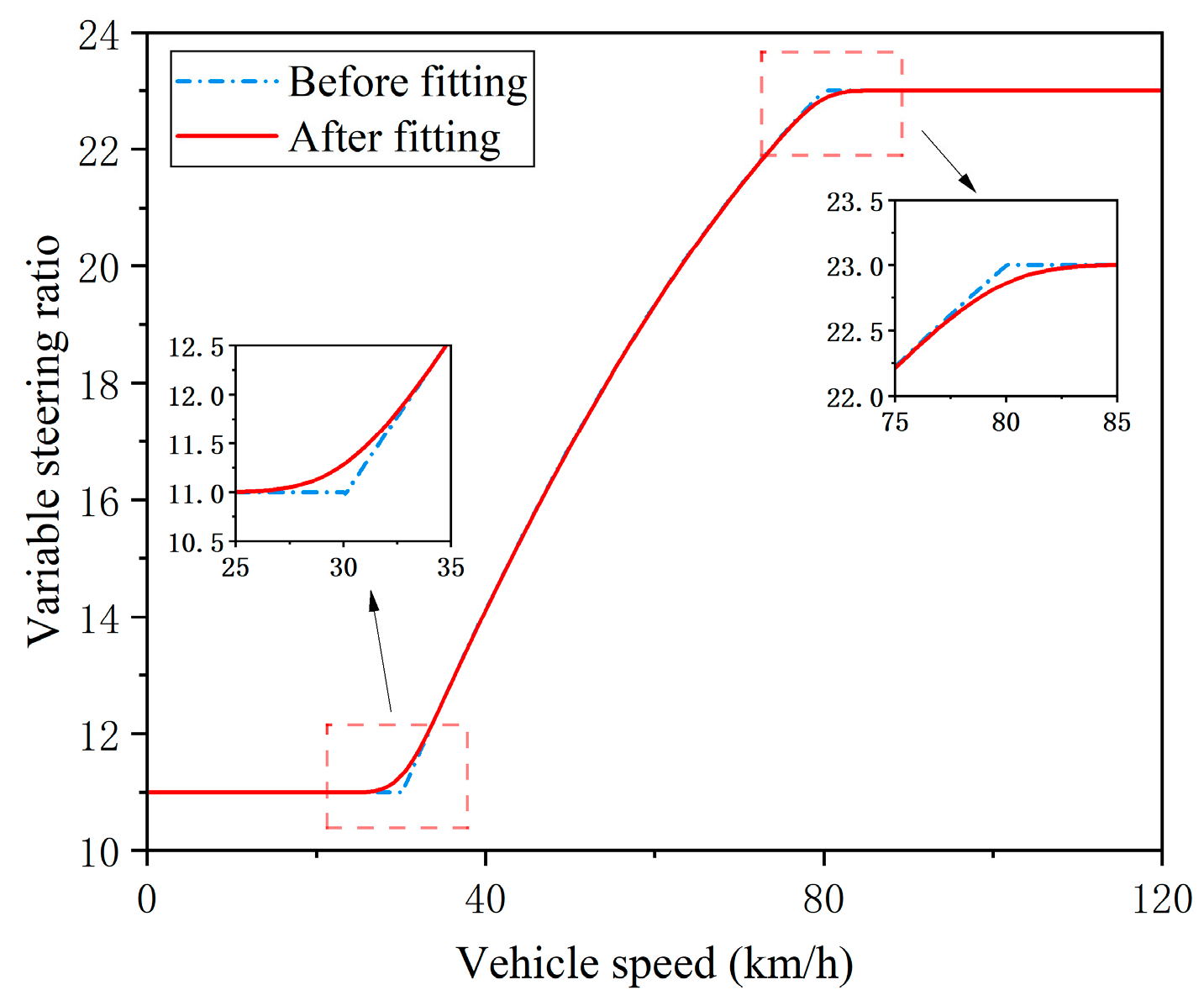
3.3. VSR Strategy Design and Curve Fitting

In order to ensure handing stability, the upper and lower speed thresholds were set. At a low speed ($v_x\le 30 \mathrm{km}/\mathrm{h}$), a fixed steering ratio ($i_w=11$) was set. At a high speed ($v_x\ge 80 \mathrm{km}/\mathrm{h}$), a fixed steering ratio ($i_w=23$) was set.

The ideal VSR function after design is expressed as:

$$i_{wd}=\left\{\begin{array}{ll}11\hfill & v_x\le 30 \mathrm{km}/\mathrm{h}\hfill \\ {\displaystyle \frac{v_x/L}{G_{\mathrm{h}}\left(1+K{v}_x^2\right) }}\hfill & 30 \mathrm{km}/\mathrm{h}<v_x<80 \mathrm{km}/\mathrm{h}\hfill \\ 23\hfill & v_x\ge 80 \mathrm{km}/\mathrm{h}\hfill \end{array}\right.$$

(13)

The VSR curve can be shown as:

From Figure 4, the VSR curve is not smooth at the critical speed, and the function is continuous but not differentiable at the segment point, which will cause sudden changes and fluctuations in steering near the critical speed during acceleration and deceleration, resulting in a reduction in stability.

Therefore, it is necessary to fit the curve. The B-spline curve fitting method approximates the given data point by using basic function, and the curve modification is more flexible. The B-spline curve of order $k$ is defined as [38]:

$$P\left(j\right)=\left[\begin{array}{cccc}{P}_0& P_1& \dots & P_n\end{array}\right]\left[\begin{array}{c}{B}_{0,k}\left(j\right)\\ B_{1,k}\left(j\right)\\ ⋮\\ B_{n,k}\left(j\right)\end{array}\right]={\displaystyle \sum }_0^n{P}_i{B}_{i,k}\left(j\right)$$

(14)

where $P_i$ are the control points, corresponding to the $i\text{-}th$ $k\text{-}th$ order B-spline basic function $B_{i,k}\left(j\right)$; $k$ is the order; $j$ is the independent variable, $j\in \left[\begin{array}{c}{j}_{k-1},j_{n+1}\end{array}\right]$; $B_{i,k}\left(j\right)$ is the basic function; its de Boor–Cox recurrence can be expressed as

$$B_{i,k}\left(j\right)=\left\{\begin{array}{ll}\left\{\begin{array}{cc}1& j_i\le j\le j_{i+1}\\ 0& else\end{array}\right.\hfill & k=1\hfill \\ {\displaystyle \frac{j-j_i}{j_{i+k-1}-j_i}}{B}_{i,k-1}\left(j\right)+{\displaystyle \frac{j_{i+k}-j}{j_{i+k}-j_{i+1}}}{B}_{i+1,k-1}\left(j\right)\hfill & k\ge 2\hfill \end{array}\right.$$

(15)

where knot vector $J=\left\{j_0,j_1,\dots ,j_{i+k}\right\}$ is a monotone non-decreasing sequence.

The quasi-uniform B-spline end node repeatability is $k$, and the other nodes are uniformly distributed in an equivariant non-decreasing sequence. A cubic interpolation basic function is used with a higher number of polynomials to make the curve smoother; its node distribution parameters can be expressed as:

$$J=\left\{0,0,0,1,2,3,\dots n,n,n\right\}$$

(16)

The VSR curve is smoothly fitted and the data interpolated by cubic quasi-uniform B-spline, and the fitted VSR curve can be represented as Figure 5.

The fitted curve is continuously differentiable everywhere and closely approximates the original curve, thereby meeting the design requirements of the steering system and contributing to the enhancement in the vehicle’s handling stability.

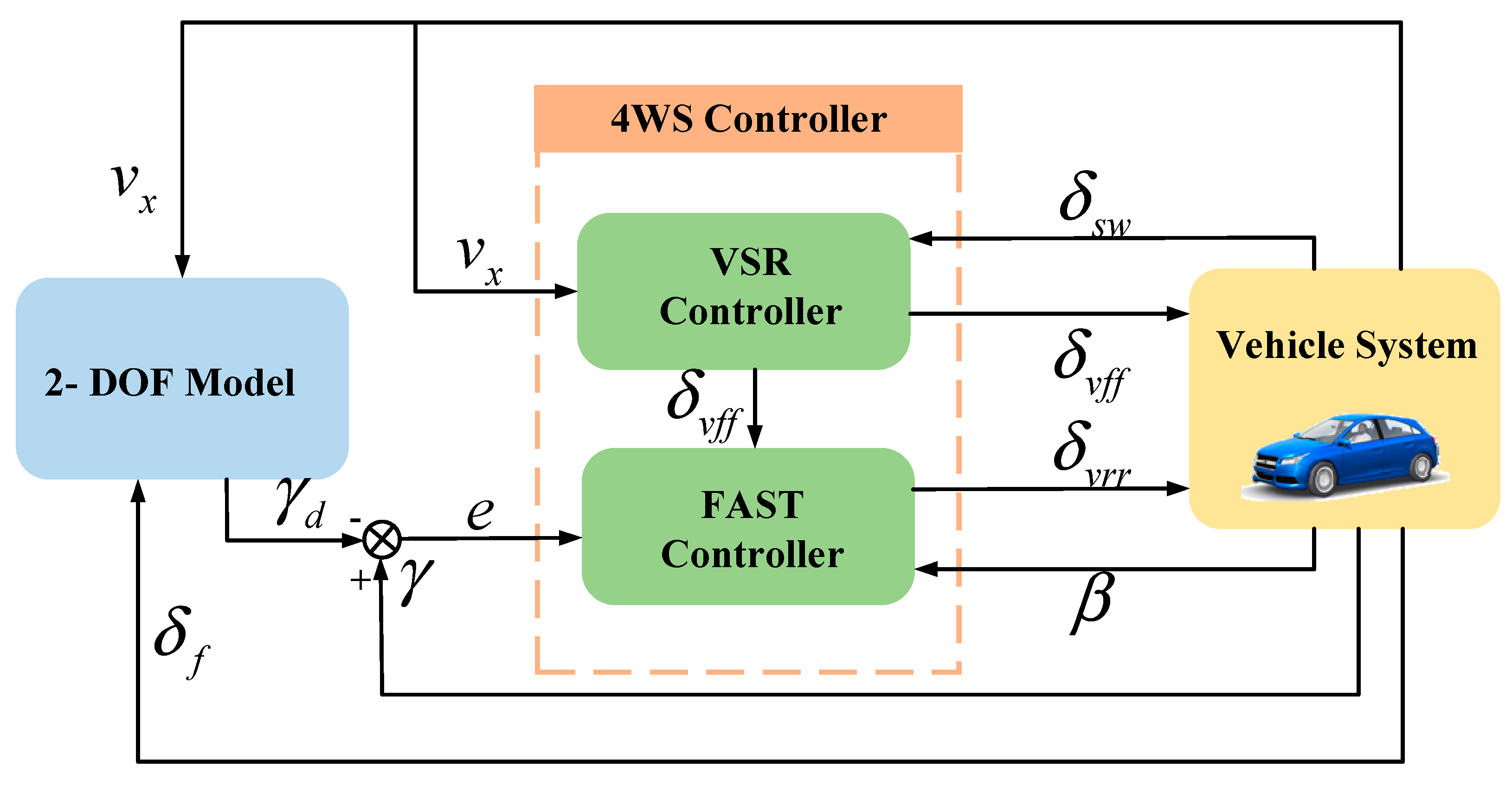
4. WS Controller Design

The structure of the 4WS system based on VSR-FAST is shown in Figure 6. The vehicle inputs signals, such as steering wheel angle, speed, front and rear wheel angles into 2-DOF vehicle model, VSR controller, and FAST controller, and calculates the reference front wheel angle and the additional rear wheel angle, which are applied to the vehicle to form the closed-loop control of 4WS and improve the dynamic stability performance.

4.1. FAST Sliding Mode Control Algorithm

From Equation (1), the 2-DOF 4WS vehicle model can be considered as a system of relative order 1:

$$\dot{x}=u_c+G$$

(17)

where system state $x\in R$, control input $u_c\in R$, and uncertain item $G\in R$.

In uncertain item $G=G_1\left(x,t\right)+G_2\left(x,t\right)$, $G_1\left(x,t\right)$ represents the non-differentiable uncertainty of the system, and $G_2\left(x,t\right)$ represents the differentiable uncertainty of the system.

Assume that $G_1\left(x,t\right)$, $G_2\left(x,t\right)$ are satisfied:

$$\left\{\begin{array}{c}{\displaystyle \frac{\left|G_1\left(x,t\right)\right|}{q_1}}\le \left|{\sigma }_1\left(x\right)\right|\\ {\displaystyle \frac{\left|{\dot{G}}_2\left(x,t\right)\right|}{q_2}}\le \left|{\sigma }_2\left(x\right)\right|\\ G_1\left(0,0\right)=0\end{array}\right.$$

(18)

where $q_1$, $q_2$ are unknown positive numbers, and ${\sigma }_1\left(x\right)$, ${\sigma }_2\left(x\right)$ are sliding mode variable functions.

FAST control law of system (17) is designed as follows [39]:

$$\left\{\begin{array}{l}{u}_c=u_{eq}+u_{sw}\hfill \\ u_{sw}=-c_1{\sigma }_1\left(x\right)+u_1\hfill \\ {\dot{u}}_1=-c_2{\sigma }_2\left(x\right)\hfill \end{array}\right.$$

(19)

where $u_{eq}$ is the sliding mode control item, $u_{sw}$ is the sliding mode switch item, and $c_1$, $c_2$ are parameters to be designed,

$$\left\{\begin{array}{l}{\sigma }_1\left(x\right)={\left|x\right|}^{{\displaystyle \frac{1}{2}}}\mathrm{sgn}\left(x\right)+x\hfill \\ {\sigma }_2\left(x\right)={\displaystyle \frac{1}{2}}\mathrm{sgn}\left(x\right)+{\displaystyle \frac{3}{2}}{\left|x\right|}^{{\displaystyle \frac{1}{2}}}\mathrm{sgn}\left(x\right)+x\hfill \end{array}\right.$$

(20)

In order to improve the convergence speed and enhance the stability of the system, an adaptive parameter controller is designed as

$$\left\{\begin{array}{l}{\dot{c}}_1=\left\{\begin{array}{cc}{\displaystyle \frac{4\left(2d_1+d_2\right)sgn\left(\left|x\right|-\tau \right)}{1+d_2^2}}\cdot \left({\displaystyle \frac{1}{2}}{\left|x\right|}^{-{\displaystyle \frac{1}{2}}}+1\right){\sigma }_1^2\left(x\right)& \left|x\right|>0\\ 0& \left|x\right|=0\end{array}\right.\hfill \\ c_2={\displaystyle \frac{c_1{d}_2}{2}}+{\displaystyle \frac{4d_1+d_2^2}{2}}-{\displaystyle \frac{d_2}{2d_3}}-{\displaystyle \frac{d_2\left(4d_1+d_2^2\right)}{4d_4}}\hfill \end{array}\right.$$

(21)

where $d_1$, $d_2$, $d_3$, and $d_4$ are any rear numbers, and $\tau$ is a smaller positive number.

4.2. Design of 4WS Controller Based on VSR-FAST

The deviation between the actual yaw rate $\gamma$ and the desired yaw rate ${\gamma }_d$ is taken as the tracking error of the system, which can be expressed as:

$$e=\gamma -{\gamma }_d$$

(22)

Define the sliding mode surface $s$ as

$$s=e=\gamma -{\gamma }_d$$

(23)

The derivation yields:

$$\dot{s}=\dot{e}=\dot{\gamma }-{\dot{\gamma }}_d$$

(24)

Substitute Equation (1) into Equation (24) to obtain

$$\dot{s}={\displaystyle \frac{a{k}_1-b{k}_2}{I_z}}\beta +{\displaystyle \frac{a^2{k}_1+b^2{k}_2}{I_z{v}_x}}\gamma -{\displaystyle \frac{a{k}_1}{I_z}}{\delta }_{vff}+{\displaystyle \frac{b{k}_2}{I_z}}{\delta }_{vrr}-{\dot{\gamma }}_d$$

(25)

where ${\delta }_{vrr}$ is the additional rear wheel angle, and ${\delta }_{vff}$ is the reference front wheel angle, which can be calculated from the ideal VSR after design:

$${\delta }_{vff}={\displaystyle \frac{{\delta }_{sw}}{i_{wd}}}$$

(26)

According to the FAST algorithm, the equivalent sliding mode control law can be designed as

$$u_{eq}={\displaystyle \frac{I_z}{b{k}_2}}\left(-{\displaystyle \frac{a{k}_1-b{k}_2}{I_z}}\beta -{\displaystyle \frac{a^2{k}_1+b^2{k}_2}{I_z{v}_x}}\gamma +{\displaystyle \frac{a{k}_1}{I_z}}{\delta }_{vff}+{\dot{\gamma }}_d\right)$$

(27)

According to Equations (19) and (27), the control law can be obtained as

$$\begin{array}{ll}{u}_c& ={\delta }_{vrr}\\ & ={\displaystyle \frac{I_z}{b{k}_2}}\left(-{\displaystyle \frac{a{k}_1-b{k}_2}{I_z}}\beta -{\displaystyle \frac{a^2{k}_1+b^2{k}_2}{I_z{v}_x}}\gamma +{\displaystyle \frac{a{k}_1}{I_z}}{\delta }_{vff}+{\dot{\gamma }}_d\right)-c_1{\sigma }_1\left(s\right)-{\displaystyle \int c_2{\sigma }_2\left(s\right)}\end{array}$$

(28)

4.3. Stability Proof of FAST Controller

Lemma [40]: For nonlinear systems:

$$\dot{x}=f\left(x\right) \left(x\in R^n\right)$$

(29)

Suppose there is a continuously differentiable $V\left(x\right):U\to R$ satisfies

(1)

$V\left(x\right)$ is a positive definite;

(2)

The existence of positive real numbers ${\xi }_1>0$, ${\xi }_2>0$, $\alpha \in \left(0,1\right)$, and an open neighborhood $U_0\subset U$, containing the origin, makes the equation hold:

$$\begin{array}{cc}\dot{V}\left(x\right)+{\xi }_{1}V{\left(x\right)}^{\alpha }+{\xi }_{2}V\left(x\right) \le 0& x\in U_0\backslash \left\{0\right\}\end{array}$$

(30)

Then, System (29) is finite time stable;

If $U=U_0=R^n$, System (29) is global finite time stable. Convergence time $t_r$ meets:

$$t_r⩽{\displaystyle \frac{1}{{\xi }_2\left(1-\alpha \right)}}\ln {\displaystyle \frac{{\xi }_{2}V{\left(\begin{array}{c}{x}_0\end{array}\right)}^{1-\alpha }+{\xi }_1}{{\xi }_1}}$$

(31)

Substituting Equation (19) into Equation (17), the control system can be obtained as

$$\left\{\begin{array}{l}{\dot{x}}_1=-c_1{\sigma }_1\left(\begin{array}{c}{x}_1\end{array}\right)+x_2+{\epsilon }_1\hfill \\ {\dot{x}}_2=-c_2{\sigma }_2\left(\begin{array}{c}{x}_1\end{array}\right)+{\epsilon }_2\hfill \end{array}\right.$$

(32)

Define a Lyapunov function of quadratic type $V=Z^{T}YZ$, where

$$\begin{array}{ccc}Y=\left[\begin{array}{cc}{\displaystyle \frac{4d_1+d_2^2}{2}}& {\displaystyle \frac{-d_2}{2}}\\ {\displaystyle \frac{-d_2}{2}}& 1\end{array}\right]& d_1>0& d_2>0\end{array}$$

(33)

$$Z=\left[\begin{array}{cc}{\sigma }_1\left(x_1\right)& x_2\end{array}\right]$$

(34)

By

$$\left\{\begin{array}{l}{{\sigma }^{\prime }}_1\left(x_1\right)={\displaystyle \frac{1}{2}}{\left|x_1\right|}^{-{\displaystyle \frac{1}{2}}}+1\ge 0\\ {\sigma }_2\left(x_1\right)={\sigma }_1\left(x_1\right){{\sigma }^{\prime }}_1\left(x_1\right)\end{array}\right.$$

(35)

where ${{\sigma }^{\prime }}_1\left(x_1\right)$ represents the derivative of ${\sigma }_1\left(x_1\right)$ with respect to the independent variable. Thus, it can be obtained as

$$\begin{array}{ll}\dot{Z}& =\left[\left.\begin{array}{c}{\dot{\sigma }}_1\left(x_1\right)\\ {\dot{x}}_2\end{array}\right]\right.\\ & ={{\sigma }^{\prime }}_1\left(x_1\right)\left(\left[\begin{array}{cc}-c_1& 1\\ -c_2& 0\end{array}\right]\left[\begin{array}{c}{\mathsf{\sigma }}_1\left(x_1\right)\\ x_2\end{array}\right]+\left[\begin{array}{c}{\epsilon }_1\\ {\displaystyle \frac{{\epsilon }_2}{{{\sigma }^{\prime }}_1\left(x_1\right)}}\end{array}\right]\right)\\ & ={{\sigma }^{\prime }}_1\left(x_1\right)\left(AZ+B\right)\end{array}$$

(36)

where ${\dot{\sigma }}_1\left(x_1\right)$ represents the derivative of ${\sigma }_1\left(x_1\right)$ with respect to time.

Substitute Equation (36) into Equation (18) to obtain

$$W={\left[\begin{array}{c}Z\\ B\end{array}\right]}^T\left[\begin{array}{cc}\left(d_3{q}_1^2+d_4{q}_2^2\right)C^{T}C& \\ & -D\end{array}\right]\left[\begin{array}{c}Z\\ B\end{array}\right]\ge 0$$

(37)

where $C=\left[\begin{array}{c}1\\ 0\end{array}\right]$, $D=\left[\begin{array}{cc}{d}_3& \\ & d_4\end{array}\right]$.

The following equation can be obtained from Equations (35) and (36).

$$\begin{array}{ll}\dot{V}& ={\dot{Z}}^{T}YZ+Z^{T}Y\dot{Z}\\ & ={\tilde{\sigma }}_1\left(x_1\right)\left[Z^T\left(A^{T}Y+YA\right)Z+B^{T}YZ+Z^{T}YB\right]\\ & = {\tilde{\sigma }}_1\left(x_1\right)\left({\left[\begin{array}{c}Z\\ B\end{array}\right]}^T\left[\begin{array}{cc}{A}^{T}Y+YA& Y\\ Y& 0\end{array}\right]\left[\begin{array}{c}Z\\ B\end{array}\right]\right)\\ & \le {\tilde{\sigma }}_1\left(x_1\right)\left({\left[\begin{array}{c}Z\\ B\end{array}\right]}^T\left[\begin{array}{cc}{A}^{T}Y+YA& Y\\ Y& 0\end{array}\right]\left[\begin{array}{c}Z\\ B\end{array}\right]+W\right)\end{array}$$

(38)

By

$${\lambda }_{min}\left(Y\right){‖Z‖}_2^2\le Z^{T}YZ\le {\lambda }_{max}\left(Y\right){‖Z‖}_2^2$$

(39)

can obtain

$$\dot{V}\le {\displaystyle \frac{V}{{\lambda }_{\max }\left(Y\right)}}{\tilde{\sigma }}_1\left(x_1\right){\tau }_1=-{\displaystyle \frac{{\tau }_1}{2{\lambda }_{\max }\left(Y\right)}}{\left|x_1\right|}^{-{\displaystyle \frac{1}{2}}}V-{\displaystyle \frac{{\tau }_1}{{\lambda }_{\max }\left(Y\right)}}V$$

(40)

Then,

$$\dot{V}\le -{\displaystyle \frac{{\tau }_1{\lambda }_{\min }^{\frac{1}{2}}\left(Y\right)}{2{\lambda }_{max}\left(Y\right)}}{V}^{{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{{\tau }_1}{{\lambda }_{max}\left(Y\right)}}V$$

(41)

According to the lemma, if there exists any parameter $c_1$, $c_2$ satisfying:

$$\left\{\begin{array}{l}{c}_1>{\displaystyle \frac{2}{8d_1+d_2^2}}\left[{\tau }_1+d_3{q}_1^2+d_4{q}_2^2-{\displaystyle \frac{d_2^2}{4d_3}}-{\displaystyle \frac{{\left(4d_1+d_2^2\right)}^2}{4d_4}}\right]\hfill \\ \hfill \\ c_2={\displaystyle \frac{d_2}{2}}{c}_1+{\displaystyle \frac{4d_1+d_2^2}{2}}-{\displaystyle \frac{d_2}{2d_3}}-{\displaystyle \frac{d_2\left(4d_1+d_2^2\right)}{4d_4}}\hfill \\ {\tau }_1<d_2-{\displaystyle \frac{1}{d_3}}-{\displaystyle \frac{d_2^2}{4d_4}}\hfill \end{array}\right.$$

(42)

Then, $Z=\left[\begin{array}{cc}{\sigma }_1\left(x_1\right)& x_2\end{array}\right]$ converges to 0 in finite time, and the convergence time satisfies:

$$t_{restrain} \le {\displaystyle \frac{2{\lambda }_{max}\left(Y\right)}{{\tau }_1}}ln\left(1+{\displaystyle \frac{2}{{\lambda }_{min}^{\frac{1}{2}} \left(Y\right)}}V{\left(0\right)}^{{\displaystyle \frac{1}{2}}}\right)$$

(43)

That is, the system is stable within a finite time.

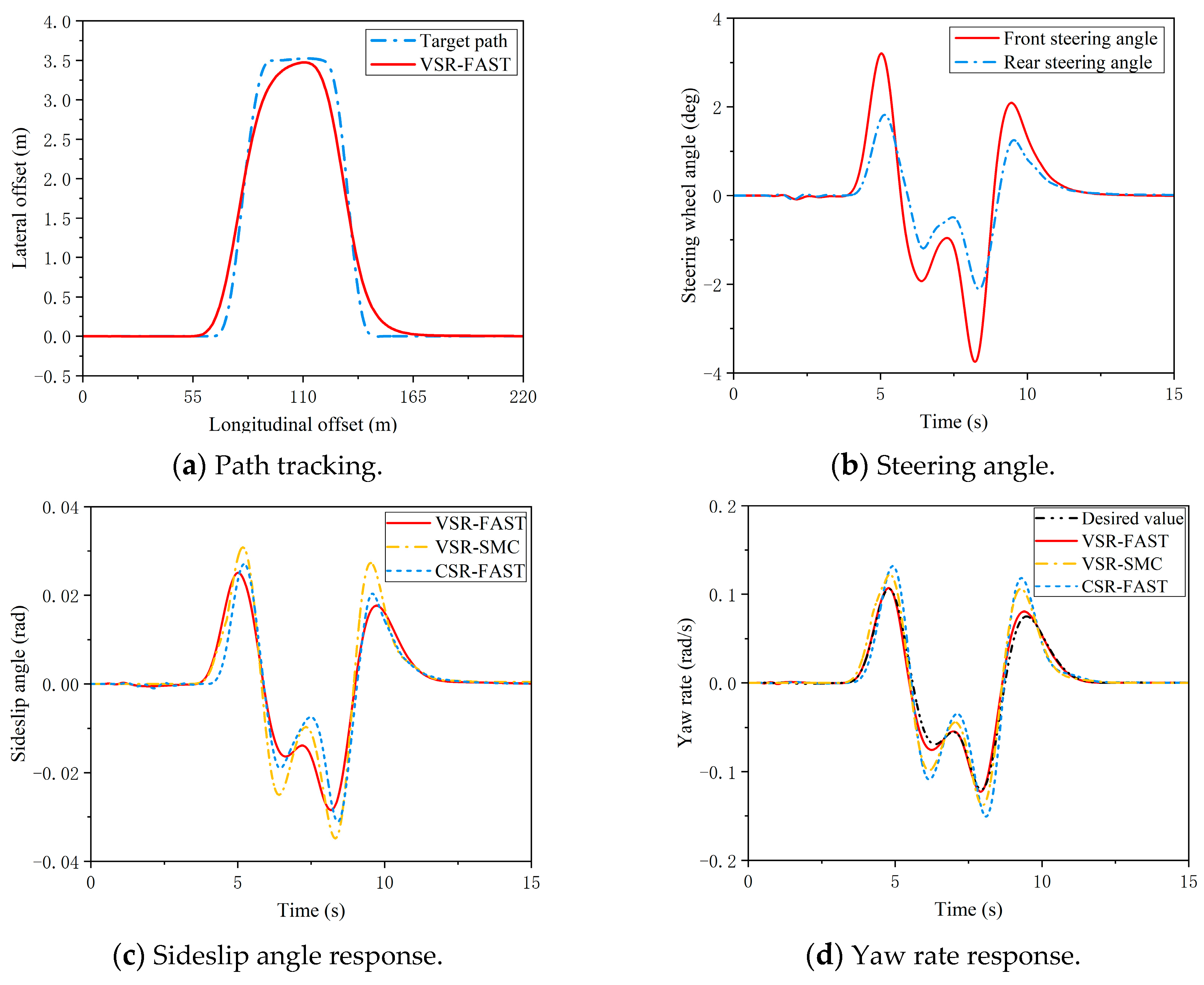
5. Simulation Results’ Analysis

5.1. Vehicle Parameters

This paper constructed the 4WS controller of electric vehicle using the MATLAB/Simulink and CarSim simulation platforms and conducted co-simulation experiments. The main parameters of the electric vehicle model are shown in

Table 1. The main parameters of the electric vehicle model.

Symbol	Parameter	Value/Unit
$m$	Vehicle mass	1412/kg
$a$	Distance from CG to front axle	1.015/m
$b$	Distance from CG to rear axle	1.895/m
$L$	Wheelbase	2.91/m
$I_z$	Yaw moment of inertia	1536.7/kg·m2
$h_g$	Center of gravity	0.54/m
$R$	Wheel radius	0.31/m

.

5.2. VSR Fitting Results’ Analysis

In order to verify the effect of VSR curve after cubic quasi-uniform B-spline fitting, this section, based on FAST controller, simulated the double-lane change condition at variable speeds within the critical speed range. In Figure 7, the values of the fitted SR change in the speed regions of 25–35 km/h and 75–85 km/h.

Figure 8a,b shows the sideslip angle and yaw rate responses of VSR at 25–35 km/h. From Figure 8a, it can be observed that the fitted sideslip angle is reduced by 0.0044 radians, indicating an enhancement in stability. In the yaw rate response in Figure 8b, the fitting treatment significantly weakened the buffeting problem when the vehicle initially reaches the critical speed, and somewhat reduces the impact of sudden change in the steering ratio.

Figure 9a,b show the response of the vehicle sideslip angle and yaw rate with VSR in the 75–85 km/h critical speed region. The response time of the sideslip angle obtained after fitting is advanced. Moreover, compared to the pre-fitting state, the responses of both the sideslip angle and the yaw rate exhibit greater stability, with respective improvements of 16.3% and 52.3%.

The above results indicate that the VSR curve obtained after fitting is conducive to enhancing the vehicle’s handling stability and mitigating the adverse effects of abrupt changes in SR within the critical speed range on the steering performance.

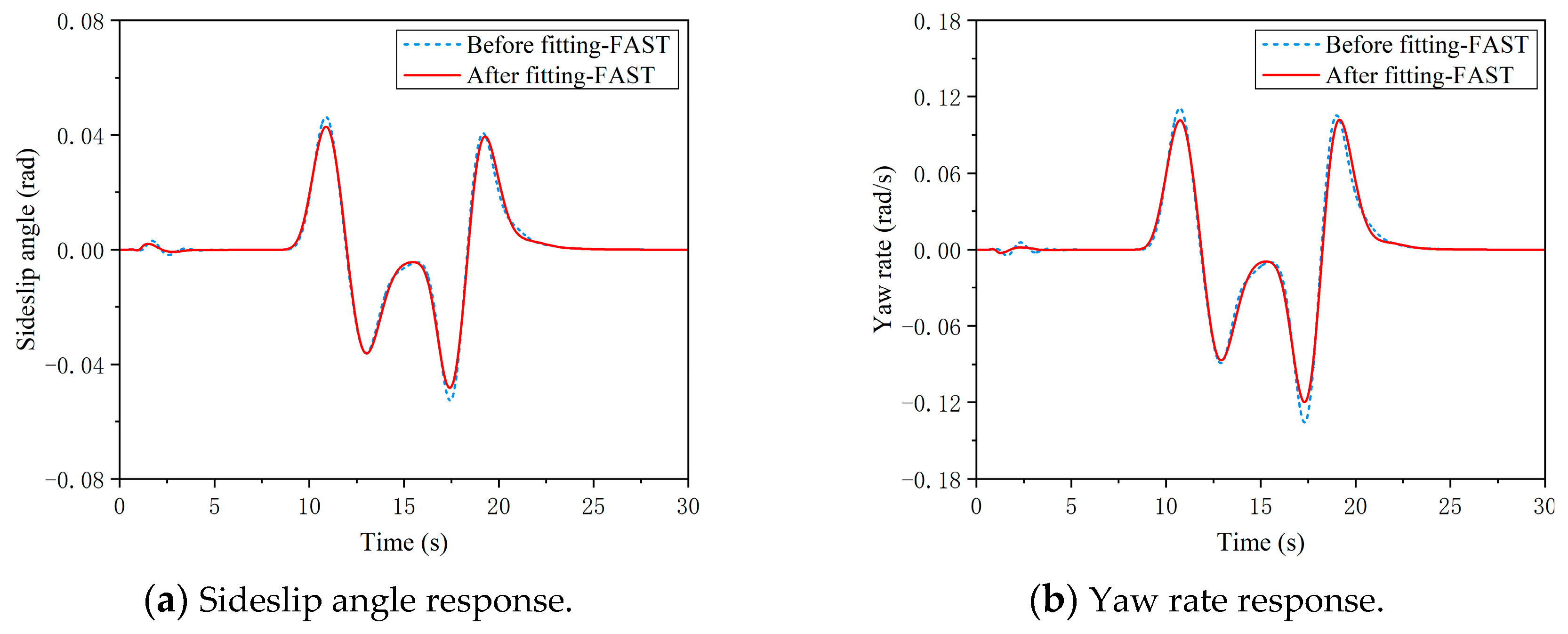
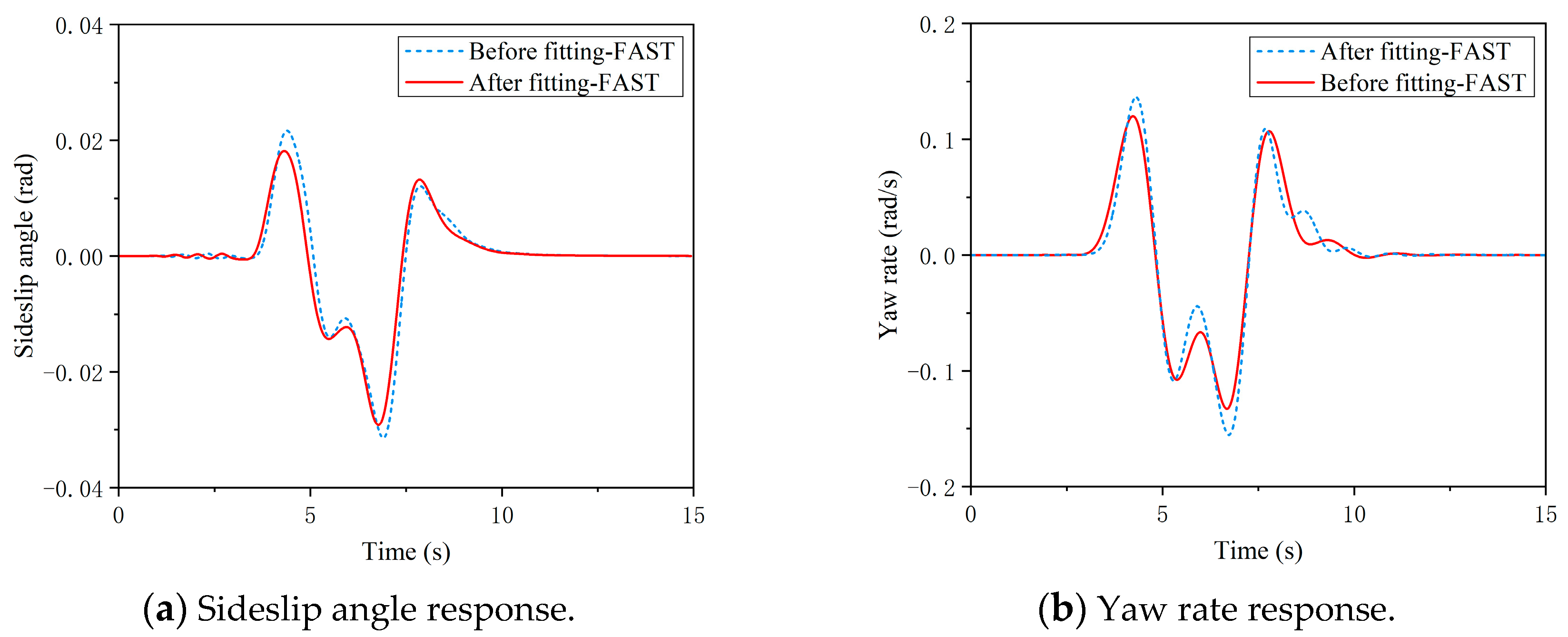
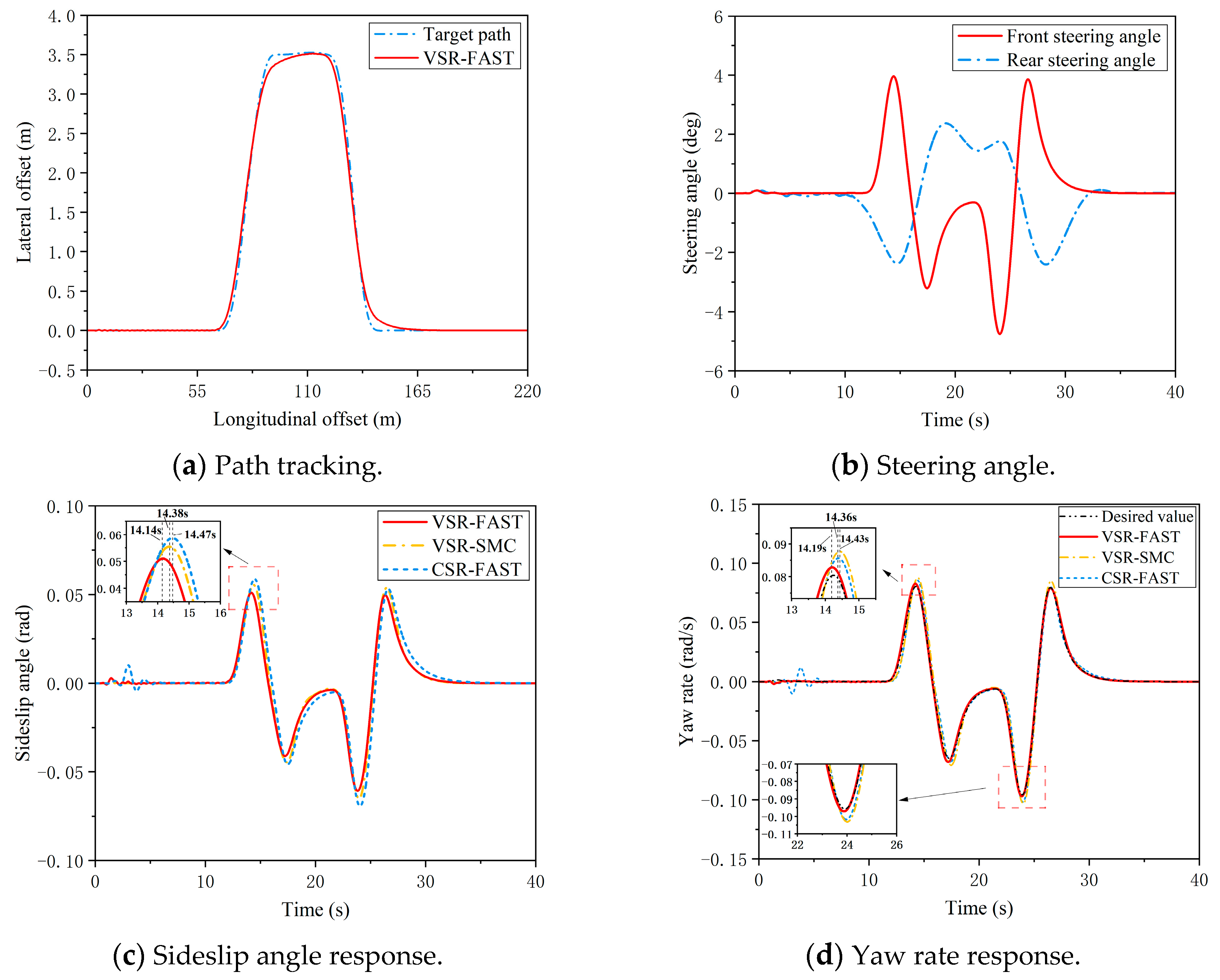
5.3. VSR-FAST Controller Simulation

In order to verify the effectiveness of 4WS control system based on VSR-FAST, the double-lane change condition was taken as road input; three speed conditions of low (20 km/h), medium (60 km/h), and high (90 km/h) speeds were set; and the road surface coefficient of friction was selected as 0.85. The simulations were conducted and analyzed for three types of 4WS control systems: VSR-FAST, VSR-SMC, and CSR (constant steering ratio)-FAST.

(1)

Low speed

The simulation results for vehicle path tracking response, front and rear wheel steering angles, sideslip angle, and yaw rate at 20 km/h are presented in Figure 10. From Figure 10a, the VSR-FAST controller effectively performs the double-lane change maneuver with a small tracking error and trajectories that are essentially coincident. Furthermore, Figure 10b, Figure 11b, and Figure 12b display the front- and rear-wheel steering angles output by the vehicle at low, medium, and high speed conditions, respectively. The front-wheel steering angle is maintained within ±6°, and the rear-wheel steering angle is within ±5°, which aligns with practical conditions. At low speeds, the rear wheels turn in the opposite direction to the front wheels. This not only enhances stability but also aligns with the characteristics of a four-wheel steering system.

As depicted in Figure 10c, the peak sideslip angle under CSR-FAST control is 0.009 rad larger than that under VSR-FAST control. The VSR strategy optimizes the sideslip angle by 13.6%, thereby enhancing system stability. Compared to CSR, VSR advances the steering response by 0.33 s, improving agility. In contrast to VSR-FAST, VSR-SMC exhibits a larger steady-state error in the sideslip angle, with a peak value of 0.065 rad, indicating that SMC sacrifices some control precision in its efforts to suppress chattering. However, the incorporation of the FAST control strategy optimizes the sideslip angle by 7.3%, enhancing both control precision and disturbance rejection capability. The FAST controller reaches the peak value 0.24 s earlier than the SMC, demonstrating a quicker system response and convergence rate.

Figure 10d reveals that CSR-FAST exhibits noticeable oscillations during the initial vehicle startup phase (0–5 s), which is detrimental to low-speed stability. VSR-FAST maintains the maximum deviation between the actual and desired yaw rates at 0.0037 rad/s, improving the tracking performance by 41% compared to CSR’s 0.0063 rad/s, thereby strengthening steering stability. Additionally, VSR-FAST responds more rapidly to yaw rate changes than CSR-FAST, with an advance of 0.17 s, indicating a more timely response to fluctuations and suggesting that VSR can enhance steering sensitivity, allowing the vehicle to handle path-steering maneuvers more adeptly. Under SMC control, the deviation is 0.0077 rad/s, whereas the introduction of the FAST control strategy optimizes the tracking performance by 64%, enhancing the system’s disturbance rejection capability.

(2)

Medium speed

Figure 11a shows path tracking at medium speed. The tracking trajectory of VSR-FAST controller is basically identical. The tracking error is 0.38 m, which is larger than that at low speed.

As illustrated in Figure 11c, the peak sideslip angles for VSR-FAST and CSR-FAST are 0.025 rad and 0.027 rad, respectively, with VSR-FAST achieving a 7.4% optimization in sideslip angle. When comparing the overall response curves of sideslip angle between VSR and CSR, the VSR-controlled response exhibits smaller fluctuations relative to the desired value, thereby enhancing steering stability at medium speeds. The FAST controller reaches its peak 0.21 s earlier than the SMC, and during the second steering maneuver, it stabilizes near the desired value in 0.6115 s, whereas the SMC takes 0.928 s, demonstrating the superior rapid convergence of FAST under medium-speed conditions. The maximum sideslip angle for VSR-SMC is 0.031 rad, and VSR-FAST further optimizes this by an additional 7.3%, indicating that FAST enhances control precision and reduces steady-state error while maintaining robustness.

From Figure 11d, it is evident that the actual yaw rate of the VSR-FAST controller closely aligns with the desired yaw rate curve. In comparison with CSR-FAST, the VSR-FAST controller significantly reduces the peak yaw rate by 0.0461 rad/s, thereby enhancing the handling stability during the steering phase. When compared to SMC-FAST, the VSR-FAST controller reduces the deviation by 76%, improving the system’s disturbance rejection capability.

Under medium-speed conditions, there is a commonality in the response curves of sideslip angle and yaw rate: compared to VSR-SMC and CSR-FAST controllers, the first peak response of VSR-FAST is relatively rapid, which enhances the steering sensitivity and safety. The second peak response is relatively delayed, which mitigates the sensation of vehicle tilt during steering, thereby enhancing driving comfort and stability.

(3)

High speed

The results for the double-lane change condition at 90 km/h are shown in Figure 12.

From Figure 12a, the tracking error of VSR-FAST controller is 0.577 m, and the tracking accuracy is lower than that at low and medium speeds. As shown in Figure 12c, the peak sideslip angles for the VSR-FAST and CSR-FAST controllers are 0.016 rad and 0.019 rad, respectively. The VSR controller stabilizes the sideslip angle response by achieving a 16% optimization over CSR-FAST. During high-speed operation, CSR-FAST experiences significant oscillations between 2 s and 3 s, likely due to the CSR system’s inability to adjust steering sensitivity in real time according to changes in steering demands, resulting in a poorer steering stability. In contrast, VSR-FAST performs steering maneuvers smoothly at the 2.5 s mark, indicating that VSR enhances adaptability to driving conditions and further improves steering stability. The VSR-SMC controller has a peak sideslip angle of 0.018 rad, and compared to VSR-SMC, the FAST controller improves performance by 11%, thereby enhancing the system’s control accuracy.

In Figure 12d, the maximum yaw rate deviations for the VSR-FAST and CSR-FAST controllers are 0.0106 rad/s and 0.0547 rad/s, respectively. The implementation of VSR improves the actual yaw rate tracking performance by 81%, thereby enhancing stability at high speeds. VSR-FAST rapidly approaches the desired yaw rate curve during steering maneuvers, demonstrating the FAST control strategy’s rapid convergence speed. Within the response fluctuation region from 3.8 s to 5.8 s, the FAST controller also maintains a smaller deviation from the desired value, exhibiting strong disturbance rejection capabilities. The VSR-SMC controller’s maximum yaw rate deviation is 0.0273 rad/s, and the introduction of FAST improves the actual yaw rate tracking performance by 61%, which is beneficial for maintaining high-speed stability.

In summary, the VSR algorithm enhances the agility at low speeds and stability at high speeds for 4WS, thereby improving the system’s adaptability to various driving conditions. Meanwhile, the FAST algorithm effectively suppresses the chattering issues associated with the traditional sliding mode control, strengthening the system’s disturbance rejection capabilities and enhancing the convergence speed and control precision when far from the equilibrium point. Under double-lane change conditions at any vehicle speed, the designed VSR-FAST controller adeptly tracks the desired yaw rate and centroidal sideslip angle, demonstrating a strong trajectory tracking capability. It achieves an integrated enhancement in control precision, disturbance rejection, adaptability, and rapid convergence, thereby reinforcing the maneuverability and stability of four-wheel steering systems.

6. Conclusions

In this paper, a 4WS controller based on VSR strategy and FAST sliding mode control algorithm was designed to control and output four wheel angles of vehicle. The simulation results show that:

(1)

The VSR curve after cubic quasi-uniform B-spline fitting reduces the steering fluctuation and improves the adverse influence of sudden change in SR in the critical speed region on the steering stability;

(2)

Compared to CSR, the VSR enhances the low-speed agility and high-speed stability of 4WS, improving adaptability to diverse conditions. The FAST algorithm, compared to SMC, effectively mitigates chattering, boosts disturbance rejection, and enhances convergence speed and precision away from equilibrium. The VSR-FAST controller efficiently handles double-lane changes at various speeds, tracking the desired sideslip angle and yaw rate effectively. It achieves superior path tracking, high control precision, strong disturbance rejection, adaptability, and rapid convergence, thereby enhancing 4WS maneuverability and stability.

In addition, due to the limitation of test equipment and site, the control algorithm proposed in this paper was only simulated. In future research, testing on real vehicles will be considered.