Porous and Magnetic Effects on Axial Couette Flows of Second Grade Fluids in Cylindrical Domains
Abstract
1. Introduction
2. Problem Presentation
3. Fluid Velocity for Flows Through a Circular Cylinder
3.1. Case or (Motion in a Cylinder)
3.2. Case (Motion in a Cylinder)
3.3. Case When
4. Fluid Velocity for Flows Between Infinite Coaxial Circular Cylinders
4.1. Case or (Motion Between Two Cylinders)
4.2. Case (Motion Between Two Cylinders)
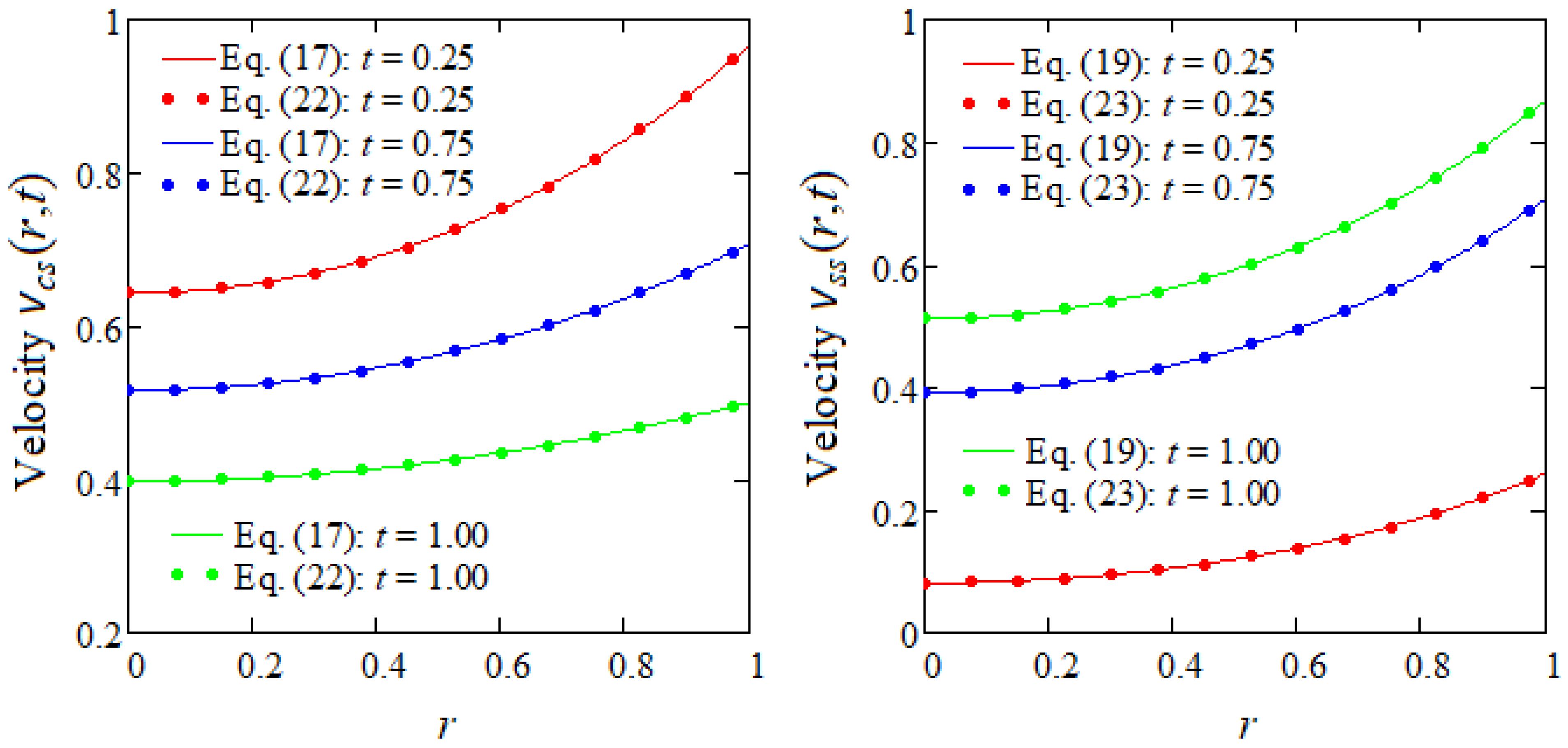
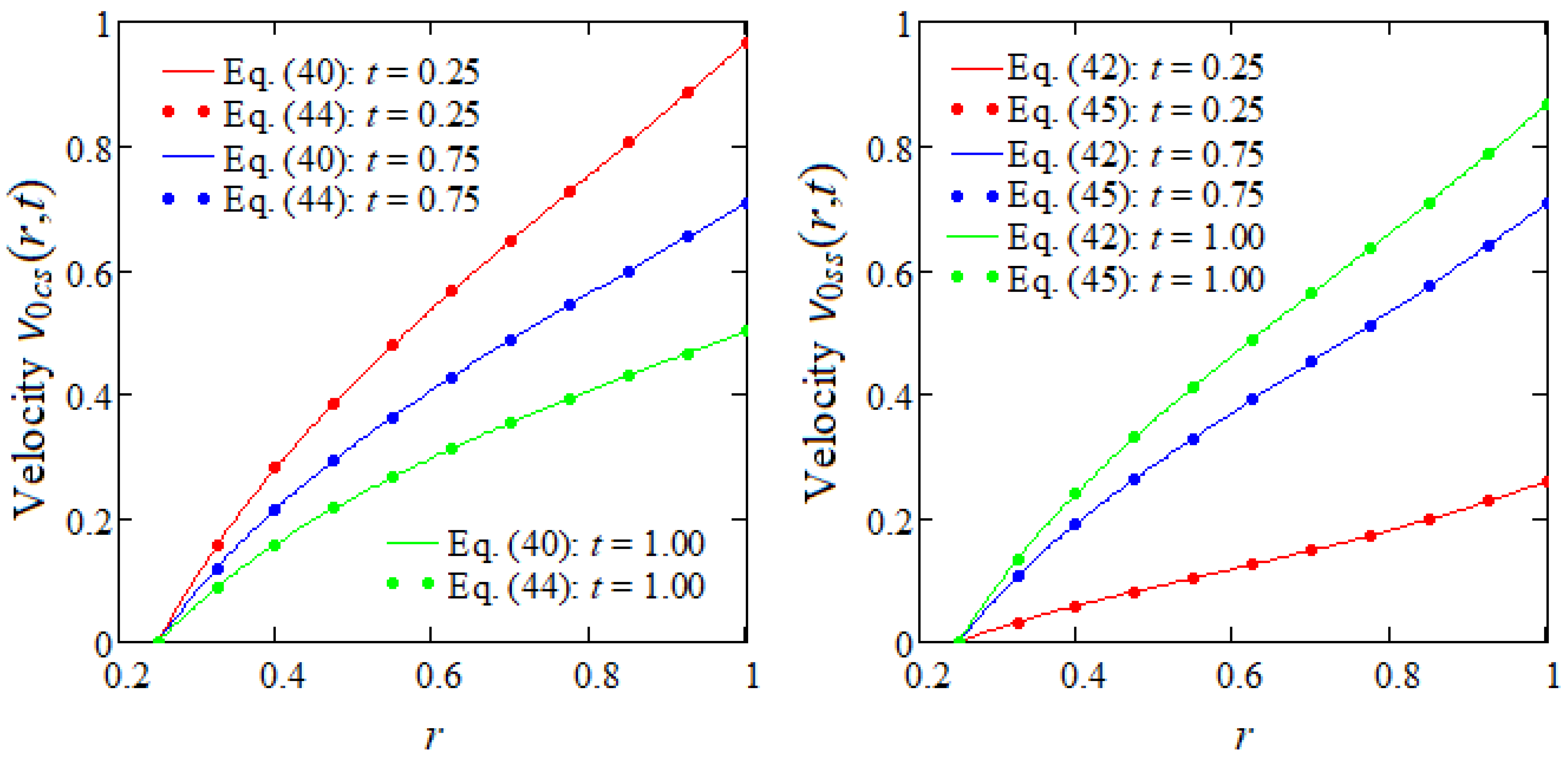
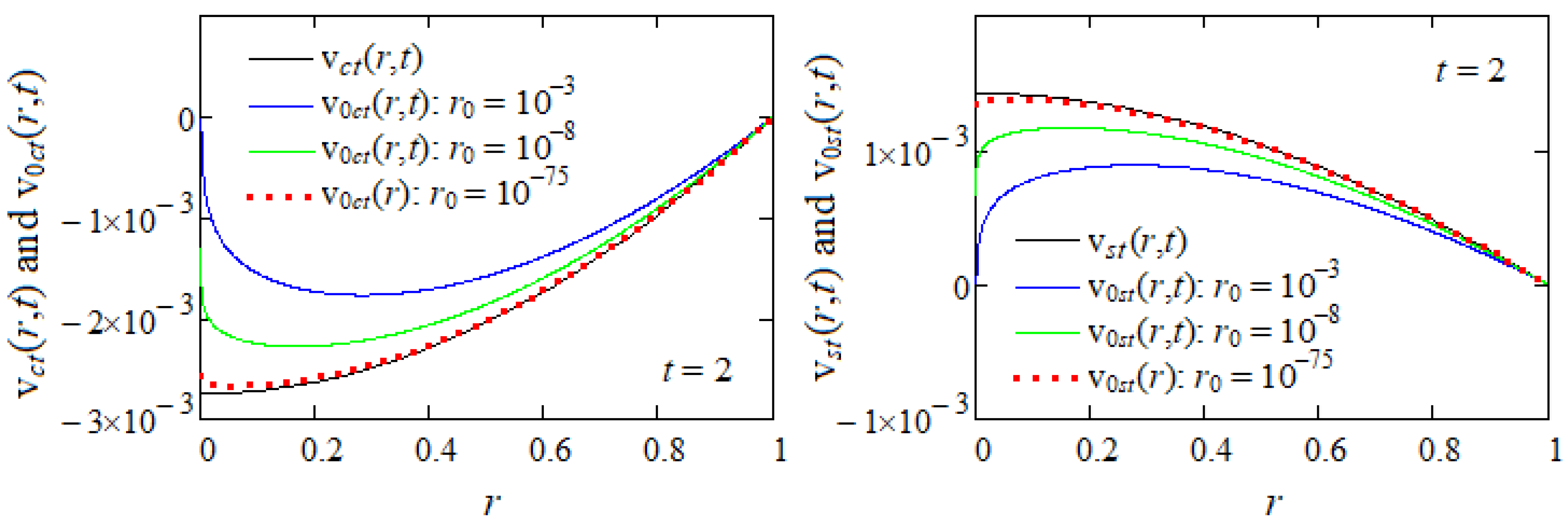
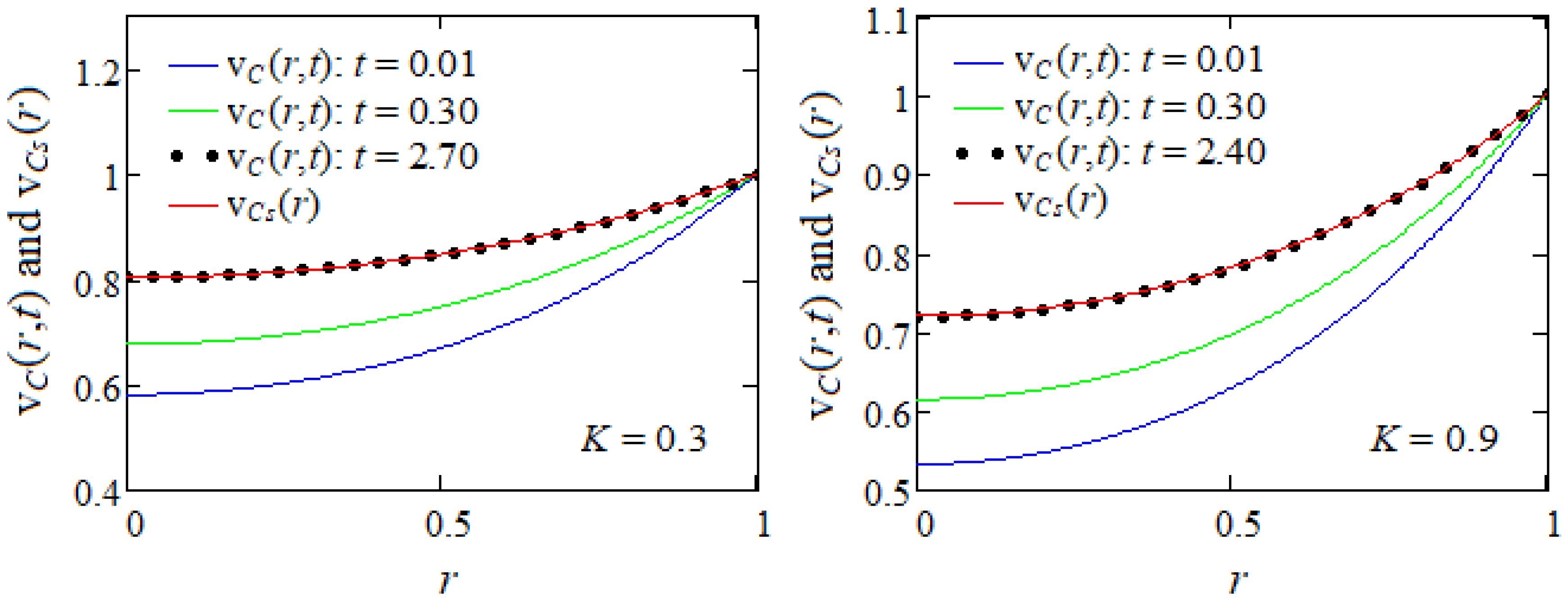
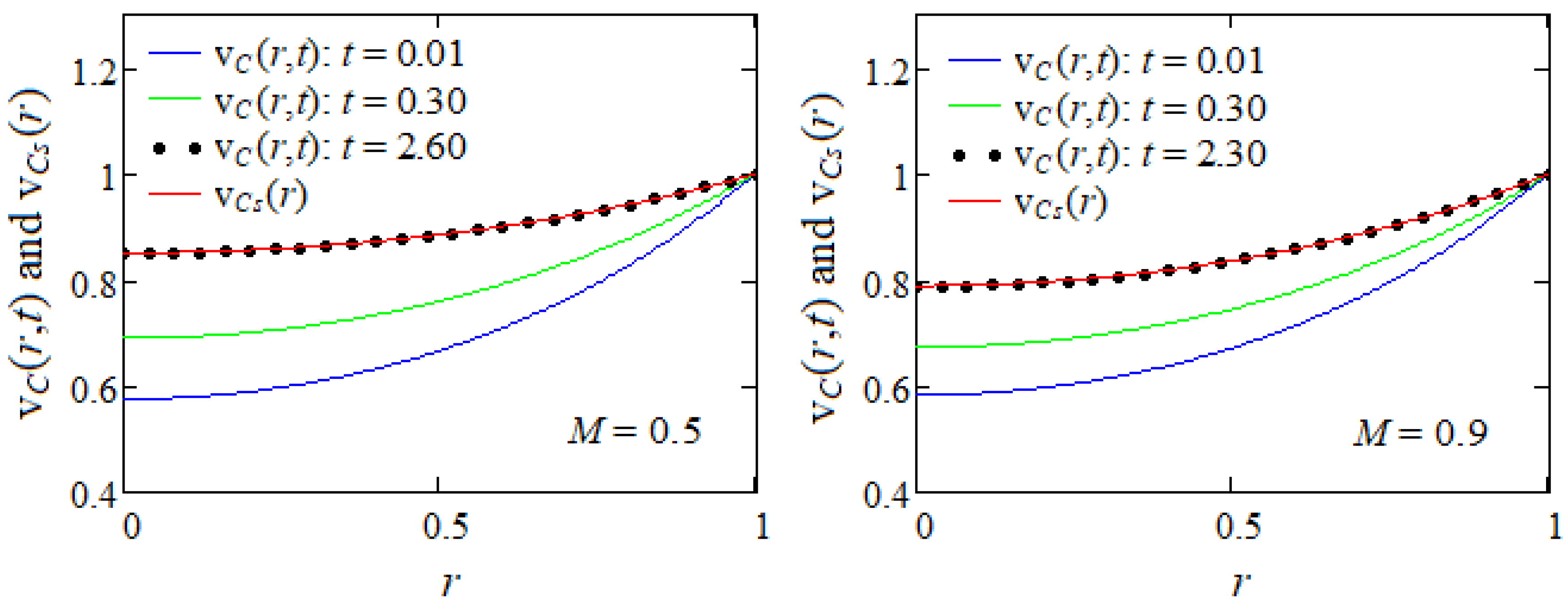
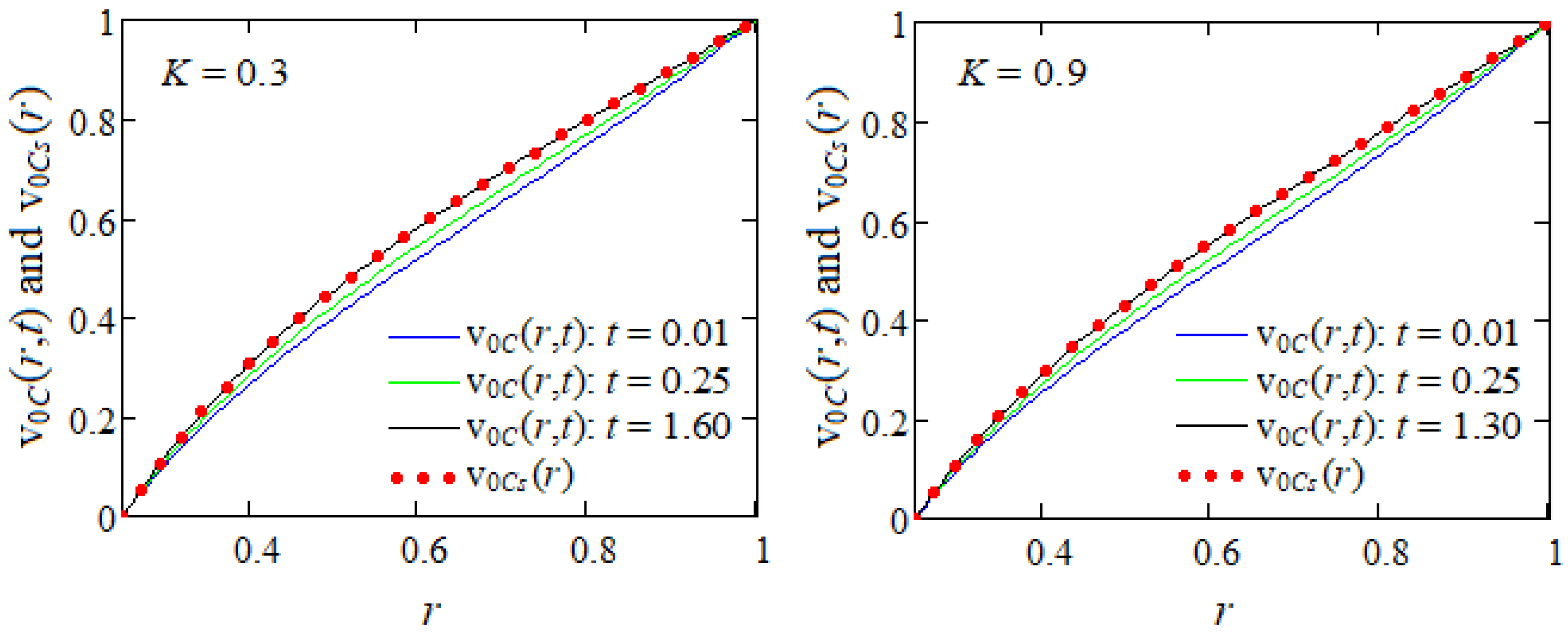
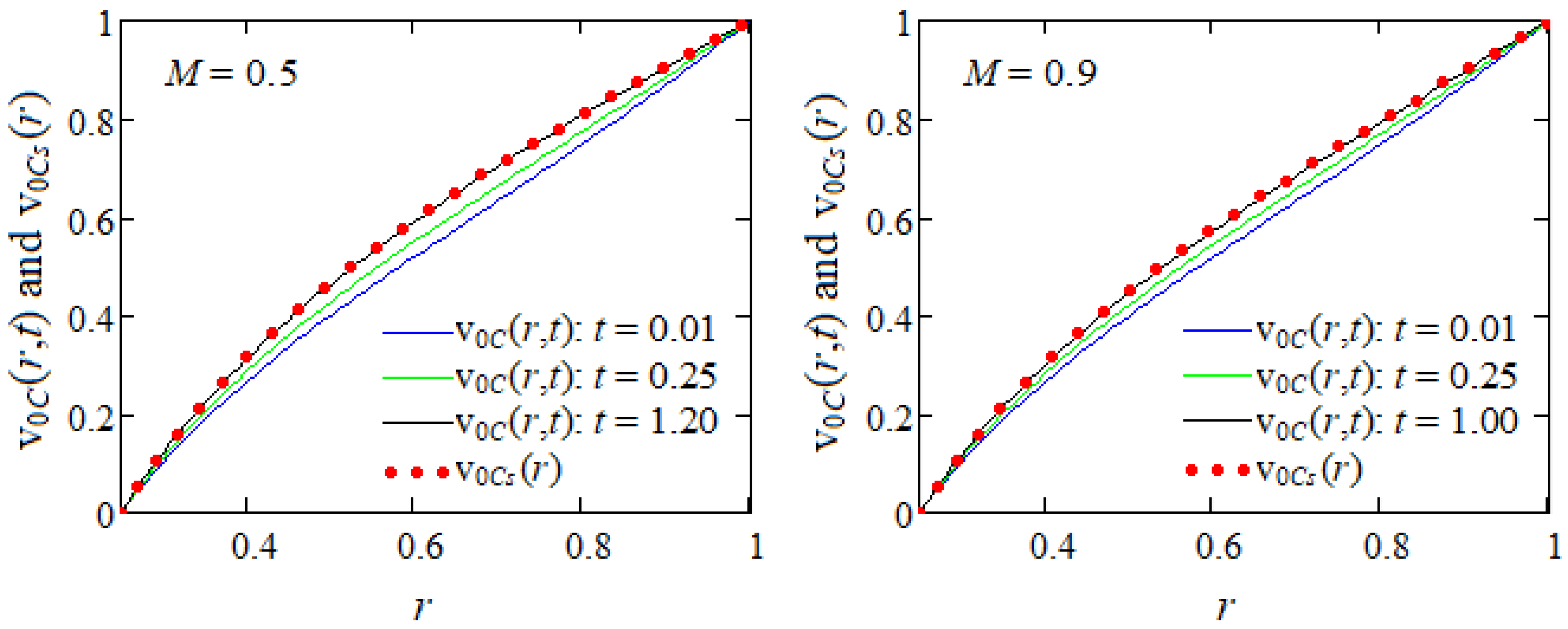
5. Numerical Results
6. Conclusions
- -
- MHD axial Couette flows of ECISGFs through a porous medium in two cylindrical domains were analytically investigated. The fluid motion was induced by a circular cylinder that moves along its symmetry axis with the time-dependent velocity .
- -
- General expressions have been established for the corresponding dimensionless velocity fields. They can generate exact solutions for any motion of this type of the respective fluids and the motion problems in discussion are completely solved.
- -
- For illustration, some particular cases have been considered and the corresponding velocity fields were derived. For validation, the steady components of these velocities were presented in different forms and their equivalence was graphically proved.
- -
- As application, since the considered motions become steady in time, the necessary time to reach the steady state was graphically determined. That time, which is important for experimental researchers, declines for increasing values of K or M.
- -
- Consequently, the steady state for such motions of ECISGFs is earlier touched in the presence of a porous medium or magnetic field. It is also rather touched for flows between infinite circular cylinders than in an infinite circular cylinder.
- -
- The fluid flows faster in the absence of a porous medium or magnetic field.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ting, T.W. Certain unsteady flows of second grade fluids. Arch. Ration. Mech. Anal. 1963, 14, 1–26. [Google Scholar] [CrossRef]
- Rajagopal, K.R. Longitudinal and torsional oscillations of a rod in a non-Newtonian fluid. Acta Mech. 1983, 49, 281–285. [Google Scholar] [CrossRef]
- Bandelli, R.; Rajagopal, K.R. Start-up flows of second grade fluids in domains with one finite dimension. Int. J. Non-Linear Mech. 1995, 30, 817–839. [Google Scholar] [CrossRef]
- Fetecau, C. Starting solutions for the motion of a second grade fluid due to longitudinal and torsional oscillations of a circular cylinder. Int. J. Eng. Sci. 2006, 44, 788–795. [Google Scholar] [CrossRef]
- Erdogan, M.E.; Imrak, C.E. On the comparison of the methods used for the solutions of the governing equation for unsteady unidirectional flows of second grade fluids. Int. J. Eng. Sci. 2007, 45, 786–796. [Google Scholar] [CrossRef]
- Bano, Z.; Shah, N.F.; Islam, S.; Haroon, T. Exact solution to longitudinal and torsional oscillations of an electrically conducting second grade fluid. Int. J. Phys. Sci. 2011, 6, 2939–2943. [Google Scholar] [CrossRef]
- Fetecau, C.; Mocanu, C.; Samiulhaq; Fetecau, C. Exact solutions for motions of second grade fluids induced by an infinite cylinder that applies arbitrary shear stresses to fluid. J. Comput. Theor. Nanosci. 2012, 17, 266–270. [Google Scholar] [CrossRef]
- Javaid, M.; Imran, M.A.; Khan, I.; Nisar, K.S. Natural convection flow of a second grade fluid in an infinite vertical cylinder. Sci. Rep. 2020, 10, 8327. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, M.E. On unsteady motions of a second-order fluid over a plane wall. Int. J. Non-Linear Mech. 2003, 38, 1045–1051. [Google Scholar] [CrossRef]
- Erdogan, M.E.; Imrak, C.E. Effects of the side walls on unsteady flow of a second grade fluid over a plane wall. Int. J. Non-Linear Mech. 2008, 43, 779–782. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, Y. Some unsteady flows of a second grade fluid over a plane wall. Nonlinear Anal. Real World Appl. 2010, 11, 4442–4450. [Google Scholar] [CrossRef]
- Sultan, Q.; Nazar, M.; Ahmad, I.; Ali, U. Flow of second-grade fluid between two walls induced by rectified sine pulses shear stress. J. Mech. 2015, 31, 573–582. [Google Scholar] [CrossRef]
- Imran, M.; Tahir, M.; Nazar, M.; Kamran, M. Some Couette flows of a second-grade fluid due to tangential stresses. Sci. Int. 2015, 27, 829–834. [Google Scholar]
- Baranovskii, E.S.; Artemov, M.A. Steady flows of second grade fluids subject to stick-slip boundary conditions. In Proceedings of the 23rd International Conference Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; pp. 110–113. [Google Scholar]
- VeeraKrishna, M.; Reddy, G.S. Unsteady MHD reactive flow of second grade fluid through porous medium in a rotating parallel plate channel. J. Anal. 2018, 27, 103–120. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D. General solutions for some MHD motions of second-grade fluids between parallel plates embedded in a porous medium. Symmetry 2023, 15, 183. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Analytical solutions to the unsteady Poiseuille flow of a second grade fluid with slip boundary conditions. Polymers 2024, 16, 179. [Google Scholar] [CrossRef] [PubMed]
- Kanuri, J.V.; Chandra Sekhar, K.V.; Brahmanandam, P.S.; Ramanaiah, J.V. Analytical solutions of Poiseuille flow of second-grade fluid. J. Nav. Archit. Mar. Eng. 2024, 21, 67–77. [Google Scholar] [CrossRef]
- Jamil, M.; Zafarullah, M. MHD flows of second grade fluid through the moving porous cylindrical domain. Eur. J. Pure Appl. Math. 2019, 12, 1149–1175. [Google Scholar] [CrossRef]
- Fetecau, C.; Akhtar, S.; Forna, N.C.; Moroşanu, C. General solutions for MHD motions of second grade fluids through a circular cylinder filled with porous medium. Symmetry 2025, 17, 319. [Google Scholar] [CrossRef]
- Hamza, S.E.E. MHD flow of an Oldroyd-B fluid through porous medium in a circular channel under the effect of time dependent pressure gradient. Am. J. Fluid Dyn. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Sneddon, I.N. Fourier Transforms; McGRAW-Hill: New-York, NY, USA, 1951. [Google Scholar]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
| r | Figure 6 | Figure 7 | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.30 | 0.118 | 0.119 | 0.111 | 0.112 | 0.121 | 0.122 | 0.116 | 0.117 |
| 0.35 | 0.218 | 0.219 | 0.206 | 0.208 | 0.223 | 0.225 | 0.214 | 0.217 |
| 0.40 | 0.306 | 0.307 | 0.289 | 0.291 | 0.312 | 0.315 | 0.300 | 0.304 |
| 0.45 | 0.384 | 0.385 | 0.363 | 0.366 | 0.391 | 0.395 | 0.377 | 0.382 |
| 0.50 | 0.454 | 0.456 | 0.431 | 0.434 | 0.462 | 0.467 | 0.447 | 0.452 |
| 0.55 | 0.520 | 0.521 | 0.495 | 0.498 | 0.528 | 0.534 | 0.511 | 0.517 |
| 0.60 | 0.580 | 0.582 | 0.555 | 0.558 | 0.590 | 0.595 | 0.572 | 0.578 |
| 0.65 | 0.638 | 0.640 | 0.612 | 0.615 | 0.647 | 0.653 | 0.629 | 0.636 |
| 0.70 | 0.693 | 0.695 | 0.668 | 0.671 | 0.702 | 0.707 | 0.685 | 0.691 |
| 0.75 | 0.747 | 0.748 | 0.723 | 0.726 | 0.755 | 0.760 | 0.739 | 0.744 |
| 0.80 | 0.798 | 0.800 | 0.778 | 0.780 | 0.806 | 0.810 | 0.791 | 0.796 |
| 0.85 | 0.849 | 0.850 | 0.832 | 0.834 | 0.856 | 0.859 | 0.844 | 0.848 |
| 0.90 | 0.900 | 0.900 | 0.887 | 0.889 | 0.904 | 0.907 | 0.896 | 0.898 |
| 0.95 | 0.950 | 0.900 | 0.943 | 0.944 | 0.952 | 0.954 | 0.948 | 0.949 |
| 1.00 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fetecau, C.; Vieru, D. Porous and Magnetic Effects on Axial Couette Flows of Second Grade Fluids in Cylindrical Domains. Symmetry 2025, 17, 706. https://doi.org/10.3390/sym17050706
Fetecau C, Vieru D. Porous and Magnetic Effects on Axial Couette Flows of Second Grade Fluids in Cylindrical Domains. Symmetry. 2025; 17(5):706. https://doi.org/10.3390/sym17050706
Chicago/Turabian StyleFetecau, Constantin, and Dumitru Vieru. 2025. "Porous and Magnetic Effects on Axial Couette Flows of Second Grade Fluids in Cylindrical Domains" Symmetry 17, no. 5: 706. https://doi.org/10.3390/sym17050706
APA StyleFetecau, C., & Vieru, D. (2025). Porous and Magnetic Effects on Axial Couette Flows of Second Grade Fluids in Cylindrical Domains. Symmetry, 17(5), 706. https://doi.org/10.3390/sym17050706







