Abstract
In cloud computing environments, security challenges emerge due to compromised firmware and supply chain attacks that target devices deployed within data centers. The Secure Protocol and Data Model (SPDM) has been widely adopted for device attestation, which verifies device identity and firmware integrity. However, the scalability of the SPDM is challenged by the resource constraints of peripheral devices and the inherent asymmetry of the protocol, where a heavy verification burden on the central requester leads to a potential bottleneck. In order to solve these problems, we propose a secure and scalable device attestation protocol, SPDM-AggSig, that integrates a chainless-certificate-based aggregate signature scheme within the SPDM framework supporting group messaging. Our protocol reduces the communication overhead by replacing the conventional X.509 certificates with lightweight chainless certificates. It also improves the scalability through group-based attestation with constant-size aggregated signatures. The proposed delegation mitigates the asymmetry in the attestation, introducing a tendency toward functional symmetry by distributing the verification burdens from the central requester to group leaders. We also provide a formal security proof demonstrating existential unforgeability under an adaptive chosen message attack (EUF-ACMA). SPDM-AggSig achieves an approximately 84.18% improvement in the computation overhead and a 96.22% decrease in the communication overhead compared to the baseline.
1. Introduction
In cloud computing environments, various IT infrastructure components, such as storage, networking, and computing devices, are tightly connected and managed in an integrated manner. As these architectures grow increasingly sophisticated and large-scale, hardware-based security threats such as firmware tampering pose a significant concern [1,2,3]. Through a supply chain attack, attackers can manipulate a device’s firmware to inject malware or distribute malicious updates containing compromised firmware. Once infected, malicious code can persist from the system boot phase, making it difficult to detect or mitigate by leveraging conventional OS-level protection mechanisms. As a result, a single compromised device can rapidly spread the threat to other devices deployed in the data center. In other words, without guaranteeing the integrity of the hardware and firmware, attackers can stealthily deploy compromised devices into the system or tamper with devices in regular operation to perform malicious activities. Therefore, we need a security mechanism to verify the authenticity of devices and ensure that they function properly from the initial boot phase to runtime.
In order to resolve this problem, the Distributed Management Task Force (DMTF) [4], an industry consortium that develops IT infrastructure management standards, comprising members such as Intel, Broadcom, Google, and Microsoft, published the Secure Protocol and Data Model (SPDM) [5] in 2019 as a device attestation protocol. The SPDM is designed to guarantee the authenticity of hardware devices, such as peripheral devices, by verifying their provisioned identity and running firmware. After confirming devices’ identity, the SPDM allows the requester and the responder to establish secure communication channels, providing confidentiality and integrity in data exchange.
The SPDM shares many properties at a high level with TLS [6], a de facto standard for Internet security. Specifically, the SPDM employs PKI-based X.509 certificates [7] as a core component of authentication, following the same approach as that in web environments. However, we have concerns about the standard SPDM protocol in that its communication structure and use of X.509 certificates can raise scalability and efficiency problems.
- Bottlenecks due to centralized requests. Numerous peripheral devices are connected to the host platform. Each device receives an authentication request from the central requester and must respond to it. Thus, all authentication responses are concentrated on the requester, which can cause heavy computation and network loads. As the number of connected devices increases, requesters consume more computing resources and bandwidth, increasing the risk of bottlenecks, potentially delaying the system boot time, and degrading the overall performance. This architecture exhibits an inherent asymmetry, where the central requester is solely responsible for verifying all responders, incurring a potential performance bottleneck. Similar phenomena are evident in large-scale computing installations [8,9], where centralized authentication systems have historically suffered from scalability challenges, demonstrating that an optimized approach is critical to mitigating such performance issues.
- Limitations of resource-constrained devices. While the existing X.509 certificates are typically hundreds of bytes to several kilobytes (KB) in size, they are transmitted in chain form, usually including the certificates of the issuing Certificate Authority (CA), rather than as a single certificate, so the data conveyed during the authentication phase are expected to be several KB in size on average. Regarding the web server and the client, sufficient computing resources and network bandwidths are available for addressing such X.509 certificates. However, transmitting and verifying certificates can lead to a substantial network overhead in resource-constrained environments, such as on peripheral devices or IoT devices, potentially degrading system performance. From a scalability perspective, the size of the certificates, which can be several KB, can significantly burden these devices.
In this paper, we aim to design a secure and scalable device attestation protocol by (1) minimizing the load on the requester and (2) reducing the communication overhead during the authentication process.
A naive approach to minimizing the load of the requester is to extend the current SPDM with a group-based messaging functionality (referred to as SPDM-Group in Section 6.2), which allows multiple devices to be grouped so that the authentication process is performed at the group level, thereby reducing the burden on the requester. During the negotiation phase, the requester sends predefined group information (Multiple scenarios for group formation exist. For simplicity, in this paper, we assume that group membership is already defined at the time of deployment.) to the leader. It then retrieves certificates from all group members to verify them on behalf of the requester. After authenticating their identities, the leader forwards only its own certificate rather than sending all individual certificates to the requester. In other words, the leader offloads the verification process from the requester, thereby reducing both the bandwidth usage and computation overhead. However, in this case, the requester’s trust anchor (that is, the list of the root CA certificates that the entity trusts) must be shared with the leader. In addition, since the size of the certificate chain remains within the kilobyte range, the leader—who has relatively limited computing power compared to that of the requester—can face impractical overheads caused by verification.
To address the root cause of this problem, we replace the conventional X.509 certificates with a lightweight certificate format, chainless certificates (While the original term is “certificate”, we refer to this as a “chainless certificate” in this paper to avoid confusion with X.509 certificates.) [10,11]. As the name suggests, the chainless certificate is used as a commitment to bind the public key of a device while ensuring that it has been legitimately issued by an authority trusted by the verifier without the chain structure of the X.509 certificate. This allows the certificate sizes to remain small—varying depending on the security strength but at most around 300 bytes—significantly reducing the communication overhead during identity verification (referred to as SPDM-Chainless in Section 6.2).
Finally, we propose SPDM-AggSig, which integrates the chainless-certificate-based aggregate signature scheme into the SPDM-Group framework. Specifically, the group leader aggregates the signatures retrieved from each member and produces a constant-size aggregated signature, regardless of the number of group members, which the requester then verifies; additionally, the leader can aggregate certificates for verification, further reducing the overall size of the transmitted data. Thus, SPDM-AggSig not only minimizes the overall computation and communication overhead but also offers a scalable alternative to traditional SPDM-based methods without compromising the individual authentication for each group member. More importantly, the proposed scheme reduces the asymmetry in the attestation process by distributing the verification responsibilities between the requester and group leaders, resulting in a more balanced and scalable architecture that reflects a tendency toward functional symmetry.
We summarize these contributions as follows:
- We propose a secure and scalable device attestation protocol based on the SPDM with a chainless-certificate-based aggregate signature scheme;
- The proposed scheme introduces group-based attestation, where the group leader aggregates both signatures and certificates from multiple devices, significantly reducing the computation and communication overhead;
- We replace the traditional X.509 certificates with chainless certificates, reducing the size of the identity and improving the overall performance in resource-constrained environments;
- A formal security model and proof are provided to demonstrate the existential unforgeability of the proposed scheme under an adaptive chosen message attack (EUF-ACMA);
- We present both theoretical and experimental evaluations to demonstrate the efficiency and scalability of SPDM-AggSig compared to those of the SPDM-based implementations, resulting in an approximately 84.18% lower computation overhead and 96.22% lower communication overhead (evaluated using ECC P-384 for 1000 devices);
- The proposed scheme reduces the attestation asymmetry by balancing the burdens between the requesters and responders, leading to a more functionally symmetric attestation system.
The rest of this paper is organized as follows. In Section 2, we describe the background knowledge. In Section 3, we describe the cryptographic background, the system architecture, and security goals. In Section 4, we introduce the construction of the proposed scheme. In Section 5, we provide a security analysis of the proposed scheme. In Section 6, we present a comparative and performance analysis, comparing our scheme with existing CBAS schemes and evaluating its performance against that of SPDM-based implementations. In Section 7, we conclude this paper.
2. Background
In this section, we provide background information on the SPDM and the chainless-based aggregate signature scheme.
2.1. Overview of SPDM
Security Protocol and Data Model (SPDM) [5], introduced by the Distributed Management Task Force (DMTF) [4], plays a crucial role in hardware security architectures, particularly for device attestation and secure communication. SPDM has been introduced in various industrial standards, including Compute Express Link (CXL) [12], Mobile Industry Processor Interface (MIPI) [13], and Trusted Computing Group (TCG) [14], for constructing trustworthy computing environments. In particular, Intel’s Trust Domain Extension (TDX) Connect [15] and AMD’s Secure Encrypted Virtualization Trusted I/O (SEV-TIO) [16], which are promising technologies for enhancing the hardware-based security in confidential computing and confidential virtual machine environments, adopt the SPDM as the device attestation protocol.
Since its initial release, SPDM has continuously been updated to meet evolving hardware security requirements. The latest version, SPDM v1.3 [5], was recently announced. SPDM involves a series of message exchanges between the requester and the responder, starting with the negotiation phase and providing three key features: (1) device attestation, (2) secure session establishment, and (3) identity provisioning. Among these, we describe the negotiation and device attestation phase, which aligns with our research focus. Figure 1 illustrates the SPDM message flow between the requester and the responder, which consists of two phases: negotiation and device attestation.
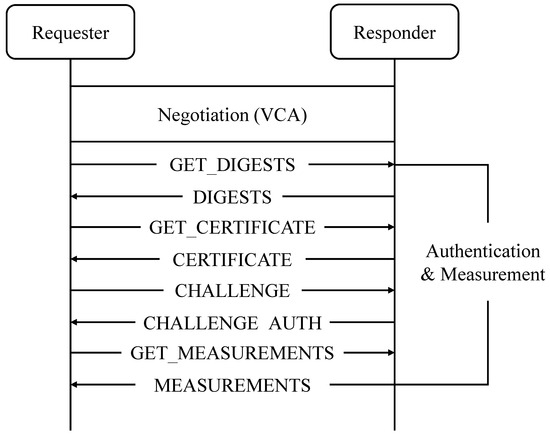
Figure 1.
Standard SPDM message flow for negotiation and device attestation.
- The negotiation phase. In this phase, SPDM ensures that both the requester and the responder agree on the supported versions, capabilities, and cryptographic algorithms, commonly abbreviated as VCA. The requester and the responder exchange messages to negotiate the compatibility between protocol versions, identify supported features and capabilities, and agree upon the cryptographic algorithms for the device attestation phase.
- The device attestation phase. In this phase, SPDM focuses on verifying the identity of the device and ensuring the integrity of its firmware and hardware configuration. They exchange messages as follows:
- GET_DIGESTS/DIGESTS: The requester initiates the authentication by sending a GET_DIGESTS message to retrieve the hash value of the responder’s certificate chain. If the hash value matches a previously verified identity cached by the requester, the process of retrieving the entire certificate chain can be omitted.
- GET_CERTIFICATE/CERTIFICATE: The requester sends a GET_CERTIFICATE message to retrieve the responder’s X.509 certificate. The responder provides the whole certificate chain in the CERTIFICATE response.
- CHALLENGE/CHALLENGE_AUTH: To verify the responder’s possession of the secret key associated with the certificate, the requester sends a CHALLENGE message. The responder replies with the CHALLENGE_AUTH message containing the signature signed by its own secret key. In SPDM, the message to be signed is referred to as the message transcript.
- GET_MEASUREMENTS/MEASUREMENTS: The requester sends the GET_MEASUR EMENTS message to obtain specific measurements from the responder, such as the current state of the firmware, the hardware configuration, or other security-related data.
As the requester is solely responsible for device attestation, SPDM follows a centralized model in which functional asymmetry remains between the entities.
2.2. X.509 Certificates
X.509 certificates [7] are a widely used format for public key infrastructure (PKI) and play an essential role in authenticating entities in web environments. As shown in Figure 2, X.509 certificates follow a hierarchical trust model, where each certificate is signed by a Certificate Authority (CA). Each certificate in the chain is verified using the public key of its upper certificate, continuing until the root CA certificate—a self-signed certificate—is reached. If the root CA certificate is in the trust anchor of the verifier, it eventually trusts the leaf certificate.
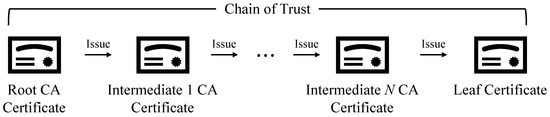
Figure 2.
Hierarchical certificate chain from the root CA to the leaf certificate via intermediate CAs.
While SPDM also employs X.509 certificates to identify devices, it differs from web environments, where X.509 certificates are typically issued by trusted third-party root CAs such as DigiCert [17], Let’s Encrypt [18], or GlobalSign [19]. These root CAs are widely identified and trusted by most web browsers. When web servers obtain certificates from the CA, they usually have no direct relationship beyond the certificate issuance process. However, in the SPDM ecosystem, the root CA in the certificate chain often belongs to the device manufacturer rather than a public CA. In many cases, SPDM-supported devices are expected to have a hardware root of trust (RoT), such as TCG DICE (Device Identifier Composition Engine) [20], from which they derive a unique public key. As a result, certificates can be tightly linked to the hardware RoT and provisioned into the device at the manufacturing step, allowing manufacturers complete control over the certificate issuance process. This enables flexibility in defining the certificate structures, including the addition of SPDM-specific extensions that can carry device-related attributes such as the firmware version or hardware configuration. Moreover, the manufacturer acts as both the hardware provider and the certificate issuer, guaranteeing supply chain security and permitting only trusted devices with manufacturer-issued certificates to participate in secure communication. A real-world example of this approach can be found in Samsung’s SPDM-supported products [21]. Samsung publicly provides the root CA certificates for its DRAM and SSD products to facilitate device attestation with SPDM.
Recently, short-lived certificates have emerged as a practical alternative to traditional revocation methods, such as Certificate Revocation Lists (CRLs) or Online Certificate Status Protocol (OCSP), simplifying the certificate management and minimizing the exposure to certificate compromise. Industry examples include Netflix’s short-lived SSH certificates [22] and Let’s Encrypt’s short-validity (90-day) TLS certificates [18], demonstrating their real-world adoption and effectiveness.
2.3. Aggregate Signatures
Aggregate signature schemes provide an efficient cryptographic solution that combines individual signatures into a compact signature. The aggregate signature scheme is a promising solution for resource-constrained environments, such as peripheral devices, the industrial Internet of Things (IIoT), and vehicular ad hoc networks (VANETs), because it reduces the communication overhead and verification costs. Among the various approaches to aggregate signature schemes, two prominent categories are certificateless aggregate signature (CLAS) and certificate-based aggregate signature (CBAS) schemes.
CLAS schemes [23,24,25,26,27,28,29] aim to eliminate the dependency on traditional PKI by allowing a trusted authority (TA) (The TA in CLASs is similar to the CA in CBASs.) to generate partial secret keys for users. While removing the need for users to manage certificates, they introduce a significant security concern known as key escrow, where the TA can reconstruct the user’s complete secret key.
On the other hand, CBAS schemes [10,11,30,31,32,33,34] leverage PKI to achieve efficient signature aggregation. In CBAS schemes, users generate their own secret keys, and the CA then issues certificates to bind their identities to public keys. Unlike traditional X.509 certificates, these certificates take the form of a commitment that conceals the CA’s secret key. We refer to these as chainless certificates. Recent advancements in CBASs have introduced pairing-free constructions, significantly reducing the computation costs while maintaining strong security properties based on the discrete logarithm problem (DLP).
CBAS schemes can be compatible with SPDM, as both utilize certificates issued by a CA for authentication. However, the existing CBAS schemes generally lack mechanisms allowing independent third-party verifiers to publicly authenticate the device certificates issued by a CA. Such verification is critical in attestation protocols like SPDM, where a requester authenticates multiple devices by validating certificates issued by a trusted CA and verifying possession of the corresponding private keys through signature verification. To overcome this limitation, we enhanced the current CBAS techniques by incorporating an explicit certificate verification phase, enabling public validation of the certificates during the attestation phase. Consequently, the proposed scheme delivers notable improvements in functionality and performance, specifically optimized for SPDM environments. A comprehensive evaluation comparing our scheme with recent CBAS proposals is detailed in Section 6.1.
3. Description of the System and Security Goals
3.1. The System Model
As shown in Figure 3, we consider a device attestation framework based on SPDM with key entities: the Certificate Authority (CA), the requester, and the responder, who can be further classified as the group leader and the group member. In this paper, we use “responder” and “device” interchangeably.
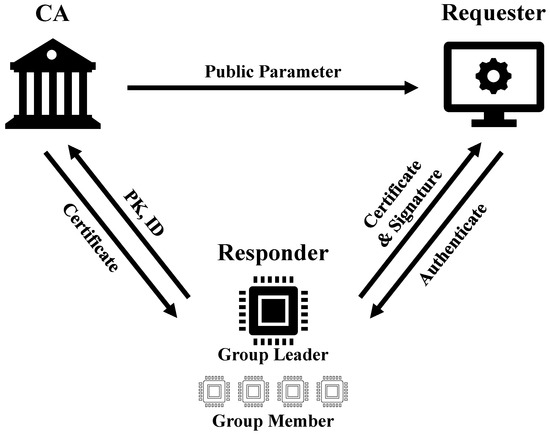
Figure 3.
A system model of SPDM-AggSig, illustrating the key entities for the group-based attestation.
- Certificate Authority. As the root of trust in the system, the CA issues the device certificates. These certificates are used to bind a device’s public key to its unique identity. Unlike in web environments, the CA in this system is often controlled by the device manufacturer, providing more control over the certificate structures and supply chain security. Furthermore, by adopting short-lived certificates issued securely at the time of manufacturing, the system inherently mitigates the potential risks associated with compromised or vulnerable certificates, as any compromised certificate can be quickly replaced with a newly updated one. This frequent update process effectively eliminates the need for complex revocation mechanisms such as CRLs or OCSP, substantially simplifying the certificate lifecycle management and strengthening the system’s overall resilience. Certificate issuance can conveniently leverage SPDM’s existing identity provisioning mechanisms.
- Requester. As shown in Figure 3, the requester initiates the authentication process to verify the identity and integrity of the responder. For example, in a data center, the host platform may act as the requester when verifying the authenticity of numerous peripheral devices. The primary role of the requester is to authenticate responders by verifying their certificates and ensuring that they possess the secret key corresponding to the public key included in the certificate.
- Responder. The responder sends the information required for authentication to the requester. As shown in Figure 3, each responder obtains a certificate from the CA corresponding to its own key pair. In our scheme, responders can be categorized into group leaders and group members depending on their roles.
- Group leader: The group leader acts as an intermediary between the requester and the group. It collects authentication data—such as certificates or signatures—from group members at different stages. The group leader can aggregate such authentication data into a constant size, reducing the computation and communication overhead for the requester.
- Group member: Group members are individual devices within the group, with each holding a chainless certificate issued by the CA. They provide their authentication data to the group leader in the device attestation phase.
Group-based attestation transforms the validation process from a fully centralized into a partially distributed model, introducing a more symmetric operational system across the requester and the responder. We assume that each responder is equipped with a hardware root of trust (RoT).
3.2. Preliminaries
3.2.1. The Elliptic Curve Cryptosystem and Assumptions
Let be an elliptic curve over a finite field , where p is a large prime and . Additionally, ensures that the curve has no singularities. We consider an additive cyclic subgroup of with a generator P and an order q, where q is a large prime and the special point (the point at infinity) acts as the identity element for the group operation. For , the point addition is performed according to the chord-and-tangent rule [35,36]. The scalar multiplication on can be computed as , where and .
The Elliptic Curve Discrete Logarithm Problem (ECDLP): Given , it is computationally infeasible to determine the integer so that the equation holds. In other words, for any probabilistic polynomial time (PPT) algorithm , the success probability of finding s given P and is negligible:
where is the security parameter, and negl represents a negligible function in .
3.2.2. Algorithm Definition
We present the definition of the algorithm for a chainless-certification-based aggregate signature scheme as follows:
- : This algorithm takes the security parameter as input. It outputs the public parameter and the secret key of the CA .
- : This algorithm takes the identity as the input. It outputs the public/secret key pair .
- : This algorithm takes , , and as the input. It outputs the corresponding certificate .
- : This algorithm takes as the input. It outputs a commitment that can be used to verify whether corresponds to associated with .
- : This algorithm takes , and as input. It outputs 1 if the commitment is valid, confirming that corresponds to associated with ; otherwise, it outputs 0, indicating that the certificate verification failed.
- (: This algorithm takes proofs as input. It outputs the corresponding aggregation proof .
- : This algorithm takes , , and as input. If is valid, it outputs 1; otherwise, it outputs 0.
- (: This algorithm takes , and message m as input. It outputs the signature .
- : This algorithm takes , the public key of the CA , , and m as input. If is valid, it outputs 1; otherwise, it outputs 0.
- (: This algorithm takes the signatures as input. It outputs the corresponding aggregation signature .
- : This algorithm takes , , , and as input. If is valid, it outputs 1; otherwise, it outputs 0.
3.3. The Security Model
In traditional certificate-based aggregate signature schemes [10,11], security models typically define two types of adversaries.
- Type I (malicious device) adversary : An external attacker cannot access the master secret key used to generate the certificate (i.e., the secret key of the CA). Instead, it can replace the public keys of other devices.
- Type II (malicious CA) adversary : A malicious or compromised CA can generate a valid certificate for the target public key pair.
However, in SPDM environments, where the manufacturer acts as the CA, the assumptions for the security models need to be fine-tuned to reflect the practical SPDM framework. Unlike traditional PKI systems, where the CA is an independent third party, the manufacturer itself is the root of trust. The security assumptions underlying SPDM rely on the manufacturer acting as a trusted entity, particularly during the device manufacturing and provisioning phases. Specifically, SPDM assumes that peripheral devices intended for deployment in data centers are securely produced, with device-specific key pairs and certificates generated and provisioned within a trusted manufacturing environment. Under these assumptions, SPDM explicitly targets threat scenarios where a legitimate device is replaced with an entirely unauthorized device or cases in which the original device’s firmware becomes maliciously modified or corrupted after manufacturing. Consequently, the manufacturing and initial provisioning processes, protected by a robust hardware RoT, are inherently considered trustworthy. For example, a compromised group leader can be effectively detected through the attestation phase by validating measurements securely recorded within the device’s hardware RoT, enabling the rapid identification and exclusion of unauthorized or tampered devices. Thus, we focus on Type I adversaries to ensure the proposed scheme is secure against external attackers who attempt to generate valid signatures without possessing the secret key.
We provide the security game of existential unforgeability under an adaptive chosen message attack (EUF-ACMA) for a challenger and an adversary . We briefly outline how the security game proceeds: A challenger initializes the system by generating the primary system keys and only provides the attacker with publicly available information, securely retaining the private keys. The attacker possesses considerable capabilities, including obtaining secret keys, requesting legitimate certificates, querying signatures for chosen messages, and replacing public keys with malicious alternatives. Finally, to break the security, the attacker must successfully produce a valid signature for a new message attributed to the challenger whose secret key and corresponding signature have never been revealed or issued. The signature scheme is considered secure if the probability of the attacker winning this game remains negligible, ensuring strong resistance against forgery attacks. The security game is formally summarized below.
- The initialize phase: runs Setup(·) to generate and . keeps securely and sends to .
- The query phase:
- KeyExtract: Upon receiving the identity , == KeyGen(·) to create the key pairs () and send to .
- PubKeyReplace: For an identity , can replace with . It is not required to possess the corresponding secret key, and the process can be performed repeatedly.
- CertExtract: runs CertGen(·) and sends the certificate on the requested () to .
- SecKeyExtract: Upon receiving the identity , checks the recorded output from the KeyExtract query and sends to .
- SignExtract: Upon receiving the identity and message m, can run Sign(·) to generate a signature and send it to .
- The forgery phase: outputs a forged signature for the challenge identity and message , where was never queried during PriKeyExtract and the pair was never queried during SignExtract. The corresponding certificate cannot be captured by . In addition, of cannot be replaced.
- The output phase: Upon receiving the forged signature tuple , if Verify(·) returns 1, then wins the game, and outputs 1; otherwise, it outputs 0.
Notice that the advantage of winning in is denoted as
Definition 1.
The chainless-certificate-based aggregate signature scheme is EUF-ACMA-secure if the advantage is negligible.
4. The Proposed Scheme
In this section, we introduce SPDM-AggSig, a chainless-certificate-based device attestation protocol that leverages an aggregate signature scheme to enhance the efficiency while preserving robust security guarantees. Finally, we discuss the implications and potential challenges when deploying SPDM-AggSig in practical environments.
4.1. SPDM-AggSig
We first extend SPDM to support group-based messaging and expand the concept of the chainless certificate based on the recently proposed CBAS scheme [10] by incorporating additional features, such as enabling third-party verification of the certificates and providing a constant-size signature. Figure 4 illustrates group-based attestation with the proposed aggregate signature scheme.
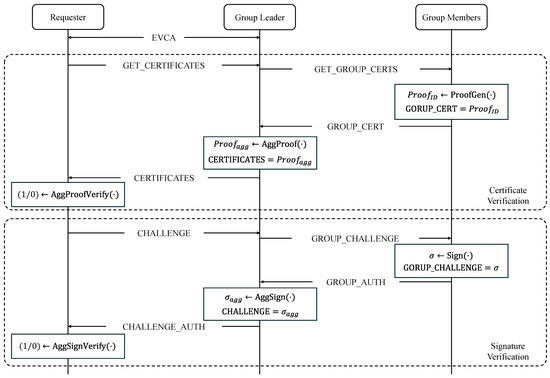
Figure 4.
The newly added message flow to support group-based authentication with the proposed aggregate signature scheme.
4.1.1. Group-Based Attestation
The standard SPDM message flow consists of direct communication between the requester and the responder. As the requester performs repetitive verification processes for each responder, it can become a bottleneck when dealing with multiple devices. In order to solve this problem, we propose the SPDM-AggSig message flow, which employs group-based attestation with the roles of the group leader and members, improving the scalability and efficiency. The explanation of GET_DIGESTS and GET_MEASUREMENTS is excluded, as they can easily be integrated into group-based attestation. The group leader acts as an intermediary between the requester and multiple group members, managing the verification process for the group. To interact with the members, the group leader can leverage mechanisms such as PCIe peer-to-peer communication.
As shown in Figure 4, we introduce new message types and functionalities as follows:
- EVCA (Extended Version, Capability, Algorithm Negotiation): The requester sends an extended version of VCA to the leader, including group-based authentication parameters, such as group member identifiers.
- Group certificate management (GET_GROUP_CERTS/GROUP_CERT): The group leader retrieves the certificates from all group members using the GET_GROUP_ CERTS message. Each group member responds with their certificate using the GROUP_CERT message. In the proposed scheme, the responder runs ProofGen(·) to generate and transmit a publicly verifiable certificate proof, allowing a third party to validate its authenticity without disclosing sensitive information (see Section 4.1.2 for details). The group leader then collects these certificates from multiple responders, including its own, and produces an aggregated proof . The requester eventually verifies that a trusted CA has issued using AggProofVerify(·). The GET_GROUP_CERTS message additionally includes the negotiated features and the cipher suite, which is determined during the EVCA phase.
- Group-based authentication (GROUP_CHALLENGE/GROUP_AUTH): The group leader issues GROUP_CHALLENGE to all group members, driving each member to run Sign(·) and generate an individual signature for the challenge message. The group leader then collects these signatures through GROUP_AUTH and aggregates them into a constant-size aggregated signature using AggSign(·). On receiving , the requester verifies the signature through AggSignVerify(·) to confirm that each device possesses the secret key corresponding to its certificate, thereby completing the authentication process. The GROUP_CHALLENGE message additionally includes the message transcript to be signed.
Our scheme allows the requester to receive a compact response—an aggregated certificate and signature—rather than multiple individual responses from each group member, thereby minimizing the network overhead and computational effort on the requester side. It is important to note that this aggregation process might not be strictly mandatory. Suppose a scenario does not leverage the group leader’s aggregation capability. In that case, the requester can still communicate directly with individual devices using the chainless certificate (i.e., SPDM-Chainless) without compromising the authentication capabilities. Instead, the overall communication overhead becomes higher, as the requester must manage separate attestation exchanges and collect the responses from each device individually.
4.1.2. Chainless-Certificate-Based Aggregate Signatures
We describe the details of SPMD-SigAgg, including the certificate and signature verification. Setup(·) is conducted by the CA, at which time each device—both group leaders and member devices—executes KeyGen(·) to generate a public and private key pair. The CA then issues a corresponding certificate via CertGen(·). Subsequently, as shown in Figure 4, each participant follows the specified message flow and invokes the necessary cryptographic functions to achieve the attestation process.
- : The CA can run the setup algorithm with a security parameter . This generates the public parameters , and its key pair , where a random , and P is the generator of the elliptic curve group . The cryptographic hash functions are defined as follows:
- ;
- .
- : The responder can generate its key pair with the identity . The secret key , and the corresponding public key is , where a random .
- : The CA can generate the certificate for the device as follows:
- , where a random ;
- , where .
- : The responder can generate the proof used to verify whether the certificate was issued by the CA as follows:
- , where a random ;
- .
- : This requester can verify the received proof by checking whether the commitment in correctly matches as follows:where . It outputs 1 if the verification succeeds and 0 otherwise.
- (: The group leader can combine n proofs {} into the aggregated proof as follows:
- ;
- and .
- : The requester can verify the aggregated proof as follows:where . It outputs 1 if the verification succeeds and 0 otherwise.
- : The responder can generate a signature on the message m as follows:
- , where a random ;
- where .
- : The requester can verify the signature as follows:where and . It outputs 1 if the verification succeeds and 0 otherwise.
- : The group leader can combine n signatures {} into a single aggregated signature as follows:
- and .
- : The requester can verify the aggregated signature as follows:where , and . It outputs 1 if the verification succeeds and 0 otherwise.
4.2. The Correctness Proof
We demonstrate the verification of the certificate proof and the signature of the proposed scheme. Since the aggregate schemes (both the proof and the signature) combine multiple individual responses into an aggregated compact response without altering the original structure, their correctness is inherently derived from the correctness of the individual schemes. Therefore, the correctness of the aggregate schemes can be directly reduced to that of the individual schemes.
- Aggregated certificate correctness proof. Given the aggregated certificate proof , the AggProofVerify(·) algorithm computes
- Aggregated signature correctness. Given the aggregated signature , the AggSignVerify(·) algorithm computes
4.3. Discussion and Future Work
4.3.1. Peer-to-Peer Communication
Peripheral devices typically rely on well-established communication protocols such as PCI Express (PCIe) and Compute Express Link (CXL). Both protocols support peer-to-peer (P2P) communication, enabling devices to directly exchange data without routing through the central host platform. For example, GPUDirect [37] allows GPUs to transmit data to each other over the PCIe bus directly, reducing the overhead associated with host-managed memory transfers. However, achieving interoperability between devices from different manufacturers remains a significant implementation challenge. Due to the lack of standardized protocols and interfaces across different manufacturers’ devices, achieving interoperability often requires significant effort to change the hardware-level configuration and firmware. Therefore, as part of our future work, we will consider exploring a low-level group messaging functionality at the hardware and firmware levels to improve the interoperability and enable seamless peer-to-peer communication across heterogeneous devices.
4.3.2. Compatibility with SPDM-Origin
SPDM-AggSig employs a chainless certificate structure managed directly by the device manufacturer, which differs fundamentally from the X.509-based certificates used in traditional SPDM protocols (SPDM-Origin). Nevertheless, compatibility with SPDM-Origin can be straightforwardly maintained through the requester’s capability to support both authentication mechanisms. Suppose some devices in a deployment environment use traditional X.509 certificates while other devices or groups of devices leverage the chainless certificate approach. In this case, the requester can distinguish these devices during the negotiation phase and request attestation accordingly. Thus, as long as the requester is equipped to handle both certificate types and respective message formats, each device only needs to support its native authentication mechanism. This ensures seamless coexistence and interoperability between the legacy SPDM and newly introduced SPDM-AggSig deployments without requiring modifications to the existing device implementations.
4.3.3. Handling Failure Scenarios
- Network failures. In practical deployment scenarios, network conditions such as latency or packet loss may occasionally lead to attestation failures. However, SPDM inherently resolves such failures through straightforward mechanisms, including session re-initialization and requester-initiated retries. Given these inherent recovery capabilities, SPDM-AggSig naturally achieves sufficient robustness against typical network disruptions without relying on further specialized mechanisms, thus maintaining operational simplicity.
- Device and firmware compromise. SPDM explicitly assumes trust in the manufacturing process, where the devices and firmware are provisioned securely based on hardware RoTs. Consequently, SPDM-AggSig is primarily designed to detect and handle scenarios where a genuine device is replaced with an unauthorized one or a device’s firmware becomes compromised after provisioning. Measurement-based attestation ensures that compromised devices or firmware modifications are readily observable, enabling immediate exclusion and replacement.
- Group leader compromise. Another critical failure scenario involves the potential compromise or failure of group leaders in SPDM-AggSig, which could introduce single-point-of-failure vulnerabilities. Our scheme proactively addresses the issue through built-in measurement validation mechanisms that leverage the hardware RoT, facilitating the rapid detection and immediate exclusion of compromised or faulty leaders. In addition, further enhancements such as deploying fallback mechanisms with secondary leaders pre-designated by the manufacturers or integrating dynamic leader election processes can be readily incorporated to ensure continuous and secure group operation under diverse operational conditions. We will leave these enhancements as directions for future work.
4.3.4. Further Security Enhancements
Although we provide rigorous security proofs, formal verification tools such as the Tamarin prover [38] could offer complementary benefits by systematically verifying the security properties and cryptographic assumptions and detecting subtle vulnerabilities. A recent study applied formal verification methods to rigorously analyzing the security properties of the SPDM 1.2 protocol [39]. Formal verification approaches could also be extended to addressing more comprehensive scenarios, such as dynamic session management and multi-party interactions within SPDM. Moreover, the emergence of the quantum computing area could significantly threaten the conventional cryptographic primitives, including ECC. Recent research has explored hybrid cryptographic solutions combining ECC with post-quantum cryptographic (PQC) algorithms within the SPDM protocol [40]. Consequently, designing efficient and secure aggregate signatures leveraging PQC schemes represents another crucial future research direction, ensuring long-term cryptographic resilience and interoperability with evolving security practices.
5. Security Analysis
In this section, we provide a formal security proof, along with a high-level sketch of the key ideas of the proof, and analyze the security properties of the proposed scheme.
5.1. Sketch of the Proof
SPDM-AggSig achieves existential unforgeability under an adaptive chosen message attack (EUF-ACMA) security based on the widely accepted hardness assumption of the Elliptic Curve Discrete Logarithm Problem (ECDLP) in the random oracle model. At a high level, the proof leverages the idea that an adversary capable of forging a valid signature without possessing the legitimate private key and certificate would implicitly solve the underlying ECDLP, a problem known to be computationally infeasible. More specifically, the security proof utilizes a challenger who initially embeds an ECDLP instance into the key of the CA during system setup. The adversary is allowed to adaptively request various keys, certificates, and signatures. Suppose the adversary succeeds in producing a valid yet previously unseen signature. In this case, the challenger can apply the Forking lemma [41] to extract two related but distinct signatures from the forgery, thereby solving the embedded ECDLP instance. Consequently, through the reduction of security into the computational infeasibility of solving the ECDLP, our scheme is EUF-ACMA-secure.
5.2. Security Proof
As described in Section 3.3, we prove the proposed scheme is EUF-ACMA-secure against in the random oracle model (ROM) based on the ECDLP assumption.
Theorem 1.
If the ECDLP assumption holds, the proposed scheme is EUF-ACMA-secure against the adversary in ROM.
Proof of Theorem 1.
Suppose the adversary can forge a valid signature under the proposed scheme. Then, given a random ECDLP instance , a challenger can solve the ECDLP and the output s by interacting with in the following game.
The initialization phase: sets , implicitly implying , and generates the system parameter , q, P, , , , where is a random oracle and the cryptographic hash function . The responses to the queries—KeyExtract, , CertExtract, and SignExtract—are recorded in the corresponding lists—, , , and —all of which are initially empty. Then, selects a random identity as the challenge identity.
The query phase: In this phase, can adaptively request the following queries.
- KeyExtract: Upon receiving a public key request query for , the challenger checks for an existing tuple . If such a tuple is found, it responds with . Otherwise, it generates a new key pair , where is chosen uniformly at random, and returns . The newly generated tuple is then added to .
- SecKeyExtract: Upon receiving a secret key request for , the challenger checks for an existing tuple . If such a tuple is found, it responds with . Otherwise, it generates a new key pair , where is chosen uniformly at random, returns , and adds the newly created tuple to .
- CertExtract: Upon receiving a certificate request for and , the challenger first checks whether . If so, aborts. Otherwise, generates the certificate , where , are chosen uniformly at random. It then returns and adds the tuple to .
- PubKeyReplace: Upon receiving a public key replacement request for , the challenger first checks whether . If so, the query is ignored. Otherwise, the challenger searches for the tuple . Once found, it replaces the tuple with , indicating that the corresponding secret key is no longer available.
- : Upon receiving an hash oracle request for , the challenger checks for an existing tuple . If the tuple exists, returns . If the tuple does not exist, follows the same process as for a certificate generation request for , obtaining along with the corresponding certificate tuple . The newly created tuple is then added to , and is returned.
- SignExtract: Upon receiving a signature generation request for , if , the challenger generates the signature , where , with chosen uniformly at random and . The tuple is then added to . The certificate can be obtained through a CertExtract query. Otherwise, aborts the game.
The forgery phase: Finally, outputs a forged signature , for the tuple , where . If or , the challenger aborts. Otherwise, by applying the Forking lemma [41], another valid forged signature can be generated through a probabilistic polynomial time (PPT) adversary using the same random tape but with a different response from the oracle. As a result, is able to produce a second valid forged signatures , where , while remains the same, . Thus, from the valid forged signature and , we obtain the following two equations:
From these equations, can solve for as the solution of the ECDLP.
Based on the simulation presented above, the probability that can solve the ECDLP can be computed using the following three events:
- : does not abort during the query phase;
- : The adversary produces a valid forged signature.;
- : The forgery corresponds to the target identity .
We can then compute the probability of each event, , , and , where q is the maximum number of queries. Thus, the probability that successfully solves the ECDLP is at least
□
5.3. Security Properties
We highlight the practical implications of the proposed scheme and demonstrate how it protects against common security threats.
- Device Authentication.
- Certificate verification: We ensure that the device cannot generate a valid certificate without knowledge of the CA secret key. The certificate proof verification determines whether the certificate is valid and issued by a trusted CA.
- Signature verification: We guarantee that the device holds the secret key corresponding to the public key in the verified certificate. The successful verification of the signature demonstrates proof of possession of the secret key without revealing it.
Together, they enable the verification of the authenticity of the device.
- Replay attack protection. Since the signature scheme is probabilistic, it produces a different signature each time, even for the same message. This randomness ensures that identical messages do not result in identical signatures, effectively preventing replay attacks. Any attempt to resend a captured old signature will easily be detected and rejected.
- Man-in-the-middle (MITM) attack protection.
- Impersonation attack prevention: The combination of certificate and signature verification ensures that only devices with valid certificates and the correct secret key can participate in the protocol. Without them, any attempt to impersonate a legitimate device is detected at the verification phase.
- Modification attack prevention: We ensure the integrity of the message by verifying each corresponding signature. An alteration in a single bit of the message means that the signature no longer matches, which protects the system from tampering or data injection by malicious attackers.
Thus, we can ensure that attackers cannot impersonate a legitimate device or modify the communication.
6. Comparative and Performance Analysis
In this section, we present a comparative analysis with other CBAS schemes (Section 6.1) and a performance analysis from the deployment perspective by comparing SPDM-based implementations (Section 6.2). The notation used in the analysis is explained in Table 1. We also provide a common experimental setup designed explicitly for proof-of-concept (PoC) evaluations. All experiments were conducted using a standard desktop environment equipped with an Intel Core i5-13600KF (3.5 GHz) CPU and 32 GB of DDR5 RAM, running on Windows 10. We implemented the proposed scheme and all of the comparative schemes as PoC prototypes in C++, utilizing the OpenSSL 3.4.0 library [42], to evaluate their practical performance relative to that of the existing SPDM baseline implementation. The experiments use NIST ECC curves [43], specifically P-256 (secp256r1) and P-384 (secp384r1) while varying the number of devices (group members), to analyze the efficiency and scalability of the schemes.

Table 1.
Definitions of notations used for the analysis.
6.1. A Comparative Analysis with Existing CBAS Schemes
In this section, we comparatively evaluate the proposed scheme with recent certificate-based aggregate signature (CBAS) schemes, namely Q-CBAS [10] and V-CBAS [11]. Specifically, we selected Q-CBAS because it represents that most recently introduced in the literature, thus serving as a current state-of-the-art benchmark. Meanwhile, V-CBAS was included due to its constant-size signature generation, which closely aligns with the design objectives of our scheme, particularly regarding the minimized communication overhead. The comparison is structured into three distinct aspects: functionality (Section 6.1.1), security (Section 6.1.2), and performance (Section 6.1.3). The detailed results are summarized in Table 2 and Table 3.

Table 2.
Comparative evaluation of CBAS schemes.

Table 3.
Performance analysis of CBAS schemes.
6.1.1. Functionality Comparison
As shown in Table 2, a critical limitation of the existing CBAS schemes (Q-CBAS and V-CBAS) is their inability to provide publicly verifiable certificates, a fundamental requirement for integration with SPDM. In SPDM-based attestation, the certificate serves to establish trust in the device’s claimed identity, while signature verification ensures that the device legitimately possesses the corresponding private key. The absence of public verifiability in the existing schemes thus renders them fundamentally incompatible with the SPDM protocol. In order to address this limitation, our scheme introduces publicly verifiable certificates and further enhances the efficiency through the aggregation of multiple certificates into a compact form. Consequently, among the evaluated CBAS schemes, the proposed scheme uniquely meets the functional requirements for effective integration into SPDM-based attestation environments.
6.1.2. Security Comparison
Table 2 further compares the security guarantees provided by Q-CBAS, V-CBAS, and the proposed scheme, considering two distinct attacker models and . Q-CBAS explicitly assumes and proves security against both outsider and insider adversaries. Similarly, V-CBAS aimed initially to provide comprehensive security under both attacker models; however, Qiao et al. [10] identified vulnerabilities against insider adversaries , undermining its original security claim. In contrast, the proposed scheme specifically targets security under the outsider adversary model without addressing insider threats explicitly. Although this implies that our scheme does not provide stronger protection from insider threats compared to that with Q-CBAS, the outsider-only assumption is practically sufficient within SPDM deployment scenarios. Specifically, in SPDM environments, the device certificates are securely provisioned and strictly controlled by trusted manufacturers, inherently minimizing the impact of insider threats. Thus, the security guarantees provided by our scheme adequately address the threat landscape relevant to typical SPDM use cases.
6.1.3. Performance Comparison
- Theoretical evaluation. Table 3 compares the computation and communication overheads of the three evaluated CBAS schemes. In terms of the computation cost, a critical observation is that the signature verification cost, particularly involving the relatively expensive scalar multiplication operation , is notably higher in Q-CBAS compared to that in the other schemes. The increased overhead in Q-CBAS reflects a trade-off arising from its stronger security assumptions discussed in Section 6.1.2. On the other hand, our scheme and V-CBAS exhibit a similar computational efficiency. Regarding the communication overhead, the aggregate signature size in Q-CBAS increases linearly with the number of devices m, whereas both V-CBAS and the proposed scheme maintain a constant signature size regardless of m. The constant-size characteristic significantly enhances scalability and efficiency, particularly in large-scale deployments, highlighting a clear advantage over Q-CBAS in practical SPDM scenarios.Experimental evaluation. Figure 5 illustrates the results of the experimental evaluation of the CBAS schemes. The left y-axis represents the computation overhead, while the right y-axis indicates the communication overhead. The bar graphs illustrate the computation overhead, divided into the signature generation, signature verification, and overall cost, whereas the green line graph with markers indicates the aggregate signature size, representing the communication overhead. Specifically, Q-CBAS exhibits a significantly higher computational overhead, particularly during the signature verification stage, due to the larger number of costly scalar multiplications. This overhead notably increases as the number of aggregated devices grows from 100 to 1000, demonstrating the scalability limitations of the Q-CBAS scheme. In contrast, V-CBAS and our scheme show a comparable computation overhead, maintaining efficiency across varying device scales. Moreover, regarding the communication overhead, the linear growth in the aggregate signature size of Q-CBAS is evident as the number of devices increases. In contrast, both V-CBAS and our scheme retain constant-size signatures. Consequently, these experimental results underscore the proposed scheme’s prominent scalability and practicality for large-scale SPDM-based attestation deployments.
 Figure 5. A comparison of the experimental computation and communication costs based on ECC P-384 and the number of devices for Q-CBAS [10], V-CBAS [11], and the proposed scheme.
Figure 5. A comparison of the experimental computation and communication costs based on ECC P-384 and the number of devices for Q-CBAS [10], V-CBAS [11], and the proposed scheme.
6.2. Performance Analysis in SPDM-Based Implementations
In this section, we demonstrate the efficiency and scalability of the proposed SPDM-AggSig scheme through theoretical and experimental evaluations, comparing it with SPDM-Origin (the standard SPDM protocol); SPDM-Group, which integrates a group concept into the existing SPDM message flow; and SPDM-Chainless, which replaces the X.509 certificates with chainless certificates, as described in Section 1. Specifically, we examine whether the proposed scheme relieves the bottleneck from the requester’s perspective and addresses the burden of the computing resource constraints on the device side. We assume that the signature algorithm in the certificates and authentication messages for both SPDM-Origin and SPDM-Group is based on elliptic curve cryptography (ECC).
6.2.1. Theoretical Evaluation
We conduct a theoretical comparative analysis of the four schemes regarding the communication and computation costs. Specifically, we examine the entity cost, which represents the total cost incurred by each entity—categorized as the requester, the group leader, and the responder (group member)—as well as the overall cost, which represents the total cost incurred by each scheme. In terms of the communication overhead, the overall cost corresponds to the total sum of messages transmitted over the network, while the computation overhead represents the total sum of the computation costs incurred by all entities.
The communication overhead. As shown in Table 4, we compare the size of the exchanged SPDM messages by focusing on key distinctions among the schemes, such as whether VCA or EVCA is used in the negotiation phase, the size of the certificates retrieved for verification, group-based messages, and the signature transmission in the authentication phase. The bandwidth overhead is based on the size of the messages sent and received by each entity. For example, in SPDM-Group, the group leader’s certificate retrieval cost is given by . The leader first receives from the requester and forwards to the members. Then, it receives from the members and finally sends to the requester.

Table 4.
Comparison of communication costs.
In terms of the overall cost, the group-based scheme (SPDM-Group and SPDM-AggSig) is comparable to the other schemes (SPDM-Origin and SPDM-Chainless). However, when analyzing the entity cost of the requester, the group-based scheme offloads the requester’s overhead to the leader, effectively mitigating the potential bottleneck for the requester. In SPDM-Origin and SPDM-Chainless, the requester’s entity cost is linear to the number of devices. In contrast, SPDM-Group maintains a constant message size , while SPDM-AggSig keeps the requester’s entity cost primarily independent of the number of devices.
Certificate size is another key factor affecting the communication overhead. It is primarily determined by two factors: the number of certificates in the chain, denoted by d, and the actual size of the individual certificates in practical scenarios. Given that the size of chainless certificates is relatively smaller than that of standard X.509 certificates , SPDM schemes based on chainless certificates are more efficient from the perspective of the overall communication overhead (see Section 6.2.2 for details).
- The computational overhead. The computational overhead incurred during the certificate and signature verification phases for the four schemes is shown in Table 5 and Table 6, respectively. When calculating the overall cost, we include the overhead introduced by all m devices in the system. In other words, the overall cost is represented as the sum of the requester’s cost and the cost of m responders. In schemes employing a group leader, the overall cost is revised to account for the leader’s overheads: .
 Table 5. Comparison of computation cost: certificate verification.
Table 5. Comparison of computation cost: certificate verification. Table 6. Comparison of computation cost: signature verification.
Table 6. Comparison of computation cost: signature verification.
Contrary to X.509-certificate-based schemes, the chainless certificate cannot be revealed directly because is used to generate the signature. Instead, as shown in Table 5, the certificate proof must be generated by the responders, which incurs . Nevertheless, the computational overhead is significantly reduced since the requester can check the certificate without being affected by the chain structure.
Moreover, while SPDM-Chainless produces , where the expensive scalar multiplication increases proportionally with the number of devices, SPDM-AggSig requires , where only a fixed cost of is incurred, which enhances the scalability. The requester in SPDM-Group is the only entity whose overhead is not linearly related to the number of responders. However, this burden is entirely shifted to the leader, who verifies all group members’ certificates on behalf of the requester. In contrast, SPDM-AggSig significantly reduces the requester’s cost while imposing only a relatively small overhead on the group leader.
As shown in Table 6, similar to certificate verification, the requester in SPDM-Group demonstrates the best performance. However, it is important to highlight that this benefit comes with the drawback of shifting the entire burden to the group leader. In contrast, SPDM-AggSig performs efficiently by delegating only a tiny portion of the cost to the leader while keeping the requester’s overhead minimal. Regarding the individual responders, all schemes require a comparable computation cost to generate the signature. However, in terms of the overall cost, SPDM-AggSig outperforms the others, achieving a higher efficiency and improved performance compared to those of the other schemes (see Section 6.2.2 for details).
6.2.2. Experimental Evaluation
We conducted the implementation and testing as described in Section 6. Additionally, the number of certificates in the chain, denoted as d, was set to 3, considering the typical chain structure consisting of a root CA certificate, an intermediate CA certificate, and a leaf certificate.
- The communication overhead. As shown in Figure 6, the communication cost for the four schemes—SPDM-Origin, SPDM-Group, SPDM-Chainless, and SPDM-AggSig—is analyzed across different numbers of devices (1, 200, 400, 600, 800, and 1000). The size of the X.509 certificate is set to 600 bytes, following the example provided in the SPDM v1.3 standard document [5]. In the case of EVCA, the main difference from VCA is the inclusion of a group member identifier (4 bytes each) (Typically, 2 bytes are used as device identifiers in PCIe and CXL, but 4 bytes are chosen here for scalability.).
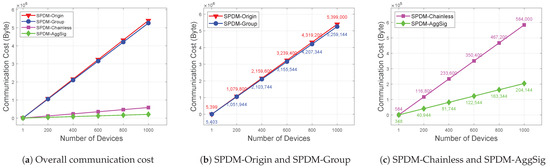 Figure 6. A comparison of the experimental communication costs based on ECC P-384 and the number of devices.
Figure 6. A comparison of the experimental communication costs based on ECC P-384 and the number of devices.
In Figure 6a, SPDM-Origin and SPDM-Group incur significantly higher communication costs than those for SPDM-Chainless and SPDM-AggSig as the number of devices increases. This difference is primarily due to the certificate size, which plays the most significant role in the communication overhead. While the cost of signature generation remains similar across the schemes, the larger size of the X.509 certificates in SPDM-Origin and SPDM-Group leads to substantially higher communication costs compared to those with the compact chainless certificates used in SPDM-Chainless and SPDM-AggSig. As observed in Figure 6b, SPDM-Origin produces slightly higher costs than those for SPDM-Group due to the initial negotiation message () being broadcast to all of the responders, affecting the communication overhead. In Figure 6c, SPDM-AggSig outperforms the others by aggregating both the certificate proofs and signatures, significantly reducing the communication costs. As a result, SPDM-AggSig offers the most efficient communication cost, achieving an approximately 96.22% decrease in the communication overhead, making it highly scalable for large-scale deployments.
- Computation overhead. In Figure 7, the computation cost for SPDM-Origin, SPDM-Chainless, and SPDM-AggSig is analyzed across different numbers of devices (100, 500, and 1000) and the ECC curves P-256 and P-384. Since the overall computation cost of SPDM-Origin and SPDM-Group is equivalent, as shown in Table 5 and Table 6, only the cost for SPDM-Origin is presented.
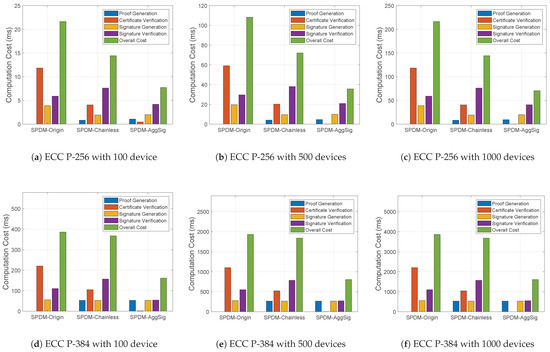 Figure 7. A comparison of the experimental computation costs based on ECC curves and the number of devices.
Figure 7. A comparison of the experimental computation costs based on ECC curves and the number of devices.
In Figure 7a–c, SPDM-Origin exhibits the highest computational cost regardless of the number of devices and the curve parameters due to the use of the X.509 certificate, even though it does not incur any certificate proof generation costs. Conversely, SPDM-AggSig achieves the best performance, benefiting from the considerable computational efficiency gained through verifying aggregated certificates and signatures. Interestingly, with the P-384 curve, as shown in Figure 7d–f, the computation cost of SPDM-Chainless approaches that of SPDM-Origin because the cost of ECC operations grows with larger key sizes (that is, the size of element in and ). Nevertheless, SPDM-AggSig continues to provide the highest performance, enhancing scalability and efficiency. As a result, SPDM-AggSig demonstrates outstanding scalability and performance, achieving approximately an 84.18% improvement in computation overhead by leveraging aggregated proofs and signatures.
The experimental evaluation indicates that SPDM-AggSig not only improves the communication and computation performance but also enables a more balanced attestation system, relieving the asymmetry of the traditional central requester-based message flows. Nevertheless, we acknowledge the importance of exploring the energy efficiency further and conducting precise evaluations on resource-constrained MCU-class devices (e.g., the ARM Cortex-M), which could strengthen the proposed scheme’s practicality in deployment environments.
7. Conclusions
In this paper, we proposed SPDM-AggSig, a novel device attestation protocol that addresses the scalability and efficiency challenges in traditional SPDM-based methods. By adopting a chainless-certificate-based aggregate signature scheme, SPDM-AggSig minimizes the communication and computation costs. In addition, group-based attestation reduces the burden on the requester by offloading authentication tasks, allowing it to handle multiple devices more efficiently. We rigorously proved the security of the proposed scheme in terms of existential unforgeability under an adaptive chosen message attack (EUF-ACMA), ensuring its resilience against various threats. The experimental results demonstrate that SPDM-AggSig significantly outperforms the conventional SPDM-Origin, achieving improvements of approximately 84.18% and 96.22% in the computation and communication overhead, respectively. Furthermore, SPDM-AggSig mitigates the asymmetry inherent in conventional SPDM protocols by distributing the burdens, thereby establishing a more functionally symmetric and scalable attestation system.
Funding
This work was supported by INHA UNIVERSITY Research Grant. This research was funded by INHA UNIVERSITY Research Grant grant number 71335-1. The APC was funded by INHA UNIVERSITY.
Data Availability Statement
The dataset is available from the author on request.
Acknowledgments
The author wishes to thank all of the reviewers for their useful comments and discussions.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Ryan, C. Tech Tampering: Are Hardware Supply Chain Attacks on the Rise? 2024. Online Resource. Available online: https://www.siliconrepublic.com/enterprise/hp-wolf-security-hardware-attacks-tampering (accessed on 29 April 2025).
- Plumb, T. HP Wolf: Not Just Software Attacks; Hackers Are Coming for Enterprise Hardware, Too. Online Resource. 2024. Available online: https://venturebeat.com/security/hp-wolf-not-just-software-attacks-hackers-are-coming-for-enterprise-hardware-too/ (accessed on 29 April 2025).
- Holland, A. Hardware Supply Chain Threats Can Undermine Your Endpoint Infrastructure. Online Resource. 2025. Available online: https://www.techradar.com/pro/hardware-supply-chain-threats-can-undermine-your-endpoint-infrastructure (accessed on 29 April 2025).
- DMTF. Distributed Management Task Force. Online Resource. Available online: https://www.dmtf.org/ (accessed on 29 April 2025).
- DMTF. DSP0274 Security Protocol and Data Model (SPDM) Specification. Version 1.3. Online Resource. 2023. Available online: https://www.dmtf.org/sites/default/files/standards/documents/DSP0274_1.3.0.pdf (accessed on 29 April 2025).
- Rescorla, E. The Transport Layer Security (TLS) Protocol Version 1.3. RFC 8446. 2018. Available online: https://www.rfc-editor.org/info/rfc8446 (accessed on 29 April 2025).
- Boeyen, S.; Santesson, S.; Polk, T.; Housley, R.; Farrell, S.; Cooper, D. Internet X.509 Public Key Infrastructure Certificate and Certificate Revocation List (CRL) Profile. RFC 5280. 2008. Available online: https://www.rfc-editor.org/info/rfc5280 (accessed on 29 April 2025).
- Niu, Z.; Jiang, H.; Zhou, K.; Yang, T.; Yan, W. Identification and authentication in large-scale storage systems. In Proceedings of the 2009 IEEE International Conference on Networking, Architecture, and Storage, Zhangjiajie, China, 9–11 July 2009; IEEE: New York, NY, USA, 2009; pp. 421–427. [Google Scholar]
- Goel, A.; Rahulamathavan, Y. A Comparative Survey of Centralised and Decentralised Identity Management Systems: Analysing Scalability, Security, and Feasibility. Future Internet 2024, 17, 1. [Google Scholar] [CrossRef]
- Qiao, Z.; Yang, Q.; Zhou, Y.; Yang, B.; Xia, Z.; Zhang, M.; Wang, T. An efficient certificate-based aggregate signature scheme with provable security for Industrial Internet of Things. IEEE Syst. J. 2022, 17, 72–82. [Google Scholar] [CrossRef]
- Verma, G.K.; Singh, B.; Kumar, N.; Chamola, V. CB-CAS: Certificate-based efficient signature scheme with compact aggregation for industrial Internet of Things environment. IEEE Internet Things J. 2019, 7, 2563–2572. [Google Scholar] [CrossRef]
- CXL. Compute Express Link. Online Resource. Available online: https://computeexpresslink.org/ (accessed on 29 April 2025).
- MIPI. Mobile Industry Processor Interface. Online Resource. Available online: https://www.mipi.org/ (accessed on 29 April 2025).
- TCG. Trusted Computing Group. Online Resource. Available online: https://trustedcomputinggroup.org/ (accessed on 29 April 2025).
- Intel Corporation. Intel® Trust Domain Extensions (Intel® TDX); Technical Report; Intel Corporation: Santa Clara, CA, USA, 2022; Available online: https://www.intel.com/content/www/us/en/developer/articles/technical/intel-trust-domain-extensions.html (accessed on 29 April 2025).
- Kaplan, D.; Powell, J.; Woller, T. AMD memory encryption. White Pap. 2016, 13, 12. [Google Scholar]
- DigiCert. DigiCert Website. Online Resource. 2024. Available online: https://www.digicert.com/ (accessed on 29 April 2025).
- Encrypt, L. Let’s Encrypt Website. Online. 2017. Available online: https://letsencrypt.org/ (accessed on 29 April 2025).
- GlobalSign. GlobalSign Website. Online Resource. 2024. Available online: https://www.globalsign.com/en (accessed on 29 April 2025).
- TCG. Device Identifier Composition Engine (DICE). Online Resource. 2024. Available online: https://trustedcomputinggroup.org/wp-content/uploads/DICE-Layering-Architecture-r19_pub.pdf (accessed on 29 April 2025).
- Samsung. Root CA Certificate for SSD Attestation. Online Resource. 2024. Available online: https://download.semiconductor.samsung.com/resources/certificate/Samsung_Memory_RootCA.crt (accessed on 29 April 2025).
- Netflix. Bless: SSH Certificate Authority. 2023. Available online: https://github.com/Netflix/bless (accessed on 29 April 2025).
- Horng, S.J.; Tzeng, S.F.; Huang, P.H.; Wang, X.; Li, T.; Khan, M.K. An efficient certificateless aggregate signature with conditional privacy-preserving for vehicular sensor networks. Inf. Sci. 2015, 317, 48–66. [Google Scholar] [CrossRef]
- Kumar, P.; Kumari, S.; Sharma, V.; Sangaiah, A.K.; Wei, J.; Li, X. A certificateless aggregate signature scheme for healthcare wireless sensor network. Sustain. Comput. Inform. Syst. 2018, 18, 80–89. [Google Scholar] [CrossRef]
- Cheng, L.; Wen, Q.; Jin, Z.; Zhang, H.; Zhou, L. Cryptanalysis and improvement of a certificateless aggregate signature scheme. Inf. Sci. 2015, 295, 337–346. [Google Scholar] [CrossRef]
- Han, Y.; Song, W.; Zhou, Z.; Wang, H.; Yuan, B. eCLAS: An efficient pairing-free certificateless aggregate signature for secure VANET communication. IEEE Syst. J. 2021, 16, 1637–1648. [Google Scholar] [CrossRef]
- Thumbur, G.; Rao, G.S.; Reddy, P.V.; Gayathri, N.; Reddy, D.K.; Padmavathamma, M. Efficient and secure certificateless aggregate signature-based authentication scheme for vehicular ad hoc networks. IEEE Internet Things J. 2020, 8, 1908–1920. [Google Scholar] [CrossRef]
- Wu, W.; Ye, F. IPCAS: An improved conditional privacy-preserving certificateless aggregate signature scheme without bilinear pairing for VANETs. J. Syst. Archit. 2024, 152, 103175. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, Y.; Yang, Q.; Yang, K.; Han, Y.; Yang, B.; Xia, Z. An efficient and secure certificateless aggregate signature scheme. J. Syst. Archit. 2024, 147, 103030. [Google Scholar] [CrossRef]
- Hwang, Y.W.; Lee, Y. A Lightweight Certificate-Based Aggregate Signature Scheme Providing Key Insulation. Comput. Mater. Contin. 2021, 69, 1747. [Google Scholar] [CrossRef]
- Verma, G.K.; Singh, B.; Kumar, N.; Kaiwartya, O.; Obaidat, M.S. PFCBAS: Pairing free and provable certificate-based aggregate signature scheme for the e-healthcare monitoring system. IEEE Syst. J. 2019, 14, 1704–1715. [Google Scholar] [CrossRef]
- Verma, G.K.; Kumar, N.; Gope, P.; Singh, B.; Singh, H. SCBS: A short certificate-based signature scheme with efficient aggregation for industrial-internet-of-things environment. IEEE Internet Things J. 2021, 8, 9305–9316. [Google Scholar] [CrossRef]
- Verma, G.K.; Gope, P.; Saxena, N.; Kumar, N. CB-DA: Lightweight and escrow-free certificate-based data aggregation for smart grid. IEEE Trans. Dependable Secur. Comput. 2022, 20, 2011–2024. [Google Scholar] [CrossRef]
- Chen, J.N.; Huang, Z.J.; Zhou, Y.P.; Zou, F.M.; Chen, C.M.; Wu, J.M.T.; Wu, T.Y. Efficient certificate-based aggregate signature scheme for vehicular ad hoc networks. IET Netw. 2020, 9, 290–297. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Conference on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- NVIDIA. GPUDirect RDMA. Online Resource. Available online: https://docs.nvidia.com/cuda/gpudirect-rdma/ (accessed on 29 April 2025).
- Meier, S.; Schmidt, B.; Cremers, C.; Basin, D. The TAMARIN prover for the symbolic analysis of security protocols. In Proceedings of the Computer Aided Verification: 25th International Conference, CAV 2013, Saint Petersburg, Russia, 13–19 July 2013; Proceedings 25. Springer: Berlin/Heidelberg, Germany, 2013; pp. 696–701. [Google Scholar]
- Cremers, C.; Dax, A.; Naska, A. Formal Analysis of {SPDM}: Security Protocol and Data Model version 1.2. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 6611–6628. [Google Scholar]
- Yao, J.; Matusiewicz, K.; Zimmer, V. Post quantum design in SPDM for device authentication and key establishment. Cryptography 2022, 6, 48. [Google Scholar] [CrossRef]
- Pointcheval, D.; Stern, J. Security arguments for digital signatures and blind signatures. J. Cryptol. 2000, 13, 361–396. [Google Scholar] [CrossRef]
- OpenSSL. OpenSSL Library 3.4.0. Online Resource. Available online: https://openssl-library.org/source/ (accessed on 29 April 2025).
- NIST. Elliptic Curve Cryptographic Curve. Online Resource. Available online: https://csrc.nist.gov/projects/elliptic-curve-cryptography (accessed on 29 April 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).