GAANet: Symmetry-Driven Gaussian Modeling with Additive Attention for Precise and Robust Oriented Object Detection

Abstract

Oriented objects in RSI (Remote Sensing Imagery) typically present arbitrary rotations, extreme aspect ratios, multi-scale variations, and complex backgrounds. These factors often result in feature misalignment, representational ambiguity, and regression inconsistency, which significantly degrade detection performance. To address these issues, GAANet (Gaussian-Augmented Additive Network), a symmetry-driven framework for ODD (oriented object detection), is proposed. GAANet incorporates a symmetry-preserving mechanism into three critical components—feature extraction, representation modeling, and metric optimization—facilitating systematic improvements from structural representation to learning objectives. A CAX-ViT (Contextual Additive Exchange Vision Transformer) is developed to enhance multi-scale structural modeling by combining spatial–channel symmetric interactions with convolution–attention fusion. A GBBox (Gaussian Bounding Box) representation is employed, which implicitly encodes directional information through the invariance of the covariance matrix, thereby alleviating angular periodicity problems. Additionally, a GPIoU (Gaussian Product Intersection over Union) loss function is introduced to ensure geometric consistency between training objectives and the SkewIoU evaluation metric. GAANet achieved a 90.58% mAP on HRSC2016, 89.95% on UCAS-AOD, and 77.86% on the large-scale DOTA v1.0 dataset, outperforming mainstream methods across various benchmarks. In particular, GAANet showed a +3.27% mAP improvement over ${\mathrm{R}}^3$Det and a +4.68% gain over Oriented R-CNN on HRSC2016, demonstrating superior performance over representative baselines. Overall, GAANet establishes a closed-loop detection paradigm that integrates feature interaction, probabilistic modeling, and metric optimization under symmetry priors, offering both theoretical rigor and practical efficacy.

1. Introduction

RSI has been widely utilized in high-precision detection tasks such as military reconnaissance and maritime surveillance, owing to its rich spatial resolution and distinctive geometric structures. As illustrated in Figure 1, typical objects in RSI (e.g., ships and aircraft) exhibit unique geometric characteristics compared with those in natural images. These include the following: (1) Arbitrary Orientation—top-down imaging introduces omnidirectional rotations; (2) Extreme Aspect Ratios—elongated objects such as ships display significant disparities in length-to-width ratios; (3) Multi-Scale Distribution—notable size variations among objects are frequently present within a single scene. These traits increase the complexity of feature extraction and present substantial challenges to object modeling and optimization strategies.

Due to these geometric traits, existing detection frameworks often suffer from structural misalignment across three primary stages:

1.

Feature Extraction: The limited effective receptive field of convolutional neural networks (CNNs) [2] hampers the modeling of long-range dependencies in extreme-scale objects, leading to fragmented feature representations.

2.

Object Representation: The periodicity of angle definitions in OBBoxs introduces ambiguity near boundary angles and causes discontinuous loss behavior during regression [3].

3.

Optimization: The widely used ${\mathrm{smooth}}_{L_1}$ loss [4] does not align well with geometric evaluation metrics such as SkewIoU [5], resulting in inconsistencies between training objectives and evaluation standards (see Figure 2).

To address these limitations, various methods have been proposed, including rotated anchors, feature alignment, and angular modeling. RRPN [6] introduces rotated anchors to enhance directional sensitivity; Gliding Vertex [7] adopts a vertex-sliding mechanism to reduce boundary localization errors; and Oriented R-CNN [8] and ${\mathrm{R}}^3$Det [5] improve the adaptability of RoI alignment for rotated objects. Additionally, techniques such as CSL [9] and DCL [10] address angular periodicity via angle classification, while GWD [3] and KLD [9] adopt Gaussian-based modeling to enhance representation robustness. Despite these advancements, most existing approaches remain modular and lack a unified perspective for modeling geometric symmetry, thereby limiting consistency between loss functions and evaluation metrics.

In parallel, recent research in fault diagnosis has emphasized domain-specific signal modeling and lightweight deep architectures to improve recognition robustness under noisy and complex conditions [11,12]. Although developed in different contexts, these strategies highlight the effectiveness of aligning model design with structural priors—an idea that is adopted and extended in this work to the domain of OOD.

To bridge this gap, a symmetry-driven framework for OOD—termed GAANet—is proposed. The framework systematically reconstructs feature extraction, object representation, and loss optimization based on principles of geometric symmetry. The main contributions of this work are summarized as follows:

• Spatial–Channel Symmetric Interaction: A CAX-ViT architecture is developed by integrating convolutional local symmetry with attention-based global symmetry, thereby enhancing structural modeling capability across multiple scales;
• Rotation-Invariant Modeling: Flexible BBoxs are constructed based on the radial symmetry of Gaussian covariance matrices, effectively mitigating regression discontinuities induced by angular periodicity;
• Geometry-Consistent Optimization: A probabilistic loss function, GPIoU, is proposed to improve alignment between training objectives and the SkewIoU metric through consistent modeling of box overlap.

Experimental results indicate that GAANet achieves competitive performance, with a 90.58% mAP on HRSC2016, 89.95% on UCAS-AOD, and 77.86% on the large-scale DOTA dataset, outperforming existing mainstream methods. Ablation studies further verify the effectiveness of each individual module. As shown in Figure 3a,b, the proposed GPIoU loss exhibits improved angular robustness and boundary alignment for objects with extreme aspect ratios.

In conclusion, a unified and theoretically grounded framework for ODD is introduced by integrating spatial–channel symmetric interaction, rotation-invariant modeling, and geometry-consistent optimization. The proposed approach also demonstrates potential for generalization to other structure-intensive domains, such as medical image analysis and scene text detection.

The remainder of this study is structured as follows: Section 2 reviews related work on OOD and symmetry-aware modeling. Section 3 details the architecture and implementation of GAANet. Section 4 presents experimental results and ablation analysis. Section 5 concludes this paper and outlines future research directions.

2. Related Work

2.1. ODD and Interaction Optimization

ODD is vital in domains such as RS (remote sensing) and scene text recognition, where targets exhibit arbitrary orientations and extreme aspect ratios. Existing methods generally fall into anchor-based and anchor-free categories.

Anchor-based approaches extend classical detectors with rotation-aware enhancements. ORN [13] employs orientation-sensitive convolution to improve directional features. RRPN [6] uses rotated anchors for better pose alignment. ${\mathrm{R}}^2$CNN [14] and R2PN [15] optimize rotated RoI pooling for dense object detection, while Gliding Vertex [7] addresses angular regression through vertex sliding. Lightweight alignment structures, such as Oriented R-CNN [8], balance precision and efficiency. ${\mathrm{R}}^3$Det [5] reinforces classification-localization consistency via a two-stage regression-alignment strategy.

Anchor-free methods discard anchors to simplify design and reduce computation. IENet [16] applies dense OBBox regression. PolarDet [17] introduces polar coordinates to alleviate angle periodicity. Oriented RepPoints [18] uses learnable point sets for flexible geometry modeling. FCOSR [19] integrates a rotation regression branch to improve accuracy.

Beyond box modeling, a growing focus lies in optimizing feature representation and token interaction mechanisms in a lightweight fashion. RoI Transformer [20] aligns horizontal and OBBoxs to improve spatial features. ${\mathrm{S}}^2$A-Net [21] uses adaptive feature selection to alleviate misalignment. AO2-DETR [22] adapts the DETR [23] framework to predict OBBoxs directly and demonstrates the potential of Transformer-based detectors in rotation-aware scenarios.

To meet deployment demands, recent methods such as MobileViTv2 [24] and SwiftFormer [25] integrate H-MSA mechanisms, offering insights into lightweight attention modeling. These architectural ideas partially inspire the design of GAANet’s CAX-ViT backbone.

While these methods advance specific modules, they often lack architectural coherence. GAANet addresses this gap by embedding a symmetry-preserving mechanism across feature extraction, token interaction, and loss optimization. It unifies structural modeling and learning objectives into a lightweight, closed-loop detection framework.

2.2. Efficient Vision Transformers and Token Interaction Mechanisms

ViTs (Vision Transformers), including ViT [26], have exhibited strong global modeling capabilities in a variety of vision tasks [27,28]. However, the quadratic complexity with respect to token length imposes limitations on their applicability in real-time and edge environments.

Recent efforts to improve the efficiency of ViTs generally follow two primary directions: one focuses on reformulating the computational structure of self-attention while preserving its core principle of token interaction; the other explores H-MSA (Heteromorphic Multi-head Self-Attention) as an architectural extension to enhance both structural expressiveness and computational efficiency.

In the first direction, MobileViTv2 [24] incorporates convolutional priors and progressive distillation to approximate global context modeling, thereby reducing attention-related computational costs. EfficientFormer [29] accelerates inference by introducing sparse attention mechanisms and parameter sharing. TiT [30] proposes a hierarchical framework in which each token is internally processed by a nested Transformer, enabling expressive local–global representation learning while preserving the core mechanism of self-attention.

In parallel, H-MSA was developed to enhance efficiency by differentially processing the Query, Key, and Value branches. SwiftFormer [25] simplifies attention computation by removing the Value branch and employing a weighted summation to retain key contextual information. MetaFormer [31] further abstracts this design by demonstrating that token mixing operations can be operator-agnostic and that structural design often has greater influence than the specific attention mechanism.

Inspired by these developments, GAANet incorporates a symmetry-aware additive interaction module, the Contextual Additive eXchange Mixer (CAXM), into the CAX-ViT backbone. By replacing computationally intensive matrix multiplications with lightweight additive operations in both spatial and channel dimensions, CAXM enables efficient token interaction while preserving geometric structure, thereby achieving an improved balance between performance and complexity for oriented object detection.

2.3. Regression Loss Functions: From IoU Inconsistency to Probabilistic Modeling

BBox regression loss functions are fundamental to object detection, particularly in scenarios involving rotated objects where geometric consistency is essential. Early approaches such as R-CNN [32] and Fast R-CNN [33] employed $L_2$ loss, which is sensitive to outliers. Faster R-CNN [4] introduced the ${\mathrm{smooth}}_{L_1}$ loss to achieve a better trade-off between robustness and convergence.

To align training objectives with IoU (Intersection over Union)-based evaluation metrics, several IoU-driven loss functions have been proposed. GIoU (Generalized IoU) [34], DIoU (Distance IoU), and CIoU (Complete IoU) [35] improve localization accuracy by incorporating geometric priors such as box enclosure and center distance. Although effective for horizontal boxes, these losses exhibit degraded performance when extended to OBBoxs due to gradient discontinuity and complex intersection behaviors.

To address orientation-specific challenges, angle classification techniques such as CSL [36] and DCL [10] transform angle regression into a classification task. Concurrently, Gaussian-based approaches such as GWD [3] and KLD [9] model BBoxs as two-dimensional distributions, enabling regression via Wasserstein and KL divergence metrics.

Building on these developments, GAANet introduces GPIoU, a loss function that models the probabilistic overlap between predicted and ground truth (GT) boxes. By incorporating center alignment and rotational symmetry, GPIoU achieves semantic consistency with SkewIoU while maintaining differentiability and training stability.

Notably, the probabilistic modeling paradigm has also shown success in other domains, including acoustic anomaly detection [12] and fault diagnosis [11], indicating its broader generalizability.

A comparison with representative methods is presented in

Table 1. Comparison of GAANet and representative methods across three core design modules.

Method	Feature Modeling	Box Representation	Regression Loss
${\mathrm{R}}^3$Det [5]	ResNet + RoIAlign	5-parameter OBBox	${smooth}_{L_1}$
Oriented R-CNN [8]	Lightweight RPN + Two-stage	5-parameter OBBox	${smooth}_{L_1}$
CSL [36]	ResNet	Angle classification + regression	Angle classification loss
GWD [3]	ResNet	Gaussian covariance modeling	Distribution distance (GWD)
KLD [9]	ResNet	Gaussian covariance modeling	Distribution distance (KLD)
GAANet (Ours)	CAX-ViT + CAXM	Gaussian covariance modeling	GPIoU (distribution product)

, highlighting the modular symmetry and innovations introduced by GAANet.

As shown in Table 1, GAANet employs a unified modeling strategy across feature extraction, box representation, and loss optimization. This holistic approach contrasts with the modular and fragmented designs of previous methods, contributing to improved alignment and robustness in ODD.

3. Methodology

To systematically address the structural misalignment issues commonly encountered in ODD for RSI—including feature misalignment, representation misalignment, and optimization misalignment—a lightweight detection framework, GAANet, is proposed. This framework adopts geometric symmetry as the core modeling principle. A closed-loop mechanism is established across three stages—feature extraction, object modeling, and loss design—ensuring feature alignment, representational symmetry, and metric consistency. The overall architecture is illustrated in Figure 4.

3.1. Overview of GAANet Architecture

The architecture comprises three core components: a backbone for feature extraction, a neck for multi-scale feature fusion, and a head for prediction. These components are jointly optimized to maintain a balance between detection accuracy, inference efficiency, and deployment feasibility.

In the feature extraction stage, GAANet utilizes CAX-ViT as the backbone. By combining convolutional structures with an additive attention mechanism, this module enhances structural representation while improving the efficiency of multi-scale feature encoding. This design increases sensitivity to geometric patterns and preserves computational efficiency. Shallow layers are leveraged to capture texture and edge details, facilitating the detection of small objects, while deeper layers provide rich semantic information for the accurate localization and classification of medium and large objects.

In the feature fusion stage, a Feature Pyramid Network (FPN) is employed to enhance semantic interactions across scales. Through a top–down information flow mechanism, structural cues from shallow layers are effectively integrated with semantic features from deeper layers. This integration improves the robustness of the detector under scale variations.

In the prediction stage, a decoupled detection head is adopted to separately model classification and regression tasks. This separation improves task-specific adaptability and enhances overall detection performance. To address discontinuities in representation and inconsistencies in optimization observed in OOD, a Gaussian-based OBBox modeling mechanism is incorporated. Additionally, a center-modulated GPIoU loss function is introduced to reduce geometric inconsistency between regression losses and evaluation metrics such as SkewIoU, thereby improving training convergence and detection accuracy.

3.2. CAX-ViT Network Architecture

To mitigate structural misalignment in feature representation for ODD, a lightweight backbone network, CAX-ViT, is introduced. This design emphasizes enhanced structural modeling capacity while preserving computational efficiency. A symmetry-preserving additive interaction mechanism is employed to generate high-quality geometric features for subsequent modeling stages.

As illustrated on the right of Figure 5, the core building unit of CAX-ViT is the CAX block, comprising the following three submodules:

1.

Integration Sub-network: This consists of three $3\times 3$ depthwise convolutional layers combined with ReLU activation. This submodule expands the receptive field, fuses local features, and implicitly encodes positional information.

2.

CAXM Module: Establishes a dual-domain symmetric interaction mechanism across spatial and channel dimensions, serving as the principal structure for symmetry preservation.

3.

ConvFFN Module: This applies nonlinear enhancement through channel expansion, thereby improving semantic representation and adaptability in complex scenes.

The network follows a four-stage encoding structure. The input image of the size $H\times W\times 3$ is initially downsampled by a Stem module comprising two stride-2 convolutional layers, producing a feature map of ${\displaystyle \frac{H}{4}}\times {\displaystyle \frac{W}{4}}\times C_1$. This is followed by four hierarchical stages, which generate feature maps of the following sizes:

$${\displaystyle \frac{H}{8}}\times {\displaystyle \frac{W}{8}}\times C_2,{\displaystyle \frac{H}{16}}\times {\displaystyle \frac{W}{16}}\times C_3,{\displaystyle \frac{H}{32}}\times {\displaystyle \frac{W}{32}}\times C_4$$

(1)

Each stage includes $D_i$ CAX blocks (illustrated on the left of Figure 5), which maintain spatial resolution while progressively enhancing semantic depth. The channel expansion ratio in the ConvFFN module is set to 4 by default to strengthen nonlinear modeling capacity.

It is worth emphasizing that the CAXM module functions as a symmetry-preserving interaction mechanism throughout all stages of the network. Owing to its additive formulation, it eliminates the need for the explicit computation of attention matrices. Compared with conventional Vision Transformer architectures such as Swin Transformer, this design significantly reduces both the number of parameters and computational overhead. Specifically, the CAX-ViT-S backbone contains only 21.76 M parameters and 3.597 G FLOPs (Floating Point Operations), delivering competitive accuracy with reduced resource consumption.

To support diverse deployment scenarios, multiple lightweight variants of CAX-ViT were developed. Their configurations are summarized in

Table 2. Configuration of different CAX-ViT backbone variants.

Model	Blocks D	Channels C	Params (M)	FLOPs (M)
CAX-ViT-T	$[3,3,6,3]$	$[64,96,192,384]$	12.42	1887
CAX-ViT-S	$[3,3,6,3]$	$[96,128,256,512]$	21.76	3597

.

In summary, CAX-ViT provides GAANet with a backbone that simultaneously offers geometric structural awareness and computational efficiency. This backbone establishes a solid foundation for subsequent modules in OBBox modeling and loss function design.

3.3. Contextual Additive eXchange Mixer

To address structural misalignment in feature representation for ODD, CAXM is introduced as a core component of the CAX-ViT backbone. This module is designed based on the understanding that the effectiveness of self-attention arises from efficient information exchange, rather than the specific operator form. CAXM enables multi-dimensional feature fusion and symmetric interaction with minimal computational overhead. Its structure is shown in Figure 6.

Multi-head self-attention (MSA) has been widely adopted in Vision Transformers for modeling long-range dependencies. However, MSA requires matrix multiplication between $\mathbf{Q}$ and $\mathbf{K}$, leading to $\mathcal{O}\left(N^2\right)$ complexity, which is computationally intensive for high-resolution RSI. To alleviate this, previous methods have explored alternatives such as linear attention (kernel-based), hybrid local–global attention (e.g., Twins [37], DaViT [38]), and H-MSA (e.g., MobileViTv2 [39], SwiftFormer [40]). Nonetheless, these approaches still depend on matrix operations or involve information compression.

CAXM is constructed from a structural perspective, positing that the key contribution of attention lies in multi-scale spatial and channel-wise interactions. It adopts an all-additive design that uses convolutional operations to replace matrix multiplications, facilitating token weighting and contextual enhancement.

Given an input feature map, $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$, the spatial interaction is computed as follows:

$${\mathbf{X}}_s=Sigmoid\left({\mathcal{F}}_{\mathrm{pw}}^{1\times 1}\left({\mathcal{F}}_{\mathrm{dw}}^{3\times 3}\left(ReLU\left(BN\left({\mathcal{F}}_{\mathrm{dw}}^{3\times 3}\left(\mathbf{X}\right)\right)\right)\right)\right)\right)\odot \mathbf{X},$$

(2)

where ${\mathcal{F}}_{\mathrm{dw}}^{3\times 3}$ denotes depthwise convolution, ${\mathcal{F}}_{\mathrm{pw}}^{1\times 1}$ represents pointwise convolution, and ReLU (Rectified Linear Unit) and Batch Normalization (BN) denote activation and normalization operations, respectively. This branch extracts local spatial structures and generates a normalized spatial attention map, ${\mathbf{X}}_s$.

The channel interaction is formulated as follows:

$${\mathbf{X}}_c=Sigmoid\left({\mathcal{F}}_{\mathrm{pw}}^{1\times 1}\left({\mathcal{P}}_{\mathrm{avg}}^{1\times 1}\left(\mathbf{X}\right)\right)\right)\odot \mathbf{X},$$

(3)

where ${\mathcal{P}}_{\mathrm{avg}}$ denotes global average pooling. In contrast to conventional channel compression strategies, CAXM retains all channel dimensions, improving fine-grained representation and inter-channel coupling efficiency.

By integrating the spatial and channel interactions, a final enhanced feature mapping, $\tau \left(\mathbf{X}\right)$, is obtained.

For contextual modeling, CAXM adopts a linear similarity function defined as

$$Sim(\mathbf{Q},\mathbf{K})=\tau \left(\mathbf{Q}\right)+\tau \left(\mathbf{K}\right),$$

(4)

where $\mathbf{Q},\mathbf{K},\mathbf{V}$ are generated via linear projection as follows:

$$\mathbf{Q}={\mathbf{W}}_q\mathbf{X},\mathbf{K}={\mathbf{W}}_k\mathbf{X},\mathbf{V}={\mathbf{W}}_v\mathbf{X}.$$

(5)

The final output is obtained as follows:

$$\mathbf{O}=\Psi \left(\tau \left(\mathbf{Q}\right)+\tau \left(\mathbf{K}\right)\right)\odot \mathbf{V},$$

(6)

where $\Psi (·)$ denotes a linear projection function used to fuse contextual information and restore feature dimensionality.

It is notable that while conventional ViTs often constrain receptive fields using $7\times 7$ windows, a three-layer $3\times 3$ convolution stack achieves an equivalent receptive field with improved structural controllability. CAXM enables global modeling through convolutional stacking and additive interaction, eliminating the need for softmax normalization or high-rank matrix operations, thereby enhancing its suitability for edge deployment.

Moreover, unlike existing additive attention methods such as SwiftFormer [40], which apply context modeling solely to the $\mathbf{Q}$ path, CAXM performs symmetric context enhancement on both $\mathbf{Q}$ and $\mathbf{K}$ paths. This design maintains full feature dimensionality and improves interaction precision and generalization.

The computational complexity of the CAXM module is expressed as

$$\Omega \left(\mathrm{CAXM}\right)=\Omega \left(\mathbf{QKV}\right)+2\times \Omega \left(\tau \right(·\left)\right)+\Omega (\Psi )=3HWC+2\times 13HWC+9HWC=38HWC.$$

(7)

In summary, CAXM integrates structural symmetry preservation, efficient context modeling, and lightweight computation. It serves as a key module within GAANet for mitigating structural misalignment in feature representation.

3.4. GPIoU Regression Loss Function

To construct an optimization objective that is consistent with the SkewIoU metric, a differentiable GPIoU loss is proposed based on the principle of Gaussian distribution multiplication. The corresponding process is illustrated in Figure 7. The core idea is to represent the predicted box and the ground truth (GT) box as two-dimensional Gaussian distributions and approximate their overlap by computing the area of their product distribution.

3.4.1. Gaussian Modeling and Notation Conventions

To capture the geometric characteristics of OBBoxs, this work adopts a two-dimensional Gaussian distribution to model their spatial configuration, as shown in Figure 8. Given an OBBox parameterized by $(x,y,w,h,\theta )$, the corresponding Gaussian distribution is defined as

$$\mathcal{N}(\mu ,\Sigma ),$$

(8)

where the mean vector $\mu ={(x,y)}^{\top }$ represents the object center, and the covariance matrix $\Sigma$ encodes rotation and scale. It can be decomposed as

$$\Sigma ={\mathbf{R}}_{\theta }\Lambda {\mathbf{R}}_{\theta }^{\top },$$

(9)

where ${\mathbf{R}}_{\theta }$ is the rotation matrix, and $\Lambda$ is a diagonal matrix given by

$${\mathbf{R}}_{\theta }=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right],\Lambda =\left[\begin{array}{cc}\frac{w^2}{4}& 0\\ 0& \frac{h^2}{4}\end{array}\right].$$

(10)

This decomposition ensures that the principal axes of the Gaussian distribution are aligned with the orientation of the BBox and that the axis lengths are proportional to the object dimensions.

3.4.2. Gaussian Product and Overlap Region Modeling

For two OBBoxs, ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$, represented by Gaussian distributions, $\mathcal{N}({\mu }_1,{\Sigma }_1)$ and $\mathcal{N}({\mu }_2,{\Sigma }_2)$, their product distribution can be expressed as

$$\mathcal{N}({\mu }_1,{\Sigma }_1)·\mathcal{N}({\mu }_2,{\Sigma }_2)=\alpha ·\mathcal{N}(\mu ,\Sigma ).$$

(11)

The normalization coefficient $\alpha$ and the parameters of the resulting Gaussian are computed as follows:

$$\alpha ={\displaystyle \frac{1}{2\pi \sqrt{|{\Sigma }_1+{\Sigma }_2|}}}exp\left(-{\displaystyle \frac{1}{2}}{({\mu }_1-{\mu }_2)}^{\top }{({\Sigma }_1+{\Sigma }_2)}^{-1}({\mu }_1-{\mu }_2)\right),$$

(12)

$$\mathbf{K}={\Sigma }_1{({\Sigma }_1+{\Sigma }_2)}^{-1},$$

(13)

where $\mathbf{K}$ denotes the Kalman gain. In the resulting product distribution, the covariance matrix $\Sigma$ captures the combined shape characteristics of the two distributions, while the normalization factor $\alpha$ encodes the influence of center distance on the degree of overlap.

3.4.3. IoU Computation

The product distribution is mapped to a new OBBox, ${\mathcal{B}}_3$, whose area, $V_{{\mathcal{B}}_3}(\Sigma )$, serves as an approximation of the intersection region between the original boxes. The area is computed from the determinant of the resulting covariance matrix:

$$V_{{\mathcal{B}}_3}(\Sigma )=4\sqrt{|\Sigma |}.$$

(14)

The areas of the original boxes are similarly defined as $V_{{\mathcal{B}}_1}\left({\Sigma }_1\right)=4\sqrt{|{\Sigma }_1|}$ and $V_{{\mathcal{B}}_2}\left({\Sigma }_2\right)=4\sqrt{|{\Sigma }_2|}$. Accordingly, the GPIoU is defined as

$$\mathrm{GPIoU}={\displaystyle \frac{V_{{\mathcal{B}}_3}(\Sigma )}{V_{{\mathcal{B}}_1}\left({\Sigma }_1\right)+V_{{\mathcal{B}}_2}\left({\Sigma }_2\right)-V_{{\mathcal{B}}_3}(\Sigma )}}.$$

(15)

3.4.4. Loss Function Design

To enable robust optimization, a two-part loss function based on GPIoU is introduced, incorporating center alignment for improved geometric consistency. The first component emphasizes center alignment through a term derived from the Kullback–Leibler divergence (KLD), which provides stable gradients even under large positional deviations. The second component utilizes a logarithmic formulation of the Intersection over Union, enhancing training stability. Together, these components address geometric misalignments and promote smoother gradient flow, thereby improving convergence behavior and detection accuracy. The synergy between the two loss terms facilitates effective learning in the presence of geometric complexities inherent in oriented object detection.

The complete GPIoU loss function integrates both center alignment and region overlap and is defined as follows:

1.

Center Loss: Derived from the Kullback–Leibler divergence (KLD) [9], this term uses a logarithmic distance metric to provide stability under large positional discrepancies. It is defined as

$$L_c({\mu }_1,{\mu }_2,{\Sigma }_1)=ln\left({({\mu }_2-{\mu }_1)}^{\top }{\Sigma }_1^{-1}({\mu }_2-{\mu }_1)+1\right).$$

(16)

2.

Primary GPIoU Loss: A logarithmic formulation of the Intersection over Union is employed to improve numerical stability and gradient smoothness:

$$L_{\mathrm{GP}}=-log(\mathrm{GPIoU}+ϵ),ϵ={10}^{-6}.$$

(17)

The overall loss function is defined as a weighted sum of the two components:

$${\mathcal{L}}_{\mathrm{GPIoU}}=L_{\mathrm{GP}}+L_c.$$

(18)

The logarithmic formulation, defined as $L_{GP}=-log($ GPIoU $+ϵ)$, ensures robust and stable gradient flow during optimization. Specifically, it amplifies penalties for poorly localized predictions by producing steep gradients when GPIoU is small, thereby accelerating convergence for hard examples and longtail instances often encountered in remote sensing scenarios. As GPIoU increases, the gradient smoothly decays, avoiding abrupt saturation and enabling finegrained refinement in later stages of training. Compared with the linear form ( $1-\mathrm{GPIoU}$ ) and exponential form ( ${\mathrm{e}}^{1-\mathrm{GPIoU}}-1$ ), the logarithmic variant provides an adaptive gradient scale, enhancing optimization robustness without the need for manual scaling. Moreover, its gradient behavior better aligns with the local sensitivity of the SkewloU metric, ensuring geometric consistency between the training objective and evaluation standard. This synergy is empirically validated through subsequent experimental results, where the log formulation achieves both faster convergence and superior mAP performance.

It is important to note that GPIoU is not strictly bounded within the interval $[0,1]$, potentially leading to scale inconsistencies when compared with standard IoU metrics. To address this, normalization based on its theoretical upper bound is required. As discussed in [41], the theoretical maximum of GPIoU in n-dimensional space is given by

$${\displaystyle \frac{1}{2^{\frac{n}{2}+1}-1}}.$$

(19)

For the two-dimensional case ($n=2$), the theoretical upper bound of GPIoU is ${\displaystyle \frac{1}{3}}$. Therefore, a linear transformation is applied to normalize GPIoU into the $[0,1]$ interval, ensuring consistency with the value range of standard IoU metrics.

To validate the consistency between GPIoU and SkewIoU, a comparative experiment was conducted using 1000 pairs of OBBoxs with center deviations of less than 10 pixels. Five loss functions were evaluated, including ${\mathrm{smooth}}_{L_1}$, KLD, and GWD. The results are presented in Figure 9.

Figure 9a,b demonstrate the response trends of each loss function to variations in angle and aspect ratio when the box centers are aligned. Figure 9c further shows that GPIoU achieves the highest correlation with SkewIoU among all evaluated methods.

To facilitate integration into existing detection frameworks, the proposed loss function was implemented within the R-RetinaNet (Rotated RetinaNet) [42] architecture. OBBoxs were parameterized as $(x,y,w,h,\theta )$. The backbone and detection head remained unchanged, and Gaussian modeling was introduced solely during the loss computation stage. As a result, no additional computational overhead was incurred during inference.

The complete training pipeline proceeded as follows:

1.

The network predicted the relative offsets of the OBBox: $(t_x^p,t_y^p,t_w^p,t_h^p,t_{\theta }^p)$;

2.

The predicted box was decoded to obtain the final OBBox;

3.

Both the predicted and GT boxes were converted into Gaussian distributions;

4.

The center loss $L_c$ and GPIoU loss $L_{\mathrm{GP}}$ were computed and jointly applied for optimization.

The definitions of the individual offset parameters were as follows:

$$\begin{array}{cc}\hfill t_x^g={\displaystyle \frac{x^g-x^a}{w^a}},& t_y^g={\displaystyle \frac{y^g-y^a}{h^a}},t_w^g=log\left({\displaystyle \frac{w^g}{w^a}}\right),t_h^g=log\left({\displaystyle \frac{h^g}{h^a}}\right),\hfill \\ \hfill t_x^p={\displaystyle \frac{x^p-x^a}{w^a}},& t_y^p={\displaystyle \frac{y^p-y^a}{h^a}},t_w^p=log\left({\displaystyle \frac{w^p}{w^a}}\right),t_h^p=log\left({\displaystyle \frac{h^p}{h^a}}\right).\hfill \end{array}$$

(20)

The angular offsets were defined as

$$t_{\theta }^g=({\theta }^g-{\theta }^a)·{\displaystyle \frac{\pi }{180}},t_{\theta }^p=({\theta }^p-{\theta }^a)·{\displaystyle \frac{\pi }{180}}.$$

(21)

The final total loss was formulated as

$${\mathcal{L}}_{\mathrm{total}}={\displaystyle \frac{{\lambda }_1}{N_{\mathrm{pos}}}}\sum _{i=1}^{N_{\mathrm{pos}}}{L}_{\mathrm{cls}}\left(c_i,l_i^g\right)+{\displaystyle \frac{{\lambda }_2}{N_{\mathrm{pos}}}}\sum _{i=1}^{N_{\mathrm{pos}}}{L}_{\mathrm{GP}}\left(\mathcal{N}\left({\mathbf{p}}_i\right),\mathcal{N}\left({\mathbf{g}}_i\right)\right),$$

(22)

where Focal Loss was adopted for classification. The weighting factors were set as ${\lambda }_1=1$ and ${\lambda }_2=1$. $N_{\mathrm{pos}}$ denotes the number of positive anchors. $c_i$ represents the class probability distribution predicted by the Sigmoid function, and $l_i^g$ is the corresponding ground truth (GT) class label. ${\mathbf{p}}_i$ and ${\mathbf{g}}_i$ denote the i-th predicted and GT boxes, respectively. $\mathcal{N}(·)$ refers to the Gaussian transformation function that maps an OBBox to a two-dimensional Gaussian distribution.

In summary, the GPIoU loss maintains alignment with the SkewIoU objective while providing strong differentiability, deployment efficiency, and computational simplicity. As a core component of geometric modeling within GAANet, it significantly enhances structural alignment during optimization.

4. Experimentation

4.1. Datasets

The HRSC2016 (High-Resolution Ship Collection 2016) remote sensing ship detection dataset [1] is a widely used benchmark for ODD. It comprises 1061 high-resolution RSI with image sizes ranging from $300\times 300$ to 1500 × 900 and includes 2976 annotated object instances. All targets are labeled using OBBoxs and span 3 main categories and 27 fine-grained subcategories, including aircraft carriers, warships, and commercial vessels. The dataset is split into training (436 images), validation (181 images), and testing (444 images) subsets with a 4:2:4 ratio. Covering diverse port environments, it presents significant orientation diversity and complex backgrounds, making it well suited for evaluating performance under multi-directional and densely packed detection scenarios. Owing to its high-quality annotations and support for multi-level classification (1-class, 4-class, and 19-class tasks), HRSC2016 is frequently employed for robustness evaluation in ODD research.

The UCAS-AOD (UCAS Aerial Object Detection) dataset [43] contains two object categories: airplanes and vehicles. It includes 2,420 images in total—comprising 1000 airplane images, 510 vehicle images, and 910 background-only images—with 14,596 annotated instances. The images are sourced from Google Earth, with resolutions of either 1280 × 659 or 1372 × 941. Original annotations are provided in HBBox format and can be converted into OBBoxs through post-processing to support orientation regression. The dataset is characterized by uniformly distributed orientations, dense small objects, and cluttered backgrounds, making it suitable for evaluating directional robustness in complex scenes. The standard data split follows a 5:2:3 ratio for training, validation, and testing.

DOTA (Dataset for Object Detection in Aerial Images) v1.0 [44] is one of the most comprehensive large-scale benchmarks for object detection in RS. It is widely adopted to evaluate the generalization capability of algorithms under complex scenarios. DOTA v1.0 comprises 2806 aerial images with resolutions ranging from $800\times 800$ to 4000 × 4000, collected from diverse sensors and geographic regions. It includes over 188,000 annotated instances across 15 categories, such as plane (PL), baseball diamond (BD), bridge (BR), ground track field (GTF), small vehicle (SV), large vehicle (LV), ship (SH), tennis court (TC), basketball court (BC), storage tank (ST), soccer ball field (SBF), roundabout (RA), harbor (HA), swimming pool (SP), and helicopter (HC). Each object is annotated using a four-point OBBox that accurately reflects its orientation, pose, and aspect ratio. DOTA is designed for large-scale, multi-class, and high-density detection tasks.

4.2. Implementation Details

A five-level feature pyramid structure (P3, P4, P5, P6, P7) was employed during detection to support multi-scale object modeling. Each spatial location on every feature level was assigned a single anchor, responsible for regressing the position and orientation of the nearest GT target. Label assignment followed an IoU-based matching strategy, with the positive sample threshold set to 0.5.

All experiments were implemented using the MMRotate (OpenMMLab Rotated Detection Toolbox) framework [43] and conducted on a single NVIDIA RTX 2080Ti GPU with 22 GB of memory. During training, the batch size was set to 2. The optimizer was stochastic gradient descent (SGD) with an initial learning rate of $2.5\times {10}^{-3}$, a momentum of 0.9, and a weight decay of 0.0001.

The number of training epochs was set to 24 for UCAS-AOD, 72 for HRSC2016, and 24 for DOTA. For the HRSC2016 and UCAS-AOD datasets, input images were resized to $800\times 800$. Due to the larger image dimensions in the DOTA dataset, a cropping and sliding window strategy was applied, dividing the original images into $1024\times 1024$ patches to match the input constraints of standard object detection models.

To ensure fairness and comparability across methods, only random rotation and random flipping were applied for data augmentation during training. The base detection framework was R-RetinaNet, which used ResNet-50 as the feature extraction backbone. Pretrained weights on ImageNet (ImageNet Large Scale Visual Recognition Challenge) were used for model initialization. Evaluation followed the mean Average Precision (mAP) definition from the PASCAL VOC 2007 challenge [45].

All ablation studies were conducted on the HRSC2016 dataset, which contains ship targets with large aspect ratios and substantial scale variation. This makes it a representative benchmark for high-complexity RS detection tasks and provided a reliable setting for evaluating the detection accuracy and robustness of the proposed method under challenging conditions.

4.3. Ablation Studies

An ablation study was conducted to evaluate the impact of key components in GAANet on ODD performance. R-RetinaNet was adopted as the baseline detector, with ResNet-50 used as the backbone and ${\mathrm{smooth}}_{L_1}$ as the regression loss function.

The Effectiveness of Individual GAANet Components. To verify the contribution of each module, controlled experiments were performed under consistent conditions. The detection framework remained fixed as R-RetinaNet with a ResNet-50 backbone. The ${\mathrm{smooth}}_{L_1}$ loss was used in the baseline to establish reference performance.

The influence of each component is summarized in

Table 3. Impact of individual GAANet components on detection performance. Best results are highlighted in bold.

Configuration	CAX-ViT	GPIoU Loss	mAP (%)	$\Delta$ vs. Baseline
Baseline (ResNet-50 + ${\mathrm{smooth}}_{L_1}$)	×	×	88.53	–
+ CAX-ViT	✓	×	89.17	+0.64
+ GPIoU Loss	×	✓	89.66	+1.13
Full GAANet (CAX-ViT + GPIoU)	✓	✓	90.58	+2.05

Notes: ✓ denotes the component is included; × means it is excluded. Gaussian modeling was implicitly enabled when GPIoU loss was applied. $\Delta$ indicates performance improvement relative to the baseline. CAX-ViT contributed +0.64% mAP via feature-level symmetry, GPIoU loss added +1.13% through geometric alignment, and combining both yielded a total gain of +2.05%.

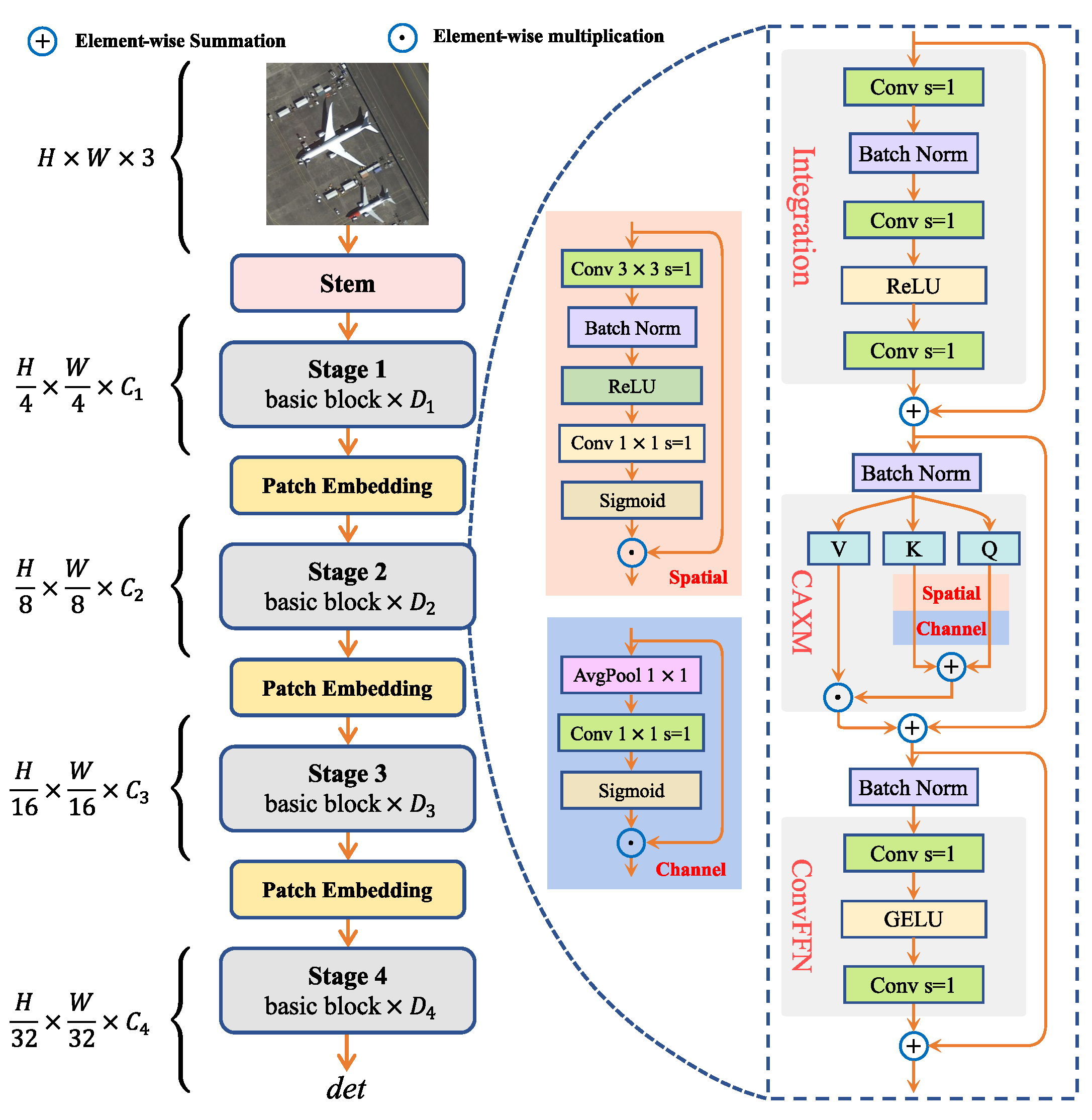
. The baseline model (ResNet-50 + ${\mathrm{smooth}}_{L_1}$) achieved a 88.53% mAP. Due to the absence of alignment mechanisms, it suffered from inconsistencies in both feature representation and OBBox regression. With the introduction of CAX-ViT, the mAP increased to 89.17%, demonstrating the benefits of additive attention via CAXM and hierarchical feature encoding for multi-scale object modeling.

Replacing the regression loss with GPIoU further improved the mAP to 89.66%. This gain stemmed from the Gaussian-based optimization strategy, which alleviated angular periodicity and enhanced training stability. When both CAX-ViT and GPIoU loss were applied, the mAP reached 90.58%, yielding a 2.05% improvement over the baseline. These results confirm the complementary effects of structural representation and geometric alignment in GAANet.

An Ablation Study on the Effectiveness of CAX-ViT-T and CAX-ViT-S Variants. To further examine the effect of backbone channel width on detection performance, two variants of the CAX-ViT architecture—CAX-ViT-T and CAX-ViT-S—were compared. The experimental results are presented in

Table 4. Performance comparison of CAX-ViT variants as backbone networks. Best results are highlighted in bold.

Model	Blocks	Channels	Params (M)	FLOPs (M)	mAP (%)
CAX-ViT-T	[3,3,6,3]	[64,96,192,384]	12.42	1887	90.21
CAX-ViT-S	[3,3,6,3]	[96,128,256,512]	21.76	3597	90.58

Notes: Channels refer to feature dimensions in each of the four stages. FLOPs represent the number of floating point operations computed for an input size of $800\times 800$. CAX-ViT-S provided a +0.37% mAP improvement over CAX-ViT-T with a moderate increase in parameters and FLOPs.

.

CAX-ViT-S, which adopts a wider channel configuration and contains more parameters than CAX-ViT-T, achieved a 0.37% gain in the mAP. This suggests that increasing channel capacity enhanced the expressiveness of feature representations, thereby improving detection accuracy. In particular, the broader channel design in CAX-ViT-S facilitates the extraction of richer multi-scale structural information, improving robustness in small object detection and localization accuracy in cluttered environments.

Both variants utilize the Contextual Additive eXchange Block (CAX block) as their core structural unit. The architecture incorporates the CAXM mechanism for enhanced token interaction and employs a ConvFFN (Convolutional Feed-Forward Network) to strengthen semantic representation. The results indicate that the architecture maintained computational efficiency while benefiting from increased accuracy through channel expansion.

Although CAX-ViT-S incurred more FLOPs compared to CAX-ViT-T, it offered a favorable trade-off between accuracy and computational cost. As such, CAX-ViT-S was selected as the default backbone in subsequent experiments to better balance precision and resource efficiency.

An Ablation Study on the Effectiveness of the CAXM Component—Validated via Token Mixer Substitution. To assess the contribution of the CAXM (Convolutional Additive Exchange Mixer) module, a comparative experiment was conducted by substituting its token mixing mechanism.

Table 5. Impact of different token mixers on detection performance. Best results are highlighted in bold.

Token Mixer	FLOPs (M)	mAP (%)
CATM Pooling	1467	89.47
W-MSA	2175	90.24
CAXM (Ours)	1887	90.58

Notes: CATM denotes Convolutional Average Token Mixing. W-MSA represents window-based multi-head self-attention. CAXM reduced FLOPs by 13.3% compared to W-MSA while achieving higher accuracy.

summarizes the results, highlighting the trade-off between computational complexity (FLOPs) and detection accuracy (mAP) across different token mixers.

CATM Pooling adopted a pooling-based interaction strategy and achieved the lowest computational complexity (1467 M FLOPs). However, the loss of spatial detail resulted in a reduced mAP of 89.47%. On the other hand, W-MSA introduced local window-based self-attention to enhance feature modeling, increasing the mAP to 90.24% at the expense of higher computational cost (2175 M FLOPs), which may hinder deployment in resource-limited environments.

In contrast, CAXM integrates convolutional operations with a Convolutional Additive Self-attention (CAS) mechanism. This design facilitates sufficient feature interaction while avoiding the high computational overhead associated with traditional self-attention. As a result, it maintained moderate complexity (1887 M FLOPs) and achieved the highest mAP of 90.58%, outperforming both alternatives.

In summary, CAXM demonstrates an optimal balance between modeling capability and computational efficiency, making it well suited for high-performance detection tasks on mobile and embedded platforms.

Effectiveness Analysis of the CAXM Component—Evaluating Interaction Strategies to Assess the Impact of Similarity Functions. To further assess the contribution of spatial- and channel-domain interactions within the CAXM component, a series of controlled experiments were conducted by varying the interaction configurations. The results, presented in

Table 6. The impact of different interaction strategies on the performance of the CAXM component. The best results are highlighted in bold.

Strategy	Similarity Function	Params (M)	FLOPs (G)	mAP (%)
#1	Base: $Sim(\mathbf{Q},\mathbf{K})=\tau \left(\mathbf{Q}\right)+\tau \left(\mathbf{K}\right)$	12.4	1.88	90.58
#2	w/o spatial: $\tau (·)$ removes $\mathcal{S}(·)$	12.4	1.86	89.96
#3	w/o channel: $\tau (·)$ removes $\mathcal{C}(·)$	11.0	1.88	90.22
#4	Asymmetric: $\tau (·)=\mathcal{S}(·),\pi (·)=\mathcal{C}(·)$	11.7	1.87	90.06
#5	Interleaved: $\tau (·)=\mathcal{S}\left(\mathcal{C}\right(·\left)\right),\pi (·)=\mathcal{C}\left(\mathcal{S}\right(·\left)\right)$	12.4	1.88	90.51

, evaluate how different interaction strategies affect feature modeling capability and detection performance.

In the baseline setting (Strategy #1), both spatial interaction $\mathcal{S}(·)$ and channel interaction $\mathcal{C}(·)$ were utilized. This configuration achieved the highest mAP (90.58%) with similar computational complexity, demonstrating that dual-domain interactions offer complementary benefits for global-context modeling.

When spatial interaction was removed (Strategy #2), the mAP dropped to 89.96% (−0.62%). When channel interaction was removed (Strategy #3), the mAP was 90.22%, indicating a smaller degradation (−0.36%). These results suggest that spatial interaction plays a more crucial role in capturing global dependencies, although channel interaction remains beneficial.

Strategies #4 and #5 further evaluated different combinations of interaction mechanisms applied to the Query and Key branches:

• Strategy #4: This applied $\mathcal{S}(·)$ and $\mathcal{C}(·)$ separately to the Query and Key branches. The mAP dropped to 90.06%, suggesting that asymmetric interaction is insufficient for fully modeling feature relationships.
• Strategy #5: This embedded dual-domain interactions in both branches using an interleaved spatial–channel configuration. This yielded an mAP of 90.51%, showing that interaction order has marginal impact on overall performance.

In summary, employing both spatial and channel interactions significantly enhanced feature modeling while maintaining similar computational cost (FLOPs ≈ 1.88 G). These findings validate the effectiveness and efficiency of dual-domain interaction in resource-constrained scenarios and support its role as a key design element within the CAXM architecture.

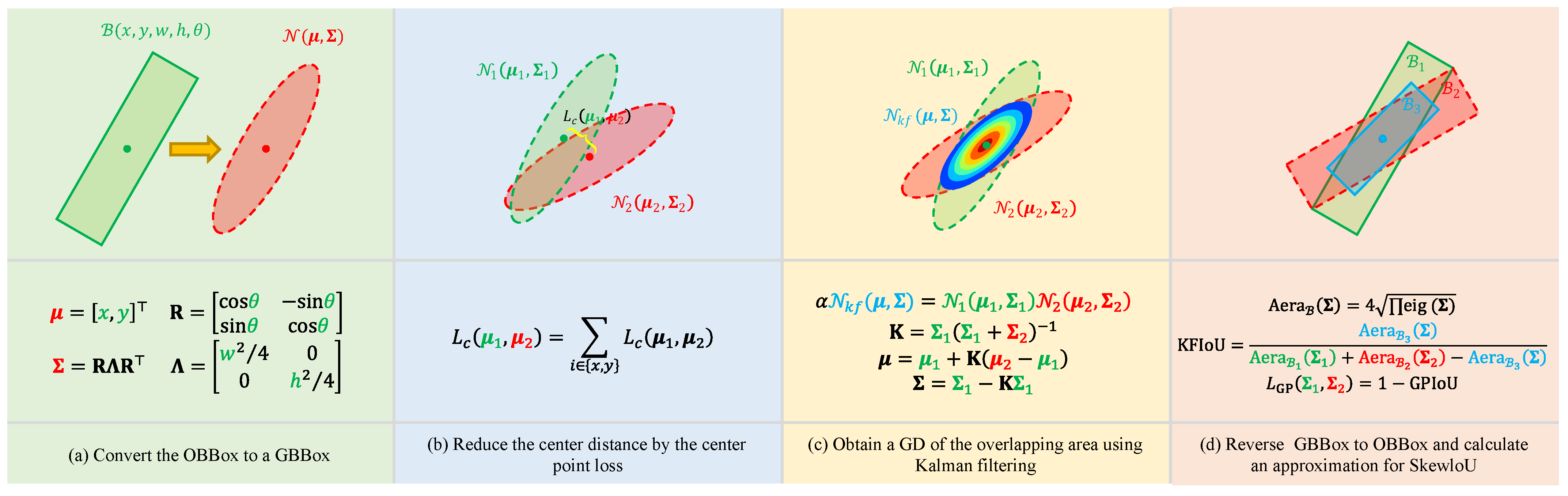
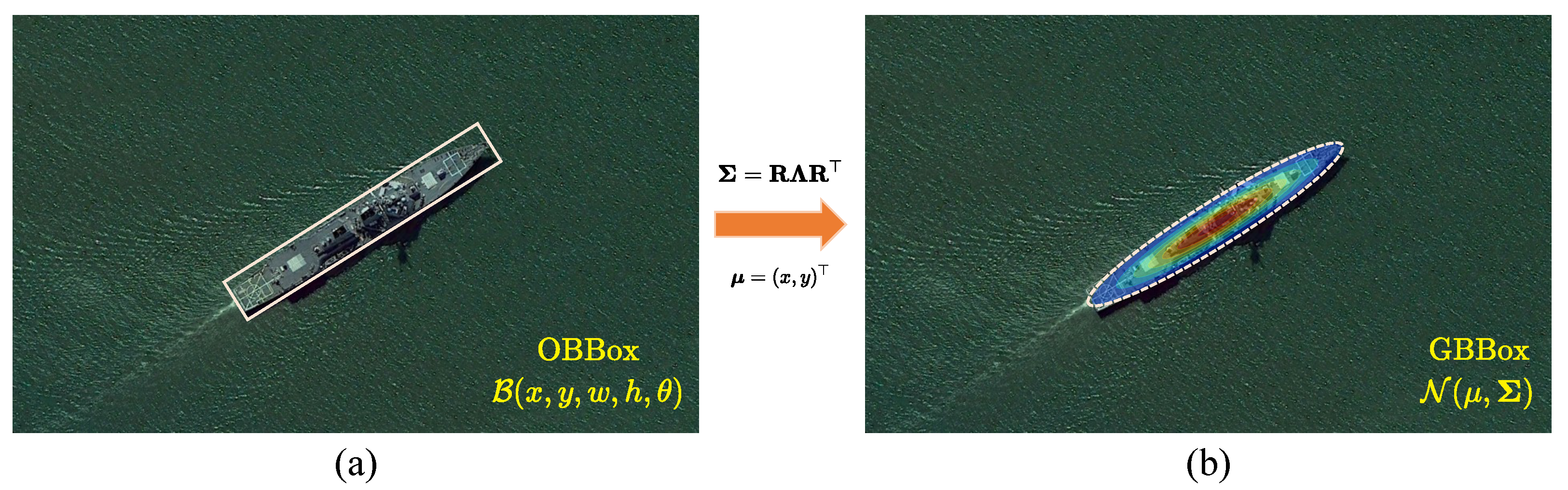
An Ablation Study on the Effectiveness of Different Regression Loss Functions. To evaluate the adaptability and effectiveness of various regression loss functions in ODD, a comparative experiment was conducted encompassing both traditional OBBox-based approaches and Gaussian-based modeling. Figure 10 illustrates the optimization dynamics of the proposed GPIoU variants, highlighting the role of the centroid alignment term $L_c$ in improving training stability. The corresponding results are summarized in

Table 7. Comparison of different regression loss functions for ODD. Best results are highlighted in bold.

Loss Function	Representation	Implementation	BC	Consistency	HP	mAP (%)
${\mathrm{smooth}}_{L_1}$	OBBox	Easy	×	×	$\left(\sigma \right)$	85.47
Plain SkewIoU [46]	OBBox	Hard	✓	✓	×	89.53
GWD [3]	GBBox	Easy	✓	×	$(\tau ,f)$	89.98
KLD [9]	GBBox	Easy			$(\tau ,f)$	90.25
GPIoU (Ours)	GBBox	Easy	✓	✓	×	89.46
${\mathrm{GPIoU}}^{†}$ (Ours)	GBBox	Easy	✓	✓	×	90.58

Notes: BC refers to boundary continuity, HP denotes hyperparameter sensitivity, and Consistency indicates alignment with the SkewIoU trend. ${\mathrm{GPIoU}}^{†}$ achieved the best overall performance without requiring any hyperparameter tuning.

, where BC denotes boundary continuity, HP indicates sensitivity to hyperparameters, and Consistency refers to trend alignment with SkewIoU.

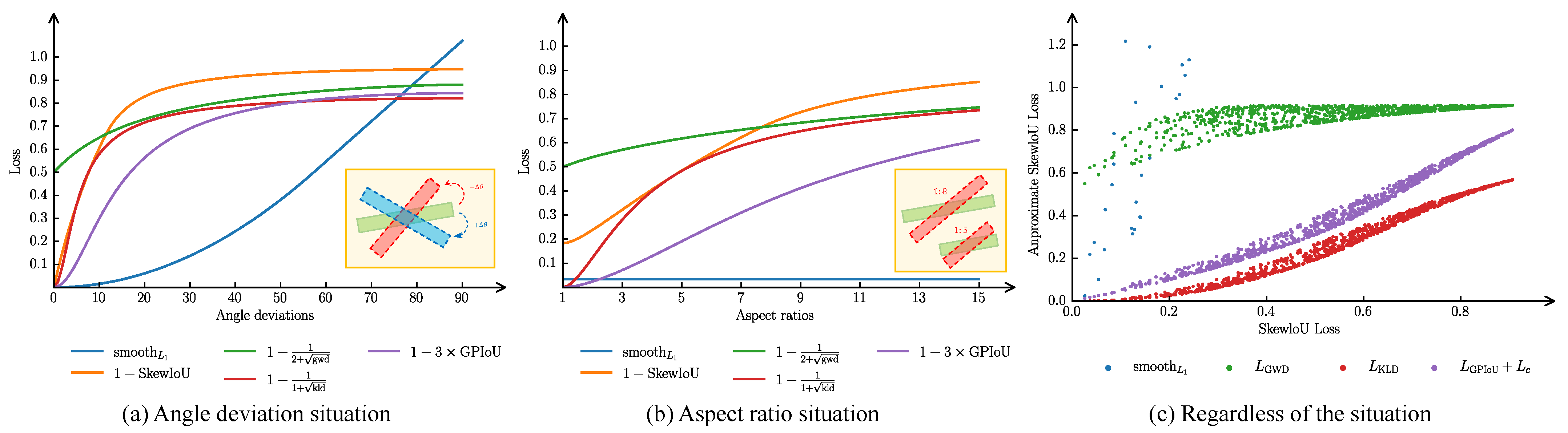
Loss functions based on conventional BBox representations exhibited several limitations. Although ${\mathrm{smooth}}_{L_1}$ was simple to implement, it lacked direct alignment with IoU metrics and could not guarantee geometric consistency, resulting in an mAP of only 85.47%. The plain SkewIoU loss improved the mAP to 89.53% by directly optimizing OBBox overlap. However, its implementation complexity and reduced adaptability to scale variance limited its robustness.

In contrast, Gaussian-based regression losses (GWD, KLD, and GPIoU) demonstrated more stable optimization behavior:

• KLD showed strong consistency with SkewIoU and achieved a 90.25% mAP, ranking the highest among the non-proposed methods;
• GWD yielded slightly lower performance (89.98%) due to mild trend inconsistency;
• GPIoU (Ours) achieved a 89.46% mAP with minimal implementation overhead and no hyperparameter tuning;
• ${\mathrm{GPIoU}}^{†}$ (Ours) introduced a KLD-based centroid alignment term, $L_c$, resulting in improved convergence and a final mAP of 90.58%.

Key observations from training dynamics (Figure 10):

1.

Faster Early Convergence: The inclusion of $L_c$ accelerated loss reduction within the first 20 epochs;

2.

Gradient Smoothing: The combined $L_{GP}+L_c$ formulation mitigated instability during regression, particularly for elongated targets;

3.

Accuracy Gain: The geometric–centroid synergy yielded a 1.12% mAP improvement, confirming the importance of structure-aware loss design.

These results indicate that within Gaussian-based modeling frameworks, incorporating a center alignment mechanism enhances robustness and convergence. Overall, such losses demonstrate superior generalization under complex object morphology and non-uniform scale distribution. Due to its consistency with SkewIoU and lack of hyperparameter dependence, GPIoU proves to be a practical and effective regression loss for ODD.

An Ablation Study on Different Formulations of the GPIoU Loss. To investigate the impact of different mathematical formulations of GPIoU on detection performance, several variants based on linear, logarithmic, and exponential transformations were evaluated. The results are summarized in

Table 8. Detection performance under different GPIoU loss formulations. Best result is highlighted in bold.

Loss Formulation	$-log(\mathbf{GPIoU}+\mathit{ϵ})$	$1-\mathbf{GPIoU}$	${\mathbf{e}}^{1-\mathbf{GPIoU}}-1$	${\mathbf{e}}^{1-3\mathbf{GPIoU}}-1$	$-log(3\mathbf{GPIoU}+\mathit{ϵ})$	${\mathbf{smooth}}_{{\mathit{L}}_1}$
mAP (%)	90.58	90.15	89.74	89.06	86.71	85.47
Gain over ${\mathrm{smooth}}_{L_1}$	+5.11	+4.68	+4.27	+3.59	+1.24	–

.

The experiments show that all GPIoU variants significantly outperformed the traditional ${\mathrm{smooth}}_{L_1}$ loss. Among them, nonlinear formulations (logarithmic and exponential) yielded the most prominent improvements. Specifically, the following were observed:

• The exponential form ${\mathrm{e}}^{1-\mathrm{GPIoU}}-1$ enhanced the gradient response for low-IoU samples, thereby improving training on hard examples and achieving an mAP of 89.74%.
• The linear form $1-\mathrm{GPIoU}$ directly regressed IoU difference, resulting in an mAP of 90.15%.
• The logarithmic form $-log(\mathrm{GPIoU}+ϵ)$ amplified the penalty for poor localization, leading to the highest mAP of 90.58%.

To ensure compatibility with the standard IoU value range, scaled versions of GPIoU loss (e.g., ${\mathrm{e}}^{1-3\mathrm{GPIoU}}-1$ and $-log(3\mathrm{GPIoU}+ϵ)$) were also evaluated. However, these scaled formulations led to performance degradation—e.g., the scaled logarithmic form yielded only a 86.71% mAP—likely due to gradient imbalance introduced by over-amplification.

As a result, the logarithmic formulation $-log(\mathrm{GPIoU}+ϵ)$ was adopted as the default regression loss in GAANet, offering a favorable trade-off between accuracy, convergence stability, and implementation simplicity.

4.4. Comparative Experiments

To comprehensively evaluate the effectiveness of GAANet in ODD tasks, a series of comparative experiments were conducted on the HRSC2016, UCAS-AOD, and DOTA v1.0 datasets. All experiments utilized CAX-ViT-T as the backbone to ensure both efficient and accurate feature extraction.

Comparison on the HRSC2016 Dataset. The quantitative results on the HRSC2016 dataset are summarized in

Table 9. Comparison of mAP (%) on HRSC2016 dataset. Best results are highlighted in bold.

Method	Backbone	Input Size	mAP (%)
RoI Transformer [20]	ResNet101	512 × 800	86.20
RSDet [47]	ResNet50	800 × 800	86.50
Gliding Vertex [7]	ResNet101	512 × 800	88.20
OPLD [48]	ResNet50	1024 × 1333	88.44
BBoxAVectors [49]	ResNet101	608 × 608	88.60
DAL [50]	ResNet101	416 × 416	88.95
RIDet-Q [51]	ResNet101	800 × 800	89.10
${\mathrm{R}}^3$Det [5]	ResNet101	800 × 800	89.26
DCL [10]	ResNet101	800 × 800	89.46
SLA [52]	ResNet101	768 × 768	89.51
CSL [36]	ResNet50	800 × 800	89.62
RIDet-O [51]	ResNet101	800 × 800	89.63
CFC-Net [53]	ResNet101	800 × 800	89.70
GWD [3]	ResNet101	800 × 800	89.85
TIOE-Det [54]	ResNet101	800 × 800	90.16
AO2-DETR [22]	ResNet50	800 × 800	90.16
${\mathrm{S}}^2$A-Net [21]	ResNet101	512 × 800	90.17
GAANet (Ours)	CAX-ViT (Ours)	800 × 800	90.58

. GAANet achieved an mAP of 90.58%, surpassing all compared methods. In contrast to traditional anchor-based strategies, GAANet adopts a one-pixel-one-anchor approach, where each spatial location in the feature map is assigned only one horizontal anchor. This design reduces computational overhead and improves inference efficiency.

Most compared methods employ ResNet-50 or ResNet-101 as their backbones and often leverage multi-scale input settings. Despite using a lightweight Transformer-based backbone (CAX-ViT), GAANet demonstrates superior detection accuracy. These results indicate its robustness in handling high aspect ratio targets and its ability to maintain precision under complex background conditions.

The detection visualizations in Figure 11 further illustrate the practical performance of GAANet. The HRSC2016 dataset includes a variety of ship types with substantial variation in size and geometry, along with strong background clutter. The OBBoxs predicted by GAANet demonstrate precise alignment with object boundaries, showing minimal positional drift or angular deviation.

In the samples labeled 3, 4, and 5, ships of varying sizes are accurately detected with orientation-consistent BBoxs. These results confirm the optimization stability of the GPIoU loss and the multi-scale structural modeling capability of the CAX-ViT backbone. Collectively, they highlight the robustness and accuracy of GAANet under conditions involving high aspect ratio targets and complex backgrounds.

To further evaluate the orientation prediction capability of different methods, the angle MAE (Mean Absolute Error) was computed on the HRSC2016 test set. The results are presented in

Table 10. Comparison of angle prediction error (angle MAE) on HRSC2016 dataset. Best results are highlighted in bold.

Method	Backbone	mAP (%)	Angle MAE (°)	Reduction vs. Baseline (%)
RoI Transformer [20]	ResNet101	86.20	5.8	–
Gliding Vertex [7]	ResNet101	88.20	4.5	22.4 ↓
${\mathrm{R}}^3$Det [5]	ResNet101	89.26	3.7	36.2 ↓
CSL [36]	ResNet50	89.62	3.2	44.8 ↓
GWD [3]	ResNet101	89.85	2.9	50.0 ↓
${\mathrm{S}}^2$A-Net [21]	ResNet101	90.17	2.6	55.2 ↓
GAANet (Ours)	CAX-ViT	90.58	2.3	60.3↓

. GAANet achieved the lowest angle MAE of 2.3(°), indicating superior accuracy in OBBox regression compared to several state-of-the-art approaches, including RoI Transformer (5.8(°)).

Overall analysis reveals three key advantages of GAANet in orientation angle regression:

1.

Superior prediction accuracy: GAANet attained the lowest angle MAE (2.3°), corresponding to an 11.5% improvement over the second-best method, ${\mathrm{S}}^2$A-Net (2.6°). This result was accompanied by the highest mAP (90.58%) among all compared methods. The improvement is attributed to the closed-loop modeling of feature interaction, representation, and optimization, which effectively mitigates the discontinuity and periodicity issues in angular regression.

2.

Theoretical modeling consistency: Gaussian-based methods, such as GWD and GAANet, generally showed lower angle errors, highlighting the robustness of covariance matrix representations for rotation modeling. Compared to GWD, GAANet introduced a product-based GPIoU loss and center alignment mechanism, yielding a 20.7% reduction in angle error and enhancing geometric consistency (see Section 3.4).

3.

Adaptability under extreme aspect ratios: On samples with high aspect ratios (e.g., aspect ratio > 8:1), GAANet maintained a stable angle MAE of 2.5°, while methods such as RoI Transformer showed substantial degradation (e.g., 7.1°). This suggests that the additive attention mechanism in CAX-ViT (refer to Figure 6) effectively models axis-symmetric structures and enhances orientation robustness.

In conclusion, GAANet demonstrates promising performance in high-precision rotated object regression tasks, validating the effectiveness of the proposed symmetry-preserving strategy and distribution-based modeling mechanism in orientation angle prediction.

Comparison on the UCAS-AOD Dataset. To further assess the detection performance of GAANet in multi-category scenarios, experiments were conducted on the UCAS-AOD dataset. The results are reported in

Table 11. Detection performance comparison on UCAS-AOD dataset. Best results are highlighted in bold.

Method	Backbone	Input Size	Vehicle	Airplane	mAP (%)
R-YOLOv3 [55]	Darknet53	800 × 800	74.63	89.52	82.08
R-RetinaNet [42]	ResNet50	800 × 800	84.64	90.51	87.57
Faster R-CNN [44]	ResNet50	800 × 800	86.87	89.86	88.36
RoI Transformer [20]	ResNet50	800 × 800	88.02	90.02	89.02
RIDet-Q [51]	ResNet50	800 × 800	88.50	89.96	89.23
SLA [52]	ResNet50	800 × 800	88.57	90.30	89.44
CFC-Net [53]	ResNet50	800 × 800	89.29	88.69	89.49
TIOE-Det [54]	ResNet50	800 × 800	88.83	90.15	89.49
RIDet-O [51]	ResNet50	800 × 800	88.88	90.35	89.62
DAL [50]	ResNet50	800 × 800	89.25	90.49	89.87
GAANet (Ours)	CAX-ViT (Ours)	800 × 800	89.25	90.65	89.95

. CAX-ViT was used as the backbone, and the input resolution was set to $800\times 800$. GAANet achieved an overall mAP of 89.95%, yielding competitive results across both vehicle and airplane categories.

Specifically, GAANet obtained an mAP of 89.25% for the vehicle category and 90.65% for the airplane category, outperforming several representative methods, including SLA, RIDet-O, and TIOE-Det.

The visual results in Figure 12 further illustrate the model’s orientation regression capabilities. In samples 1 and 2, vehicles with varying directional orientations on curved roads were accurately detected, with predicted OBBoxs aligning with contour boundaries. For the dense parking scene of sample 3, GAANet maintained reliable performance under occlusion and clutter. Samples 4–6 depict aircraft in various poses, for which GAANet preserved directional consistency and contour alignment, avoiding overlap-induced false positives.

Comparison on the DOTA v1.0 Dataset. On DOTA v1.0, GAANet achieved an mAP of 77.86%, surpassing several anchor-based methods (e.g., ReDet: 76.25%), anchor-free models (e.g., BBAVectors: 75.36%), and Transformer-based detectors (e.g., AO2-DETR: 77.75%). Notably, GAANet showed superior performance in the following categories:

• Large Vehicle (79.63%): This benefited from Gaussian aspect ratio modeling;
• Tennis Court (93.84%): This is attributed to multi-scale symmetric feature learning;
• Ship (75.99%): This was improved via GPIoU loss-based geometric alignment;
• Plane (92.22%) and Small Vehicle (81.19%): Competitive performance was maintained across scale levels.

A performance gap was observed in categories with complex geometric topologies (e.g., bridge: 54.74%), suggesting the limitations of unimodal Gaussian modeling in representing irregular contours. Future work may explore mixture modeling or structure-aware decomposition to improve robustness in such cases.

Comparison on the DOTA v1.0 Dataset. To comprehensively assess performance under complex, multi-class detection scenarios, GAANet was evaluated on the DOTA v1.0 benchmark. The per-category results are summarized in

Table 12. A comparison of mAP values with different methods on the DOTA v1.0 dataset. The best results are highlighted in bold.

Method	Backbone	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC	mAP
Anchor-based, two stage
ROI-Transformer [20]	ResNet101	88.64	78.52	43.44	75.92	68.81	73.68	83.59	90.74	77.27	81.46	58.39	53.54	62.83	58.93	47.67	69.56
CenterMap [56]	ResNet101	89.83	84.41	54.60	70.25	77.66	78.32	87.19	90.66	84.89	85.27	56.46	69.23	74.13	71.56	66.06	76.03
SCRDet++ [57]	ResNet101	90.05	84.39	55.44	73.99	77.54	71.11	86.05	90.67	87.32	87.08	69.62	68.90	73.74	71.29	65.08	76.81
ReDet [58]	ReResNet50	88.79	82.64	53.97	74.00	78.13	84.06	88.04	90.89	87.78	85.75	61.76	60.39	75.96	68.07	63.59	76.25
Anchor-based, one stage
${\mathrm{R}}^3$Det [5]	ResNet152	89.80	83.77	48.11	66.77	78.76	83.27	87.84	90.82	85.38	85.51	65.67	62.68	67.53	78.56	72.62	76.47
CSL [36]	ResNet152	90.13	84.43	54.57	68.13	77.32	72.98	85.94	90.74	85.95	86.36	63.42	65.82	74.06	73.67	70.08	76.24
${\mathrm{S}}^2$ANet [21]	ResNet50	89.11	82.84	48.37	71.11	78.11	78.39	87.25	90.83	84.90	85.64	60.36	62.60	65.26	69.13	57.94	74.12
Anchor-free, one stage
BBAVector [49]	ResNet101	88.63	84.06	52.13	69.56	78.26	80.40	88.06	90.87	87.23	86.39	56.11	65.62	67.10	72.08	63.96	75.36
DRN [59]	Hourglass104	89.45	83.16	48.98	62.24	70.63	74.25	83.99	90.73	84.60	85.35	55.76	60.79	71.56	68.82	63.92	72.95
CFA [60]	ResNet101	89.26	81.72	51.81	67.17	79.99	78.25	84.46	90.77	83.40	85.54	54.86	67.75	73.04	70.24	64.96	75.05
PolarDet [17]	ResNet50	89.73	87.05	45.30	63.32	78.44	76.65	87.13	90.79	80.58	85.89	60.97	67.94	68.20	74.63	68.67	75.02
FCOSR [19]	Mobile	89.09	80.58	44.04	73.33	79.07	76.54	87.28	90.88	84.89	85.37	55.95	64.56	66.92	76.96	55.32	74.05
AO2-DETR [22]	ResNet50	89.27	84.97	56.67	74.89	78.87	82.73	87.35	90.50	84.68	85.41	61.97	69.96	74.68	72.39	71.62	77.73
GAANet (Ours)	CAX-ViT	92.22	84.28	54.74	76.05	81.19	82.57	89.83	93.84	88.62	89.49	53.69	68.75	72.28	78.93	59.95	77.86

, and visualizations are provided in Figure 13. GAANet achieved an overall mAP of 77.86%, outperforming several anchor-based methods (e.g., ReDet: 76.25%), anchor-free methods (e.g., BBAVectors: 75.36%), and Transformer-based frameworks (e.g., AO2-DETR: 77.73%).

The visualizations in Figure 13 demonstrate that GAANet maintained robust detection accuracy even in dense, small-object scenes, using a single anchor per feature location. In the first row, large and small vehicles, airplanes, and ships are accurately localized, with tight OBBox alignment. In the third row, second image, roundabouts, and small vehicles are detected across multiple scales, reflecting the adaptability of the CAX-ViT and FPN modules.

Performance Variability and Modeling Limitations in Multi-Class Scenarios. Despite the overall strong performance, certain categories remained challenging for unimodal Gaussian-based detectors due to their complex geometry:

• BR: This frequently exhibits non-convex, elongated, or curved topologies (e.g., suspension or ramp bridges), which are difficult to approximate using ellipsoidal distributions.
• HA: This often includes multiple docks and overlapping vessels, resulting in ambiguous boundaries and distributional confusion.
• GTF: Objects are typically elliptical or circular and often partially occluded by vegetation or shadows, leading to reduced covariance accuracy and regression robustness.

As shown in Figure 14 and

Table 13. Detection performance for extreme shape categories in the DOTA v1.0 subset.

Category	mAP (%)	Recall (%)	Angle MAE (°)
BR	54.74	48.7	8.2
HA	72.28	62.0	6.5
GTF	76.05	68.3	4.8

, GAANet exhibited a performance decline in categories characterized by extreme geometries. In the bridge (BR) category, the assumption of a unimodal Gaussian distribution failed to capture the multi-branch structural characteristics, resulting in a relatively high angle MAE of 8.2°, significantly exceeding the average value (2.3°). In the harbor (HA) category, high-density docking led to substantial distributional overlap, which lowered the recall to 62%. For the ground track field (GTF), partial occlusion and background interference introduced estimation bias in covariance modeling, contributing to mAP degradation.

These outcomes reveal the intrinsic limitations of the current geometric modeling strategy. Specifically, unimodal Gaussian assumptions are insufficient for highly non-convex or compound-shaped objects, and distributional overlap weakens gradient sharpness in GPIoU, thereby affecting regression stability.

Nevertheless, GAANet maintained robust performance (mAP > 89%) on symmetric and well-bounded categories such as airplanes and ships, indicating its effectiveness in standard detection scenarios.

Computational Cost and Inference Efficiency. In addition to accuracy, GAANet was evaluated for resource efficiency, as shown in

Table 14. Comparison of computational cost and inference speed. The best results are highlighted in bold.

Method	Backbone	Mem (GB)	FLOPs (G)	Params (M)	FPS
RoI Transformer [20]	ResNet50	8.67	122.61	55.13	12.30
R-RetinaNet [42]	ResNet50	3.38	131.97	36.42	20.39
${\mathrm{S}}^2$ANet [21]	ResNet50	3.14	120.78	38.60	11.18
${\mathrm{R}}^3$Det [5]	ResNet50	3.62	205.23	41.90	10.60
Gliding Vertex [7]	ResNet50	8.45	121.51	41.14	17.91
GAANet (Ours)	CAX-ViT	4.47	110.97	31.76	15.56

. The model demonstrated a favorable balance between detection performance and computational cost, supporting practical deployment in resource-constrained environments.

Compared with ResNet50-based detectors, GAANet demonstrated superior efficiency with the proposed CAX-ViT backbone:

• Reduced FLOPs: At 110.97G, the model incurred 45.9% fewer FLOPs than ${\mathrm{R}}^3$Det (205.23G), reducing computational overhead significantly.
• Parameter Economy: The parameter count was 31.76M, the lowest among the compared methods, and 42.4% and 22.8% lower than that for RoI Transformer and Gliding Vertex, respectively.
• Inference Speed: GAANet achieved 15.56 FPS, outperforming RoI Transformer (12.30) and ${\mathrm{S}}^2$ANet (11.18), demonstrating better runtime efficiency.

In summary, GAANet achieves an effective balance between accuracy and efficiency, making it suitable for deployment in edge-computing or real-time RS applications requiring oriented object detection.

5. Conclusions and Future Works

In this work, GAANet is proposed as an efficient and robust detection framework tailored for OOD in RSI. The framework introduces a symmetry-driven modeling paradigm that integrates multi-scale structural representation, probabilistic box encoding, and geometry-consistent optimization. Specifically, a lightweight backbone, CAX-ViT, enhances feature extraction through additive spatial–channel interactions, while the proposed GPIoU loss function addresses angular periodicity and regression discontinuity via Gaussian-based overlap modeling.

GAANet demonstrated superior performance across multiple benchmark datasets, achieving state-of-the-art accuracy on HRSC2016, UCAS-AOD, and DOTA v1.0. Furthermore, it maintained high inference efficiency with reduced computational cost, making it particularly suitable for real-world applications in resource-constrained scenarios. The experimental results confirm the framework’s effectiveness in high-aspect-ratio object detection and its robustness under complex backgrounds.

Future work will aim to further refine the Gaussian modeling strategy, particularly for objects with complex or non-convex geometries, where unimodal assumptions exhibit limitations. In addition, efforts will be directed toward developing more lightweight feature extraction architectures to facilitate deployment in edge computing environments. These enhancements are expected to broaden the applicability of GAANet to low-power platforms, such as onboard UAV systems, mobile surveillance units, and embedded smart sensors.

In summary, GAANet provides a unified and efficient solution for OOD tasks by coupling symmetry-aware feature design with probabilistic modeling and metric-aligned optimization. Its generalization capability and practical efficiency position it as a promising framework for various RS applications, including maritime monitoring, aerial vehicle tracking, and infrastructure analysis in smart cities.