Electroencephalogram-Based Familiar and Unfamiliar Face Perception Classification Underlying Event-Related Potential Analysis and Confident Learning
Abstract
1. Introduction
- We collect the FUFP dataset. As the largest publicly available dataset, it enables researchers to invest in signal processing and familiarity classification algorithms quickly and compare the pros and cons of existing algorithms. Six labels allow researchers to analyze face perception from more perspectives. Compared to the label “label”, “label 2” offers an extra category of whether the face is the subject’s own face for further analysis.
- We construct a benchmark for the EEG-based face familiarity study. The results of five baseline classification algorithms, ERP analysis, and power spectral density (PSD) analysis are provided.
- We propose an algorithm called ECL (ERP analysis and confident learning) to classify the UF and FF stimulus. Experiments on FUFP show the effectiveness of the algorithm.
- Install Git LFS from the official website: https://git-lfs.com, accessed on 15 February 2025.
- Clone the repository using Git LFS to download the large files.
- Once the files are downloaded, they can be opened and processed in MATLAB as usual.
2. Informed Consent Statement
3. Dataset Design and Collection
3.1. Participants
3.2. Stimulus Material
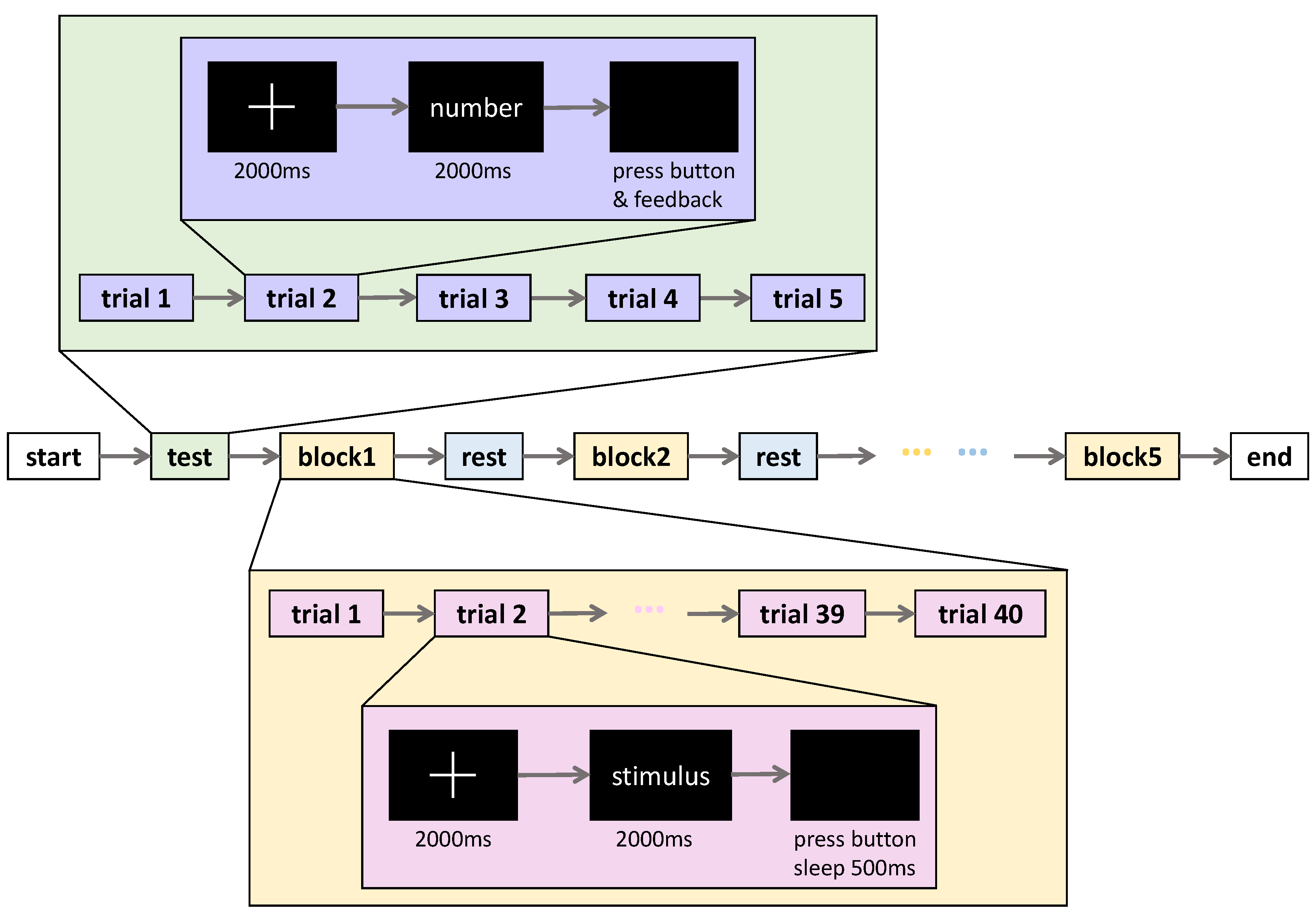
3.3. Experimental Paradigm
3.4. Preprocessing
- Electrode repositioning: By adjusting the electrodes of different subjects collected at different time points to the standard position in a mathematical way using Curry8, the minor variations in electrode placement across subjects or sessions could be eliminated, thereby reducing inter-subject variability and improving the consistency and quality of the EEG data for subsequent analysis.
- Apply baseline correction to remove the influence of linear drift caused by DC acquisition mode.
- Apply a bandpass filter with a frequency range of 0–30 Hz to the raw EEG data. The cutoff frequencies for the bandpass filter are set at 0 Hz (low cutoff) and 30 Hz (high cutoff).
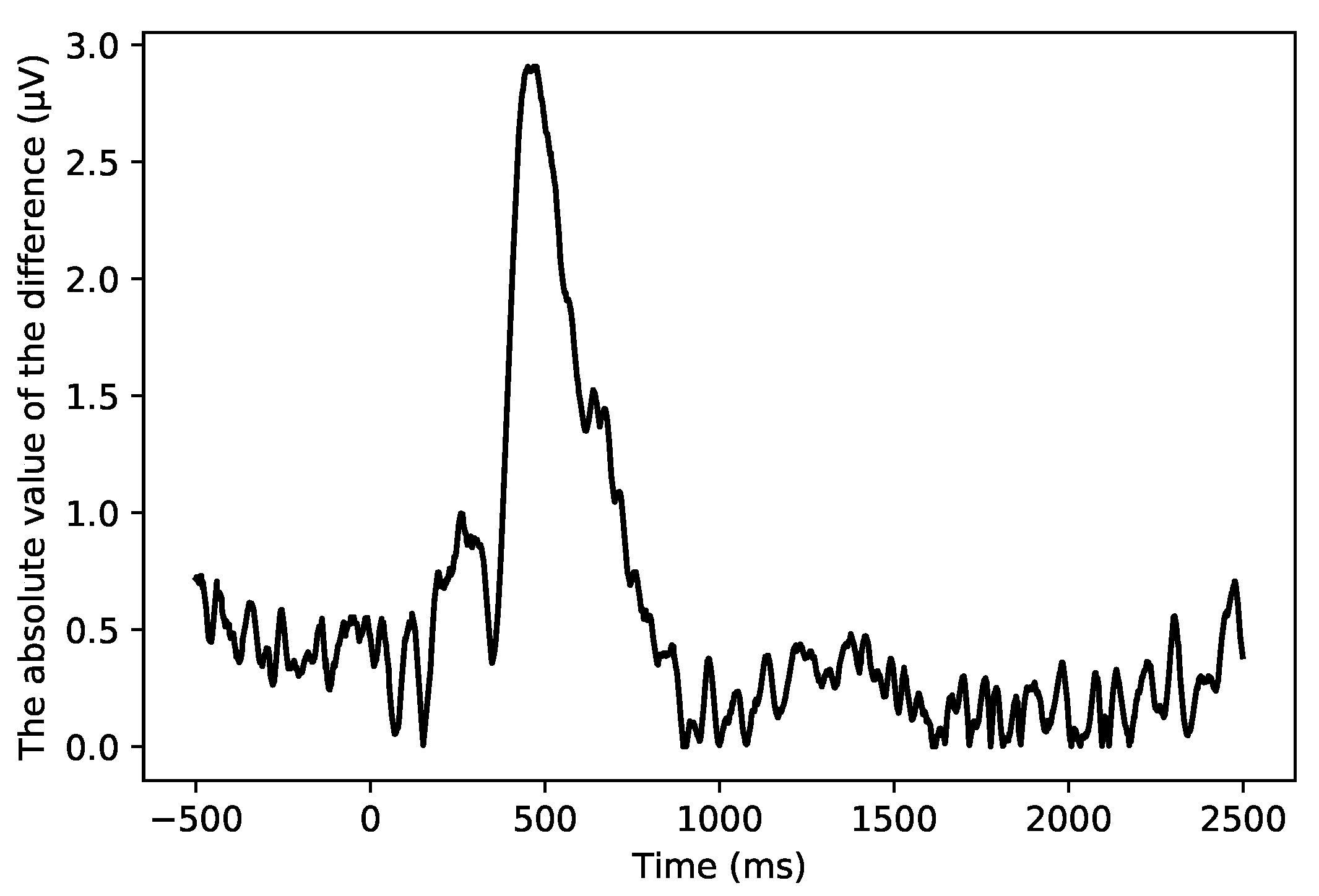
- Reject the vertical electrooculogram artifacts: Since the amplitude of electrical signals generated by eye movement artifacts (such as blinking and vertical eye movements) is usually much larger than that of EEG signals, and the frequency range of eye movement artifacts usually overlaps with that of EEG signals, these artifacts can significantly distort EEG signals. To remove these artifacts, independent component analysis (ICA) is used to identify and isolate components corresponding to the vertical electrooculogram activity. Specifically, ICA involves decomposing the EEG signals into independent components, identifying artifact-related components based on their temporal and spatial characteristics, and removing these components from the signal. The components are then rejected from the EEG data to ensure the integrity of the EEG signals. Figure 5 shows the time series diagram of independent component 28 (IC 28). At 900 ms, a transient peak lasting about 200 ms appears, which may mean that this component is produced by eye movement, so it is marked as an electrooculogram artifact and removed to avoid its interference with the subsequent ERP analysis and PSD analysis.
4. Benchmark Experiment
4.1. Baseline Evaluations
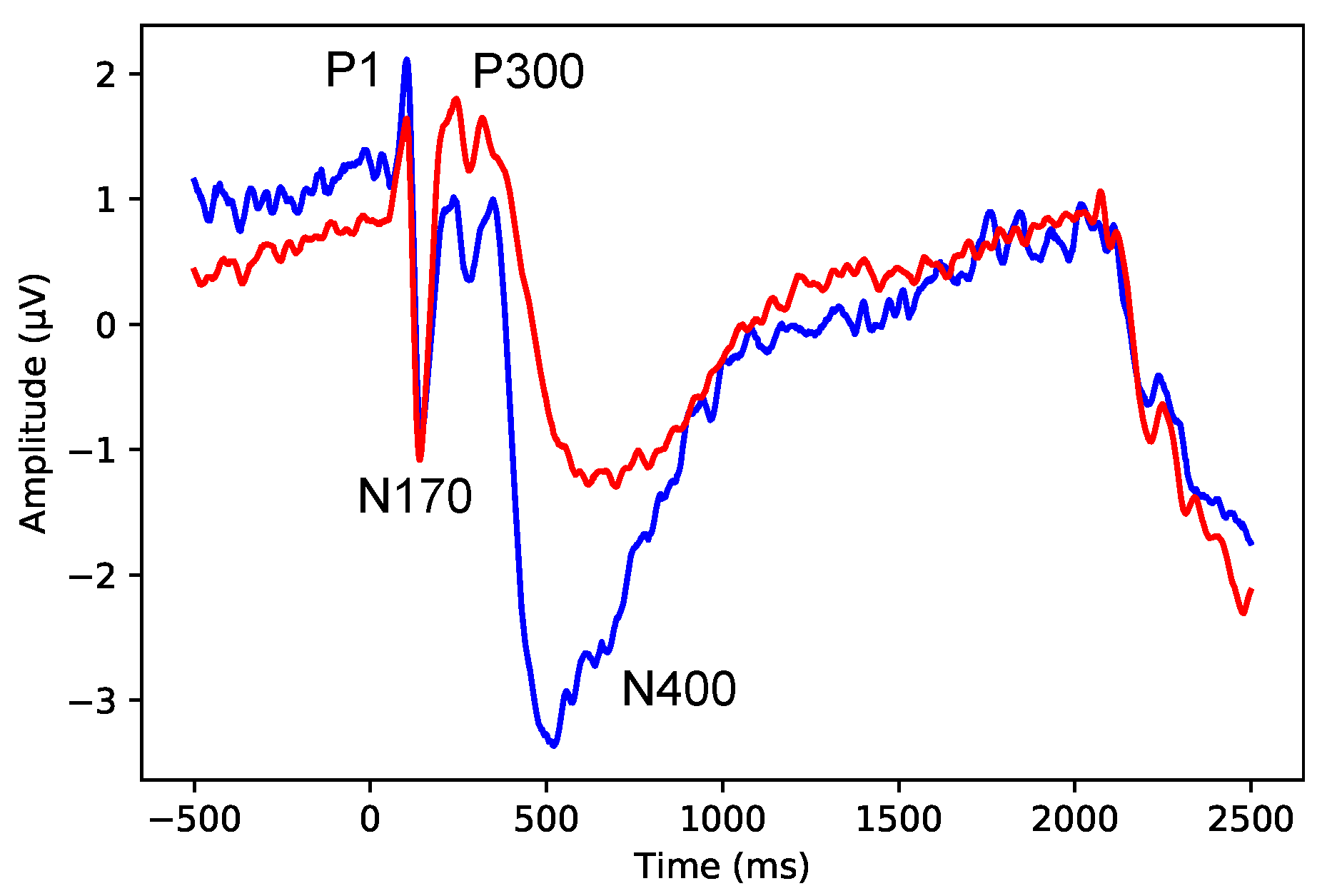
4.2. ERP Analysis
- Crop the original EEG signals obtained from the subject’s scalp into 3000 ms duration epochs offline, which include a 500 ms pre-stimulus baseline and a 500 ms post-stimulus baseline.
- Remove the epochs with obviously abnormal amplitudes (only retain the epochs within ±100 μV).
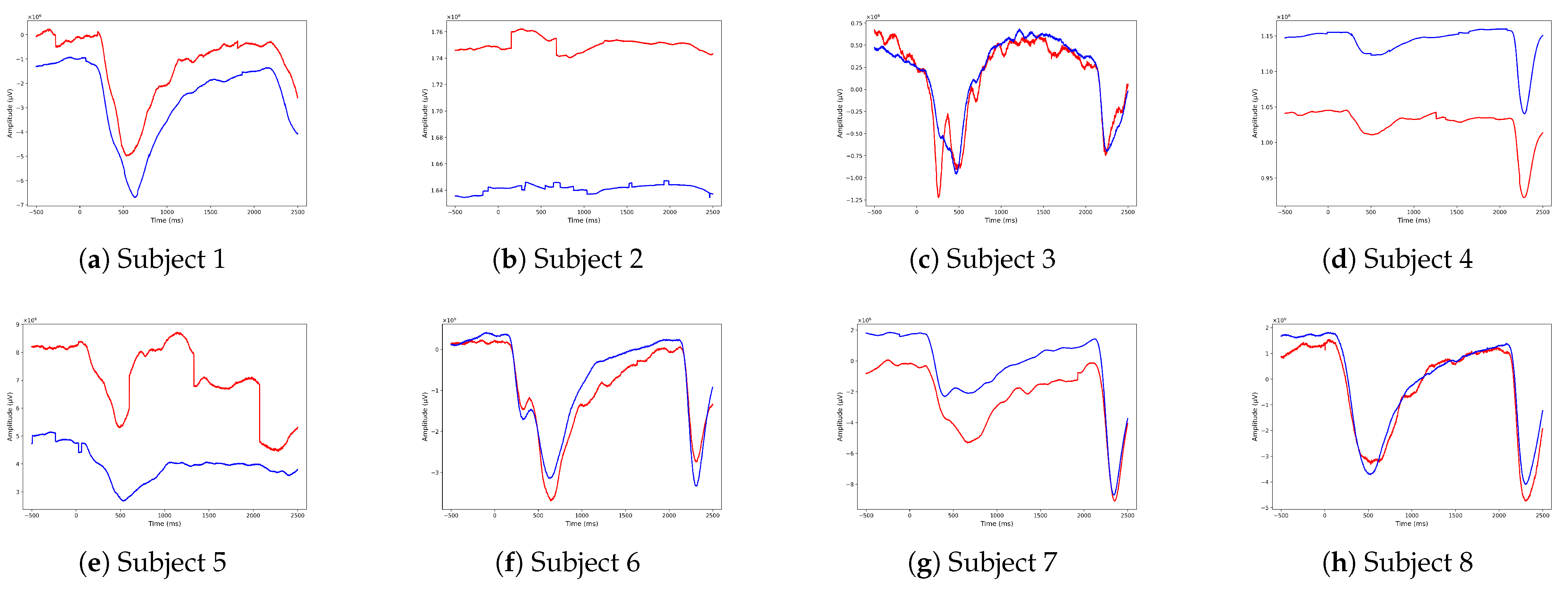
- Average the epochs for each condition (familiar and unfamiliar faces) and each subject (Subjects 1–8) to obtain the overall mean ERP values.
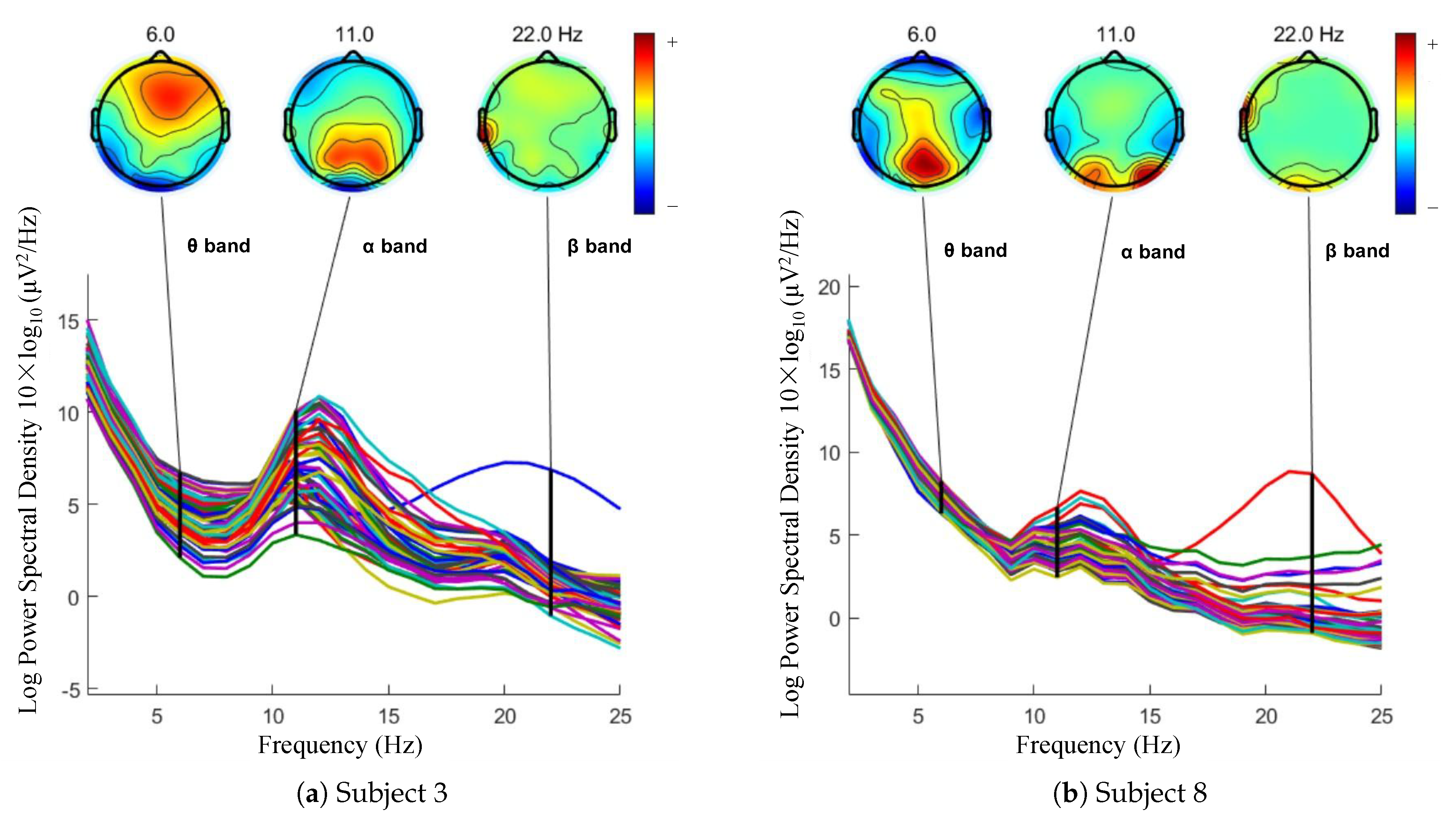
4.3. PSD Analysis
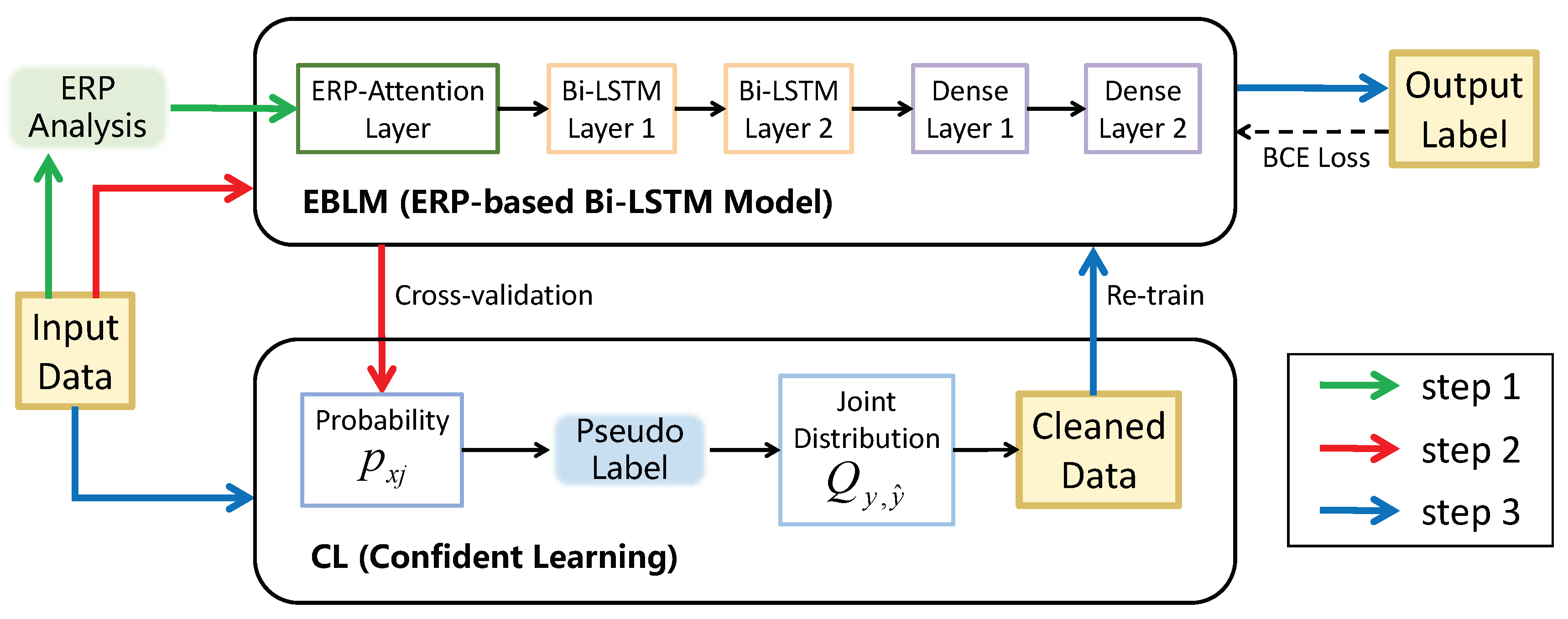
5. Familiarity Classification with ECL
5.1. Method
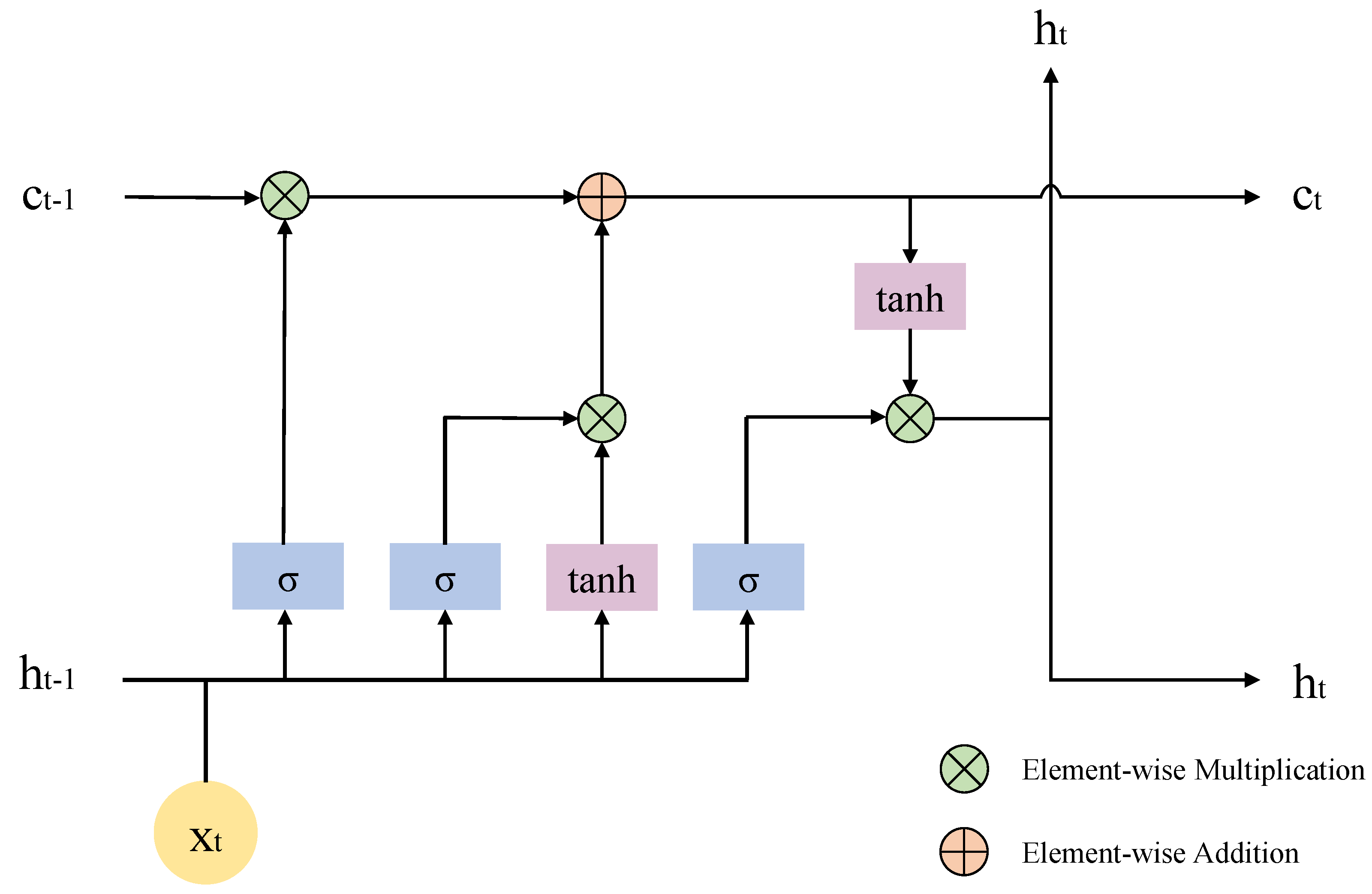
5.1.1. EBLM (ERP-Based Bi-LSTM Model)
5.1.2. CL (Confident Learning)
| Algorithm 1 ECL Algorithm for Familiarity Classification |
| Require: EEG dataset , where is the EEG signal and is the label Ensure: Trained EBLM model for familiarity classification
|
5.2. Experiment Results
5.2.1. Ablation Study
5.2.2. Comparison Experiments
5.3. Model Complexity
5.3.1. Time Complexity
5.3.2. Memory Complexity
6. Discussion
6.1. The Fufp Dataset and Methodology
6.2. Benefits and Limitations
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Young, A.W. Faces, people and the brain: The 45th Sir Frederic Bartlett Lecture. Q. J. Exp. Psychol. 2018, 71, 569–594. [Google Scholar] [CrossRef] [PubMed]
- Crouzet, S.M.; Kirchner, H.; Thorpe, S.J. Fast saccades toward faces: Face detection in just 100 ms. J. Vision 2010, 10, 16. [Google Scholar] [CrossRef]
- Morrisey, M.N.; Hofrichter, R.; Rutherford, M. Human faces capture attention and attract first saccades without longer fixation. Vis. Cogn. 2019, 27, 158–170. [Google Scholar] [CrossRef]
- Visconti, M.; Gobbini, M.I. Familiar face detection in 180 ms. PLoS ONE 2015, 10, e0136548. [Google Scholar]
- Zhang, J.; Liu, J.; Xu, Y. Neural decoding reveals impaired face configural processing in the right fusiform face area of individuals with developmental prosopagnosia. J. Neurosci. 2015, 35, 1539–1548. [Google Scholar] [CrossRef] [PubMed]
- DeGutis, J.; Bahierathan, K.; Barahona, K.; Lee, E.; Evans, T.; Shin, H.M.; Mishra, M.; Likitlersuang, J.; Wilmer, J. What is the prevalence of developmental prosopagnosia? An empirical assessment of different diagnostic cutoffs. Cortex 2023, 161, 51–64. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhen, Z.; Liu, X.; Song, Y.; Liu, J. The neural network for face recognition: Insights from an fMRI study on developmental prosopagnosia. Neuroimage 2018, 169, 151–161. [Google Scholar] [CrossRef]
- Duchaine, B.; Yovel, G.; Nakayama, K. No global processing deficit in the navon task in 14 developmental prosopagnosics. Soc. Cogn. Affect. Neur. 2007, 2, 104–113. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, C.; Ni, T. A hierarchical discriminative sparse representation classifier for EEG signal detection. IEEE/ACM Trans. Comput. BioL. Bioinf. 2021, 10, 1679–1687. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Pan, W.; Bai, H.; Liu, W.; Wang, L.; Lin, C. Epilepsy signal recognition using online transfer tsk fuzzy classifier underlying classification error and joint distribution consensus regularization. IEEE/ACM Trans. Comput. BioL. Bioinf. 2021, 18, 1667–1678. [Google Scholar] [CrossRef]
- Toyoda, A.; Ogawa, T.; Haseyama, M. MvLFDA-based video preference estimation using complementary properties of features. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 635–639. [Google Scholar]
- Sokolovsky, M.; Guerrero, F.; Paisarnsrisomsuk, S.; Ruiz, C.; Alvarez, S.A. Deep learning for automated feature discovery and classification of sleep stages. IEEE/ACM Trans. Comput. BioL. Bioinf. 2020, 17, 1835–1845. [Google Scholar] [CrossRef]
- Kanwal, S.; Uzair, M.; Ullah, H.; Khan, S.D.; Ullah, M.; Cheikh, F.A. An image based prediction model for sleep stage identification. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, China, 22–25 September 2019; pp. 1366–1370. [Google Scholar]
- Arnau-Gonzalez, P.; Katsigiannis, S.; Arevalillo-Herraez, M.; Ramzan, N. Image-evoked affect and its impact on eeg-based biometrics. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, China, 22–25 September 2019; pp. 2591–2595. [Google Scholar]
- Mukherjee, P.; Das, A.; Bhunia, A.K.; Roy, P.P. Cogni-net: Cognitive feature learning through deep visual perception. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Taipei, China, 22–25 September 2019; pp. 4539–4543. [Google Scholar]
- Guo, Y.; Nejati, H.; Cheung, N.M. Deep neural networks on graph signals for brain imaging analysis. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3295–3299. [Google Scholar]
- Eimer, M.; Gosling, A.; Duchaine, B. Electrophysiological markers of covert face recognition in developmental prosopagnosia. Brain 2012, 135, 542–554. [Google Scholar] [CrossRef]
- Williams, P.; White, A.; Merino, R.B.; Hardin, S.; Mizelle, J.C.; Kim, S. Facial recognition task for the classification of mild cognitive impairment with ensemble sparse classifier. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany,, 23–27 July 2019; pp. 2242–2245. [Google Scholar]
- Tasci, I.; Baygin, M.; Barua, P.D.; Hafeez-Baig, A.; Dogan, S.; Tuncer, T.; Tan, R.S.; Acharya, U.R. Black-white hole pattern: An investigation on the automated chronic neuropathic pain detection using EEG signals. Cogn. Neurodynamics 2024, 18, 2193–2210. [Google Scholar] [CrossRef] [PubMed]
- Tasci, I.; Tasci, B.; Barua, P.D.; Dogan, S.; Tuncer, T.; Palmer, E.E.; Fujita, H.; Acharya, U.R. Epilepsy detection in 121 patient populations using hypercube pattern from EEG signals. Inf. Fusion 2023, 96, 252–268. [Google Scholar] [CrossRef]
- Lan, Z.; Liu, Y.; Sourina, O.; Wang, L.; Scherer, R.; Muller-Putz, G. SAFE: An EEG dataset for stable affective feature selection. Adv. Eng. Inf. 2020, 44, 101047. [Google Scholar] [CrossRef]
- Li, R.; Wang, L.; Suganthan, P.N.; Sourina, O. Sample-based data augmentation based on electroencephalogram intrinsic characteristics. IEEE J. Biomed. Health Inf. 2022, 26, 4996–5003. [Google Scholar] [CrossRef] [PubMed]
- Lan, Z.; Sourina, O.; Wang, L.; Scherer, R.; Muller-Putz, G.R. Domain adaptation techniques for EEG-based emotion recognition: A comparative study on two public datasets. IEEE Trans. Cogn. Dev. Syst. 2018, 11, 85–94. [Google Scholar] [CrossRef]
- Kumari, A.; Edla, D.R.; Reddy, R.R.; Jannu, S.; Vidyarthi, A.; Alkhayyat, A.; de Marin, M.S.G. EEG-based motor imagery channel selection and classification using hybrid optimization and two-tier deep learning. J. Neurosci. Methods 2024, 409, 110215. [Google Scholar] [CrossRef]
- Li, R.; Wang, L.; Sourina, O. Subject matching for cross-subject EEG-based recognition of driver states related to situation awareness. Methods 2022, 202, 136–143. [Google Scholar] [CrossRef]
- Li, R.; Hu, M.; Gao, R.; Wang, L.; Suganthan, P.; Sourina, O. TFormer: A time–frequency transformer with batch normalization for driver fatigue recognition. Adv. Eng. Inf. 2024, 62, 102575. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Subasi, A. LEDPatNet19: Automated emotion recognition model based on nonlinear LED pattern feature extraction function using EEG signals. Cogn. Neurodynamics 2022, 16, 779–790. [Google Scholar] [CrossRef] [PubMed]
- Özbeyaz, A.; Arıca, S. Familiar/unfamiliar face classification from EEG signals by utilizing pairwise distant channels and distinctive time interval. Signal Image Video Process. 2018, 12, 1181–1188. [Google Scholar] [CrossRef]
- Ghosh, L.; Dewan, D.; Chowdhury, A.; Konar, A. Exploration of face-perceptual ability by EEG induced deep learning algorithm. Biomed. Signal Process. Control 2021, 66, 102368. [Google Scholar] [CrossRef]
- Bablani, A.; Edla, D.R.; Kupilli, V.; Dharavath, R. Lie detection using fuzzy ensemble approach with novel defuzzification method for classification of EEG signals. IEEE Trans. Instrum. Meas. 2021, 70, 2509413. [Google Scholar] [CrossRef]
- Chang, W.; Wang, H.; Yan, G.; Liu, C. An EEG based familiar and unfamiliar person identification and classification system using feature extraction and directed functional brain network. Expert Sys. Appl. 2020, 158, 113448. [Google Scholar] [CrossRef]
- William, F.; Aygun, R. ConvoForest classification of new and familiar faces using EEG. In Proceedings of the 16th IEEE International Conference on Semantic Computing (ICSC), Virtual, 26–28 January 2022; pp. 274–279. [Google Scholar]
- Wiese, H.; Anderson, D.; Beierholm, U.; Tuttenberg, S.C.; Young, A.W.; Burton, A.M. Detecting a viewer’s familiarity with a face: Evidence from event-related brain potentials and classifier analyses. Psychophysiology 2022, 59, e13950. [Google Scholar] [CrossRef]
- Sutton, S.; Braren, M.; Zubin, J.; John, E.R. Evoked-potential correlates of stimulus uncertainty. Science 1965, 150, 1187–1188. [Google Scholar] [CrossRef]
- Gao, W.; Cao, B.; Shan, S.; Chen, X.; Zhou, D.; Zhang, X.; Zhao, D. The CAS-PEAL large-scale chinese face database and baseline evaluations. IEEE Trans. Syst. Man. Cybern. Pt. A Syst. Humans 2008, 38, 149–161. [Google Scholar]
- Muramatsu, D.; Makihara, Y.; Iwama, H.; Tanoue, T.; Yagi, Y. Gait verification system for supporting criminal investigation. In Proceedings of the 2nd IAPR Asian Conference on Pattern Recognition (ACPR), Okinawa, Japan, 5–8 November 2013; pp. 747–748. [Google Scholar]
- Zeng, Y.; Wu, Q.; Yang, K.; Tong, L.; Yan, B.; Shu, J.; Yao, D. EEG-based identity authentication framework using face rapid serial visual presentation with optimized channels. Sensors 2019, 19, 6. [Google Scholar] [CrossRef]
- Rossion, B.; Jacques, C. The N170: Understanding the time course of face perception in the human brain. In Oxford Handbook of Event-Related Potential Components; Oxford University Press: Oxford, UK, 2012; pp. 115–141. [Google Scholar]
- Duncan-Johnson, C.C.; Donchin, E. On quantifying surprise: The variation of event-related potentials with subjective probability. Psychophysiology 1977, 14, 456–467. [Google Scholar] [CrossRef]
- Rugg, M.D.; Curran, T. Event-related potentials and recognition memory. Trends Cogn. Sci. 2007, 11, 251–257. [Google Scholar] [CrossRef] [PubMed]
- Voss, J.L.; Lucas, H.D.; Paller, K.A. More than a feeling: Pervasive influences of memory without awareness of retrieval. Cogn. Neurosci. 2012, 3, 193–207. [Google Scholar] [CrossRef] [PubMed]
- Curran, T.; Hancock, J. The FN400 indexes familiarity-based recognition of faces. Neuroimage 2007, 36, 464–471. [Google Scholar] [CrossRef] [PubMed]
- Luck, S.J. An Introduction to the Event-Related Potential Technique; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Wiener, N. Generalized harmonic analysis. Acta Math. 1930, 55, 117–258. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 2003, 15, 70–73. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. The Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comp. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Northcutt, C.; Jiang, L.; Chuang, I. Confident learning: Estimating uncertainty in dataset labels. J. Artif. Intell. Res. 2021, 70, 1373–1411. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ozbeyaz, A.; Arica, S. Classification of EEG signals of familiar and unfamiliar face stimuli exploiting most discriminative channels. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 3342–3354. [Google Scholar] [CrossRef]





| Author | Subject | Stimulus | Repeat Time | Number of Samples | Dataset |
|---|---|---|---|---|---|
| Özbeyaz et al. [28] | 10 | 61 FFs, 59 UFs | 1 | 1200 | Public (without labels) |
| Ghosh et al. [29] | 38 | 10 FFs, 10 UFs | 200 | 152,000 | local |
| Williams et al. [18] | 13 | 8 FFs, 16 UFs, 8 objects | 5 | 2080 | local |
| Bablani et al. [30] | 10 | 10 face images | 60 | 6000 | local |
| Chang et al. [31] | 20 | 2 FFs, 6 UFs | / | / | local |
| William et al. [32] | 11 | 10 FFs, 10 UFs | 10 | 2200 | local |
| Wiese et al. [33] | 19 | 1 FF, 2 UFs | 50 | 2850 | public |
| Ours (FUFP) | 8 | 8 FFs, 32 UFs | 20 | 6400 | Public (with 6 labels) |
| Channel | 66 channels (64 EEG and 2 EOG) |
| Frequency | 1000 Hz |
| Subject | 8 subjects (4 males and 4 females) |
| Stimuli | 40 faces (8 FFs and 32 UFs) |
| Repeat time | 20 times |
| Number of samples | 6400 (8 × 40 × 20) |
| Sample duration | 3 s |
| Label | “label”: 0 is UF, 1 is FF “resp”: subject’s button response “acc”: accuracy “RT”: response time “sti”: stimulus “label 2”: 0 is UF, 1 is FF, 2 is the subject’s own face |
| Variable Name | Shape | Contents |
|---|---|---|
| label | 1 × 800 | 0 is UF, 1 is FF |
| resp | 1 × 800 | Subject’s button response; 1 is FF, 2 is UF |
| acc | 1 × 800 | Whether the subject responds correctly to the stimulus; 1 is correctness, 2 is error |
| RT | 1 × 800 | The response time of the subject recorded in milliseconds |
| sti | 1 × 800 | The stimuli numbered from “1” to “40”, where the first 8 stimuli represent FF and the remaining 32 stimuli represent UF |
| label 2 | 1 × 800 | 0 is UF, 1 is FF, 2 is the subject’s own face |
| data | 800 × 66 × 3000 | The EEG signal |
| Terms and Notions | Full Name | Explanation |
|---|---|---|
| EEG | Electroencephalogram | A technique for recording brain activity |
| EOG | Electrooculogram | A technique for recording electrical signals produced by eye movements and blinking |
| ERP | Event-related potential | A kind of electrophysiological response induced by specific stimuli or cognitive tasks |
| PSD | Power spectral density | A measure of the distribution of signal power across different frequencies |
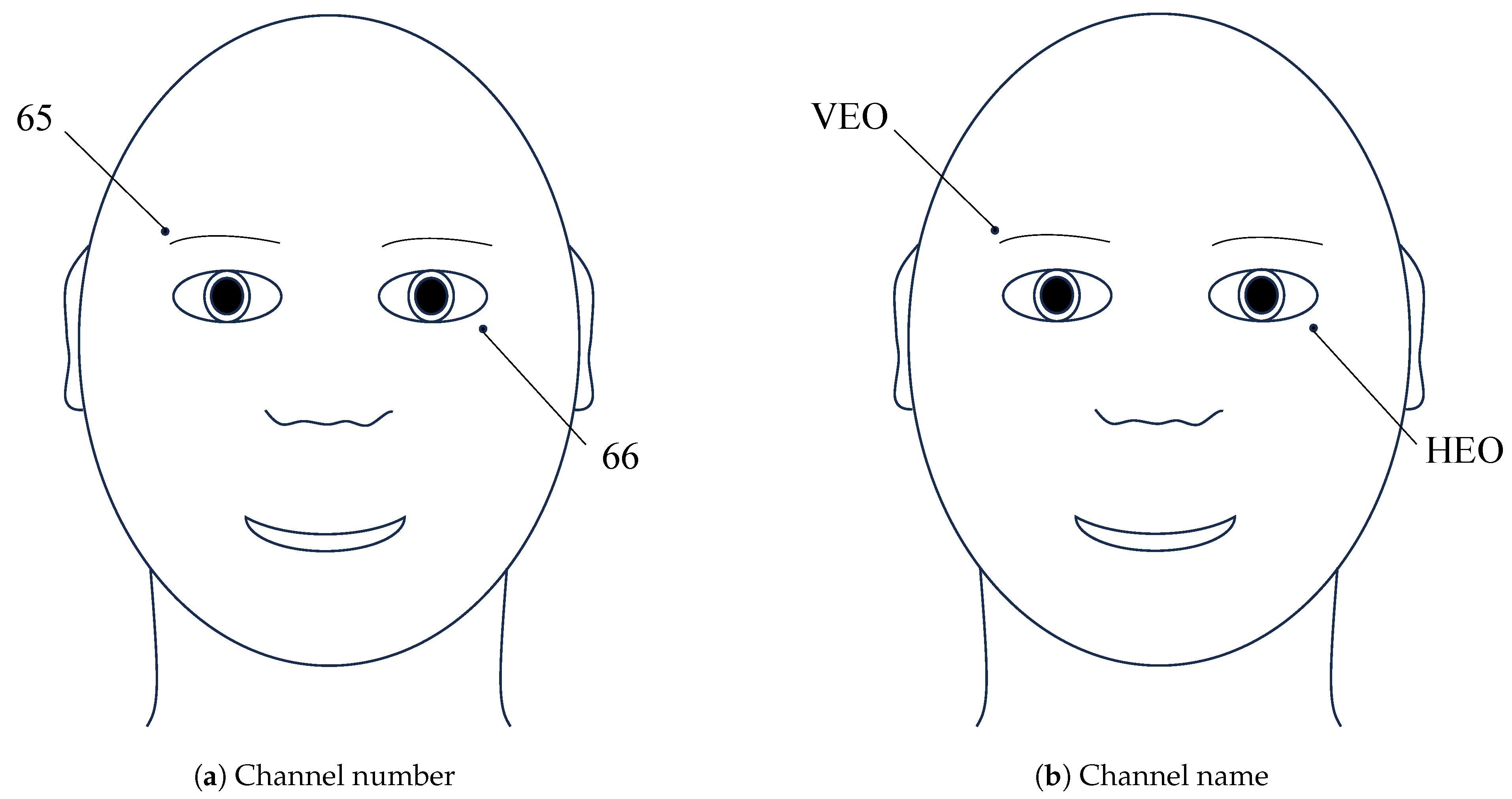
| VEO | Vertical electrooculogram | Electrical signals generated by eye movements in the vertical direction |
| HEO | Horizontal electrooculogram | Electrical signals generated by eye movements in the horizontal direction |
| epoch | Epoch | A data segment with a fixed time length extracted from continuous EEG signals |
| Method | Accuracy (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sub. 1 | Sub. 2 | Sub. 3 | Sub. 4 | Sub. 5 | Sub. 6 | Sub. 7 | Sub. 8 | FUFP | |
| RF | 75 | 65.63 | 77.03 | 64.38 | 70.78 | 72.19 | 66.09 | 70.63 | 77.03 |
| DT | 63.75 | 61.72 | 69.22 | 62.97 | 67.66 | 65.94 | 70.63 | 63.28 | 67.34 |
| LR | 63.75 | 64.84 | 60.94 | 63.28 | 62.19 | 62.19 | 63.59 | 62.03 | 64.21 |
| SVM | 76.25 | 71.88 | 76.25 | 67.19 | 71.25 | 71.72 | 76.41 | 74.53 | 77.00 |
| KNN | 77.5 | 70.31 | 78.13 | 74.38 | 73.28 | 73.59 | 78.13 | 76.09 | 79.84 |
| Avg. | 71.25 | 66.87 | 72.31 | 66.44 | 69.03 | 69.13 | 70.97 | 69.31 | 73.08 |
| Stimuli | Sample Size of Subject No. | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| FF | 151 | 26 | 160 | 48 | 156 | 128 | 159 | 159 |
| UF | 602 | 90 | 640 | 185 | 618 | 518 | 627 | 639 |
| Layer Name | Input Dimension | Output Dimension | Activation Function |
|---|---|---|---|
| ERP-Attention Layer | 3000 | 198 | / |
| Bi-LSTM Layer 1 | 198 | 128 | / |
| Bi-LSTM Layer 2 | 128 | 64 | / |
| Dense Layer 1 | 64 | 64 | ReLU |
| Dense Layer 2 | 64 | 2 | SoftMax |
| Method | Accuracy (%) | |
|---|---|---|
| FUFP Dataset | Wiese Dataset | |
| EBLM without ERP-attention layer | 78.44 | 78.25 |
| EBLM | 82.97 | 78.60 |
| EBLM + CL (baseline) | 92.66 | 85.61 |
| EBLM + CL (ours) | 94.59 | 86.67 |
| CL Strategy | Accuracy (%) |
|---|---|
| Prune all the examples in the off-diagonals of | 92.66 |
| Prune examples in the off-diagonals of | 93.44 |
| Change the labels of n × samples in , filter n × samples in | 89.38 |
| Filter n × samples in , change the labels of n × samples in | 94.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Z.; Zhou, M.; Lyu, Z.; Fang, Y. Electroencephalogram-Based Familiar and Unfamiliar Face Perception Classification Underlying Event-Related Potential Analysis and Confident Learning. Symmetry 2025, 17, 623. https://doi.org/10.3390/sym17040623
Zuo Z, Zhou M, Lyu Z, Fang Y. Electroencephalogram-Based Familiar and Unfamiliar Face Perception Classification Underlying Event-Related Potential Analysis and Confident Learning. Symmetry. 2025; 17(4):623. https://doi.org/10.3390/sym17040623
Chicago/Turabian StyleZuo, Zhihan, Menglu Zhou, Zhihe Lyu, and Yuchun Fang. 2025. "Electroencephalogram-Based Familiar and Unfamiliar Face Perception Classification Underlying Event-Related Potential Analysis and Confident Learning" Symmetry 17, no. 4: 623. https://doi.org/10.3390/sym17040623
APA StyleZuo, Z., Zhou, M., Lyu, Z., & Fang, Y. (2025). Electroencephalogram-Based Familiar and Unfamiliar Face Perception Classification Underlying Event-Related Potential Analysis and Confident Learning. Symmetry, 17(4), 623. https://doi.org/10.3390/sym17040623







