Abstract
This study addresses the dual challenges of complex road environments and diverse task-safety requirements in mobile-robot path planning by proposing an innovative method that integrates a dual-layer fuzzy control system with an improved genetic algorithm. Initially, an expert system-based dual-layer fuzzy control system is developed. The first layer translates complex road conditions and obstacles into road-safety levels, while the second layer combines these with task-safety levels to generate fitness weights for the genetic algorithm. Furthermore, road-safety factors are incorporated into the genetic algorithm’s fitness function to enhance safety considerations in path planning. The algorithm implementation incorporates Bernoulli chaotic mapping, Gaussian operators, and Symmetrical Sigmoid operators to optimize the selection, crossover, and mutation processes, significantly boosting the algorithm’s global search capability and efficiency. Experimental results indicate that the proposed method reduces path distance by up to 5.9% and decreases the number of turns by up to 85.7%, demonstrating superior universality and robustness across various comparative experiments. This research contributes to resolving the issues posed by complex road environments and varying task-safety requirements in mobile-robot path planning.
1. Introduction
In recent years, the rapid development of artificial-intelligence technology has brought new development opportunities for mobile robots, which are gradually adapting to increasingly complex tasks and forming a benign iterative development pattern from cutting-edge theoretical explorations, key technology breakthroughs to application scenario demonstrations [1,2,3]. Mobile robotic vehicles are widely used in typical scenarios such as intelligent manufacturing, material transportation, logistics sorting container ports, etc. They can replace manual labor to complete a large number of transportation operations, which effectively improves task efficiency and accuracy and reduces human errors and safety risks [4,5,6].
For mobile robotic vehicles, path-planning algorithms have been the focus of research. Path planning [7] is a path strategy that constitutes a sequence of points or curves at the start position and the end position, and its objective and constraint functions are nonlinear functions of the optimization variables, and it is mainly used to solve planning problems that can be topologized as a network of points and lines, and it is mainly used in the path planning of industrial robots [8], the trajectory planning of unmanned aerial vehicles [9], the traveler’s problem [10], and the path planning of underwater unmanned aerial vehicles [11]. After a long period of development, more and more path optimization algorithms have been proposed by scholars, and the common algorithms mainly include: the A* algorithm [12], the artificial potential field algorithm [13], the genetic algorithm [14], the particle swarm algorithm [15], the biologically inspired neural network algorithm [16,17,18], the gray wolf algorithm [19,20], the whale algorithm [21,22], the sparrow algorithm [23], the fuzzy control algorithm [24], These algorithms play a good role in optimizing the path planning for robots, but there are many more in real-world environments.
Fuzzy control is an intelligent control method based on fuzzy theory, fuzzy linguistic variables, and fuzzy logic reasoning, which solves the problems that are difficult to establish an accurate mathematical model by imitating human fuzzy reasoning and decision-making and adopts the fuzzy control method based on an expert system. Zhao et al. [25] establish a hierarchical interval Type-2 fuzzy control model, which is a better way to improve the robot path uncertainty in planning. Li et al. [26] proposed an interval Type-2 fuzzy control model in order to solve the complexity and uncertainty in robot local path planning. Dong et al. [27] used fuzzy control algorithms to adaptively control the path optimization parameters for the path planning of UAVs in complex environments. While fuzzy control and genetic algorithms have been extensively utilized in path planning, there is a scarcity of studies that closely integrate a dual-layer fuzzy control system with an improved genetic algorithm, particularly tailored for path planning of mobile robots in complex road and multi-task environments.
Facing the real working environment, mobile robotic vehicles need to consider a great number of environmental factors in the movement process. At present, some scholars have already considered the complex road environment when studying the path planning of mobile robots. Feng et al. [28] considered the relationship between complex road conditions and tasks and proposed a hybrid genetic algorithm, which effectively solved the task-safety problem of mobile robots in complex environments, but there was no categorization of different obstacles to be considered, and it was only simple to link the task with the environment, which was not comprehensive and in-depth enough. Wang et al. [29] proposed a motion framework for autonomous driving in complex urban environments, which effectively improved the efficiency and quality of autonomous driving in urban environments. Guo et al. [30] proposed a vehicle formation control method based on a road disturbance observer for rugged road environments, which effectively improved the stability of the vehicle’s horizontal and vertical formation. Li et al. [31] proposed an improved ant colony algorithm, which comprehensively solves the task-safety problem of mobile robots in complex environments. Wang et al. [32] proposed a prescribed performance adaptive robust control (PPARC) scheme for uncertain robotic manipulators and transformed the optimization of control parameters into an optimal design problem, for which they proposed a fuzzy-based cost function. Li et al. [33] proposed an integrated framework for decision-making and motion planning with oscillation-free capability. They enhanced computational efficiency by constructing a state transition model based on predictive uncertainty. Mohammadzadeh et al. [34] proposed a robust Type-3 (T3) fuzzy controller implementation for path-tracking tasks of autonomous vehicles under critical driving conditions and exogenous disturbances. By utilizing the Lyapunov stability theorem and Barbalat’s lemma to ensure stability, they constructed control inputs to enhance robustness, thereby eliminating error boundaries. Liang et al. [35] adopted a bootstrapped Deep Q-Network (DQN) to enhance deep exploration in reinforcement learning methods, achieving adaptive decision-making for autonomous vehicles. To enable surrounding human-driven vehicles (HDVs) to understand the behavior of autonomous vehicles (AVs) and prevent accidents caused by misunderstandings, they derived an Inverse Reinforcement Learning (IRL) method to learn the reward function of skilled drivers for lane-changing path planning. Yin et al. [36] addressed the issue of drone navigation in low-altitude environments by constructing autonomous drone navigation in a 3D environment, using adaptive control as a Markov decision process, and proposing a deep reinforcement learning algorithm. They also introduced a new velocity constraint loss function and added it to the original actor loss to improve the drone’s velocity control capability. Shi et al. [37] were inspired by the attachment and grasping abilities of Dynastes Hercules. By utilizing the microstructures of its feet to achieve effective contact and firm grip with surfaces, they proposed a bio-inspired robotic foot connection mechanism that enables climbing on trusses of different heights. Zou et al. [38] adopted a deep learning approach that combines particle swarm optimization (PSO) with long short-term memory (LSTM) networks to anticipate and mitigate trajectory tracking errors, thereby significantly improving the reliability and safety of task execution. Existing literature often delves deeply into specific tasks or environments when considering complex settings. However, the relationship between diversified tasks and the safety of complex road conditions is frequently overlooked. Presently, there is no effective method to address this issue.
To comprehensively address the safety challenges posed by complex road conditions and diverse obstacles encountered by mobile robots during the execution of multiple tasks, the system prioritizes the safest path for high-risk tasks and employs strict obstacle avoidance strategies to evade any potential risks. For tasks with moderate risk, while ensuring the safety of the path, the system focuses on the smoothness of the path to avoid damage to items due to severe vibrations and collisions. As for low-risk tasks, the system, while ensuring basic safety, prioritizes paths with higher efficiency to optimize the overall task execution time and resource utilization. Through this hierarchical path-planning strategy, the method proposed in this paper can flexibly adjust the path-planning scheme according to the specific requirements of the task and environmental conditions, thereby ensuring that mobile robots can efficiently and safely complete multi-task execution in complex road environments. This paper innovatively proposes a multi-task path-planning method that integrates dual-layer fuzzy control with an improved genetic algorithm. The main contributions of this method are clearly reflected in the following three aspects:
(1) This study pioneers the integration of a dual-layer fuzzy control system with an improved genetic algorithm for mobile-robot path planning. The first layer of fuzzy logic processes complex road environments, including road conditions and obstacles, into quantifiable safety levels. The second layer incorporates the safety requirements of tasks to generate fitness weights for the genetic algorithm. This design effectively merges the complexities of road environments with the safety demands of tasks.
(2) This paper enhances path-planning safety by incorporating road-safety factors into the fitness function model of the genetic algorithm. This innovative method enables the algorithm to thoroughly consider road-safety conditions during the search for the optimal path, resulting in safer and more reliable routes.
(3) This study employs Bernoulli chaotic mapping, Gaussian operators, and Symmetrical Sigmoid operators to optimize the selection, crossover, and mutation processes of the genetic algorithm. These enhancements not only improve the algorithm’s global search capability but also significantly boost its execution efficiency, resulting in a faster and more effective path-planning process.
The structure of the remaining sections is as follows: Section 2 establishes the dual-layer fuzzy control system model. Section 3 discusses improvements to the genetic algorithm. Section 4 is the Robot Motion Model. Section 5 integrates the dual-layer fuzzy control system with the improved genetic algorithm. Section 6 presents experiments and analysis. Section 7 offers conclusions and future outlook.
2. A Dual Layered Fuzzy Control System Based on Expert Systems
Because the fuzzy logic method can well simulate human control strategies and experience, it has good robustness and adaptability to complex and unknown environments. Therefore, many scholars use fuzzy control methods to plan the path of robots, and have achieved good results. However, the number of fuzzy rules for a single fuzzy controller increases exponentially with the increase of fuzzy inputs, and when the number of input variables increases, there will be a problem of “fuzzy rule explosion”, which will cause the controller to respond very slowly. In 2004, Emara and Elshafei [39] jointly proposed and derived a hierarchical adaptive fuzzy algorithm, which effectively solved the regular explosion phenomenon of the traditional single-layer fuzzy control system. The hierarchical fuzzy control system can guide the robot to carry out more efficient complex path planning and realize the safe path planning of multi-task mobile robots in complex environments. In this paper, a two-layer fuzzy control system based on an expert system is established. The first layer is the road-safety fuzzy control system, which outputs the road-safety level by inputting complex road conditions and complex obstacles, which mainly processes the environmental information obtained by the sensor, describes the relationship between the mobile robot and the road environment, and determines the safety degree of the mobile robot moving on the complex road. The second layer is the task-safety fuzzy control system, which outputs the fitness weight coefficient level of the genetic algorithm by inputting the road-safety level and the task level and dynamically adjusts the fitness weight of the genetic algorithm according to the safety level of the task and the road-safety level output by the first layer.
2.1. Road-Safety Fuzzy Control System
The first layer of fuzzy control is a road-safety fuzzy control system for mobile robots. Due to the lack of understanding of complex road environments when conducting path-planning research on mobile robots in real environments, they are unable to make intelligent decisions based on environmental characteristics. Input different road conditions and obstacles into the fuzzy controller, use the knowledge base of the expert system to perform fuzzy discrimination on the input of the fuzzy controller, and output corresponding road-safety levels based on different environmental characteristics.
The actual road conditions are complex, including asphalt, cement, soil, gravel, uphill, downhill, and sloping roads, as well as lawn, gravel, standing water, ice and snow, and potholes. The actual obstacles are also diverse, including large and immovable buildings, streetlights, trees, movable animals, people, and vehicles, as well as small and immovable branches, small stones, small plastic objects, and other obstacles. Different obstacles and road conditions can have different impacts on the driving safety of robots. For the evaluation criteria of environmental characteristics, we comprehensively analyze based on the following four factors: 1. The shaking size factor of mobile robots; 2. The attachment size factor of mobile robots; 3. Possible collision factors of mobile robots; 4. Possible factors for mobile-robot rollover. Therefore, we first established a small knowledge base of environmental feature categories, allowing the expert system to have rich knowledge and experience. Then, we imitated the thinking of experts to design fuzzy control rules. Finally, by identifying and classifying environmental features, we gave the road-safety level. The output of the first layer of fuzzy control will serve as the input for the second layer of task safety-level fuzzy control. Therefore, the level of road safety directly determines the driving safety of the mobile robot. The fuzzy control process for road safety of mobile robots is shown in Figure 1.
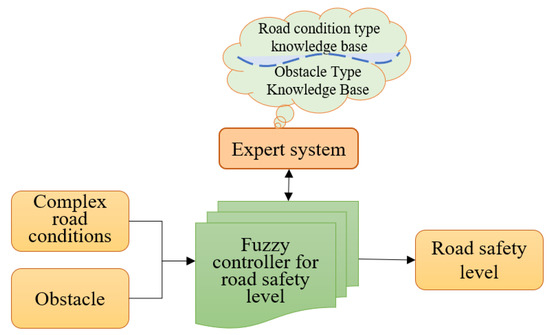
Figure 1.
Fuzzy control process for road safety.
For the definition of road grades, the higher the safety level of a road, the drier, smoother, and more wear-resistant its surface tends to be, and the more comfortable the driving experience. A dry and smooth asphalt road is the safest road, with a road condition level of I; Asphalt roads and cement roads with a small amount of water accumulation, with a road condition level of II; Roads with small slopes and potholes, with a road condition level of III; There are many roads with accumulated water, a small amount of snow, many potholes, large slopes, sand and stones, good soil, lawns, etc., and the road condition level is IV; Other dangerous roads with high water accumulation, snow accumulation, icing, many potholes, steep slopes, poor soil, etc., have a road condition level of V. Other very dangerous roads, such as steep slopes, stairs, cliffs, etc., are impassable obstacles that we consider useless roads to walk on. We input road-type knowledge in advance for the system to learn and form a road-condition-type knowledge base in the expert system.
For the definition of obstacle level, we believe that obstacles with smaller, softer, smaller areas and less damage have a higher safety level. Smaller leaves are the safest obstacles, with an obstacle level of I; Obstacles with a large accumulation of leaves, with an obstacle level of II; Obstacles such as smaller branches, smaller gravel, smaller movable animals, and smaller plastic objects are classified as level IV obstacles; Dangerous obstacles such as moving pedestrians, large movable animals, moving vehicles, large branches, and large debris are classified as level V. Other very dangerous obstacles, such as trees, buildings, large stones, immovable vehicles, and other large obstacles that cannot be passed through, are considered as having no roads to walk through. We input obstacle-type knowledge in advance for the system to learn and form an obstacle-type knowledge base in the expert system.
For the definition of road-safety level, we believe that road-safety level is determined by complex road environmental factors, which are mainly influenced by complex road conditions and obstacles, i.e., the road-safety level is determined by both road condition level and obstacle level. When the road condition level and obstacle level are different, we consider the more dangerous level to be the road-safety level. For example, when the road condition level is II, and the obstacle level is III, the road-safety level is III. The determination method of road-safety level can be regarded as the same as the fuzzy control rules for road-safety.
The road-safety fuzzy controller is a dual input single output system with a range of input and output changes of [0, 1]. The input variables are complex road conditions and obstacles, described using language variables such as Road Condition I, Road Condition II, Road Condition III, Road Condition IV, and Road Condition V, and language variables such as Obstacle I, Obstacle II, Obstacle III, Obstacle IV, and Obstacle V. The output variable is the road-safety level, which can be described by language variables as: road-safety level I, road-safety level II, road-safety level III, road-safety level IV, and road-safety level V.
Commonly used affiliation functions include Gaussian function and trigonometric function, etc. In this paper, the form of trigonometric function is used, and the affiliation function of input and output variables in the fuzzy control system for road safety is shown in Figure 2.
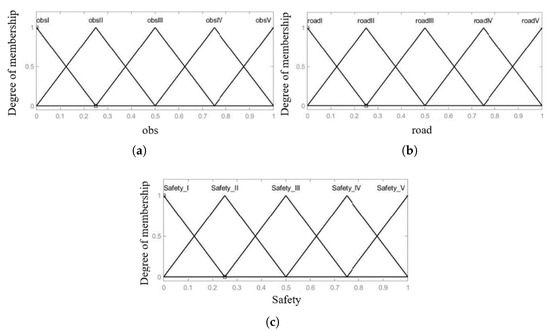
Figure 2.
The membership function diagram of inputs and outputs in the fuzzy control system for road safety are listed as: (a) Obstacle level membership function diagram. (b) Road level membership function diagram. (c) Road-safety level membership function diagram.
Since there are 2 inputs to the road-safety fuzzy control system and the number of fuzzy gradations for each input is 5, the number of fuzzy control rules at the first level is 25. The road-safety fuzzy control rules are shown in Table 1.

Table 1.
Fuzzy control rules for road safety.
2.2. Task-Safety Fuzzy Control System
In the proposed dual-layer fuzzy control system, the interaction between the road-safety fuzzy control system and the task-safety fuzzy control system is crucial for achieving path-planning safety. The road-safety level output from the first layer is quantified into Grades I to V. This quantified result serves as one of the inputs for the second layer, where it is combined with the task safety level to form the input variables.
The second layer of fuzzy control is a task-safety fuzzy controller for mobile robots. Due to the fact that mobile robots can perform various tasks, the safety level of different tasks is also different. Therefore, we need to consider the safety of different road environment characteristics based on the safety of the tasks. Firstly, we select road environments that meet safety conditions based on different task-safety levels. Then, we input the safety levels of different tasks and road-safety levels that meet the conditions into the fuzzy controller. Finally, we use the knowledge base of the expert system to perform fuzzy discrimination on the input of the fuzzy controller and output corresponding fitness weight coefficients based on different task-safety levels.
The actual tasks have diversity, which may involve transporting different items such as fruits, grains, fertilizers, ammunition, chemical reagents, glass products, etc., or performing different tasks such as handling, inspection, sweeping, etc. For different tasks, the safety level we need to consider is also different. For the evaluation criteria of task safety level, we comprehensively analyze three factors: 1. Factors affecting human health; 2. Health factors that affect the environment; 3. One’s own risk factors. Therefore, we first establish a small knowledge base for task-safety levels, allowing the expert system to have rich knowledge and experience. Then, we design fuzzy control rules by imitating the thinking of experts. Finally, by identifying task-safety levels and road-safety levels, we provide fitness weight coefficients. The fuzzy control process for mobile-robot task safety is shown in Figure 3.
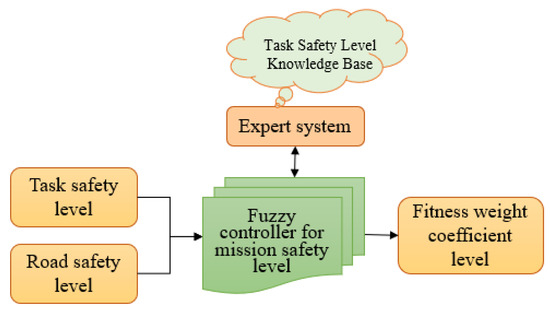
Figure 3.
Task security fuzzy control process.
For the definition of task safety level, we believe that the higher the impact of a task on human health, the greater the impact on the environment, and the greater the danger of transporting goods themselves, the higher the task safety level. The most dangerous task is to transport toxic and harmful chemical reagents, flammable and explosive materials such as gunpowder, and the safety level of the task is level I; Transport of fragile items, precision equipment, and other sub-hazardous tasks, with a task safety level of II; The general hazardous tasks of transporting takeout, harmless chemicals, express delivery, general equipment, etc. have a safety level of III; Perform outdoor inspections, transport less harmless and non-safety-required items, and other less hazardous tasks with a safety level of IV; The mobile robot performs a non-hazardous task of quickly and shortest distance reaching the target point without load, with a task safety level of V. We input task type knowledge in advance for the system to learn, and form a task-safety-level knowledge base in the expert system.
For the definition of the fitness weight level of genetic algorithms, we believe that the fitness weight level is determined by both the road-safety level and the task-safety level. Mobile robots first screen the road-safety level that meets the safety conditions based on the level of task safety, as shown in Table 2. After screening the road-safety level, when the task safety level is different from the road-safety level, we consider the road-safety level as the genetic algorithm fitness weight level. For example, when the task safety level is III and the road-safety level is II, the genetic algorithm fitness weight level is II. The determination of the fitness weight level of the genetic algorithm can be regarded as the same as the task-safety fuzzy control rules.

Table 2.
Relationship between mission safety level and roadway safety level selection.
The task-safety fuzzy controller is a dual input single output system with a range of input and output variations of [0, 1]. The input variables are task level and road-safety level, described using language variables: task safety level I, task safety level II, task safety level III, task safety level IV, task safety level V, and language variables: road-safety level I, road-safety level II, road-safety level III, road-safety level IV, and road-safety level V. The output variable is the fitness weight coefficient level, which can be described as fitness weight level I, fitness weight level II, fitness weight level III, fitness weight level IV, and fitness weight level V.
In this paper, the form of trigonometric function is used, and the affiliation function of the input and output variables in the fuzzy control system for task safety is shown in Figure 4.
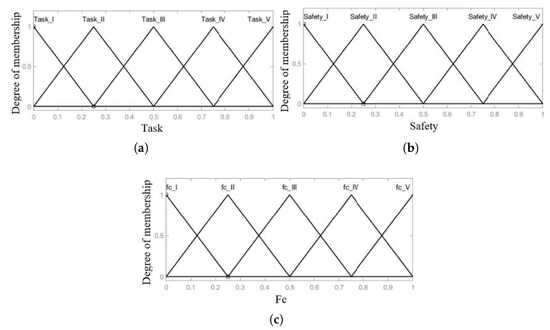
Figure 4.
The membership function diagram of inputs and outputs in the fuzzy control system for road safety are listed as: (a) Task-safety-level membership function diagram. (b) Road-safety level membership function diagram. (c) Fitness weight level membership function diagram.
Since there are 2 inputs to the task-safety fuzzy control system and the number of fuzzy gradations for each input is 5, the number of fuzzy control rules at the second level is 25. The mission safety fuzzy control rules are shown in Table 3.

Table 3.
Fuzzy control rules for task safety.
2.3. The Dual-Layer Fuzzy Control System in This Article
In order to consider the relationship between complex road conditions, complex obstacles, and different tasks at the same time, this paper innovatively proposes a two-layer fuzzy control system based on an expert system, which effectively combines the complex road environment with the safety level of the task, and its main working principle is shown in Figure 5.
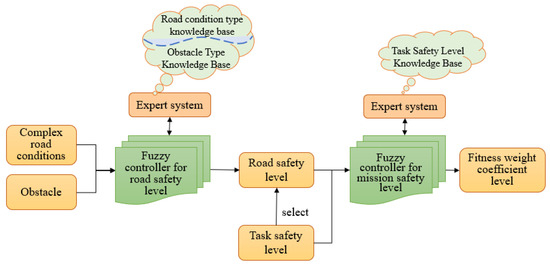
Figure 5.
Working principle of dual-layer fuzzy control system.
3. Improving the Genetic Algorithm
As early as the 1970s, John Holland was the first to propose genetic algorithms, whose main idea is to find the optimal solution to the search by simulating biological evolution. The population is all the solutions of the search process, and the individuals are the separate solutions of the search process. Each solution is a chromosome, and the initial chromosome formation is formed by generating consecutive feasible paths through random numbers, as shown in Figure 6 and Figure 7.
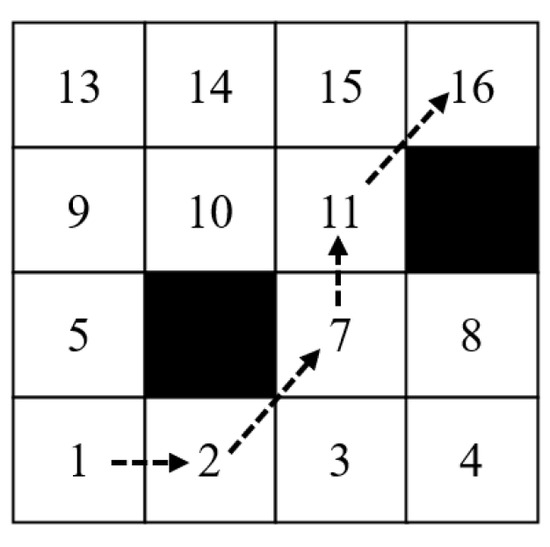
Figure 6.
Raster maps.
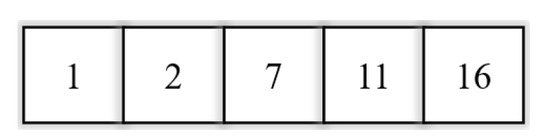
Figure 7.
Continuously passable paths.
Genetic algorithm has a great dependence on selection, crossover and mutation operations, and its parameter selection seriously affects the effect of genetic algorithm. In order to overcome the problem that traditional GA is easy to fall into local extremes prematurely, this paper proposes an improved adaptive genetic algorithm (IGA). The selection operation is optimized using the Bernoulli chaotic mapping operator, the adaptive crossover operation is optimized using the Gaussian operator, and the adaptive mutation operation is optimized using the Symmetrical Sigmoid operator.
3.1. Improving the Fitness Function
The fitness function plays a crucial role in the final outcome of genetic algorithms, determining the evolutionary direction of the population, and is therefore also known as the objective function. Currently, in most GA calculations, the objective function only includes path distance and turning energy consumption without considering road environmental safety. Therefore, we introduce road environmental safety factors into the fitness function of genetic algorithms. Finally, a new multi-objective optimization model is established as the fitness function of the genetic algorithm, and Formula (1) is obtained:
In Equation (1), , , and are the path distance, turning energy consumption, and road environmental safety functions of the k-th optimized path, respectively. , , and are the weight values of the corresponding objective function.
At present, the path distance and turning energy consumption of the genetic algorithm fitness function are calculated using Formulas (2)–(5).
In Equations (2)–(5), (, ) and (, ) represent the positions of the previous grid and the next grid, respectively; is the square of the distance between adjacent three grid positions; ti is the penalty value size of the current grid; T is the size of the penalty value for the path.
For road environmental safety factors, we mainly assign subjective values based on the level of road conditions and the size of obstacles and distinguish them by assigning different values. The road environmental safety function is calculated using Formulas (6)–(8).
In Equations (6)–(8), , assigns values to different obstacles and road conditions in complex road environments, , , They are the weight value of obstacle property rights, road condition weight value, and road environmental safety correction value, where is a nonzero positive number.
In this paper, fuzzy weights are generated by the task-safety fuzzy controller and quantified into fitness weight coefficient grades (Grade I to Grade V). These grades are then mapped to specific numerical values to be integrated into the fitness function of the genetic algorithm. By doing so, the fuzzy weights are effectively incorporated into the fitness function, enabling the genetic algorithm to comprehensively consider the safety of the road environment and the specific requirements of the task during the path selection and optimization process, thereby achieving safer and more efficient path planning.
3.2. Select Operation
In order to achieve better optimization results, Bernoulli chaotic mapping is introduced into a genetic algorithm, which utilizes the randomness, traversal, and nonlinearity of chaotic operations to improve the selection operator. Introduce the Bernoulli chaotic mapping formula in the selection operation, such as Formulas (9) and (10):
In Equations (9) and (10), To control the parameters, N represents the number of populations, represents the random number of Bernoulli chaotic maps generated after the t-th iteration, represents the number of individuals in the selection operation population, and int() is the rounding function. The initial value of Bernoulli chaotic mapping is set to a uniform random number within the (0, 1) interval.
The genetic algorithm uses binary random tournaments for selection operations, and the specific steps are as follows:
Step 1: Generate 2 random numbers based on the Bernoulli chaotic mapping formula, select 2 individuals with corresponding numbers from the population, compare their fitness, and pass on the individual with the highest fitness to the next generation population;
Step 2: Repeat step 1 to obtain N individuals from the next generation population.
3.3. Adaptive Crossover Operations
The crossover operation of the genetic algorithm is to exchange partial genes of two parent individuals to generate new individuals. The size of crossover probability has a significant impact on the evolutionary speed of a population. A higher crossover probability in the early stages helps accelerate population evolution, while a lower crossover probability in the later stages helps protect excellent individual genes. Therefore, in the process of evolution, we need to dynamically and adaptively adjust the crossover probability. This article first calculates individual fitness through Formula (11) and then uses the Gaussian operator to adaptively and dynamically adjust the crossover probability.
In Equations (11) and (12), and are the minimum and maximum values of crossover probability, and are the maximum and average values of fitness, and t and T are the current and final values of evolution, respectively.
3.4. Adaptive Mutation Operation
The mutation operation of a genetic algorithm is to mutate some genes of an individual, mainly through deletion, exchange, mutation, and other means to generate new gene fragments, thereby forming a new individual. The size of mutation probability has a significant impact on population richness. In the early stage, there are significant differences in the population, and adopting a smaller mutation probability can help accelerate population evolution. In the later stage, the population difference is small, and it is easy to fall into local optima. Using a higher mutation probability can help increase the richness of the population and enhance the ability to escape from local optima. Therefore, in the process of evolution, we need to dynamically and adaptively adjust the mutation probability. This article first calculates individual fitness through Formula (13) and then uses the Symmetrical Sigmoid operator to adaptively and dynamically adjust the mutation probability.
In Equations (13) and (14), and are the minimum and maximum values of the mutation probability, respectively.
3.5. The Improved Genetic Algorithm in This Article
By adding the Bernoulli chaotic mapping operator, Gaussian operator, and Symmetrical Sigmoid operator to the selection, adaptive crossover, and adaptive mutation operations, and taking environmental safety factors, path distance, and turning energy consumption as the fitness of the genetic algorithm, the improved genetic algorithm in this paper is finally obtained. The working principle is shown in Figure 8.
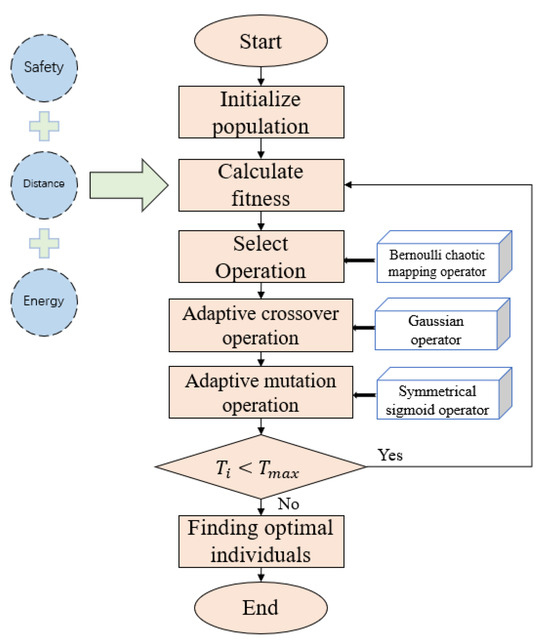
Figure 8.
Improving the working principle of genetic algorithms.
4. Kinematic Model of the Robot
Assuming that the robot’s trajectory can be decomposed into multiple time slices, within each time slice , the robot can be approximated as moving at a constant velocity in a straight line. In this case, the kinematic model of the robot (Figure 9) can be expressed as:
where , , and represent the position of the robot on the x-axis and y-axis and its orientation at time t, respectively; and represent the velocity and angular velocity of the robot at time t, respectively.
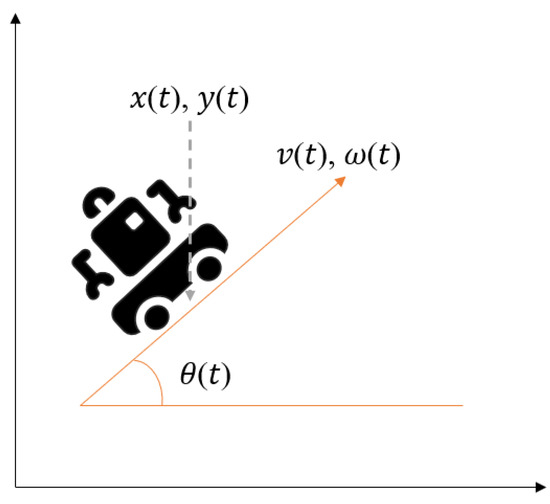
Figure 9.
Kinematic model of the robot.
5. Methodology
To simultaneously consider the relationships between complex road conditions, intricate obstacles, and various tasks, this paper proposes an innovative method that combines a dual-layer fuzzy control system with an improved genetic algorithm to address the path-planning problem for mobile robots in complex road environments and under diverse task-safety requirements. Firstly, by constructing a dual-layer fuzzy control system based on an expert system, we achieve an effective assessment of complex road conditions and obstacles. In this system, the first layer of the fuzzy control system categorizes complex road conditions and obstacles and translates them into road-safety levels. The second layer then combines these with task-safety levels to dynamically adjust the fitness weights of the genetic algorithm, thereby optimizing the weights of the fuzzy rules. This method not only effectively avoids the “fuzzy rule explosion” problem but also ensures that the path-planning process can be flexibly adjusted according to different task requirements and environmental conditions, significantly enhancing the safety and reliability of the path.
The dual-layer fuzzy controller dynamically adjusts the weight coefficients of the improved genetic algorithm’s fitness based on different environmental characteristics and task levels, effectively integrating the safety levels of the complex road environment with those of the tasks. This integration fully leverages the fuzzy inference capability of fuzzy control and the global search capability of the genetic algorithm. The improvements to the genetic algorithm not only enhance its global search capability but also significantly increase the algorithm’s execution efficiency, making the path-planning process faster and more effective. This method achieves intelligent path planning for multi-task mobile robots in complex road environments. The working principle of the proposed method is illustrated in Figure 10.
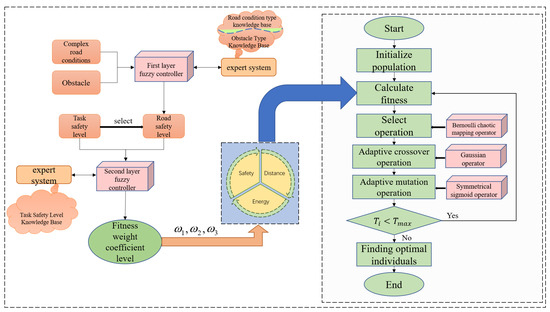
Figure 10.
Method schematic diagram in this article.
6. Performance Analysis
In order to verify the performance of the Improved Genetic Algorithm (IGA) proposed in this paper, it is compared with the traditional Genetic Algorithm (GA), Hybrid Adaptive Genetic Algorithm (HAGA), Ref. [28] Enhanced Genetic Algorithm (EGA), Ref. [40] and Ant Colony Algorithm (ACO), with a raster dimension of 20 × 20 and the number of obstacles of 48. The parameter settings are shown in Table 4.

Table 4.
Parameter settings for different algorithms.
In Table 4, N represents the population, T represents the number of iterations, pc represents the crossover probability, pm represents the mutation probability, pn represents the domain search probability, and Alpha, Beta, and Rho represent the pheromone importance, heuristic factor importance, and pheromone coefficient of the ant colony algorithm, respectively.
The path optimization effects of different algorithms are shown in Figure 11.
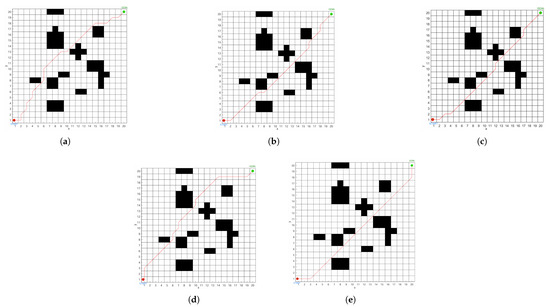
Figure 11.
Different algorithms, they are listed as: (a) GA Planning results. (b) HAGA Planning results. (c) EGA Planning results. (d) ACO Planning results. (e) IGA Planning results.

Table 5.
Different algorithm path planning data.
In Figure 11 and Table 5, this article compares GA, HAGA, EGA, ACO, and IGA and finds that under the same conditions, the number of turns for IGA is 2, which is a maximum reduction of 85.7% compared to other algorithms. The path length of IGA is 28.042, which is the highest improvement of 5.9% compared to the comparison algorithm. The runtime of IGA is 1.52, which is the highest improvement of 25% compared to the comparison algorithm. We found that the IGA proposed in this article has significant advantages in path planning, effectively improving the global and local optimization capabilities of mobile robots.
In order to make the results fair and objective while avoiding accidental errors and verifying the robustness of the algorithm, we conducted 15 repeated experiments and obtained the results in Table 6.

Table 6.
Analysis of data from different algorithms.
In Table 6, after running different algorithms 15 times, we analyzed the optimized path distance data. By comparing and analyzing the mean, standard error, IQR, and coefficient of variation (CV), we found that the IGA optimization results in this paper were significantly better than those of GA, HAGA, EGA, and ACO, and at the same time, the standard error, IQR, and CV of the algorithms in this paper are kept at a lower level, which effectively proves that this paper’s algorithms have a better optimization ability and robustness.
6.1. Analysis of Different Experimental Environments
In order to verify the robustness and universality of the algorithm, this paper conducted experiments on maps with different numbers of obstacles, different grid dimensions, and dynamic environments. The experiment mainly involves comparing a few obstacles with multiple obstacles, comparing 10 × 10 and 50 × 50 grid dimensions, and comparing dynamic obstacles before and after movement. The results are shown in Figure 12, Figure 13 and Figure 14.
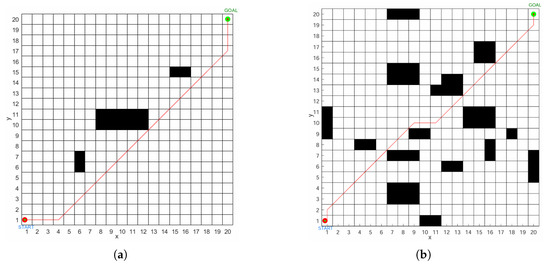
Figure 12.
Comparison of the number of obstacles, they are listed as: (a) Less obstacle situation. (b) Multiple obstacle situations.
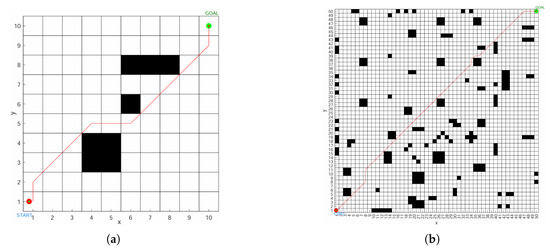
Figure 13.
Comparison of different grid dimensions, they are listed as: (a) 10 × 10 Dimension. (b) 50 × 50 Dimension.
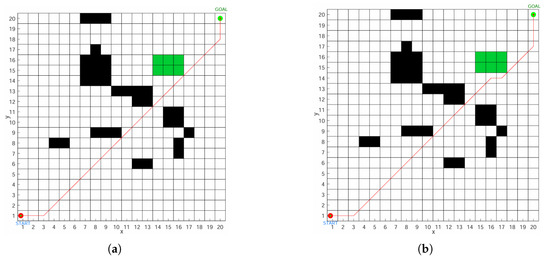
Figure 14.
Comparison before and after obstacle movement, they are listed as: (a) Before moving obstacles. (b) After the obstacle moves.
Through Figure 12, Figure 13 and Figure 14, we can observe that the algorithm proposed in this paper exhibits good path optimization performance in comparative experiments with different numbers of obstacles, different grid dimensions, and dynamic obstacles. The short path distance and few turns effectively demonstrate its good robustness and wide adaptability.
6.2. Analysis of Different Task Situations
In order to verify the universality and reliability of the algorithm, in this paper, five tasks with different safety levels are experimented in the same complex environment, using different colors to simulate different road environments, and different task-safety levels need to choose the road that meets the safety conditions. The security level is from high to low, where level I is the highest security level and level V is the lowest security level, and the path-finding results obtained are shown in Figure 15.
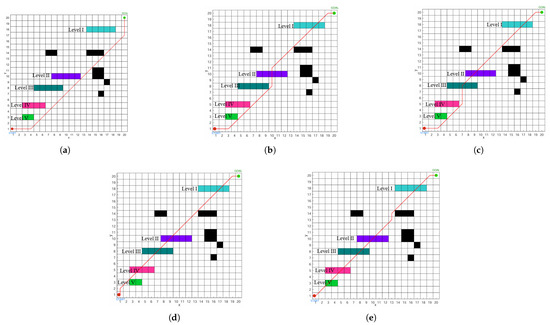
Figure 15.
Different task security levels are listed as: (a) Task Safety Level I. (b) Task Safety Level II. (c) Task Safety Level III. (d) Task Safety Level IV. (e) Task Safety Level V.
As shown in Figure 15, we observe that tasks with five different safety levels exhibit excellent path optimization under the same complex environmental conditions. The mobile robot intelligently plans optimal paths that meet the respective road-safety conditions based on the task’s safety level. Specifically, higher task-safety levels result in safer paths, and these paths traverse roads with corresponding or higher safety levels. Notably, roads with higher safety levels can also accommodate tasks with lower safety levels, enhancing the system’s flexibility. Consequently, the mobile robot efficiently and safely completes path-planning tasks in complex and variable road environments, demonstrating its wide applicability and high reliability.
6.3. Real Machine Testing
Based on the relevant research conducted earlier, the improved algorithm has been successfully simulated in Matlab 2022b and has shown certain advantages compared to other algorithms. In order to verify the effectiveness and adaptability of the proposed algorithm in real-world scenarios, the algorithm was applied to a mobile robot developed by our team, as shown in Figure 16. The mobile robot uses the RPLIDAR A3 laser scanner to obtain 2D point cloud data, integrates IMU and odometry data, and finally constructs the real-time scene through the Gmapping algorithm.

Figure 16.
Mobile robot.
The experimental environment was selected as a corridor area with a length of 12 m and a width of 2.2 m for simulation experiments. The vehicle was placed at the yellow starting point, with unevenly distributed obstacles of varying sizes, and a green target position was set. The vehicle was then started to perform path planning, and the experiment was repeated 20 times (Figure 17).

Figure 17.
Experimental environment.
As shown in the results of Table 7, under different numbers of randomly distributed obstacles, the mobile robot using the algorithm proposed in this paper can safely, collision-free, and effectively reach the target position.

Table 7.
Path results under different numbers of obstacles.
7. Conclusions
This paper introduces an innovative method that combines a dual-layer fuzzy control system with an improved genetic algorithm to address the path-planning challenges of mobile robots in complex road environments with diverse safety requirements. The dual-layer fuzzy control system, built on an expert system, enables efficient evaluation of complex road conditions and obstacles. It dynamically adjusts the genetic algorithm’s fitness weights based on task-safety levels, enhancing both the practicality and safety of the planned paths. Furthermore, by incorporating road-safety factors into the genetic algorithm’s fitness function model, the method significantly improves safety considerations in the path-planning process.
In our algorithm implementation, we utilized Bernoulli chaotic mapping, Gaussian operators, and Symmetrical Sigmoid operators as optimization measures. These enhancements significantly improved the global search ability and convergence speed of the genetic algorithm, ensuring efficient and stable operation. Experimental results indicate that the proposed method can reduce path distance by up to 5.9% and decrease the number of turns by as much as 85.7%. Additionally, it exhibits exceptional universality and robustness across various comparative experiments.
To further validate the algorithm’s universality and reliability, we conducted experiments on tasks with five different safety levels in the same complex environment, using different colors to simulate various road conditions. The experimental results indicate that the mobile robot can find optimal paths that meet road-safety conditions according to the varying safety levels of the tasks. Higher task-safety levels correspond to safer paths, higher road-safety ratings, shorter path lengths, and fewer turns. These results convincingly demonstrate the algorithm’s strong universality and reliability.
However, due to time constraints, this study has not yet addressed the spatial state of obstacles. In future work, we will further consider the spatial relationship between obstacles and the robot, conduct in-depth research in a three-dimensional environment, and introduce a deep reinforcement learning adaptive mechanism, enabling the fuzzy controller to dynamically adjust rules based on real-time data, thereby reducing reliance on predefined rules. This will further improve the algorithm. This research introduces new ideas and methods to the field of mobile-robot path planning and provides strong support for balancing complex road environments with varying task-safety requirements. It is significant for enhancing the safety of multi-task mobile-robot operations in complex environments.
Author Contributions
Conceptualization, Y.T. and T.F.; formal analysis, C.S.; funding acquisition, C.S. and J.L.; methodology, Y.T. and T.F.; resources, S.X.Y.; supervision, H.Z.; writing—original draft, Y.T. and T.F.; writing—review and editing, C.S., J.L., S.X.Y. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Sichuan Provincial Science and Technology Plan Project (Grant No. 2022NZZJ0036).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Armanini, C.; Boyer, F.; Mathew, A.T.; Duriez, C.; Renda, F. Soft Robots Modeling: A Structured Overview. IEEE Trans. Robot. 2023, 39, 1728–1748. [Google Scholar] [CrossRef]
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum Robots: An Overview. Adv. Intell. Syst. 2023, 5, 2200367. [Google Scholar] [CrossRef]
- Heidari, A.; Navimipour, N.J.; Unal, M.; Zhang, G.D. Machine Learning Applications in Internet-of-Drones: Systematic Review, Recent Deployments, and Open Issues. ACM Comput. Surv. 2023, 55, 247. [Google Scholar] [CrossRef]
- Gao, H.; Feng, J.H.; Xiao, Y.; Zhang, B.; Wang, W.D. A UAV-Assisted Multi-Task Allocation Method for Mobile Crowd Sensing. IEEE Trans. Mob. Comput. 2024, 22, 3790–3804. [Google Scholar] [CrossRef]
- Liu, L.X.; Wang, X.; Yang, X.; Liu, H.J.; Li, J.P.; Wang, P.F. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Wan, S.H.; Gu, Z.H.; Ni, Q. Cognitive computing and wireless communications on the edge for healthcare service robots. Adv. Intell. Syst. 2020, 149, 99–106. [Google Scholar] [CrossRef]
- Patle, B.K.; Babu, L.G.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- Sun, Y.W.; Jia, J.J.; Xu, J.T.; Chen, M.S.; Niu, J.B. Path, feedrate and trajectory planning for free-form surface machining: A state-of-the-art review. Chin. J. Aeronaut. 2022, 35, 12–29. [Google Scholar] [CrossRef]
- Chen, J.C.; Ling, F.Y.; Zhang, Y.; You, T.; Liu, Y.F.; Du, X.Y. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system. Swarm Evol. Comput. 2022, 69, 101005. [Google Scholar] [CrossRef]
- Datsko, D.; Nekovar, F.; Penica, R.; Saska, M. Energy-Aware Multi-UAV Coverage Mission Planning with Optimal Speed of Flight. IEEE Robot. Autom. Lett. 2024, 9, 2893–2900. [Google Scholar] [CrossRef]
- Zhu, D.J.; Yang, S.X. Bio-Inspired Neural Network-Based Optimal Path Planning for UUVs Under the Effect of Ocean Currents. IEEE Trans. Intell. Veh. 2022, 7, 231–239. [Google Scholar] [CrossRef]
- Zhao, S.M.; Hwang, S.H. Complete coverage path planning scheme for autonomous navigation ROS-based robots. ICT Express 2024, 10, 83–89. [Google Scholar] [CrossRef]
- Sang, H.Q.; You, Y.S.; Sun, X.J.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.Z.; Sun, Y.; Kong, J.Y.; Tong, X.L.; Zhao, G.J.; Chen, B.J. Genetic Algorithm-Based Trajectory Optimization for Digital Twin Robots. Front. Bioeng. Biotechnol. 2022, 9, 793782. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.B.; Ran, X.J.; Wang, J.M.; Chen, H.Y.; Deng, W. Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning. Eng. Appl. Artif. Intell. 2023, 121, 105942. [Google Scholar] [CrossRef]
- Shen, D.; Liu, G.L.; Li, T.C.; Yu, F.W.; Gu, F.Q.; Xiao, K.; Zhu, X.W. ORB-NeuroSLAM: A Brain-Inspired 3-D SLAM System Based on ORB Features. IEEE Internet Things J. 2024, 11, 12408–12418. [Google Scholar] [CrossRef]
- Zhu, D.Q.; Cao, X.; Sun, B.; Luo, C.M. Biologically Inspired Self-Organizing Map Applied to Task Assignment and Path Planning of an AUV System. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 304–313. [Google Scholar] [CrossRef]
- Teng, Y.X.; Feng, T.P.; Li, J.M.; Chen, S.Y.; Tang, X.C. A Dual-Layer Symmetric Multi-Robot Path Planning System Based on an Improved Neural Network-DWA Algorithm. Symmetry 2025, 17, 85. [Google Scholar] [CrossRef]
- Liu, J.Y.; Wei, X.X.; Huang, H.J. An Improved Grey Wolf Optimization Algorithm and its Application in Path Planning. IEEE Access 2021, 9, 121944–121956. [Google Scholar] [CrossRef]
- Li, H.R.; Lv, T.L.; Shui, Y.C.; Zhang, J.; Zhang, H.; Zhao, H.; Ma, S.B. An Improved grey wolf optimizer with weighting functions and its application to Unmanned Aerial Vehicles path planning. Comput. Electr. Eng. 2023, 111, 108893. [Google Scholar] [CrossRef]
- Dai, Y.N.; Yu, J.Y.; Zhang, C.; Zhan, B.W.; Zheng, X.T. A novel whale optimization algorithm of path planning strategy for mobile robots. Appl. Intell. 2022, 53, 10843–10857. [Google Scholar] [CrossRef]
- Huang, Y.J.; Li, Y.B.; Zhang, Z.T.; Sun, Q. A novel path planning approach for AUV based on improved whale optimization algorithm using segment learning and adaptive operator selection. Ocean Eng. 2023, 280, 114591. [Google Scholar] [CrossRef]
- Yue, Y.G.; Cao, L.; Lu, D.W.; Hu, Z.Y.; Xu, M.H.; Wang, S.X.; Li, B.; Ding, H.H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhao, J. Role Dynamic Assignment of Human–Robot Collaboration Based on Target Prediction and Fuzzy Inference. IEEE Trans. Ind. Inform. 2024, 20, 471–481. [Google Scholar] [CrossRef]
- Zhao, T.; Xiang, Y.F.; Dian, S.Y.; Guo, R.; Li, S.C. Hierarchical interval type-2 fuzzy path planning based on genetic optimization. J. Intell. Fuzzy Syst. 2020, 39, 937–948. [Google Scholar] [CrossRef]
- Li, K.; Zhang, X.; Han, Y. Robot Path Planning Based on Interval Type-2 Fuzzy Controller Optimized by an Improved Aquila Optimization Algorithm. IEEE Access 2023, 11, 111655–111671. [Google Scholar] [CrossRef]
- Dong, Z.N.; Zhang, R.L.; Chen, Z.J.; Zhou, R. Study on UAV Path Planning Approach Based on Fuzzy Virtual Force. Chin. J. Aeronaut. 2010, 23, 341–350. [Google Scholar] [CrossRef]
- Feng, T.P.; Li, J.M.; Jiang, H.; Yang, S.X.; Wang, P.X.; Teng, Y.X.; Chen, S.Y.; Fu, Q.; Luo, B.J. The Optimal Global Path Planning of Mobile Robot Based on Improved Hybrid Adaptive Genetic Algorithm in Different Tasks and Complex Road Environments. IEEE Access 2024, 12, 18400–18415. [Google Scholar] [CrossRef]
- Wan, H.M.; Zhang, L.L.; Kong, Q.; Zhu, W.C.; Zheng, J.; Zhuang, L.; Xu, X. Motion planning in complex urban environments: An industrial application on autonomous last-mile delivery vehicles. J. Field Robot. 2022, 39, 1258–1285. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, Q. Finite-Time Command-Filtered Lateral-Longitudinal Formation Control of Vehicles on Rough Roads. IEEE Trans. Intell. Veh. 2023, 8, 4331–4340. [Google Scholar] [CrossRef]
- Liu, X.W.; Li, Q.; Zhang, J.H. Research on global path planning of unmanned vehicles based on improved ant colony algorithm in the complex road environment. Meas. Control 2022, 55, 945–959. [Google Scholar] [CrossRef]
- Wang, F.L.; Chen, k.; Zhen, S.C.; Chen, X.F.; Zheng, H.M.; Wang, Z.D. Prescribed Performance Adaptive Robust Control for Robotic Manipulators With Fuzzy Uncertainty. IEEE Trans. Fuzzy Syst. 2024, 32, 1318–1330. [Google Scholar] [CrossRef]
- Li, Z.R.; Hu, J.; Leng, B.; Xiong, L.; Fu, Z.Q. An Integrated of Decision Making and Motion Planning Framework for Enhanced Oscillation-Free Capability. IEEE Trans. Fuzzy Syst. 2024, 25, 5718–5732. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Taghavifar, H.; Zhang, C.W.; Alattas, K.A.; Liu, J.P.; Vu, M.T. A non-linear fractional-order type-3 fuzzy control for enhanced path-tracking performance of autonomous cars. IET Control Theory Appl. 2024, 18, 40–54. [Google Scholar] [CrossRef]
- Liang, J.H.; Yang, K.D.; Tan, C.P.; Wang, J.X.; Yin, G.D. Enhancing High-Speed Cruising Performance of Autonomous Vehicles Through Integrated Deep Reinforcement Learning Framework. IEEE Trans. Intell. Transp. Syst. 2024, 26, 835–848. [Google Scholar] [CrossRef]
- Yin, Y.F.; Wang, Z.T.; Zheng, L.L.; Su, Q.R.; Guo, Y. Autonomous UAV Navigation with Adaptive Control Based on Deep Reinforcement Learning. Electronics 2024, 13, 2432. [Google Scholar] [CrossRef]
- Shi, Y.T.; Hou, X.Y.; Na, Z.L.; Zhou, J.; Yu, N.; Liu, S.; Xin, L.B.; Gao, G.W.; Liu, Y.H. Bio-inspired Attachment Mechanism of Dynastes Hercules: Vertical Climbing for On-Orbit Assembly Legged Robots. J. Bionic Eng. 2024, 21, 137–148. [Google Scholar] [CrossRef]
- Zou, Z.M.; Yang, S.M.; Zhao, L. Dual-loop control and state prediction analysis of QUAV trajectory tracking based on biological swarm intelligent optimization algorithm. Sci. Rep. 2024, 14, 19091. [Google Scholar] [CrossRef]
- Emara, H.; Elshafei, A.L. Robust robot control enhanced by a hierarchical adaptive fuzzy algorithm. Eng. Appl. Artif. Intell. 2004, 17, 187–198. [Google Scholar] [CrossRef]
- Ab, M.N.; Nazir, A.; Khalil, A.; Ho, W.J.; Akbar, M.F.; Noor, M.H.M.; Mohamed, A.S.A. Improved genetic algorithm for mobile robot path planning in static environments. Expert Syst. Appl. 2024, 249, 123762. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).