Approximation Properties of a New (p,q)-Post-Widder Operator
Abstract
1. Introduction
2. Preliminary Results
3. Convergence Estimate
4. Difference of Operators
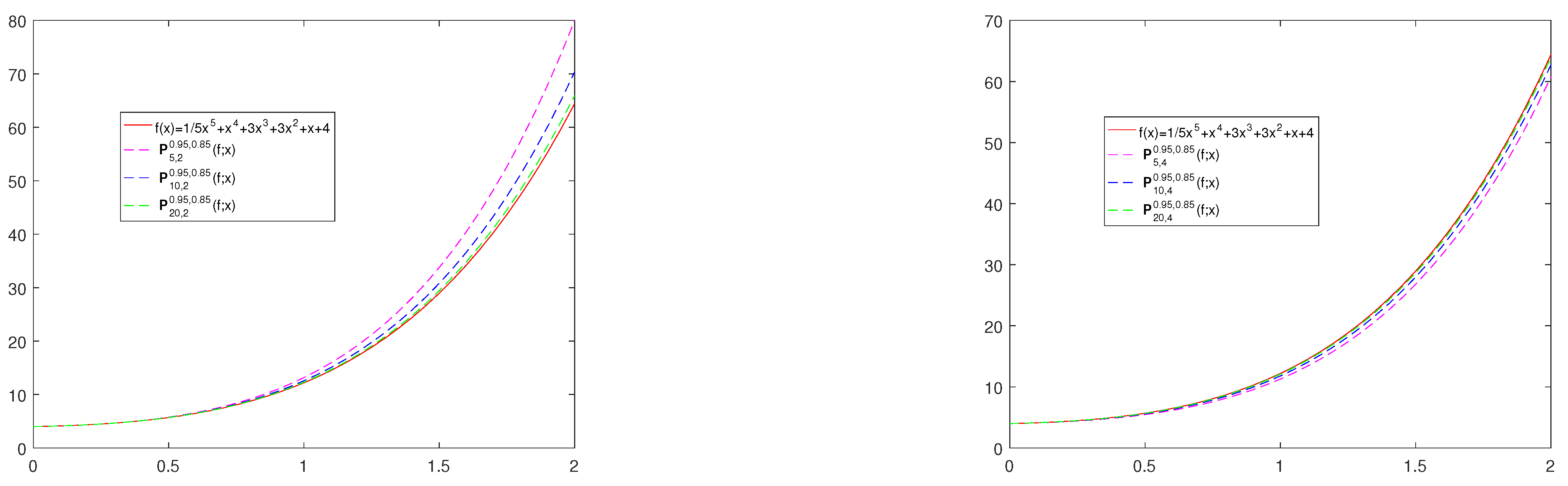
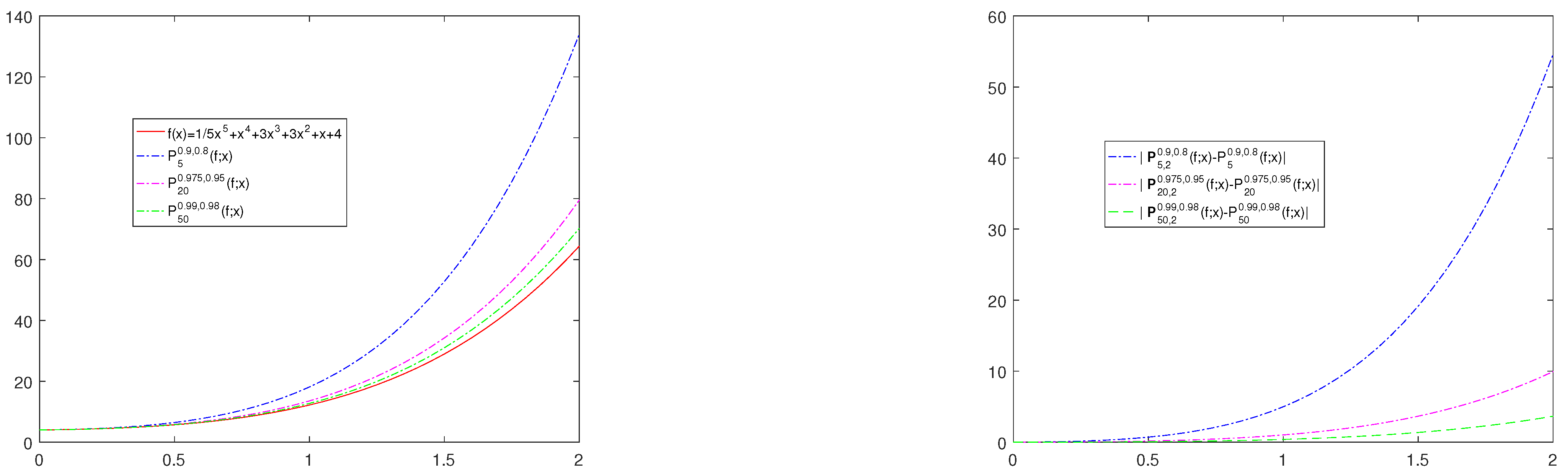
5. Graphical Analysis
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ditzian, Z.; Totik, V. Moduli of Smoothness; Springer: New York, NY, USA, 1987. [Google Scholar]
- Rempulska, L.; Rempulska, M. The Voronovskaya-type theorems for Post-Widder and Stancu operators. Int. J. Pure Appl. Math. 2007, 38, 467. [Google Scholar]
- King, J. Positive linear operators which preserve x2. Acta Math. Hungar. 2003, 99, 203–208. [Google Scholar]
- Aldaz, J.M.; Kounchev, O.; Render, H. Shape preserving properties of generalized Bernstein operators on extended Chebyshev spaces. Numer. Math. 2009, 114, 1–25. [Google Scholar]
- Rempulska, L.; Skorupka, M. On Approximation by Post-Widder and Stancu Operators Preserving x2. Kyungpook Math. J. 2009, 49, 57–65. [Google Scholar] [CrossRef]
- May, C. Saturation and inverse theorems for combinations of a class of exponential-type operators. Can. J. Math. 1976, 28, 1224–1250. [Google Scholar] [CrossRef]
- Siddiqui, M.A.; Agrawal, R.R. A Voronovskaya Type Theorem on Modified Post-Widder Operators Preserving x2. Kyungpook Math. J. 2011, 51, 87–91. [Google Scholar]
- Gupta, V.; Agrawal, D. Convergence by modified Post-Widder operators. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. A Matemáticas 2019, 113, 1475–1486. [Google Scholar]
- Gupta, V.; Tachev, G. Some results on Post-Widder operators preserving test function xr. Kragujev. J. Math. 2022, 46, 149–165. [Google Scholar]
- Srivastav, R.K.; Deshwal, S. Convergence: New Post-Widder operators. Int. J. Math. Trends Technol.-IJMTT 2021, 67, 43–52. [Google Scholar]
- Abel, U.; Acu, A.M.; Heilmann, M.; Raşa, I. Positive linear operators preserving certain monomials on [0,∞). Dolomites Res. Notes Approx. 2023, 16, 1–9. [Google Scholar]
- Jackson, F.H. On q-definite integrals. Quart. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- De Sole, A.; Kac, V. On integral representations of q-gamma and q-beta functions. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Nat. IX Ser. Rend. Lincei Mat. Appl. 2005, 16, 11–29. [Google Scholar]
- Ünal, Z.; Özarslan, M.A.; Duman, O. Approximation properties of real and complex post-widder operators based on q-integers. Miskolc Math. Notes 2012, 13, 581–603. [Google Scholar] [CrossRef]
- Mursaleen, M.; Ansari, K.J.; Khan, A. On (p, q)-analogue of bernstein operators. Appl. Math. Comput. 2015, 266, 874–882. [Google Scholar] [CrossRef]
- Mursaleen, M.; Alotaibi, A.; Ansari, K.J. On a Kantorovich Variant of (p, q)-Szász-Mirakjan Operators. J. Funct. Space 2016, 2016, 035253. [Google Scholar] [CrossRef]
- Mursaleen, M.; Ansari, K.J.; Khan, A. Some approximation results by (p, q)-analogue of Bernstein-Stancu operators. Appl. Math. Comput. 2015, 264, 392–402. [Google Scholar] [CrossRef]
- Malik, N.; Gupta, V. Approximation by (p, q)-Baskakov-Beta operators. Appl. Math. Comput. 2017, 293, 49–56. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Alotaibi, A. Durrmeyer type (p, q)-Baskakov operators preserving linear functions. J. Math. Inequal. 2018, 12, 961–973. [Google Scholar] [CrossRef]
- Kantar, U.D.; Yuksel, I. Investigating (p, q)-hybrid Durrmeyer–type operators in terms of their approximation properties. Gazi Univ. J. Sci. Part A Eng. Innov. 2022, 2022, 1–11. [Google Scholar]
- Gupta, V.; Rassias, T.M.; Agrawal, P.; Acu, A.M. Recent Advances in Constructive Approximation Theory; Springer: New York, NY, USA, 2018. [Google Scholar]
- Aral, A.; Gupta, V. Applications of (p,q)-Gamma functions to Szász-Durrmeyer operators. Publ. Inst. Math. 2017, 102, 211–220. [Google Scholar] [CrossRef]
- Mishra, V.N.; Pandey, S.; Mishra, L.N. On King Type Modification of (p,q)-Baskakov Operators which preserves x2. arXiv 2016, arXiv:1603.05510. [Google Scholar]
- Cheng, W.T.; Zhang, W.H.; Cai, Q.B. (p,q)-gamma operators which preserve x2. J. Inequal. Appl. 2019, 2019, 108. [Google Scholar] [CrossRef]
- Ispir, N. On modified Baskakov operators on weighted spaces. Turk. J. Math. 2001, 25, 355–365. [Google Scholar]
- DeVore, R. Constructive Approximation; Springer: Berlin, Germany, 1993. [Google Scholar]
- Aral, A.; Inoan, D.; Raşa, I. On differences of linear positive operators. Anal. Math. Phys. 2019, 9, 1227–1239. [Google Scholar] [CrossRef]
- Li, F.; Wang, J. Analysis of an HIV infection model with logistic target-cell growth and cell-to-cell transmission. Chaos Solitons Fractals 2015, 81, 136–145. [Google Scholar] [CrossRef]
- Li, F.; Yu, P.; Tian, Y.; Liu, Y. Center and isochronous center conditions for switching systems associated with elementary singular points. Commun. Nonlinear Sci. 2015, 28, 81–97. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y.; Liu, Y.; Yu, P. Bi-center problem and bifurcation of limit cycles from nilpotent singular points in Z2-equivariant cubic vector fields. J. Differ. Equations 2018, 265, 4965–4992. [Google Scholar] [CrossRef]
- Li, F.; Yu, P.; Liu, Y.; Liu, Y. Centers and isochronous centers of a class of quasi-analytic switching systems. Sci. China Math. 2018, 61, 1201–1218. [Google Scholar] [CrossRef]
- Chen, T.; Li, F.; Yu, P. Nilpotent center conditions in cubic switching polynomial Liénard systems by higher-order analysis. J. Differ. Equations 2024, 379, 258–289. [Google Scholar] [CrossRef]


| n | |||||
|---|---|---|---|---|---|
| 1 | 0.6500112460x | 0.5684376699x | 0.5460098343x | 0.5481623430x | 0.5599198421x |
| 2 | 0.5155136408x | 0.4715008341x | 0.4586055131x | 0.4611483255x | 0.4708714274x |
| 5 | 0.3330338798x | 0.3200984310x | 0.3160333664x | 0.3175769845x | 0.3225043240x |
| 10 | 0.2094704922x | 0.2061183719x | 0.2050302752x | 0.2055871628x | 0.2073071687x |
| 20 | 0.1061774863x | 0.1057318488x | 0.1055848555x | 0.1056725604x | 0.1059422998x |
| 50 | 0.0190597401x | 0.0190571443x | 0.0190562834x | 0.0190568250x | 0.0190584917x |
| 100 | 0.0011796543x | 0.0011796537x | 0.0011796535x | 0.0011796536x | 0.0011796540x |
| n | |||||
|---|---|---|---|---|---|
| 1 | 0.6904248749x | 0.5951190729x | 0.5691154513x | 0.5726075886x | 0.5877166349x |
| 2 | 0.5592141272x | 0.5043842406x | 0.4884490433x | 0.4924044957x | 0.5057550612x |
| 5 | 0.3859008863x | 0.3662152533x | 0.3600806295x | 0.3628977742x | 0.3712804626x |
| 10 | 0.2734295975x | 0.2661140905x | 0.2637572176x | 0.2652266629x | 0.2695357143x |
| 20 | 0.1815753046x | 0.1793770242x | 0.1786552990x | 0.1791976930x | 0.1808005124x |
| 50 | 0.0878522537x | 0.0875992467x | 0.0875152362x | 0.0875864032x | 0.0877992403x |
| 100 | 0.0363155512x | 0.0362976064x | 0.0362916309x | 0.0362968539x | 0.0363125380x |
| 200 | 0.0072789758x | 0.0072788312x | 0.0072787830x | 0.0072788254x | 0.0072789528x |
| n | |||||
|---|---|---|---|---|---|
| 1 | 0.6473797410x | 0.5666616874x | 0.5444595799x | 0.5465330454x | 0.5580839204x |
| 2 | 0.5126813590x | 0.4693234779x | 0.4566145638x | 0.4590763080x | 0.4685829583x |
| 5 | 0.5126813590x | 0.4693234779x | 0.4566145638x | 0.4590763080x | 0.4685829583x |
| 10 | 0.2055548154x | 0.2023839811x | 0.2013544854x | 0.2018730421x | 0.2034810102x |
| 20 | 0.1020811086x | 0.1016848692x | 0.1015541781x | 0.1016306825x | 0.1018667152x |
| 50 | 0.0170102994x | 0.0170084541x | 0.0170078423x | 0.0170082185x | 0.0170093793x |
| 100 | 0.0009223449x | 0.0009223446x | 0.0009223445x | 0.0009223446x | 0.0009223448x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Q. Approximation Properties of a New (p,q)-Post-Widder Operator. Symmetry 2025, 17, 553. https://doi.org/10.3390/sym17040553
Lin Q. Approximation Properties of a New (p,q)-Post-Widder Operator. Symmetry. 2025; 17(4):553. https://doi.org/10.3390/sym17040553
Chicago/Turabian StyleLin, Qiu. 2025. "Approximation Properties of a New (p,q)-Post-Widder Operator" Symmetry 17, no. 4: 553. https://doi.org/10.3390/sym17040553
APA StyleLin, Q. (2025). Approximation Properties of a New (p,q)-Post-Widder Operator. Symmetry, 17(4), 553. https://doi.org/10.3390/sym17040553






