Abstract
This paper is based on the shape invariance of the solvable superpotentials and uses the series expansion method to study the approximate expansion forms of these superpotentials. Firstly, this paper examines the differential equations satisfied by the first-order approximations of the superpotentials. Through an example, namely Rosen–Morse (trigonometric) superpotentials, the specific forms of these first-order approximations are analyzed. Based on these simple first-order approximations, this paper then delves into the ground-state wave functions of the superpotential. Secondly, this paper derives the differential equations satisfied by the second-order approximations with the first-order approximations. Using the harmonic oscillator superpotentials as an example, similarly, non-unique forms for the second-order approximations are obtained. By selecting simpler forms for the first- and second-order approximations, the authors further investigate the ground-state wave functions of the superpotential with the second-order approximation. Thirdly, the authors discuss the Hamiltonians of the potential with the first- and second-order approximations, concluding that the additional term originates from the corrections to the superpotential. Finally, conclusions and prospects are provided.
1. Introduction
The Schrödinger equation serves as the fundamental equation governing the behavior of quantum systems [1]. By solving this equation, we can obtain critical information regarding particle states in various potential fields, including wave function evolution and energy level structures. These insights are essential in understanding the properties of atoms, molecules, crystals, and elementary particles in the microscopic world [2,3]. Consequently, obtaining exact solutions to the Schrödinger equation (including the Klein–Gordon equation and Dirac equation) has remained a central focus in quantum mechanics research. To date, numerous researchers have employed transformations and supersymmetric quantum mechanics (SUSYQM) approaches to derive exact solutions for the Schrödinger equation, Klein–Gordon equation, and Dirac equation [4,5,6].
SUSYQM theory can be utilized to conveniently and swiftly obtain the exact solutions of the Schrödinger equation [6,7]. SUSYQM introduces supersymmetric algebra, which is an algebraic structure that is distinct from that of conventional quantum mechanics. This algebraic structure provides a new mathematical framework for the solution of the Schrödinger equation, making it easier to deal with various quantum systems, including those with very complex potential fields. Even for nonstationary problems, which are difficult to solve in quantum mechanics, SUSYQM provides an effective method by introducing supersymmetric generators. Thus, nonstationary problems can be transformed into stationary problems, which are easier to solve. SUSYQM can also be used to study the energy spectrum structure of the system [7], including finding the energy levels and determining the degeneracy of the energy levels. This is very important in understanding the energy spectrum structure in molecular, atomic, and nuclear physics [8]. SUSYQM also reveals the symmetry in nature according to supersymmetry. This is of great significance in understanding the basic properties and interactions of matter. Supersymmetry also plays a key role in high-energy physics, particle physics, and related fields [6,9].
The earliest research on the exact solutions of the Schrödinger equation can be traced back to the beginning of the 20th century [10,11]. First, Natanzon derived the general properties of potentials that can be solved by hypergeometric functions, confluent hypergeometric functions, and Bessel functions in the Schrödinger equation [12]. Later, in 1926, Erwin Schrödinger and Hermann Weyl found the exact solution of the Schrödinger equation for the harmonic oscillator potential [13]. In the 1980s, Dutt, Ranabir, Khare, Avinash, Sukhatme, Uday P., and others pioneered a new field by constructing 11 solvable superpotentials [11]. They used supersymmetric techniques to solve the energy levels and wave functions of solvable superpotentials in quantum mechanics; surprisingly, they found that the partner potentials corresponding to these superpotentials all belonged to shape-invariant potentials [14,15]. This finding provided important clues for an understanding of the properties of quantum systems. In 1997, Dutt, Gangopadhyaya, and other researchers extended the supersymmetric solution techniques to non-central potentials and spherical harmonic potentials [16]. They derived these techniques in detail and successfully obtained the exact solutions of the energy levels and wave functions with vector potentials and non-central scalar potentials as examples. In 2022, members of our team, including Zhong Shikun, Li Min, and Xiong Lulin, constructed new solvable superpotentials using the additivity of superpotentials in SUSYQM [10,17,18]. These studies have all expanded the understanding of supersymmetric properties and further promoted the research and application of superpotentials in quantum mechanics.
In SUSYQM, superpotentials play a crucial role. If we obtain the superpotential of a solvable potential, we can conveniently obtain the eigenvalues and wave functions of that potential using SUSYQM methods [17]. Around 1986, Pursey and others proposed the concept of isospectral superpotentials and established a set of methods for the construction of isospectral superpotentials [19]. Isospectral superpotentials can be used to calculate a series of different potentials with the same energy spectrum using SUSYQM methods, providing new ideas for the discovery of more solvable superpotentials. In 1988, Dutt and others obtained additive shape-invariant potentials using the aforementioned method [15], such as the harmonic oscillator, three-dimensional harmonic oscillator, Coulomb superpotential, and more than ten other superpotentials. In 2010, Bougie and others proved the uniqueness of these isospectral potentials [20]. The introduction of the concept of isospectral potentials has opened up new possibilities for the derivation of exactly solvable superpotentials. Therefore, it is also necessary to construct new isospectral superpotentials based on the existing solvable superpotentials.
This paper is based on SUSYQM and presents in-depth research on one-dimensional isospectral superpotentials. Initially, by leveraging the principle of shape invariance and the intrinsic dependency between ℏ and the superpotential, we derived the power series expansion of in terms of ℏ. Subsequently, based on the relationship where is a function of a in , we expanded into a Taylor series centered around a. This formed the basis for our construction of first- and second-order approximations of isospectral supersymmetric potentials. It also enabled us to establish the intricate relationships between , and . Thereafter, we extended our research to conventional solvable potentials. Utilizing these approximate relationships, in the first-order approximation, taking the Rosen–Morse (trigonometric) superpotentials as an example, the potential function and eigen ground-state wave function were obtained. In the second-order approximation, taking the harmonic oscillator superpotential as an example, its potential function and eigen ground-state wave function were obtained.
2. Approximate Expansion of Superpotential
In quantum mechanics, the power series expansion is a common mathematical method for the solution of the involved differential equations, especially when discussing wave functions, potential energy functions, or other physical quantities. Supersymmetric quantum mechanics explores the symmetry of particles by introducing supersymmetric algebra and can be used to study the energy level structure and wave function properties in quantum systems [5]. Based on this, the introduction of the idea of power series expansion, and the study of finite-order approximations or infinite-order expansions of superpotentials, is undoubtedly of great significance. The superpotential is a core concept in this theory, and researchers may also describe certain approximations to the superpotential. Such approximation methods may include ignoring higher-order terms or simplifying the superpotential using physical principles such as symmetry and conservation [21,22].
For the sake of simplicity in description, references related to supersymmetric quantum mechanics generally assume before further discussion. This paper focuses on the study of ℏ while preserving it as an infinitesimal quantity (where , h is a Planck constant) [9]. The time-independent Schrödinger equation in one dimension is
Let , and define the raising and lowering operators (where is a superpotential and a is a parameter). Define the partner Hamiltonians , and we can obtain the partner potentials :
According to the shape invariance satisfied by the partner potentials in SUSYQM (where the relationship between parameters a and is , and g is a function of ) [7], while retaining ℏ, the shape invariance satisfied by the superpotential (equivalent to the shape invariance satisfied by the partner potentials) is
In Equation (3), the superpotential is a function of two real variables (x and a) that possess at least third-order partial derivatives concerning the arguments x and a. Then, the Taylor series in a circular vicinity with radii ℏ and center point a is convergent if the parameter ℏ is small enough. The above equation can be re-expressed as a series with ℏ. Firstly, and must be expanded into a series of ℏ:
Then, we expand into a Taylor series centered around a:
Because this paper only discusses second-order approximation problems, to ensure computational effectiveness, the high-order infinitesimal of is ignored. Substituting Equations (4)–(6) into Equation (3), the left-hand side of Equation (3) is
The first term on the right-hand side of Equation (3) can be simplified to
The second term on the right-hand side of Equation (3) is
Since Equation (3), after considering Equations (7)–(9), holds for any ℏ, it is required that the coefficients obtained after collecting similar terms according to the exponent of parameter ℏ must be zero. Therefore, it becomes possible to obtain the expressions of the superpotentials under first- and second-order approximations based on shape invariance in SUSYQM.
3. The Equation Satisfied by the Zeroth-Order Approximation of the Superpotential
According to Equations (3) and (7)–(9), when only considering the zeroth-order approximation of the ℏ term, it can be deduced that satisfies
Equation (10) is derived based on the shape invariance, through substitution, and considering only the zeroth-order approximation of the ℏ term. It is equivalent to the physical meaning of shape invariance. Solving the differential equation through Equation (10) allows for the determination of the superpotential forms for all traditionally solvable potentials [7]. This reflects the relationship between the superpotential and the parameter function . It implies that the traditionally solvable superpotentials also satisfy Equation (10).
4. The First-Order Approximation of the Superpotential
Based on Equation (3), which describes shape invariance and uses the zeroth-order approximation , we can easily obtain the first-order approximation of the superpotential.
4.1. The Equation Satisfied by the First-Order Approximation of the Superpotential
According to Equations (7)–(9), it can be demonstrated that, when the first-order approximation of ℏ (the terms of in the expanded series) is only considered, and are found to satisfy
By reusing Equation (10), we can obtain
Substituting Equation (12) into Equation (11), we obtain
Analyzing Equation (13), the following two points are clear. First, Equation (13) enables us to obtain under the first-order approximation based on and . This provides a new approach to solving solvable superpotentials. Second, since and represent the zeroth- and first-order approximations (where we set ), respectively, and both are derived from Equation (3) through relevant approximations, they undoubtedly satisfy the requirement of shape invariance in Equation (3). Therefore, it can be considered that , and all belong to approximately isospectral superpotentials. However, the eigen-wave functions will differ.
4.2. Example—The First-Order Approximation of the Rosen–Morse (Trigonometric) Superpotential
In the following discussion, the Rosen–Morse (trigonometric) superpotential is taken as an example to further discuss the issues related to the first-order approximation of the superpotential. Firstly, the aforementioned form of the superpotential is substituted into Equation (13) to obtain the general solution expression for . At this point, becomes a solvable potential, and the existence of the general solution expression for implies that, after considering the first-order approximation, a series of new solvable superpotentials can be constructed based on the traditionally exactly solvable superpotentials. This undoubtedly significantly supplements the number of solvable potentials. According to reference [23], we have the superpotential and ground-state wave function of the Rosen–Morse (trigonometric) superpotential:
Substituting Equation (14) into Equation (13) yields the general solution of ,
where is an arbitrary function of . (Similarly, in the following text, refers to an arbitrary function of ‘*’). For the convenience of subsequent calculations, we set , and then
The new superpotential is
Its eigen-wave function is
If we take the arbitrary constants , we can draw the figures of the superpotentials and the ground-state wave functions as shown in Figure 1. According to Figure 1, after taking into account the first-order approximation, the superpotential’s curve exhibits noticeable changes. The form of the change depends on the choice of . The waveform of the ground-state wave function has also changed. It can be inferred that the waveforms of other eigenfunctions will also undergo corresponding changes.
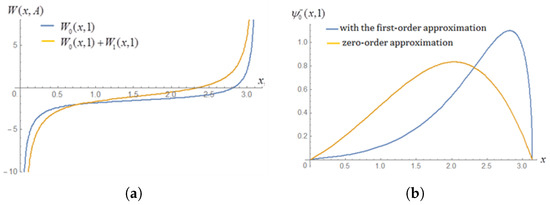
Figure 1.
The superpotential figure (a) and the ground-state wave function (normalized) figure (b) for the Rosen–Morse (trigonometric) potential.
In this section, based on the series expansion and the shape invariance, the relationship expression between and , namely Equation (13), is constructed. The specific expressions for the isospectral superpotential and wave function under the first-order approximation are thereby obtained. Using a similar construction method, the derivation of the second-order approximation will subsequently be carried out.
5. The Second-Order Approximation of the Superpotential
In the first-order approximation, the terms containing are taken into account, while, in the second-order approximation, the terms containing need to be considered. This section is based on this expansion; firstly, the equation satisfied by the second-order approximation is derived. Since the differential equation satisfied by the second-order approximation contains the first-order approximation , the second part of this section discusses the selection of . Finally, the harmonic oscillator superpotential is used as an example for further research.
5.1. The Equation Satisfied by the Second-Order Approximation of the Superpotential
According to the aforementioned Equations (5)–(7), if we only consider the term , we can obtain
Utilizing
we obtain
and then
Substituting Equation (21) into Equation (22), we obtain
According to Equation (10), taking the partial derivatives on both sides gives
Simplifying Equation (23), we obtain
Analyzing Equation (25), we clarify two points. First, given the specific expressions of and , we can solve the differential equation to obtain the precise expression of the new superpotential under the second-order approximation, offering a new method to determine newly solvable superpotentials. Second, since is a second-order approximation of , a result obtained by correlation approximation derivation from Equation (3), it must also satisfy the requirement of shape invariance of Equation (3). Thus, it can be assumed that and all belong to the family of isospectral superpotentials (where we set ). However, the eigenfunctions will be different.
5.2. The Choice of the Specific Solution of
Based on the previous discussion, it can be seen that the traditional solvable superpotential is , which satisfies Equation (10). The first-order approximation of the superpotential satisfies Equation (13), and its solution is related to . Given any traditional superpotential , the general solution form of the corresponding can be determined. The second-order approximation of the superpotential satisfies Equation (25), and its solution is related to both and . Given any traditional superpotential , to obtain the general solution of , the expression of must be determined. Therefore, the complexity or simplicity of the particular solution of chosen based on its general solution directly determines the complexity or simplicity of the general solution form of , and even whether Equation (25) is solvable. Hence, the selection of the particular solution of is crucial.
Therefore, the selection of the particular solution form for is determined by whether a simplified general solution for can be obtained. In most cases, is selected based on the general solution of , as this typically yields simpler general solution expressions for . However, for certain solvable superpotentials, such as the harmonic oscillator superpotential, choosing according to its general solution leads to exhibiting identical general solution forms to those of . Under such circumstances, a non-zero particular solution form of with greater simplicity should be selected instead. Furthermore, when selecting based on its general solution produces a general solution for where any derived particular solution induces wave function divergence, such as the Morse potential, a non-zero simplified particular solution form of must also be adopted. In other words, the selection of ’s particular solution form from its general solution should strictly follow three principles: computational simplicity, expression uniqueness, and wave function convergence. Therefore, the direct assignment of without justification in reference [7] is considered untenable, which further validates the significance of this study.
5.3. Example—the Second-Order Approximation of the Harmonic Oscillator Superpotential
Through the previous theoretical calculations, we have obtained the relationships between , and and discussed the selection of . Next, we take the existing solvable harmonic oscillator as an example to calculate the corresponding new superpotential expressions with second-order approximation. If is a solvable superpotential, then the general solution for implies that a series of solvable superpotentials can be constructed based on traditional solvable superpotentials, after we consider first- and second-order approximations.
According to reference [24], we present the superpotential , the expression of and the ground-state wave function for the Harmonic Oscillator superpotential:
Substituting Equation (26) into Equation (13), we can obtain the general solution of :
Choose
and, substituting Equations (26) and (28) into Equation (25), we can work out the general solution of :
where is function ; taking the arbitrary function as zero, we obtain a simple :
We obtain the superpotential after considering the second-order approximation as
The wave function (the second-order approximation considered) is
These results are much more complicated. If both arbitrary constants are taken as , we can draw the comparison figures of the superpotentials and the ground-state wave functions, as shown in Figure 2. From Figure 2, a comparative analysis of the superpotential curve before and after approximation correction reveals differences induced by the first- and second-order terms. The form of the change depends on the result of . The waveform of the ground-state wave function has also changed. It can be inferred that the waveforms of the excited eigenfunctions will also undergo changes.
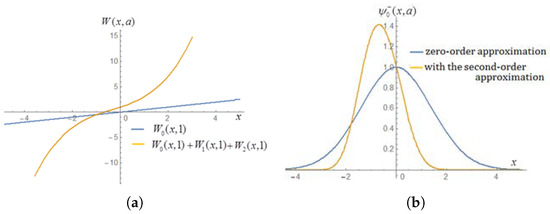
Figure 2.
The superpotential figure (a) and the ground-state wave function (non-normalized) figure (b) for the harmonic oscillator potential.
We have obtained the expression for the second-order approximation of the superpotential based on the coefficient of the term being zero. Detailed discussions have been provided for . Furthermore, using the exactly solvable superpotential, we have also calculated the second-order approximation expressions of the other superpotentials (we will not repeat them in this paper).
6. Discussions of
The introduction of first-order and second-order approximations of the superpotential inevitably leads to changes in the Hamiltonian. Therefore, further discussions are needed regarding the Hamiltonian.
6.1. of the First-Order Approximation
According to the definition of the raising and lowering operators , , which considered the first-order approximation, we have
The partner Hamiltonians also change to
If we define
then the residual terms are defined as
and we have
According to Equation (37), it can be seen that there is an additional term in the energy when using the first-order approximation of the superpotential. After being approximated, the shape invariance should be satisfied, i.e.,
and the zero-order naturally satisfies the shape invariance relation
Thus, without considering the approximate expansion of , we have
or
where is a function with respect to (independent of x). Accordingly one can further limit , which matches with Equation (13). If also applies the same approximation, the situation will become more complex, and this will be our next research focus.
6.2. of the Second-Order Approximation
Similarly, after considering the second-order approximation, it is clear that follows.
The partner Hamiltonians are
and the first term of the above two equations is still . The remaining term can be defined as
and we have
According to Equation (45), it can be seen that there is an additional term in the partner Hamiltonians when considering the second-order approximation of the superpotential. According to the shape invariance, there is
It can be demonstrated that the zero-order is consistent with the shape invariance relation.
Thus, without considering the approximate expansion of , there are
or
where is a function with respect to (independent of x). We can further qualify , which satisfies Equation (13). If has been determined earlier, then we can further qualify , which satisfies Equation (13). Moreover, if we take into account the first-order approximation when , it implies that , where is a function of (independent of x).
By further investigating the Hamiltonian with the first-order approximation and the second-order approximation, we find that the Hamiltonians in both approximations have an additional value that does not cause a change in the energy spectrum if the shape invariance relation is followed and when the approximation of is not considered. However, we need to impose further restrictions on and .
7. Conclusions and Prospects
In this paper, we have constructed a new isospectral potential that can be used for precise solutions, while maintaining shape invariance. Initially, we introduced the concept of the superpotential, which is a function related to infinitesimals ℏ, and established an inherent connection between ℏ and the superpotential. By expanding in a series, we obtained its approximate expansion expression. Furthermore, based on the relationship between parameters and , with the existence of a connection to , we derived the relationship expression between and through a Taylor expansion. Through the application of shape invariance conditions, we successfully derived the expressions for the superperpotential under first-order and second-order approximations, providing new possibilities for the derivation of the exact solvable potential of the Schrödinger equation.
We further discussed the energy spectrum of the corrections, arguing that, since and , etc., were all approximate corrections in the following shape invariance relation, regardless of the order of the correction, the energy spectra of the corresponding potentials were the same. Nevertheless, we discussed some solvable superpotentials, derived the expressions for some superpotentials while considering the first- and second-order approximations, and plotted the graphs of these superpotentials and the ground-state wave functions. We also discussed the Hamiltonian after correction and the additional Hamiltonian due to the correction.
According to the research results given in this article, it can be deduced that there is a possibility for further research on the series expansion of superpotentials, which is also of great research value. We will carry out higher-order series expansions and seek the laws under each-order approximation, even deriving the expression of the sum of the whole series, and attempt to construct strictly shape-invariant isospectral superpotentials from the existing solvable superpotentials. It should be noted that the computational challenges and complexity rise exponentially with increasing approximation orders. Currently, our team is preparing for the next stage of research based on this paper.
Author Contributions
Conceptualization, G.L.; Methodology, G.L.; Software, Y.L. and Y.Y.; Validation, Y.L. and Y.Y.; Formal analysis, Y.L. and Y.Y.; Investigation, W.Q., W.C. and H.L.; Resources, G.L.; Data curation, Y.L. and Y.Y.; Writing—original draft, Y.L. and Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schleich, W.P.; Greenberger, D.M.; Kobe, D.H.; Scully, M.O. Schrödinger equation revisited. Proc. Natl. Acad. Sci. USA 2013, 110, 5374–5379. [Google Scholar] [PubMed]
- Bhatta, V.S. Plurality of wave-particle duality. Curr. Sci. 2020, 118, 1365–1374. [Google Scholar]
- George, C.; Prigogine, I.; Rosenfeld, L. The macroscopic level of quantum mechanics. Nature 1972, 240, 25–27. [Google Scholar]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and quantum mechanics. Phys. Rep. 1995, 251, 267–385. [Google Scholar]
- Junker, G. Supersymmetric Methods in Quantum and Statistical Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Bagchi, B.K. Supersymmetry in Quantum and Classical Mechanics; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Gangopadhyaya, A.; Mallow, J.; Rasinariu, C. Supersymmetric Quantum Mechanics: An Introduction; World Scientific Publishing: Singapore, 2017. [Google Scholar]
- Junker, G. Supersymmetric Methods in Quantum, Statistical and Solid State Physics: Enlarged and Revised Edition; IOP Publishing: London, UK, 2019. [Google Scholar]
- Bougie, J.; Gangopadhyaya, A.; Mallow, J.V. Generation of a complete set of additive shape-invariant potentials from an Euler equation. Phys. Rev. Lett. 2010, 105, 210402. [Google Scholar] [CrossRef] [PubMed]
- Zhong, S.K.; Xie, T.Y.; Dong, L.; Yang, C.X.; Xiong, L.L.; Li, M.; Luo, G. Shape invariance of solvable Schrödinger equations with a generalized hyperbolic tangent superpotential. Results Phys. 2022, 35, 105369. [Google Scholar] [CrossRef]
- Gendenshteîn, L.É. Derivation of exact spectra of the Schrodinger equation by means of supersymmetry. Jetp. Lett. 1983, 38, 356–359. [Google Scholar]
- Natanzon, G.A. General properties of potentials for which the Schrodinger equation can be solved by means of hypergeometric functions. Teor. Mat. Fiz. 1979, 38, 219–229. [Google Scholar]
- Schrödinger, E. Quantisierung als eigenwertproblem. Ann. Phys. 1926, 386, 109–139. [Google Scholar]
- Cooper, F.; Ginocchio, J.N.; Khare, A. Relationship between supersymmetry and solvable potentials. Phys. Rev. D 1987, 36, 2458. [Google Scholar]
- Dutt, R.; Khare, A.; Sukhatme, U.P. Supersymmetry, shape invariance, and exactly solvable potentials. Am. J. Phys. 1988, 56, 163–168. [Google Scholar]
- Dutt, R.; Gangopadhyaya, A.; Sukhatme, U.P. Noncentral potentials and spherical harmonics using supersymmetry and shape invariance. Am. J. Phys. 1997, 65, 400–403. [Google Scholar]
- Xiong, L.; Tan, X.; Zhong, S.; Cheng, W.; Luo, G. A New Solvable Generalized Trigonometric Tangent Potential Based on SUSYQM. Symmetry 2022, 14, 1593. [Google Scholar] [CrossRef]
- Li, M.; Zhong, S.K.; Dong, L.; Xiong, L.L.; Luo, G. Shape Invariance of Solvable Schrödinger Equations with the Generalized Hyperbolic Pöschl-Teller Potential. Adv. Math. Phys. 2022, 2022, 4345342. [Google Scholar] [CrossRef]
- Mallow, J.V.; Gangopadhyaya, A.; Bougie, J.; Rasinariu, C. Inter-relations between additive shape invariant superpotentials. Phys. Lett. 2020, 384, 126129. [Google Scholar]
- Bagchi, B.; Grandati, Y.; Quesne, C. Rational extensions of the trigonometric Darboux-Pöschl-Teller potential based on para-Jacobi polynomials. J. Math. Phys. 2015, 56, 062103. [Google Scholar] [CrossRef]
- Bougie, J.; Gangopadhyaya, A.; Rasinariu, C. The supersymmetric WKB formalism is not exact for all additive shape invariant potentials. J. Phys. A Math. Theor. 2018, 51, 375202. [Google Scholar]
- Quesne, C. Deformed shape invariant superpotentials in quantum mechanics and expansions in powers of ℏ. Symmetry 2020, 12, 1853. [Google Scholar] [CrossRef]
- Fernández, D.J.; Reyes, R. Spectral manipulation of the trigonometric Rosen-Morse potential through supersymmetry. Phys. Scr. 2021, 96, 125250. [Google Scholar] [CrossRef]
- Koohrokhi, T.; Izadpanah, A.; Gerayloo, M. A unified scheme of central symmetric shape-invariant potentials. Pramana 2024, 98, 140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).