Abstract
In this paper, an improved model-free adaptive predictive control method is presented for unknown nonlinear systems with quantization to handle the limited network transmission capacity and denial of service (DoS) attacks. Firstly, to reduce the impact of the DoS attacks on the control system, an attack compensation mechanism is designed, which can be adjusted based on different attack strategies of attackers, and the elastic control of DoS attack can be realized for systems with different complexity and attack intensity. Secondly, a uniform quantizer with encoding and decoding mechanism is presented to tackle the network bandwidth limitation and to reduce the effects of quantization errors. Subsequently, an improved model-free adaptive predictive control method is designed, which can realize the tracking control task of the system with quantization under DoS Attacks. The boundedness of the tracking error of the control system is strictly proved by theoretical analysis. The proposed algorithm has certain symmetry in the prediction time domain and the control time domain. It predicts the state and output of the system at multiple times in the future at each sampling time, and calculates the optimal control sequence according to the predicted results. This kind of symmetric relationship between the prediction of the future and the optimization of the current control is reflected in time, so as to achieve the optimal performance of the system in the whole prediction interval. Finally, the effectiveness and robustness of the presented control method are verified by simulation results under both undisturbed and disturbed conditions.
1. Introduction
Data-driven control (DDC) proposed in [1,2,3] is an effective method for complex nonlinear systems. By only utilizing system input/output (I/O) data to design the control algorithm, the DDC method can get rid of the dependence on the precise system model. Due to the advantages of DDC, it has been rapidly developed in method theory and practical application, such as PID control, iterative feedback tuning [4], virtual reference feedback tuning [5], iterative learning control (ILC) [6], model-free adaptive control (MFAC) [7], robot trajectory tracking control problem [8], and train operation control [9,10].
Among these DDC methods, the MFAC method [11] is the fastest developing and most complete method in theory and application. For unknown nonlinear multiagent systems consensus tracking problem, a distributed MFAC strategy is presented in [12]. In [13], an event triggered model-free adaptive iterative learning control (MFAILC) method is proposed to deal with the fading phenomenon of nonlinear systems. For false data injection attacks problem of MIMO nonlinear cyber–physical systems, according to partial form dynamic linearization, a new MFAC strategy is proposed in [14]. Considering disturbances and the over-speed protection of subway train control systems, an extended-state observer-based model-free adaptive iterative-learning energy-efficient control is presented in [15]. For the path tracking control problem, an enhanced MFAC method [16] is designed for a self-driving wheel excavator. In addition, due to its excellent control performance, robustness to model uncertainty and external disturbances, model predictive control (MPC) [17] is the most widely used control strategy. On the basis of the advantages of MPC and MFAC, a model-free adaptive predictive control (MFAPC) method is proposed in [18], which can handle the problem of the traditional MPC relying on the models. In [19], the MFAPC algorithm is also investigated for MIMO nonlinear discrete time systems. As can be seen from the above references, the MFAC method has received a lot of attention.
Currently, a network control systems (NCS) [20,21,22] composed of network channels, sensors, actuators, and controllers have been rapidly developed and widely used. The distinguishing feature of the NCS is that it connects cyberspace with physical space, making it possible to perform multiple tasks remotely. The NCS has many significant advantages. The control system only needs to transmit data through the network, which eliminates complex wiring. In addition, the NCS can reduce the complexity and cost of setting up the system, while increasing the flexibility of the system and reducing installation and maintenance costs. However, with the development of information technology, the network control system becomes more and more complex, and it is difficult to establish an accurate mathematical model.
In addition, for the NCS, there are also some issues with communication delay [23], packet loss [24], and quantization [25,26], where quantization is a pivotal problem that needs to be handled. Due to the limited transmission capacity of certain devices in networks and closed-loop systems, such as A/D and D/A converters, the data transmitted in practical NCS needs to be quantized before it can be sent to the next network node. Moreover, the network transmission burden is a significant problem to be dealt with in the NCS. Quantization is an effective method to reduce the amount of data and solve the network transmission burden while meeting the control requirements. In [27], a quantized feedback control method was proposed for discrete-time MIMO linear systems with input and output quantization. A quantized ILC for discrete-time systems [28] was presented, which can obtains bounded convergence of tracking errors. In [29], for the zero-error tracking issue, by using an encoding and decoding mechanism, a quantized ILC is also proposed. In [30,31], by only using I/O data, a quantized MFAC method is designed to ensure that the tracking error is convergent. In [32], a quantized data-driven MFAPC approach is designed for nonlinear systems, but the tracking error convergence analysis is lacking. For nonlinear multi-agent systems with uniform quantization, an event-triggered MFAC algorithm is presented in [33]. The literature reviewed above only considers quantitative problem. If the system is subjected to network attacks, the above works are no longer applicable.
Moreover, the introduction of communication network makes the NCS more open, but it also brings the risk of network attacks to the system. Network attacks not only destroy the performance of the control system, but also bring about disastrous consequences. Denial of service (DoS) [34,35,36,37] attacks send a large number of useless data packets to the system, blocking communication channels and preventing normal system data packets from being transmitted to the control center in a timely manner, resulting in the control center being unable to generate effective control signals in a timely manner. Therefore, the control problem of DoS attacks has been subject to wide concern. In [38], for networked control systems under DoS attacks, an adaptive event-triggered method is proposed. For nonlinear multiagent systems with output constraints and DoS attacks, a robust fuzzy adaptive event-triggered control scheme is designed in [39]. In [40], for high-speed train speed tracking with aperiodic DoS attacks and communication delays, an extended-state observer-based MFAILC algorithm is proposed. In [34], a distributed MFAC method is presented for nonlinear multiagent systems subjected to DoS attacks. In [41], an new event-triggered MFAC method was presented for unknown nonlinear systems under frequency duration constrained DoS attacks.
In conclusion, none of the references reviewed above have the ability to deal with both network bandwidth limitations and DoS attacks, and the DDC methods reviewed can only deal with a single DoS attack problem. Motivated by these observations, this paper investigates an improved model-free adaptive predictive control (IMFAPC) strategy for nonlinear systems with quantization to tackle limited network transmission capacity and DoS attacks. Compared with the existing works, the main contributions of this paper are addressed as follows.
- Network bandwidth limitation and DoS attacks are handled simultaneously for nonlinear systems only utilizing the I/O data to design control methods. The proposed IMFAPC method can eliminate the dependence on the system model, which is a data-driven control method.
- An attack compensation mechanism is presented to reduce the impact of the DoS attacks on the control system, which can be adjusted according to the different attack strategies of attackers, and the elastic control of the DoS attack can be realized for systems with different complexity and attack intensity.
- A uniform quantizer with encoding and decoding mechanisms is proposed to settle the network bandwidth limitation and to reduce the effects of quantization errors. Furthermore, the convergence analysis of the proposed control method is carried out, and the tracking error is proved to be bound.
The rest of the paper is given as follows. Section 2 addresses the problem formulation. The design and analysis of the IMFAPC method for the nonlinear system with quantization under DoS attacks are developed in Section 3. In Section 4, simulations are given to illustrate the effectiveness and robustness of proposed method. Section 5 summarizes this paper.
2. Problem Formulation
The following unknown discrete time single-input single-output (SISO) nonlinear system is considered:
where t signifies the time. stands for the system output. represents the system input. and denote two unknown integers. stands for the unknown nonlinear function.
The following two assumptions are given for the nonlinear system (1).
Assumption 1.
The partial derivative of is continuously differentiable for all t with finite exceptions.
Assumption 2.
The system (1) is a generalized Lipschitz system, which satisfies , where , , and b represents a positive constant.
Remark 1.
From a practical point of view, these assumptions imposed on the system are reasonable and acceptable. Assumption 1 is a typical constraint for general nonlinear systems in the field of control system design. Assumption 2 imposes an upper bound on the change rate of the system output driven by the change in the control input, where b depends on the system parameters. From an energy viewpoint, the energy change inside a system cannot go to infinity if the energy change in the control input is at a finite level.
Theorem 1.
([42]). For the unknown nonlinear system (1) satisfying Assumptions 1–2, if , system (1) can be converted to a compact-form dynamic linearization data model with the time-varying parameter .
where , denotes a constant. , .
2.1. DoS Attacks
DoS attacks send a large number of useless packets to the network channel to prevent the transmission of real data and thus destroy the data availability. Therefore, the attacker launches DoS attacks on the network control system, resulting in packet loss and failure of the control task.
When DoS attacks occur on the network’s control system, the system out data packet is represented as follows:
where is a random variable that satisfies the Bernoulli distribution. indicates that the attacks succeed and that the controller cannot receive the data packet. indicates that the attacks have failed and that the controller can receive data packets normally. Considering the energy limitation of the attacker, assuming the probability of attack failure is , . The probability of attack success is .
To reduce the impact of the DoS attacks on the control system, the attack compensation mechanism can be conducted as follows:
where is the last unattacked output signal before time t. The attack compensation mechanism (4) can be adjusted according to different attack strategies of attackers, which can handle DoS attacks of different complexity and intensity.
The control task in this article is to design suitable data driven control method to track the reference trajectory .
2.2. Prediction Equation
On the basis of data model (2) and the attack compensation mechanism (4), the one-step-ahead prediction equation is
Hance, in terms of (5), the following N-step ahead prediction equations are obtained:
To facilitate the design of control method and analysis, (6) can be converted to a compact form.
in which , , and .
Furthermore, if , it can be derived that
where , denotes the control horizon.
2.3. Uniform Quantizer and Encoding and Decoding Mechanism
In this article, a quantification of the output data is utilized to settle the problem of the network bandwidth limitations of the system (1). On the basis of [43,44], the uniform quantizer is proposed by
where z is the variable of the uniform quantizer. . stands for the largest quantization level.
The quantization error is defined as . According to the properties of the uniform quantizer (9), is qualified by a constant, namely . Obviously, the uniform quantizer can cause persistent errors that cannot be eliminated naturally. Therefore, the encoding and decoding mechanism is adopted to reduce the impact of quantization errors and improve quantization accuracy. The output data of the system are first encoded and quantified and then decoded, and the decoded data are applied to the control system. In this article, the following encoding and decoding mechanism is given.
According to [45], the encoder is constructed as
The decoder is given by
in which is the output of the encoder and also the input of the decoder. and are the input and internal state of encoder, respectively. is the decoder’s output, which can be considered as an estimate of . is utilized to adjust the difference between the encoder estimation and the system output. , .
In terms of (10) and (11), if is the quantization information, we have the following the encoder:
The decoder is given by
in which , , and denote the input, output, and internal state of the encoder, respectively. is the output of the decoder. .
3. Control Algorithm Design and Analysis
The following performance index functions are given to design the control algorithm.
where .
By minimizing the performance index functions (14) and (15), an IMFAPC strategy with attack compensation mechanism is presented as follows.
where and are weighting factors, and stands for step size factor, . and M denote positive constants. and denote the estimated values of and , , respectively. and . is the parameter of the auto-regressive model (20) which can be obtained using algorithm (18). According to the past estimated sequence , the auto-regressive model (20) is utilized to estimate . . . is the prediction order. . Equation (17) is a reset algorithm that can make the parameter estimation algorithm (16) have strong time-varying parameter tracking ability. Equation (19) is used to ensure the boundedness of . Equation (21) is to guarantee that the prediction parameters’ sign remains unchanged.
Remark 2.
The proposed IMFAPC algorithm (16)–(22) has a certain symmetry in the prediction time domain and the control time domain. It predicts the state and output of the system at multiple times in the future at each sampling time and calculates the optimal control sequence according to the predicted results. This kind of symmetric relationship between the prediction of the future and the optimization of the current control is reflected in time, so as to achieve the optimal performance of the system in the whole prediction interval.
Figure 1 is a block diagram of the control system under a DoS attack that uses the proposed IMFAPC method. According to Figure 1, firstly, the network attack occurs at the output of the system, and the system output data after the attack are processed by the attack compensation mechanism. Secondly, a uniform quantizer with an encoding and decoding mechanism is given to deal with the network bandwidth limitation and to reduce the effects of quantization errors. Finally, based on the quantized output data, the designed IMFAPC method is applied to the system.
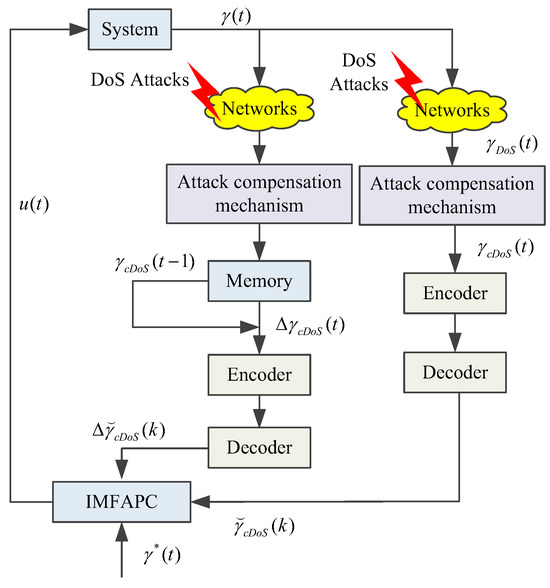
Figure 1.
Block diagram of IMFAPC under DoS attacks.
The IMFAPC algorithm working procedure is summarized in Algorithm 1. According to the IMFAPC method (16)–(22), it is clear that the proposed control algorithm is designed only utilizing I/O data, which is a data-driven control method. In addition, an attack compensation mechanism (4) is introduced, which can be adjusted according to the different attack strategies of attackers, and the elastic control of the DoS attack can be realized for systems with different complexities and attack intensities.
| Algorithm 1: IMFAPC Design for network bandwidth limitation and DoS attacks |
|
Theorem 2.
Consider the nonlinear system (1) satisfying Assumptions 1–2 with the IMFAPC algorithm (17)–(24). If and the parameter meets condition , the tracking error of the system is uniformly ultimate bounded, as t goes to infinity.
Proof of Theorem 2.
The proof of Theorem 2 consists of three parts. Part A is the boundedness of . Part B proves that the tracking error of the system (5) is uniformly ultimate bounded. Part C proves that the tracking error of the system (2) is uniformly ultimate bounded.
Part A is to prove boundedness of .
From (4), (5), and (11), one has
From the uniform quantizer and encoding and decoding mechanisms, we have
According to (23) and (24), it can be derived that
In the same way, one yields
where , .
The parameter estimation error is defined as .
From (16) and (5), it follows that
According to in Theorem 1, we have . Taking the absolute value on both sides of (27) yields
Due to and , there must exist a positive constant such that
Take ; there must exist a positive constant such that
In the light of (28)–(30), it leads to
Therefore, is bounded. Since is bounded, is also bounded. From (18)–(21), it is clear that the boundedness of the prediction values is guaranteed.
Part B proves that the tracking error of the system (5) is uniformly ultimate bounded.
The tracking error of the system is .
From (23) and (25), one has
Since , . Taking absolute value on both sides of (32), it further leads to
Define . Because is a semi-positive definite matrix, and are the positive definite matrixes for .
It is clear that ,
where is the adjoint matrix of . is the algebraic cofactor of .
Therefore, it can be derived that
Since is bounded, (34) is bounded and its upper bound is constant.
Because is a positive definite matrix, is monic polynomial in of degree . is monic polynomial in of degree . is monic polynomial in of degree , where . There must exists a constant , such that (34) has the same positive sign as for .
Hence, there must exist a positive constant such that
From (33) and (35), one can conclude that
According to (36), it can be seen that the tracking error of the system is uniformly ultimate bounded, and the bound is .
Part C proves that the tracking error of the system (2) is uniformly ultimate bounded. Define the tracking error of the system (2) as .
Case 1: When , the system is not attacked. We have
From (25), It follows that
Take the absolute values on both sides of (38) and according to part B, one has
Hence, the tracking error of the system (2) is bounded.
Case 2: When , the system is attacked. One has
According to (25), we have
From part B, it further leads to
Thus, the proof of Theorem 2 is finished. □
4. Simulation Study
In this section, to show the correctness and robustness of the proposed IMFAPC approach, numerical simulations are conducted compared to a quantized data-driven model-free adaptive predictive control (QDDMFAPC) [32]. The following nonlinear system is given for the simulation.
The reference trajectory is .
4.1. Without Disturbance
The initial values of the control system are given by , . The parameters selection for the IMFAPC method is , , , , , , , , , , , . The parameter of DoS attacks is given by . Figure 2 is random variable .
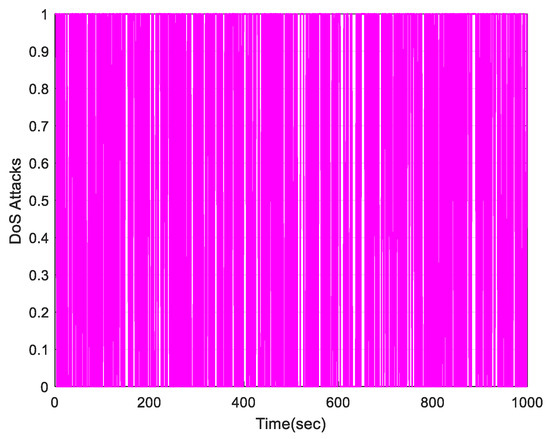
Figure 2.
DoS attacks.
Figure 3 plots the output tracking profiles of the system output and . Figure 4 is the control input profile. Figure 5 plots the tracking error of the system output and . It can be seen from Figure 3 and Figure 5 that the presented IMFAPC algorithm has better control performance under DoS attacks than the QDDMFAPC method.
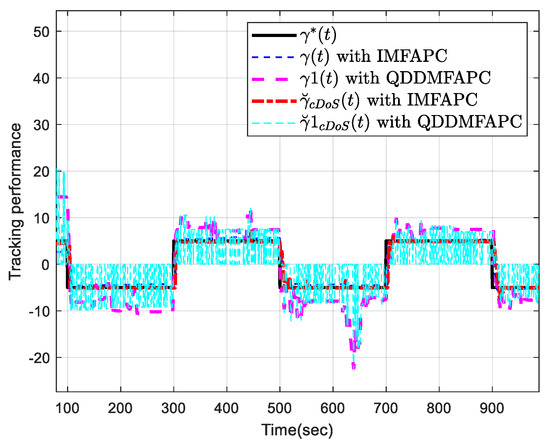
Figure 3.
Output tracking performance.
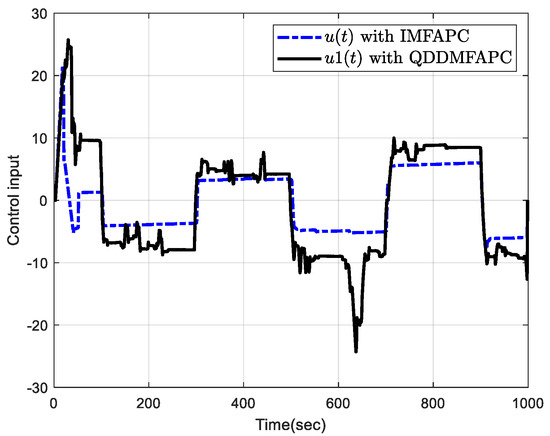
Figure 4.
Control input.
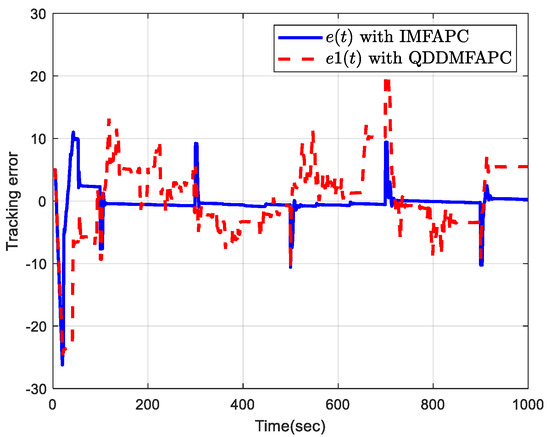
Figure 5.
Tracking error.
Table 1 shows the average error of the proposed IMFAPC algorithm and the existing QDDMFAPC algorithm. It can be seen from Table 1 that the proposed control algorithm has better tracking performance under network attacks and quantization without disturbance.

Table 1.
Comparison of different algorithms without disturbance.
4.2. With Disturbance
In order to verify the correctness and robustness of the presented method, the disturbance d(t) is considered, as shown in Figure 6.
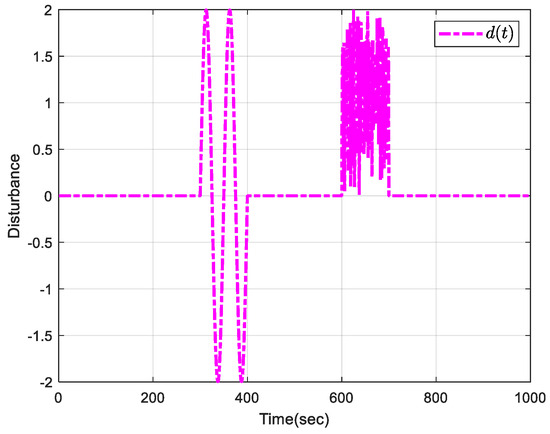
Figure 6.
Disturbance signal.
Under the disturbance, Figure 7 shows random variable with . Figure 8 is the tracking profiles of the control system output and . Figure 9 plots the control input profile with disturbance by using IMFAPC and QDDMFAPC. Figure 10 plots the tracking error. From Figure 8 and Figure 10, it is clear that the system can still achieve good tracking performance under DoS attacks and disturbance, which indicates that the proposed control algorithm is robust.
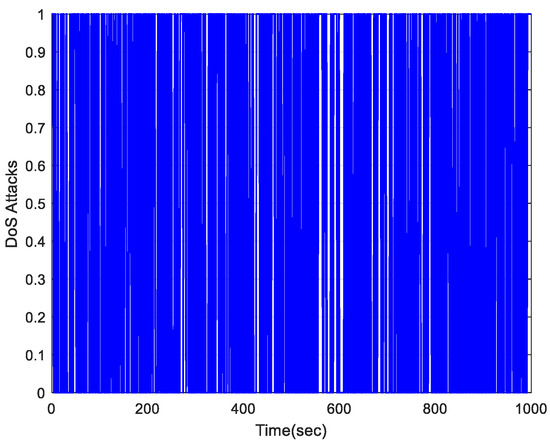
Figure 7.
DoS attacks under disturbance.
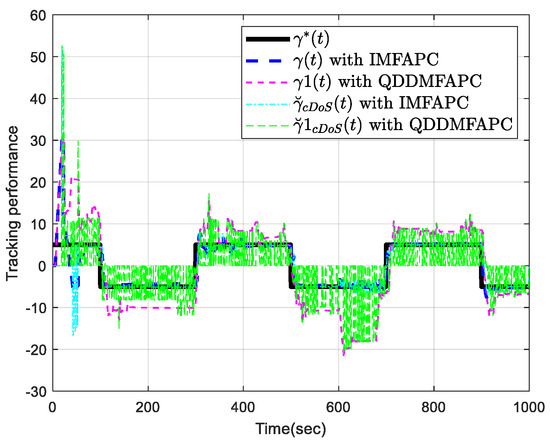
Figure 8.
Tracking performance with disturbance.
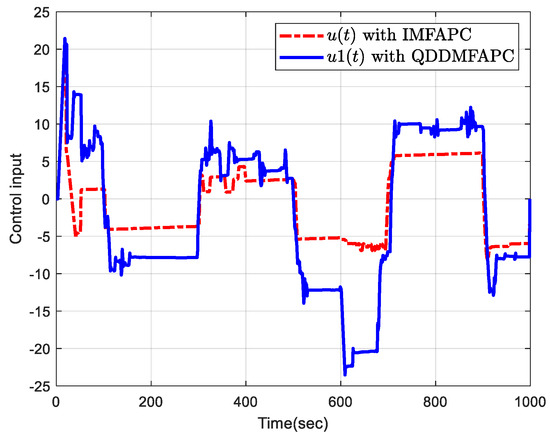
Figure 9.
Control input with disturbance.
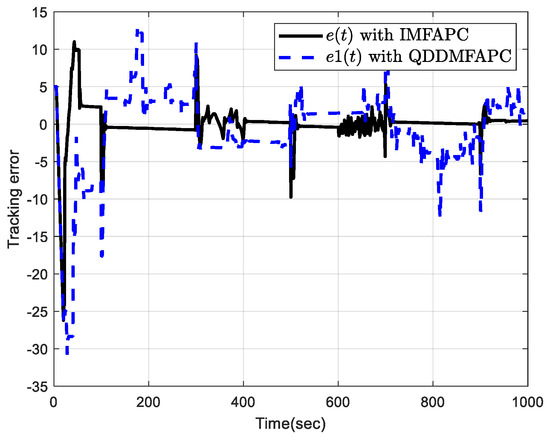
Figure 10.
Tracking error with disturbance.
Table 2 shows the average error of the proposed IMFAPC algorithm and the existing QDDMFAPC algorithm under disturbance. It can be seen from Table 2 that the proposed control algorithm has strong robustness compared to QDDMFAPC.

Table 2.
Comparison of different algorithms with disturbance.
Under the without disturbance and with disturbance conditions, the system control performance can be obtained when data quantization and DoS attacks are considered, which verifies the effectiveness and robustness of the proposed method. Therefore, the simulation results demonstrate the conclusion of Theorem 2.
Table 3 shows the abbreviations that appear in the paper and some primary notation definitions.

Table 3.
Abbreviations/primary notations.
5. Conclusions
In this paper, for unknown nonlinear systems, in order to handle the limited network transmission capacity and DoS attacks, an IMFAPC method is designed. Firstly, considering the impact of the DoS attacks on the control system, an attack compensation mechanism is proposed. Secondly, a uniform quantizer and an encoding and decoding mechanism are proposed to handle the network bandwidth limitation and to reduce the effects of quantization errors. A theoretical analysis of the proposed control method is conducted to illustrate that the tracking error is bounded. Finally, the effectiveness and robustness of the presented control method are verified using simulation results under both undisturbed and disturbed conditions compared to QDDMFAPC. In this paper, the proposed method can only deal with a single-network attack problem, but it is powerless to deal with hybrid network attacks. In the future, we will study data-driven control methods under hybrid attacks.
Author Contributions
Conceptualization, G.L.; methodology, G.L.; software, G.L. and J.Z.; validation, G.L., J.Z., Y.W. (Yule Wang) and Y.W. (Yangyang Wang); formal analysis, G.L. and Y.W. (Yangyang Wang); investigation, G.L.; writing—original draft preparation, G.L.; writing—review and editing, G.L. and Y.W. (Yangyang Wang); supervision, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 62203151, Scientific and Technological Project of Henan Province of China under Grant 252102240132, and High-level Talents Fund Project of Henan University of Technology under Grant 2021BS084.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the anonymous reviewers for their helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hou, Z.S.; Xu, J.X. On data-driven control theory: The state of the art and perspective. Acta Autom. Sin. 2009, 35, 650–667. [Google Scholar] [CrossRef]
- Hou, Z.S.; Chi, R.; Gao, H. An overview of dynamic-linearization-based data-driven control and applications. IEEE Trans. Ind. Electron. 2017, 64, 4076–4090. [Google Scholar] [CrossRef]
- Hou, Z.; Gao, H.; Lewis, F.L. Data-driven control and learning systems. IEEE Trans. Ind. Electron. 2017, 64, 4070–4075. [Google Scholar]
- Hjalmarsson, H.; Gunnarsson, S.; Gevers, M. A Convergent Iterative Restricted Complexity Control Design Scheme. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 1735–1740. [Google Scholar]
- Guardabassi, G.; Savaresi, S. Virtual reference direct design method: An off-line approach to data-based control system design. IEEE Trans. Automat. Contr. 2000, 45, 954–959. [Google Scholar] [CrossRef]
- Liu, G.; Hou, Z. Adaptive iterative learning fault-tolerant control for state constrained nonlinear systems with randomly varying iteration lengths. IEEE Trans. Neural. Networ. 2024, 35, 1735–1749. [Google Scholar] [CrossRef] [PubMed]
- Hou, Z.; Xiong, S. On model-free adaptive control and its stability analysis. IEEE Trans. Automat. Contr. 2019, 64, 4555–4569. [Google Scholar] [CrossRef]
- Liu, S.; Li, Z.; Ji, H.; Hou, Z.; Chen, L. Data learning-based model-free adaptive control and application to an NAO robot. Int. J. Robust Nonlinear Control 2023, 33, 2722–2747. [Google Scholar] [CrossRef]
- Liu, G.; Hou, Z.S. Cooperative adaptive iterative learning fault-tolerant control scheme for multiple subway trains. IEEE Trans. Cybern. 2022, 52, 1098–1111. [Google Scholar] [CrossRef]
- Liu, G.; Hou, Z.S. RBFNN-based adaptive iterative learning fault-tolerant control for subway trains with actuator faults and speed constraint. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5785–5799. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. Model Free Adaptive Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bu, X.; Hou, Z.; Zhang, H. Data-driven multiagent systems consensus tracking using model free adaptive control. IEEE Trans. Neural. Networ. 2018, 29, 1514–1524. [Google Scholar] [CrossRef]
- Bu, X.; Yu, W.; Yu, Q.; Hou, Z.; Yang, J. Event-Triggered Model-Free Adaptive Iterative Learning Control for a Class of Nonlinear Systems Over Fading Channels. IEEE Trans. Cybern. 2022, 52, 9597–9608. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Jin, S.; Bu, X.; Hou, Z.; Yin, C. Model-free adaptive control for a class of MIMO nonlinear cyberphysical systems under false data injection attacks. IEEE Trans Control Netw Syst. 2023, 10, 467–478. [Google Scholar] [CrossRef]
- Zheng, J.; Hou, Z. ESO-Based Model-Free Adaptive Iterative Learning Energy-Efficient Control for Subway Train with Disturbances and Over-Speed Protection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8136–8148. [Google Scholar] [CrossRef]
- Liu, S.; Hou, Z.; Tian, T.; Deng, Z.; Guo, L. Path tracking control of a self-driving wheel excavator via an enhanced data-driven model-free adaptive control approach. IET Control Theory Appl. 2020, 14, 220–232. [Google Scholar] [CrossRef]
- Han, T.; Zhu, H.; Yu, D. Data-Driven Model Predictive Control for Uncalibrated Visual Servoing. Symmetry 2024, 16, 48. [Google Scholar] [CrossRef]
- Jin, S.; Hou, Z.; Chi, R.; Bu, X. Model free adaptive predictive control approach for phase splits of urban traffic network. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5750–5754. [Google Scholar]
- Guo, Y.; Hou, Z.; Liu, S.; Jin, S. Data-driven model-free adaptive predictive control for a class of MIMO nonlinear discrete-time systems with stability analysis. IEEE Access 2019, 7, 102852–102866. [Google Scholar] [CrossRef]
- Hespanha, J.; Naghshtabrizi, P.; Xu, Y. A Survey of Recent Results in Networked Control Systems. Proc. IEEE 2007, 95, 138–162. [Google Scholar] [CrossRef]
- Li, H.; Sun, Z.; Sun, F. Networked control systems: An overview of state-of-the-art and the prospect in future research. Control Theory Appl. 2010, 27, 238–243. [Google Scholar]
- Zhang, X.M.; Han, Q.L.; Yu, X. Survey on Recent Advances in Networked Control Systems. IEEE Trans. Ind. Inform. 2016, 12, 1740–1752. [Google Scholar] [CrossRef]
- Schlotterbeck, C.; Gallegos, J.A.; Teel, A.R.; Núñez, F. Stability guarantees for a class of networked control systems subject to stochastic delays. IEEE Trans. Automat. Contr. 2024, 69, 8884–8891. [Google Scholar] [CrossRef]
- Zhang, W.-A.; Yu, L. Modeling and control of networked control systems with both network-induced delay and packet-dropout. Automatica 2008, 44, 3206–3210. [Google Scholar] [CrossRef]
- Li, T.; Xie, L. Distributed Coordination of Multi-Agent Systems with Quantized-Observer Based Encoding-Decoding. IEEE Trans. Automat. Contr. 2012, 57, 3023–3037. [Google Scholar] [CrossRef]
- Jiang, K.; Mao, L.; Su, Y.; Zheng, Y. Trajectory Tracking Control for Underactuated USV with Prescribed Performance and Input Quantization. Symmetry 2021, 13, 2208. [Google Scholar] [CrossRef]
- Wang, J. Quantized Feedback Control of Discrete-Time MIMO Linear Systems with Input and Output Quantization Over Finite Data Rate Channels. IEEE Trans. Automat. Contr. 2023, 68, 6277–6284. [Google Scholar] [CrossRef]
- Bu, X.; Cheng, Z.; Hou, Z. Iterative learning control for discrete-time systems with quantised measurements. IET Control Theory Appl. 2015, 9, 1455–1460. [Google Scholar] [CrossRef]
- Shen, D.; Zhang, C. Zero-error tracking control under unified quantized iterative learning framework via encoding–decoding method. IEEE Trans. Cybern. 2022, 52, 1979–1991. [Google Scholar] [CrossRef] [PubMed]
- Bu, X.; Qiao, Y.; Hou, Z.; Yang, J. Model Free Adaptive Control for a Class of Nonlinear Systems Using Quantized Information. Asian J. Control 2018, 20, 962–968. [Google Scholar] [CrossRef]
- Zhu, P.; Bu, X.; Liang, J.; Shen, D. Data driven control for a class of nonlinear SISO systems with uniform quantizer using encoding and decoding mechanism. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 7–12. [Google Scholar]
- Liu, G.; Hou, Z. Quantized data driven model-free adaptive predictive control for a class of nonlinear systems. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 12–14 May 2023; pp. 1105–1110. [Google Scholar]
- Ren, H.; Liu, R.; Cheng, Z.; Ma, H.; Li, H. Data-Driven Event-Triggered Control for Nonlinear Multi-Agent Systems with Uniform Quantization. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 712–716. [Google Scholar] [CrossRef]
- Ma, Y.; Che, W.; Deng, C.; Wu, Z. Distributed Model-Free Adaptive Control for Learning Nonlinear MASs Under DoS Attacks. IEEE Trans. Neural. Networ. 2023, 34, 1146–1155. [Google Scholar] [CrossRef]
- Wan, K.; Chen, Y.; Zhao, J.; Yu, M. Event-triggered secure consensus control for DC microgrids under DoS attacks. IEEE Trans. Ind. Electron. 2024, 72, 908–918. [Google Scholar] [CrossRef]
- Tan, C.; Di, J.; Guo, G.; Li, Y.; Wong, W.S. Exponential mean-square stabilization control for cyber-physical systems under random DoS attacks and transmission delay. IEEE Trans. Automat. Contr. 2024, 70, 190–202. [Google Scholar] [CrossRef]
- Xu, X.; Luo, H.; Chen, W.; Gao, L. Containment Control Problem of Linear Multiagent Systems with External Disturbance and DoS Attacks. Symmetry 2023, 15, 384. [Google Scholar] [CrossRef]
- Zhao, N.; Shi, P.; Xing, W.; Lim, C.P. Event-triggered control for networked systems under denial of service attacks and applications. IEEE Trans. Circuits Syst. I Reg. Papers 2022, 69, 811–820. [Google Scholar] [CrossRef]
- Li, Y.; Lu, G.; Li, K. Fuzzy adaptive event-triggered consensus control for nonlinear multiagent systems with output constraints and DoS attacks. IEEE Trans. Cybern. 2024, 55, 2–13. [Google Scholar] [CrossRef]
- Tan, W.; Hou, Z.; Li, Y.X. Robust data-driven iterative learning control for high-speed train with aperiodic DoS attacks and communication delays. IEEE Trans. Intell. Vehicl. 2024, 1–10. [Google Scholar] [CrossRef]
- Bu, X.; Yu, W.; Yin, Y.; Hou, Z. Event-triggered data-driven control for nonlinear systems under frequency-duration-constrained DoS attacks. IEEE Trans. Inf. Forensic. Secur. 2023, 18, 1449–1460. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. A novel data-driven control approach for a class of discrete-time nonlinear systems. IEEE Trans. Contr. Syst. Technol. 2011, 19, 1549–1558. [Google Scholar]
- Zhu, P.; Jin, S.; Bu, X.; Hou, Z. Improved model-free adaptive control for MIMO nonlinear systems with event-triggered transmission scheme and quantization. IEEE Trans. Cybern. 2023, 53, 5867–5880. [Google Scholar] [CrossRef]
- Huo, N.; Shen, D. Encoding–decoding mechanism-based finite-level quantized iterative learning control with random data dropouts. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1343–1360. [Google Scholar] [CrossRef]
- Bu, X.; Zhu, P.; Yu, Q.; Hou, Z.; Liang, J. Model-free adaptive control for a class of nonlinear systems with uniform quantizer. Int. J. Robust Nonlinear Control 2020, 30, 6383–6398. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
