Homogeneous Weights of Linear Codes over 𝔽pm[u, v] of Order p4m
Abstract
1. Introduction
2. Preliminaries
3. On the Ring with Order
- (i)
- If , and where are in then this means that the cyclic code, in , is of the formand this is isomorphic, in , to the cyclic code
- (ii)
- If , and where and then, in , we haveIn , this corresponds to
- (iii)
- Assume that , and where In , we obtainThen, as a correspondent in the ring , the code C is of the form
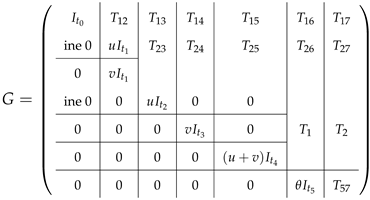
4. Matrices Associated with the MacWilliams Relation for the SWE
5. Homogeneous Weight
- H1.
- If then where
- H2.
- There is such that
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Norton, G.; Sălăgean, A. On the structure of linear cyclic codes over finite chain rings. Appl. Algebra Eng. Commun. Comput. 2000, 10, 489–506. [Google Scholar] [CrossRef]
- Voloch, J.; Walker, J. Homogeneous weights and exponential sums. Finite Fields Their Appl. 2003, 9, 310–321. [Google Scholar] [CrossRef]
- Shi, M.; Ozbudak, F.; Xu, L.; Sol’e, P. LCD codes from tridiagonal Toeplitz matrices. Finite Fields Their Appl. 2021, 75, 101892. [Google Scholar] [CrossRef]
- Shi, M.; Zhu, S.; Yang, S. A class of optimal p-ary codes from one-weight codes over . J. Frankl. Inst. 2013, 350, 929–937. [Google Scholar] [CrossRef]
- Norton, G.H.; Sălăgean, A. On the Hamming distance of linear codes over a finite chain ring. IEEE Trans. Inform. Theory 2000, 46, 1060–1067. [Google Scholar] [CrossRef]
- Alabiad, S.; Alhomaidhi, A.A.; Alsarori, N.A. On linear codes over local rings of order p4. Mathematics 2024, 12, 3069. [Google Scholar] [CrossRef]
- Honold, T. Characterization of finite Frobenius rings. Arch. Math. 2001, 76, 406–415. [Google Scholar] [CrossRef]
- Corbas, B.; Williams, G. Rings of order p5 Part II. Local Rings. J. Algebra 2000, 231, 691–704. [Google Scholar] [CrossRef]
- McDonald, B.R. Finite Rings with Identity; Marcel Dekker: New York, NY, USA, 1974. [Google Scholar]
- Zariski, O.; Samuel, P. Commutative Algebra; Springer: New York, NY, USA, 1960; Volume II. [Google Scholar]
- Matsumura, H. Commutative Ring Theory; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Raghavendran, R. Finite associative rings. Compos. Math. 1969, 21, 195–229. [Google Scholar]
- Wood, J.A. Duality for modules over finite rings and applications to coding theory. Am. J. Math. 1999, 121, 555–575. [Google Scholar] [CrossRef]
- Ayoub, C. On the group of units of certain rings. J. Number Theory 1972, 4, 383–403. [Google Scholar] [CrossRef]
- Alabiad, S.; Alhomaidhi, A.A.; Alsarori, N.A. On linear codes over finite singleton local rings. Mathematics 2024, 12, 1099. [Google Scholar] [CrossRef]
- Castillo-Guillén, C.A.; Rentería-Márquez, C.; Tapia-Recillas, H. Constacyclic codes over finite local Frobenius non-chain rings with nilpotency index 3. Finite Fields Their Appl. 2017, 43, 1–21. [Google Scholar] [CrossRef]
- Alhomaidhi, A.A.; Alabiad, S.; Alsarori, N.A. Generator matrices and symmetrized weight enumerators of linear codes over 𝔽pm + u𝔽pm + v𝔽pm + w𝔽pm. Symmetry 2024, 16, 1169. [Google Scholar] [CrossRef]
| Ring | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhomaidhi, A.A.; Alabiad, S. Homogeneous Weights of Linear Codes over 𝔽pm[u, v] of Order p4m. Symmetry 2025, 17, 440. https://doi.org/10.3390/sym17030440
Alhomaidhi AA, Alabiad S. Homogeneous Weights of Linear Codes over 𝔽pm[u, v] of Order p4m. Symmetry. 2025; 17(3):440. https://doi.org/10.3390/sym17030440
Chicago/Turabian StyleAlhomaidhi, Alhanouf Ali, and Sami Alabiad. 2025. "Homogeneous Weights of Linear Codes over 𝔽pm[u, v] of Order p4m" Symmetry 17, no. 3: 440. https://doi.org/10.3390/sym17030440
APA StyleAlhomaidhi, A. A., & Alabiad, S. (2025). Homogeneous Weights of Linear Codes over 𝔽pm[u, v] of Order p4m. Symmetry, 17(3), 440. https://doi.org/10.3390/sym17030440






