Fractional Optimal Control Problem for Symmetric System Involving Distributed-Order Atangana–Baleanu Derivatives with Non-Singular Kernel
Abstract
1. Introduction
2. Preliminaries
3. Distributed-Order Fractional Atangana–Baleanu Derivatives Using Fractional Variational Principles
4. The Canonical Momenta of Fractions
5. Constrained Systems and Fractional Variational Principles in Distributed-Order Atangana–Baleanu Derivatives
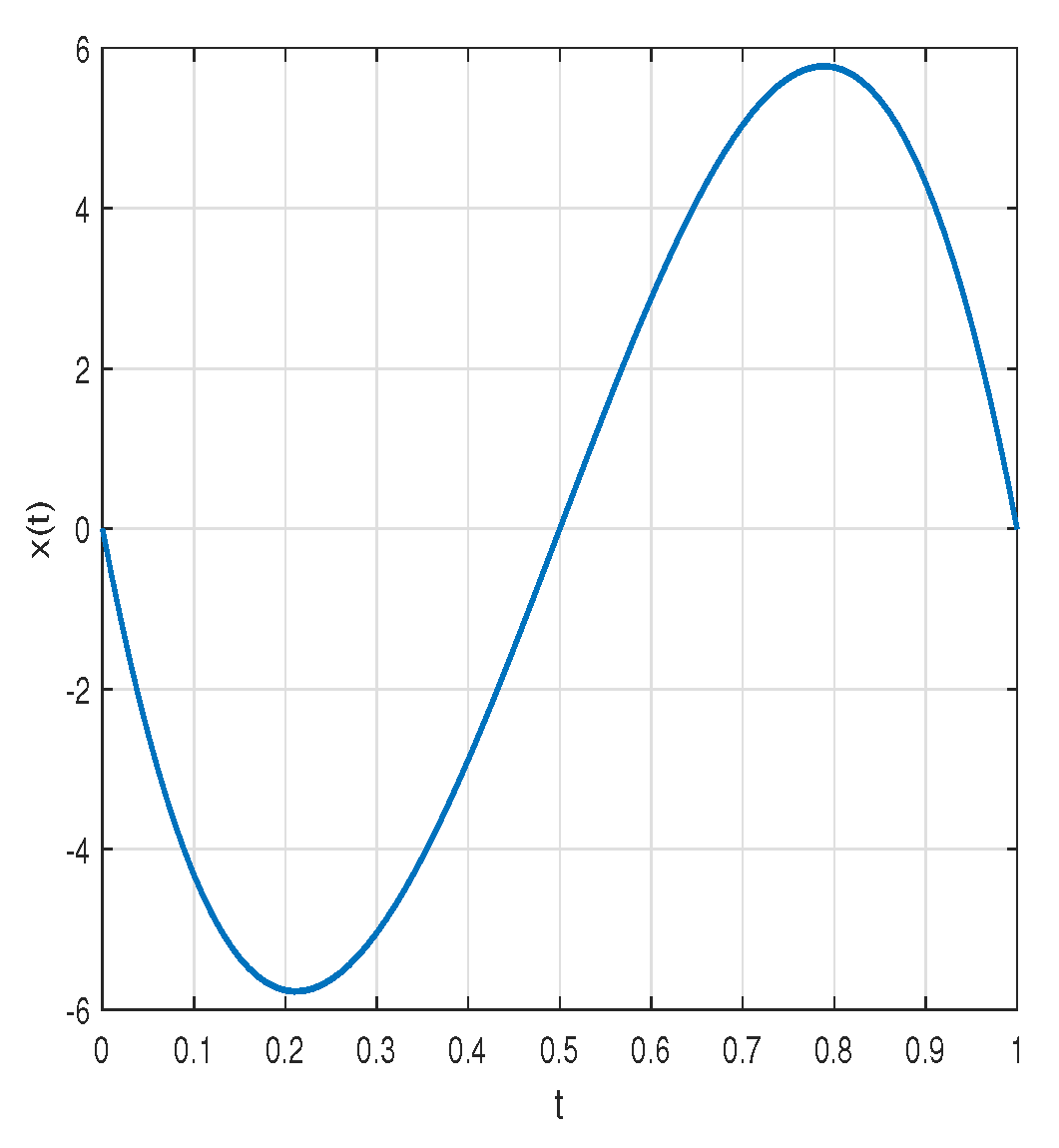
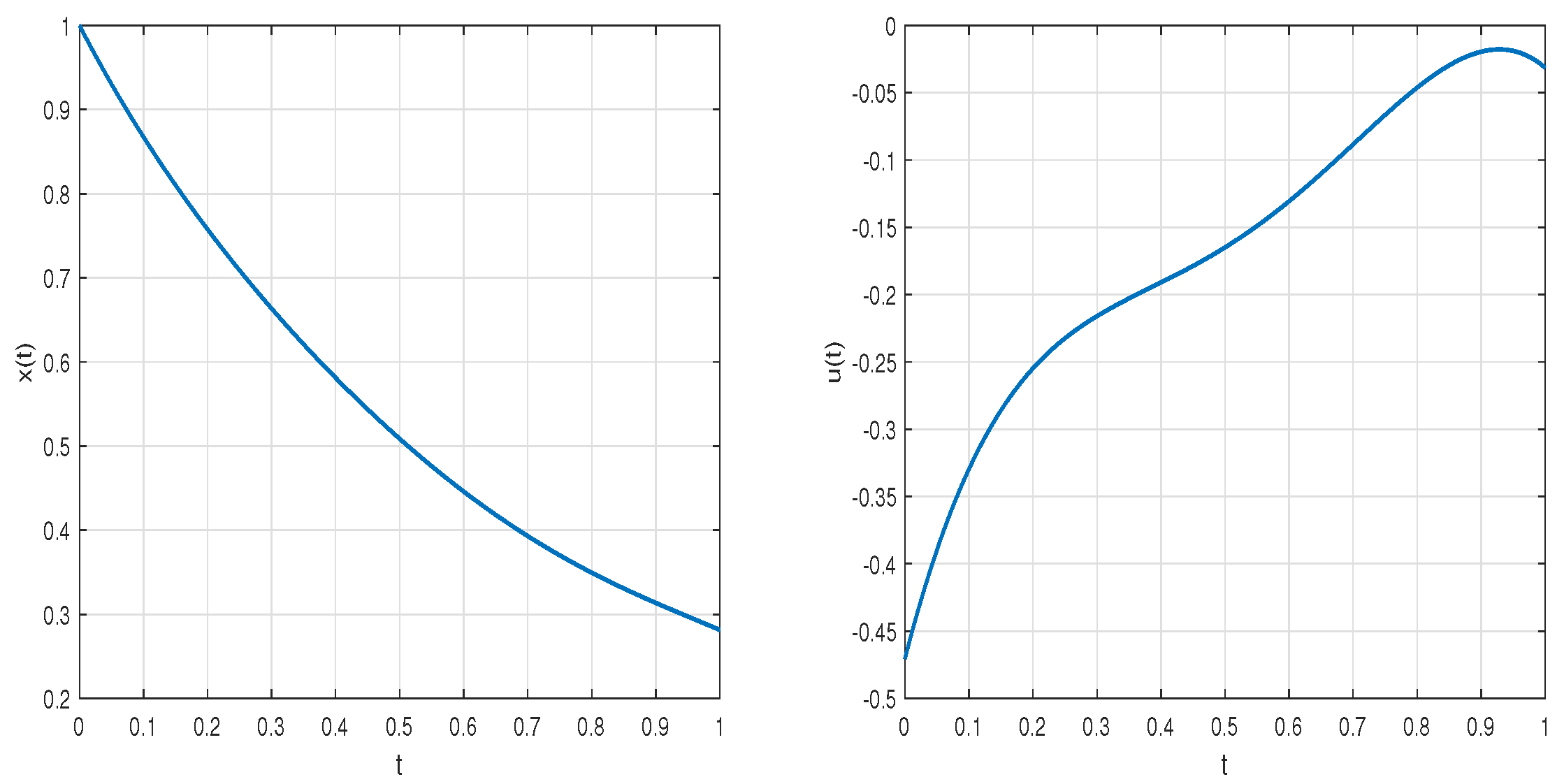
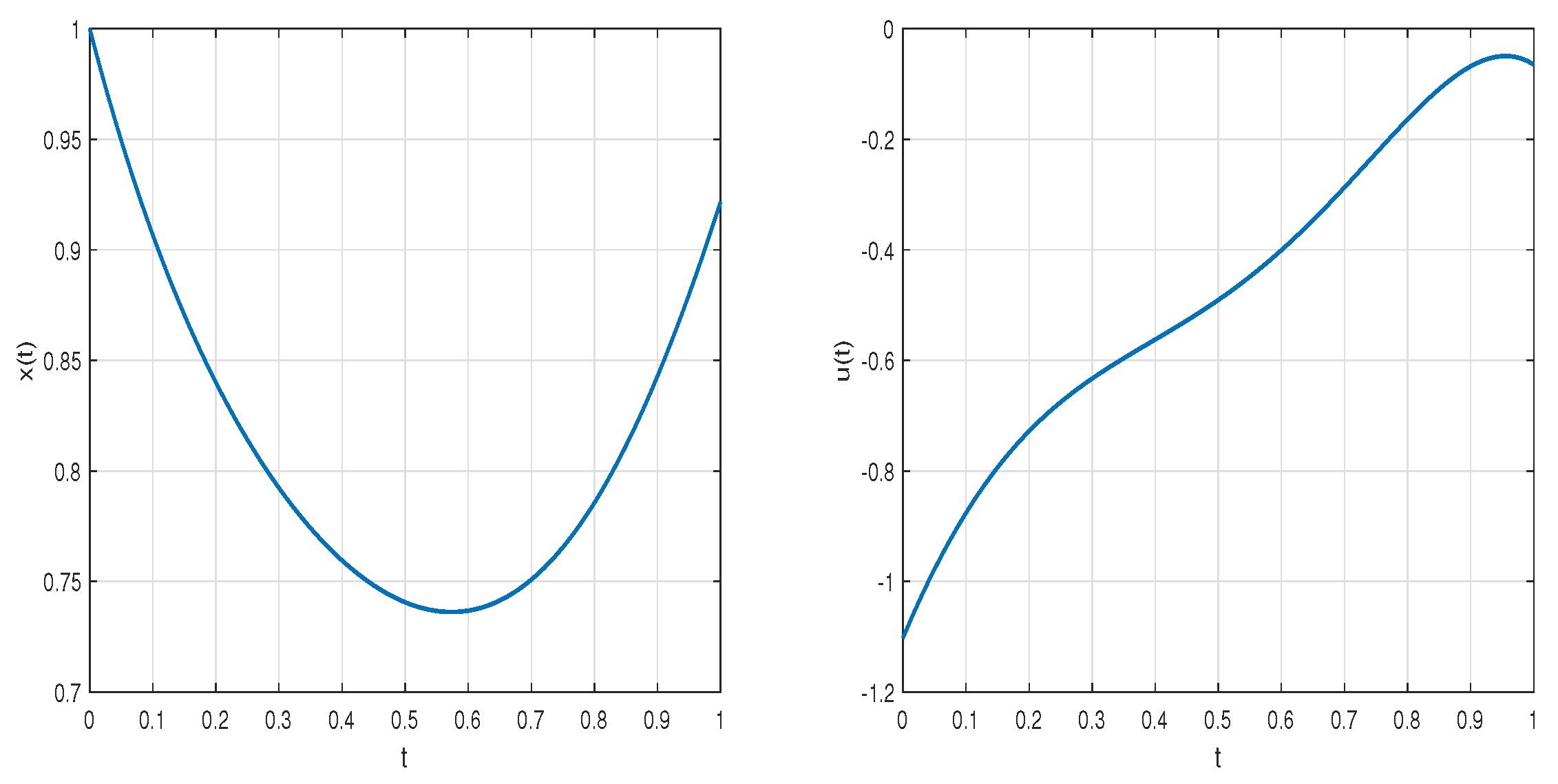
6. Problem of Fractional Optimal Control with Distributed-Order Derivatives of Atangana–Baleanu Derivatives
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2001, 1, 73–85. [Google Scholar]
- Jarad, F.; Ugurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Bahaa, G.M. Optimal control problem for variable-order fractional differential systems with time delay involving Atangana-Baleanu derivatives. Chaos Solitons Fractals (Nonlinear Sci. Nonequilib. Complex Phenom.) 2019, 122, 129–142. [Google Scholar] [CrossRef]
- Sadek, L.; Ounamane, S.; Abouzaid, B.; Sadek, E.M. The Galerkin Bell method to solve the fractional optimal control problems with inequality constraints. J. Comput. Sci. 2024, 77, 102244. [Google Scholar] [CrossRef]
- Sadek, L. Control theory for fractional differential Sylvester matrix equations with Caputo fractional derivative. J. Vib. Control 2024. [Google Scholar] [CrossRef]
- Sadek, L.; Baleanu, D.; Abdo, M.S.; Shatanawi, W. Introducing novel θ-fractional operators: Advances in fractional calculus. J. King Saud Univ.-Sci. 2024, 36, 103352. [Google Scholar] [CrossRef]
- Sadek, L. A cotangent fractional derivative with the application. Fractal Fract. 2023, 7, 44. [Google Scholar] [CrossRef]
- Riewe, F. Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 1996, 53, 1890–1899. [Google Scholar] [CrossRef]
- Riewe, F. Mechanics with fractional derivatives. Phys. Rev. E 1997, 55, 3581–3592. [Google Scholar] [CrossRef]
- Agrawal, O.P. Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 2002, 272, 368–379. [Google Scholar] [CrossRef]
- Agrawal, O.P. A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 2004, 38, 323–337. [Google Scholar] [CrossRef]
- Agrawal, O.P.; Baleanu, D.A. Hamiltonian formulation and direct numerical scheme for fractional optimal control problems. J. Vib. Control 2007, 13, 1269–1281. [Google Scholar] [CrossRef]
- Baleanu, D.; Muslih, S.I. Lagrangian formulation on classical fields within Riemann-Liouville fractional derivatives. Phys. Scr. 2005, 72, 119–121. [Google Scholar] [CrossRef]
- Baleanu, D.; Avkar, T. Lagrangian with linear velocities within Riemann-Liouville fractional derivatives. Nuovo Cimnto B 2004, 119, 73–79. [Google Scholar]
- Baleanu, D.; Agrawal, O.M.P. Fractional Hamilton formalism within Caputo’s derivative. Czechoslov. J. Phys. 2000, 56, 1087–1092. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Hajipour, M. A new formulation of the fractional optimal control problems involving Mittag-Leffler nonsingular kernel. J. Optim. Theory. Appl. 2017, 175, 718–737. [Google Scholar] [CrossRef]
- Bahaa, G.M.; Torres, D.F.M. Time-Fractional Optimal Control of Initial Value Problems on Time Scales. In Nonlinear Analysis and Boundary Value Problems; Area, I., Cabada, A., Cid, J.Á., Franco, D., Liz, E., Pouso, R.L., Rodríguez-López, R., Eds.; Springer International Publishing AG: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Mophou, G.M. Optimal control of fractional diffusion equation. Comput. Math. Appl. 2011, 61, 68–78. [Google Scholar] [CrossRef]
- Mophou, G.M. Optimal control of fractional diffusion equation with state constraints. Comput. Math. Appl. 2011, 62, 1413–1426. [Google Scholar] [CrossRef]
- Abdel-Gaid, S.H.; Qamlo, A.H.; Bahaa, G.M. Bang-bang property and time optimal control for Caputo fractional differential systems. Fractal Fract. 2024, 8, 84. [Google Scholar] [CrossRef]
- Bahaa, G.M. Fractional optimal control problem for variable-order differential systems. Fract. Calc. Appl. Anal. 2017, 20, 1447–1470. [Google Scholar] [CrossRef]
- Bahaa, G.M.; Atangana, A. Necessary and Sufficient Optimality Conditions for Fractional Problems Involving Atangana-Baleanu’s Derivatives. In Fractional Derivatives with Mittag-Leffler Kernel; Studies in Systems, Decision and Control; Gómez, J.F., Torres, L., Escobar, R.F., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 194. [Google Scholar] [CrossRef]
- Bahaa, G.M.; Abdeljawad, T.; Jarad, F. On Mittag-Leffler Kernel-Dependent Fractional Operators with Variable Order. In Fractional Calculus and Fractional Differential Equations; Daftardar-Gejji, V., Ed.; Springer Nature Singapore Pte Ltd.: Singapore, 2019; pp. 41–58. [Google Scholar] [CrossRef]
- Ounamane, S.; Sadek, L.; Abouzaid, B.; Sadek, E.M. Fractional truncated exponential method for linear fractional optimal control problems. Math. Comput. Simul. 2025, 232, 408–426. [Google Scholar] [CrossRef]
- Nosrati, K.; Belikov, J.; Tepljakov, A.; Petlenkov, E. Robust fractional order singular Kalman filter. Int. J. Robust Nonlinear Control 2023, 34, 602–627. [Google Scholar] [CrossRef]
- Bota, C.; Caruntu, B. Analytic approximate solutions for a class of variable order fractional differential equations using the polynomial least squares method. Fract. Calc. Appl. Anal. 2017, 20, 1043–1050. [Google Scholar] [CrossRef]
- Caputo, M. Mean fractional-order-derivatives differential equations and filters. Ann. dell’Univ. Ferrara 1995, 41, 73–84. [Google Scholar] [CrossRef]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Chechkin, A.; Gorenflo, R.; Sokolov, I. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef]
- Djida, J.D.; Atangana, A.; Area, I. Numerical Computation of a Fractional Derivative with Non-Local and Non-Singular Kernel. Math. Model. Nat. Phenom. 2017, 12, 4–13. [Google Scholar] [CrossRef]
- Djida, J.D.; Mophou, G.M.; Area, I. Optimal control of diffusion equation with fractional time derivative with nonlocal and nonsingular mittag-leffler kernel. arXiv 2017, arXiv:1711.09070. [Google Scholar] [CrossRef]
- Eab, C.H.; Lim, S.C. Fractional Langevin equations of distributed order. Phys. Rev. E 2011, 83, 031136. [Google Scholar] [CrossRef]
- Frederico, G.S.F.; Torres, D.F.M. Fractional optimal control in the sense of Caputo and the fractional Noether’s theorem. Int. Math. Forum 2008, 3, 479–493. [Google Scholar]
- Ford, N.; Morgado, M. Distributed order equations as boundary value problems. Comput. Math. Appl. 2012, 64, 2973–2981. [Google Scholar] [CrossRef][Green Version]
- Gòmez-Aguilar, J.F. Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fractals 2017, 35, 179–186. [Google Scholar] [CrossRef]
- Gòmez-Aguilar, J.F. Space-time fractional diffusion equation using a derivative with nonsingular and regular kernel. Phys. A Stat. Mech. Its Appl. 2017, 465, 562–572. [Google Scholar] [CrossRef]
- Gòmez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, J.F. Electrical circuits RC, LC, and RL described by Atangana-Baleanu fractional derivatives. Int. J. Circ. Theor. Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Hartley, T.T.; Lorenzo, C.F. Fractional System Identification: An Approach Using Continuous Order-Distributions; Technical Report; NASA: Washington, DC, USA, 1999.
- Ma, X.-X.; Liu, S.; Li, X.; Zhao, X.-W. Fractional optimal control problems with both integer-order and Atangana–Baleanu Caputo derivatives. Asian J. Control 2023, 25, 4624–4637. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo fractional derivative. Adv. Differ. Equations 2020, 2020, 334. [Google Scholar] [CrossRef]
- Tajadodi, H.; Khan, A.; Francisco Gómez-Aguilar, J.; Khan, H. Optimal control problems with Atangana-Baleanu fractional derivative. Optim. Control Appl. Meth. 2021, 42, 96–109. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlin. Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Pilipovic, S.; Zorica, D. Time distributed-order diffusion-wave equation. I. Volterra-type equation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 1869–1891. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the existence of the order domain and the solution of distributed order equations—Part I. Int. J. Appl. Math. 2000, 2, 865–882. [Google Scholar]
- Jarad, F.; Maraba, T.; Baleanu, D. Fractional variational optimal control problems with delayed arguments. Nonlinear Dyn. 2010, 62, 609–614. [Google Scholar] [CrossRef]
- Jarad, F.; Maraba, T.; Baleanu, D. Higher order fractional variational optimal control problems with delayed arguments. Appl. Math. Comput. 2012, 218, 9234–9240. [Google Scholar] [CrossRef]
- Jafari, H.; Ganji, R.M.; Sayevand, K.; Baleanu, D. A numerical approach for solving fractional optimal control problems with Mittag-Leffler kernel. J. Vibr. Control 2021, 28, 2596–2606. [Google Scholar] [CrossRef]
- Jiao, Z.; Chen, Y.; Podlubny, I. Distributed-Order Dynamic Systems: Stability, Simulation, Applications and Perspectives; Springer: London, UK, 2012. [Google Scholar]
- Liu, Z.; Zeng, S.; Bai, Y. Maximum principles for multi-term space-time variable-order fractional diffusion equations and their applications. Fract. Calc. Appl. Anal. 2016, 19, 188–211. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Mura, A.; Gorenflo, R. Time fractional diffusion of distributed order. J. Vib. Control 2008, 14, 1267–1290. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Scheffler, H.P. Stochastic model for ultraslow diffusion. Stoch. Process. Appl. 2006, 116, 1215–1235. [Google Scholar] [CrossRef]
- Nosrati, K.; Belikov, J.; Tepljakov, A.; Petlenkov, E. Extended fractional singular Kalman filter. Appl. Math. Comput. 2023, 448, 127950. [Google Scholar] [CrossRef]
- Ozdemir, N.; Karadeniz, D.; Iskender, B.B. Fractional optimal control problem of a distributed system in cylindrical coordinates. Phys. Lett. A 2009, 373, 221–226. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.V.; Korabel, N.; Kantz, H.; Sokolov, I.M.; Metzler, R. Distributed-order diffusion equations and multifractality: Models and solutions. Phys. Rev. E 2015, 92, 042117. [Google Scholar] [CrossRef]
- Sokolov, I.; Chechkin, A.; Klafter, J. Distributed-order fractional kinetics. Acta Phys. Pol. B 2004, 35, 1323–1341. [Google Scholar]
- Zaky, M.A. A Legendre spectral quadrature tau method for the multi-term time-fractional diffusion equations. Comp. Appl. Math. 2017, 37, 3525–3538. [Google Scholar] [CrossRef]
- Atanackovic, T.M. A generalized model for the uniaxial isothermal deformation of a viscoelastic body. Acta Mech. 2002, 159, 77–86. [Google Scholar] [CrossRef]
- Luchko, Y. Boundary value problems for the generalized time-fractional diffusion equation of distributed order. Fract. Calc. Appl. Anal. 2009, 12, 409–422. [Google Scholar]
- Abdeljawad, T.; Baleanu, D. Integration by parts and its applications of a new nonlocal fractional derivative with Mittag-Leffler nonsingular kernel. J. Nonlinear Sci. Appl. 2017, 10, 1098–1107. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Int. Tran. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Kochubei, A.N. Distributed order calculus and equations of ultraslow diffusion. J. Math. Anal. Appl. 2008, 340, 252–281. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Baghli, S.; Benchohra, M. Controllability for semilinear functional and neutral functional evolution equations with infinite delay in Frechet spaces. Appl. Math. Optim. 2009, 60, 253–274. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, B.G.; Qamlo, A.H. Fractional Optimal Control Problem for Symmetric System Involving Distributed-Order Atangana–Baleanu Derivatives with Non-Singular Kernel. Symmetry 2025, 17, 417. https://doi.org/10.3390/sym17030417
Mohamed BG, Qamlo AH. Fractional Optimal Control Problem for Symmetric System Involving Distributed-Order Atangana–Baleanu Derivatives with Non-Singular Kernel. Symmetry. 2025; 17(3):417. https://doi.org/10.3390/sym17030417
Chicago/Turabian StyleMohamed, Bahaa Gaber, and Ahlam Hasan Qamlo. 2025. "Fractional Optimal Control Problem for Symmetric System Involving Distributed-Order Atangana–Baleanu Derivatives with Non-Singular Kernel" Symmetry 17, no. 3: 417. https://doi.org/10.3390/sym17030417
APA StyleMohamed, B. G., & Qamlo, A. H. (2025). Fractional Optimal Control Problem for Symmetric System Involving Distributed-Order Atangana–Baleanu Derivatives with Non-Singular Kernel. Symmetry, 17(3), 417. https://doi.org/10.3390/sym17030417





