Riemannian Topological Analysis of Neuronal Activity

Abstract

Cerebral dynamics emerge from the brain’s substrate due to the anatomical patterns of its physical connections, which we know are not a fixed structure but are subject to temporal and local modifications. This circumstance makes it possible for a more or less fixed number of neurons to generate a range of complex networks. By studying the topological space associated with these physical connections and their geometric dynamics, we can use Differential Geometry to study the foundations of the brain’s connectome.

1. Introduction

Our work aims to better understand how brain spiral waves arise by studying the geometric properties of the regular surfaces of a given brain topological space, to which a metric has been incorporated, and, in particular, their minimizing properties, in order to demonstrate that the spiral patterns of neuronal dynamics emerge naturally as the geodesics of this topological space.

Neural networks exhibit an information flow generated by electrical and electrochemical reactions that move within an $n$-dimensional topological space [1]. From this perspective, axonal and neuronal orientation is not arbitrary but governed by the topological dynamics of the brain [2,3]. In this sense, Luo et al. employed a symmetry-based approach as an improvement on neural network architecture to detect and process different network protocol levels [4].

Specifically, Gardner et al. [5] have applied symplectic reconstruction techniques and homological calculus to the modeling of neural activation networks in the VNS. Through a theoretical–experimental study, they have determined neuronal patterns, both locally and globally, and their results, which are based on Algebraic Topology, show that the space used for processing and transferring information in this brain region is topologically equivalent to a toroid. The proposed mathematical modeling of neural network activity reconstructs information locally using directed complete graphs and globally using mathematical structures called simplices [6]. The topological information in these simplicial structures is extracted as Betti numbers, which are associated with the homological holes in the structure [7]. The computational analysis of the homological information from these simplicial complexes enabled them not only to count the number of holes in each dimension of the complex but also to trace the path in adjacent temporal complexes [8]. Thus, they demonstrated that the brain uses complex topological spaces to process information. From a topological perspective, the local flow of information in the VNS is embedded in a toroid.

On the other hand, starting from the concept of Hopf symmetry, which is closely related to most non-linear oscillations, Xu et al. [9] conducted a theoretical–experimental study on the behavior of brain spiral waves. Their work was guided by a linear analysis of a system of equations, performed around a fixed point that was different from the one used to obtain Turing patterns. The richness of the obtained patterns is due to the proximity of two critical lines in the parameter space. This allows for a transition region between the Hopf bifurcation and a saddle-node bifurcation, where the former exhibits regular oscillations within a limit cycle and the latter presents a bistable situation in which spiral traveling wavefronts can appear [10].

They were able to observe how, through successive symmetry breaking, both with respect to the phase and the amplitude of the oscillation, the motion described by the spiral waves became increasingly complex, transitioning from a rotation around a point to circular motion and eventually to a circular helix. Through these symmetry breakings, it was observed that the properties of the spiral waves around the cerebral cortex are ubiquitous. This discovery opens a new approach to understanding how the brain functions, as spiral waves participate in intricate interactions and play a crucial role in the organization of the brain’s complex activities [11].

However, the relationship between the state variables used in these models and the structural and functional peculiarities of brain tissue has not been clarified. The theory of Riemannian manifolds, and particularly the concept of geodesics in these spaces, allows for a more precise specification of this relationship, expressing the bioelectrical and physico-chemical tissue parameters as a function of the topological properties of the fields at the mesoscopic scale [12,13,14,15].

Building upon two apparently unconnected previous results—(i) the shape of the visual nervous system (VNS)-associated topological space is a toroid and (ii) spiral waves are the natural and ubiquitous method used for communication between neurons—we show that (i) and (ii) are intrinsically connected by the existence of certain topological geometric constraints imposed on the associated Riemannian manifold. To this end, we prove that stable circular helices are the solution (the geodesics of the metric manifold) to the minimum equivalent path problem in the toroid. Finally, a local gauge theory is proposed.

2. Preliminary

Definition 1. 

Let $Q$ be a differentiable manifold. An affine connection on $Q$ is the map ∇:

$$\nabla :\mathfrak{X}\left(Q\right)\times \mathfrak{X}\left(Q\right)\to \mathfrak{X}\left(Q\right)$$

$$\left(X,Y\right)\mapsto {\nabla }_{X}Y$$

which satisfies [16]

• ${\nabla }_X\left(aY+b\overline{Y}\right)=a{\nabla }_{X}Y+b{\nabla }_X\overline{Y},\forall a,b\in \mathbb{R},\forall X,Y,\overline{Y}\in \mathfrak{X}\left(Q\right).$
• ${\nabla }_X\left(fY\right)=X\left(f\right)Y+f{\nabla }_{X}Y,\forall f\in C^{\mathrm{\infty }},\forall X,Y\in \mathfrak{X}\left(Q\right).$
• ${\nabla }_{aX+b\overline{X}}\left(Y\right)=a{\nabla }_{X}Y+b{\nabla }_{\overline{X}}\left(Y\right),\forall a,b\in \mathbb{R},\forall X,\overline{X,}Y\in \mathfrak{X}\left(Q\right).$
• ${\nabla }_{fX}Y=f{\nabla }_{X}Y,\forall f\in C^{\mathrm{\infty }},\forall X,Y\in \mathfrak{X}\left(Q\right).$

Proposition 1. 

Let $X,\overline{X}\in \mathfrak{X}\left(Q\right)$ such that $X_p={\overline{X}}_p$ for some $p$ $\in$ $Q$. Then,

$${\left({\nabla }_{X}Y\right)}_p={\left({\nabla }_{\overline{X}}Y\right)}_p,\forall Y\in \mathfrak{X}\left(Q\right).$$

Definition 2. 

Given an affine manifold $\left(Q,\nabla \right)$, a vector field $X$ $\in \mathfrak{X}\left(Q\right)$ is said to be parallel if $\nabla \mathrm{X}\equiv 0$; that is, if

$${\nabla }_{v}Y=0,\forall \hspace{1em}v\in \mathrm{T}\mathrm{Q}.$$

An affine manifold may not admit parallel vector fields.

Definition 3. 

Let $\left(Q,\nabla \right)$ be an affine manifold and let $\left(U,q^1,\dots ,q^n\right)$ be a coordinate neighborhood of $Q$. As we know, the set $\left({\partial }_1\equiv {\displaystyle \frac{\partial }{\partial q^1}},\dots ,{\displaystyle \frac{\partial }{\partial q^n}}\right)$ forms a basis of vector fields on $U$. Since ${\nabla }_{{\partial }_i}{\partial }_j$ is also a vector field on $U$, we can express it pointwise as a linear combination of the coordinate vector fields $\left({\partial }_1,\dots ,{\partial }_n\right)$. Consequently, there exist $n^3$ differentiable functions ${\Gamma }_{ij}^k,i,j,k\in \left\{1,\dots ,n\right\}$, known as the Christoffel symbols of $\nabla$ in the coordinates $\left(q^1,\dots ,q^n\right)$, which satisfy the following properties [17]:

• The values of ${\Gamma }_{ij}^k,i,j,k\in \left\{1,\dots ,n\right\}$ determine the connection $\nabla$ on the open set $U$.
• Conversely, given a coordinate neighborhood $\left(U,q^1,\dots ,q^n\right)$ and an arbitrary set of $n^3$ differentiable functions ${\Gamma }_{ij}^k,i,j,k\in \left\{1,\dots ,n\right\}$ on $U$, there exists a unique affine connection $\nabla$ on $U$ whose Christoffel symbols in the coordinates $\left(q^1,\dots ,q^n\right)$ are ${\Gamma }_{ij}^k$.
• Let ${\Gamma }_{ij}^k$ be the Christoffel symbols of a connection $\nabla$ on $Q$ for the coordinate neighborhood $\left(U,q^1,\dots ,q^n\right)$. It follows that $\nabla$ is symmetric on $U$ (see Definition 1) if and only if ${\Gamma }_{ij}^k={\Gamma }_{ji}^k$ for all $i,j,k$.
• Let $\nabla$ be a connection on $Q$, and let $\left(q^1,\dots ,q^n\right)$ and $\left({\overline{q}}^1,\dots ,{\overline{q}}^n\right)$ be two coordinate systems on the same open set $U\subseteq Q$. The relationship between the Christoffel symbols ${\Gamma }_{ij}^k$ and ${\overline{\Gamma }}_{ij}^k$, which are associated with their respective coordinate systems, is

$${\overline{\Gamma }}_{ij}^s={\displaystyle \sum _{r=1}^n}{\displaystyle \frac{\partial {\overline{q}}^s}{\partial q^r}}{\displaystyle \frac{{\partial q}^r}{\partial {\overline{q}}^i\partial {\overline{q}}^j}}+{\displaystyle \sum _{l,m,r=1}^n}{\displaystyle \frac{\partial q^l}{\partial {\overline{q}}^i}}{\displaystyle \frac{{\partial q}^m}{\partial {\overline{q}}^j}}{\displaystyle \frac{\partial {\overline{q}}^s}{\partial q^r}}{\Gamma }_{lm}^r$$

Definition 4. 

We define the covariant derivative of $X\in \mathfrak{X}\left(Q\right)$ along $\mathsf{\gamma }:I\to Q$ as the following map:

$${\displaystyle \frac{DX}{dt}}:I\to TQ$$

$$t\mapsto {\nabla }_{{\mathsf{\gamma }}^{\prime }\left(\mathrm{t}\right)}X\in T_{{\mathsf{\gamma }}^{\prime }\left(\mathrm{t}\right)}Q.$$

Using the properties of the affine connection from Definition 1, the following are obtained [18]:

1.

The covariant derivative is $\mathbb{R}$-linear, that is,

$${\displaystyle \frac{D\left(aX+b\overline{X}\right)}{dt}}=a{\displaystyle \frac{DX}{dt}}+b{\displaystyle \frac{D\overline{X}}{dt}}.$$

2.

The Leibniz rule for the product holds, that is,

$${\displaystyle \frac{D\left(fX\right)}{dt}}={\mathsf{\gamma }}^{\prime }\left(f\right)X+f{\displaystyle \frac{D\left(X\right)}{dt}}={\displaystyle \frac{d\left(f\circ \mathsf{\gamma }\right)}{dt}}X+f{\displaystyle \frac{DX}{dt}}.$$

The expression for the covariant derivative, in coordinates, is

$${\displaystyle \frac{DX}{dt}}\left(t\right)=\left({\displaystyle \frac{d\left(X^k\circ \mathsf{\gamma }\right)}{dt}}+{\displaystyle \sum _{i,j=1}^n}{X}^i\left(\mathsf{\gamma }\left(\mathrm{t}\right)\right){\dot{q}}^j(t){\Gamma }_{ij}^k\left(\mathsf{\gamma }\left(\mathrm{t}\right)\right)\right){\partial }_k{|}_{\mathsf{\gamma }\left(\mathrm{t}\right)}.$$

The definition of the covariant derivative can be extended to more general vector fields along $\mathsf{\gamma }$, as shown in the following definitions.

Definition 5. 

Given a differentiable curve $\mathsf{\gamma }:I\to Q$, we say that $\widehat{X}$ is a vector field along $\mathsf{\gamma }$ if it is a differentiable map:

$$\widehat{X}:I\to TQ$$

$$t\mapsto \widehat{X}(t)$$

such that $\widehat{X}(t)$ $\in {\mathrm{T}}_{\mathsf{\gamma }\left(\mathrm{t}\right)}Q$, $\forall$ $t$ $\in I$ (that is, such that $\pi \circ \widehat{X}=\mathsf{\gamma }$, where $\pi :TQ\to Q$ is the canonical projection) [19].

Definition 6. 

From Definition 4, it can be shown that the covariant derivative of a vector field along a curve $\mathsf{\gamma }$ depends only on the values of the field along the curve. This allows us to define the covariant derivative along $\mathsf{\gamma }$ of a vector field $\widehat{X}$ along $\mathsf{\gamma }$ that does not necessarily come from a field defined over the entire manifold. In fact, if $\widehat{X}\left(t\right)={\displaystyle \sum _{k=1}^n}{\widehat{X}}^i(t){\displaystyle \frac{\partial }{\partial q^i}}{|}_{\mathsf{\gamma }\left(\mathrm{t}\right)}$, then we define it as follows:

$${\displaystyle \frac{D\widehat{X}}{dt}}\left(t\right)≔\left({\displaystyle \frac{d{\widehat{X}}^k}{dt}}+{\displaystyle \sum _{i,j=1}^n}{\widehat{X}}^i\left(\mathsf{\gamma }\left(\mathrm{t}\right)\right){\dot{q}}^j(t){\Gamma }_{ij}^k\left(\mathsf{\gamma }\left(\mathrm{t}\right)\right)\right){\partial }_k{|}_{\mathsf{\gamma }\left(\mathrm{t}\right)}.$$

This definition is independent of the chosen coordinates.

Definition 7. 

Let $\widehat{X}:I\to TQ$ be a vector field along a curve $\mathsf{\gamma }$. We will say that $\widehat{X}$ is parallel if ${\displaystyle \frac{D\widehat{X}}{dt}}\equiv 0$.

Next, we will see that there is a unique way to parallel transport a vector $v$ along a curve $\mathsf{\gamma }$.

Theorem 1. 

Given a curve $\mathsf{\gamma }:I\to Q$ and a vector $v\in T_{\mathsf{\gamma }\left(t_0\right)}Q$, $t_0\in I$, there exists a unique vector field $V$ along $\mathsf{\gamma }$ such that $V\left(t_0\right)=v$ y ${\displaystyle \frac{DV}{dt}}\equiv 0$.

Let ${\overline{T}}_{t_0}^t\left(v\right)$ denote the vector in $T_{\mathsf{\gamma }\left(t\right)}Q$ obtained by parallel transporting $v$ $\in$ $T_{\mathsf{\gamma }\left(t_0\right)}Q$ along $\mathsf{\gamma }$. Then, the following properties hold [20]:

• The parallel transport map

  $${\overline{T}}_{t_0}^t:T_{\mathsf{\gamma }\left(t_0\right)}Q\to T_{\mathsf{\gamma }\left(t\right)}Q$$

  $$v\mapsto {\overline{T}}_{t_0}^t\left(v\right)$$

  is a vector space isomorphism.
• If $\left(e_1,\dots ,e_n\right)$ is a basis of $T_{\mathsf{\gamma }\left(t_0\right)}Q$ and $E_1,\dots ,E_n$ are the corresponding vector fields along $\mathsf{\gamma }$ obtained by the parallel transport of the vectors $e_1,\dots ,e_n$, respectively, then any parallel vector field $V$ along $\mathsf{\gamma }$ can be written as

  $$V={\displaystyle \sum _{i=1}^n}{a}^i{E}_i{a}^i\in \mathbb{R},\forall i\in \left\{1,\dots ,n\right\}.$$
• The following equality holds: ${\overline{T}}_{t_0}^{t_2}\circ {\overline{T}}_{t_0}^{t_1}={\overline{T}}_{t_0}^{t_2}$, $\forall$ $t_0,t_1,t_2\in I.$
• It is possible to reconstruct the connection from the parallel transport. Indeed, for each vector field $X\in \mathfrak{X}\left(Q\right)$ and each curve $\mathsf{\gamma }$ in $Q$, the vector field $T_{\mathsf{\gamma }\prime \left(t\right)}X$ can be expressed in terms of the parallel transport map, which is as follows:

  $${\nabla }_{{\mathsf{\gamma }}^{\prime }\left(\mathrm{t}\right)}X={lim}_{h\to 0}{\displaystyle \frac{{\overline{T}}_{t+h}^t\left(X_{\mathsf{\gamma }(t+h)}\right)-X_{\mathsf{\gamma }\left(t\right)}}{h}}$$

Up to this point, we have defined the velocity $\mathsf{\gamma }\prime \left(t\right)$ of a differentiable curve $\mathsf{\gamma }\left(t\right)$in $Q$, but not its acceleration. Next, we will see how the connection above allows us to define the latter, and with it, the concept of a geodesic.

Definition 8. 

Let $\left(Q,\nabla \right)$ be an affine manifold and $\mathsf{\gamma }:I\to Q$ a differentiable curve. We will call the acceleration of $\mathsf{\gamma }$ the covariant derivative of its velocity ${\displaystyle \frac{D\mathsf{\gamma }\prime }{dt}}$.

We will say that $\mathsf{\gamma }$ is a geodesic if it has zero acceleration, ${\displaystyle \frac{D\mathsf{\gamma }\prime }{dt}}\equiv 0$, that is, if the vector field $\mathsf{\gamma }\prime \left(t\right)$ is a parallel vector field.

Next, let us study the equation that defines geodesics in coordinates. Given a coordinate neighborhood $\left(U,q^1,\dots ,q^n\right)$ of $Q$ and a vector field $\widehat{X}$ along a curve $\mathsf{\gamma }$ in $U$, the expression of the covariant derivative is given by Definition 6. Therefore, if we take $\widehat{X}\equiv \mathsf{\gamma }\prime$, then [21]

$${\displaystyle \frac{D{\mathsf{\gamma }}^{\prime }}{dt}}\left(t\right)=\left({\displaystyle \frac{d^2{q}^k}{d{t}^2}}(t)+{\displaystyle \sum _{i,j=1}^n}{\dot{q}}^i(t){\dot{q}}^j(t){\Gamma }_{ij}^k\left(\mathsf{\gamma }\left(\mathrm{t}\right)\right)\right){\displaystyle \frac{\partial y}{\partial q^k}}{|}_{\mathsf{\gamma }\left(\mathrm{t}\right)}.$$

Consequently, $\mathsf{\gamma }$ will be a geodesic if and only if the following holds:

$${\displaystyle \frac{d^2{q}^k}{d{t}^2}}\left(t\right)+{\displaystyle \sum _{i,j=1}^n}{\dot{q}}^i(t){\dot{q}}^j(t){\Gamma }_{ij}^k=0,\forall k\in \left\{1,\dots ,n\right\}.$$

Theorem 2. 

Let $\left(Q,\nabla \right)$ be an affine manifold. For each $t_0\in \mathbb{R},p\in \mathrm{Q}$ y ${v\in T}_{p}Q$, there exists a unique geodesic $\mathsf{\gamma }:(a,b)\to Q$ such that [22] the following hold:

(i)

$\mathsf{\gamma }$($t_0)=p,{\mathsf{\gamma }}^{\prime (t_0)}=v$;

(ii)

$\mathsf{\gamma }$ is inextensible (or maximal), that is, there does not exist another geodesic $\overline{\mathsf{\gamma }}$ that satisfies (i) and whose domain of definition strictly contains $(a,b)$.

That is, the initial point and velocity determine the geodesic [23].

3. Results

Here, we use methods from Differential Geometry to solve path optimization problems. Any minimum path problem can be solved by finding geodesics [24]. Minimum paths are the geodesics of their associated manifold, and in a Riemannian manifold in particular, any two points can be connected by at least one geodesic [25].

Consider a surface of revolution $S$ obtained by rotating the circle $C_2$ of radius $b$ around an axis contained in the same plane as $C_2$ in such a way that its center describes a circle $C_1$ of radius $a$. $S$ is called the torus (see Figure 1).

Thus, the coordinates of a point $P$ on $S$ are given by

$$\left\{\begin{array}{c}x=\left(a+b·cos\theta \right)·cos\phi \\ y=\left(a+b·cos\theta \right)·sin\phi \\ z=b·sin\theta \end{array}\right.$$

where

$$\left\{\begin{array}{c}dx=-b·sin\theta ·cos\phi d\theta -\left(a+b·cos\theta \right)·sin\phi d\phi \\ dy=-b·sin\theta ·sin\phi d\theta +\left(a+b·cos\theta \right)·cos\phi d\phi \\ dz=b·cos\theta d\theta \end{array}\right.$$

The tangent plane to $S$ at a point $P$ with coordinates $\left(\theta ,\phi \right)$is the plane spanned by the vectors

$$\left\{\begin{array}{c}{f}_{\theta }\left(\theta ,\phi \right)=(-b·sin\theta ·cos\phi ,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-b·sin\theta ·sin\phi ,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}b·cos\theta )\\ f_{\phi }\left(\theta ,\phi \right)=(-\left(a+b·cos\theta \right)·sin\phi ,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(a+b·cos\theta \right)·cos\phi ,\hspace{1em}\hspace{1em}0)\end{array}\right.$$

and the components $g_{ij}$ of the metric are

$$\left\{\begin{array}{c}{g}_{11}=\left(f_{\theta },f_{\theta }\right)=b^2\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ g_{12}=g_{21}=\left(f_{\theta },f_{\phi }\right)=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ g_{22}=\left(f_{\phi },f_{\phi }\right)={\left(a+b·cos\theta \right)}^2\end{array}\right.$$

That is, $g$ is the $2$-form ${\overline{T}}_2$:

$${\overline{T}}_2={ds}^2{=b}^2{d\theta }^2+{\left(a+b·cos\theta \right)}^2{d\phi }^2$$

$${\overline{T}}_2=\left(\begin{array}{cc}{b}^2& 0\\ 0& {\left(a+b·cos\theta \right)}^2\end{array}\right)$$

$\left(S,g\right)$ is then a Riemannian manifold.

Let us consider curves in $R^3$, that is, $C^{\mathrm{\infty }}$-differentiable submanifolds of dimension $2$ of $R^2$ (and their relative topology). Since $P\in c\subset R^2$, we will write the curve as $x^i=x^i(t)$, $t\in I$, $i=\mathrm{1,2},3$. Furthermore, $R^3$ is a Riemannian manifold with the tensor field $T_2={dx}^1\otimes {dx}^1+{dx}^2\otimes {dx}^2+{dx}^3\otimes {dx}^3$, and $c$ is a Riemannian submanifold of $R^3$ with the restriction ${\overline{T}}_2=T_{2/c}$. At each point of $c$, this field ${\overline{T}}_2$ is the Euclidean inner product and therefore defines a norm [26].

Let us now find the expression, in coordinates, of the first fundamental form. Let $S$ be parametrized as $x^i=x^i\left(\theta ,\phi \right)$, $i=\mathrm{1,2},3$. Then, ${\displaystyle \frac{\partial }{\partial \theta }}$, ${\displaystyle \frac{\partial }{\partial \phi }}$ is a basis of the tangent vector fields to $S$, i.e., $T_{x}S=\left({\left({\displaystyle \frac{\partial }{\partial \theta }}\right)}_x,{\left({\displaystyle \frac{\partial }{\partial \phi }}\right)}_x\right)$. Since

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial }{\partial \theta }}={\displaystyle \sum _{i=1}^3}{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\displaystyle \frac{\partial }{\partial x^i}}\\ {\displaystyle \frac{\partial }{\partial \phi }}={\displaystyle \sum _{i=1}^3}{\displaystyle \frac{\partial x^i}{\partial \phi }}·{\displaystyle \frac{\partial }{\partial x^i}}\end{array}\right.$$

it follows that

$$E={\overline{T}}_2\left({\displaystyle \frac{\partial }{\partial \theta }},{\displaystyle \frac{\partial }{\partial \theta }}\right)=\sum _{i,j}{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\displaystyle \frac{\partial x^j}{\partial \theta }}·T_2\left({\displaystyle \frac{\partial }{\partial x^i}},{\displaystyle \frac{\partial }{\partial x^j}}\right)=\sum _{i,j}{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\displaystyle \frac{\partial x^j}{\partial \theta }}{\delta }_{ij}={\displaystyle \sum _{i=1}^3}{\left({\displaystyle \frac{\partial x^i}{\partial \theta }}\right)}^2$$

Analogously, $F$ and $H$

$$\left\{\begin{array}{c}E={\displaystyle \sum _{i=1}^3}{\left({\displaystyle \frac{\partial x^i}{\partial \theta }}\right)}^2\\ F={\displaystyle \sum _{i=1}^3}{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\displaystyle \frac{\partial x^i}{\partial \phi }}\\ H={\displaystyle \sum _{i=1}^3}{\left({\displaystyle \frac{\partial x^i}{\partial \phi }}\right)}^2\end{array}\right.\hspace{1em}$$

Let $n$ be a normal (unit) field to $S$. Since $n·n=1$, it follows that $n·D_{v}n=0$, i.e., $D_{v}n$ $\in TS$. This allows us to define the following linear map, known as the Weingarten map [27]:

$${Ø}_1^1:TS\to TS$$

$$v\to D_{v}n$$

From it, the tensor can be constructed:

$${Ø}_2\left(v,w\right)=-{\overline{T}}_2\left(v,{Ø}_1^1\left(w\right)\right)=-v·D_{w}n$$

That is,

$${Ø}_2=-i\left({\overline{T}}_2\otimes {Ø}_1^1\right)$$

${\mathrm{Ø}}_2$ is the second fundamental form on the surface $S$ and has the following explicit expression:

$${Ø}_2=e{d\theta }^2+2fd\theta d\phi +{hd\phi }^2$$

Let $n=n^i{\displaystyle \frac{\partial }{\partial x^i}}$ be the unit normal field to $S$. It holds that

$$e={Ø}_2\left({\displaystyle \frac{\partial }{\partial \theta }},{\displaystyle \frac{\partial }{\partial \theta }}\right)=-{Ø}_1^1\left({\displaystyle \frac{\partial }{\partial \theta }}\right)·{\displaystyle \frac{\partial }{\partial \theta }}=-\left(D_{{\displaystyle \frac{\partial }{\partial \theta }}}n\right)·\theta =-{\displaystyle \frac{\partial n^j}{\partial \theta }}·{\displaystyle \frac{\partial }{\partial x^j}}·{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\displaystyle \frac{\partial }{\partial x^i}}=-{\displaystyle \frac{\partial n^j}{\partial \theta }}·{\displaystyle \frac{\partial x^i}{\partial \theta }}·{\delta }_{ij}=-{\displaystyle \frac{\partial n^i}{\partial \theta }}·{\displaystyle \frac{\partial x^i}{\partial \theta }}$$

Analogously, $f$ and $h$

$$\left\{\begin{array}{c}e=-{\displaystyle \frac{\partial n^i}{\partial \theta }}·{\displaystyle \frac{\partial x^i}{\partial \theta }}\\ f=-{\displaystyle \frac{\partial n^i}{\partial \theta }}·{\displaystyle \frac{\partial x^i}{\partial \phi }}\\ h=-{\displaystyle \frac{\partial n^i}{\partial \phi }}·{\displaystyle \frac{\partial x^i}{\partial \phi }}\end{array}\right.\hspace{1em}$$

On the other hand, the Weingarten endomorphism ${\mathrm{Ø}}_1^1=-i\left({\overline{T}}^2\otimes {\mathrm{Ø}}_2\right)$. Let $A,B$, and $C$ be the matrices of ${\overline{T}}_2$, ${\mathrm{Ø}}_1^1$, and ${\mathrm{Ø}}_2$, respectively. It holds that [28]

$$C=-AB=-B^{t}A$$

Furthermore,

$$\left\{\begin{array}{c}A=\left(\begin{array}{cc}E& F\\ F& H\end{array}\right)\\ C=\left(\begin{array}{cc}e& f\\ f& h\end{array}\right)\\ B=-A^{-1}C\end{array}\right.$$

Thus,

$${\overline{T}}^2={\displaystyle \frac{1}{EH-F^2}}·\left(\begin{array}{cc}H& -F\\ -F& E\end{array}\right)$$

from which we find that

$${Ø}_1^1=-{\displaystyle \frac{1}{EH-F^2}}·\left(\begin{array}{cc}eH-fF& fH-hF\\ fE-eF& hE-fF\end{array}\right)$$

The eigenvalues of the Weingarten map ${\mathrm{Ø}}_1^1$ are called the principal curvatures $\left({\lambda }_1 y {\lambda }_2\right)$. The corresponding eigenvectors are called the principal curvature directions. By definition, $k=det{\mathrm{Ø}}_1^1={\lambda }_1·{\lambda }_2$ is the total curvature or Gauss curvature, and $tr=tr{\mathrm{Ø}}_1^1={\lambda }_1+{\lambda }_2$ is the mean curvature. These are the only two invariants of ${\mathrm{Ø}}_1^1$ in $S\subset R^3$ [29].

If $D$ is the Riemannian connection of ${\mathbb{R}}^3$, it follows that, in general, $D_{u}v\notin TS$, $\forall u,v\in \mathrm{T}\mathrm{S}$. Now, the first fundamental form ${\overline{T}}_2$ endows $S$ with the structure of a Riemannian manifold, and therefore there exists a (unique) Riemannian connection on $S$. Let us denote it by ${\overline{D}}_{u}v$ $\in \mathrm{T}\mathrm{S},\forall u,v\in \mathrm{T}\mathrm{S}$. The Gauss equation holds [30]:

$$D_{u}v={\overline{D}}_{u}v+{Ø}_2\left(u,v\right)n,\forall u,v\in \mathrm{T}\mathrm{S}$$

Let $v$ be a unit tangent vector field to a curve on the surface $s$ $\in \mathrm{S}$. As a particular case of the Gauss equation, we have the expression $D_{v}v={\overline{D}}_{v}v+{Ø}_2\left(v,v\right)n$. As we know, the field $D_{v}v$ is the curvature vector of the curve $s$, and its norm $‖D_{v}v‖$ is the curvature of $s$ at each point. ${\overline{D}}_{v}v$ and ${Ø}_2\left(v,v\right)n$ are called the intrinsic (or geodesic) curvature vector and the normal curvature vector, respectively, and their norms $‖D_{v}v‖$ and ${Ø}_2\left(v,v\right)$are the geodesic curvature and normal curvature, respectively. From Meusnier’s Theorem, we know that all curves on $\mathrm{S}$ $\in$ ${\mathbb{R}}^3$ passing through $p$ $\in \mathrm{S}$ and tangent to the same direction have the same normal curvature vector.

As we will see below, from the condition $D_{\overrightarrow{v}}{T}_2=0,\forall \overrightarrow{v}\in TM$, $\forall \overrightarrow{v}\in TM$, where $M$ is a Riemannian manifold, and the requirement that the Christoffel symbols be symmetric in their two lower indices, we can derive the Christoffel symbols as functions of the components of the metric tensor [31].

Let us consider the particular case of the torus:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial }{\partial \mathrm{\theta }}}=\left(-\mathrm{b}·\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\theta }·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\phi },-\mathrm{b}·\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\theta }·\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\phi },\mathrm{b}·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }\right)\\ {\displaystyle \frac{\partial }{\partial \mathrm{\phi }}}=(-\left(\mathrm{a}+\mathrm{b}·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }\right)·\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\phi },\left(\mathrm{a}+\mathrm{b}·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }\right)·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\phi },0)\end{array}\right.$$

$${\displaystyle \frac{\partial }{\partial \mathrm{\theta }}}\times {\displaystyle \frac{\partial }{\partial \mathrm{\phi }}}=\mathrm{b}·\left(\mathrm{a}+\mathrm{b}·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }\right)·\left(-\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\phi },-\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\theta }·\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\phi },-\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{\theta }\right)$$

$$\left\{\begin{array}{c}k={\displaystyle \frac{cos\theta }{b·(a+b·cos\theta )}}\\ tr={\displaystyle \frac{a+2b·cos\theta }{b·(a+b·cos\theta )}}\end{array}\right.$$

$$\left\{\begin{array}{c}e=-N_{\theta }·{\displaystyle \frac{\partial }{\partial \theta }}=-\left(b·{sin}^2\theta ·{sin}^2\phi +b·{sin}^2\theta ·{cos}^2\phi +b·{cos}^2\theta \right)=-b\\ f=-N_{\theta }·{\displaystyle \frac{\partial }{\partial \phi }}=0\\ h=-N_{\phi }·{\displaystyle \frac{\partial }{\partial \phi }}=-\left(a+b·cos\theta \right)·\left(cos\theta ·{sin}^2\theta +cos\theta ·{cos}^2\phi \right)=-\left(a+b·cos\theta \right)·cos\theta \end{array}\right.$$

$$\left\{\begin{array}{c}{Ø}_2=\left(\begin{array}{cc}-b& 0\\ 0& -\left(a+b·cos\theta \right)·cos\theta \end{array}\right)\\ {Ø}_1^1=\left(\begin{array}{cc}{\displaystyle \frac{1}{b}}& 0\\ 0& {\displaystyle \frac{cos\theta }{a+b·cos\theta }}\end{array}\right)\end{array}\right.$$

$$\left\{\begin{array}{c}{\lambda }_1={\displaystyle \frac{1}{b}}\\ {\lambda }_2={\displaystyle \frac{cos\theta }{a+b·cos\theta }}\end{array}\right.$$

$$\left\{\begin{array}{c}k={\displaystyle \frac{cos\theta }{b·(a+b·cos\theta )}}\\ tr={\displaystyle \frac{a+2b·cos\theta }{b·(a+b·cos\theta )}}\end{array}\right.$$

For $\theta =\pm {\displaystyle \frac{\pi }{2}}$, $k=0.$

Now our interest lies in studying the behavior of the geodesics of the torus for this metric $g$. The geodesics on a Riemannian manifold are the curves that solve the following system of differential equations:

$${\displaystyle \frac{d^2{u}^k}{d{t}^2}}+{\displaystyle \sum _{i,j=1}^n}{\Gamma }_{ij}^k{\displaystyle \frac{d{u}^i}{dt}}·{\displaystyle \frac{d{u}^j}{dt}}=0\hspace{1em}k=\mathrm{1,2},\dots ,n,$$

(1)

where $n$ is the dimension of the manifold.

$\left(u^j\right)$ is a coordinate system, and the constants ${\Gamma }_{ik}^l$ are given in terms of the derivatives of the coefficients $g_{ij}$ of the metric $g$.

$${\Gamma }_{ik}^l={\displaystyle \frac{1}{2}}·\sum _j{g}^{lj}·\left({\displaystyle \frac{{\delta }_{g_{ij}}}{\delta u^k}}+{\displaystyle \frac{{\delta }_{g_{jk}}}{\delta u^i}}-{\displaystyle \frac{{\delta }_{g_{ki}}}{\delta u^j}}\right)$$

$g^{lj}$ denotes the coefficients of the inverse of $g$:

$$\sum _k{g}^{lj}·g_{kj}={\delta }_{ij}$$

In the case of the torus, $g_{ij}=0,i\ne j$; hence,

$$\left\{\begin{array}{c}{g}^{ii}={\displaystyle \frac{1}{g_{ii}}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ g^{ij}=0,\hspace{1em}i\ne j\end{array}\right.$$

$$\left\{\begin{array}{c}\begin{array}{c}{\Gamma }_{ik}^k={\displaystyle \frac{1}{2g_{kk}}}·{\displaystyle \frac{{\delta }_{g_{kk}}}{\delta u^i}}\hspace{1em}\\ {\Gamma }_{ik}^k=-{\displaystyle \frac{1}{2g_{kk}}}·{\displaystyle \frac{{\delta }_{g_{ii}}}{\delta u^k}}\end{array}\end{array}\right.$$

Then,

$$\left\{\begin{array}{c}{\Gamma }_{11}^1={\Gamma }_{11}^2={\Gamma }_{12}^1={\Gamma }_{21}^1={\Gamma }_{22}^2=0\\ {\Gamma }_{12}^2={\Gamma }_{21}^2=-{\displaystyle \frac{b·sin\theta }{a+b·cos\theta }}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ {\Gamma }_{22}^1={\displaystyle \frac{sin\theta }{b}}·\left(a+b·cos\theta \right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}\right.$$

and System (1) is then reduced to the following system:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2\theta }{d{t}^2}}+{\displaystyle \frac{sin\theta }{b}}·\left(a+b·cos\theta \right){\left({\displaystyle \frac{d\phi }{dt}}\right)}^2=0\\ {\displaystyle \frac{d^2\phi }{d{t}^2}}-{\displaystyle \frac{2·b·sin\theta }{a+b·cos\theta }}·{\displaystyle \frac{d\theta }{dt}}·{\displaystyle \frac{d\phi }{dt}}=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}\hspace{1em}\right.$$

(2)

To simplify, let us take $b=1$ and $a=R$, reducing System (2) to

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2\theta }{d{t}^2}}+(R+cos\theta )·sin\theta {\left({\displaystyle \frac{d\phi }{dt}}\right)}^2=0\\ {\displaystyle \frac{d^2\phi }{d{t}^2}}-{\displaystyle \frac{2sin\theta }{R+cos\theta }}·{\displaystyle \frac{d\theta }{dt}}·{\displaystyle \frac{d\phi }{dt}}=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}\right.$$

(3)

The problem of finding the geodesics of the torus for the metric $g$ is reduced to finding the solutions for the system of differential equations in (3).

A preliminary trivial solution to the system is $\theta =d,$ $\phi =m$, where $d$ and $m$ are constants, yielding constant geodesics, which are of no further interest.

Non-trivial solutions are readily obtained as shown below.

For a constant $\phi$, ${\displaystyle \frac{d^2\theta }{d{t}^2}}=0$, ${\displaystyle \frac{d\theta }{dt}}=m_1$, and $\theta \left(t\right)=m_{1}t+m_2$, where the values $m_1$ and $m_2$ depend on the initial conditions. These geodesics correspond to the meridional circles of the torus.

For constant $\theta$, System (3) reduces to

$$\left\{\begin{array}{c}(R+cos\theta )·sin\theta {\left({\displaystyle \frac{d\phi }{dt}}\right)}^2=0\\ {\displaystyle \frac{d^2\phi }{d{t}^2}}=0\end{array}\right.$$

(4)

If ${\displaystyle \frac{d\phi }{dt}}=0$, the solution is the trivial case, where $\theta$ and $\phi$ are constant.

Now, let ${\displaystyle \frac{d\phi }{dt}}\ne 0$. From the first equation of System (4), we find that $sin\theta$ must be zero, as $R+cos\theta \ne 0$. Therefore, the only acceptable values for $\theta$ are $\theta =n\pi$.

From the second equation of System (4), we conclude that $\phi \left(t\right)=m_{1}t+m_2$. These solutions correspond to the inner and outer circles of the torus, which are associated with the values $\theta =\pi$ and $\theta =0$, respectively.

In addition to these straightforward solutions, there exist other geodesics whose behavior is not as apparent. Let us study System (3) in detail. If in the second equation of (3) we set $z={\displaystyle \frac{d\phi }{dt}}$, the equation transforms into

$$z\prime -{\displaystyle \frac{2sin\theta }{R+cos\theta }}·{\displaystyle \frac{d\theta }{dt}}·z=0$$

$${\displaystyle \frac{dz}{z}}={\displaystyle \frac{2sin\theta }{R+cos\theta }}d\theta =-2\left(\log \left(R+cos\theta \right)\right)\prime$$

Then,

$${\displaystyle \frac{d\phi }{dt}}=z={\displaystyle \frac{m}{{\left(R+cos\theta \right)}^2}}$$

From this, it follows that this first derivative $\left({\displaystyle \frac{d\phi }{dt}}\right)—$which need not be continuous—does not change sign, so function $\phi$ is monotic, i.e., it is either entirely non-increasing or non-decreasing.

Substituting the value of ${\displaystyle \frac{d\phi }{dt}}$ into the first equation of (3), we obtain

$${\displaystyle \frac{d^2\theta }{d{t}^2}}+\left(R+cos\theta \right)·sin\theta ·{\displaystyle \frac{m^2}{{\left(R+cos\theta \right)}^4}}=0$$

By integrating the previous equation, we obtain

$${\left({\displaystyle \frac{d\theta }{dt}}\right)}^2=-{\displaystyle \frac{m^2}{{\left(R+cos\theta \right)}^2}}+d$$

By imposing the geodesic condition on the previous solution, we obtain the following separable differential equation:

$${\displaystyle \frac{R+cos\theta }{\sqrt{{\left(R+cos\theta \right)}^2-\frac{m^2}{d}}}}d\theta =\sqrt{d}dt$$

And by integrating we obtain

$${\int }_{{\theta }_0}^{\theta }{\displaystyle \frac{R+cos\theta }{\sqrt{{\left(R+cos\theta \right)}^2-\frac{m^2}{d}}}}d\theta =(t-t_0)\sqrt{d}$$

Now, ${\left(R-1\right)}^2\le {\left(R+cos\theta \right)}^2$, which leads us to consider three cases:

(a)

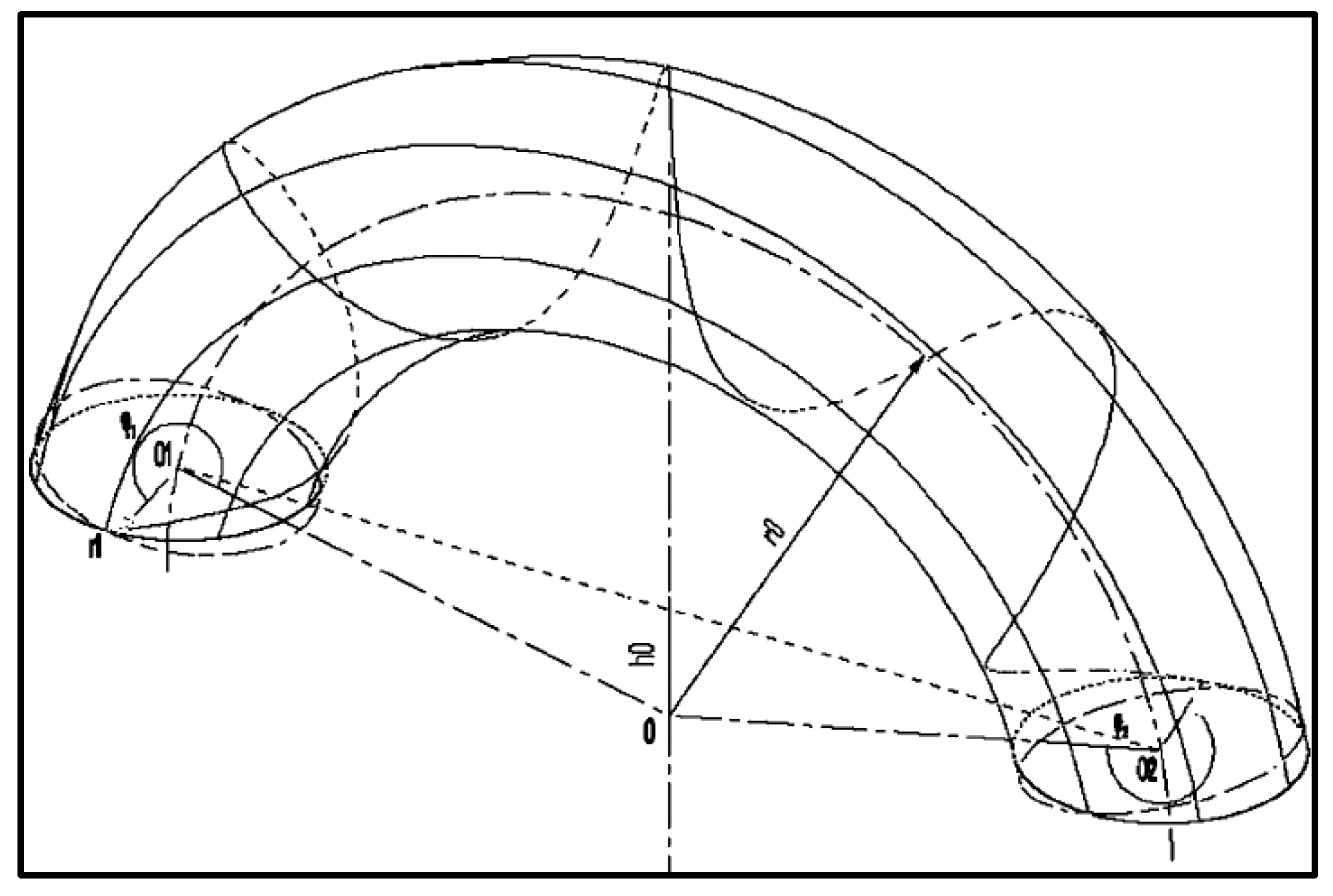
$d$ and $m$ have values such that ${\displaystyle \frac{m^2}{d}}<{\left(R-1\right)}^2$, and the geodesics wind around the torus.

(b)

$d$ and $m$ have values such that ${\displaystyle \frac{m^2}{d}}={\left(R-1\right)}^2$, and then the geodesic is asymptotic to the circle $\theta =\pi .$

(c)

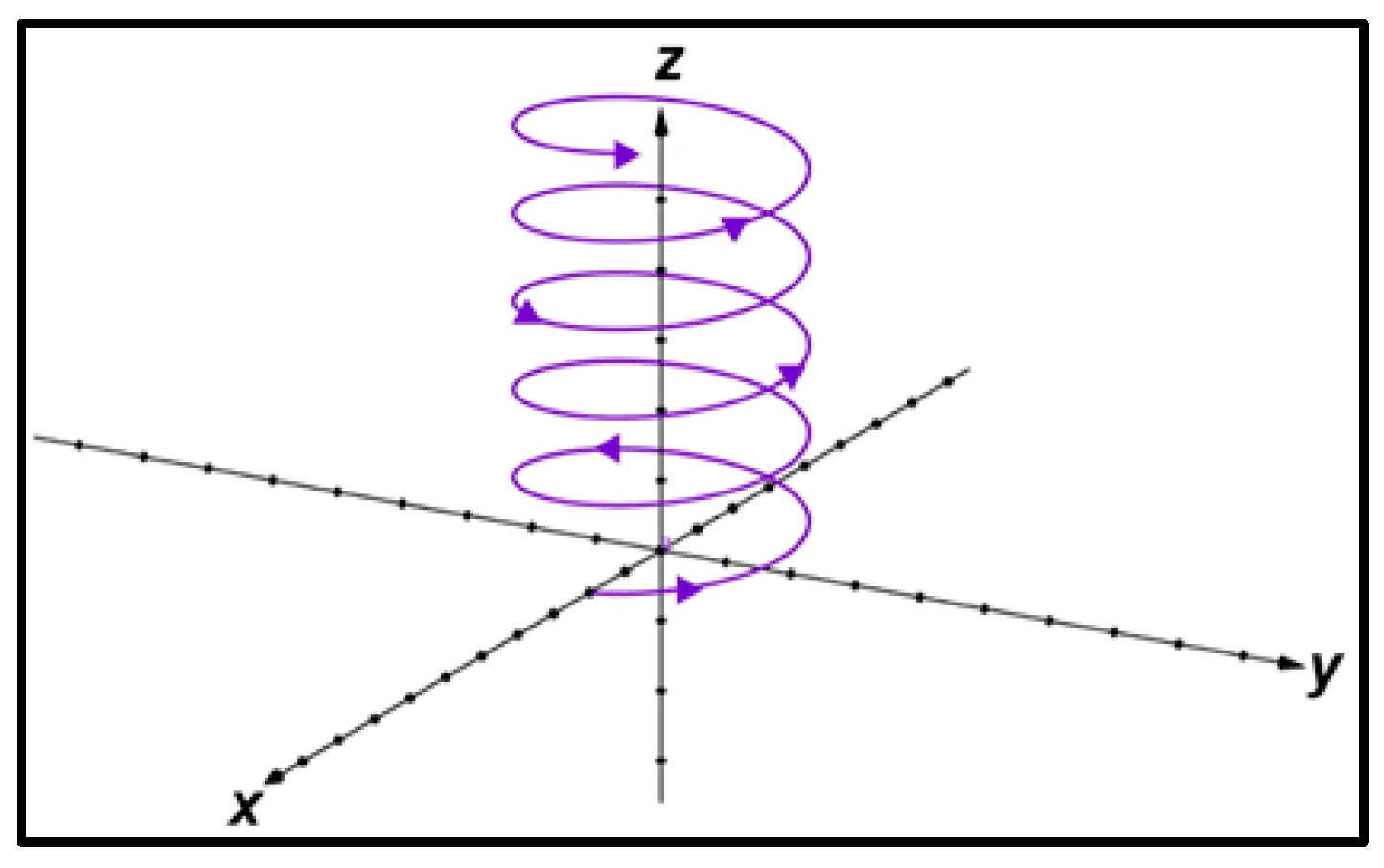
$d$ and $m$ have values such that ${\displaystyle \frac{m^2}{d}}>{\left(R-1\right)}^2$, and then the only geodesics in this case are the curves that wind around the torus in the manner of circular helices on a cylinder (see Figure 2), the meridians, and the parallels.

This can be justified by using the fact that the plane and the torus are homeomorphic and locally isometric. The straight lines, which are the geodesics of the plane, will become helices; thus, they are geodesics on the torus [32].

Now we may observe that not every geodesic on the torus minimizes the distance. Consider two distinct points on the same meridian. We can consider a helix that wraps around the torus and connects the two points. This helix is a geodesic, but it does not minimize the distance between the points. However, every geodesic is locally minimized. Let $\left(S,g\right)$ be a Riemannian manifold and let $\gamma :\left[p_1,p_2\right]\to M$, with $p_1,p_2\in R$, being an admissible curve in $S$. $\gamma$ is said to be minimizing if, for every other admissible curve $\tilde{\gamma }$ with the same endpoints, $L(\gamma )\le L(\tilde{\gamma })$, where $L$ is the length function associated with the metric $g$. Equivalently, the curve $\gamma$ is minimizing if its length is equal to the Riemannian distance between the two endpoints. Next, we will see under which conditions we can guarantee that given two points, $p_1,p_2\in S$, there exists a minimizing geodesic connecting them.

The Hopf–Rinow theorem states that given a complete, simply connected Riemannian manifold of dimension $\ge 2$ and constant curvature $c$, we can guarantee that for any two points $p$ and $q$ on the Riemannian manifold, there exists a minimizing geodesic connecting them [33]. That is, the Hopf–Rinow theorem links metric completeness with geodesic completeness, which is a fundamental result considering that circular helices are the only curves (up to congruence) with constant curvature and torsion.

Let $v$be a unit tangent field to γ. We will take $v={‖{\displaystyle \frac{d}{dt}}‖}^{-1}{\displaystyle \frac{d}{dt}}$, where $‖{\displaystyle \frac{d}{dt}}‖=\sqrt{{\left({\dot{x}}^1\right)}^2+{\left({\dot{x}}^2\right)}^2{+\left({\dot{x}}^3\right)}^2}$, ${\dot{x}}^i={\displaystyle \frac{d{x}^i}{dt}}$.

$v·v=1$ where $v·D_{v}v=0$, and thus $D_{v}v$ is orthogonal to $v$. We also define the (unit) normal field to $\gamma$ as follows: $n={‖D_{v}v‖}^{-1}$. The function along the curve $k=‖D_{v}v‖$ will be called the curvature of $\gamma$. Then, $D_{v}v=kn$. Moreover, the field $D_{v}n+kv$ is orthogonal to both $n$ and $v.$

By definition, the field $q={‖D_{v}v+kv‖}^{-1}\left(D_{v}v+kv\right)$, which is unitary and orthogonal to both $v$ and $n$, will be called the binormal field of $\gamma$. The function over the curve $\tau =‖D_{v}v+kv‖$ is called the torsion of $\gamma$. Therefore, we find that $D_{v}n=-kv+\tau q$.

The trihedron $\left(v,n,q\right)$ is called the Frenet trihedron of the curve. The plane $〈n,q〉$ is called the normal plane, $〈v,n〉$ is the osculating plane, and $〈v,q〉$ is the rectifying plane of $c$ (see Figure 3).

It is possible to completely describe a three-dimensional trajectory by determining how it curves at each instant. Curvature not only measures the variation in the direction in which the trajectory moves but also the time it takes for this direction to change [34]. Thus, the spatiotemporal stability of trajectories depends on their curvature. For domains with increasing curvature, the Hopf instability, which gives rise to oscillating spatial patterns, has been studied as a function of curvature [35,36]. Furthermore, any stability condition on a trajectory induces torsion conditions [37,38].

The parametric equations of a circular helix with radius $r$ and pitch $\rho$ are as follows:

$$\left\{\begin{array}{c}x=r·cos\theta \\ y=r·sin\theta \\ z=\rho ·\theta \hspace{1em}\hspace{1em}\hspace{1em}\end{array}\right.$$

$${\displaystyle \frac{d}{d\theta }}=\left(-r·sin\theta ,r·cos\theta ,\rho \right)$$

$$T={\displaystyle \frac{1}{r^2+{\rho }^2}}·\left(-r·cos\theta ,-r·sin\theta ,0\right)=-{\displaystyle \frac{r}{r^2+{\rho }^2}}·\left(cos\theta ,sin\theta ,0\right)$$

$$N=\left(-cos\theta ,sin\theta ,0\right)$$

$$k={\displaystyle \frac{r}{r^2+{\rho }^2}}$$

$$radius of curvature=\sigma ={\displaystyle \frac{r^2+{\rho }^2}{r}}$$

The center of curvature is as follows:

$${\overrightarrow{x}}^{\prime }=\left(r·cos\theta ,r·sin\theta ,\rho ·\theta \right)-{\displaystyle \frac{r^2+{\rho }^2}{a}}·\left(cos\theta ,sin\theta ,0\right)\Rightarrow$$

$${\overrightarrow{x}}^{\prime }=\left(-{\displaystyle \frac{{\rho }^2}{r}}·cos\theta ,r·sin\theta ,\rho ·\theta \right)$$

This is the equation of another circular helix with

$$\left\{\begin{array}{c}{r}^{\prime }=-{\displaystyle \frac{{\rho }^2}{r}}\\ {\rho }^{\prime }=\rho \hspace{1em}\hspace{1em}\end{array}\right.$$

(5)

It is coaxial and has the same pitch as the original helix:

$$r^{\prime }=-{\displaystyle \frac{{{\rho }^{\prime }}^2}{r^{\prime }}}=-{\displaystyle \frac{{\rho }^2}{\frac{-{\rho }^2}{r}}}=r,{\rho }^{″}={\rho }^{\prime }=\rho$$

(6)

We thus recover the original helix:

$${\overrightarrow{x}}^{″}={\overrightarrow{x}}^{\prime }$$

(7)

Furthermore,

$$k^{\prime }={\displaystyle \frac{r^{\prime }}{{r^{\prime }}^2+{{\rho }^{\prime }}^2}}=-{\displaystyle \frac{r}{r^2+{\rho }^2}}=-k\hspace{1em}$$

(8)

Now we calculate the torsions:

$$\tau ={\displaystyle \frac{\mathrm{d}\mathrm{e}\mathrm{t}(\dot{x},\ddot{x},\stackrel{⃛}{x})}{k^2}}={\displaystyle \frac{1}{{\left(r^2+{\rho }^2\right)}^3}}·{\left({\displaystyle \frac{r^2+{\rho }^2}{r}}\right)}^2·\left|\begin{array}{ccc}-r·sin\theta & -r·cos\theta & r·sin\theta \\ r·cos\theta & -r·sin\theta & -r·cos\theta \\ \rho & 0& 0\end{array}\right|={\displaystyle \frac{\rho ·r^2}{r^2·(r^2+{\rho }^2)}}={\displaystyle \frac{\rho }{r^2+{\rho }^2}}$$

(9)

$${\tau }^{\prime }={\displaystyle \frac{{\rho }^{\prime }}{{r^{\prime }}^2+{{\rho }^{\prime }}^2}}={\displaystyle \frac{r^2}{\rho ·(r^2+{\rho }^2)}}={\displaystyle \frac{r^2}{{\rho }^2}}·\tau$$

(10)

Both the center of curvature and the radius of curvature vary depending on the point of the trajectory. The center of curvature is also contained in the osculating plane. We can define it as the plane defined by two infinitely close tangents that contain a differential element in their trajectory, so that the trajectory can be locally considered flat in the osculating plane. The tangential and normal components of acceleration have a defined physical interpretation. The tangential component arises from the variation in the speed modulus over time, while the normal component arises from the variation in the direction of velocity over time [39,40]. The osculating plane coincides with the plane of motion, as both the tangential acceleration vector and the normal acceleration vector for each point on the trajectory (or, equivalently, for each instant) are contained within the osculating plane [41].

In summary, the motion of a particle moving along a defined trajectory is fully determined if the equation of that trajectory is known; more specifically, if the osculating plane associated with that trajectory and the associated parameters are known. The analysis of the trajectory, and, specifically, of its curvature and torsion, allows for the determination of the direction and stability of the unit normal vector and, by extension, of the trajectory, or, in our case, of the geodesics (see Figure 4).

4. Discussion

Our geometric approach can be interpreted as a spatial averaging operation of the voltages and currents in the intracellular space and the interstitial space, eliminating unnecessary details. In particular, we demonstrate that the existence of a synaptic propagation with a spiral (helical) shape in the VNS naturally arises from the structure of the Riemannian manifold associated with the VNS: a toroid. Our final result (Equations (5)–(10)) guarantees the stability of the spiral solutions obtained previously. If we assume this stability, then the synaptic activity is in an almost circular helicoidal orbit, whose radius is approximately constant.

In general, it is very difficult, and sometimes impossible, to solve Differential Geometry problems explicitly in terms of formulas or geometric constructions involving simple known elements. Instead, it is often sufficient to simply prove the existence of a solution under certain conditions and then investigate the properties of the solution afterward. In many cases, when such an existence proof turns out to be more or less difficult, it can be useful to simulate the mathematical conditions of the problem with corresponding physical artifacts or, rather, to consider the mathematical problem as an interpretation of a physical phenomenon. The existence of the physical phenomenon then represents the solution to the mathematical problem.

Einstein’s theory of gravitation geometrizes the gravitational field from the moment it interprets the potentials $g_{ij}$ as components of the metric tensor and identifies the geometric structure of spacetime as having the structure of what, from the classical perspective, would be a gravitational field. No such analogy is found in relation to the electromagnetic (EM) field: the fundamental elements of the Maxwell–Lorentz field, the components of electromagnetic potential, remain purely physical quantities, with no connection to any possible geometric meaning. They do, however, feature as components of the spacetime structure, but at the same level as pressure or matter density: their influence on that structure occurs solely through the energy–momentum tensor, nothing more.

Another consequence of incorporating electromagnetism into relativistic theory is that the equations of the worldlines of an incoherent, electrically charged material fluid are no longer geodesics of spacetime, if spacetime is considered a four-dimensional Riemannian space. Certain terms appear in them that correspond to the ponderomotive forces of Lorentz’s theory. This result is nothing more than the geometric manifestation of the fact that the EM field in Einstein’s original theory appears as juxtaposed to the material gravitational field, as a term added to the energy–momentum mass tensor, without its characteristic elements receiving a geometric interpretation.

Geometrizing the EM field was one of the methods adopted to attempt its unification with the gravitational field, which led to Weyl’s theory [42]. The aim was to attribute to the former a geometric meaning somewhat similar to the one Einstein was able to assign to the latter. This was not possible without departing from the Riemannian framework. To achieve this, Weyl generalized the concept of Riemannian space, modifying its metric connection and making it a non-integrable connection. Although the theory failed, Weyl had managed to describe a geometric generalization of Riemannian space, the Weyl space, thereby initiating what would become known as gauge theories.

The ultimate goal of any physical theory is to make predictions about observable quantities. Certain theories exhibit structural ambiguities, where the functions describing the states of a given physical system are not uniquely determined. If the observables predicted by a given physical system are invariant under changes or transformations allowed by the structure of the theory, then these changes are physically irrelevant. In this case, the theory is said to have gauge freedom.

Before Einstein, a physical law followed a methodological sequence: experiments ⇒ equations of interaction ⇒ symmetry (invariance). After Einstein, this scheme was reversed; it is now symmetry that dictates the interaction [43]. Consequently, the most straightforward approach to formulating a covariant theory of neuronal activity would be through a gauge theory, modifying the Lagrangian but not the pseudo-Riemannian geometry. So, we propose an intuitive gauge formulation constructed by imposing local Lorentz invariance and covariance under diffeomorphisms.

5. Conclusions

There is a clear missing link in research between the structure of a neural network and its emerging function [44]. Understanding the connectivity of the network reveals how changes in the intrinsic structures within that neural network seem to accompany neurological and psychological disorders and may even be used as diagnostic markers for pathologies such as Alzheimer’s disease, strokes, and autism [45,46]. Researchers are using topological tools to understand states of consciousness, sensory neuroscience, and the morphological properties of brain arteries throughout life [47,48].

Through neurotopology, it is possible to define the trajectories of synaptic signals in specific brain regions, which subsequently release different electrical, chemical, and electrochemical impulses that trigger a cascade of multiple recurrent inter- and intraneuronal connectivity factors [49,50,51,52]. These factors are optimized as the neuroelectric morphology is modified, minimizing the resources invested in this process while maximizing the processing and storage of information [53,54].

Attempting to apply the canonical methods typically employed in the classical theory of neuronal activity to complex brain connectome dynamics can lead to significant challenges [55,56,57]. It is well known that Einstein, originally, starting from the principles of equivalence (weak and strong) and general covariance, generalized Newton’s theory of gravitation, not in its original form, as a theory of point particles (although he later generalized it to the geodesic law, i.e., the Newtonian law of motion), but in its Lagrange–Laplace–Poisson formulation, i.e., as a field theory that can be used when bodies are extended and not rigid—such as the brain—based on the Poisson equation and with the presence of sources (masses) in the gravitational field [58]. Ordinarily, physical theories provide a clear distinction between physical phenomena and the arena in which these phenomena take place. For example, in electrodynamics, the arena is Minkowski spacetime and the phenomenon is the Maxwell–Faraday field; in classical mechanics, the arena is physical space (or configuration space) and the phenomenon is the dynamic trajectories of particles. In General Relativity, this distinction no longer holds, as the pseudo-Riemannian metric of the arena is simultaneously the gravitational potential. Here, we propose an alternative method for describing the emerging ideas about brain connectome–EM interactions by applying both Einstein’s original theory and the gauge formulation.

Hamiltonian and Lagrangian formulations are two basic, elegant, and general formulations of classical mechanics in the sense that they provide a unified framework with which to address seemingly distinct mechanical systems. When studying systems of particles and rigid bodies, the presence of symmetries and their associated invariants play an essential role. In our approach, the research on the differential geometric analysis of differential equations includes the inverse problem of variational calculus. The latter is equivalent to a Lagrangian system, and more specifically to the minimum path calculation problem. The minimum path problem is the problem of finding a point in a certain region where the function attains its minimum (or maximum) value; in some cases, the existence of a minimum is by no means evident, and it turns out to be an extremely difficult issue. There are many examples that confirm that caution is truly necessary regarding the existence of a solution in minimum problems with a complex structure [59,60]. While in classical problems solved using differential calculus, the quantity to be minimized depended only on one or more numerical variables, in these complex problems, the quantity considered, the elapsed time, depends on the entire curve.