Investigation of Turbulence Characteristics Influenced by Flow Velocity, Roughness, and Eccentricity in Horizontal Annuli Based on Numerical Simulation
Abstract
1. Introduction
2. Methods and Procedures
2.1. Numerical Simulation
2.1.1. Numerical Model
- (1)
- Governing equation
- (2)
- Turbulence model
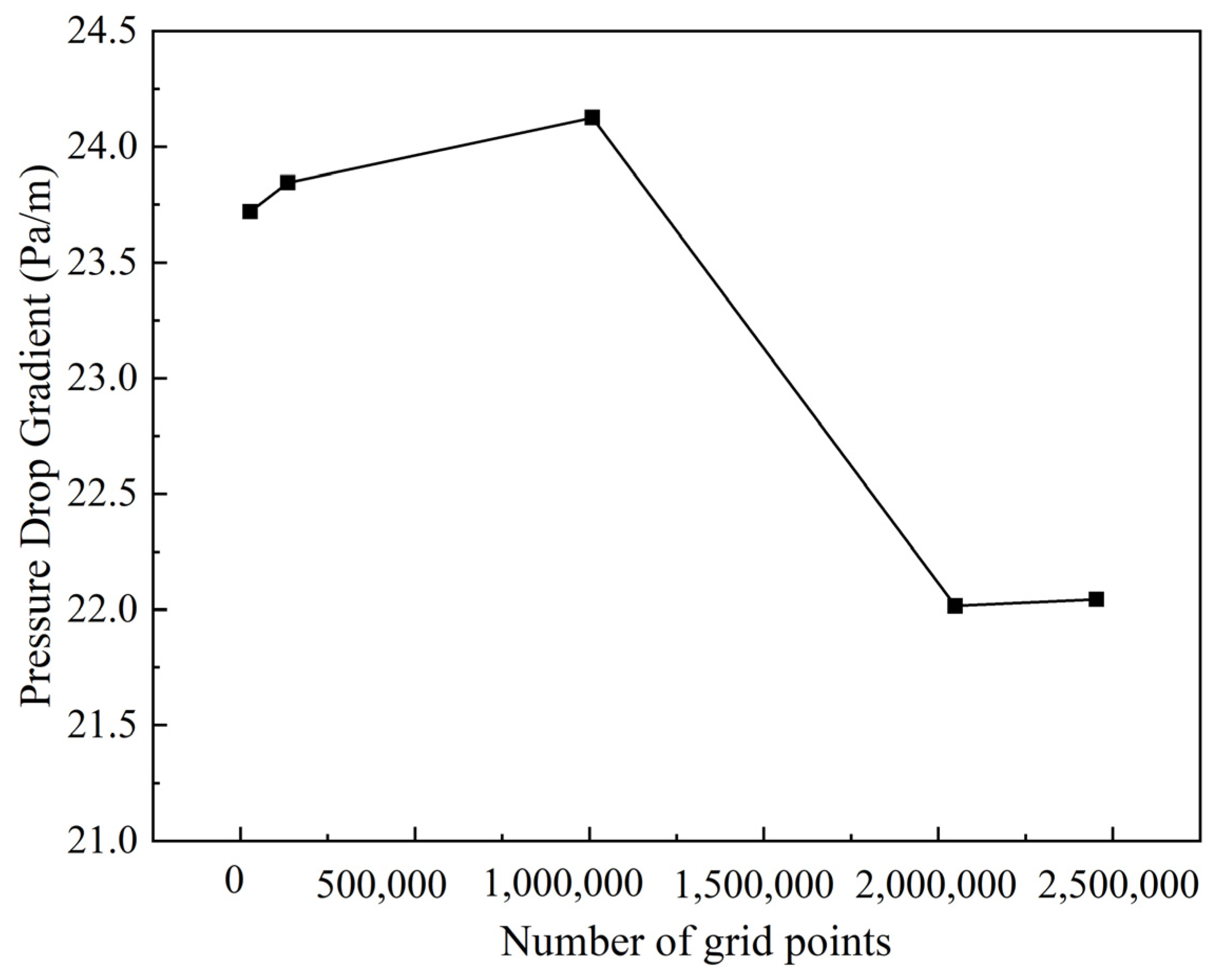
2.1.2. Model Validation
3. Results and Discussion
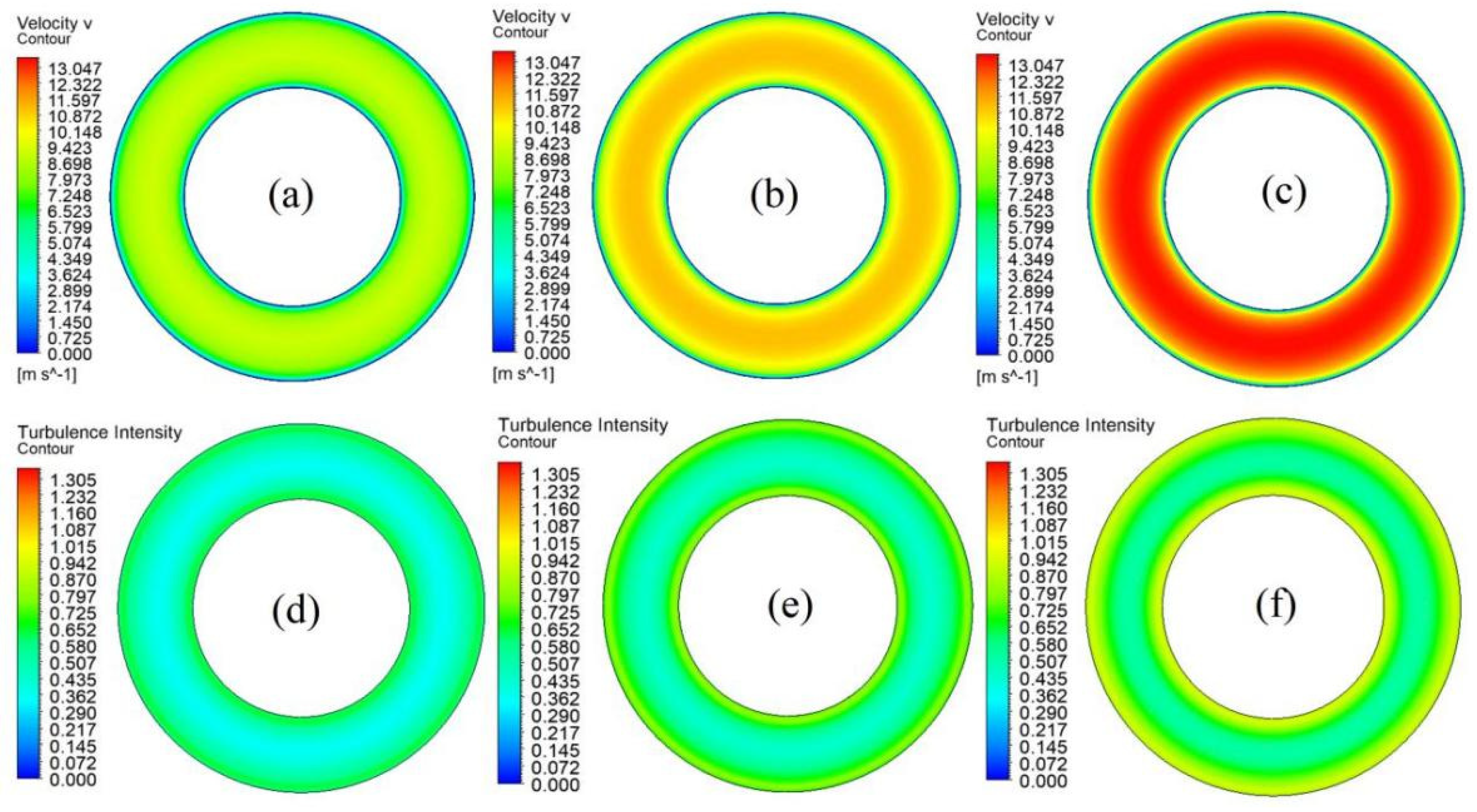
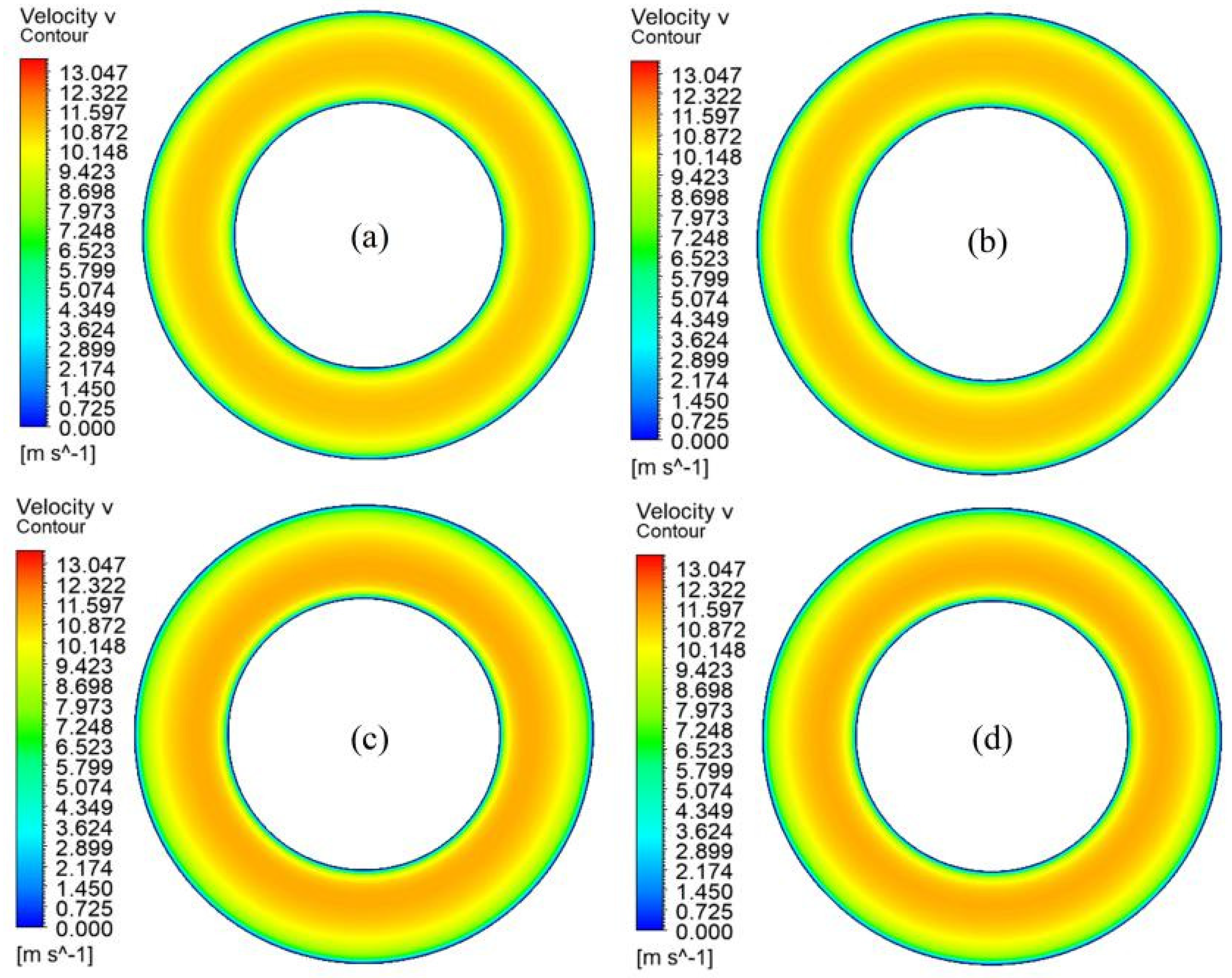
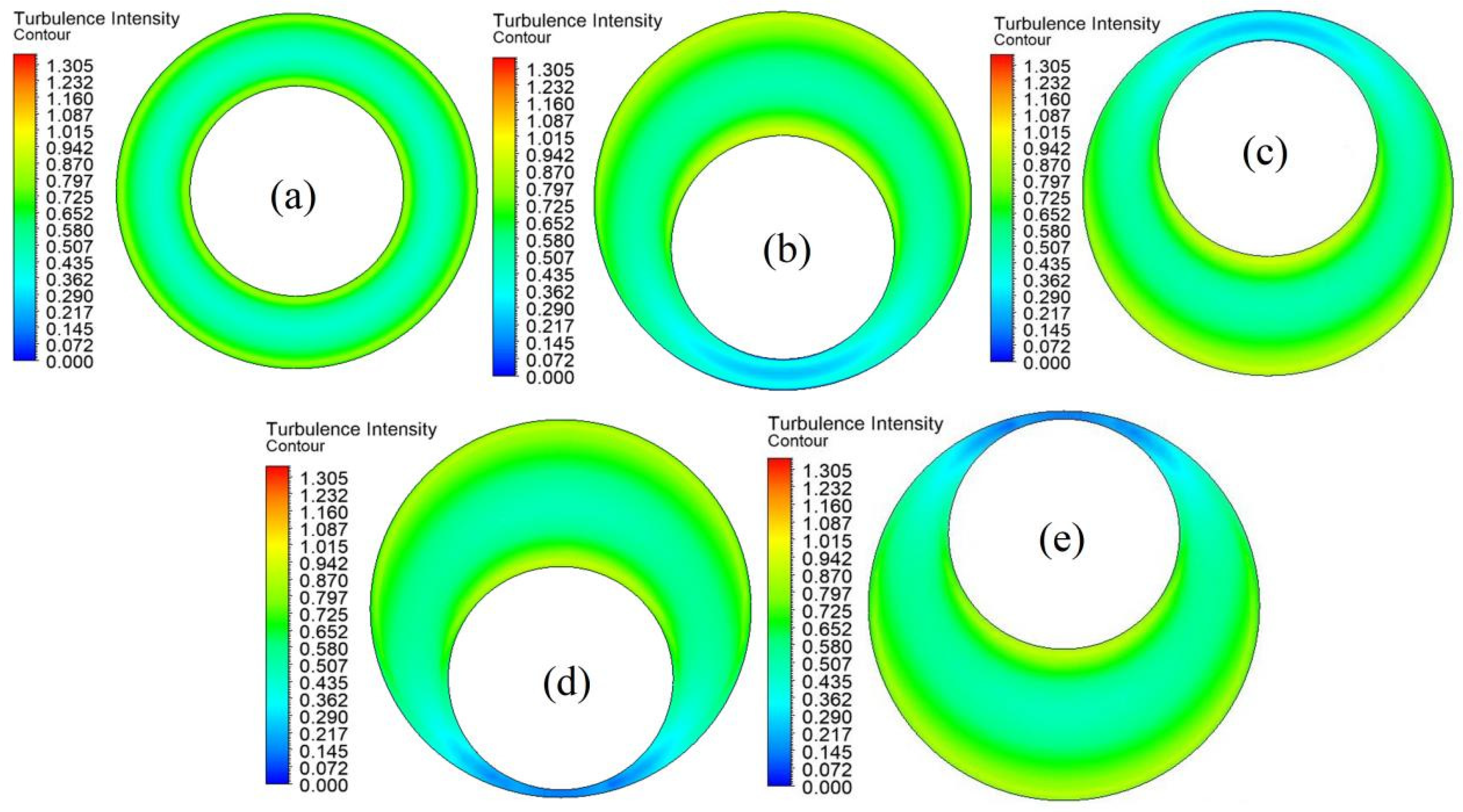
Turbulence and Wall Shear Stress Characteristics
4. Conclusions
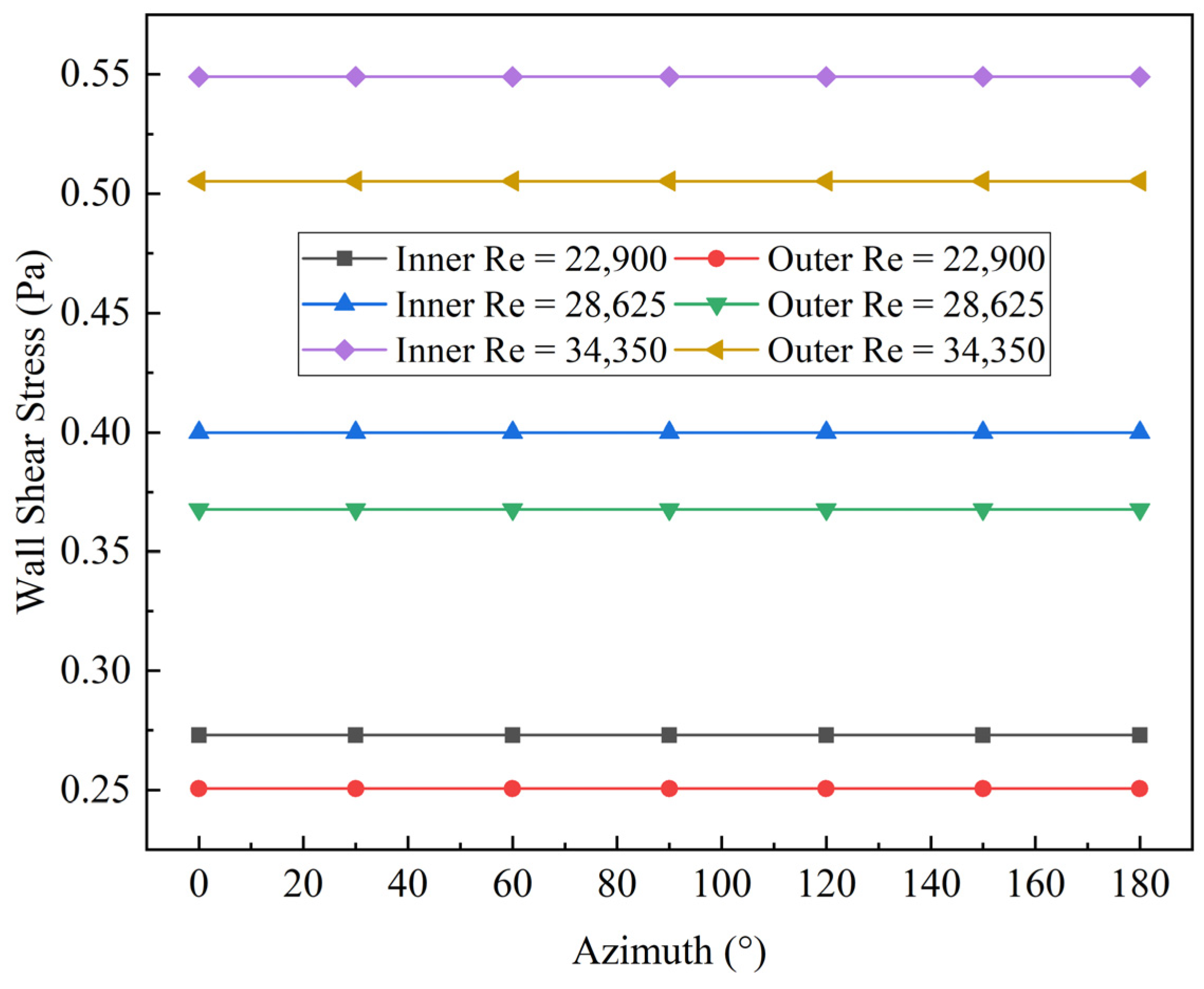
- Across various Reynolds numbers, the wall shear force and turbulence characteristics display a distinct central symmetry, with the inner pipe experiencing a notably higher wall shear force compared to the outer pipe. As the Reynolds number intensifies, there is a corresponding augmentation in the wall shear force on both pipes, and the disparity between their wall shear forces widens as the Reynolds number increases.
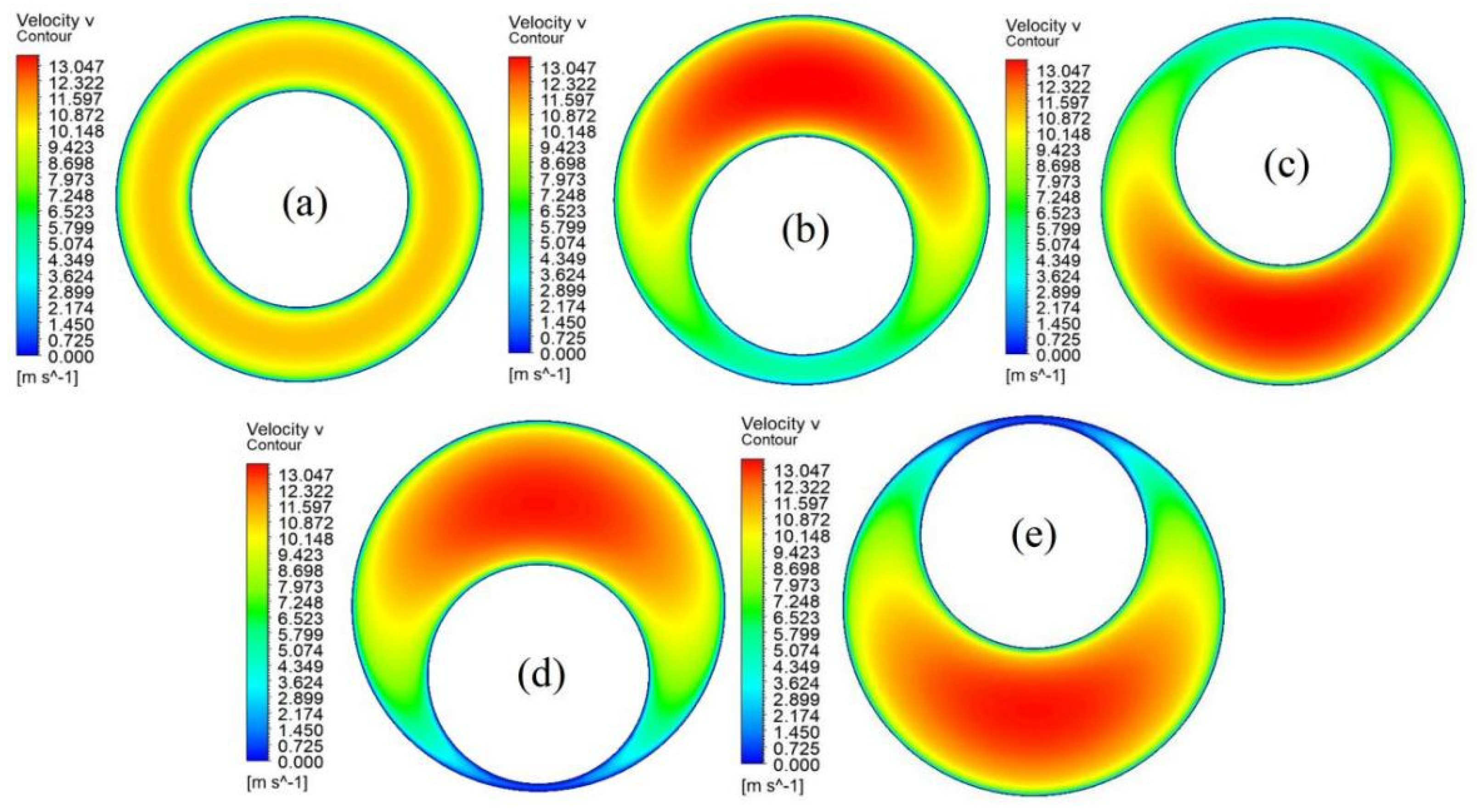
- Numerical simulations reveal that an escalation in the roughness of the inner pipe significantly amplifies the wall shear force acting upon it, while concurrently elevating the wall shear force on the outer pipe. Conversely, when the outer pipe’s roughness increases, the wall shear force on the inner pipe also undergoes an augmentation.
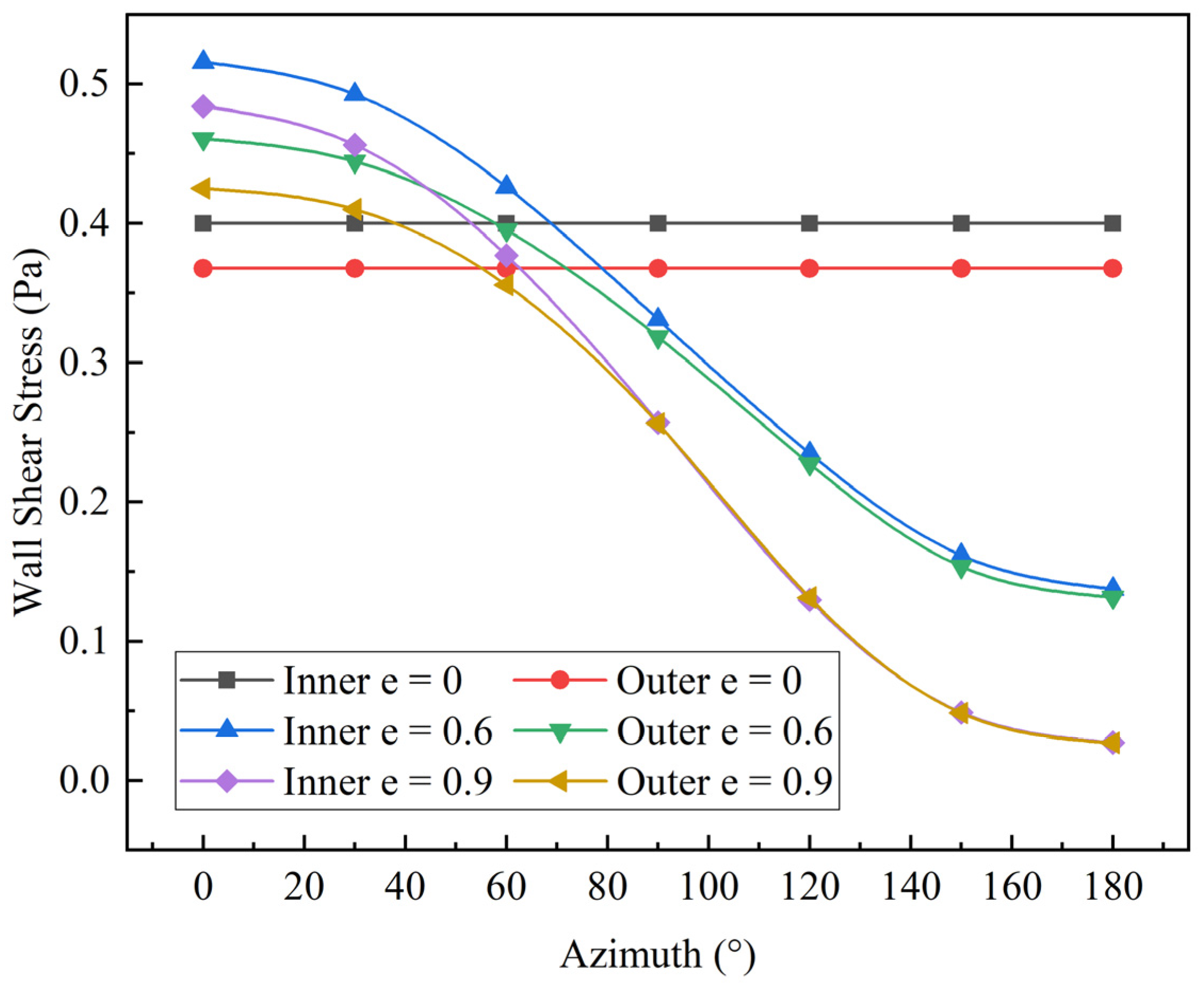
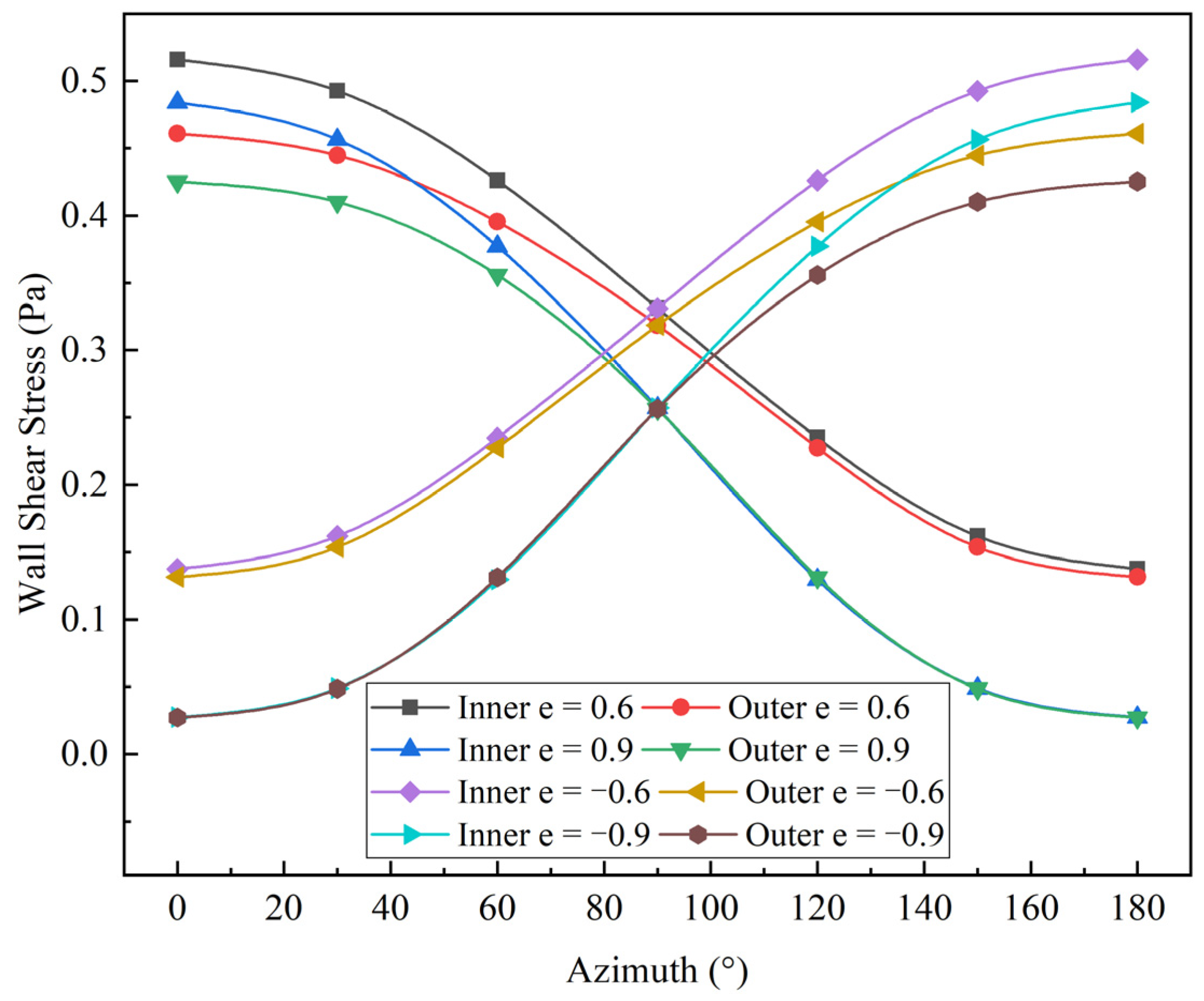
- The introduction of eccentricity leads to an uneven distribution of wall shear force across both the inner and outer pipes. In larger annular spaces, the shear force distribution surpasses that observed in concentric configurations, whereas in smaller annular spaces, it diminishes. Notably, during instances of negative eccentricity, a reversal in this distribution pattern is evident. Furthermore, the wall shear force and turbulence characteristics exhibit axial symmetry, regardless of whether the eccentricity is positive or negative.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| turbulent, time-averaged, and fluctuating variables in the RANS model, respectively | |
| ui, uj | time-varying velocities in x, y, and z directions, respectively (m/s) |
| Ui, Uj | time-averaged velocities in x, y, and z directions, respectively (m/s) |
| υ | kinetic viscosity (m2/s) |
| k | turbulent kinetic energy (m2/s2) |
| F1, F2 | blending functions in the turbulence model |
| Pk | production of turbulent kinetic energy (m2/s3) |
| modified production of turbulent kinetic energy (m2/s3) | |
| Din, Dout | inner and outer diameter of the annulus, respectively (m) |
| Re = ρUbD/μ | Reynolds number based on bulk mean velocity |
| Ub | bulk mean velocity (m/s) |
| μ | dynamic viscosity (Pa·s) |
| ρ | density (kg/m3) |
| S | average shear strain rate (1/s) |
| sij, Sij | average shear strain tensor for fluctuating and average velocity field, respectively (1/s) |
| U, U | vector and magnitude of velocity (m/s) |
| ε | viscous dissipation of turbulent kinetic energy (m2/s3) |
| υt | eddy viscosity (m2/s) |
| ω | turbulent eddy frequency (1/s) |
| R | represents roughness |
| i | stands for inner pipe |
| o | stands for outer pipe |
| e | eccentricity |
References
- Bagheri, E.; Wang, B.C.; Yang, Z. Influenceof domain size on direct numerical simulation of turbulent flow in a moderately curved concentric annular pipe. Phys. Fluids. 2020, 32, 065105. [Google Scholar] [CrossRef]
- Bagheri, E.; Wang, B.C. Effects of radius ratio on turbulent concentric annular pipe flow and structures. Int. J. Heat Fluid Flow. 2020, 86, 108725. [Google Scholar] [CrossRef]
- Xiong, X.; Rahman, A.M.; Zhang, Y. RANS Based Computational Fluid Dynamics Simulation of Fully Developed Turbulent Newtonian Flow in Concentric Annuli. J. Fluids Eng. 2016, 138, 091202. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, Y.; Rahman, A.M. Reynolds-Averaged Simulation of the Fully Developed Turbulent Drag Reduction Flow in Concentric Annuli. J. Fluids Eng. 2020, 142, 101209. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, N. Numerical Simulation of Turbulent Flow for non-Newtonian Fluid in two kinds Complex Annulus Channel. J. Phys. Conf. Ser. 2021, 1985, 012062. [Google Scholar] [CrossRef]
- Bekiri, F.; Benchabane, A. Numerical study of drilling fluids flow in drilling operation with pipe rotation. Mater. Today Proc. 2021, 49, 950–954. [Google Scholar] [CrossRef]
- Najafabadi, M.F.; Farhadi, M.; Rostami, H.T. Numerically analysis of a Phase-change Material in concentric double-pipe helical coil with turbulent flow as thermal storage unit in solar water heaters. J. Energy Storage 2022, 55, 105712. [Google Scholar] [CrossRef]
- Himanshu, O.P.; Kurmi, S.J.; Tyagi, S.K. Performance assessment of an improved gasifier stove using biomass pellets: An experimental and numerical investigation. Sustain. Energy Technol. Assess. 2022, 53, 102432. [Google Scholar] [CrossRef]
- Motaman, S.; Eltaweel, M.; Herfatmanesh, M.R.; Knichel, T.; Deakin, A. Numerical analysis of a flywheel energy storage system for low carbon powertrain applications. J. Energy Storage 2023, 61, 106808. [Google Scholar] [CrossRef]
- Jing, J.; Huang, W.; Karimov, R.; Sun, J.; Li, Y. Numerical investigation on oil-water flow characteristics and construction optimization for novel wellbore lubrication fitting. AIP Adv. 2024, 14, 035306. [Google Scholar] [CrossRef]
- Dokhani, V.; Ma, Y.; Li, Z. An Accurate Model for Prediction of Turbulent Frictional Pressure Loss of Power-Law Fluids in Eccentric Geometries. SPE Drill. Complet. 2021, 36, 913–930. [Google Scholar] [CrossRef]
- Haciislamoglu, M.; Langlinais, J. Non-Newtonian Flow in Eccentric Annuli. J. Energy Resour. Technol. 1990, 112, 163–169. [Google Scholar] [CrossRef]
- Erge, O.; Ozbayoglu, E.M.; Miska, S.Z.; Yu, M.; Takach, N.; Saasen, A.; May, R. CFD Analysis and Model Comparison of Annular Frictional Pressure Losses While Circulating Yield Power Law Fluids. In Proceedings of the SPE Bergen One Day Seminar, Bergen, Norway, 22 April 2015. [Google Scholar]
- Ferroudji, H.; Hadjadj, A.; Haddad, A.; Ofei, T.N. Numerical study of parameters affecting pressure drop of power-law fluid in horizontal annulus for laminar and turbulent flows. J. Pet. Explor. Prod. Technol. 2019, 9, 3091–3101. [Google Scholar] [CrossRef]
- Ferroudji, H.; Hadjadj, A.; Ofei, T.N.; Rahman, M.A.; Hassan, I.; Haddad, A. CFD method for analysis of the effect of drill pipe orbital motion speed and eccentricity on the velocity profiles and pressure drop of drilling fluid in laminar regime. Petrol Coal 2019, 61, 1241–1251. [Google Scholar]
- Ferroudji, H.; Hadjadj, A.; Rahman, M.A.; Hassan, I.; Ofei, T.N.; Haddad, A. The impact of orbital motion of drill pipe on pressure drop of non-Newtonian fluids in eccentric annulus. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 65, 94–108. [Google Scholar]
- Belimane, Z.; Hadjadj, A.; Ferroudji, H.; Rahman, M.A.; Qureshi, M.F. Modeling surge pressures during tripping operations in eccentric annuli. J. Nat. Gas Sci. Eng. 2021, 96, 104233. [Google Scholar] [CrossRef]
- Liu, Y.; Mitchell, T.; Upchurch, E.R.; Ozbayoglu, E.M.; Baldino, S. Investigation of Taylor bubble dynamics in annular conduits with counter-current flow. Int. J. Multiph. Flow. 2024, 170, 104626. [Google Scholar] [CrossRef]
- Rushd, S.; Shazed, A.R.; Faiz, T. CFD Simulation of pressure losses in eccentric horzontal wells. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Bahrain, 6 March 2017. [Google Scholar]
- Francois, G.S. About Boussinesq’s Turbulent Viscosity Hypothesis: Historical Remarks and a Direct Evaluation of Its Validity. C.R. Mec. 2007, 335, 617–627. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Multiscale Model for Turbulent Flows. In Proceedings of the 24th Fluid Dynamics Conference, American Institute of Aeronautics and Astronautics, Orlando, FL, USA; 1993. [Google Scholar]
- Keshmiri, A.; Uribe, J.; Shokri, N. Benchmarking of Three Different CFD Codes in Simulating Natural, Forced and Mixed Convection Flows. Int. J. Comput. Method. 2015, 67, 1324–1351. [Google Scholar] [CrossRef]
- Knudsen, J.G.; Katz, D.V. Fluid Dynamics and Heat Transfer. Phys. Today 1958, 12, 40–44. [Google Scholar] [CrossRef]
- Chadwick, A.; John, M.; Martin, B. Hydraulics in Civil and Environmental Engineering, 5th ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill Series in Mechanical Engineering: New York, NY, USA, 2011. [Google Scholar]
- Huque, M.M.; Butt, S.; Zendehboudi, S.; Imtiaz, S. Systematic sensitivity analysis of cuttings transport in drilling operation using computational fluid dynamics approach. J. Nat. Gas Sci. Eng. 2020, 81, 103386. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS Fluent 19.0. ANSYS Fluent Users Guide; Ansys Inc.: Canonsburg, PA, USA, 2019. [Google Scholar]
- Kalitzin, G.; Medic, G.; Iaccarino, G.; Durbin, P. Near-Wall Behavior of RANS Turbulence Models and Implications for Wall Functions. J. Comput. Phys. 2005, 204, 265–291. [Google Scholar] [CrossRef]

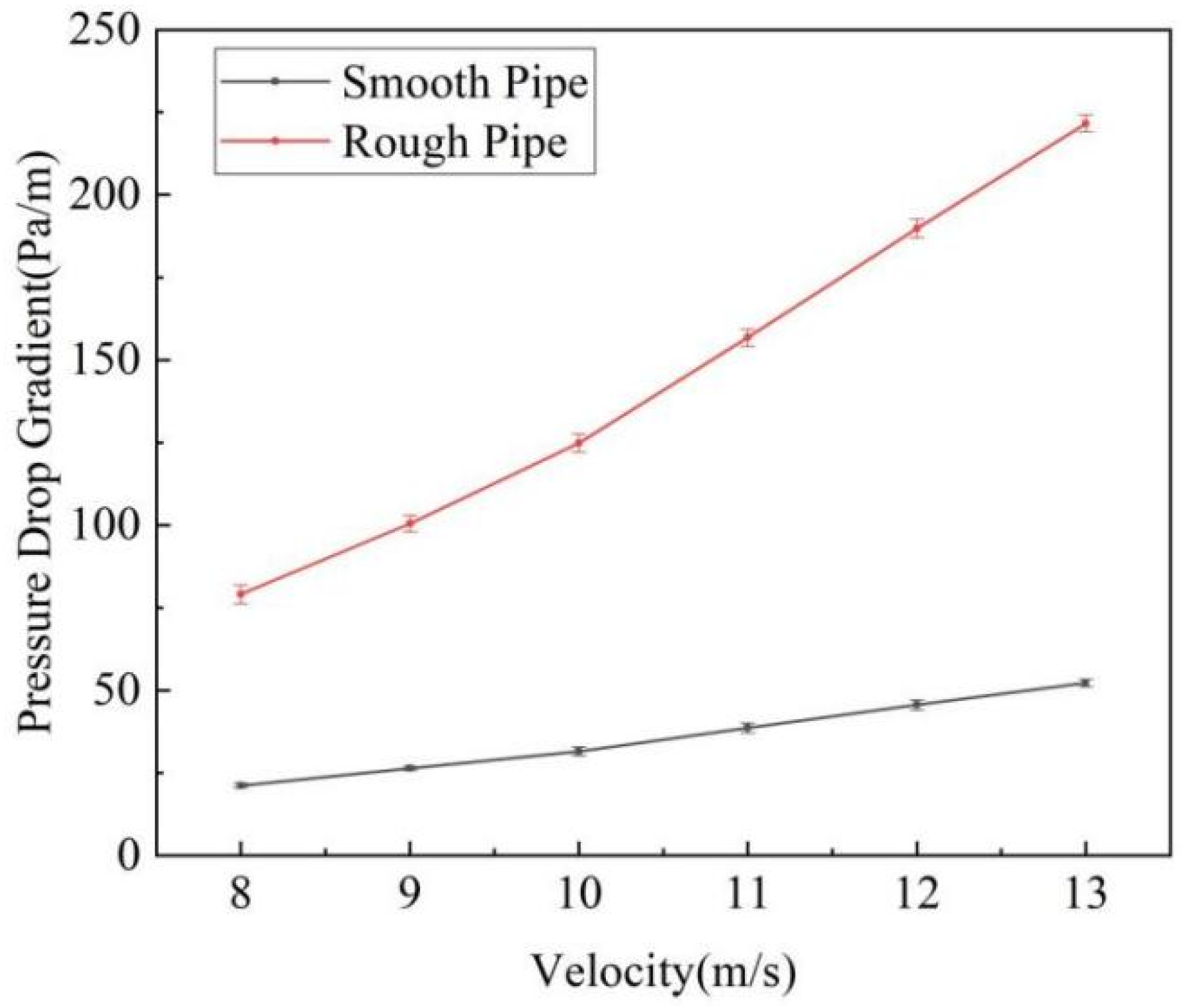
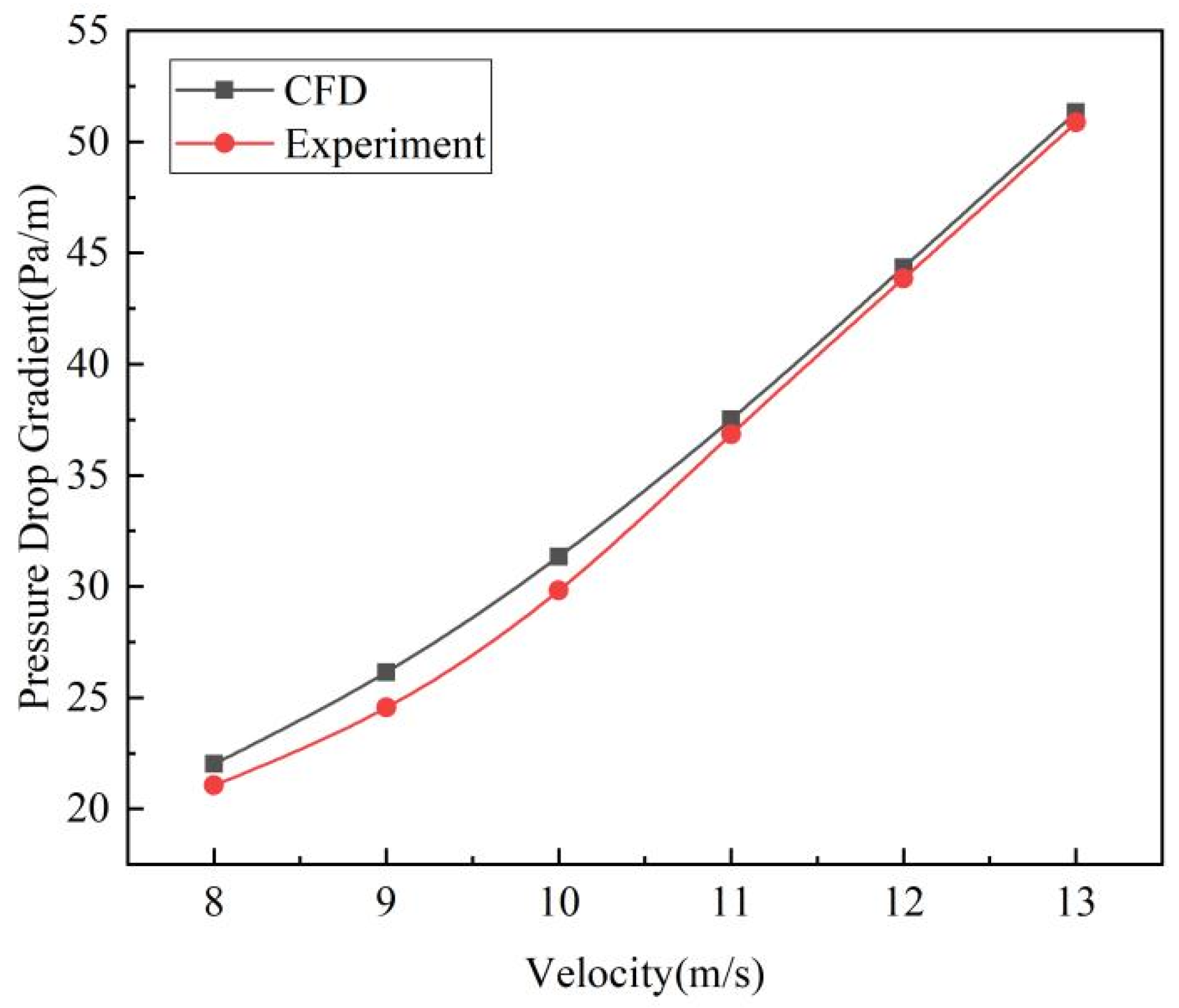


| Velocity (m/s) | Smooth Tube | Rough Tube |
|---|---|---|
| Mean ± Standard Deviation | Mean ± Standard Deviation | |
| 8 | 21.17 ± 0.71 | 79.06 ± 2.81 |
| 9 | 26.37 ± 0.62 | 100.46 ± 2.51 |
| 10 | 31.52 ± 1.31 | 124.85 ± 2.73 |
| 11 | 38.65 ± 1.50 | 156.78 ± 2.60 |
| 12 | 45.61 ± 1.58 | 189.82 ± 2.82 |
| 13 | 52.28 ± 1.09 | 221.58 ± 2.58 |
| Parameters | Value |
|---|---|
| Velocity (m/s) | 8, 10, 12 |
| Roughness (mm) | 0, 0.25 (inner); 0, 1 (outer) |
| Eccentricity | 0, 0.6, 0.9 |
| Parameter | Tube | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|---|
| Roughness (mm) | Inner (Ri) | 0 | 0.25 | 0 | 0.25 |
| Outer (Ro) | 0 | 0 | 1 | 1 |
| Parameter | Tube | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|---|
| wall shear stress (Pa) | inner 0° | 0.4 | 0.5 | 0.47 | 0.59 |
| inner 30° | 0.4 | 0.5 | 0.47 | 0.59 | |
| inner 60° | 0.4 | 0.5 | 0.47 | 0.59 | |
| inner 90° | 0.4 | 0.5 | 0.47 | 0.59 | |
| inner 120° | 0.4 | 0.5 | 0.47 | 0.59 | |
| inner 150° | 0.4 | 0.5 | 0.47 | 0.59 | |
| inner 180° | 0.4 | 0.5 | 0.47 | 0.59 | |
| outer 0° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 30° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 60° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 90° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 120° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 150° | 0.37 | 0.38 | 0.76 | 0.78 | |
| outer 180° | 0.37 | 0.38 | 0.76 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Sun, J.; Zhang, J.; Huang, N. Investigation of Turbulence Characteristics Influenced by Flow Velocity, Roughness, and Eccentricity in Horizontal Annuli Based on Numerical Simulation. Symmetry 2025, 17, 409. https://doi.org/10.3390/sym17030409
Sun Y, Sun J, Zhang J, Huang N. Investigation of Turbulence Characteristics Influenced by Flow Velocity, Roughness, and Eccentricity in Horizontal Annuli Based on Numerical Simulation. Symmetry. 2025; 17(3):409. https://doi.org/10.3390/sym17030409
Chicago/Turabian StyleSun, Yanchao, Jialiang Sun, Jie Zhang, and Ning Huang. 2025. "Investigation of Turbulence Characteristics Influenced by Flow Velocity, Roughness, and Eccentricity in Horizontal Annuli Based on Numerical Simulation" Symmetry 17, no. 3: 409. https://doi.org/10.3390/sym17030409
APA StyleSun, Y., Sun, J., Zhang, J., & Huang, N. (2025). Investigation of Turbulence Characteristics Influenced by Flow Velocity, Roughness, and Eccentricity in Horizontal Annuli Based on Numerical Simulation. Symmetry, 17(3), 409. https://doi.org/10.3390/sym17030409







