1. Introduction
The theory of fixed points is one of the most enjoyable and energetic areas of research in the evolution of mathematical analysis. In this context, the most well-established and useful theorem is the Banach contraction principle [
1]. This theorem is just a primer on the subject of fixed points for mathematicians. It has been developed considerably over more than a hundred years of studies and has found applications in many branches of science, especially mathematics. In parallel with the development of fixed-point theory, many mapping classes and iteration techniques have been developed [
2,
3,
4,
5,
6,
7,
8,
9].
Many fixed point and approximation theorems have been studied by many authors in reflexive Banach space by imposing different restrictions on the operators. Asymptotically nonexpansive mappings, which form the basis of our work, were introduced by Goebel and Kirk in 1972. In fact, asymptotically nonexpansive mappings are a generalization of class nonexpansive mappings. Also, Goebel and Kirk demonstrated the existence of a fixed point of asymptotically nonexpansive mappings in uniformly convex Banach spaces [
10,
11]. Halpern first introduced the following iteration scheme for a nonexpansive
mapping for
, known as the Halpern iteration [
12]:
In the last forty years, many important studies have been conducted on the strong convergence of approximate fixed points of
under different additional conditions using the (1) iteration scheme. The findings of these studies can be briefly summarized as follows. Lions obtained strong convergence with
where
in iteration (1) [
13]. Wittmann obtained strong convergence under certain conditions in iteration (1) [
14]. Reich obtained strong convergence using iteration (1) in a Hilbert space [
15]. Shioji and Takahashi showed strong convergence in uniformly convex Banach spaces with a uniformly Gâteaux differentiable norm in iteration (1) [
16,
17]. In particular, since the early 2000s, research on nonexpansive mappings has gained momentum, leading to the definition of new classes of mappings. These classes of mappings have found extensive applications in fixed-point theory within metric and Banach spaces, as well as in approximation theory. Researchers can explore the literature in this field in greater depth by referring to sources [
18,
19,
20,
21,
22,
23,
24,
25,
26] and the references therein.
On the other hand, researchers have conducted extensive work on ergodic theory using asymptotically nonexpansive mappings. For this purpose, various iteration techniques such as Mann, viscosity, and Halpern in Cesàro means iterations were used. Now, some work on the approximation of the fixed point for nonexpansive and asymptotically nonexpansive mapping will be presented. Baillon first proved the following nonlinear ergodic theorem in 1975 [
27]: “Let
be a nonempty closed convex subset of a Hilbert space
, and the mapping
satisfy
. Then for each
,
Cesàro summability converges weakly to a fixed point of the mapping
. In 1979, Bruck conducted a study that established the nonlinear ergodic theorem for nonexpansive mappings in uniformly convex Banach spaces equipped with Fréchet differentiable norms [
28]. Hirano and Takahashi extended Baillon’s theorem for nonexpansive mappings in their work [
29]. Song and Chen [
30] defined the following viscosity iteration in Cesàro means for the nonexpansive
mapping:
Song studied strong convergence using Mann iteration within Cesàro means for nonexpansive mappings [
31]. Then, Zhang and Song introduced the theorem on the strong convergence of Halpern iteration Cesàro means for asymptotically nonexpansive mappings [
32]. That is, they proved the strong convergence of
by the following iteration (4) for a nonexpansive
mapping in uniformly convex Banach spaces:
Moreover, the same authors proved that the weak continuous dual mappings of the sequence
defined in a uniformly convex Banach space converge strongly to some fixed points
. Zhu and Chen [
33] defined the following iterations (5 and 6) for viscosity iteration in Cesàro means for nonexpansive mappings:
They considered as a nonempty closed convex subset of a uniformly Banach space and as a nonexpansive mapping such that , and assumed that the sequences and in (0, 1) satisfy the following conditions for all :
Then, they proved that the sequence defined by (5) strongly converges to a fixed point of . Moreover, the same authors proved that for an arbitrary point , the sequence defined by (6) strongly converges to a fixed point of .
In the first section of this article, studies in the literature are examined. In the second section, the basic concepts underlying this study are included. The third section, inspired by the results presented above, investigates under what conditions the sequence defined by Kirk iteration in the Cesàro means converges strongly and weakly for an asymptotically nonexpansive self-mapping . The last section includes numerical sections. Now, before moving on to the preliminary information, let us introduce some concepts that we will use in our study.
2. Preliminaries
Let be a Banach space. Throughout this paper, when is a sequence in , then will denote the strong convergence of to , and will denote the weak convergence of to .
is a nonempty set. If the distance function satisfies for all then is symmetric. endowed with metric forms a symmetric space. A set equipped with a symmetric distance function is called a symmetric space. It is well known that Banach space has symmetry and metric spaces inherently possess this symmetry. However, pseudo-metric spaces do not always exhibit this symmetric property.
Definition 1 ([34]). E is called uniformly convex, if there exists
such that where , is a strictly increasing convex and continuous function with .
If satisfiesthen the Banach space is uniformly convex. Definition 2 ([2]). Let the unit sphere of a normed space be defined as . If the limit for exists, then the norm of the space is said to be as Gâteaux differentiable at the point . If the norm is Gâteaux differentiable at all points of , then the norm of is said to be Gâteaux differentiable. Summability methods aim to assign limits to divergent series and enhance their rate of convergence. The Cesàro summation method is one of the most fundamental and widely used techniques for summing divergent series, alongside methods such as Riesz, Nörlund, and Hölder [
35,
36]. Cesàro introduced the first formal approach to summing divergent series using such methods.
Definition 3 ([36]). Let be a field of real or complex numbers and let be an infinite matrix, with for and be a sequence. In this case, a mapping from to is thatThe sequence is called a mapping sequence of the sequence and or a mapping from sequence to sequence. For this mapping to exist, the infinite sum in (8) must be convergent for every .
Definition 4 ([36]). Let be the sequence of partial sums . Then, let the mapping sequence, which is created with the help of the matrix of the sequence, be defined as in (8). If , the series or the series be a summable to the value of .
Definition 5 ([35]). Let be the sequence of partial sums . Matrix elements of series or series mapping sequence obtained with the help of the matrix given byIt is Cesàro summable and said to be for short if .
Definition 6 ([9]). Let be a non-empty set and be a mapping. If there is that satisfies the equationthen is called a fixed point of mapping . The set of all fixed points of mapping is denoted by , , or .
notation will be used throughout this study. Definition 7 ([9]). Let be a metric space and be a mapping. If at least one real number can be found that satisfies the condition such thatthen is called a contraction mapping for all . The real number is called the contraction ratio. Definition 8 ([9]). Let be a metric space and be a Lipschitz mapping. If for all ,the condition is met; is called a nonexpasive mapping.
Definition 9 ([10]). Let be a normed space and be a nonempty closed convex subset of . Let be a mapping. If for each there exists a sequence of nonnegative real numbers satisfying such thatthen mapping is said to be asymptotically nonexpansive. Here, when , is called nonexpansive mapping. The iteration method was first defined by the Italian mathematician Picard [
3]. Since then, many iteration methods have been introduced by researchers. There are two important issues when defining the iteration method. The first is that the newly defined iteration method should be faster than the iteration methods in the literature, and the second is that this defined iteration method should be simple. Let
be a metric space and
a mapping. In its most general form, a fixed-point iteration method, with
being a function, is defined by the iteration
Definition 10 ([3]). For , if in the iteration (11) such thatthen this iteration method is called the Picard iteration method. Definition 11 ([6]). In iteration (11), if for and we have and if the iteration function is given bythis iteration is called Kirk iteration, and this method is called the Kirk iteration method. Now, let us state the following two lemmas, which are very important for our study [
31].
Lemma 1. Let , , and be sequences of nonnegative real numbers satisfying the inequality for If and , then exists. In particular, whenever there exists a subsequence in which strongly converges to zero.
Lemma 2. Let be a nonempty closed convex subset of a uniformly convex Banach space . Assume is an asymptotically nonexpansive mapping with . Suppose that for the bounded sequence in , there exists a subsequence satisfying one of two conditions for each :
and
and
Under these conditions, there exists a unique such that Additionally, a Banach space
is said to satisfy Opial’s condition if, for any sequence
in
such that
, the following inequality holds:
Corollary 1. Let be a nonempty closed convex subset of uniformly convex Banach space . Assume is an asymptotically nonexpansive mapping with . Furthermore, let there exist a bounded sequence in ; there exists a subsequence that fulfills one of the following two conditions:
If either or and satisfies Opial’s condition, then .
3. Results
Ergodic theory, which emerged through the work of Neumann and Birkhoff in 1931, can be expressed as a part of dynamical systems theory, or in other words, as the mathematical formulation of designed physical thought. Later, it was frequently used in many fields such as functional analysis, probability theory, measure theory, and number theory, and research in this area continues today. To express the relationship of ergodic theory with functional analysis and summability theory in the most general way, let , be a linear operator on Banach space, and let and be an iteration sequence that . It examines the convergence of the mapping sequence given in the form and the consequences of this situation.
In our study, we define the Kirk iteration in the Cesaro means for the asymptotically nonexpansive mapping
condition as
where
and
Lemma 3. Let be a uniformly convex Banach space given by the uniformly Gâteaux differentiable norm. Assume that is a nonempty closed convex subset of and let be an asymptotically nonexpansive mapping with . Let be defined by Equation (12). Also, suppose that is defined as satisfying the condition . Then, sequences and are bounded.
Proof. Let
and we estimate as follows from the iteration process (12):
Applying Lemma 1 to yield the existence of the limit , the boundedness of the sequence is thus proven.
On the other hand, let
. We show the bounded of
. Therefore,
and if the necessary operations are made by taking the norm of both sides in this last equation, then
Thus, we determine that is bounded. □
Theorem 1. Let be a uniformly convex Banach space given by the uniformly Gâteaux differentiable norm. Suppose that is a nonempty closed convex subset of and is an asymptotically nonexpansive mapping with . Let be defined by Equation (12). Also, suppose that is defined as satisfying the condition . In this case, the sequence given by Equation (12) is strongly convergent to some fixed points of
Proof. According to Lemma 3, we know that the sequences
and
are bounded. First, let us show that
under the hypotheses of Theorem 1:
Due to the compactness of
, the sequence
has a strongly convergent subsequence
, which converges to a limit denoted by
:
From Corollary 1, it follows that . Moreover, since the limit exists as established by inequality (13), is indeed the strong limit of the sequence . □
Theorem 2. Let be a nonempty closed convex subset of uniformly convex Banach space with Opial’s condition. Suppose that is an asymptotically nonexpansive mapping with . Assume that is defined bywhere and . Suppose that and . Then, as , weakly converges to some fixed point of .
Proof. It follows from the reflexivity of
that there exists a subsequence
of
such that
. By Theorem 1,
By applying Corollary 1, it follows that
. We now demonstrate that
converges weakly to
. If this were not the case, there would exist a subsequence
of
that weakly converges to some
. We also have
Because
exists for each
by inequality (13) and
satisfies Opial’s condition,
This leads to a contradiction, so we conclude that . Therefore, converges weakly to . The proof is complete. □
4. Numerical Examples
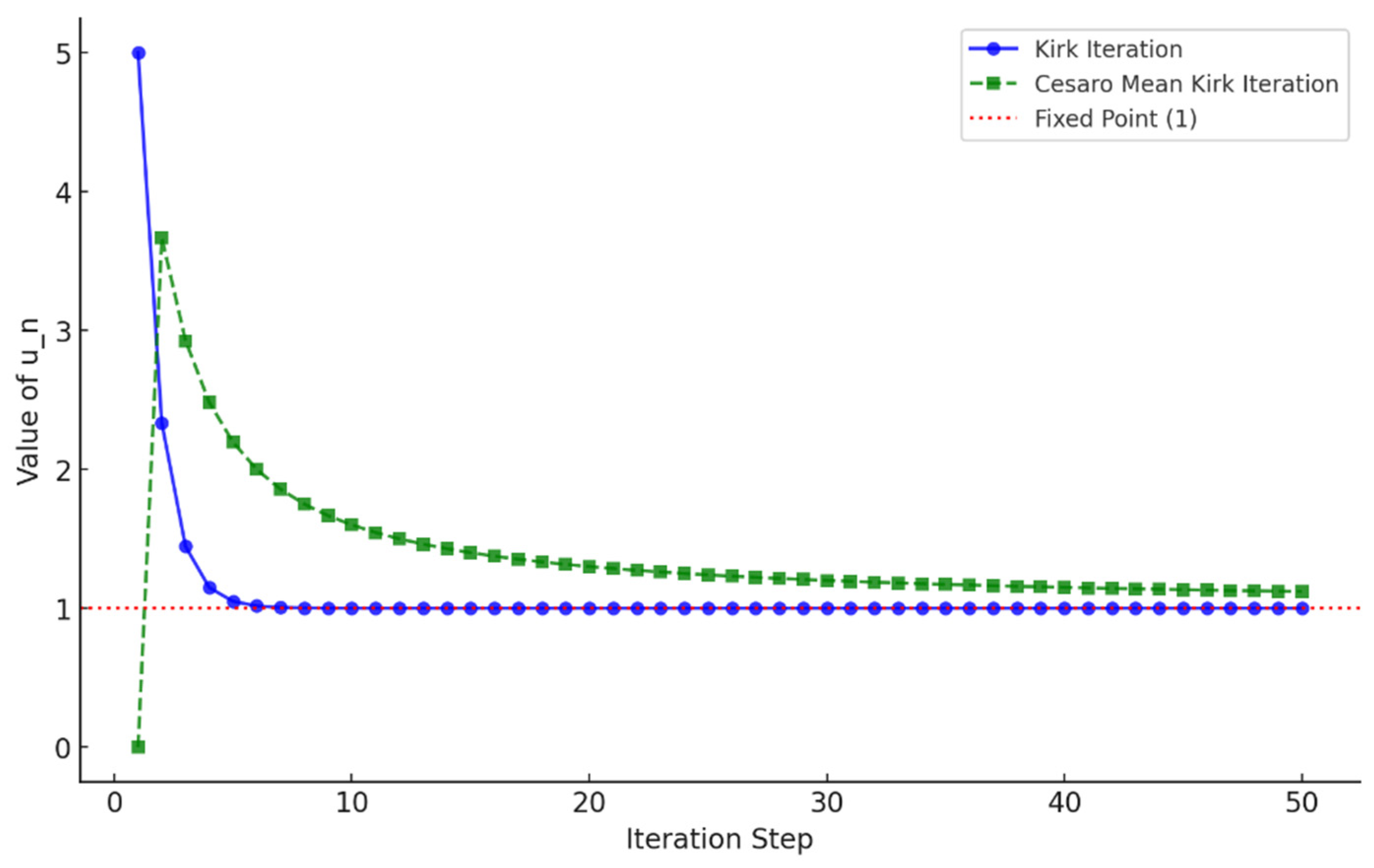
Let us start with a numerical example that shows that the Kirk iteration we prefer in our study is faster and more useful than the Mann iteration and Halpern iteration techniques used previously in ergodic theory.
Example 1: Let us take a mapping
that is asymptotically nonexpansive on a Banach space
. Let us see the convergence speed of this transformation to the fixed point
with the three-iteration method on the graph as shown in
Figure 1.
The Kirk iteration outperforms Mann and Halpern iterations by incorporating a weighted summation of multiple iterates, ensuring faster and more stable convergence. While the Mann iteration progresses with smaller steps and converges slowly, the Halpern iteration initially converges rapidly but slows down over time. In contrast, the Kirk iteration is both fast in the beginning and maintains efficiency in the long run, making it particularly advantageous for optimization problems and numerical approximations. By ensuring that the weights in the summation sum to 1 , the Kirk iteration stabilizes the sequence and enhances performance in nonexpansive and asymptotically nonexpansive settings. However, in some cases, standard Kirk iteration may experience oscillatory behavior or slow convergence when applied to sequences that do not naturally stabilize.
To address these limitations, Cesàro summability is introduced, improving stability and accelerating convergence by acting as an averaging process that reduces oscillations. This aligns the Kirk iteration with ergodic theory, where summability techniques have been effective in stabilizing iteration sequences. The Cesàro mean Kirk iteration enhances standard Kirk iteration by ensuring strong convergence in Banach spaces, eliminating oscillatory effects, and improving efficiency in practical applications. Therefore, when dealing with asymptotically nonexpansive mappings or numerical fixed-point problems, Cesàro mean Kirk iteration should be preferred for superior performance and reliability.
Now, consider the linear mapping
in Example 1 as shown in
Figure 2.
Let us take a mapping
that is asymptotically nonexpansive on a Banach space
. Let us compare the Kirk iteration for the nonlinear
mapping and the Cesàro mean Kirk iteration as shown in
Figure 3.
As can be seen from both examples, the Kirk iteration shows a direct approach to the fixed point, with oscillations gradually decreasing. Cesàro mean Kirk iteration smooths out fluctuations, leading to a more stable convergence. Both methods ultimately reach the same limit, but the Cesàro mean provides a more stable and averaged trajectory.
Now, let us give numerical examples for the lemmas and theorems presented in the results section.
Example 2: Let us consider the Banach space
and the closed convex subset
. We define an asymptotically nonexpansive mapping
as follows:
This mapping satisfies the asymptotic nonexpansiveness condition because for any
,
Since the contraction factor
is less than
,
is an asymptotically nonexpansive mapping. We define the parameters
and
as follows:
From the properties of the harmonic series, we know that
which ensures the boundedness of the sequence.
We initialize the sequence with
and generate the next terms using
Computing the first few terms:
Observing the sequence, we notice that
which means the sequence is bounded. Since
is bounded and remains within
, iterating the function
multiple times will also produce values within the same interval. Therefore,
will remain bounded, and the conditions of Lemma 3 will be satisfied.
We can give the following examples for Theorem 1 and Theorem 2, which we put forward in the results.
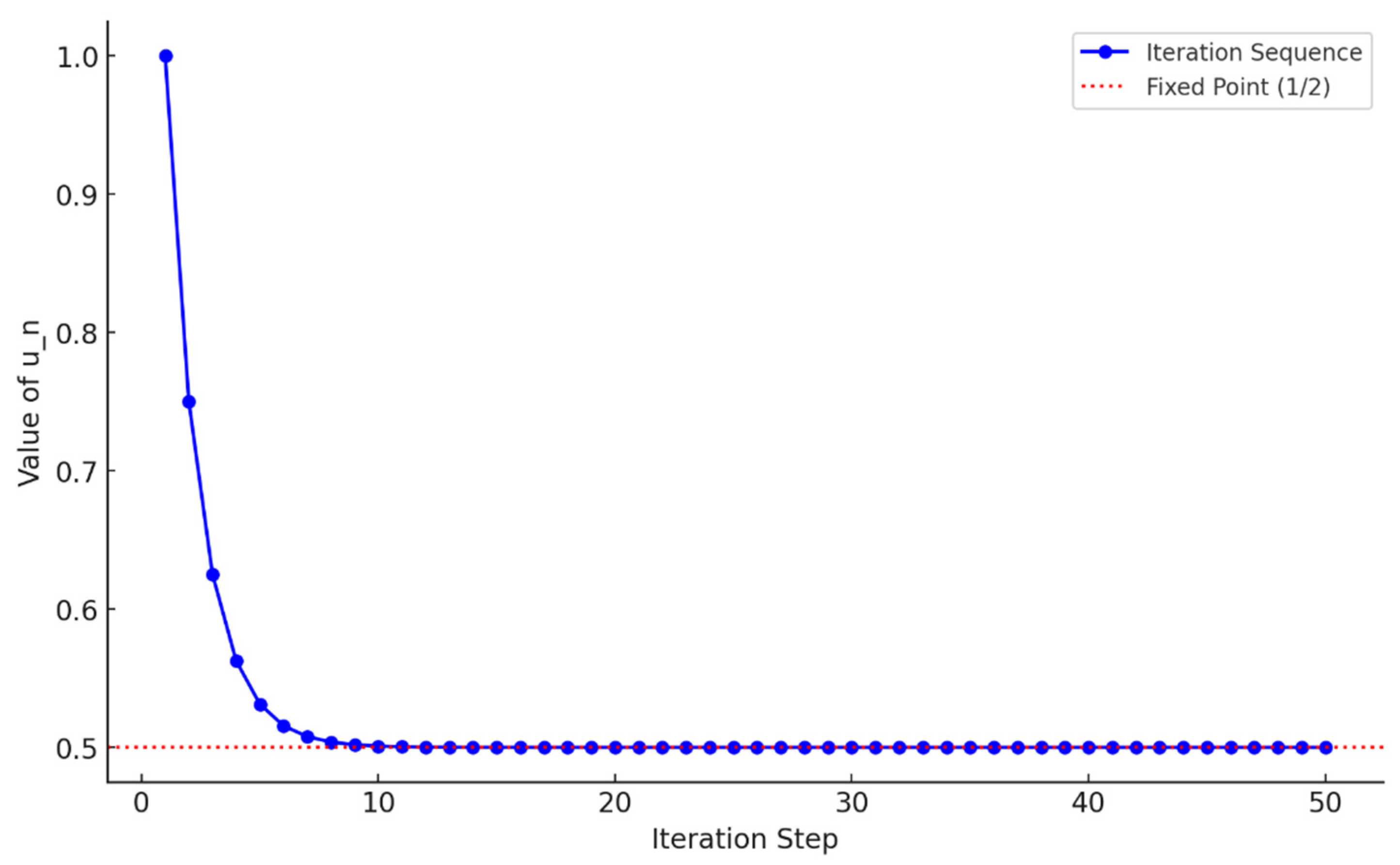
Example 3: Let
with the standard absolute value norm and
, which is a nonempty closed convex subset. Let us consider the mapping
given in Example 2. Also, let
. We know the sequence
is bounded in
, and the mapping
is asymptotically nonexpansive. Then,
is given by
From the harmonic series property, we know that
which satisfies Theorem 1’s requirement. Now, let us create the iterative sequence for
and compute iterates using
Compute the first few iterations:
We notice from observing the sequence that
as
which suggests strong convergence to the fixed point
. On the other hand,
from
. Thus, Since the sequence
converges to
, this satisfies Theorem 1. Let us examine this situation on the graph as shown in
Figure 4.
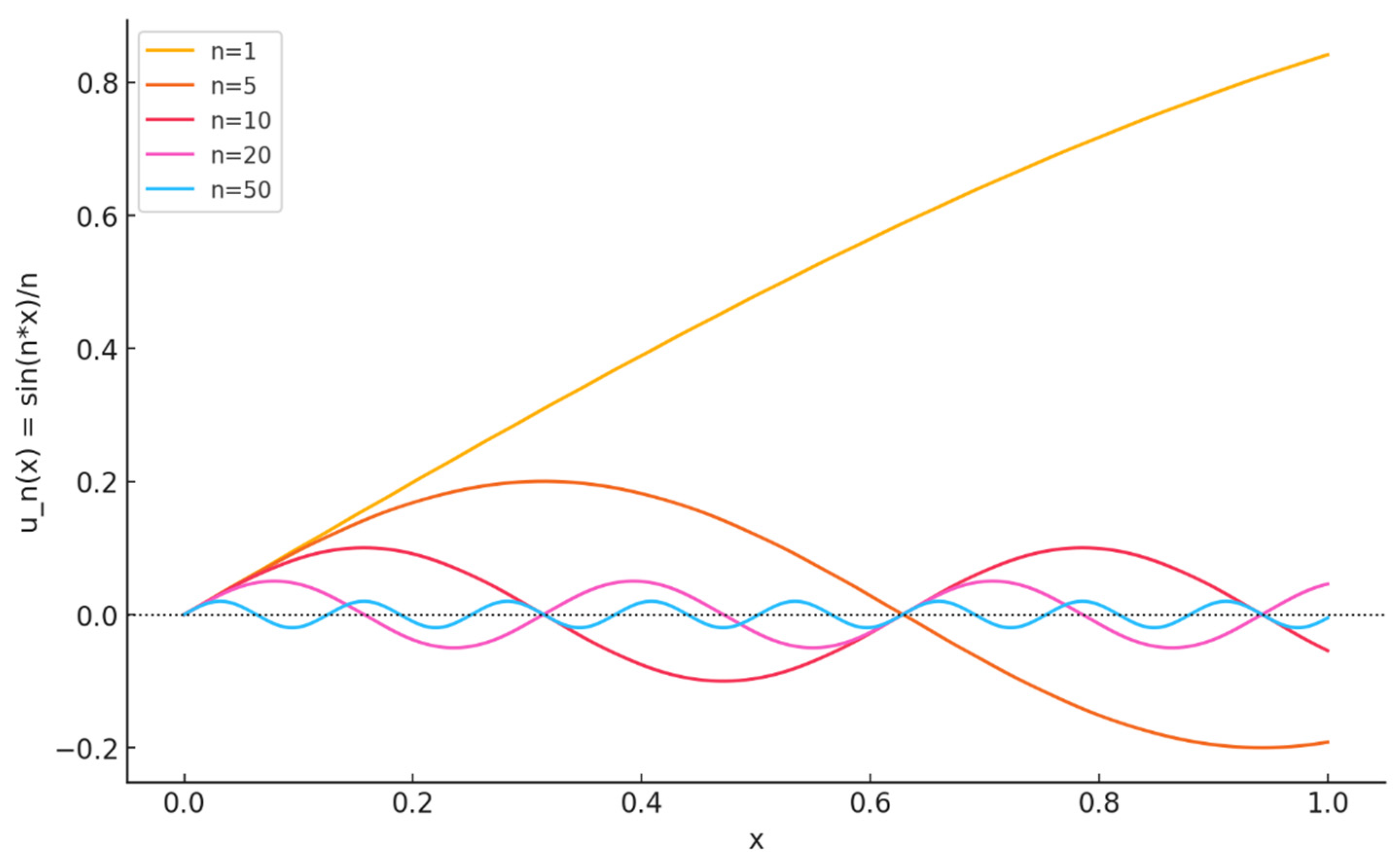
Example 4: Let
with the standard absolute value norm and
be a convex subset of
, such as
.
is a nonempty closed convex subset of a uniformly convex Banach space
with Opial’s condition. Consider the mapping
This mapping satisfies asymptotic nonexpansiveness because
if
is taken
the inequality holds. Also,
From the harmonic series, we know .
On the other hand,
considering two weighted terms for
. Let
,
, and
, then compute
Therefore, following this process, we see that the sequence remains oscillatory but bounded. All conditions of Theorem 2 are verified, here, we need to solve
to find the fixed point
.
approaching
, which only holds if
. The oscillatory term
causes weak convergence rather than strong convergence. As
the Cesàro mean smooths out oscillations, making
weakly converge to zero. This means that the sequence
weakly converges to a fixed point of
in
. Now, let us examine this situation on the graph as shown in
Figure 5.