Estimation of Biresponse Semiparametric Regression Model for Longitudinal Data Using Local Polynomial Kernel Estimator

Abstract

When handling longitudinal data in regression models, we often encounter problems involving two interrelated response variables. These response variables may display an unknown curve shape in their relationship with one predictor variable, referred to as the nonparametric component, while maintaining a linear relationship with other predictor variables, referred to as the parametric component. In such cases, a Biresponse Semiparametric Regression (BSR) approach is a suitable solution. This research aims to estimate the BSR model for longitudinal data using the Local Polynomial Kernel (LPK) estimator by considering a symmetrical variance–covariance matrix estimate validated on simulation data and apply it to a real dataset of Dengue Hemorrhagic Fever (DHF) disease. The parameter estimation method used is a combination of Least Squares (LS) and Weighted Least Squares (WLS). For determining the optimal bandwidth, we use a Generalized Cross–Validation (GCV) method. The simulation study results indicate that with kernel weighting, employing weights derived from the inverse of the variance–covariance matrix significantly enhances the estimation accuracy of the BSR model. In addition, the results of the estimation for modeling the DHF disease, where platelets and hematocrit are response variables, and hemoglobin and examination time are predictor variables, produced an R-Square value of 92.8%.

1. Introduction

Regression analysis has long been used to identify patterns of functional relationships through the form of the regression curve and the effect between predictor variables (independent) and response variables (dependent) by estimating the regression curve. First, we create a scatter diagram to determine the curve shape between these variables. In the regression model, the curve has a patterned shape, including curve shapes such as linear, quadratic, or exponential patterns [1]. Parametric and nonparametric regression models are the two types used in regression analysis. The nonparametric regression model includes the assumption that a curve’s form is unknown, which can be interpreted as no previous information available. The parametric regression provides the assumption that the regression curve’s shape is known, or it can be said that there is information about the shape of the regression curve. The nonparametric regression has great flexibility because the pattern of the nonparametric regression curve is assumed to be smooth [2].

Nonparametric regression (NR) is a regression analysis approach in which the predictor is built based on the information obtained from the data rather than having a preset form, meaning that there is an unknown specific curve shape connecting the predictor with the response variable. The NR model does not have assumptions like parametric regression. In the NR model, the regression curve is only assumed to be smooth, meaning it is in a certain function space. In estimating the NR curve, it is not influenced by the researcher’s subjectivity, so it has high flexibility. Next, a regression analysis that uses both parametric and nonparametric models is defined as Semiparametric Regression (SR). The SR model is formed by at least two predictors. The SR model assumes that a functional connection between the response with predictor variables follows certain patterns, while the shape of the pattern for other predictor variables is unknown [3].

In some problems with multipredictors, the response variable has a curve shape whose relationship pattern with the predictor variable is unknown, but with other predictor variables, the shape of the curve is known. In this condition, the SR model approach is suggested [4]. The SR models utilize certain estimators, such as kernel, spline, Fourier series, and local polynomial estimators. Several studies regarding one-response SR have been conducted by researchers, including Asrini [5] who used the Fourier series estimator; Diana et al. [6] who used a Bayesian approach; and Mohaisen and Abdulhussein [7] who used the spline estimators. Meanwhile, modeling biresponse or multi-response regression in the NR model has been conducted by Lestari et al. [8,9] who estimated the regression curve with a smoothing spline estimator.

The regression model has three types of data, namely cross-sectional, time series, and longitudinal data. The features of cross-sectional data differ from those of longitudinal data. The observations in the cross-sectional data contain $n$ independent subjects, and only one observation is made for each subject. Time series data can be interpreted as a series of data obtained by observations at different times periodically at certain intervals [1]. Longitudinal data are a collection of data observed from $n$ independent objects, each observed repeatedly at different times. Longitudinal data have advantages over cross-sectional data. That is, with the same number of subjects, the results of error observations provide a better estimate of the treatment effect than cross-sectional data because the data are estimated for each observation. In addition, longitudinal studies are more powerful than cross-sectional studies because fewer subjects are needed to obtain the same statistical power [10].

The main objective of SR modeling is to obtain an estimate of the regression curve. Several estimators can be used to estimate the regression curve, including the Local Polynomial Kernel (LPK). The LPK estimates the regression curve based on the polynomial form with the polynomial order according to the data pattern. The LPK estimator is based on assigning weights to each observation using the kernel function. In contrast, the weight is determined by the smoothing parameter, namely the bandwidth. LPK has several advantages, including reducing asymptotic bias and providing good estimation results [11]. In the estimating process of the regression curve using the LPK estimator, we optimize a WLS (Weighted Least Squares) function based on the GCV criterion. The GCV approach can be used to determine the smoothing parameters (bandwidth). Furthermore, the WLS method is a form of development of OLS (Ordinary Least Squares) used to overcome heteroscedasticity. Heteroscedasticity in the regression model occurs due to the inequality of the variance of the error vector. The WLS is a special case of generalized Least Squares. The WLS method can maintain the efficiency properties of its estimator without losing its bias and consistency properties [12]. Determination of the optimum bandwidth in nonparametric regression can be performed using the GCV method. The GCV method is often used because it has optimal asymptotic properties, and invariance to transformation and unknown variance of population. The optimum bandwidth is selected based on the minimum of GCV [13,14].

The Biresponse Nonparametric Regression (BNR) model for longitudinal data has been widely studied, and estimates of regression model parameters have been produced. The SR approach to longitudinal data, time series, and cross-section one-response regression models has been widely used by researchers. Longitudinal data have advantages compared to other types of data. Longitudinal data are able to capture changes and patterns over time of the observed subjects. In addition, longitudinal data are able to control the heterogeneity of the subject because the subject is observed repeatedly. It provides the advantage of investigating the changes in the subject over time, which the cross-section data are unable to achieve. Previous studies for longitudinal data were limited to one-response SR models, while some real cases involve biresponse or multi-response variables. This research examines the estimation of SR models using biresponse variables on longitudinal data.

The biresponse regression model differs from the one-response regression model, where the biresponse model consists of several equations assuming a correlation between responses. Therefore, the novelty of this research is the estimation of the BSR model using the Local Polynomal Kernel estimator by considering variance–covariance matrix estimates. In the estimation process of the BSR model, we use the WLS (Weighted Least Squares) optimization method by including a weight matrix, which is the inverse of the variance–covariance matrix, into the Least Squares optimization function based on the GCV criterion. Therefore, the estimation of the variance–covariance matrix is very necessary in this research. This is what distinguishes it from the classical estimation methods that have existed before. In this research, the LPK estimator is combined with the variance–covariance matrix estimation, which is validated on the simulation data. The simulation results are combined with DHF data of hospitalized patients. The response variables used are platelets and hematocrit of DHF patients during hospitalization, while the predictor variables are the examination time and hemoglobin levels. The predictor variable of examination time is a nonparametric component, while the hemoglobin is a parametric component. The original contribution of this research is the development of a semiparametric model involving two responses in longitudinal data with LPK function. In addition, this model is applied to model DHF data, where platelets and hematocrit are correlated, while time and hemoglobin variables are predictor variables with nonparametric and parametric components, respectively.

2. Literature Review

In this section, we provide brief discussions of research concepts based on studies from various references. This is provided to show research that has been carried out previously regarding the problems examined in this study so as to provide an aspect of originality to this research.

2.1. Nonparametric Regression (NR) Model

The approach of using NR models, both one-response and biresponse, has been widely used by previous researchers using longitudinal, cross-section and time series data. The following previous researchers who have conducted research on one-response or bi-response modeling in the NR model include the following: Mardianto et al. [13], Ketrin et al. [14], and Iriany and Fernandes [15] used the Fourier series estimator; Rahmawati et al. [16] used the spline smoothing estimator; Geller and Neumann [17] and Fan and Gijbels [18] discussed local polynomials in the NR models; Araveeporn [19] used truncated spline estimators in time series data; and Mariati et al. [20] used a mixed estimator of smoothing spline and Fourier series to estimate the NR model. Studies on longitudinal data using the NR model have been widely conducted, including spline regression estimation with Least Squares [21], truncated spline regression estimation [22,23], smoothing spline estimation [24], kernel NR estimation [25,26], and mixed estimators of NR [27]. These studies are limited to one response even though some cases involve several correlated response variables. In research on longitudinal data, biresponse or multiresponse variables are often found in NR modeling. Previous studies on Biresponse Nonparametric Regression (BNR) using longitudinal data include those by Xiang et al. [28] who used the Local Polynomial Kernel approach; Fernandes et al. [29] who used spline smoothing. The researchers mentioned above discussed nonparametric regression models for longitudinal data only. In other words, these researchers have not discussed semiparametric regression models for longitudinal data yet.

2.2. Semiparametric Regression (SR) Model

Several studies on estimating SR models using different estimators have been conducted by some researchers. For example, Asrini [5] used the Fourier series estimator; Diana et al. [6] estimated an SR model using the Bayesian approach; Nisa and Budiantara [30] used a mixed estimator of truncated spline and Fourier series; Mohaisen and Abdulhussein [7] used the spline estimator; and Ampa et al. [31] used the kernel estimator. In addition, various studies on estimating SR models for longitudinal data have also been conducted by some researchers, for example Sun and You [32] who used the Least Squares spline approach; Jazi and Pullenayegum [33] selected the variables of a longitudinal SR model; and Utami et al. [34] used the local polynomial estimator. These previous studies are limited to one-response SR models only. In the real cases, we frequently find some correlated response variables of SR models for longitudinal data that must be analyzed. In this case, we should employ a biresponse or multiresponse SR model for longitudinal data. Several previous researchers who studied biresponse or multiresponse SR modeling for longitudinal data include Li [35] and Jia et al. [36] who estimated the covariance matrix of errors to improve estimation efficiency for coefficients of the longitudinal SR model; Jiao et al. [37] who analyzed longitudinal data based on the Bayesian method, and Chamidah et al. [38] who estimated the multiresponse SR model using the smoothing spline estimator.

Researchers generally accommodate this correlation using a symmetrical variance–covariance matrix when estimating model parameters. The variance–covariance matrix is theoretically assumed to be a fixed variable, while in real cases, its value is unknown. Several studies have been carried out on the estimation of the variance–covariance matrix in nonparametric and semiparametric regression models, including the studies by Lestari et al. [8,9], Li [35], Jia et al. [36], and Ampulembang et al. [39]. This means that the variance–covariance matrix must be estimated from the data. In previous research, the implementation of the estimation results was only carried out on simulated data. Based on the simulation results from previous research, the results showed that estimates using the variance–covariance matrix were better than estimates without using the variance–covariance matrix. Therefore, it is necessary to carry out research regarding the estimation of the SBR model for longitudinal data using local polynomials. Based on the estimation results, it is then simulated using a variance–covariance, which is then implemented on real data, namely DHF patients. Compared to previous methods, SBR for longitudinal data with the LPK estimator using the variance–covariance matrix as the weighted estimator provides the advantage of being able to model data with two correlated responses in longitudinal data phenomena with a semiparametric pattern, so that the model estimate fits.

3. Materials and Methods

In order to accomplish the research goals, this section provides a brief explanation of the materials and research steps used, such as the Weighted Least Squares (WLS) estimator, the SR model of longitudinal data, the Local Polynomial Kernel estimator in the NBR model, the goodness of fit of the estimated model, the DHF, and research steps.

3.1. Weighted Least Squares (WLS) Estimator

According to Montgomery et al. [40], deviations in error assumptions can usually occur in observations in regression analysis. The deviation is indicated by $Var\left(\mathsf{\epsilon }\right)\ne \mathbf{I}{\sigma }^2$, so that to overcome the regression model, the WLS method is used. This method can overcome violations of the heteroscedasticity assumption and can eliminate the unbiased and consistent properties of the OLS (Ordinary Least Squares) model. The deviation can be seen from the following regression model:

$$\mathbf{y}=\mathbf{X}\mathsf{\beta }+\mathsf{\epsilon }$$

where $\mathbf{y}$ represents a response variable, $\mathbf{X}$ represents a predictor variable, $\mathsf{\beta }$ represents a parameter of predictor variable, and $\mathsf{\epsilon }$ represents a random error. Here, $\mathit{E}\left(\mathsf{\epsilon }\right)=\mathbf{0}$, and $Var\left(\mathsf{\epsilon }\right)=\mathbf{V}{\sigma }^2$ where $\mathbf{V}$ is a weighting matrix, and $\mathsf{\epsilon }~N_n(\mathbf{0},\mathbf{V}{\sigma }^2)$, where $\mathsf{\epsilon }$ demonstrates Multivariate normal distribution. This regression model shows the deviation form, namely the matrix $\mathbf{V}{\sigma }^2\ne \mathbf{I}{\sigma }^2$. This means that the estimator for the parameter of the regression model based on Least Squares, namely $\widehat{\mathsf{\beta }}={\left({\mathbf{X}}^{\mathbf{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y},$ is not valid. Hence, another method is needed to obtain the estimator for the parameter of the regression model, namely the Weighted Least Squares (WLS) method, so that we can obtain the estimator for the parameter of the regression model based on the WLS, where $\widehat{\mathsf{\beta }}={\left({\mathbf{X}}^{\mathbf{T}}{\mathbf{V}}^{-1}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathbf{T}}{\mathbf{V}}^{-1}\mathbf{y}$.

3.2. Semiparametric Regression (SR) Model for Longitudinal Data

Longitudinal data are obtained by repeatedly observing each subject at different periods. Longitudinal data have different characteristics from cross-sectional data. The difference between longitudinal and cross-sectional data is that cross-sectional data are independent, while longitudinal data are dependent on the same subject and independent from different subjects [10]. Between responses and between observations on the same subject are correlated when longitudinal data include multiple responses [38]. The SR model combines two regression models, namely the parametric regression model and nonparametric model, so the SR model has at least two predictor variables. The SR model assumes that the functional association between the response and predictor variables follows a certain pattern, while the other predictor has an unknown pattern. For example, $y_i$ denotes the response variable for the i-th subject while $x_i$ and $t_i$ represent the predictor variables. If the form of the function between $y_i$ and $x_i$ is known and the form of curve for $t_i$ is unknown (if linear), the data can be modeled using the SR model as follows:

$$y_i={\beta }_0+{\beta }_1{x}_{1i}+{\beta }_2{x}_{2i}+\dots +{\beta }_p{x}_{pi}+\eta \left(t_i\right)+{\epsilon }_i, i=1,2,\dots ,n$$

(1)

where $y_{i }$ is the response variable at the i-th observation; ${x_{1i}, x_{2i},\dots ,x}_{pi}$ are parametric components of the predictor variable; ${\beta }_0, {\beta }_1, {\beta }_2,\dots ,{\beta }_p$ are parameters of the parametric components; $\eta \left(t_i\right)$ is a nonparametric component of predictor variables; and ${\epsilon }_i$ is the random error with ${\epsilon }_i~N\left(0,{\sigma }^2\right)$. The function $\eta \left(t_i\right)$ is a function whose curve shape is not known yet, and it is assumed to be smooth. Model (1) can be represented by the following matrix equation:

$$\mathbf{y}=\mathbf{X}\mathsf{\beta }+\mathsf{\eta }+\mathsf{\epsilon }$$

(2)

where $\mathbf{y}$ is the response variable with dimensions $(n\times 1)$, $\mathbf{X}$ is the parametric component of the predictor variable with the dimensions $(n\times \left(p+1\right))$, $\mathsf{\beta }$ is the parameter of the parametric component with the dimensions $\left(\right(p+1)\times 1)$ and $\mathsf{\eta }$ is the nonparametric component of the predictor variable with the dimensions ($n\times 1$) that are assumed to be smooth and $\mathsf{\epsilon }~N_n(0,\mathbf{I}{\sigma }^2)$ [38,41].

Next, the SR model for longitudinal data is given as follows [38]:

$$y_{ij}=x_{ij}^T\mathsf{\beta }+\mathrm{\eta }\left(t_{ij}\right)+{\epsilon }_{ij}, i=1,2,\dots ,n; j=1,2,\dots ,m_i$$

(3)

where $y_{ij}$ is the response variable, $x_{ij}^T\mathsf{\beta }$ is the parametric component of the regression function, $\eta \left(t_{ij}\right)$ is an unknown function called the nonparametric component of the regression function that is estimated by the Local Polynomial Kernel (LPK) estimator, and ${\epsilon }_{ij}~N\left(0,{\sigma }^2\right)$ is the observation error.

Model (3) can be written as the following matrix equation:

$$\mathbf{y}=\mathbf{X}\mathsf{\beta }+\mathsf{\eta }+\mathsf{\epsilon }.$$

(4)

Therefore, Equation (4) is as follows:

$${\mathbf{y}}^{\mathbf{\ast }}=\mathsf{\eta }+\mathsf{\epsilon }$$

(5)

where ${\mathbf{y}}^{\mathbf{\ast }}=\mathbf{y}-\mathbf{X}\mathsf{\beta }$. Furthermore, if the estimation of $\mathsf{\beta }$, namely $\widehat{\mathsf{\beta }}$, is known, then the nonparametric function $\mathsf{\eta }$ can be estimated by using WLS optimization.

Therefore, Equation (2) can be expressed as follows:

$$\eta \left(t_{ij}\right)\approx {\mathit{z}}_{ij}^T\mathit{\theta }\left(t_0\right).$$

Next, let $\widehat{\mathit{\theta }}$ be an estimator of $\theta$ obtained by using the following WLS optimization:

$$\mathit{Q}=\underset{\theta }{\mathrm{Min}}\{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{\left(y_{ij}-{\mathit{z}}_{ij}^T\mathsf{\theta }\left(t_0\right)\right)}^2(t_{ij}-t_0)\}.$$

(6)

The WLS optimization in Equation (6) can be written as follows:

$$\mathit{Q}={{\mathrm{M}\mathrm{i}\mathrm{n}}_{\mathsf{\theta }}\left\{\right(\mathbf{y}-{\mathit{Z}}_{t_0}\mathit{\theta }\left(t_0\right))}^T(\mathbf{y}-{\mathit{Z}}_{t_0}\mathit{\theta }(t_0))\}$$

(7)

where ${\mathit{Z}}_{\mathit{i}}=[{\mathit{z}}_{\mathit{i}1},{\mathit{z}}_{\mathit{i}2},\dots ,{\mathit{z}}_{\mathit{i}{\mathit{n}}_{\mathit{i}}}{]}^T$ and ${\mathit{Z}}_{t_0}=[{\mathit{Z}}_1^{\mathit{T}},\dots ,{\mathit{Z}}_{\mathit{n}}^{\mathit{T}}]$. Therefore, the value for $\widehat{\mathit{\theta }}\left(t_0\right)$ can be obtained by adjusting Equation (7) with respect to $\mathit{\theta }\left(t_0\right)$, and setting to zero. Hence, we obtain the following equation:

$$\widehat{\mathsf{\theta }}\left(t_0\right)={\left({\mathbf{Z}}_{t_0}^T{\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^T{\mathbf{y}}^{\mathbf{\ast }}.$$

(8)

Then, we obtain the LPK estimator, $\widehat{\mathit{\eta }}$, as follows:

$$\widehat{\mathit{\eta }}={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^T{\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^T{\mathbf{y}}^{\mathbf{\ast }}={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^T{\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^T(\mathbf{y}-\mathbf{X}\widehat{\mathsf{\beta }})$$

Thus, based on Equation (8), the following equation can be obtained:

$$\widehat{\mathit{\eta }}=\mathbf{A}{\mathbf{y}}^{\mathbf{\ast }}=\mathbf{A}(\mathbf{y}-\mathbf{X}\widehat{\mathsf{\beta }})$$

where A $={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^T{\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^T$.

Next, we determine $\widehat{\mathsf{\beta }}$ by minimizing the Least Squares (LS) function as follows:

$$\mathit{Q}\left(\mathsf{\beta }\right)={(\left(\mathbf{I}-\mathbf{A}\right)\mathbf{y}-(\mathbf{I}-\mathbf{A}\left)\mathbf{X}\mathsf{\beta }\right)}^{\mathbf{T}}(\left(\mathbf{I}-\mathbf{A}\right)\mathbf{y}-(\mathbf{I}-\mathbf{A}\left)\mathbf{X}\mathsf{\beta }\right).$$

(9)

Hence, we obtain $\widehat{\mathsf{\beta }}$ as follows:

$$\widehat{\mathsf{\beta }}={\left[{\mathbf{X}}^{\mathrm{T}}{\left(\mathbf{I}-\mathbf{A}\right)}^{\mathrm{T}}\left(\mathbf{I}-\mathbf{A}\right)\mathbf{X}\right]}^{-1}{\mathbf{X}}^{\mathrm{T}}{\left(\mathbf{I}-\mathbf{A}\right)}^{\mathrm{T}}\left(\mathbf{I}-\mathbf{A}\right)\mathbf{y}$$

(10)

where ${\mathbf{A}}_{\mathbf{p}\mathbf{a}\mathbf{r}}=\mathbf{X}{\left[{\mathbf{X}}^{\mathrm{T}}{\left(\mathbf{I}-\mathbf{A}\right)}^{\mathrm{T}}\left(\mathbf{I}-\mathbf{A}\right)\mathbf{X}\right]}^{-1}{\mathbf{X}}^{\mathrm{T}}{\left(\mathbf{I}-\mathbf{A}\right)}^{\mathrm{T}}\left(\mathbf{I}-\mathbf{A}\right)$, ${\mathbf{A}}_{\mathbf{n}\mathbf{o}\mathbf{n}\mathbf{p}\mathbf{a}\mathbf{r}}=\mathbf{A}(\mathbf{I}-{\mathbf{A}}_{\mathbf{p}\mathbf{a}\mathbf{r}})$, and

$${\mathbf{A}}^{\mathbf{\ast }}\left(\mathbf{h}\right)={\mathbf{A}}_{\mathbf{p}\mathbf{a}\mathbf{r}}+{\mathbf{A}(\mathbf{I}-\mathbf{A}}_{\mathbf{p}\mathbf{a}\mathbf{r}}).$$

3.3. Local Polynomial Kernel Estimator in Biresponse Nonparametric Regression (BNR) Model

In regression analysis, if the response variable has two correlated variables, then it is called the biresponse regression (BR) model. The BR model can be written as follows:

$${\mathbf{y}}_i=\mathbf{f}\left(x_i\right)+{\mathsf{\epsilon }}_{\mathit{i}}, i=1,2,\dots ,n$$

where ${\mathbf{y}}_{\mathit{i}}={({\mathbf{y}}_{\mathit{i}}^{\left(1\right)},{\mathbf{y}}_{\mathit{i}}^{\left(2\right)})}^{\mathrm{T}}$ is the response variable, $\mathbf{f}\left(x_i\right)={\left({\mathbf{f}}^{\left(1\right)}\right(x_i),{\mathbf{f}}^{\left(2\right)}(x_i\left)\right)}^{\mathrm{T}}$ is the regression function, and ${\mathsf{\epsilon }}_i={({\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)},{\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)})}^{\mathrm{T}}$ is the observation error with the variance–covariance matrix of each observation, ${\mathsf{\Sigma }}_i$, given by the following expression:

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_i& =Cov\left({\mathsf{\epsilon }}_{\mathit{i}}\right)=Cov\left(\begin{array}{c}{\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)}\\ {\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)}\end{array}\right)\hfill \\ & =\left(\begin{array}{cc}\mathrm{V}\mathrm{a}\mathrm{r}\left({\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)}\right)& \mathrm{C}\mathrm{o}\mathrm{v}({\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)},{\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)})\\ \mathrm{C}\mathrm{o}\mathrm{v}({\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)},{\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)})& \mathrm{V}\mathrm{a}\mathrm{r}\left({\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)}\right)\end{array}\right)\hfill \\ & =\left(\begin{array}{cc}{\sigma }_{1i}^2& {\sigma }_{1i}{\sigma }_{2i}{\rho }_i\\ {\sigma }_{1i}{\sigma }_{2i}{\rho }_i& {\sigma }_{2i}^2\end{array}\right)\hfill \end{array}$$

where ${\sigma }_1^2$ and ${\sigma }_2^2$ are two variance components, and $\rho$ is the correlation coefficient [41].

The Biresponse Nonparametric Regression (BNR) model is a regression model consisting of two response variables that are correlated with each other. The BNR model can be written as follows:

$${\mathbf{y}}_i=\mathsf{\eta }\left(t_i\right)+{\mathsf{\epsilon }}_{\mathit{i}}, i=1,2,\dots ,n$$

(11)

where ${\mathbf{y}}_{\mathit{i}}={({\mathbf{y}}_{\mathit{i}}^{\left(1\right)},{\mathbf{y}}_{\mathit{i}}^{\left(2\right)})}^{\mathrm{T}}$ represents two response variables that are correlated with each other, $\mathsf{\eta }\left(t_i\right)={\left({\mathsf{\eta }}_1\right(t_i),{\mathsf{\eta }}_2(t_i\left)\right)}^{\mathrm{T}}$ is the regression function, and ${\mathsf{\epsilon }}_{\mathit{i}}={({\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)},{\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)})}^{\mathrm{T}}$ is the observation error with the variance–covariance matrix ${\mathsf{\Sigma }}_{\mathit{i}}$, where index i indicates the observation. Here, ${\mathbf{y}}_{\mathit{i}}^{\left(1\right)}$ and ${\mathbf{y}}_{\mathit{i}}^{\left(2\right)}$ are correlated with each other. The function $\mathsf{\eta }\left(t_i\right)$ is a nonparametric biresponse curve estimated using the LPK estimator by considering the kernel function $K_h$ and a weighting matrix $\mathbf{W}$. The matrix $\mathbf{W}$ is a $(2n\times 2n)$ weighting matrix obtained from the inverse of the variance–covariance matrix, as shown below:

$$\mathbf{W}={\left(\begin{array}{cc}{\mathsf{\Sigma }}_{11}& {\mathsf{\Sigma }}_{12}\\ {\mathsf{\Sigma }}_{21}& {\mathsf{\Sigma }}_{22}\end{array}\right)}^{-1}$$

(12)

where ${\mathsf{\Sigma }}_{rr}=diag({\sigma }_1^{2\left(r\right)},{\sigma }_2^{2\left(r\right)},\dots ,{\sigma }_n^{2\left(r\right)})$, and ${\mathsf{\Sigma }}_{sr}=diag({\sigma }_1^{\left(s\right)\left(r\right)},{\sigma }_2^{\left(s\right)\left(r\right)},\dots ,{\sigma }_n^{\left(s\right)\left(r\right)})$.

The function $\mathsf{\eta }\left(t_i\right)={\left({\mathsf{\eta }}_1\right(t_i),{\mathsf{\eta }}_2(t_i\left)\right)}^{\mathrm{T}}$ is approximated locally with a Taylor Series of p-degree polynomials at point $t_0$ as follows [41]:

$${\eta }_r\left(t_i\right)\approx {\theta }_0^{\left(r\right)}\left(t_0\right)+\left(t_i-t_0\right){\theta }_1^{\left(r\right)}\left(t_0\right)+\cdots +{\left(t_i-t_0\right)}^p{\theta }_p^{\left(r\right)}\left(t_0\right), r=1,2$$

(13)

where ${\theta }_k^{\left(r\right)}\left(t_0\right)={\displaystyle \frac{{\eta }_r^{\left(k\right)}\left(t_0\right)}{k !}}$, $k=\mathrm{0,1},2,\dots ,p$.

Let $\mathbf{y}=\left(\begin{array}{c}{\mathbf{y}}_1\\ {\mathbf{y}}_2\end{array}\right)$; ${\mathbf{y}}_r=\left(\begin{array}{c}{\mathbf{y}}_1^{\left(r\right)}\\ {\mathbf{y}}_2^{\left(r\right)}\\ \begin{array}{c}⋮\\ {\mathbf{y}}_n^{\left(r\right)}\end{array}\end{array}\right)$; $\mathsf{\theta }\left(t_0\right)=\left(\begin{array}{c}{\mathsf{\theta }}^1\\ {\mathsf{\theta }}^2\end{array}\right)$; ${\mathsf{\theta }}^{\mathit{r}}=\left(\begin{array}{c}{\theta }_0^{\left(r\right)}\left(t_0\right)\\ {\theta }_1^{\left(r\right)}\left(t_0\right)\\ \begin{array}{c}⋮\\ {\theta }_p^{\left(r\right)}\left(t_0\right)\end{array}\end{array}\right)$; ${\mathbf{Z}}_{t_0}=\left(\begin{array}{cc}{Z}^{\left(1\right)}\left(t_0\right)& \mathbf{0}\\ \mathbf{0}& Z^{\left(2\right)}\left(t_0\right)\end{array}\right)$; ${\mathbf{Z}}^{\mathit{r}}\left(t_0\right)=\left[{\mathbf{Z}}_1^{\mathbf{T}},\dots ,{\mathbf{Z}}_{\mathbf{n}}^{\mathbf{T}}\right]; {\mathbf{Z}}_{\mathit{i}}=[{\mathit{z}}_{\mathit{i}1},{\mathit{z}}_{\mathit{i}2},\dots ,{\mathit{z}}_{\mathit{i}p}{]}^T$; ${\mathit{z}}_{ip}=[1,(t_i-t_0),(t_i-t_0{)}^2,\dots ,(t_i-t_0{)}^p{]}^T$; $\mathsf{\epsilon }=\left(\begin{array}{c}{\mathsf{\epsilon }}_1\\ {\mathsf{\epsilon }}_2\end{array}\right)$; and ${\mathsf{\epsilon }}_r=\left(\begin{array}{c}{\mathsf{\epsilon }}_1^{\left(\mathit{r}\right)}\\ {\mathsf{\epsilon }}_2^{\left(\mathit{r}\right)}\\ \begin{array}{c}⋮\\ {\mathsf{\epsilon }}_{\mathit{n}}^{\left(\mathit{r}\right)}\end{array}\end{array}\right)$.

If ${\eta }_r\left(t_i\right)\approx {\mathit{z}}_{\mathit{i}\mathit{p}}^{\mathit{T}}{\mathsf{\theta }}^r$; $i=1,2,\dots ,n$, so Equation (13) can be transformed into the following equation:

$$\mathbf{y}={\mathbf{Z}}_{{\mathit{t}}_0}\mathsf{\theta }\left(t_0\right)+\mathsf{\epsilon }.$$

(14)

The estimation of $\mathsf{\theta }$, namely $\widehat{\mathsf{\theta }}$, is obtained by using the Weighted Least Squares (WLS) method, which minimizes the following function:

$$\mathit{Q}={\left(\mathbf{y}-{\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)\right)}^{\mathbf{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right)\left(\mathbf{y}-{\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)\right)$$

(15)

where ${\mathbf{K}}_{\mathit{h}}\left(t_0\right)=\left(\begin{array}{cc}{\mathbf{K}}_{\mathit{h}}^{\left(1\right)}& \mathbf{0}\\ \mathbf{0}& {\mathbf{K}}_{\mathit{h}}^{\left(2\right)}\end{array}\right)$; and ${\mathbf{K}}_{\mathit{h}}^{\left(\mathbf{r}\right)}=diag({\mathbf{K}}_{1h}^r,{\mathbf{K}}_{2h}^r,\dots ,{\mathbf{K}}_{nh}^r).$

Hence, we obtain the estimation of $\mathsf{\theta }\left(t_0\right)$, namely $\widehat{\mathsf{\theta }}\left(t_0\right),$ as follows:

$$\widehat{\mathsf{\theta }}\left(t_0\right)={\left({\mathbf{Z}}_{{\mathrm{t}}_0}^T\mathbf{W}{\mathbf{K}}_h\right(t_0\left){\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{{\mathrm{t}}_0}^T\mathbf{W}{\mathbf{K}}_h\left(t_0\right){\mathbf{Z}}_{t_0}\mathbf{y}.$$

The bandwidth or smoothing parameter is a controller of the balance between the smoothing function and the suitability of the function to the data. If the bandwidth is too small, the shape of the estimated curve will not be smooth, meaning that the estimated value obtained is closer to the data. An excessively wide bandwidth will result in an overly smooth estimated curve that tends to approach the response variable’s average. As a result, selecting the appropriate bandwidth for nonparametric regression is crucial. One technique for determining the optimum bandwidth $\left(h\right)$ is the following Generalized Cross-Validation (GCV) approach, as shown below [9,23]:

$$GCV\left(h\right)={\displaystyle \frac{MSE\left(h\right)}{{\left(n^{-1}tr\left[I-A\right]\right)}^2}}$$

(16)

$$\mathrm{where} MSE\left(h\right)=n^{-1}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2.$$

(17)

The bandwidth $\left(h\right)$ that generates the lowest GCV value is the optimum bandwidth $\left(h\right)$ value.

3.4. Goodness of Fit of Estimated Model

The degree to which the independent variable simultaneously influences the dependent variable is ascertained using the coefficient of determination $\left(R^2\right)$. The greater the coefficient of determination value, the greater the influence of the independent variable on the dependent variable. The formula for the coefficient of determination is given as follows [42]:

$$R^2={\displaystyle \frac{\sum _{i=1}^n\sum _{j=1}^{m_i}{\left({\widehat{y}}_{ij}-\overline{y}\right)}^2}{\sum _{i=1}^n\sum _{j=1}^{m_i}{\left(y_{ij}-\overline{y}\right)}^2}}; 0\le R^2\le 1$$

(18)

where $y_{ij}$ is the response variable in the $i$-th subject of the $j$-th observation, ${\widehat{y}}_{ij}$ is the estimated response variable in the $i$-th subject of the $j$-th observation, and $\overline{y}$ is the average response.

The average of the squared errors between the estimated and real values is known as the MSE. The best model can be identified by finding the minimum MSE value close to zero. This means that the estimation result is close to the actual data value and can be used to calculate the prediction for the next period. The formula of the MSE is given by Equation (17).

3.5. Dengue Haemorrhagic Fever (DHF)

Dengue Hemorrhagic Fever (DHF) is a disease that often occurs in tropical areas and is geographically similar to malaria. DHF is transmitted to humans by mosquitoes called Aedes Aegypti. The course of DHF is about 6 to 7 days, with a peak of mild fever at the end of the fever period. The diagnosis of dengue fever is generally based on the results of laboratory tests on patient blood samples [43]. The normal platelet count ranges from 150 thousand per microliter to 440 thousand per microliter. However, DHF patients experience a decrease in platelets to below 100,000/mm³. The laboratory diagnosis of DHF is thrombocytopenia, which is a decrease in platelets to below 100,000/mm³. Hemoconcentration is an increase in hematocrit levels by 20% or more [44].

The data used in this study are secondary data regarding platelet, hematocrit, and hemoglobin levels in hospitalized patients with DHF in 2022 at the Roemani Hospital Semarang. The number of subjects taken was ten patients, with each patient observed for seven days of observation, with the criteria of patients observed being Grade I patients, marked by symptoms of fever, followed by a positive tourniquet test and indications of viral infection with signs of bleeding [45]. This research used two response variables: platelet count and hematocrit data from hospitalized DHF patients. The parametric predictor variable is the hemoglobin level in hospitalized DHF patients, and the nonparametric predictor is the examination time (per day) in hospitalized DHF patients.

3.6. Research Steps

The research steps include estimating a two-response semiparametric regression (SR) model for longitudinal data using a local polynomial estimator and then applying it to platelet and hematocrit data from Grade 1 DHF patients. This research uses two response variables and two predictor variables.

• Determination of the components from BSR models of longitudinal data, such as parametric component regression function and nonparametric component regression function.
• Estimation of BSR model using longitudinal data with LPK estimators. The estimation method in this study was to optimize the WLS method.
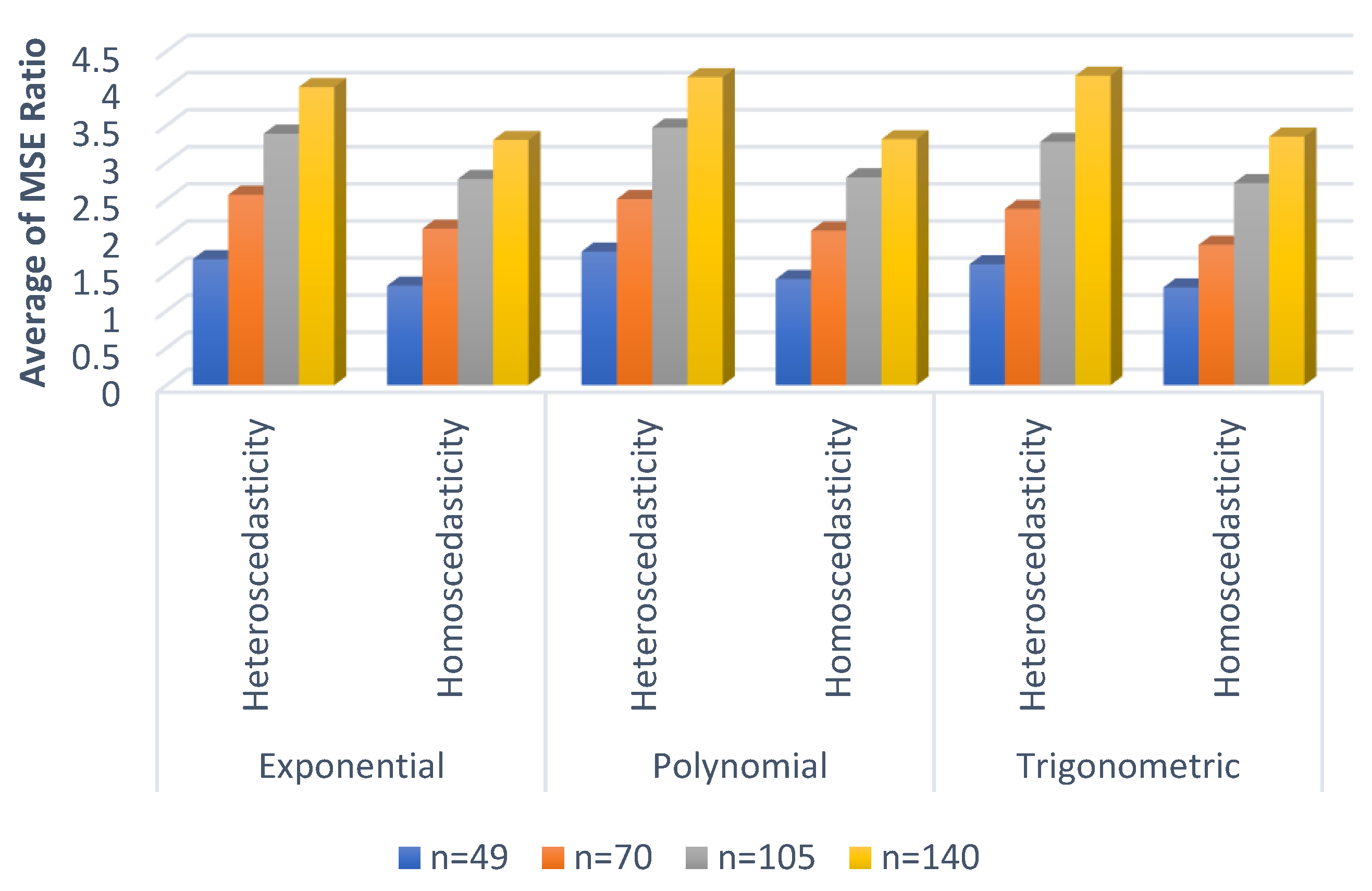
• Simulation of BSR model using the LPK estimator with longitudinal data by considering the use of variance–covariance matrix estimation and the simulation of the implementation of the BSR model in the case of homoscedasticity and heteroscedasticity using three types of functions, namely trigonometric functions, exponential functions, and polynomial functions. The simulation process was carried out with the help of open source software R. The prediction accuracy value in this simulation uses the MSE ratio; if the MSE ratio value is greater than 1, then the MSE of the second method is better than the MSE of the first method. Therefore, it can be proven that the estimation in the BSR model is better using the matrix W and kernel weighting.
• Implementation of the BSR model using the LPK estimator of longitudinal data in DHF patients. The following section will cover the application of the BSR model for the case of heteroscedasticity using two indicators for determining DHF disease, namely platelet and hematocrit levels, which are influenced by time and hemoglobin.

4. Results and Discussion

This session explains the analysis conducted following the research objectives. We discuss the estimation of the Biresponse Semiparametric Regression (BSR) model for longitudinal data using the LPK estimator. The estimation method in this research is to optimize the Weighted Least Squares (WLS) function. Then, the results of the BSR model estimation of longitudinal data using the LPK estimator are applied to the simulation data by considering the use of variance–covariance matrix estimation. The simulation results are combined with DHF data of hospitalized patients.

4.1. Determining Components of BSR Model for Longitudinal Data

In the paired longitudinal data $\left(x_{ij},t_{ij},y_{ij}^{\left(r\right)}\right),$ $j=1,2,\dots ,m$; $i=1,2,\dots ,n;r=1,2$, with m indicating the number of subjects, while n indicates the number of observations and r indicates the number of responses. The predictor variables consist of $x_{ij}$ and $t_{ij}$. $y_{ij}^{\left(1\right)}$ is the first response, and $y_{ij}^{\left(2\right)}$ is the second response. The relationship curve form between $y_{ij}^{\left(r\right)}$ and $x_{ij}$ is known, while the relationship curve form between $y_{ij}^{\left(r\right)}$ and $t_{ij}$ is unknown. Hence, the relationship between $(x_{ij},t_{ij})$ and $y_{ij}^{\left(r\right)}$ follows a semiparametric regression (SR) model as follows:

$$y_{ij}^{\left(r\right)}={\beta }_0^r+{\beta }_1^r{x}_{1i}+{\eta }_r\left(t_{ij}\right)+{\epsilon }_{ij}^{\left(r\right)}$$

(19)

If $f^r\left(x_{ij}\right)={\beta }_0^r+{\beta }_1^r{x}_{1i}$, then Equation (19) can be transformed into the following matrix equation:

$${\mathbf{y}}_{ij}=\mathbf{f}\left(x_{ij}\right)+\mathsf{\eta }\left(t_{ij}\right)+{\mathit{\epsilon }}_{ij}$$

(20)

where ${\mathbf{y}}_{ij}={\left(\begin{array}{cc}{\mathbf{y}}_{ij}^{\left(1\right)}& {\mathbf{y}}_{ij}^{\left(2\right)}\end{array}\right)}^T$ consists of two correlated response variables, $\mathbf{f}\left(x_{ij}\right)={\left(\begin{array}{cc}{\mathbf{f}}^{\left(1\right)}\left(x_{ij}\right)& {\mathbf{f}}^{\left(2\right)}\left(x_{ij}\right)\end{array}\right)}^T$ is the parametric component regression function, $\mathsf{\eta }\left(t_{ij}\right)={\left(\begin{array}{cc}{\mathsf{\eta }}^{\left(1\right)}\left(t_{ij}\right)& {\mathsf{\eta }}^{\left(2\right)}\left(t_{ij}\right)\end{array}\right)}^T$ is the nonparametric component regression function and ${\mathsf{\epsilon }}_i={\left(\begin{array}{cc}{\mathsf{\epsilon }}_{\mathit{i}}^{\left(1\right)}& {\mathsf{\epsilon }}_{\mathit{i}}^{\left(2\right)}\end{array}\right)}^T$ is the measurement error with a mean of 0 and variance of ${\mathsf{\Sigma }}_i$. The equation for each response variable can be expressed as follows:

$$y_{ij}^{\left(1\right)}={\beta }_0^1+{\beta }_1^1{x}_{1i}+{\eta }_1\left(t_{ij}\right)+{\epsilon }_{ij}^{\left(1\right)}$$

$$y_{ij}^{\left(2\right)}={\beta }_0^2+{\beta }_1^2{x}_{1i}+{\eta }_2\left(t_{ij}\right)+{\epsilon }_{ij}^{\left(2\right)}$$

In the matrix notation, we may write the equation as follows:

$$\left(\begin{array}{c}{\mathbf{y}}_{ij}^{\left(1\right)}\\ \cdots \\ {\mathbf{y}}_{ij}^{\left(2\right)}\end{array}\right)=\left(\begin{array}{c}{\mathbf{f}}^{\left(1\right)}\left(x_{ij}\right)+{\mathsf{\eta }}_1\left(t_{ij}\right)\\ \cdots \cdots \cdots \cdots \cdots \cdots \\ {\mathbf{f}}^{\left(2\right)}\left(x_{ij}\right)+{\mathsf{\eta }}_2\left(t_{ij}\right)\end{array}\right)+\left(\begin{array}{c}{\mathsf{\epsilon }}_{ij}^{\left(1\right)}\\ \cdots \\ {\mathsf{\epsilon }}_{ij}^{\left(2\right)}\end{array}\right)$$

(21)

where

$${\mathbf{y}}_{ij}^{\left(1\right)}=\left[\begin{array}{c}{\mathrm{y}}_{11}^{\left(1\right)}\\ {\mathrm{y}}_{12}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{1m}^{\left(1\right)}\\ \begin{array}{c}{\mathrm{y}}_{21}^{\left(1\right)}\\ {\mathrm{y}}_{22}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{2m}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{n1}^{\left(1\right)}\\ \begin{array}{c}{\mathrm{y}}_{n2}^{\left(1\right)}\\ ⋮\\ {\mathrm{y}}_{nm}^{\left(1\right)}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathrm{f}}^{\left(1\right)}\left(x_{11}\right)+{\mathrm{\eta }}_1\left(t_{11}\right)\\ {\mathrm{f}}^{\left(1\right)}\left(x_{12}\right)+{\mathrm{\eta }}_1\left(t_{12}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(1\right)}\left(x_{1m}\right)+{\mathrm{\eta }}_1\left(t_{1m}\right)\\ \begin{array}{c}{\mathrm{f}}^{\left(1\right)}\left(x_{21}\right)+{\mathrm{\eta }}_1\left(t_{21}\right)\\ {\mathrm{f}}^{\left(1\right)}\left(x_{22}\right)+{\mathrm{\eta }}_1\left(t_{22}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(1\right)}\left(x_{2m}\right)+{\mathrm{\eta }}_1\left(t_{2m}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(1\right)}\left(x_{n1}\right)+{\mathrm{\eta }}_1\left(t_{n1}\right)\\ \begin{array}{c}{\mathrm{f}}^{\left(1\right)}\left(x_{n2}\right)+{\mathrm{\eta }}_1\left(t_{n2}\right)\\ ⋮\\ {\mathrm{f}}^{\left(1\right)}\left(x_{nm}\right)+{\mathrm{\eta }}_1\left(t_{nm}\right)\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]+\left[\begin{array}{c}{\mathrm{\epsilon }}_{11}^{\left(1\right)}\\ {\mathrm{\epsilon }}_{12}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{1m}^{\left(1\right)}\\ \begin{array}{c}{\mathrm{\epsilon }}_{21}^{\left(1\right)}\\ {\mathrm{\epsilon }}_{22}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{2m}^{\left(1\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{n1}^{\left(1\right)}\\ \begin{array}{c}{\mathrm{\epsilon }}_{n2}^{\left(1\right)}\\ ⋮\\ {\mathrm{\epsilon }}_{nm}^{\left(1\right)}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]; {\mathbf{y}}_{ij}^{\left(2\right)}=\left[\begin{array}{c}{\mathrm{y}}_{11}^{\left(2\right)}\\ {\mathrm{y}}_{12}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{1m}^{\left(2\right)}\\ \begin{array}{c}{\mathrm{y}}_{21}^{\left(2\right)}\\ {\mathrm{y}}_{22}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{2m}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{y}}_{n1}^{\left(2\right)}\\ \begin{array}{c}{\mathrm{y}}_{n2}^{\left(2\right)}\\ ⋮\\ {\mathrm{y}}_{nm}^{\left(2\right)}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}{\mathrm{f}}^{\left(2\right)}\left(x_{11}\right)+{\mathrm{\eta }}_2\left(t_{11}\right)\\ {\mathrm{f}}^{\left(2\right)}\left(x_{12}\right)+{\mathrm{\eta }}_2\left(t_{12}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(2\right)}\left(x_{1m}\right)+{\mathrm{\eta }}_2\left(t_{1m}\right)\\ \begin{array}{c}{\mathrm{f}}^{\left(2\right)}\left(x_{21}\right)+{\mathrm{\eta }}_2\left(t_{21}\right)\\ {\mathrm{f}}^{\left(2\right)}\left(x_{22}\right)+{\mathrm{\eta }}_2\left(t_{22}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(2\right)}\left(x_{2m}\right)+{\mathrm{\eta }}_2\left(t_{2m}\right)\\ \begin{array}{c}⋮\\ {\mathrm{f}}^{\left(2\right)}\left(x_{n1}\right)+{\mathrm{\eta }}_2\left(t_{n1}\right)\\ \begin{array}{c}{\mathrm{f}}^{\left(2\right)}\left(x_{n2}\right)+{\mathrm{\eta }}_2\left(t_{n2}\right)\\ ⋮\\ {\mathrm{f}}^{\left(2\right)}\left(x_{nm}\right)+{\mathrm{\eta }}_2\left(t_{nm}\right)\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]+\left[\begin{array}{c}{\mathrm{\epsilon }}_{11}^{\left(2\right)}\\ {\mathrm{\epsilon }}_{12}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{1m}^{\left(2\right)}\\ \begin{array}{c}{\mathrm{\epsilon }}_{21}^{\left(2\right)}\\ {\mathrm{\epsilon }}_{22}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{2m}^{\left(2\right)}\\ \begin{array}{c}⋮\\ {\mathrm{\epsilon }}_{n1}^{\left(2\right)}\\ \begin{array}{c}{\mathrm{\epsilon }}_{n2}^{\left(2\right)}\\ ⋮\\ {\mathrm{\epsilon }}_{nm}^{\left(2\right)}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right].$$

Based on the nature of longitudinal data, random errors in each subject, namely $\left({\epsilon }_{i1}^{\left(r\right)},{\epsilon }_{i2}^{\left(r\right)},\dots ,{\epsilon }_{im}^{\left(r\right)}\right),$ are correlated, and errors between subjects $\left({\epsilon }_{1j}^{\left(r\right)},{\epsilon }_{2j}^{\left(r\right)},\dots ,{\epsilon }_{nj}^{\left(r\right)}\right)$ are independent, with $y_{ij}^{\left(r\right)}$ stating the response variable for $r=1,2$. On the other hand, the errors in each response, ${\epsilon }_{ij}^{\left(1\right)}$ and ${\epsilon }_{ij}^{\left(2\right)},$ are correlated. Since ${\eta }_r\left(t_{ij}\right)$ is approached by the Local Polynomial Kernel (LPK) estimator of degree p at point t around point $t_0$ as in Equation (13), we may write it as follows:

$${\eta }_r\left(t_{ij}\right)\approx {\eta }_r(t_0)+(t_{ij}-t_0){{\eta }_r}^{\left(1\right)}(t_0)+(t_{ij}-t_0{)}^2{\displaystyle \frac{{{\eta }_r}^{(2)}(t_0)}{2!}}+\dots +(t_{ij}-t{)}^p{\displaystyle \frac{{{\eta }_r}^{\left(p\right)}(t_0)}{p!}}$$

(22)

for $r=1,2$.

Next, if ${{\theta }_k}^{\left(r\right)}\left(t_0\right)={{\eta }_r}^{\left(k\right)}\left(t_0\right)/k!$; $k=0,1,2,\dots ,p$, the following equation can be obtained:

$${\eta }_r\left(t_{ij}\right)\approx {\theta }_0^{\left(r\right)}\left(t_0\right)+\left(t_{ij}-t_0\right){\theta }_1^{\left(r\right)}\left(t_0\right)+\cdots +{\left(t_{ij}-t_0\right)}^p{\theta }_p^{\left(r\right)}\left(t_0\right).$$

Hence, the Taylor series for ${\eta }_1\left(t_{ij}\right)$ is given by the following equation:

$${\eta }_1\left(t_{ij}\right)={\theta }_0^{\left(1\right)}\left(t_0\right)+\left(t_{ij}-t_0\right){\theta }_1^{\left(1\right)}\left(t_0\right)+\cdots +{\left(t_{ij}-t_0\right)}^p{\theta }_p^{\left(1\right)}\left(t_0\right).$$

(23)

Equation (23) can be expressed as follows:

$${\eta }_1\left(t_{ij}\right)={\mathbf{z}}_1^{\mathbf{\ast }}\left(t_0\right){\mathsf{\theta }}^{\left(1\right)}\left(t_0\right)$$

where ${\mathbf{z}}_1^{\mathbf{\ast }}\left(t_0\right)=\left[1,\left(t_{ij}-t_0\right),{\left(t_{ij}-t_0\right)}^2,\dots ,{\left(t_{ij}-t_0\right)}^p\right]$, and

$${\mathsf{\theta }}^{\left(1\right)}\left(t_0\right)={\left[{\theta }_0^{\left(1\right)}\left(t_0\right),{\theta }_1^{\left(1\right)}\left(t_0\right),{\theta }_2^{\left(1\right)}\left(t_0\right),\dots ,{\theta }_p^{\left(1\right)}\left(t_0\right)\right]}^T.$$

Also, the Taylor series for ${\eta }_2\left(t_{ij}\right)$ is given by the following equation:

$${\eta }_2\left(t_{ij}\right)={\theta }_0^{\left(2\right)}\left(t_0\right)+\left(t_{ij}-t_0\right){\theta }_1^{\left(2\right)}\left(t_0\right)+\cdots +{\left(t_{ij}-t_0\right)}^p{\theta }_p^{\left(2\right)}\left(t_0\right).$$

(24)

Equation (24) can be expressed as follows:

$${\eta }_2\left(t_{ij}\right)={\mathbf{z}}_2^{\mathbf{\ast }}\left(t_0\right){\mathsf{\theta }}^{\left(2\right)}\left(t_0\right)$$

where ${\mathbf{z}}_2^{\mathbf{\ast }}\left(t_0\right)=\left[1,\left(t_{ij}-t_0\right),{\left(t_{ij}-t_0\right)}^2,\dots ,{\left(t_{ij}-t_0\right)}^p\right]$, and

$${\mathsf{\theta }}^{\left(2\right)}\left(t_0\right)={\left[{\theta }_0^{\left(2\right)}\left(t_0\right),{\theta }_1^{\left(2\right)}\left(t_0\right),{\theta }_2^{\left(2\right)}\left(t_0\right),\dots ,{\theta }_p^{\left(2\right)}\left(t_0\right)\right]}^T.$$

Equations (23) and (24) can be expressed in matrix notation as follows:

$$\mathsf{\eta }\left(t_{ij}\right)=\left(\begin{array}{c}{\mathsf{\eta }}_1\left(t_{ij}\right)\\ {\mathsf{\eta }}_2\left(t_{ij}\right)\end{array}\right)={\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right).$$

(25)

Hence, the model in Equation (20) can be written as follows:

$$\mathbf{y}=\mathbf{X}\mathsf{\beta }+{\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)+\mathsf{\epsilon }.$$

(26)

The model in Equation (26) is the BSR model for longitudinal data that contains two components, namely the parametric function component ($\mathrm{i}.\mathrm{e}.,\mathbf{X}\mathsf{\beta }$) and the nonparametric function component (i.e., ${\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)$).

4.2. Estimation of BSR Model for Longitudinal Data

In the BSR model (26), estimation of the nonparametric component parameter, $\mathsf{\theta }\left(t_0\right)$, is obtained by minimizing the Weighted Least Squares (WLS) criterion by using the following kernel weighting function.

$${\mathbf{K}}_{\mathit{h}}\left(t_0\right)=\left(\begin{array}{cc}{\mathbf{K}}_{\mathit{h}}^{\left(1\right)}\left(t_0\right)& \mathbf{0}\\ \mathbf{0}& {\mathbf{K}}_{\mathit{h}}^{\left(2\right)}\left(t_0\right)\end{array}\right)$$

(27)

where ${\mathbf{K}}_{\mathit{h}}^{\left(\mathit{r}\right)}\left(t_0\right)=diag\left({\mathbf{K}}_{1\mathit{h}}^{\left(\mathit{r}\right)}\left(t_0\right),{\mathbf{K}}_{2\mathit{h}}^{\left(\mathit{r}\right)}\left(t_0\right),\dots ,{\mathbf{K}}_{\mathit{n}\mathit{h}}^{\left(\mathit{r}\right)}\left(t_0\right)\right)$, and

$${\mathbf{K}}_{\mathit{i}\mathit{h}}^{\left(\mathit{r}\right)}\left(t_0\right)=diag\left({\mathbf{K}}_{\mathit{i}1}^{\left(\mathit{r}\right)}\left({t_{i1}-t}_0\right),{\mathbf{K}}_{\mathit{i}2}^{\left(\mathit{r}\right)}\left({t_{i2}-t}_0\right),\dots ,{\mathbf{K}}_{im}^{\left(\mathit{r}\right)}\left({t_{im}-t}_0\right)\right).$$

Next, to obtain the estimation of the nonparametric component parameter, $\mathsf{\theta }\left(t_0\right)$, firstly we assume that the estimation of the parametric component parameter, $\mathsf{\beta }$, is known. Therefore, the Equation (19) becomes the following:

$${y^{\ast }}_{ij}^{\left(r\right)}={\eta }_r\left(t_{ij}\right)+{\epsilon }_{ij}^{\left(r\right)}$$

where ${y^{\ast }}_{ij}^{\left(r\right)}=y_{ij}^{\left(r\right)}-({\beta }_0^r+{\beta }_1^r{x}_{1i})$. Hereinafter, we may write the model in the matrix notation as follows:

$${\mathbf{y}}^{\mathbf{\ast }}={\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)+\mathsf{\epsilon }$$

(28)

where ${\mathbf{y}}^{\mathbf{\ast }}=\mathbf{y}-\mathbf{X}\mathsf{\beta }$.

The form of function ${\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)$ in the model (28) is unknown. So, it is estimated by using the LPK estimator and including the kernel weighting function as follows:

$$\mathit{Q}={\left({\mathbf{y}}^{\mathbf{\ast }}-{\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)\right)}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right)\left({\mathbf{y}}^{\mathbf{\ast }}-{\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right)\right)$$

(29)

$$={\mathbf{y}}^{\ast T}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}-2{\mathsf{\theta }}^{\mathit{T}}\left(t_0\right){\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}+{\mathsf{\theta }}^{\mathit{T}}\left(t_0\right){\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\mathsf{\theta }\left(t_0\right).$$

(30)

Next, by taking the partially derivative of Equation (30) with respect to $\mathsf{\theta }\left(t_0\right)$ and setting it to zero, we obtain the following results:

$$\begin{array}{cc}\hfill {\left.{\displaystyle \frac{\partial \mathit{Q}}{\partial \mathsf{\theta }\left(t_0\right)}}\right|}_{\mathsf{\theta }\left(t_0\right)=\widehat{\mathsf{\theta }}\left(t_0\right)}=0& \iff {\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}-{\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\widehat{\mathsf{\theta }}\left(t_0\right)=0\hfill \\ & \iff {\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}={\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\widehat{\mathsf{\theta }}\left(t_0\right)\hfill \\ & \iff \widehat{\mathsf{\theta }}\left(t_0\right)={\left({\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}\hfill \end{array}$$

(31)

Based on Equations (25) and (30), the LPK estimator for $\eta \left(x_{ij}\right)$ is as follows:

$$\mathbf{}\widehat{\mathsf{\eta }}\left(t_{ij}\right)={\mathbf{Z}}_{t_0}\widehat{\mathsf{\theta }}\left(t_0\right)={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}.$$

(32)

Since ${\mathbf{y}}^{\mathbf{\ast }}=\mathbf{y}-\mathbf{X}\mathsf{\beta }$, and based on Equation (32), we obtain the following equation:

$$\begin{array}{cc}\hfill \widehat{\mathsf{\eta }}\left(t_0\right)& ={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{y}}^{\mathbf{\ast }}\hfill \\ & =\mathbf{H}(\mathbf{y}-\mathbf{X}\mathsf{\beta })\hfill \end{array}$$

(33)

where $\mathbf{H}={\mathbf{Z}}_{t_0}{\left({\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right){\mathbf{Z}}_{t_0}\right)}^{-1}{\mathbf{Z}}_{t_0}^{\mathit{T}}\mathbf{W}{\mathbf{K}}_{\mathit{h}}\left(t_0\right)$.

Next, by substituting Equation (33) into Equation (26), this step gives the following equation:

$$\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}=\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\mathsf{\beta }+\mathsf{\epsilon }.$$

(34)

Hence, based on Equation (34), we have the following Least Squares (LS) expression:

$$\begin{array}{cc}\hfill \left(\mathsf{\beta }\right)& ={\left(\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}-\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\mathsf{\beta }\right)}^{\mathit{T}}\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}-\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\mathsf{\beta }\hfill \\ & ={\mathbf{y}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}-2{\mathsf{\beta }}^T{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}+{\mathsf{\beta }}^T{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\mathsf{\beta }.\hfill \end{array}$$

(35)

Next, by taking the partially derivative of Equation (35) with respect to $\mathsf{\beta }$ and setting it to zero, we obtain the following results:

$$\begin{array}{cc}\hfill {\left.{\displaystyle \frac{\partial \mathbf{L}\mathbf{S}\left(\mathsf{\beta }\right)}{\partial \mathsf{\beta }}}\right|}_{\mathsf{\beta }=\widehat{\mathsf{\beta }}}=0& \iff -2{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}+2{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\widehat{\mathsf{\beta }}=0\hfill \\ & \iff {\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\widehat{\mathsf{\beta }}={\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}\hfill \\ & \iff \widehat{\mathsf{\beta }}={\left({\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y}.\hfill \end{array}$$

(36)

Based on Equations (20) and (36), we obtain the estimation of the parametric component regression function, namely $\widehat{\mathbf{f}}$, as follows:

$$\begin{gathered} \widehat{\mathbf{f}}\left(\mathit{x}\right)=\mathbf{X}\widehat{\mathsf{\beta }}=\mathbf{X}{\left({\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{y} \\ ={\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}\mathbf{y} \end{gathered}$$

(37)

where ${\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}=\mathbf{X}{\left({\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\left(\mathbf{I}-\mathbf{H}\right)}^T\left(\mathbf{I}-\mathbf{H}\right)$.

Furthermore, by substituting Equation (37) into Equation (33), we obtain the LPK estimator of the nonparametric component of regression function as follows:

$$\begin{array}{cc}\hfill \widehat{\mathsf{\eta }}\left(\mathit{t}\right)=\mathbf{H}\left(\mathbf{y}-\mathbf{X}\mathsf{\beta }\right)& =\mathbf{H}(\mathbf{y}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}\mathbf{y})\hfill \\ & =\mathbf{H}(\mathbf{I}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}})\mathbf{y}\hfill \\ & ={\mathbf{A}}_{\mathit{n}\mathit{o}\mathit{n}\mathit{p}\mathit{a}\mathit{r}}\mathbf{y}\hfill \end{array}$$

(38)

where ${\mathbf{A}}_{\mathit{n}\mathit{o}\mathit{n}\mathit{p}\mathit{a}\mathit{r}}=\mathbf{H}(\mathbf{I}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}})$.

Finally, based on Equations (37) and (38), we obtain the estimation result of the Biresponse Semiparametric Regression (BSR) model for longitudinal data using Local Polynomial Kernel (LPK) estimator as follows:

$$\begin{array}{cc}\hfill \widehat{\mathbf{y}}& =\mathbf{X}\widehat{\mathsf{\beta }}+{\mathbf{Z}}_{t_0}\widehat{\mathsf{\theta }}\left(t_0\right)\hfill \\ & =\widehat{\mathbf{f}}\left(\mathit{x}\right)+\widehat{\mathsf{\eta }}(\mathit{t})\hfill \\ & ={\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}\mathbf{y}+{\mathbf{A}}_{\mathit{n}\mathit{o}\mathit{n}\mathit{p}\mathit{a}\mathit{r}}\mathbf{y}\hfill \\ & ={\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}\mathbf{y}+\mathbf{H}(\mathbf{I}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}})\mathbf{y}\hfill \\ & =\left({\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}+\mathbf{H}(\mathbf{I}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}})\right)\mathbf{y}\hfill \\ & ={\mathbf{A}}^{\mathbf{\ast }}\left(h\right)\mathbf{y}\hfill \end{array}$$

(39)

$$\mathrm{where} {\mathbf{A}}^{\mathbf{\ast }}\left(h\right)={\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}+\mathbf{H}(\mathbf{I}-{\mathbf{A}}_{\mathit{P}\mathit{a}\mathit{r}}).$$

(40)

4.3. Optimal Bandwidth Selection Using GCV Method

After obtaining the parameter estimates of the Biresponse Semiparametric Regression (BSR) model using the Local Polynomial Kernel estimator, the next step is determining the values of the Generalized Cross-Validation (GCV) and MSE of the model formed. The GCV criterion is one method for selecting the optimal bandwidth. The GCV function is defined as follows:

$$GCV\left(h\right)={\displaystyle \frac{2N^{-1}{\left(\mathbf{y}-\widehat{\mathbf{y}}\right)}^T\left(\mathbf{y}-\widehat{\mathbf{y}}\right)}{{\left(2N^{-1} trace\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)\right)}^2}}={\displaystyle \frac{2N^{-1}{\mathbf{y}}^T{\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)}^T\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)\mathbf{y}}{{\left(2N^{-1} trace\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)\right)}^2}}$$

(41)

where $N=n\times m$.

Furthermore, the selection of the optimal bandwidth using GCV is performed by substituting the value of the bandwidth ($h\in (0,\infty )$) into the ${\mathit{A}}^{\mathbf{\ast }}\left(h\right)$ in Equation (40) until the minimum GCV(h) value is obtained. In addition to GCV, other measures of model goodness, such as MSE (Mean Square Error), are also considered.

The MSE is the average of the squared errors between the actual value and the estimated value. The best model can be determined by determining the minimum MSE value that is the closest to zero. This means that the estimated results are close to the actual values, and can be used to calculate prediction values for future periods. The formula for the MSE value of the BSR model is defined as follows:

$$MSE\left(h\right)=N^{-1}\left({\mathbf{y}}^T{\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)}^T\left(\mathbf{I}-{\mathit{A}}^{\mathbf{\ast }}\left(h\right)\right)\mathbf{y}\right).$$

(42)

4.4. Simulation Study

This section discusses the simulation of the implementation of the BSR model in the case of homoscedasticity and heteroscedasticity using three types of functions, namely trigonometric functions, exponential functions, and polynomial functions. The number of responses used is two responses (biresponse), and only uses two predictors, i.e., one predictor for the nonparametric component and one predictor for the parametric component.

The stages of generating data are as follows:

• Generating predictor variable values as parametric components (x) with uniform distribution. The notation for uniform distribution is $x~U(a=10, b=15)$, where α is the lowest value of x, and b is the highest value of x.
• Generating predictor variable values as nonparametric components (t) with uniform distribution. The notation for uniform distribution is $\mathrm{t}~U(a=1, b=7)$, where α is the lowest value of t, and b is the highest value of t.
• Generating error ($\epsilon$) values based on the bivariate normal distribution with a mean of 0 (namely, ${\mu }_1={\mu }_2=0$) and a variance–covariance matrix Σ according to the specified correlation and variance, where the variance of the first response (${\sigma }_1^2$) is 10, and the variance of the second response (${\sigma }_2^2$) is 2, and the value of its covariance ($Cov({\epsilon }_1,{\epsilon }_2)$) is 3.

$$\begin{gathered} \mathsf{\epsilon }=\left(\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\end{array}\right)~N\left[\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right),\left(\begin{array}{cc}{\sigma }_1^2& Cov({\epsilon }_1,{\epsilon }_2)\\ Cov({\epsilon }_1,{\epsilon }_2)& {\sigma }_2^2\end{array}\right)\right], \\ \mathsf{\Sigma }=\left(\begin{array}{cc}{\sigma }_1^2& Cov({\epsilon }_1,{\epsilon }_2)\\ Cov({\epsilon }_1,{\epsilon }_2)& {\sigma }_2^2\end{array}\right)=\left(\begin{array}{cc}10& 3\\ 3& 2\end{array}\right). \end{gathered}$$

• Calculating the value of the response variable by substituting the values of $x$ and $t$ for the specified function plus the error value according to the simulation scenario form equation.

This simulation study aims to prove that in the case of biresponses, the best estimate can be obtained by using the weighting matrix (W) in addition to kernel weighting. In this simulation, the prediction accuracy value, namely the MSE of the model estimation results with the first method, is compared with the MSE of the model estimation results with the second method. The first method is an estimation method that only uses the kernel weighting without using the W, while the second method is an estimation method that uses the kernel weighting and the inverse weighting of the response error variance–covariance matrix W. Thus,

$$MSE Ratio={\displaystyle \frac{MSE of 1^{st} method}{MSE of 2^{nd} method}}$$

(43)

If the MSE ratio value is greater than one, it indicates that the MSE of the second method is better than the first method because it has a smaller MSE value, and vice versa. This means that if the MSE ratio value is greater than one, it is proven that the estimation in the biresponse regression is better using the W weighting and kernel weighting. This simulation study uses two responses with three different types of functions: trigonometric, exponential, and polynomial. In addition, this simulation has several scenarios, namely sample size, type of function and type of case. The simulation study scenario is presented in

Table 1. Simulation scenario.

No.	Scenario	Description
1	Longitudinal Data Sample Size	49, 70, 105, 140
2	Type of Cases	Heteroscedasticity/Homoscedasticity
3	Parametric Component Functions	$g_1\left(x_{ij}\right)=6x_{ij}+3$; $g_2\left(x_{ij}\right)=2x_{ij}+0.8$
4	Nonparametric Component Functions	Polynomial Function: $f_1\left(t_{ij}\right)=t_{ij}^3+8t_{ij}^2+10t_{ij}+7$ $f_2\left(t_{ij}\right)=t_{ij}^3+3t_{ij}^2+8t_{ij}+2$ Exponential Function: $f_1\left(t_{ij}\right)=3\mathrm{E}\mathrm{x}\mathrm{p}\left(t_{ij}\right)$ $f_2\left(t_{ij}\right)=2\mathrm{E}\mathrm{x}\mathrm{p}\left(t_{ij}\right)$ Trigonometric Function: $f_1\left(t_{ij}\right)=3+5Cos\left(\pi { t}_{ij}\right)$ $f_2\left(t_{ij}\right)=2+3Sin\left(\pi { t}_{ij}\right)$

.

Simulations were carried out on scenarios with different sample sizes (n), i.e., 49, 70, 105, and 140 samples, types of cases, namely homoscedasticity and heteroscedasticity, and different functions (polynomial, exponential and trigonometric). Each scenario was simulated for 30 iterations and produced different MSE values. The simulation process was carried out with the help of open source software R and an example of the output of running the R-Code. The simulation results based on the scenario are given in

Table 2. Simulation results for calculating the MSE ratio based on each scenario.

Number of Samples (n)	Type of Case Heteroscedasticity	Average of MSE Ratio
		Polynomial	Exponential	Trigonometric
49	Yes	1.8020	1.6995	1.6300
	No	1.4305	1.3417	1.3187
70	Yes	2.5103	2.5661	2.3767
	No	2.0837	2.1096	1.8931
105	Yes	3.4717	3.3899	3.2816
	No	2.8033	2.7800	2.7251
140	Yes	4.1532	4.0189	4.1729
	No	3.3165	3.3058	3.3510

.

The results of the simulation study can be seen in Table 2 and Figure 1, which shows that the average of the MSE ratio is greater than one. It proves that weighting in inverse variance–covariance matrix W estimation and kernel weighting in biresponse regression estimation are indeed needed and have been proven to provide better estimation accuracy values when using the inverse variance–covariance matrix W compared to the method that only uses kernel weighting. Based on Figure 1, it can be concluded that the more the amount of data increases, the higher the MSE ratio value. In addition, the MSE ratio value in the case of heteroscedasticity is higher than in the case of homoscedastic data. It means that higher MSE ratio values indicate that the use of the inverse variance–covariance matrix W in biresponse regression estimation is very necessary to solve local polynomial biresponse regression models using longitudinal data, especially in cases of heteroscedasticity and increasingly large amounts of data. This is in accordance with research from Rosopa et al. [46] and Midi et al. [47], where regression parameter estimation using weighted W was used if heteroscedasticity was found in the data.

4.5. Implementation of Biresponse Semiparametric Regression (BSR) Model Using LPK Estimator for Longitudinal Data of DHF Patients

Based on the simulation results of the BSR model of longitudinal data, it can be concluded that in the case of heteroscedasticity, the best estimate is to use kernel weighting and W weighting. The following section will cover the application of the BSR model for the case of heteroscedasticity using two indicators for determining DHF disease, namely platelet and hematocrit levels, which are influenced by time and hemoglobin. This study uses secondary data from medical records of inpatients with DHF in 2023 at Roemani Hospital Semarang, Central Java Province, Indonesia. The number of subjects was 10 patients, and each patient was observed seven times for a total of 70 patients. The parametric predictor is the hemoglobin in inpatients with DHF, and the nonparametric predictor is the examination time (per day) in inpatients with DHF. The following are the characteristics of data taken from 10 samples of patients who were hospitalized for seven days suffering from Grade 1 DHF, which was characterized by symptoms of fever, followed by a positive tourniquet test indicative of viral infection with signs of bleeding, with the descriptive statistics presented below (see

Table 3. Descriptive statistics in Grade 1 DHF patients.

Variable	Mean	Min	Max
Platelets (mm3)	75,271.28	32,000	147,000
Hematocrit (%)	40.77	32.9	48.8
Hemoglobin (g/dL)	13.75	10.7	16.8
Time (days)	4	1	7

).

The first step for implementing the Local Polynomial kernel (LPK) of the BSR model for longitudinal data is to determine the optimal bandwidth and local polynomial degree of the nonparametric component. The determination uses the GCV method by selecting the bandwidth and local polynomial degree with the smallest GCV value as the optimal value. Based on the GCV method, the smallest GCV value is 72.89, with the optimal bandwidth value for the first response of 0.1 and the optimal bandwidth value for the second response of 0.6, while the local polynomial degree for the first response is 2 and the local polynomial degree on second response is 3. After obtaining the bandwidth value and local polynomial degree on each response, the next step is determining the parameter estimates of the parametric and nonparametric component models. Parameter estimation of the BSR model using the LPK estimator with the optimal bandwidth value for the first response of 0.1 and optimal bandwidth value for the second response of 0.6, in addition to a local polynomial degree for the first response of 2 and local polynomial degree for the second response of 3, produces an MSE value of 0.45. 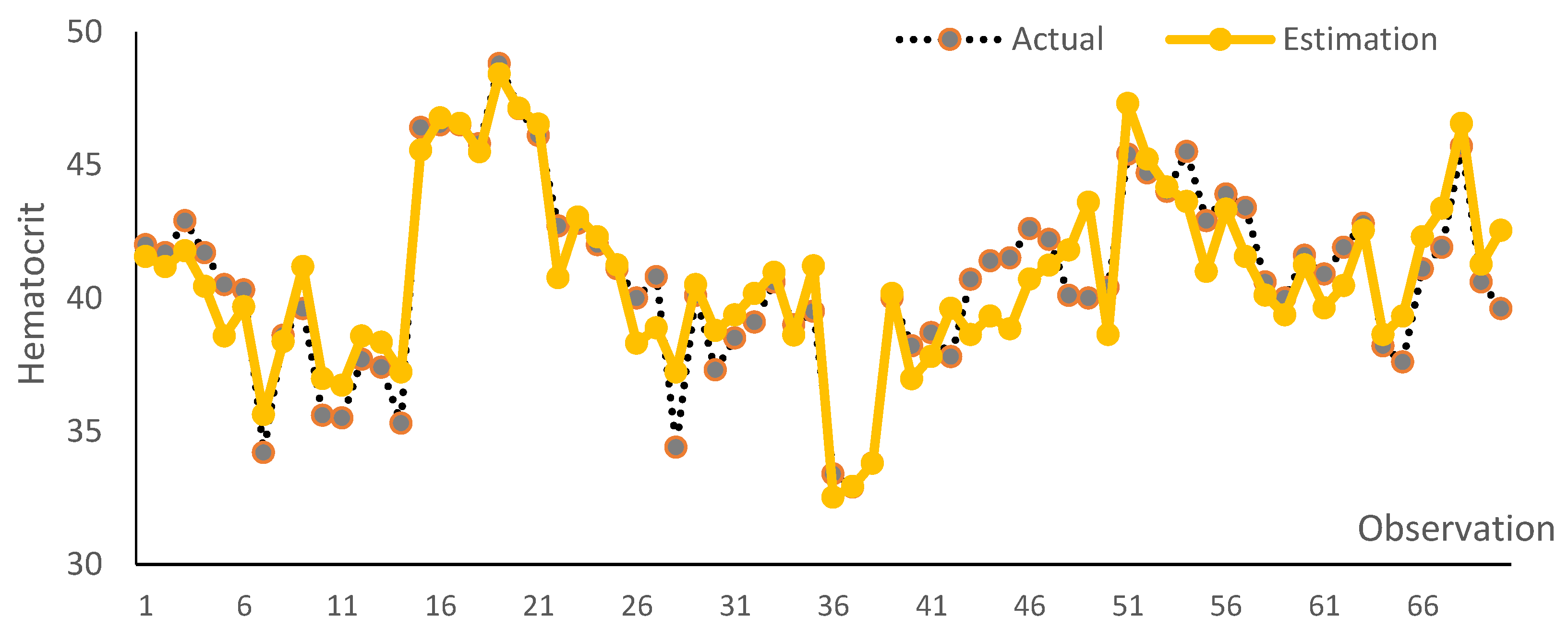The following figure (see Figure 2) is a comparison graph between the actual values and estimated values using the LPK estimator for each response.

Based on Figure 2 and Figure 3, the data pattern of the estimated BSR model using the LPK follows the actual data pattern. The results of the BSR estimation model applied to the DHF data obtained an R-square value of 92.8%, which means that according to Hair et al. [48], it can be defined as a strong estimation model because the R-square value is close to 100%. Based on Figure 1, the estimation results show that the lowest platelet levels, i.e., 32,477/mm³, were experienced by the third patient on the fifth day of being hospitalized. Figure 2 shows that the lowest hematocrit levels, 32.52%, were experienced by the sixth patient on the first day of being hospitalized. The following section will present the platelet (the first response) and hematocrit (the second response) levels in the second patient on the fourth day of being hospitalized using the Polynomial Local Kernel (LPK) estimator as follows:

$$\begin{array}{cc}\hfill y_{24}^{\left(1\right)}& ={\beta }_0^1+{\beta }_1^1{x}_{1i}+{\eta }_1\left(t_{24}\right)\hfill \\ & =290442-11778.9x+1.96\times {10}^{-17}{\left(t-4\right)}^2; 3.9<t<4.1\hfill \end{array}$$

(44)

$$\begin{array}{c}{y}_{24}^{\left(2\right)}={\beta }_0^2+{\beta }_1^2{x}_{1i}+{\eta }_2\left(t_{24}\right)\hfill \\ {\widehat{y}}_{24}^{\left(2\right)}=4.94+2.62x-9.84\times {10}^{-3}\left(t-4\right)+9.55\times {10}^{-3}{\left(t-4\right)}^2-1.53\times {10}^{-2}{\left(t-4\right)}^3; 3.4<t<4.6\hfill \end{array}$$

(45)

Based on Equations (44) and (45) and on the regression coefficient value of the hemoglobin variable, it can be concluded that every increase in the hemoglobin variable of 1 g/dL will cause platelet levels to decrease by 11,778.9/mm³, and hematocrit levels to increase by 2.62%, as experienced by the second patient on the fourth day of hospitalization. Meanwhile, the platelet modeling equation (first response) and hematocrit (the second response) modeling equation applicable to the seventh patient on the second day of hospitalization using the LPK estimator are as follows:

$$\begin{array}{cc}\hfill y_{72}^{\left(1\right)}& ={\beta }_0^1+{\beta }_1^1{x}_{1i}+{\eta }_1\left(t_{ij}\right)\hfill \\ & =300517-10637.5x-\left(6.63\times {10}^{-17}\right)\left(t-2\right)+\left(5.48\times {10}^{-17}\right){\left(t-2\right)}^2; 1.9<t<2.1\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill y_{72}^{\left(2\right)}& ={\beta }_0^2+{\beta }_1^2{x}_{1i}+{\eta }_2\left(t_{ij}\right)\hfill \\ & =5.02+2.62x+0.07\left(t-4\right)-0.02{\left(t-4\right)}^2+0.08{\left(t-4\right)}^3; 1.4<t<2.6\hfill \end{array}$$

(47)

Based on Equations (46) and (47), every 1 g/dL increase in hemoglobin variable will cause platelets to decrease by 10,637.5/mm³, and hematocrit to increase by 2.62%, which was experienced by the seventh patient on the second day of hospitalization.

5. Conclusions

Equation (39) is the result of applying LPK (Local Polynomial Kernel) estimator to estimate the Biresponse Semiparametric Regression (BSR) model for longitudinal data. The estimation method used for nonparametric functions uses WLS, while parametric functions use the LS method. In the LPK estimator using kernel weighting, the kernel weighting contains the optimal bandwidth. The selection of the optimum polynomial order and bandwidth in the model estimation is determined using the GCV method. The smallest GCV value is used to determine the optimum polynomial order and bandwidth. In addition, the use of the weighting matrix W, i.e., the inverse of the variance–covariance matrix, plays an important role in this process. It has been proven by simulating data using several iterations, which resulted in the use of weighting in the form of the inverse of the variance–covariance matrix W in biresponse regression estimation, and has been proven to provide better estimation accuracy values than methods that only use kernel weighting. The implementation of this modeling estimation is applied to DHF data, with the response variables being platelets and hematocrit, while the parametric component predictor variable is hemoglobin and the nonparametric component predictor variable is the examination time. The results of the model estimation obtained an MSE = 0.45, and R-square = 92.8%, which means that 92.8% of the variability in the dependent variable is explained by the independent variables used in this research and the remaining 7.2% are the independent variables not used in this research.

This study is only limited to data that have two responses and two predictor variables consisting of one predictor as a nonparametric component and the other predictor as a parametric component, so this topic needs to be studied further by increasing the number of response variables (multi-responses) and predictor variables (multi-predictors). In addition, the parametric component predictor variable is linear to the response variable so it needs to be expanded into a polynomial for the response variable.