Can the Solar Atmosphere Generate Very-High-Energy Cosmic Rays?

Abstract

The origin and acceleration of high-energy particles, constituting cosmic rays, is likely to remain an important topic in modern astrophysics. Among the two categories galactic and solar cosmic rays, the latter are much less investigated. The primary source of solar cosmic ray particles are impulsive explosions of the magnetized plasma, known as solar flares and coronal mass ejections. These particles, however, are characterized by relatively low energies compared to their galactic counterparts. In this work, we explore the resonance wave–wave (RWW) interaction between the polarized electromagnetic radiation emitted by the solar active regions and the quantum waves associated with high-energy, relativistic electrons generated during solar flares. Mathematically, the RWW interaction problem boils down to analyzing a Klein–Gordon Equation (spinless electrons) embedded in the electromagnetic field. We find that RWW could accelerate the relativistic electrons to enormous energies even comparable to energies in the galactic cosmic rays.

1. Introduction

The solar atmosphere is a highly effective, astrophysical engine for particle acceleration. It is well established that the primary manifestations of accelerated particles (such as electrons and protons) in the solar atmosphere are flares and coronal mass ejections [1]. The flares, the most violent explosions in the solar system, release enormous amounts of energy ($\sim {10}^{32}$ ergs) impulsively through a process assumed to be driven by what is called magnetic reconnection. The energy released by the destruction of the free energy in the magnetic field accelerates particles (also known as non-thermal particles) that propagate along coronal magnetic field lines toward the solar surface and into the interplanetary medium [2]. The evidences of accelerated, relativistic/near-relativistic particles in the flaring solar corona are provided by remote-sensing observations, including $\gamma$-ray, hard X-ray/bremsstrahlung, and radio/gyrosynchrotron measurements [3]. The flare events are, often, followed by dramatic enhancements in energetic particle fluxes, observed in in situ measurements within the heliosphere, including at ground level on Earth. These solar energetic particle (SEP) events have also been referred to as solar cosmic rays. The first detection of solar cosmic rays occurred through increased count rates in ionization chambers at ground level back in 1942 [4]. The energy of solar cosmic ray particles are, typically, lower (much lower) than galactic cosmic rays and range from a few MeV to several GeV [3].

Several particle acceleration mechanisms, describing how free magnetic energy released during a flare can be converted into particle acceleration, have been discussed and studied over the decades. These mechanisms can be categorized into three main groups: (1) electric field acceleration, when particles are accelerated in strong electric fields generated during the flare; (2) first order Fermi-type (shock) accelerations [5,6,7]; and (3) stochastic (second-order Fermi) acceleration, when particles gain energy through particle–wave interaction see chapter 11 of [8].

In this paper, we will exploit a recently explored acceleration mechanism based on resonant wave–wave (RWW) interactions [9,10]. This mechanism has already been applied to study particle energization in the magnetospheres of radio pulsars and radio Active Galactic Nuclei (AGN) [11,12]; it was shown that, under suitable conditions, RWW can boost particle energies to extremely high values—up to ${10}^{21}$ eV (AGN) and ${10}^{22}$ eV (pulsars).

The foundation work for the wave–wave resonance mechanism of acceleration was developed in [9,10], where a relativistic particle is described as a quantum wave, i.e., a Klein Gordon (KG) or a Dirac wave. The interaction between an electron and a circularly polarized electromagnetic (EM) wave is investigated as an interaction between the KG and EM waves. Thus, the acceleration of a particle is equivalent to a KG wave gaining energy at the cost of radiation—an EM wave, generated, for instance, by a nearby astrophysical object. The RWW works most efficiently when it operates on particles that are already fast. It is worth noting that the same acceleration mechanism should be applicable to Sun-like stars and other flaring stars (such as low-mass M-dwarfs, as well as young flaring stars). However, detecting cosmic rays from other stars is much more challenging due to the low flux rate and the possible overlap with other cosmic ray sources.

In what follows, we will study the reacceleration (via RWW) of already-relativistic particles generated, for instance, in solar flares; the source of the electromagnetic fields needed for the second stage of acceleration also originate in the Sun. The paper is arranged as follows: (1) In Section 2, we summarize the relevant mathematical framework of RWW, (2) Section 3 describes the solar coronal environment and parameters for efficient RWW, and (3) Section 4 and Section 5 present and summarize the main results of the study.

2. Mathematical Framework

Since the relativistic particles will be described via the quantum KG Equation, we will begin with some relativistic preliminaries. The group velocity of the KG wave, corresponding to a particle with mass m,

$${\upsilon }_g={\displaystyle \frac{\partial E}{\partial P}}={\displaystyle \frac{P}{{\left(P^2+m^2\right)}^{1/2}}},$$

(1)

tends to the speed of light ($c=1$) when $P>>m$. Here, E and P represent the particle’s energy and momentum, respectively. For a strong interaction with the EM wave (traveling with the speed of light), the initial KG (quantum) wave must be associated with highly relativistic particles. Thus, even among the energetic constituents of the solar corona [13], it is only the fastest (high Lorentz factor) that would really resonate effectively with the wave.

Following [10] and considering the circularly polarized electromagnetic wave $A^0=A^z=0$, $A^x=Acos\left(\omega t-kz\right)$ and $A^y=-Asin\left(\omega t-kz\right)$ propagating along the z-direction, we will start our analysis with the KG equation embedded in the specified EM field

$$\left({\partial }_t^2-{\partial }_z^2+2qA{K}_{\perp }cos\left(\omega t-kz\right)\right)\Psi +\left(K_{\perp }^2+m^2+q^2{A}^2\right)\Psi =0,$$

(2)

where $\omega$(k) represents the frequency (wave number) of the wave, q is the particle’s charge, and $K_{\perp }$ represents the perpendicular momentum (a constant due to the fact that the perpendicular directions are ignorable). We will seek solutions that are phase coherent with the EM, that is, $\Psi =\Psi \left(\xi \right)$ with $\xi =\omega t-kz$. Equation (2), then, reduces to the well-known Mathew equation

$$\left({\omega }^2-k^2\right){\displaystyle \frac{d^2\psi }{d{\xi }^2}}+\left(\mu +\nu cos\xi \right)=0,$$

(3)

where $\mu =K_{\perp }^2+m^2+q^2{A}^2$ and $\nu =2qA{K}_{\perp }$. It is worth noting that in a tenuous plasma (near vacuum), ${\omega }^2-k^2$ tends to zero, making (3) a singular differential equation; for a given $\mu$ and $\nu$, the derivatives of $\Psi$ must become large. The corresponding energy/momentum of the KG wave, therefore, must become commensurately large—the physical system undergoes a resonant enhancement.

After taking the WKB approximation [14] and dispersion relation, ${\omega }^2-k^2={\displaystyle \frac{{\omega }_p^2}{\sqrt{1+q^2{A}^2/m^2}}}$, into account, one can show that the rate of energy gain in physical units is given by [10,11]

$${\displaystyle \frac{dE}{dt}}\simeq eA{K}_{\perp }c{\displaystyle \frac{\sqrt{2}\hslash {\omega }^2}{{\omega }_p}}{\displaystyle \frac{{\left(1+\frac{e^2{A}^2}{m^2{c}^4}\right)}^{1/4}}{{\left(1+\frac{e^2{A}^2}{m^2{c}^4}+\frac{{\hslash }^2{K}_{\perp }^2{c}^2}{m^2{c}^4}\right)}^{1/2}}},$$

(4)

where ${\omega }_p=\sqrt{4\pi n{q}^2/m}$ is the plasma frequency and n represents the number density of particles.

The resonant enhancement, if unchecked, guarantees the maximum possible relativistic factor of the order of [9,10]

$$\gamma \simeq {\displaystyle \frac{\omega }{{\omega }_p}}{\left(1+{\displaystyle \frac{e^2{A}^2}{m^2{c}^4}}\right)}^{1/4}{\left(1+{\displaystyle \frac{e^2{A}^2}{m^2{c}^4}}+{\displaystyle \frac{{\hslash }^2{K}_{\perp }^2{c}^2}{m^2{c}^4}}\right)}^{1/2}$$

(5)

3. The Solar Active Region

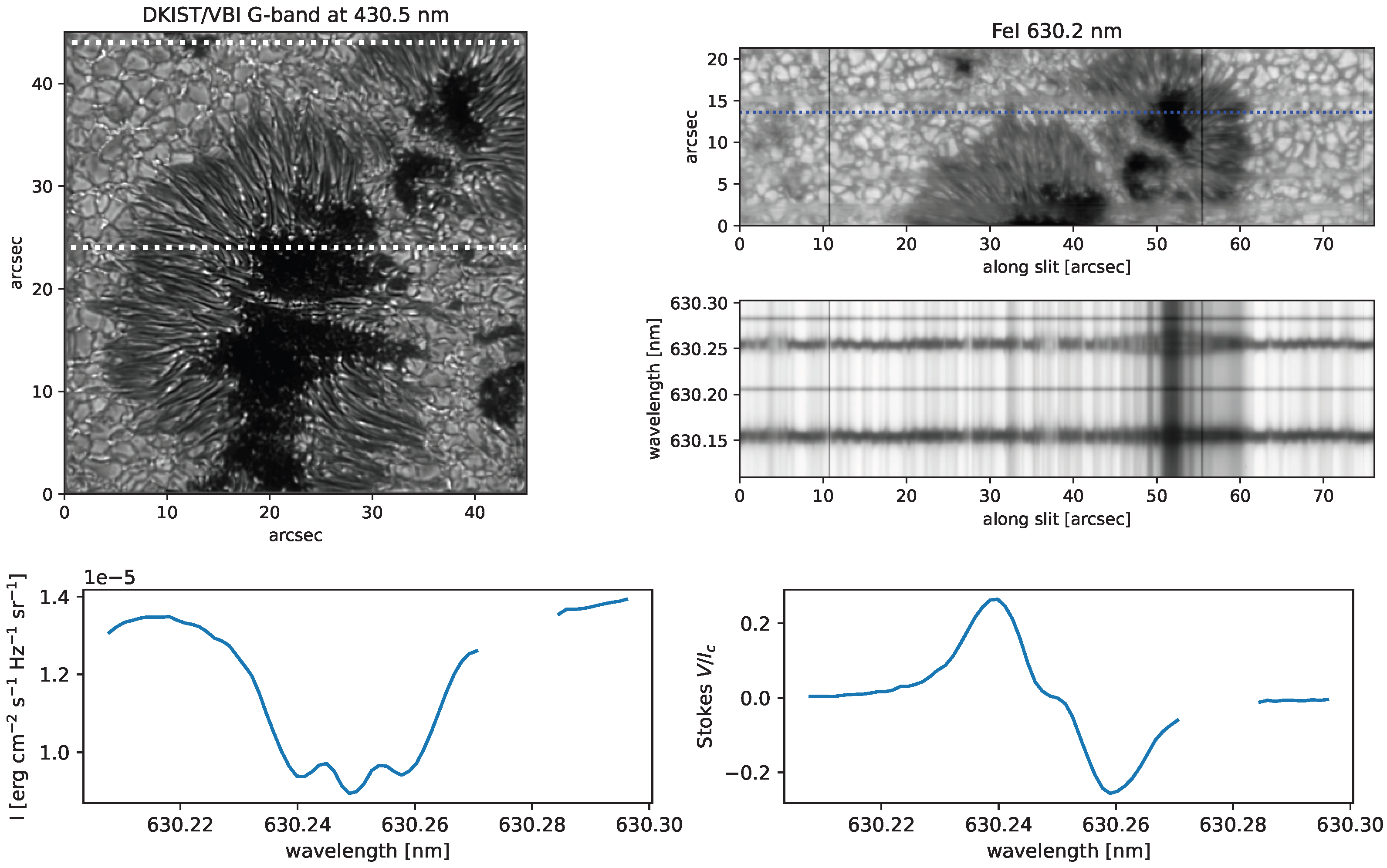
It is well known that the magnetic field of the solar active regions (ARs) induces polarized emission through the Zeeman effect in spectral lines formed across the entire electromagnetic spectrum from long radio wavelengths to GeV gamma rays. The top panels of Figure 1 display images of sunspots at G-band and Fe I 630.2 nm observed with the Visible Broadband Imager [15] and visible SpectroPolarimeter [16] on the Daniel K. Inouye Solar Telescope [17] on 16 October 2023 in AR NOAA 13645. The middle right and bottom panels of Figure 1 show Zeeman splitting of the Fe I 630.1/630.2 nm spectra along the spectrograph slit and intensity (Stokes I) and circular polarization (Stokes V) profiles of the representative pixel located in the sunspot umbra. The specific intensity of the Fe I 630.2 nm line in sunspot is around $I\approx 1.35\times {10}^{-5}\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{Hz}}^{-1}{\mathrm{sr}}^{-1}$ (Figure 1). Normalized Stokes V profile of this line indicates that around 30% of the sunspot continuum emission is circularly polarized (Figure 1).

The active region of corona is a multi-thermal (from tens of thousands to tens of millions of Kelvin), tenuous, and strongly magnetized plasma environment. The fundamental building blocks of coronal ARs are magnetic loops or open flux tubes, which are also the main contributors to coronal emissions.

Solar coronal polarimetry is challenging due to the low signal-to-noise ratios resulting from the weak magnetic field, hot and tenuous coronal environment, and large Doppler width of spectral lines. However, circular polarization of coronal emissions has been measured in various observations (see Table 1). Reference [18] reported measurements of circular polarizations in the infrared Ca 854.2 nm line in coronal loops during the 10 September 2017 X8.3 class solar flare (the second largest flare in solar cycle 24); magnetic field strengths as high as 350 G (at heights up to 25 Mm above the solar limb) were inferred.

Coronal spectropolarimetry techniques, using the near-infrared coronal emission line of Fe XIII at 1074.7 nm [19,20], have found that the degree of circular polarization of Fe XIII at 1074.7 nm line is around ∼0.1% of its disk-center intensity in AR corona. They inferred field strengths of 10 and 33 G in the two active regions at heights of 0.12, 0.15 $R_{\odot }$.

The circular polarization of low-frequency solar radio emissions has been recently explored by [21]. Their findings indicate that the average degree of circular polarization in the frequency range of 20/80 MHz varies between 10% and 80% during radio bursts.

Electron densities in the flare corona can range from ${10}^9\mathrm{to}{10}^{13}{\mathrm{cm}}^{-3}$ [8], depending on the strength of the flare and the temperature of the loops. Analyses of microwave observations of the abovementioned X8.2 solar flare suggests that large flares can accelerate nearly all electrons in a large coronal volume to mildly relativistic and relativistic speeds [22]. The estimated number density of electrons with energies above 20 keV in [22] is up to ∼${10}^{10}{\mathrm{cm}}^{-3}$. Furthermore, it has been derived that the number density of the relativistic electrons with energy above 300 keV (up to ∼1 MeV) during this event range from ${10}^2$–${10}^{4.7}$ cm⁻³ [13].

Although we have emphasized the circularly polarized radiation in the preceding discussion, RWW can take place for arbitrary polarization; hence, simple analytical expressions for energy gain (for instance) are possible for the circularly polarized waves and comparison with observation becomes easier.

4. Results

The relativistic particles in the flaring corona are illuminated by polarized emissions originating from both the corona and the photosphere, creating a promising avenue for RWW interaction. Table 1 summarizes the parameters of radiation intensity across four different wavelength ranges mentioned in Section 3, which have been successfully used for coronal magnetic field diagnostics in several studies.

As an example, we consider flare corona at H∼ 25 Mm above the photosphere. Then, by taking an average diameter, D, of the sunspot ∼20 Mm into account (Figure 1), one can estimate (order of magnitude) the corresponding solid angle $\Omega \simeq 2\pi \left(1-{\displaystyle \frac{H^2}{\sqrt{H^2+D^2}}}\right)\simeq 0.45$ sr; the flux $F_0\simeq 611.2$ erg cm⁻² s⁻¹ is, then, estimated after multiplying by the fraction of the polarized part $0.01$ for ${\lambda }_0=854.2$ nm (see Table 1).

For such a scenario, one can obtain,

$$\gamma \simeq 3.9\times {10}^9\times {\displaystyle \frac{\omega }{{\omega }_0}}\times {\left({\displaystyle \frac{{10}^2 {\mathrm{cm}}^{-3}}{n}}\right)}^{1/2},$$

(6)

where ${\omega }_0=2\pi c/{\lambda }_0$, and the flux and the cyclic frequency are normalized by the values corresponding to Fe I $630.2$ nm line. This is the maximum value of the RWW-boosted Lorentz factor. However, if there existed a mechanism that saturates the acceleration process at a lower Lorentz factor, the latter will control the final energy.

In general, there are several limiting mechanisms, which might potentially impose strict constraints on the maximum achievable energies. The solar corona magnetic field, B, can vary from tens up to hundreds of Gauss and the charged relativistic particles will inevitably experience synchrotron losses with the rate [23]

$$P_{syn}\simeq {\displaystyle \frac{2e^4{B}^2{\gamma }^2}{3m^2{c}^3}}.$$

(7)

As particles gain more and more energy (reaching higher $\gamma$), the synchrotron losses become stronger, limiting the maximum allowed energy. The synchrotron-limited ${\gamma }_{syn}^{max}$, obtained by balancing $dE/dt\simeq P_{syn}$, is estimated as

$${\gamma }_{syn}^{max}\simeq {\left({\displaystyle \frac{dE}{dt}}\times {\displaystyle \frac{3m^2{c}^3}{2e^4{B}^2}}\right)}^{1/2}\simeq 7\times {10}^8\times {\displaystyle \frac{350G}{B}}\times$$

$$\times {\left({\displaystyle \frac{\omega }{{\omega }_0}}\right)}^{1/2}\times {\left({\displaystyle \frac{F}{F_0}}\times {\displaystyle \frac{{10}^2 {\mathrm{cm}}^{-3}}{n}}\right)}^{1/4},$$

(8)

where we have taken into account the expression, $A=c\sqrt{cF}/\omega$, refs. [11,12].

Another mechanism that can potentially limit the energization process is the inverse Compton (IC) scattering when energetic electrons encounter soft thermal photons in the solar ambient. It is worth noting that the scattering will be more efficient with the radiation coming from the photosphere than with the photons corresponding to the coronal region, because the number density of the latter is much smaller. In the Thomson regime, the IC cooling rate is given by [23]

$$P_{IC}\simeq {\sigma }_{T}c{\gamma }^{2}U,$$

(9)

where ${\sigma }_T$ is the Thomson cross section, $U\simeq \sigma T^4{R}_{\odot }^2/\left({(R_{\odot }+H)}^{2}c\right)$ is radiation energy density in the corona at the altitude H, $\sigma$ denotes the Stefan-Boltzmann constant, $T\simeq 5777$ K is the photospheric temperature, and we assume that the radiation is black body. The balance condition yields

$${\gamma }_{IC}^{max}\simeq {\left({\displaystyle \frac{R_{\odot }+H}{R_{\odot }T}}\right)}^2\times {\left({\displaystyle \frac{dE/dt}{\sigma {\sigma }_T}}\right)}^{1/2}\simeq$$

$$\simeq 4.9\times {10}^{10}\times {\left({\displaystyle \frac{\omega }{{\omega }_0}}\right)}^{1/2}\times {\left({\displaystyle \frac{F}{F_0}}\times {\displaystyle \frac{{10}^2 {\mathrm{cm}}^{-3}}{n}}\right)}^{1/4}.$$

(10)

Table 1. Parameters of intensity for selected wavelengths/frequencies used for polarization measurements in the Sun.

Wavelength/Frequencies	Intensity $\left[\mathbf{erg}{\mathbf{cm}}^{-2}{\mathbf{s}}^{-1}{\mathbf{sr}}^{-1}\right]$	Circular Polarization (Stokes V/IC [%])	Coronal Magnetic Field Strength [Gauss]
Fe i 6302 Å a	$1.02\times {10}^6$	25	N/A
Ca ii 8542 Å b,c	$1.36\times {10}^5$	0.5–2	350
Fe xiii 10747 Å d,e	$1.35\times {10}^2$	0.1	10–30
20–80 MHz f	$2.40\times {10}^{-12 g}$	20–80	N/A

^a Figure 2, ^b ref. [18], ^c ref. [24], ^d ref. [19], ^e Chianti atomic line database [25], ^f ref. [21], ^g The unit of the radio flux is $\left[\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$.

Table 1. Parameters of intensity for selected wavelengths/frequencies used for polarization measurements in the Sun.

Wavelength/Frequencies	Intensity $\left[\mathbf{erg}{\mathbf{cm}}^{-2}{\mathbf{s}}^{-1}{\mathbf{sr}}^{-1}\right]$	Circular Polarization (Stokes V/IC [%])	Coronal Magnetic Field Strength [Gauss]
Fe i 6302 Å a	$1.02\times {10}^6$	25	N/A
Ca ii 8542 Å b,c	$1.36\times {10}^5$	0.5–2	350
Fe xiii 10747 Å d,e	$1.35\times {10}^2$	0.1	10–30
20–80 MHz f	$2.40\times {10}^{-12 g}$	20–80	N/A

^a Figure 2, ^b ref. [18], ^c ref. [24], ^d ref. [19], ^e Chianti atomic line database [25], ^f ref. [21], ^g The unit of the radio flux is $\left[\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$.

One should emphasize that the IC scattering in the Thomson regime works only when ${\gamma }_{IC}^{max}{ϵ}_{ph}/\left(m{c}^2\right)<<1$, where ${ϵ}_{ph}\sim k_{B}T$ is the photon energy. It is straightforward to check that, for all lines shown on Table 1, the abovementioned condition is violated. The scattering, therefore, occurs in the so-called Klein–Nishina regime. The corresponding expression for cooling power [26]

$$P_{KN}\simeq {\displaystyle \frac{\sigma {\left(mckT\right)}^2}{16{\hslash }^3}}\left(ln{\displaystyle \frac{4\gamma kT}{m{c}^2}}-1.981\right),$$

(11)

will lead to the maximum Lorentz factor

$${\gamma }_{KN}^{max}\simeq {\displaystyle \frac{m{c}^2}{4k_{B}T}}exp\left\{{\displaystyle \frac{16{\hslash }^3}{\sigma {\left(mc{k}_{B}T\right)}^2}}+1.981\right\},$$

(12)

where ℏ denotes the Planck’s constant. The preceding value of ${\gamma }_{KN}^{max}$ is unrealistically high. The IC scattering, therefore, does not impose any constraints on resonant energization.

Highly relativistic electrons might also cool in encounters with the ambient gas particles; the resulting bremsstrahlung loss occurs on time of $t_{br}\simeq 4\times {10}^7/n_p$ yr [27] with the proton number density (in the coronal region) $n_p\simeq {10}^9$ cm⁻³. One can show that the energy balance condition $t_{br}\simeq {\gamma }_{max}^{br}$ mc² /$\dot{E}$ leads to enormous Lorentz factors ∼10²⁰ for Ca II 854.2 nm. Similar situation pertains for other emission lines, and therefore, the electron bremsstrahlung does not limit the process of electron acceleration.

From Equations (6) and (8), for the parameters given in Table 1, one can show that the synchrotron mechanism is a limiting factor in all emission lines except 630.2 nm, for which the maximum relativistic factor is given by Equation (6).

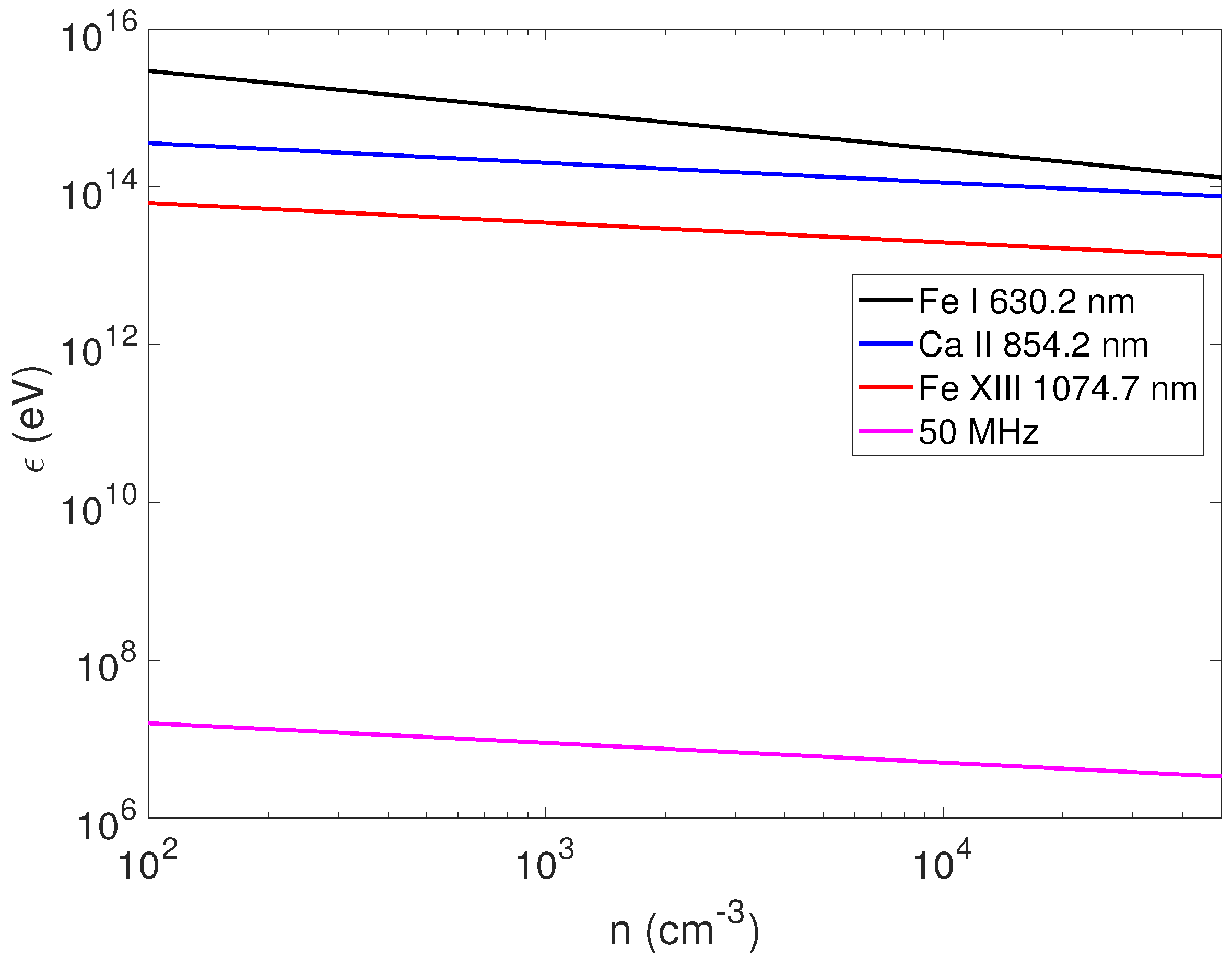
Plots of maximum achievable energies $ϵ=\gamma m{c}^2$ versus the number density are displayed in Figure 2. These plots span the set of parameters: $\lambda =630.2$ nm, $B=350$ G, $StokesV/I_c[\%]=25$ (black); $\lambda =854.2$ nm, $B=350$ G, $StokesV/I_c[\%]=1$ (blue); $\lambda =1074.6$ nm, $B=20$ G, $StokesV/I_c[\%]=0.1$ (red); $f=50$ MHz, $B=350$ G, $StokesV/I_c[\%]=50$ (magenta). As evident from (see Equations (6) and (8), all plots reveal the maximum energy decreasing with n. The line corresponding to 630.2 nm has a different inclination, because the maximum energy is not defined by the synchrotron losses. 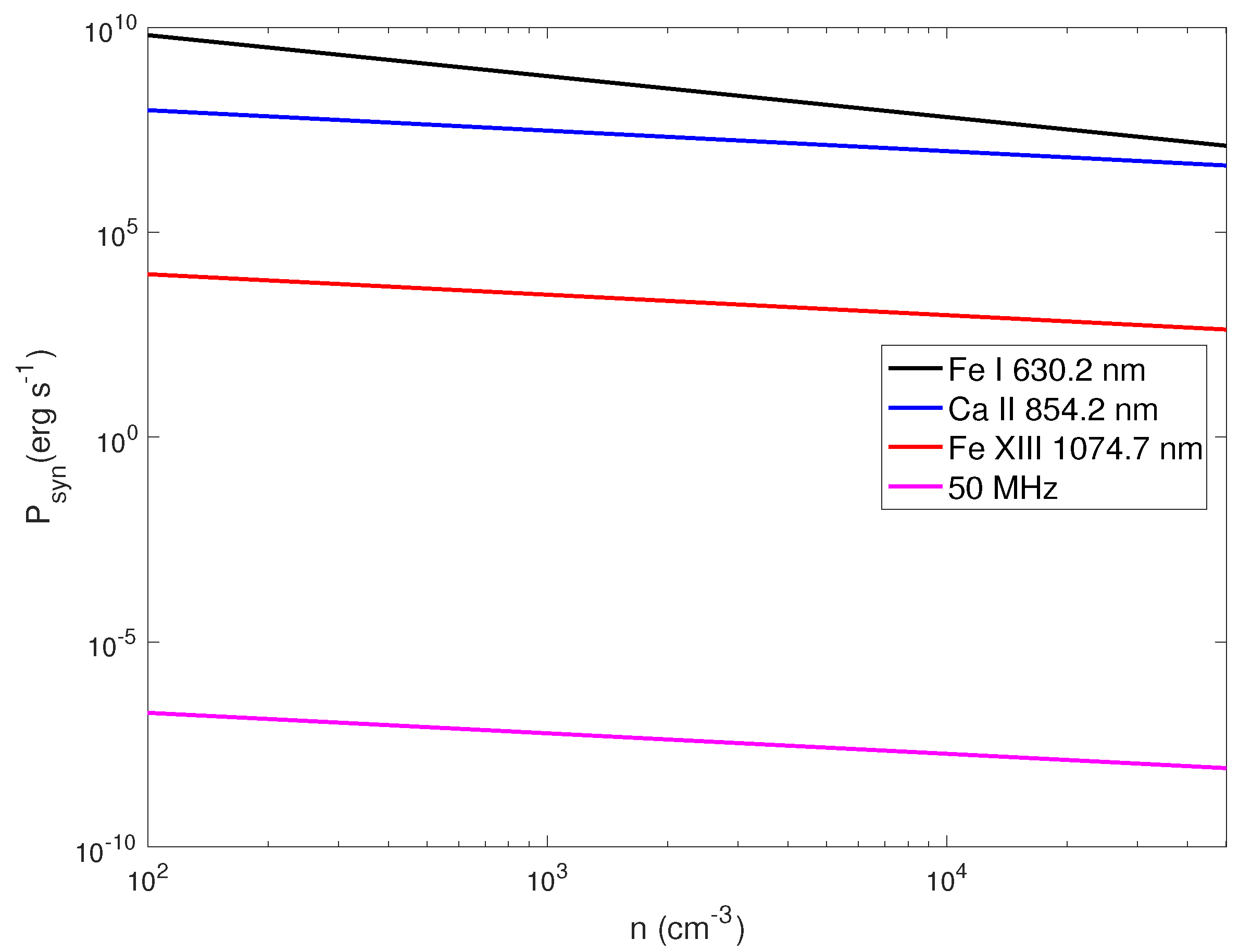In Figure 3, we show the synchrotron losses for the same set of parameters. We remind the reader that for Fe I 630.2 nm, the maximum achievable energy is not limited by the synchrotron losses, and is defined by Equation (6); the synchrotron losses still take place.

The resonance acceleration of electrons with initial energies ∼MeV, therefore, might provide energies of the order ∼1.5 $\times {10}^7$ eV for the radio band and ∼10¹⁴⁻¹⁵ eV for the rest, which means that the contribution of the Sun in the generation of high and VHE energy cosmic rays must be taken seriously. However, one must proceed with caution and realize that total flux of solar cosmic rays may not be very large. First, one must note that RWW operates on a very small subset of particles—the particles whose parallel (to the magnetic field) energy is much larger than the perpendicular component. The affected particles comprise a tiny sliver ($\approx {\omega }_p/\omega <<1$) of perpendicular energy distribution. Second, even if all particles resonated, the flux of very-high-energy (VHE) particles in the vicinity of Earth, $dN/\left(dtdA\right)\simeq F{R}_{\odot }^2/(r^2ϵ$), will be very small (here, $R_{\odot }^2/r^2$ comes from the spherical symmetry and $r=1AU$ is the distance from the Sun).

However, it is worth noting that the gyro-radius of the electrons with such high energies, $r_{gyro}\simeq ϵ/\left(eB\right)\simeq 2.5\times {10}^{10}$ cm, is smaller than $1AU$ by three orders of magnitude; therefore, some of the particles might be significantly deflected from their original directions, which is a well-known problem in cosmic ray physics. One finds that the time-scale of acceleration, $\tau =ϵ/\dot{E}$, is by many orders of magnitude smaller than the escape time-scale, ${\tau }_{esc}\simeq R_{\odot }/c$. Thus, the efficient acceleration of an individual particle as well as the continuous operation of the process is assured. A detailed study of kinematics of particles is significant to estimate the flux, but it is beyond the scope of the present paper; we intend to study this particular problem in the future.

Indirect signature of RWW could come from a secondary neutrino-related process. High-energy electrons, might produce neutrinos via the electron capture channel $e+p\to n+{\nu }_e$, which usually produces relatively low energy neutrinos, whereas the following process of $\beta$-decay $n\to p+e+{\overline{\nu }}_e$ produces high-energy neutrinos. In particular, it is well known that the beta decay spectrum has a maximum intensity for the kinetic energy of anti-neutrinos with the kinetic energy ∼1 MeV [28] in the rest frame of neutrons. On the other hand, the neutron has almost the same energy as the proton (see the previous channel). If one considers the initial energy of electrons (before scattering) ${ϵ}_0={10}^{15}$ eV, the Lorentz factor becomes of the order of ${ϵ}_0/{ϵ}_{n,r}\simeq {10}^6$, where we have taken the neutron’s rest energy, ${ϵ}_{n,r}\simeq$ 1 GeV, into account. Therefore, the energy of anti-neutrino in the lab frame is $\gamma$-times bigger and equals 1 TeV. Usually, from the Sun, one observes neutrinos in the TeV band [29], where a contribution must come from the studied mechanism and not only from cosmic rays.

5. Conclusions

We have presented here our novel investigations of the solar corona; by studying the further energization of the already-energetic coronal electrons (in a flare, for instance), we have explored a possible source of solar cosmic rays. The second stage of energization takes place by the resonant wave–wave (RWW) interaction between circularly polarized electromagnetic waves and the quantum waves of relativistic electrons. In particular, we selected the polarized radiation at 20–80 MHz, Fe I 630.2 nm, Ca II 854.2 nm, and Fe XIII 1074.7 nm, which is often used for coronal magnetic field diagnostics.

Our results demonstrate that RWW interaction can catapult the relativistic electrons to much higher energies. Since the acceleration time-scales for electrons are much shorter than their escape times scales, RWW interactions will be highly efficient, allowing particles to reach extremely high energies before they have a chance to escape from the corona.

By taking into account various (energy-dependent) processes, such as the synchrotron radiation, IC scattering, and electron bremsstrahlung, that might limit RWW energization, we find that the polarized radiation can further energize the flare-generated relativistic electrons up to ${10}^7$ eV (for the radio band) and ∼ 10¹⁵ eV (for 20–80 MHz, Fe I 630.2 nm, Ca II 854.2 nm, and Fe XIII 1074.7 nm) (Figure 2).

Typical solar cosmic rays, known as SEPs, generally have lower energy than galactic cosmic rays. However, the presented study suggests that the Sun may produce VHE electrons approaching the energy of galactic cosmic rays.

The flux of such electrons could reach to $\sim 5\times {10}^{-4}$ s⁻¹ cm⁻² during strong flare events and might be detectable through remote measurements, including at ground level. Since the electrons might experience significant deflection while traveling through the coronal magnetic field, the detection could be very challenging.

In a follow-up study, we plan to investigate the RWW interactions for protons, another primary component of solar cosmic rays.