Perrin Numbers That Are Concatenations of a Perrin Number and a Padovan Number in Base b

Abstract

Let ${\left(P_k\right)}_{k\ge 0}$ be a Padovan sequence and ${\left(R_k\right)}_{k\ge 0}$ be a Perrin sequence. Let n, m, b, and k be non-negative integers, where $2\le b\le 10$. In this paper, we are devoted to delving into the equations $R_n=b^d{P}_m+R_k$ and $R_n=b^d{R}_m+P_k$, where d is the number of digits of $R_k$ or $P_k$ in base b. We show that the sets of solutions are $R_n\in \{R_5,R_6,R_7,R_8,R_9,R_{10},R_{11},R_{12},R_{13},R_{14},R_{15},$$R_{16},R_{17},R_{19},R_{23},R_{25},R_{27}\}$ for the first equation and $R_n\in \{R_0,R_2,R_3,R_4,R_5,R_6,R_7,R_8,R_9,R_{10},R_{11},R_{12},R_{13},R_{14},R_{15},R_{16},R_{17},R_{18},R_{20},R_{21}\}$ for the second equation. Our approach employs advanced techniques in Diophantine analysis, including linear forms in logarithms, continued fractions, and the properties of Padovan and Perrin sequences in base b. We investigate both the deep structural symmetries and the complex structures that connect recurrence relations and logarithmic forms within Diophantine equations involving special number sequences.

1. Introduction

Concatenations of integer sequences have been an intriguing subject in the study of Diophantine equations. The study of concatenations within integer sequences has attracted significant interest by blending number theory and combinatorial properties. Generally, such equations exhibit certain structural and solution symmetries. The relationship between Diophantine equations and symmetry is manifested both in the structure of the equations and in the distribution of their solutions. In particular, when recursive series are analyzed using modular properties and logarithmic forms, it is seen that the solutions are in a certain order and form symmetric patterns. Today, many computer programs are used to solve Diophantine equations. One of these is PARI/GP. It is a computer program used to quickly perform arithmetic operations, especially number theory, algebraic calculations, and fast arithmetic.

The On-Line Encyclopedia of Integer Sequences (OEIS) [1] is an online encyclopedia with comprehensive, publicly available information on different integer sequences. Two of the integer sequences included here are Padovan and Perrin sequences. Let ${\left(P_k\right)}_{k\ge 0}$ and ${\left(R_k\right)}_{k\ge 0}$ denote the Padovan and Perrin sequences defined as follows:

$$\begin{array}{cc}\hfill P_0& =1,P_1=1,P_2=1,P_k=P_{k-2}+P_{k-3}\mathrm{for}k\ge 3,\hfill \\ \hfill R_0& =3,R_1=0,R_2=2,R_k=R_{k-2}+R_{k-3}\mathrm{for}k\ge 3.\hfill \end{array}$$

A few terms in these sequences are $1,1,1,2,2,3,4,5,7,9,12,\cdots \left(OEISA000931\right)$ and $3,0,2,3,$$2,5,5,7,10\cdots \left(OEISA001608\right)$, respectively.

Banks and Luca [2] established that under certain conditions, a binary recurrence sequence that can be expressed as concatenations of at least two terms has only a finite amount of solutions. Alan [3] extended this work to the Fibonacci and Lucas numbers, identifying that the Fibonacci numbers formed by concatenations of two Lucas numbers are $\{13,21,34\}$, while Lucas numbers formed by concatenations of two Fibonacci numbers are $\{1,2,3,11,18,521\}$. Similarly, Bravo [4] demonstrated that Padovan numbers formed by concatenations of two Perrin numbers are $\{2,3,5,7,12,37,35\}$, while Perrin numbers formed by concatenations of two Padovan numbers are $\{12,17,22,29,39,51,486\}$. Altassan and Alan [5] further explored the concatenations of the Fibonacci and Lucas numbers in both orders.

Erduvan [6] investigated the concatenations of Padovan and Perrin numbers. He proved that $\{12,21,37,49,265,465\}$ are all Padovan numbers formed by concatenations of two Padovan numbers, and $\left\{22\right\}$ is the unique Perrin number formed by concatenations of two Perrin numbers. Inspired by these results, we extend the analysis to Padovan and Perrin sequences in base $2\le b\le 10$. See [7,8,9,10,11,12] for more information.

Next, assume that $n,$$m,b,d,k$ are nonnegative integers. Let $2\le b\le 10.$ In this work, we consider Perrin numbers, which are the concatenation of a Padovan number and a Perrin number. These are represented by the following equations

$$\begin{array}{cc}\hfill R_n& =b^d{P}_m+R_k,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill R_n& =b^d{R}_m+P_k,\hfill \end{array}$$

(2)

where d is the number of digits of $R_k$ or $P_k$ in base b. Our analysis identifies all Perrin numbers $R_n$ that satisfy these equations.

2. Preliminaries

In this section, we present several properties and lemmas essential for reducing the upper bound of n. It is known that

$$\begin{array}{cc}\hfill P_k& =t{\alpha }^k+s{\beta }^k+r{\gamma }^k,\hfill \\ \hfill R_k& ={\alpha }^k+{\beta }^k+{\gamma }^k,\hfill \end{array}$$

where $\alpha$, $\beta$, and $\gamma$ are the roots of the characteristic polynomial $x^3-x-1=0$, and t, s, and r are the constants derived from these roots. The minimal polynomial of t over $\mathbb{Z}$ is $23x^3-23x^2+6x-1$. Key properties of the roots are as follows:

$$\begin{array}{cc}\hfill 1.32& <\alpha <1.33,\hfill \\ \hfill 0.86& <\left|\beta \right|=\left|\gamma \right|<0.87,\hfill \\ \hfill \left|s\right|& =\left|r\right|<0.25.\hfill \end{array}$$

Using these properties, we derive the following bounds for Padovan and Perrin sequences:

$$\begin{array}{cc}\hfill {\alpha }^{k-2}& \le P_k\le {\alpha }^{k-1}\mathrm{for}k\ge 1,k\ne 3,\hfill \\ \hfill {\alpha }^{k-2}& \le R_k\le {\alpha }^{k+1}\mathrm{for}k\ge 2.\hfill \end{array}$$

It is known that

$$\left|e\left(k\right)\right|:=|s{·{\beta }^k+r·\gamma }^k|\le |s{{|·|\beta |}^k+\left|r\right|·\left|\gamma \right|}^k<0.5{\alpha }^{-k/2},$$

(3)

and

$$|e^{\prime }\left(k\right)|:=|{{\beta }^k+\gamma }^k|\le {{\left|\beta \right|}^k+\left|\gamma \right|}^k<2{\alpha }^{-k/2},$$

(4)

where $e\left(k\right):=P_k-t{·{\alpha }^k=s·{\beta }^k+r·\gamma }^k$ and $e^{\prime }\left(k\right):=R_k-{{\alpha }^k={\beta }^k+\gamma }^k$ for $k\ge 1.$

Let $F:=\mathbb{Q}(\alpha ,\beta ).$ Then, $\left|Gal\right(F/\mathbb{Q}\left)\right|=[F:\mathbb{Q}]=6$, $\left[\mathbb{Q}\right(\alpha ):\mathbb{Q}]=3$ and

$$Gal(F/\mathbb{Q})\simeq \{\left(1\right),\left(\alpha \beta \right),\left(\alpha \gamma \right),\left(\beta \gamma \right),\left(\alpha \beta \gamma \right),\left(\alpha \gamma \beta \right)\}\simeq S_3.$$

Let $\eta$ be an algebraic number of degree d with a minimal polynomial, given by the following:

$$c_0{x}^d+c_1{x}^{d-1}+\cdots +c_d=c_0\prod _{i=1}^d\left(x-{\eta }^{\left(i\right)}\right)\in \mathbb{Z}\left[x\right],$$

where $c_0>0$, the coefficients $c_i$ are relatively prime integers and ${\eta }^{\left(i\right)}$ are the conjugates of $\eta$. Then, the logarithmic height of $\eta$ is defined as follows:

$$h\left(\eta \right)={\displaystyle \frac{1}{d}}\left(log{c}_0+\sum _{i=1}^{d}log\left(max\left\{|{\eta }^{\left(i\right)}|,1\right\}\right)\right).$$

In the special case where $\eta ={\displaystyle \frac{c}{f}}$ is a rational number, with $gcd(c,f)=1$ and $f\ge 1$, the logarithmic height simplifies to the following:

$$h\left(\eta \right)=log\left(max\left\{\left|c\right|,f\right\}\right).$$

Below are some properties of the logarithmic height, whose proofs can be found in [13]:

$$h(\gamma \pm \eta )\le log2+h\left(\gamma \right)+h\left(\eta \right),$$

$$h({\gamma }^{\pm t}·{\eta }^{\pm s})\le \left|t\right|h\left(\gamma \right)+\left|s\right|h\left(\eta \right).$$

The following lemma is derived from Corollary 2.3 of Matveev [14] (see also Theorem 9.4 in [15]):

Lemma 1. 

Let ${\beta }_1,{\beta }_2,\dots ,{\beta }_t$ be positive real algebraic numbers in a number field $\mathbb{K}$ of degree D. Suppose $c_1,c_2,\dots ,c_t$ are nonzero integers, and let

$$\mathsf{\Lambda }:={\beta }_1^{c_1}·{\beta }_2^{c_2}\cdots {\beta }_t^{c_t}-1\ne 0.$$

Then, we have the bound:

$$\left|\mathsf{\Lambda }\right|>exp\left(-1.4D^2{t}^{4.5}{30}^{t+3}(1+logB)C_1{C}_2\cdots C_t(1+logD)\right),$$

where $max\{0.16,Dh\left({\beta }_i\right),|log{\beta }_i\left|\right\}\le C_i$ and $max\left\{\right|c_i\left|\right\}\le B$ for all $i=1,2,\dots ,t$.

From [4], we provide the following lemma.

Lemma 2. 

If the equation $R_n=P_m$ has a solution, then $(n,m)\in \left\{\right(2,3),(2,4),(4,3),(4,4),(0,5),$ $(3,5),(5,7),(6,7),(7,8),(9,10)\}.$

Lemma 3 

([16]). Let $A,B,\mu$ be real numbers with $A>0$ and $B>1$. Let $M,u,v,w$ be positive integers, and let $p/q$ be a convergent of the continued fraction expansion of the irrational number γ, such that $q>6M$. Let

$$ϵ:=\left|\right|\mu q\left|\right|-M\left|\right|\gamma q\left|\right|.$$

If $ϵ>0$, then there are no solutions to the inequality

$$0<|u\gamma -v+\mu |<A{B}^{-w},$$

where

$$u\le M\mathit{and}w\ge {\displaystyle \frac{log(Aq/ϵ)}{logB}}.$$

Lemma 4 

([17]). Let $a,x\in \mathbb{R}$ with $0<a<1$ and $\left|x\right|<a$. Then,

$$|log(1+x)|<{\displaystyle \frac{-log(1-a)}{a}}·\left|x\right|,$$

and

$$|e^x-1|·{\displaystyle \frac{a}{1-e^{-a}}}>\left|x\right|.$$

Lemma 5 

([18]). Let N be a nonnegative integer, such that $q_N>M$. Let τ be an irrational number with $\tau =[a_0;a_1,a_2,a_3,\dots ]$ and let $\{p_n/q_n\}$ be the convergent of its continued fraction expansion. Suppose that $M,r,s$ are positive integers. Define:

$$a\left(M\right):=max\{a_i:i=0,1,2,\dots ,N\}.$$

Then, for all pairs $(r,s)$ with $0<s<M$, the following inequality holds:

$$\left|\tau -{\displaystyle \frac{r}{s}}\right|>{\displaystyle \frac{1}{(a\left(M\right)+2)s^2}}.$$

Lemma 6 

([19]). Let $2\le d\le 10$. If the equation $R_n-R_m=d^a$ has a solution, then

$$R_n\in \{2,3,5,7,10,12,17,22,29,39,51\}.$$

Lemma 7 

([20]). Let $2\le d\le 10$. If the equation $R_n=d·P_k$ has a solution, then

$$R_n\in \{2,3,5,7,10,12,90\}.$$

3. Results

Theorem 1. 

Let b be an positive integer where $2\le b\le 10$. Then, if the equation $R_n=b^d{P}_m+R_k$ has a solution, then

$$\begin{array}{cc}\hfill (n,b,m,k)\in \{& (7,2,0,0),(7,2,0,3),(7,2,1,0),(7,2,1,3),(7,2,2,0),(7,2,2,3),(8,2,3,2),\hfill \\ & (8,2,3,4),(8,2,4,2),(8,2,4,4),(11,2,7,2),(11,2,7,4),(12,2,5,5),(12,2,5,6),\hfill \\ & (13,2,9,0),(13,2,9,3),(14,2,10,0),(14,2,10,3),(16,2,7,8),(5,3,0,2),\hfill \\ & (13,2,6,7),(5,3,0,4),(5,3,1,2),(5,3,1,4),(5,3,2,2),(5,3,2,4),(6,3,0,2),\hfill \\ & (6,3,0,4),(6,3,1,2),(6,3,1,4),(6,3,2,2),(6,3,2,4),(9,3,0,0),(15,3,8,6),\hfill \\ & (9,3,0,3),(9,3,1,0),(9,3,1,3),(9,3,2,0),(9,3,2,3),(10,3,7,2),(15,3,8,5),\hfill \\ & (10,3,7,4),(12,3,9,2),(12,3,9,4),(13,3,0,9),(13,3,1,9),(7,4,1,0),\hfill \\ & (23,3,3,18),(23,3,4,18),(25,3,6,18),(7,4,0,0),(7,4,0,3),(12,6,6,6),\hfill \\ & (7,4,2,0),(7,4,2,3),(8,4,3,2),(8,4,3,4),(19,6,7,12),(13,3,2,9),(13,3,6,0),\hfill \\ & (8,4,4,2),(8,4,4,4),(11,4,7,2),(11,4,7,4),(13,4,3,7),(27,6,9,13),\hfill \\ & (13,4,4,7),(13,4,9,0),(13,4,9,3),(14,4,10,0),(14,4,10,3),(13,3,6,3),\hfill \\ & (16,4,7,8),(17,4,8,7),(19,4,5,10),(7,5,0,2),(7,5,0,4),(11,5,6,4),\hfill \\ & (7,5,1,2),(7,5,1,4),(7,5,2,2),(7,5,2,4),(9,5,3,2),(9,5,3,4),\hfill \\ & (9,5,4,2),(9,5,4,4),(10,5,5,2),(10,5,5,4),(11,5,6,2),(7,4,1,3),\hfill \\ & (10,6,3,5),(10,6,3,6),(10,6,4,5),(10,6,4,6),(12,6,6,5),(8,7,0,0),\hfill \\ & (8,7,1,0),(8,7,1,3),(8,7,2,0),(8,7,2,3),(9,7,0,5),(9,7,0,6),(8,7,0,3),\hfill \\ & (9,7,1,5),(9,7,1,6),(9,7,2,5),(9,7,2,6),(10,7,3,0),(13,9,6,3),\hfill \\ & (10,7,3,3),(10,7,4,0),(10,7,4,3),(14,7,8,2),(14,7,8,4),(13,9,6,0),\hfill \\ & (15,7,9,5),(15,7,9,6),(8,8,0,2),(8,8,0,4),(8,8,1,2),(15,9,8,5),\hfill \\ & (8,8,1,4),(8,8,2,2),(8,8,2,4),(12,8,5,5),(12,8,5,6),(15,9,8,6),\hfill \\ & (13,8,6,7),(19,8,5,10),(9,9,0,0),(9,9,0,3),(9,9,1,0),(9,10,0,2),\hfill \\ & (9,9,1,3),(9,9,2,0),(9,9,2,3),(12,9,5,2),(12,9,5,4),(11,10,4,2),\hfill \\ & (9,10,0,4),(9,10,1,2),(9,10,1,4),(9,10,2,2),(9,10,2,4),(11,10,4,4),\hfill \\ & (10,10,0,7),(10,10,1,7),(10,10,2,7),(11,10,3,2),(11,10,3,4).\}\hfill \end{array}$$

In Figure 1, the dots for each base b, where d is the length of the representation of $R_k$ in base b, visualize the relationship between the values n, m, and k for which the condition $R_n=P_m·b^d+R_k$ is satisfied. The data are plotted for the base values $b=2,3,\cdots ,10$, with unique colors assigned to each base for better differentiation. The graph given in Figure 2a,b are the nine graphs in Figure 1 shown on a single graph and Figure 2c shows the values that satisfy the equality $R_n=b^d{P}_m+R_k$. The axes represent the indices n, m, and k, and the visualization helps identify patterns in the solutions for different bases.

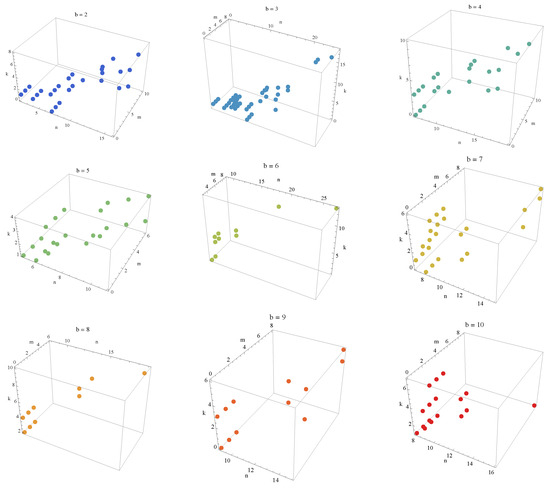
Figure 1. Visualization of the relationship between $R_n$, $P_m$, and $R_k$ in different bases b for (1).

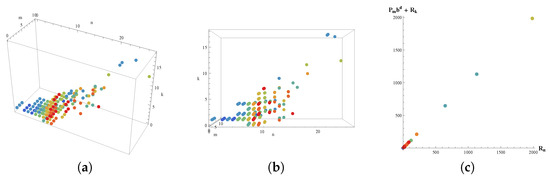
Figure 2. Three-dimensional solution distribution dased on base b and number sequences for (1).

Theorem 2. 

Let $2\le b\le 10$ be an integer. If the equation $R_n=b^d{R}_m+P_k$ has a solution, then

$$\begin{array}{cc}\hfill (n,b,m,k)\in \{& (0,2,1,5),(2,2,1,3),(2,2,1,4),(3,2,1,5),(14,10,6,2),(8,2,2,4),\hfill \\ & (4,2,1,3),(4,2,1,4),(5,2,1,7),(5,2,2,0),(5,2,2,1),(5,2,2,2),\hfill \\ & (5,2,4,0),(5,2,4,1),(5,2,4,2),(6,2,1,7),(6,2,2,0),(6,2,2,1),\hfill \\ & (6,2,2,2),(6,2,4,0),(6,2,4,1),(6,2,4,2),(7,2,0,0),(7,2,0,1),\hfill \\ & (7,2,0,2),(7,2,1,8),(7,2,3,0),(7,2,3,1),(7,2,3,2),(8,2,2,3),\hfill \\ & (14,10,6,1),(8,2,4,3),(8,2,4,4),(9,2,1,10),(11,2,5,3),\hfill \\ & (11,2,5,4),(11,2,6,3),(11,2,6,4),(12,2,0,7),(12,2,3,7),\hfill \\ & (14,2,9,5),(16,2,11,3),(16,2,11,4),(17,2,12,5),(18,2,13,3),\hfill \\ & (18,2,13,4),(0,3,1,5),(2,3,1,3),(2,3,1,4),(3,3,1,5),\hfill \\ & (4,3,1,3),(4,3,1,4),(5,3,1,7),(6,3,1,7),(7,3,1,8),(7,3,2,0),\hfill \\ & (7,3,2,1),(7,3,2,2),(7,3,4,0),(7,3,4,1),(7,3,4,2),(8,3,0,0),\hfill \\ & (8,3,0,1),(8,3,0,2),(8,3,3,0),(8,3,3,1),(8,3,3,2),(9,3,1,10),\hfill \\ & (10,3,5,3),(10,3,5,4),(10,3,6,3),(10,3,6,4),(11,3,2,6),\hfill \\ & (11,3,4,6),(11,3,7,0),(11,3,7,1),(11,3,7,2),(15,3,7,7),\hfill \\ & (15,3,11,3),(15,3,11,4),(16,3,0,9),(16,3,3,9),(17,3,13,3),\hfill \\ & (17,3,13,4),(18,3,10,7),(0,4,1,5),(2,4,1,3),(2,4,1,4),\hfill \\ & (3,4,1,5),(4,4,1,3),(4,4,1,4),(5,4,1,7),(6,4,1,7),(7,4,1,8),\hfill \\ & (8,4,2,3),(8,4,2,4),(8,4,4,3),(8,4,4,4),(9,4,1,10),(14,10,5,1),\hfill \\ & (11,4,5,3),(11,4,5,4),(11,4,6,3),(11,4,6,4),(12,4,7,0),\hfill \\ & (12,4,7,1),(12,4,7,2),(13,4,2,8),(13,4,4,8),(14,4,9,5),\hfill \\ & (16,4,11,3),(16,4,11,4),(17,4,7,8),(17,4,12,5),(18,4,13,3),\hfill \\ & (18,4,13,4),(20,4,10,7),(0,5,1,5),(2,5,1,3),(2,5,1,4),(3,5,1,5),\hfill \\ & (4,5,1,3),(4,5,1,4),(5,5,1,7),(6,5,1,7),(7,5,1,8),(9,5,1,10),\hfill \\ & (9,5,2,3),(9,5,2,4),(9,5,4,3),(9,5,4,4),(10,5,0,3),(14,10,5,0),\hfill \\ & (10,5,0,4),(10,5,3,3),(10,5,3,4),(12,5,5,6),(12,5,6,6),(14,10,5,2),\hfill \\ & (13,5,7,6),(14,5,8,0),(14,5,8,1),(14,5,8,2),(0,6,1,5),(13,10,3,9),\hfill \\ & (2,6,1,3),(2,6,1,4),(3,6,1,5),(4,6,1,3),(4,6,1,4),(5,6,1,7),(6,10,1,7),\hfill \\ & (6,6,1,7),(7,6,1,8),(9,6,1,10),(10,6,2,7),(10,6,4,7),(13,10,0,9),\hfill \\ & (11,6,0,6),(11,6,3,6),(21,6,8,8),(0,7,1,5),(2,7,1,3),(12,10,4,9),\hfill \\ & (2,7,1,4),(3,7,1,5),(4,7,1,3),(4,7,1,4),(5,7,1,7),(6,7,1,7),(5,10,1,7),\hfill \\ & (7,7,1,8),(9,7,1,10),(10,7,2,5),(10,7,4,5),(11,7,0,0),(12,10,2,9),\hfill \\ & (11,7,0,1),(11,7,0,2),(11,7,3,0),(11,7,3,1),(11,7,3,2),(11,10,4,4),\hfill \\ & (13,7,5,6),(13,7,6,6),(14,7,7,3),(14,7,7,4),(17,7,2,12),(11,10,4,3),\hfill \\ & (17,7,4,12),(18,7,11,6),(20,7,13,6),(0,8,1,5),(2,8,1,3),(11,10,2,4),\hfill \\ & (2,8,1,4),(3,8,1,5),(4,8,1,3),(4,8,1,4),(5,8,1,7),(6,8,1,7),(4,10,1,4),\hfill \\ & (7,8,1,8),(9,8,1,10),(10,8,2,0),(10,8,2,1),(10,8,2,2),(11,10,2,3),\hfill \\ & (10,8,4,0),(10,8,4,1),(10,8,4,2),(12,8,0,7),(12,8,3,7),(9,10,1,10),\hfill \\ & (0,9,1,5),(2,9,1,3),(2,9,1,4),(3,9,1,5),(4,9,1,3),(4,9,1,4),(3,10,1,5),\hfill \\ & (5,9,1,7),(6,9,1,7),(7,9,1,8),(9,9,1,10),(11,9,2,6),(14,10,6,0),\hfill \\ & (11,9,4,6),(12,9,0,3),(12,9,0,4),(12,9,3,3),(12,9,3,4),(7,10,1,8),\hfill \\ & (15,9,7,7),(18,9,10,7),(0,10,1,5),(2,10,1,3),(2,10,1,4),(4,10,1,3).\}\hfill \end{array}$$

Figure 3 and Figure 4 visualize the relationship between the parameters n, m, and k, based on the Padovan and Perrin derived from the recurrence relations. For each base b, the points represent the indices where the condition $R_n=R_m·b^d+P_k$ is satisfied. Here, d is the length of the representation of $P_k$ in base b. The data are plotted for base values $b=2,3,\cdots ,10$, with unique colors assigned to each base for better differentiation. The graph given in Figure 4a,b are the nine graphs in Figure 3 shown on a single graph and Figure 4c shows the values that satisfy the equality $R_n=b^d{R}_m+P_k$. The axes represent the indices n, m, and k, and the visualization helps to identify patterns in the solutions for different bases.

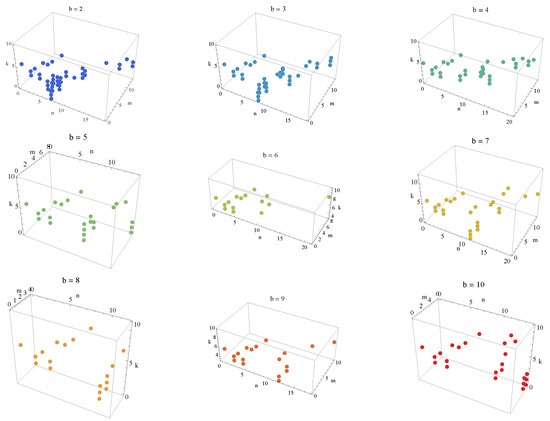
Figure 3. Visualization of the relationship between $R_n$, $R_m$, and $P_k$ in different bases b for (2).

Figure 4. Three-dimensional solution distribution based on base b and number sequences for (2).

We determine that the sets of solutions are

$$R_n\in \{5,7,10,12,17,22,29,39,51,68,90,119,209,644,1130,1983\}$$

for Equation (1) and

$$R_n\in \{2,3,5,7,10,12,17,22,29,39,51,68,90,119,158,277,367\}$$

for Equation (2). These solutions were obtained using advanced techniques in Diophantine analysis, such as properties of linear forms in logarithms, continued fractions, Baker’s Theorem, and logarithmic height functions.

Lemma 8. 

Suppose that $R_n=b^d·P_m+R_k$ is valid where d is the number of digits of $R_k$ in base b. For $n,k\ge 2,$ $m\ne 3$, and $m\ge 1$, the inequalities hold below.

(i) 

$R_k<b^d<b·R_k,$ $n-k\ge 1,$ and $\left({log}_b\alpha \right)(k-2)<d<\left({log}_b\alpha \right)(k+1)+1,$

(ii) 

$k+m-5<n<k+m+{log}_{\alpha }(b+1)+2,$

(iii) 

$d<(n-m+3){log}_2\alpha <n-m+3\le n+2.$

Proof. 

(i)

As d is the number of digits of $R_k$ in base b, we have $d=⌊{log}_{10}{R}_k⌋+1$. Then, we find

$$R_k=b^{{log}_b{R}_k}<b^d<b^{1+{log}_b{R}_k}=b·R_k,$$

$$R_n=b^d·P_m+R_k\ge b^d+R_k>R_k,$$

$$d=1+⌊{log}_b{R}_k⌋<1+{log}_b{R}_k\le 1+{log}_b{\alpha }^{k+1}=1+\left({log}_b\alpha \right)(k+1),$$

and

$$d=⌊{log}_b{R}_k⌋+1>{log}_b{R}_k\ge {log}_b{\alpha }^{k-2}=\left({log}_b\alpha \right)(k-2).$$

This completes the proof.

(ii)

As

$${\alpha }^{n-2}\le R_n=R_k+b^d·P_m<(b+1)·R_k·P_m<{\alpha }^{{log}_{\alpha }(b+1)+m+k}$$

and

$${\alpha }^{n+1}\ge R_n=R_k+b^d·P_m>R_k+R_k·P_m>R_k·P_m>{\alpha }^{k+m-4},$$

we obtain $k+m-5<n<k+m+2+{log}_{\alpha }(b+1).$

(iii)

As $R_n=b^d·P_m+R_k,$ we get $2^d\le b^d<b^d+{\displaystyle \frac{R_k}{P_m}}={\displaystyle \frac{R_n}{P_m}}\le {\alpha }^{n-m+3}$, we get $d<(n-m+3){log}_2\alpha <n-m+3\le n+2.$

□

The proof of the following lemma can be performed using a similar proof to that of the previous lemma. Therefore, it will be given without proof.

Lemma 9. 

Suppose that $R_n=b^d·R_m+P_k$ is valid, where d is the number of digits of $P_k$ in base b. For $n,m\ge 2,$ $k\ne 3$, and $k\ge 1$, the inequalities below hold.

(i) 

$P_k<b^d<b·P_k,$ $n-k\ge 3,$ and $(k-2){log}_b\alpha <d<(k-1){log}_b\alpha +1,$

(ii) 

$k+m-5<n<k+m+{log}_{\alpha }(b+1)+2,$

(iii) 

$d<(3+n-m){log}_2\alpha <2+n-m.$

4. Proof of Theorem 1

Suppose that Equation (1) is valid. Let $n<310.$ By PARI/GP, we find

$$R_n\in \left\{5,7,10,12,17,22,29,39,51,68,90,119,209,644,1130,1983\right\}.$$

(5)

Suppose that $n\ge 310.$ If $m=0,1,2$ or $k=1$, then we find the equations $R_n-R_k=b^d$ and $R_n=b{P}_m$, respectively. These are impossible by Lemmas 6 and 7. Now, suppose $n\ge 310$, $k\ge 2$, and $m\ge 3.$ As $P_3=P_4=2,$ $R_0=R_3=3,$ $R_2=R_4=2,$ we can take $k\ge 3$ and $m\ge 4.$ By (1), we write

$$R_n={\alpha }^n+{\beta }^n+{\gamma }^n=b^d(t{\alpha }^m+s{\beta }^m+r{\gamma }^m)+({\alpha }^k+{\beta }^k+{\gamma }^k).$$

This equation will be expressed in two different forms as follows:

$${\alpha }^n-b^d{\alpha }^{m}t=b^d(s{\beta }^m+r{\gamma }^m)+R_k-({\beta }^n+{\gamma }^n),$$

and

$${\alpha }^n-b^d{P}_m-{\alpha }^k=({\beta }^k+{\gamma }^k)-({\beta }^n+{\gamma }^n).$$

Using the Lemma 8, (3), and (4), rearranging these equations leads to the following results:

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{{\alpha }^{n-m}}{b^{d}t}}-1\right|& \le {\displaystyle \frac{b^d|s{\beta }^m+r{\gamma }^m|}{t{\alpha }^m{b}^d}}+{\displaystyle \frac{|{\beta }^n+{\gamma }^n|}{t{\alpha }^m{b}^d}}+{\displaystyle \frac{R_k}{t{\alpha }^m{b}^d}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{t}}\left[{\displaystyle \frac{\left|e\left(m\right)\right|}{{\alpha }^m}}+{\displaystyle \frac{\left|e^{\prime }\left(n\right)\right|}{b^d{\alpha }^m}}+{\displaystyle \frac{1}{{\alpha }^m}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{1}{{\alpha }^{m}t}}\left[{\displaystyle \frac{0.5}{{\alpha }^{m/2}}}+{\displaystyle \frac{2}{2{\alpha }^{n/2}}}+1\right]<{\displaystyle \frac{1.68}{{\alpha }^m}}\hfill \end{array}$$

(6)

and

$$\begin{array}{cc}\hfill \left|1-{\displaystyle \frac{b^d·P_m}{{\alpha }^n(1-{\alpha }^{k-n})}}\right|& \le \left|{\displaystyle \frac{1}{{\alpha }^n(1-{\alpha }^{k-n})}}\right|\left[|({\beta }^k+{\gamma }^k)|+|({\beta }^n+{\gamma }^n)|\right]\hfill \\ \hfill & \le \left|{\displaystyle \frac{1}{1-{\alpha }^{k-n}}}\right|\left[{\displaystyle \frac{\left|e^{\prime }\left(k\right)\right|}{{\alpha }^n}}+{\displaystyle \frac{\left|e^{\prime }\left(n\right)\right|}{{\alpha }^n}}\right]\hfill \\ \hfill & \le \left|{\displaystyle \frac{1}{1-{\alpha }^{-1}}}\right|\left[{\displaystyle \frac{2}{{\alpha }^n·{\alpha }^{k/2}}}+{\displaystyle \frac{2}{{\alpha }^n·{\alpha }^{n/2}}}\right]\le {\displaystyle \frac{6.16}{{\alpha }^n}}.\hfill \end{array}$$

(7)

We take

$$\begin{array}{cc}\hfill ({\mathsf{\Lambda }}_1,{\beta }_1,{\beta }_2,{\beta }_3)& :=\left({\displaystyle \frac{{\alpha }^{n-m}}{b^{d}t}}-1,\alpha ,b,t\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill (c_1,c_2,c_3)& :=\left(n-m,-d,-1\right)\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill ({\mathsf{\Lambda }}_2,{\beta }_1^{\prime },{\beta }_2^{\prime },{\beta }_3^{\prime })& :=\left(1-{\displaystyle \frac{b^d.P_m}{{\alpha }^n(1-{\alpha }^{k-n})}},\alpha ,b,{\displaystyle \frac{P_m}{1-{\alpha }^{k-n}}}\right)\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill (c_1^{\prime },c_2^{\prime },c_3^{\prime })& :=(-n,d,1)\hfill \end{array}$$

(11)

to apply Lemma 1. It can be shown that ${\mathsf{\Lambda }}_1\ne 0$ and ${\mathsf{\Lambda }}_2\ne 0.$ The logarithmic height for ${\beta }_1,$ ${\beta }_2,$ ${\beta }_3,$ ${\beta }_1^{\prime },$ ${\beta }_2^{\prime },$ ${\beta }_3^{\prime }$ are

$$\begin{array}{c}\hfill h\left(\alpha \right):={\displaystyle \frac{log\alpha }{3}},\\ \hfill h\left(t\right):={\displaystyle \frac{log23}{3}},\\ \hfill h\left({\displaystyle \frac{P_m}{1-{\alpha }^{k-n}}}\right)& \le h\left(P_m\right)+(n-k)h\left(\alpha \right)+log2\hfill \\ \hfill & \le h\left({\alpha }^{m-1}\right)+(n-k){\displaystyle \frac{log\alpha }{3}}+log2\hfill \\ \hfill & \le (m-1){\displaystyle \frac{log\alpha }{3}}+(n-k){\displaystyle \frac{log\alpha }{3}}+log2\hfill \\ \hfill & \le (m-1){\displaystyle \frac{log\alpha }{3}}+(m+2+{log}_{\alpha }(b+1)){\displaystyle \frac{log\alpha }{3}}+log2\hfill \\ \hfill & \le {\displaystyle \frac{2m+10}{3}}log\alpha +0.7.\hfill \end{array}$$

Then, we choose

$$\begin{array}{cc}\hfill (C_1,C_2,C_3)& :=(log\alpha ,3logb,3.14)\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill (C_1^{\prime },C_2^{\prime },C_3^{\prime })& :=(log\alpha ,3logb,2.1+(2m+10)log\alpha ).\hfill \end{array}$$

(13)

Also, as $d<(n-m+2){log}_2\alpha \le n,$ $B\ge max\left\{|n-m|,d,1\right\}$ and $B^{\prime }\ge max\left\{n,d,1\right\},$ we can say

$$B:=B^{\prime }:=n.$$

(14)

By using Lemma 1, (6), (8), (9), (12), and (14), we provide

$$1.68{\alpha }^{-m}>\left|{\mathsf{\Lambda }}_1\right|>exp\left(-{30}^6·\left(1.4\right)3^{7.5}3.14(1+log3)(1+logn)log\alpha logb\right),$$

i.e.,

$$mlog\alpha <1.65\times {10}^{13}(1+logn)+log1.68$$

(15)

and by using (7), (10), (11), (13), (14) and Lemma 1, we obtain

$$nlog\alpha -log6.16<5.26\times {10}^{12}(1+logn)\left((2m+10)log\alpha +2.1\right).$$

(16)

By using (15) and (16), we have $n<3.14\times {10}^{30}.$ Assume $z_1:=-(n-m)log\alpha +logt+dlogb$. For $m\ge 4$, we obtain the following inequality:

$$\left|x\right|=|e^{z_1}-1|<{\displaystyle \frac{1.68}{{\alpha }^m}}<0.55.$$

(17)

We choose $a:=0.55$ to apply Lemma 4. This provides

$$|z_1|=|log(x+1)|<{\displaystyle \frac{log(100/45)}{0.55}}·{\displaystyle \frac{1.68}{{\alpha }^m}}<2.44·{\alpha }^{-m}$$

(18)

and, consequently,

$$0<\left|d{\displaystyle \frac{logb}{log\alpha }}-(n-m)+{\displaystyle \frac{logt}{log\alpha }}\right|<8.7·{\alpha }^{-m}.$$

(19)

Next, let $\gamma :={\displaystyle \frac{logb}{log\alpha }}\notin \mathbb{Q}$, $\mu :={\displaystyle \frac{logt}{log\alpha }}$, and $M:=3.14\times {10}^{30}>n>d$. Then, we have $q_{71}$ exceeding $6M$, and we find

$$0.02<ϵ\left(\mu \right):=\left|\mu q_{71}\right|-M\left|\gamma q_{71}\right|<0.4.$$

Let $(w,A,B):=(m,8.7,\alpha )$ in Lemma 3. Then, if

$${\displaystyle \frac{log(8.7q_{71}/ϵ)}{log\alpha }}<349.8<m,$$

there is no solution to the inequality (19). This implies that

$$m\le 349.$$

By using (16), we conclude that $n<1.55\times {10}^{17}$. Now, we will find $n,m,k$ smaller than the one we found now by using Lemma 3. Let

$$z_2:=log\left({\displaystyle \frac{P_m}{1-{\alpha }^{k-n}}}\right)-nlog\alpha +dlogb.$$

(20)

From (7), we write

$$|x^{\prime }|:=\left|e^{z_2}-1\right|<{\displaystyle \frac{6.16}{{\alpha }^n}}<0.001$$

for $n\ge 310.$ To use Lemma 4, let us choose $a^{\prime }:=0.001$. Thence, we find the inequality

$$\left|log(x^{\prime }+1)\right|<{\displaystyle \frac{log(1000/999)}{0.001}}·{\displaystyle \frac{6.16}{{\alpha }^n}}<6.2·{\alpha }^{-n},$$

(21)

and

$$0<\left|d{\displaystyle \frac{logb}{log\alpha }}-n+{\displaystyle \frac{log\left(\frac{P_m}{1-{\alpha }^{k-n}}\right)}{log\alpha }}\right|<22.05·{\alpha }^{-n}.$$

(22)

If we determine $\mu :={\displaystyle \frac{log\left(\frac{P_m}{1-{\alpha }^{k-n}}\right)}{log\alpha }},\gamma ={\displaystyle \frac{logb}{log\alpha }}$$\notin \mathbb{Q}$ and $M:=1.55\times {10}^{17}>n>d,$ it can be found that $q_{54}$ exceeds $6M.$ Then, it can be shown that the inequality

$${10}^{-5}<ϵ\left(\mu \right):=\left|\right|\mu q_{54}\left|\right|-M\left|\right|\gamma q_{54}\left|\right|<0.35$$

for each $m\le 349,$ $1\le n-k$ and $m-5<n-k<m+11\le 360$ without $(m,n-k,b)=(6,1,2),$ $(6,1,4),$ $(6,2,2),$ $(6,2,4),$ $(6,3,2),$ $(6,3,4),$ $(6,5,2),$ $(6,5,4),$ $(6,7,2),$ $(6,14,2),$ $(6,14,3),$ $(6,14,4),$ $(6,14,5),$ $(6,14,6),$ $(6,14,7),$ $(6,14,8),$ $(6,14,9),$ $(6,14,10),$ $(7,2,5),$ $(7,3,5),$ $(7,5,5),$ $(8,3,7),$ $(8,5,7),$ $(9,5,3),$ $(9,5,9),$ $(9,13,3),$ $(10,7,6),$ $(10,13,2),$ $(10,13,4),$ $(10,14,3),$ $(11,7,2),$ $(11,7,8),$ $(11,14,2),$ $(11,14,4),$ $(12,13,7),$ $(13,14,7).$ By taking $A:=22.05,B:=\alpha ,$ and $w:=n$ in Lemma 3, we can demonstrate that the inequality (22) does not hold if

$${\displaystyle \frac{log(22.05q_{54}/ϵ)}{log\alpha }}<307.5<n.$$

(23)

Hence, we conclude that $n\le 307.$ This leads to a contradiction, as $310\le n.$ Now, let $(m,n-k,b)=$ $(6,1,2),$ $(6,1,4),$ $(6,2,2),$ $(6,2,4),$ $(6,3,2),$ $(6,3,4),$ $(6,5,2),$ $(6,5,4),$ $(6,7,2),$ $(6,14,2),$ $(6,14,3),$ $(6,14,4),$ $(6,14,5),$ $(6,14,6),$ $(6,14,7),$ $(6,14,8),$ $(6,14,9),$ $(6,14,10),$ $(7,2,5),$ $(7,3,5),$ $(7,5,5),$ $(8,3,7),$ $(8,5,7),$ $(9,5,3),$ $(9,5,9),$ $(9,13,3),$ $(10,7,6),$ $(10,13,2),$ $(10,13,4),$ $(10,14,3),$ $(11,7,2),$ $(11,7,8),$ $(11,14,2),$ $(11,14,4),$ $(12,13,7),$ $(13,14,7).$ It follows immediately that

$$\begin{array}{cc}\hfill R_n-R_{n-1}& =2^{d+2},2^{2d+2},\hfill \\ \hfill R_n-R_{n-2}& =R_{n-3}=2^{d+2},2^{2d+2},5^{d+1},\hfill \\ \hfill R_n-R_{n-3}& =R_{n-2}=2^{d+2},2^{2d+2},5^{d+1},7^{d+1},\hfill \\ \hfill R_n-R_{n-5}& =R_{n-1}=2^{d+2},2^{2d+2},5^{d+1},7^{d+1},3^{d+2},3^{2d+2},\hfill \\ \hfill R_n-R_{n-7}& =2R_{n-3}=2^{d+2},12·6^d,16·2^d,16·8^d,\hfill \\ \hfill R_n-R_{n-13}& =3R_{n-4}=3^{d+2},12·2^d,12·4^d,21·7^d\hfill \\ \hfill R_n-R_{n-14}& =4R_{n-5}=4·2^d,4·3^d,4·5^d,4·6^d,4·7^d,2^{2d+2},\hfill \\ \hfill & 4·8^d,4·9^d,4·{10}^d,12·3^d,2^{d+4},2^{2d+4},28·7^d.\hfill \end{array}$$

These are impossible by Lemma 6.

5. Proof of Theorem 2

Suppose that Equation (2) is valid. Suppose that $n<355.$ It can be shown that

$$R_n\in \left\{2,3,5,7,10,12,17,22,29,39,51,68,90,119,158,277,367\right\}.$$

Suppose $n\ge 355$ and $m=1$. Then, we have $R_n=P_k$, which is impossible by Lemma 2.

Now, assume $n\ge 355$ and $m\ne 1$. We can take $k\ge 2$, $k\ne 3$, and $m\ge 3$, as $P_0=P_1=P_2=1$, $P_3=P_4=2$, $R_0=R_3=3$, and $R_2=R_4=2$. By (2), we can express $R_n$ as follows:

$$R_n={\alpha }^n+{\beta }^n+{\gamma }^n=b^d({\alpha }^m+{\beta }^m+{\gamma }^m)+({\alpha }^{k}t+{\beta }^{k}s+{\gamma }^{k}r).$$

Rearranging this equation leads to the following results:

$${\alpha }^n-b^d{\alpha }^m=b^d({\beta }^m+{\gamma }^m)+P_k-({\beta }^n+{\gamma }^n),$$

and

$${\alpha }^n-b^d{R}_m-{\alpha }^{k}t=({\beta }^{k}s+{\gamma }^{k}r)-({\beta }^n+{\gamma }^n).$$

After taking the absolute values of these equations, we obtain the following representation

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{{\alpha }^{n-m}}{b^d}}-1\right|& \le {\displaystyle \frac{b^d|{\beta }^m+{\gamma }^m|}{b^d{\alpha }^m}}+{\displaystyle \frac{|{\beta }^n+{\gamma }^n|}{b^d{\alpha }^m}}+{\displaystyle \frac{P_k}{b^d{\alpha }^m}}\hfill \\ \hfill & \le {\displaystyle \frac{b^d\left|e^{\prime }\left(m\right)\right|}{b^d{\alpha }^m}}+{\displaystyle \frac{\left|e^{\prime }\left(n\right)\right|}{b^d{\alpha }^m}}+{\displaystyle \frac{1}{{\alpha }^m}}\hfill \\ \hfill & \le {\displaystyle \frac{1}{{\alpha }^m}}\left[{\displaystyle \frac{2}{{\alpha }^{m/2}}}+{\displaystyle \frac{2}{2·{\alpha }^{n/2}}}+1\right]<{\displaystyle \frac{2.32}{{\alpha }^m}}\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill \left|1-{\displaystyle \frac{b^d.R_m}{{\alpha }^n(1-t{\alpha }^{k-n})}}\right|& \le \left|{\displaystyle \frac{1}{{\alpha }^n(1-t{\alpha }^{k-n})}}\right|\left[|({\beta }^{k}s+{\gamma }^{k}r)|+|({\beta }^n+{\gamma }^n)|\right]\hfill \\ \hfill & \le \left|{\displaystyle \frac{1}{1-t{\alpha }^{k-n}}}\right|\left[{\displaystyle \frac{\left|e\left(k\right)\right|}{{\alpha }^n}}+{\displaystyle \frac{\left|e^{\prime }\left(n\right)\right|}{{\alpha }^n}}\right]\hfill \\ \hfill & \le \left|{\displaystyle \frac{1}{1-t{\alpha }^{-3}}}\right|\left[{\displaystyle \frac{0.5}{{\alpha }^n{\alpha }^{k/2}}}+{\displaystyle \frac{2}{{\alpha }^n·{\alpha }^{n/2}}}\right]\hfill \\ \hfill & \le {\displaystyle \frac{0.57}{{\alpha }^n}}\hfill \end{array}$$

(25)

by using Lemma 9, (3), and (4). To apply Lemma 1, we take

$$\begin{array}{cc}\hfill ({\mathsf{\Lambda }}_1,{\beta }_1,{\beta }_2)& :=\left({\displaystyle \frac{{\alpha }^{n-m}}{b^d}}-1,\alpha ,b\right)\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill (c_1,c_2)& :=\left(n-m,-d\right),\hfill \end{array}$$

(27)

and

$$\begin{array}{cc}\hfill ({\mathsf{\Lambda }}_2,{\beta }_1^{\prime },{\beta }_2^{\prime },{\beta }_3^{\prime })& :=\left(1-{\displaystyle \frac{b^d.R_m}{{\alpha }^n(1-t·{\alpha }^{k-n})}},\alpha ,b,{\displaystyle \frac{R_m}{1-t·{\alpha }^{k-n}}}\right)\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill (c_1^{\prime },c_2^{\prime },c_3^{\prime })& :=(-n,d,1).\hfill \end{array}$$

(29)

It can be shown that ${\mathsf{\Lambda }}_1\ne 0$ and ${\mathsf{\Lambda }}_2\ne 0.$ As

$$\begin{array}{cc}\hfill h\left(\alpha \right)& :={\displaystyle \frac{log\alpha }{3}},h\left(b\right):=logb,\hfill \\ \hfill h\left({\displaystyle \frac{R_m}{1-t·{\alpha }^{k-n}}}\right)& \le log2+h\left(t\right)+h\left(R_m\right)+(n-k)h\left(\alpha \right)\hfill \\ \hfill & \le log2+{\displaystyle \frac{1}{3}}log23+h\left({\alpha }^{m+1}\right)+(n-k){\displaystyle \frac{log\alpha }{3}}\hfill \\ \hfill & \le log2+{\displaystyle \frac{1}{3}}log23+(m+1){\displaystyle \frac{log\alpha }{3}}+(n-k){\displaystyle \frac{log\alpha }{3}}\hfill \\ \hfill & \le log2+{\displaystyle \frac{1}{3}}log23+(m+1){\displaystyle \frac{log\alpha }{3}}+(m+2+{log}_{\alpha }(b+1)){\displaystyle \frac{log\alpha }{3}}\hfill \\ \hfill & \le {\displaystyle \frac{2m+12}{3}}log\alpha +1.74.\hfill \end{array}$$

Then, we choose

$$\begin{array}{cc}\hfill (C_1,C_2)& :=(log\alpha ,log{b}^3)\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill (C_1^{\prime },C_2^{\prime },C_3^{\prime })& :=(log\alpha ,log{b}^3,5.22+(2m+12)log\alpha ).\hfill \end{array}$$

(31)

Also, as $m\ge 3,d<(n-m+3){log}_2\alpha <n,B\ge max\left\{|-d|,|n-m|\right\}$ and $B^{\prime }\ge max\left\{n,1,d\right\},$ we can choose

$$B:=B^{\prime }:=n.$$

(32)

By using Lemma 1, (24), (26), (27), (30), and (32), we provide

$${\alpha }^{-m}2.32>\left|{\mathsf{\Lambda }}_1\right|>exp\left(-{30}^5\left(1.4\right)2^{4.5}{3}^2(1+log3)log{b}^{3}log\alpha (1+logn)\right),$$

i.e.,

$$mlog\alpha <2.95\times {10}^{10}·(1+logn)+log\left(2.32\right)$$

(33)

and by using (25), (28), (29), (31), (32), and Lemma 1, we write

$${\alpha }^{-n}0.57>exp\left(-1.4(1+log3){30}^6{3}^{6.5}log{b}^{3}log\alpha (1+logn)\left(5.22+(2m+12)log\alpha \right)\right),$$

i.e.,

$$nlog\alpha -log0.57<5.48\times {10}^{12}(1+logn)\left(5.22+(2m+12)log\alpha \right).$$

(34)

By using (33) and (34), we obtain $n<4.82\times {10}^{27}.$ Assume

$$z_1:=log\alpha (n-m)-dlogb.$$

(35)

Then, we obtain

$$\left|x\right|=\left|e^{z_1}-1\right|<{\displaystyle \frac{2.32}{{\alpha }^m}}<0.998$$

(36)

as $m\ge 3.$ We take $a:=0.998$ to use Lemma 4. Then,

$$\left|log(x+1)\right|<{\displaystyle \frac{2.32}{{\alpha }^m}}{\displaystyle \frac{log\left(500\right)}{0.998}}<14.45{\alpha }^{-m}$$

(37)

and so

$$\begin{array}{cc}\hfill 0& <\left|dlogb-log\alpha (n-m)\right|<14.45{\alpha }^{-m},\hfill \\ \hfill 0& <\left|\left({\displaystyle \frac{log\alpha }{logb}}\right)-{\displaystyle \frac{d}{n-m}}\right|<{\displaystyle \frac{14.45}{(n-m)logb}}{\alpha }^{-m}<{\displaystyle \frac{21}{n-m}}{\alpha }^{-m}.\hfill \end{array}$$

(38)

Let $\tau :={\displaystyle \frac{log\alpha }{logb}}\notin \mathbb{Q}$, and define

$$M:=4.82\times {10}^{27},\mathrm{with}M>n>n-m.$$

It can be shown that $q_{65}>M$. Assume $m\ge 280$. Then, we have

$${\displaystyle \frac{{\alpha }^m}{42}}>4\times {10}^{28}>n-m,$$

and the inequality

$$\left|{\displaystyle \frac{log\alpha }{logb}}-{\displaystyle \frac{d}{n-m}}\right|<{\displaystyle \frac{21}{(n-m)}}{\alpha }^{-m}<{\displaystyle \frac{1}{2{(n-m)}^2}}$$

holds. Based on the well-known properties of continued fractions, the rational number ${\displaystyle \frac{d}{n-m}}$ is a convergent of ${\displaystyle \frac{log\alpha }{logb}}$. Let ${\displaystyle \frac{p_r}{q_r}}$ represent the r-th convergent of the continued fraction expansion of ${\displaystyle \frac{log\alpha }{logb}}$, and assume that ${\displaystyle \frac{d}{n-m}}={\displaystyle \frac{p_t}{q_t}}$ for some t. From this, we deduce that $q_{65}>2.6\times {10}^{28}$ and $a_M=max\{a_i\mid i=0,1,\cdots ,65\}=433.$ Applying Lemma 5, we establish the inequality

$${\displaystyle \frac{21}{n-m}}{\alpha }^{-m}>\left|{\displaystyle \frac{log\alpha }{logb}}-{\displaystyle \frac{p_t}{q_t}}\right|>{\displaystyle \frac{1}{435{(n-m)}^2}}.$$

From this, we derive the following bounds:

$$1.35\times {10}^{-33}>{\displaystyle \frac{21}{{\alpha }^{280}}}\ge {\displaystyle \frac{21}{{\alpha }^m}}>{\displaystyle \frac{1}{435(n-m)}}>{\displaystyle \frac{1}{435·2.6\times {10}^{28}}}>8.8\times {10}^{-32}.$$

Moreover, for $m<280$, it follows from (34) that

$$n<1.31\times {10}^{17}.$$

Now, let

$$z_2:=dlogb+log\left({\displaystyle \frac{R_m}{1-{\alpha }^{k-n}t}}\right)-nlog\alpha .$$

(39)

We have

$$\left|x^{\prime }\right|=\left|e^{z_2}-1\right|<{\displaystyle \frac{0.57}{{\alpha }^n}}<0.01\mathrm{for}n\ge 355$$

from (25). From Lemma 4, we obtain

$$|z_2|<{\displaystyle \frac{0.57}{{\alpha }^n}}{\displaystyle \frac{log(100/99)}{0.01}}<{\alpha }^{-n}0.58,$$

(40)

and

$$0<\left|d·\left({\displaystyle \frac{logb}{log\alpha }}\right)-n+{\displaystyle \frac{log\left(\frac{R_m}{1-{\alpha }^{k-n}t}\right)}{log\alpha }}\right|<2.07·{\alpha }^{-n}.$$

(41)

Let $\gamma ={\displaystyle \frac{logb}{log\alpha }}\notin \mathbb{Q}$ and define $M:=1.31\times {10}^{17},$ where $M>n>d.$ It follows that $q_{61}>6M$ and

$${10}^{-7}<ϵ\left(\mu \right):=\parallel \mu q_{61}\parallel -M\parallel \gamma q_{61}\parallel <0.35,$$

for all integers satisfying

$$2\le m<280\mathrm{and}3\le n-k<m+{log}_{\alpha }(b+1)+2.$$

By applying Lemma 3, we deduce that inequality (41) has no solution if the following condition holds:

$${\displaystyle \frac{log(2.07q_{61}/ϵ)}{log\alpha }}<350.4<n$$

(42)

where $A:=2.07,B:=\alpha ,$ and $w:=n.$ From this, we infer that $n\le 350$. However, this conclusion contradicts the fact that $n\ge 355$.

6. Conclusions

This work provided a comprehensive analysis of Perrin numbers that can be expressed as concatenations of a Padovan number and a Perrin number in a base b. The results extended existing research on combinations in integer sequences and demonstrated the power of modern techniques in Diophantine equations. The arithmetic properties of Padovan and Perrin sequences in different bases were investigated. Using linear forms in logarithms, we derived bounds with small upper values for the variables and used continued fraction expansion to improve these bounds and systematically determine all possible solutions. The obtained results reveal structural relations between different special types of numbers and contributed to the solutions of Diophantine equations involving different sequences. When the graphs of the solutions of Diophantine equations are examined, it is easily seen that the solutions have distributions in certain intervals. In the future, similar methods can be used to solve Diophantine equations with many bases or involving different sequences of numbers. In addition, similar methods can be used to find the solutions of some Diophantine equations that may be encountered in engineering problems. The distribution structure or symmetry properties of the solutions of Diophantine equations can be observed by analyzing them in different intervals.