Bounds for Hermitian Toeplitz and Hankel Determinants for a Certain Subclass of Analytic Functions Related to the Sine Function
Abstract
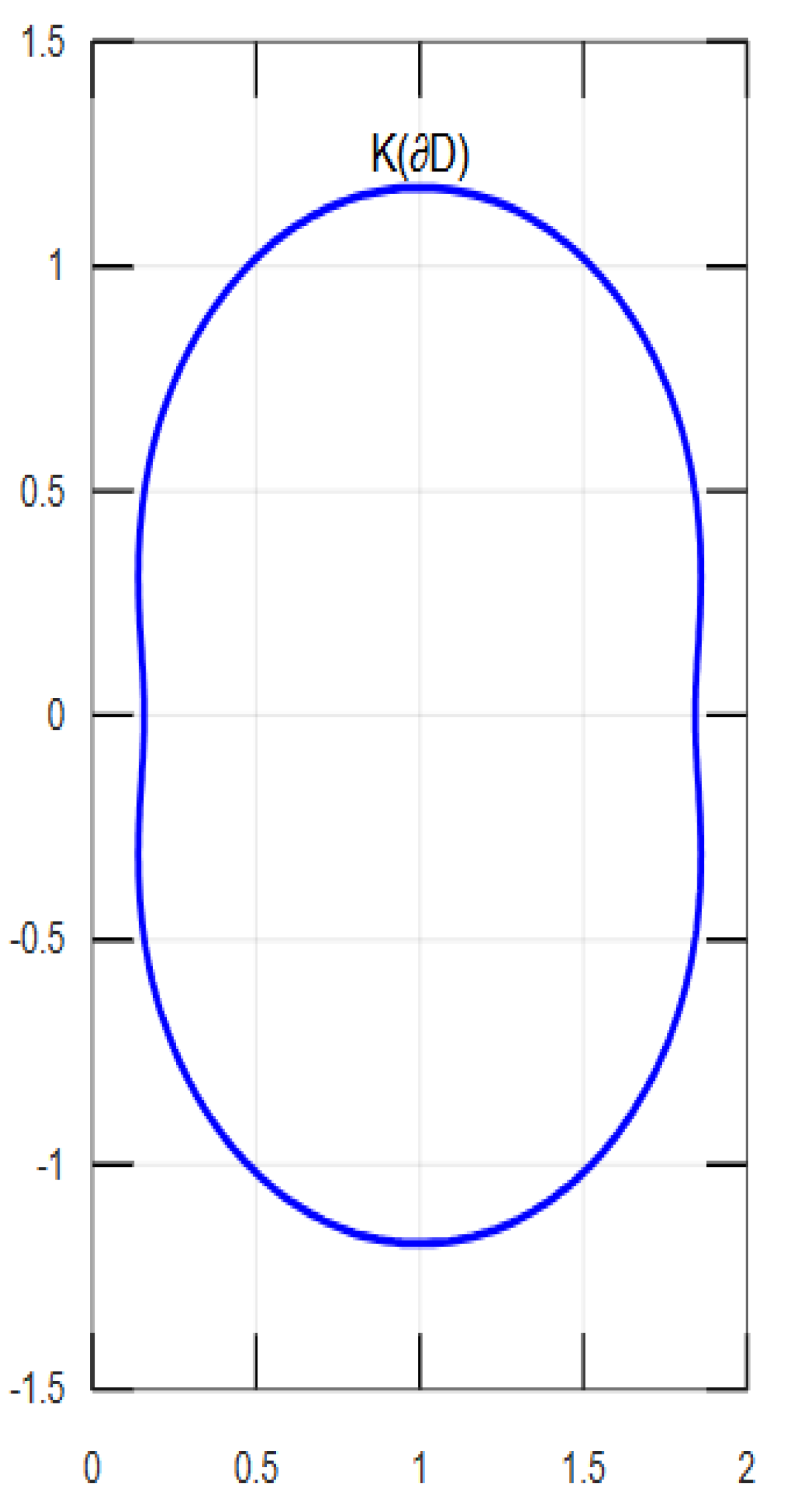
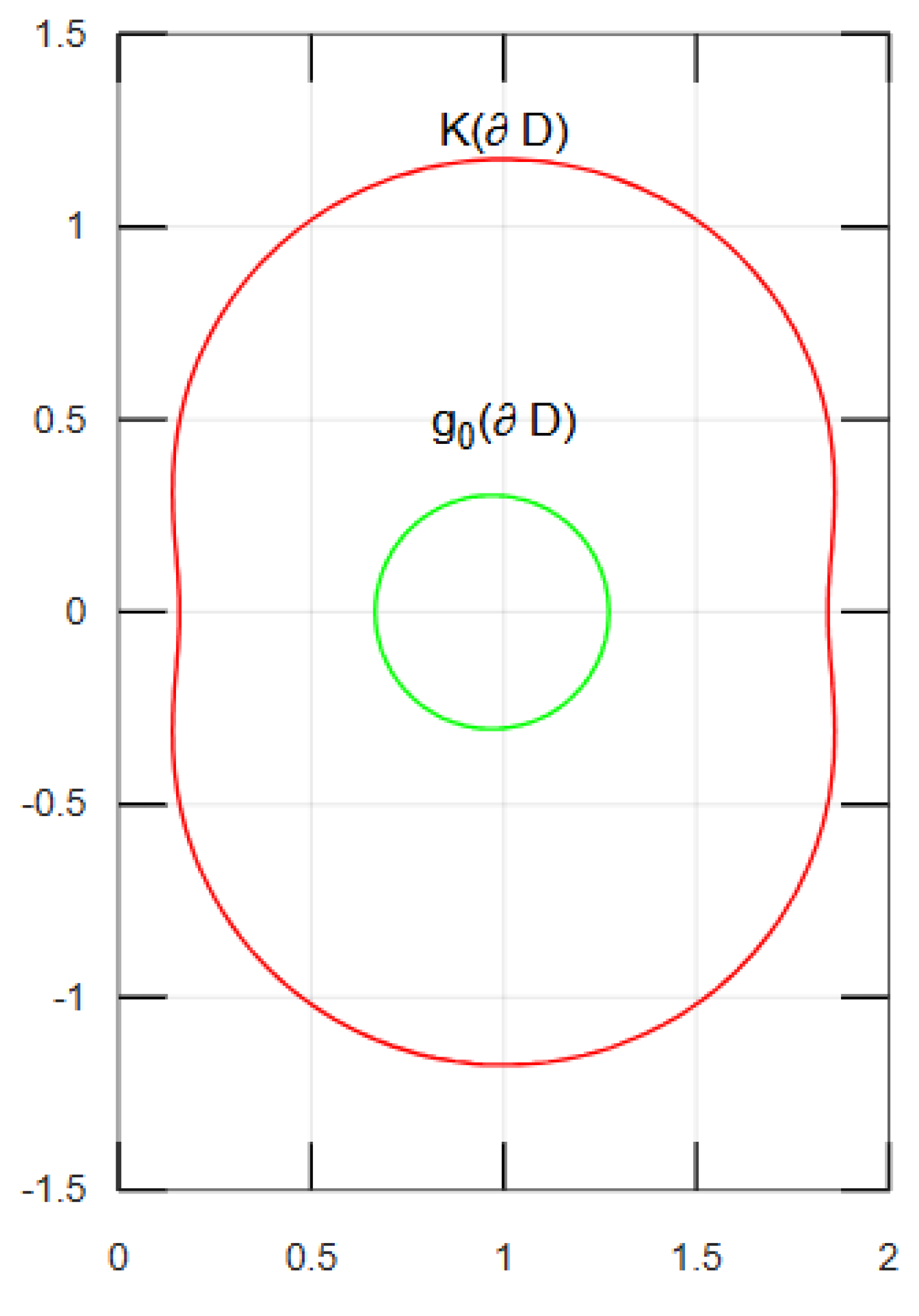
1. Introduction
2. Preliminaries
3. Coefficient Estimates
4. Hermitian Toeplitz Determinant
5. Hankel Determinant
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, W.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis; International Press Inc.: Somerville, MA, USA; New York, NY, USA, 1992; pp. 157–169. [Google Scholar]
- Darus, M.; Shanmugam, T.N.; Sivasubramanian, S. Fekete-Szegö inequality for a certain class of analytic functions. Mathematica 2007, 49, 29–34. [Google Scholar]
- Noonan, J.W.; Thomas, D.K. On the second Hankel determinant of areally mean p-valent functions. Trans. Amer. Math. Soc. 1976, 223, 337–346. [Google Scholar] [CrossRef]
- Pommerenke, C. On the coefficients and Hankel determinants of univalent functions. J. Lond. Math. Soc. 1966, 41, 111–122. [Google Scholar] [CrossRef]
- Hayman, W.K. On the second Hankel determinant of mean univalent functions. Proc. London Math. Soc. 1968, 18, 77–94. [Google Scholar] [CrossRef]
- Janteng, A.; Halim, S.A.; Darus, M. Hankel determinant for starlike and convex functions. Int. J. Math. Anal. 2007, 1, 619–625. [Google Scholar]
- Kowalczyk, B.; Lecko, A.; Sim, Y.J. The sharp bound for the Hankel determinant of the third kind for convex functions. Bull. Aust. Math. Soc. 2018, 97, 435–445. [Google Scholar] [CrossRef]
- Arif, M.; Rani, L.; Raza, M.; Zaprawa, P. Fourth Hankel determinant for the family of functions with bounded turning. Bull. Korean Math. Soc. 2018, 55, 1703–1711. [Google Scholar]
- Sokół, J.; Thomas, D.K. Further results on a class of starlike functions related to the Bernoulli lemniscate. Houston J. Math. 2018, 44, 83–95. [Google Scholar]
- Vijayalakshmi, S.P.; Sudharsan, T.V.; Breaz, D.; Subramanian, K.G. Bounds on the third order Hankel determinant for certain subclasses of analytic functions. An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 2017, 25, 199–214. [Google Scholar] [CrossRef]
- Cho, N.E.; Kumar, V. Initial coefficients and fourth Hankel determinant for certain analytic functions. Miskolc. Math. Notes 2020, 21, 763–779. [Google Scholar] [CrossRef]
- Breaz, D.; Cătaş, A.; Cotîrlă, L.T. On the upper bound of the third Hankel determinant for certain class of analytic functions related with exponential function. An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 2022, 30, 75–89. [Google Scholar] [CrossRef]
- Hartman, P.; Wintner, A. The spectra of Toeplitz’s matrices. Amer. J. Math. 1954, 76, 867–882. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Prentice Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Poisel, R.A. Digital Comunications: Fundamentals and Applications; Pearson Education: London, UK, 2001. [Google Scholar]
- Firoz Ali, M.D.; Thomas, D.K.; Vasudevarao, A. Toeplitz determinants whose elements are the coefficients of analytic and univalent functions. Bull. Aust. Math. Soc. 2018, 97, 253–264. [Google Scholar]
- Cudna, K.; Kwon, O.S.; Lecko, A.; Sim, Y.J.; Śmiarowska, B. The second and third-order Hermitian Toeplitz determinants for starlike and convex functions of order α. Bol. Soc. Mat. Mex. 2020, 26, 361–375. [Google Scholar] [CrossRef]
- Dziok, J.; Raina, R.K.; Sokół, J. Certain results for a class of convex functions related to a shell-like curve connected with Fibonacci numbers. Comput. Math. Appl. 2011, 61, 2605–2613. [Google Scholar] [CrossRef]
- Dziok, J.; Raina, R.K.; Sokół, J. On a class of starlike functions related to a shell-like curve connected with Fibonacci numbers. Math. Comput. Model. 2013, 57, 1203–1211. [Google Scholar] [CrossRef]
- Kumar, V.; Rekha, S.; Cho, N.E. Sharp estimation of Hermitian-Toeplitz determinants for Janowski type starlike and convex functions. Miskolc. Math. Notes 2020, 21, 939–952. [Google Scholar] [CrossRef]
- Lecko, A.; Śmiarowska, B. The third-order Hermitian Toeplitz determinant for some classes of analytic functions. J. Math. Inequal. 2023, 17, 931–942. [Google Scholar] [CrossRef]
- Gurusamy, P.; Jayasankar, R.; Sivasubramanian, S. The Second and Third Order Hermitian Toeplitz Determinants for Some Subclasses of Analytic Functions Associated with Exponential Function, Synergies in Analysis, Discrete Mathematics, Soft Computing and Modelling; Springer Nature: Singapore, 2023; pp. 1–16. [Google Scholar]
- Cho, N.E.; Kumar, V.; Kumar, S.S.; Ravichandran, V. Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 2019, 45, 213–232. [Google Scholar] [CrossRef]
- Arif, M.; Raza, M.; Tang, H.; Hussain, S.; Khan, H. Hankel determinant of order three for familiar subsets of analytic functions related with sine function. Open Math. 2019, 17, 1615–1630. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Tang, H. A study of fourth-order Hankel determinants for starlike functions connected with the sine function. J. Funct. Spaces 2021, 2021, 9991460. [Google Scholar] [CrossRef]
- Zulfiqar, F.; Malik, S.N.; Raza, M.; Ali, M.S. Fourth-order Hankel determinants and Toeplitz determinants for convex functions connected with sine functions. J. Math. 2022, 2022, 2871511. [Google Scholar] [CrossRef]
- Khana, M.G.; Ahmadb, B.; Murugusundaramoorthy, G.; Mashwania, W.K.; Yalçın, S.; Shabae, T.G.; Salleh, Z. Third Hankel determinant and Zalcman functional for a class of starlike functions with respect to symmetric points related with sine function. J. Math. Computer Sci. 2022, 25, 29–36. [Google Scholar] [CrossRef]
- Khan, B.; Aldawish, I.; Araci, S.; Khan, M.G. Third Hankel Determinant for the Logarithmic Coefficients of Starlike Functions Associated with Sine Function. Fractal Fract. 2022, 6, 261. [Google Scholar] [CrossRef]
- Alahmade, A.; Zeeshan Mujahid, Z.; Tawfiq, F.M.O.; Khan, B.; Khan, N.; Tchier, F. Third Hankel Determinant for Subclasses of Analytic and m-Fold Symmetric Functions Involving Cardioid Domain and Sine Function. Symmetry 2023, 15, 2039. [Google Scholar] [CrossRef]
- Giri, S.; Sivaprasad Kumar, S. Hermitian-Toeplitz determinants for certain univalent functions. Anal. Math. Phys. 2023, 13, 37. [Google Scholar] [CrossRef]
- Kamali, M.; Riskulava Alina, A. On the upper bounds of Hankel determinants for some subclasses of univalent functions associated with sine functions. Int. J. Optim. Control. Theor. Appl. 2024, 14, 41–49. [Google Scholar] [CrossRef]
- Libera, R.J.; Złotkiewicz, E. Coefficient bounds for the inverse of a function with derivative in P. Proc. Amer. Math. Soc. 1983, 87, 251–257. [Google Scholar] [CrossRef]
- Ravichandran, V.; Verma, S. Bound for the fifth coefficient of certain starlike functions. Comptes Rendus Math. 2015, 353, 505–510. [Google Scholar] [CrossRef]
- Pommerenke, C. Univalent functions. In Mathematik, Lehrbucher; Vandenhoeck and Ruprecht: Gottingen, Germany, 1975. [Google Scholar]
- Duren, P.L. Univalent functions. In Grundlehren Mathematischen Wissenschaften, 259 Fundamental Principles of Mathematical Sciences; Springer: New York, NY, USA, 1983. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thulasiram, T.; Kalaiselvan, S.; Breaz, D.; Suchithra, K.; Sudharsan, T.V. Bounds for Hermitian Toeplitz and Hankel Determinants for a Certain Subclass of Analytic Functions Related to the Sine Function. Symmetry 2025, 17, 362. https://doi.org/10.3390/sym17030362
Thulasiram T, Kalaiselvan S, Breaz D, Suchithra K, Sudharsan TV. Bounds for Hermitian Toeplitz and Hankel Determinants for a Certain Subclass of Analytic Functions Related to the Sine Function. Symmetry. 2025; 17(3):362. https://doi.org/10.3390/sym17030362
Chicago/Turabian StyleThulasiram, Thatamsetty, Sekar Kalaiselvan, Daniel Breaz, Kuppuswamy Suchithra, and Thirumalai Vinjimur Sudharsan. 2025. "Bounds for Hermitian Toeplitz and Hankel Determinants for a Certain Subclass of Analytic Functions Related to the Sine Function" Symmetry 17, no. 3: 362. https://doi.org/10.3390/sym17030362
APA StyleThulasiram, T., Kalaiselvan, S., Breaz, D., Suchithra, K., & Sudharsan, T. V. (2025). Bounds for Hermitian Toeplitz and Hankel Determinants for a Certain Subclass of Analytic Functions Related to the Sine Function. Symmetry, 17(3), 362. https://doi.org/10.3390/sym17030362





