Dynamics of a Predator-Prey System with Asymmetric Dispersal and Fear Effect
Abstract
1. Introduction
2. Mathematical Formulation
- (a)
- We first consider and as the prey populations in the source and sink patches, respectively, while y represents the predator population.
- (b)
- We further assume that the predator only captures the prey population in the source patch and intraspecific competition only among the population of the prey in the source patch.
- (c)
- It is assumed that the prey population can disperse between the sink patch and the source patch.
- (a)
- which implies that if the prey does not have fear effect or the predator does not exist, then there is no reduction in the birth and mortality rates of the prey.
- (b)
- which means that if the level of fear effect or the density of predator is extremely high, the birth rate of the prey will eventually approach to zero.
- (c)
- which means that as the level of fear effect or the density of the predator increase, the birth rate of the prey decreases.
- (d)
- which means that if the level of fear effect is large or the density of the predator is high, then the death rate of prey will reach a maximum value.
- (e)
- which means that as either the fear level or the predator population increases, the mortality rate of the prey rises.So, incorporating all of the above facts, in this paper, we propose the following system:
3. Preliminaries
3.1. Non-Negativity and Boundedness of the Solutions
3.2. Permanence of the System (6)
4. Existence and Local Stability of the Equillbria
- (a)
- it always has a trivial equilibrium ;
- (b)
- it has a boundary equilibrium when ;
- (c)
- it has a unique positive equilibrium point if condition holds.
- (a)
- locally asymptotically stable when holds;
- (b)
- unstable when holds;
- (c)
- a saddle-node when .
- (a)
- a locally asymptotically stable node when holds;
- (b)
- a saddle when holds;
- (c)
- a saddle-node when
5. Global Stability Analysis
6. Bifurcation Analysis
7. Numerical Simulations
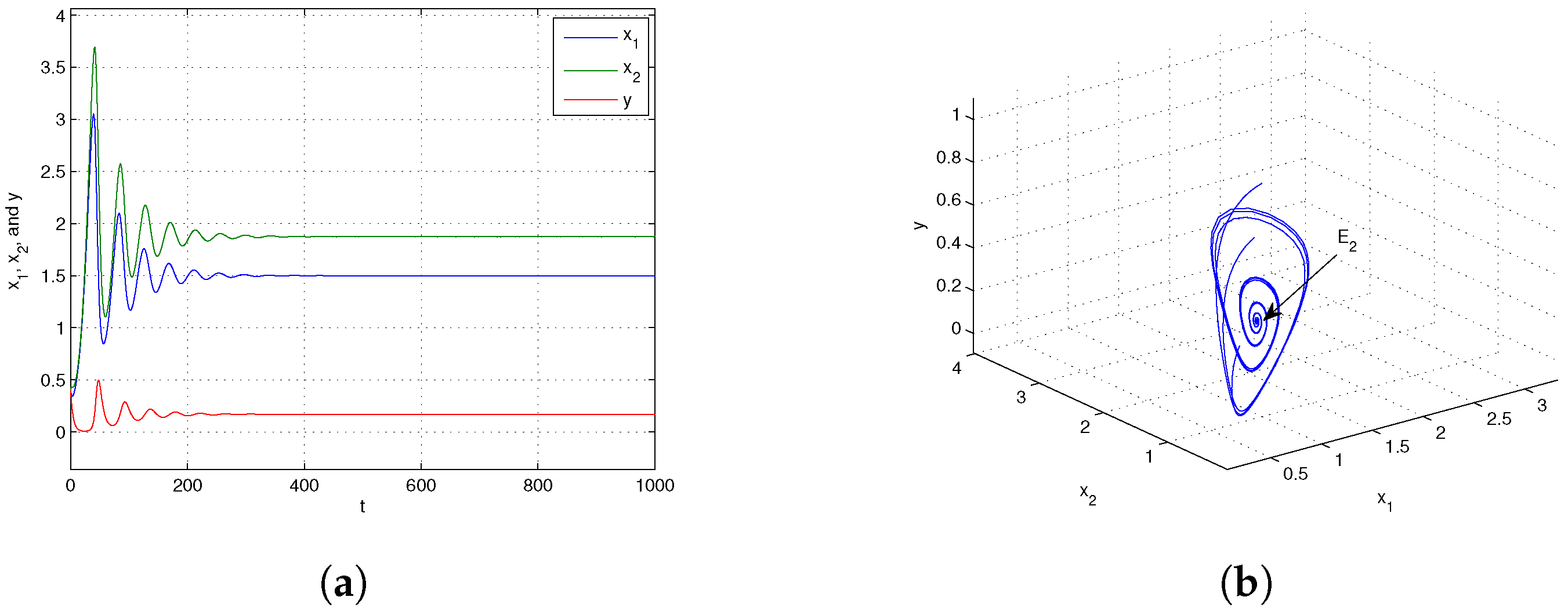
- Case I. Global stability of the equilibria
- Case II. Total population abundance
- Case III. Impact of fear effect on the system (6)
8. Conclusions
- We first investigated the non-negativity and boundedness of system (6), and proved that system (6) is persistent if . Furthermore, our research indicated that system (6) always has a trivial equilibrium point , and in the case of , there exists a boundary equilibrium point . Additionally, if condition holds, the system also possesses a unique positive equilibrium point .
- When the parameter reaches or exceeds the critical value , the equilibrium becomes globally asymptotically stable. Conversely, when and , the boundary equilibrium point is globally asymptotically stable. By applying geometric methods, we further investigated the global asymptotic stability of the system around the equilibrium point .
- When the parameter reaches the critical value , the boundary equilibrium point coincides with the trivial equilibrium point , and a transcritical bifurcation occurs near with a switch in stability. As the dispersal rate approaches or exceeds the critical value , the migration of prey between habitat patches becomes extremely sensitive, potentially leading to species collapse. This finding provides crucial guidance for species conservation and habitat connectivity management. In the construction of ecological corridors, it is essential to ensure their effectiveness and prevent excessive dispersal of prey from source patches to sink patches, which is vital for preventing species extinction.
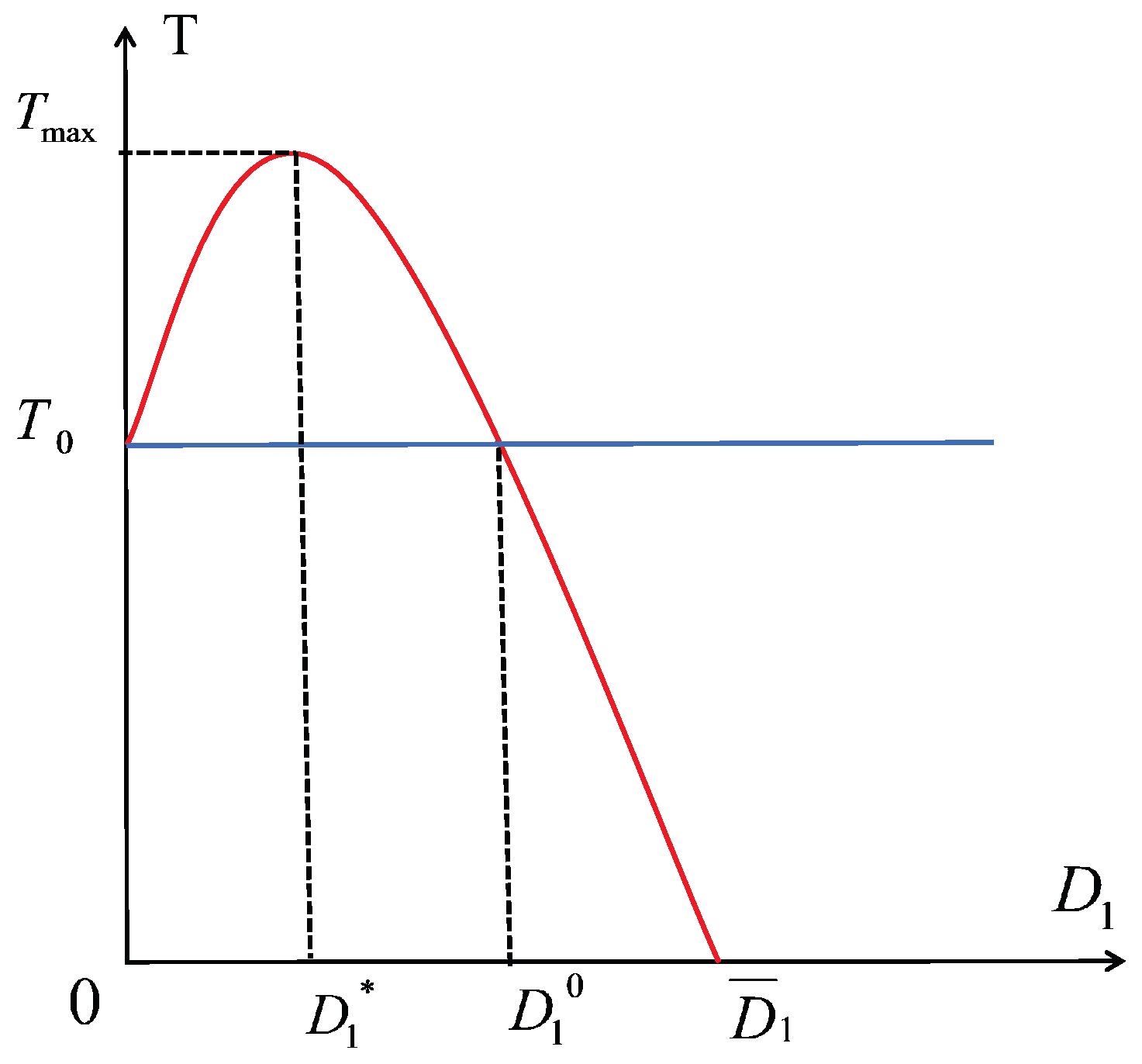
- Compared to the no-dispersal scenario, there is an optimal dispersal coefficient at which the prey population reaches its maximum. However, when exceeds , the prey population begins to decline gradually. Upon reaching , the prey population returns to the no-dispersal level, but as continues to increase, the prey population begins to fall below that of the no-dispersal case, eventually leading to extinction (see Figure 4).
- Next, we specifically investigated the impact of the fear effect parameter k and the maximum fear cost on the dynamics of system (6). Next, we specifically examined the effects of the fear effect parameter k and the maximum fear cost on the dynamics of system (6). Consistent with [42], our findings indicate that the fear effect reduces predator population density but does not alter the existence or stability of equilibrium points. However, with the introduction of maximum fear effects in our model, we further observed that higher maximum fear levels not only suppress predator density more significantly but may also accelerate population decline, potentially impacting the long-term stability of the ecosystem. From Figure 5 and Figure 6, it is evident that k and do not significantly affect the density of the prey but they lead to a continuous decrease in the final stable state of the predator.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, F.; Li, Z.; Pan, Q.; Zhu, Q. Bifurcations in a Leslie–Gower predator-prey model with strong Allee effects and constant prey refuges. Chaos Solitons Fractals 2025, 192, 115994. [Google Scholar] [CrossRef]
- Ramasamy, S.; Banjerdpongchai, D.; Park, P. Stability and Hopf-bifurcation analysis of diffusive Leslie–Gower prey–predator model with the Allee effect and carry-over effects. Math. Comput. Simul. 2025, 227, 19–40. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, L.; Chen, F. Stability and bifurcation in a two-patch commensal symbiosis model with nonlinear dispersal and additive Allee effect. Int. J. Biomath. 2024, 2450099. [Google Scholar] [CrossRef]
- Tang, D.; Ren, J. Bautin bifurcation with additive noise. Adv. Nonlinear Anal. 2022, 12, 20220277. [Google Scholar] [CrossRef]
- Winkler, M. Application of the Moser–Trudinger inequality in the construction of global solutions to a strongly degenerate migration model. Bull. Math. Sci. World Sci. 2023, 13, 1. [Google Scholar] [CrossRef]
- Alshehri, A.; Aljaber, N.; Altamimi, H.; Alessa, R.; Majdoub, M. Nonexistence of global solutions for a nonlinear parabolic equation with a forcing term. Opusc. Math. 2023, 43, 741–758. [Google Scholar] [CrossRef]
- Wang, S.; Nie, L. Global stability and asymptotic profiles of a partially degenerate reaction diffusion Cholera model with asymptomatic individuals. Adv. Nonlinear Anal. 2024, 13, 20240059. [Google Scholar] [CrossRef]
- Partohaghighi, M.; Akgül, A. New fractional modelling and simulations of prey–predator system with Mittag–Leffler kernel. Int. J. Appl. Comput. Math. 2023, 9, 43. [Google Scholar] [CrossRef]
- Ahmad, Z.; Bonanomi, G.; Cardone, A.; Iuorio, A.; Toraldo, G.; Giannino, F. Fractal-fractional Sirs model for The disease dynamics in both prey and predator with singular and nonsingular kernels. J. Biol. Syst. 2024, 1–34. [Google Scholar] [CrossRef]
- Kuipers, K.J.; Hilbers, J.P.; Garcia-Ulloa, J.; Graae, B.J.; May, R.; Verones, F.; Huijbregts, M.A.; Schipper, A.M. Habitat fragmentation amplifies threats from habitat loss to mammal diversity across the world’s terrestrial ecoregions. ONE Earth 2021, 4, 1505–1513. [Google Scholar] [CrossRef]
- Tan, W.; Herrel, A.; Rödder, D. A global analysis of habitat fragmentation research in reptiles and amphibians: What have we done so far? Biodivers. Conserv. 2023, 32, 439–468. [Google Scholar] [CrossRef]
- Tewksbury, J.J.; Levey, D.J.; Haddad, N.M.; Sargent, S.; Orrock, J.L.; Weldon, A.; Danielson, B.J.; Brinkerhoff, J.; Damschen, E.I.; Townsend, P. Corridors affect plants, animals, and their interactions in fragmented landscapes. Proc. Natl. Acad. Sci. USA 2002, 99, 12923–12926. [Google Scholar] [CrossRef]
- Franco, D.; Ruiz-Herrera, A. To connect or not to connect isolated patches. J. Theor. Biol. 2015, 370, 72–80. [Google Scholar] [CrossRef]
- Travers, E.; Härdtle, W.; Matthies, D. Corridors as a tool for linking habitats-Shortcomings and perspectives for plant conservation. J. Nat. Conserv. 2021, 60, 125974. [Google Scholar] [CrossRef]
- Sun, X.; Shen, J.; Xiao, Y.; Li, S.; Cao, M. Habitat suitability and potential biological corridors for waterbirds in Yancheng coastal wetland of China. Ecol. Indic. 2023, 148, 110090. [Google Scholar] [CrossRef]
- Freedman, H.; Waltman, P. Mathematical models of population interactions with dispersal. I: Stability of two habitats with and without a predator. SIAM J. Appl. Math. 1977, 32, 631–648. [Google Scholar] [CrossRef]
- Arditi, R.; Lobry, C.; Sari, T. Is dispersal always beneficial to carrying capacity? New insights from the multi-patch logistic equation. Theor. Popul. Biol. 2015, 106, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Kula, A.; Mack, K.M.; Zhai, L.; Ryce, A.L.; Ni, W.M.; DeAngelis, D.L.; Van Dyken, J.D. Carrying capacity in a heterogeneous environment with habitat connectivity. Ecol. Lett. 2017, 20, 1118–1128. [Google Scholar] [CrossRef] [PubMed]
- Holt, R.D. Population dynamics in two-patch environments: Some anomalous consequences of an optimal habitat distribution. Theor. Popul. Biol. 1985, 28, 181–208. [Google Scholar] [CrossRef]
- Ruiz-Herrera, A.; Torres, P.J. Effects of diffusion on total biomass in simple metacommunities. J. Theor. Biol. 2018, 447, 12–24. [Google Scholar] [CrossRef] [PubMed]
- Arditi, R.; Lobry, C.; Sari, T. Asymmetric dispersal in the multi-patch logistic equation. Theor. Popul. Biol. 2018, 120, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, Y.; Li, Y.; DeAngelis, D.L. Dispersal asymmetry in a two-patch system with source-sink populations. Theor. Popul. Biol. 2020, 131, 54–65. [Google Scholar] [CrossRef] [PubMed]
- Ban, J.; Wang, Y.; Wu, H. Dynamics of predator-prey systems with prey’s dispersal between patches. Indian J. Pure Appl. Math. 2022, 53, 550–569. [Google Scholar] [CrossRef]
- Preisser, E.L.; Bolnick, D.I.; Benard, M.F. Scared to death? The effects of intimidation and consumption in predator-prey interactions. Ecology 2005, 86, 501–509. [Google Scholar] [CrossRef]
- Cresswell, W. Predation in bird populations. J. Ornithol. 2011, 152, 251–263. [Google Scholar] [CrossRef]
- Suraci, J.P.; Clinchy, M.; Dill, L.M.; Roberts, D.; Zanette, L.Y. Fear of large carnivores causes a trophic cascade. Nat. Commun. 2016, 7, 10698. [Google Scholar] [CrossRef] [PubMed]
- Zanette, L.Y.; White, A.F.; Allen, M.C.; Clinchy, M. Perceived predation risk reduces the number of offspring songbirds produce per year. Science 2011, 334, 1398–1401. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zanette, L.; Zou, X. Modelling the fear effect in predator-prey interactions. J. Math. Biol. 2016, 73, 1179–1204. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S. Impact of fear effect on the growth of prey in a predator-prey interaction model. Ecol. Complex. 2020, 42, 100826. [Google Scholar] [CrossRef]
- Liu, T.; Chen, L.; Chen, F.; Li, Z. Dynamics of a Leslie-Gower model with weak Allee effect on prey and fear effect on predator. Int. J. Bifurc. Chaos 2023, 33, 2350008. [Google Scholar] [CrossRef]
- Benamara, I.; El Abdllaoui, A. Bifurcation in a delayed predator-prey model with Holling type IV functional response incorporating hunting cooperation and fear effect. Int. J. Dyn. Control 2023, 11, 2733–2750. [Google Scholar] [CrossRef]
- Sahoo, D.; Samanta, G. Impact of fear effect in a two prey-one predator system with switching behaviour in predation. Differ. Equ. Dyn. Syst. 2024, 32, 377–399. [Google Scholar] [CrossRef]
- Li, Q.; Chen, F.; Chen, L.; Li, Z. Dynamical analysis of a discrete amensalism system with Michaelis–Menten type harvesting for the Second Species. Qual. Theory Dyn. Syst. 2024, 23, 1–43. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Q.; Teng, Z.; Zhang, G.; Rifhat, R. Bifurcations in a discrete-time Beddington-DeAngelis prey-predator model with fear effect, prey refuge and harvesting. Nonlinear Dyn. 2025, 113, 931–969. [Google Scholar] [CrossRef]
- Creel, S.; Christianson, D.; Liley, S.; Winnie, J.A., Jr. Predation risk affects reproductive physiology and demography of elk. Science 2007, 315, 960. [Google Scholar] [CrossRef]
- Clinchy, M.; Sheriff, M.J.; Zanette, L.Y. Predator-induced stress and the ecology of fear. Funct. Ecol. 2013, 27, 56–65. [Google Scholar] [CrossRef]
- Zanette, L.Y.; Clinchy, M. Ecology of fear. Curr. Biol. 2019, 29, R309–R313. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D. Role of fear in predator-prey system with intraspecific competition. Math. Comput. Simul. 2020, 177, 263–275. [Google Scholar] [CrossRef]
- Das, B.K.; Sahoo, D.; Samanta, G. Impact of fear in a delay-induced predator-prey system with intraspecific competition within predator species. Math. Comput. Simul. 2022, 191, 134–156. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, F.; Xie, X.; Chen, S. An analysis of a predator-prey model in which fear reduces prey birth and death rates. AIMS Math. 2024, 9, 12906–12927. [Google Scholar] [CrossRef]
- Das, B.K.; Sahoo, D.; Santra, N.; Samanta, G. Modeling predator-prey interaction: Effects of perceived fear and toxicity on ecological communities. Int. J. Dyn. Control 2024, 12, 2203–2235. [Google Scholar] [CrossRef]
- Xia, Y.; Huang, X.; Chen, F.; Chen, L. Stability and bifurcation of a predator-prey system with multiple anti-predator behaviors. J. Biol. Syst. 2024, 32, 889–919. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Miller, R.K.; Michel, A.N. Ordinary Differential Equations; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Li, M.Y.; Muldowney, J.S. A geometric approach to global-stability problems. SIAM J. Math. Anal. 1996, 27, 1070–1083. [Google Scholar] [CrossRef]
- Lidicker, W. The role of dispersal in the demography of small mammals. In Small Mammals: Productivity and Dynamics of Populations; Cambridge University Press: Cambridge, UK, 1975; pp. 103–128. [Google Scholar]
- Baxter, C.V.; Fausch, K.D.; Carl Saunders, W. Tangled webs: Reciprocal flows of invertebrate prey link streams and riparian zones. Freshw. Biol. 2005, 50, 201–220. [Google Scholar] [CrossRef]
- Birkhoff, G.; Rota, G. Ordinary Differential Equation; Ginn and Co.: Boston, MA, USA, 1982. [Google Scholar]
- Wang, Z.; Wang, Y. Bifurcations in diffusive predator-prey systems with Beddington-DeAngelis functional response. Nonlinear Dyn. 2021, 105, 1045–1061. [Google Scholar] [CrossRef]
- Senan, N.A.F. A Brief Introduction to Using ode45 in MATLAB; University of California: Berkeley, MA, USA, 2007. [Google Scholar]




| Equilibrium | Existence | Stability |
|---|---|---|
| always | L.A.S. | |
| Saddle-node | ||
| Unstable | ||
| L.A.S. | ||
| Saddle-node | ||
| Unstable | ||
| L.A.S. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Chen, L.; Chen, F. Dynamics of a Predator-Prey System with Asymmetric Dispersal and Fear Effect. Symmetry 2025, 17, 329. https://doi.org/10.3390/sym17030329
Meng X, Chen L, Chen F. Dynamics of a Predator-Prey System with Asymmetric Dispersal and Fear Effect. Symmetry. 2025; 17(3):329. https://doi.org/10.3390/sym17030329
Chicago/Turabian StyleMeng, Xinyu, Lijuan Chen, and Fengde Chen. 2025. "Dynamics of a Predator-Prey System with Asymmetric Dispersal and Fear Effect" Symmetry 17, no. 3: 329. https://doi.org/10.3390/sym17030329
APA StyleMeng, X., Chen, L., & Chen, F. (2025). Dynamics of a Predator-Prey System with Asymmetric Dispersal and Fear Effect. Symmetry, 17(3), 329. https://doi.org/10.3390/sym17030329








