General Solutions for MHD Motions of Second-Grade Fluids Through a Circular Cylinder Filled with Porous Medium

Abstract

The isothermal motion of incompressible second-grade fluids induced by an infinite circular cylinder that rotates around its symmetry axis is analytically and numerically investigated when the magnetic and porous effects are taken into consideration. General closed-form expressions are established for the dimensionless velocity field and the corresponding motion problem is completely solved. For illustration, some special cases are considered, and the results’ correctness is graphically proved. Based on a simple but important observation, the obtained results have been used to provide a general expression for the shear stress corresponding to MHD motions of the same fluids through a porous medium induced by a longitudinal shear stress on the boundary. Finally, graphical representations are used to bring to light the influence of the magnetic field and porous medium on the fluid behavior. It was found that the fluid flows slower and the steady state is reached earlier in the presence of a magnetic field or porous medium.

1. Introduction

The simplest class of fluids of differential type is that of incompressible second-grade fluids whose constitutive equation is given by the relation [1]

$$\mathit{T}=-p\mathit{I}+\mu {\mathit{A}}_{\hspace{0.17em}1}+{\alpha }_1{\mathit{A}}_{\hspace{0.17em}2}+{\alpha }_2{\mathit{A}}_{\hspace{0.17em}1}^2,$$

(1)

in which T is the stress tensor, ${\mathit{A}}_{\hspace{0.17em}1}$ and ${\mathit{A}}_{\hspace{0.17em}2}$ are the first two Rivlin–Ericksen tensors, I is the unit tensor, p is the hydrostatic pressure, $\mu$ is the dynamic viscosity of the fluid, and ${\alpha }_1$ and ${\alpha }_2$ are material constants, also called normal stress moduli. If the constant ${\alpha }_1=0$ one obtains the incompressible Reiner–Rivlin fluids and if ${\alpha }_1={\alpha }_2=0$, the incompressible Newtonian fluids are recovered.

First exact solutions for isothermal motions of non-Newtonian fluids in cylindrical domains seem to be those of Ting [2] for incompressible second-grade fluids. He pointed out the fact that these solutions become unbounded if the material constant ${\alpha }_1<0$. Interesting solutions for motions of the same fluids in cylindrical domains have been established by Rajagopal [3], Bandelli and Rajagopal [4], Fetecau and Corina Fetecau [5], Erdogan and Imrak [6], and Bano et al. [7]. However, in these studies, magnetic and porous effects are not taken into consideration. The first exact general solutions for unsteady flows of incompressible second-grade fluids in such domains have been established by Corina Fetecau et al. [8] when longitudinal or rotational shear stresses are given on the boundary. Recently, Maria Javaid et al. [9] studied the natural convection flow of the same fluids in an infinite circular cylinder that oscillates along its symmetry axis. Exact solutions for unsteady motions of incompressible second-grade fluids in rectangular domains have been obtained by many authors. Among them, we remember the results of Erdogan [10], Erdogan and Imrak [11], Yao and Liu [12], Vieru et al. [13], Sultan et al. [14], Imran et al. [15], Baranovskii and Artemov [16], VeeraKrishna and Reddy [17], Fetecau and Vieru [18,19], Baranovskii [20], and Kanuri et al. [21].

The same time flows of fluids in the presence of a magnetic field or porous medium have multiple engineering applications. The interplay between the magnetic field and a moving electrical conducting fluid induces effects with applications in physics and chemistry, while flows through porous media have many practical applications in geophysical and astrophysical studies, the petroleum industry, and oil reservoir technology. Unfortunately, in the existing literature, there are few exact solutions for magneto hydrodynamic (MHD) flows of non-Newtonian fluids through cylindrical domains. Exact solutions for such flows of incompressible second-grade fluids through a porous medium between infinite coaxial circular cylinders, which move along their axis or apply time-dependent shear stresses to the fluid, were obtained by Jamil and Zafarullah [22]. However, their solutions, which were obtained using Laplace and finite Hankel transforms, are complicated and no proof of their correctness is brought to light. The influence of a magnetic field on the flow of fractional second-grade fluids in cylindrical domains has been also investigated by Danish et al. [23], Mirza et al. [24], and Uddin et al. [25].

The purpose of this note is to provide the simplest expressions for the velocity field corresponding to the MHD unsteady flow of electrical conducting incompressible second-grade fluids (ECISGFs) through a porous medium in an infinite horizontal circular cylinder that rotates around its symmetry axis with an arbitrary time-dependent velocity. The problem in discussion is completely solved using the finite Hankel transform only. For illustration, as well as to bring to light some characteristics of the fluid motion, three particular cases are considered and the correctness of the results that have been obtained is graphically proved. The velocity field corresponding to incompressible Newtonian fluids performing the same motion is immediately obtained as a limiting case of a general solution. As an application, using a simple but important observation regarding the governing equation for the non-trivial shear stress of another MHD motion of same fluids through a porous medium, a general expression is provided for the shear stress field of the respective motion.

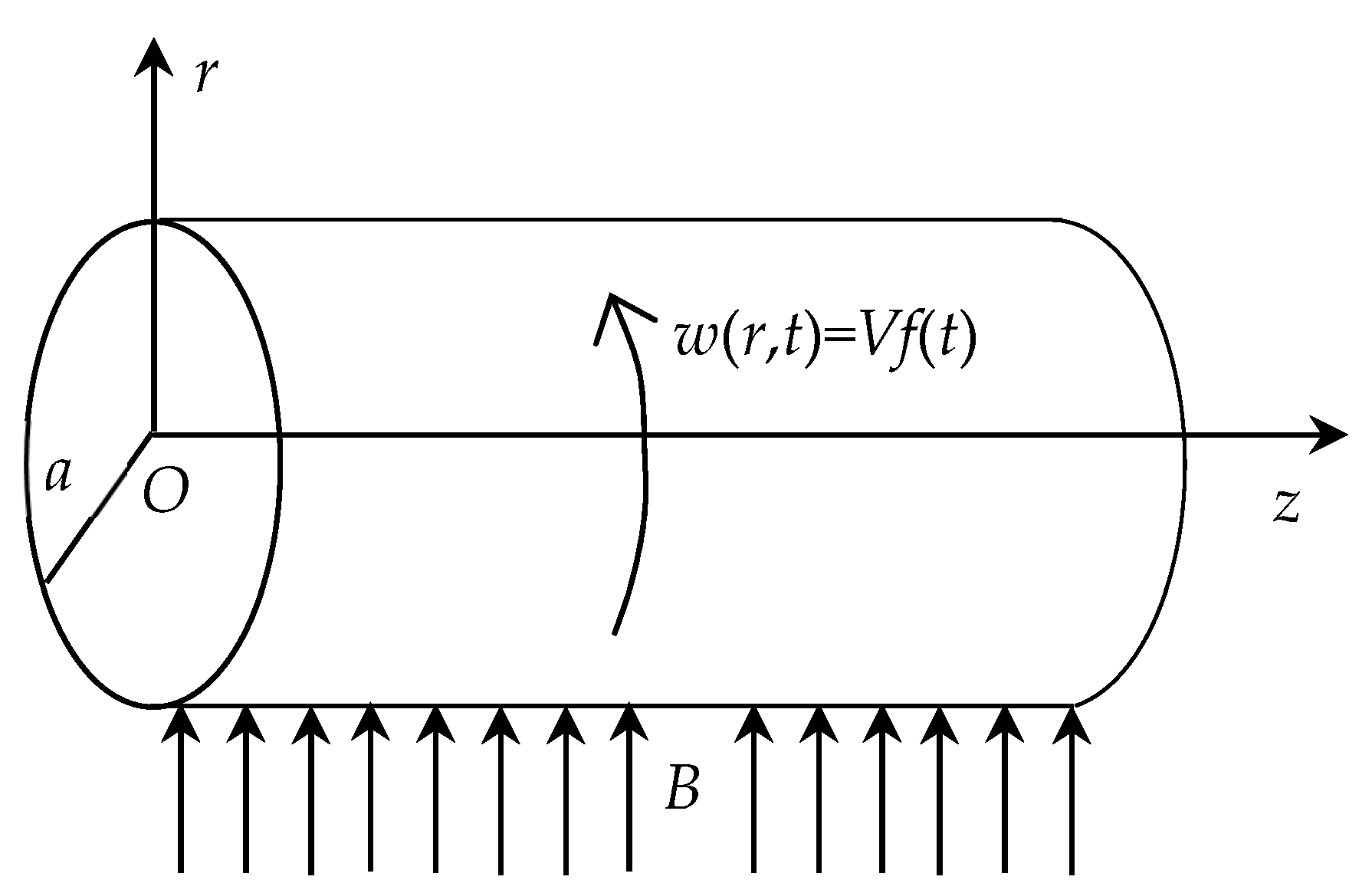
2. Problem Presentation

Let us suppose that an ECISGF is at rest in a porous medium in an infinite horizontal circular cylinder of radius a. Such a fluid allows the transport of electrical charges when placed in an electric field. At the time $t=0^{+}$, the cylinder begins to rotate around its symmetry axis with the time-dependent velocity $Vf(t)$ and a circular magnetic field of strength B acts on the azimuthally direction [26], as it is shown in Figure 1.

The function $f(\cdot )$, whose value at the moment $t=0$ is zero, is piecewise continuous and V is a constant velocity. Owing to the shear, the fluid is gradually moved and the corresponding velocity vector $\mathit{w}$ is given by the relation

$$\mathit{w}=\mathit{w}(r,t)=w(r,t){\mathit{e}}_{\theta };\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(2)

in a convenient cylindrical coordinate system r, $\theta$, and z. Here, ${\mathit{e}}_{\theta }$ is the unit vector along the $\theta$ direction. Substituting $\mathit{w}(r,t)$ from Equation (2) in (1), one obtains the following expression:

$$\tau (r,t)=\left(\mu +{\alpha }_1{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)\left({\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}-{\displaystyle \frac{1}{r}}\right)w(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(3)

for the non-trivial shear stress, $\tau (r,t)=T_{r\theta }(r,t)$.

We also assume that the fluid is finitely conducting so that the Joule heat due to the external magnetic field is negligible. In addition, there is no surplus electric charge distribution in the fluid, the magnetic permeability of the fluid is constant, and the induced magnetic field due to the applied magnetic field can be neglected. In this case, in the absence of a pressure gradient in the flow direction, the balance of linear momentum reduces to the next partial differential Equation [22]:

$$\rho {\displaystyle \frac{\mathsf{\partial }w(r,t)}{\mathsf{\partial }t}}=\left({\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}+{\displaystyle \frac{2}{r}}\right)\tau (r,t)-\sigma B^{2}w(r,t)-{\displaystyle \frac{\varphi }{k}}\left(\mu +{\alpha }_1{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)w(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(4)

where $\rho$ is the fluid density, $\sigma$ is the electrical conductivity, and $\varphi$ and k are the porosity and the permeability of the porous medium. In the following, in order to determine the dimensionless velocity and shear stress fields corresponding to the present motion, we have to solve the system of partial differential Equations (3) and (4) with the following initial and boundary conditions:

$$w(r,0)=\tau (r,0)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le r\le a;w(a,t)=Vf(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(5)

Introducing the non-dimensional variables, functions, and parameter

$$r^{\ast }={\displaystyle \frac{1}{a}}r,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{t}^{\ast }={\displaystyle \frac{\nu }{a^2}}t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}^{\ast }={\displaystyle \frac{1}{V}}w,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\tau }^{\ast }={\displaystyle \frac{a}{\mu V}}\tau ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}^{\ast }(\hspace{0.17em}{t}^{\ast })=f\left({\displaystyle \frac{a^2}{\nu }}{t}^{\ast }\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha ={\displaystyle \frac{{\alpha }_1}{\rho a^2}}$$

(6)

and neglecting the star notation, one obtains the dimensionless governing equations

$$\tau (r,t)=\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)\left({\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}-{\displaystyle \frac{1}{r}}\right)w(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(7)

$${\displaystyle \frac{\mathsf{\partial }w(r,t)}{\mathsf{\partial }t}}=\left({\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}+{\displaystyle \frac{2}{r}}\right)\tau (r,t)-Mw(r,t)-K\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)w(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(8)

In the relations (6) and (8), $\nu =\mu /\rho$ is the kinematic viscosity of the fluid and the magnetic and porous parameters M and K, respectively, are defined by the next relations:

$$M={\displaystyle \frac{a^2}{\mu }}\sigma B^2={\displaystyle \frac{a^2}{\nu }}{\displaystyle \frac{\sigma B^2}{\rho }},K={\displaystyle \frac{\varphi }{k}}{a}^2.$$

(9)

By eliminating the dimensionless shear stress $\tau (r,t)$ between Equations (7) and (8), one finds the following governing equation:

$$\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }w(r,t)}{\mathsf{\partial }t}}=\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)\left({\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}-{\displaystyle \frac{1}{r^2}}\right)w(r,t)\\ -Mw(r,t)-K\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)w(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.\end{array}$$

(10)

For the dimensionless velocity field $w(r,t)$, the initial and boundary conditions are

$$w(r,0)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\le r\le 1;w(1,t)=f(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(11)

In the next section, the governing Equation (10), together with the initial and boundary conditions (11), will be solved in the simplest way using only the finite Hankel transform and its inverse defined by the following relations [27]:

$${\chi }_H(r_n)=H\{\chi (r)\}={\displaystyle \underset{0}{\overset{1}{\int }}r\chi (r)J_1(r{r}_n)dr,}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\chi (r)=2{\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{{[{J^{\prime }}_1(r_n)]}^2}}{\chi }_H(r_n),$$

(12)

where $J_1(\cdot )$ is a standard Bessel function of the first kind of order, ${J^{\prime }}_1(\cdot )$ is its derivative, $r_n$ are the positive roots of the transcendental equation $J_1(r)=0$, and ${\chi }_H(r_n)$ is the finite Hankel transform of the function $\chi (r)$. The following identity ([23], Section 14, Equation (59)),

$$H\left\{{\displaystyle \frac{d^2\chi (r)}{d{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{d\chi (r)}{dr}}-{\displaystyle \frac{1}{r^2}}\chi (r)\right\}=-r_n^2{\chi }_H(r_n)-r_n\chi (1){J^{\prime }}_1(r_n),$$

(13)

is satisfied for any function $\chi (r)$ which satisfies the Dirichlet’s conditions on $0<r<1$.

3. Solution

Applying the finite Hankel transform to Equality (10), and bearing in mind the initial and boundary conditions (11) and the identity (13), one attains the following initial value problem

$$\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }{w}_H(r_n,t)}{\mathsf{\partial }t}}+{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}{w}_H(r_n,t)\\ -{\displaystyle \frac{f(t)+\alpha f^{\prime }(t)}{1+\alpha (r_n^2+K)}}{r}_n{J}_2(r_n)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_H(r_n,0)=0,\end{array}$$

(14)

for the function $w_H(r_n,t)$, in which $K_{eff}=M+K$ is the effective permeability. The solution of this initial value problem is given by the relation

$$w_H(r_n,t)={\displaystyle \frac{r_n{J}_2(r_n)}{1+\alpha (r_n^2+K)}}{\displaystyle \underset{0}{\overset{t}{\int }}[f(s)+}\alpha f^{\prime }(s)]\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}(t-s)\right]ds,$$

(15)

or equivalently

$$\begin{array}{l}{w}_H(r_n,t)=\alpha f(t){\displaystyle \frac{r_n{J}_2(r_n)}{1+\alpha (r_n^2+K)}}\\ +(1-\alpha M){\displaystyle \frac{r_n{J}_2(r_n)}{{[1+\alpha (r_n^2+K)]}^2}}{\displaystyle \underset{0}{\overset{t}{\int }}f(s)}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}(t-s)\right]ds.\end{array}$$

(16)

Now, applying the inverse finite Hankel transform to the last equality and using entry 1 of Table X from [27], one finds the dimensionless velocity field

$$\begin{array}{l}w(r,t)=rf(t)-2(1+\alpha K)f(t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{{[1+\alpha (r_n^2+K)]}^2{J}_2(r_n)}}{\displaystyle \underset{0}{\overset{t}{\int }}f(s)}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}(t-s)\right]ds,\end{array}$$

(17)

which clearly satisfies the initial and boundary conditions (11).

As the function $f(\cdot )$ is arbitrary, the isothermal MHD motion problem of ECISGFs through a porous medium in an infinite horizontal circular cylinder that slides along its symmetry axis is completely solved. For illustration, as well as for the results’ validation, three particular cases are considered, and the corresponding velocity fields are used to bring to light the influence of the magnetic field and porous medium on the fluid behavior. Moreover, the present results are later used to generate dimensionless exact solutions for a new class of MHD motions of the same fluids through a porous medium in an infinite circular cylinder that applies a time-dependent shear stress to the fluid. Finally, it is worth to point out the fact that by taking $\alpha =0$ in Equation (17), one finds the dimensionless velocity field

$$w_N(r,t)=rf(t)-2f(t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{r_n{J}_2(r_n)}}+2{\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{J_2(r_n)}}{\displaystyle \underset{0}{\overset{t}{\int }}f(s)}\hspace{0.17em}{\mathrm{e}}^{-(r_n^2+K_{eff})(t-s)}ds,$$

(18)

corresponding to the MHD motion of electrically conducting incompressible Newtonian fluids through a porous medium in an infinite circular cylinder that moves along its axis with the time-dependent velocity $Vf(t)$. From the last relation, it is clear that the velocity $w_N(r,t)$ does not depend on the parameters M and K independently, but only on a combination of them, which is the effective permeability. Consequently, a two-parameter approach is superfluous in this case.

4. Some Study Cases and the Results’ Validation

4.1. The Cylinder Oscillates Along Its Symmetry Axis

Substituting the function $f(t)$ by $H(t)\cos (\omega t)$ or $H(t)\sin (\omega t)$ in Equation (17), one obtains the dimensionless starting velocity fields $w_c(r,t)$ and $w_s(r,t)$ corresponding to MHD motions of ECISGFs through a porous medium induced by cosine or sine oscillations of the cylinder. Here, $H(\cdot )$ is the Heaviside unit step function and $\omega$ is the dimensionless oscillations’ frequency. The two motions become steady in time and the corresponding velocity fields can be written as the sum of their steady state and transient components, i.e.,

$$w_c(r,t)=[w_{cs}(r,t)+w_{ct}(r,t)]H(t),w_s(r,t)=[w_{ss}(r,t)+w_{st}(r,t)]H(t).$$

(19)

Direct computations show that these components are given by the relations

$$\begin{array}{l}{w}_{cs}(r,t)=r\cos (\omega t)-2(1+\alpha K)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}+2\omega (1-\alpha M)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}},\end{array}$$

(20)

$$w_{ct}(r,t)=-2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right],$$

(21)

$$\begin{array}{l}{w}_{ss}(r,t)=r\sin (\omega t)-2(1+\alpha K)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}-2\omega (1-\alpha M)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}},\end{array}$$

(22)

$$w_{st}(r,t)=2\omega (1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right],$$

(23)

in which the constants $a_n$ have the expression

$$a_n={(r_n^2+K_{eff})}^2+{\omega }^2{[1+\alpha (r_n^2+K)]}^2;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}n=1,2,3,\dots$$

(24)

Now, the Method of Lines (MOL) is used to numerically solve Equation (10) with the corresponding initial and boundary conditions. The numerical implementation is carried out using Mathematica software. As expected, Figure 2 shows an excellent agreement between the analytical expressions of the dimensionless velocity fields $w_c(r,t)$ and $w_s(r,t)$ from Equations (19), and the corresponding numerical solutions.

Equivalent forms for the dimensionless steady state (permanent or long time) velocities $w_{cs}(r,t)$ and $w_{ss}(r,t)$, namely

$$w_{cs}(r,t)=\mathrm{Re}\left\{{\displaystyle \frac{I_1(r\sqrt{\gamma })}{I_1(\sqrt{\gamma })}}{e}^{i\omega t}\right\}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{w}_{ss}(r,t)=\mathrm{Im}\left\{{\displaystyle \frac{I_1(r\sqrt{\gamma })}{I_1(\sqrt{\gamma })}}{e}^{i\omega t}\right\}\hspace{0.17em},$$

(25)

have been directly obtained using the dimensionless complex permanent velocity $w_p(r,t)=w_{cs}(r,t)+i{w}_{ss}(r,t)$. Here, i is the imaginary unit and the complex constant $\gamma =[K_{eff}+i\omega (1+\alpha K)]/(1+i\omega \alpha )$.

Figure 3 shows the equivalence of the expressions of $w_{cs}(r,t)$ and $w_{ss}(r,t)$ given by Equations (20), (25)₁ (first relation from Equations (25)) and (22), (25)₂ (second relation from Equations (25)), respectively.

4.2. The Cylinder Slides Along Its Symmetry Axis with the Constant Velocity V

Substituting $f(t)$ by $H(t)$ in the general solution (17), or taking $\omega =0$ in Equation (19)₁ (first relation from Equations (19)), one finds the dimensionless velocity field $w_C(r,t)$ corresponding to the MHD motion of ECISGFs through a porous medium induced by the circular cylinder that slides along its axis with the constant velocity V. This velocity field, as well as those corresponding to oscillatory motions of the cylinder, can be written as the sum of its steady and transient components, i.e.,

$$w_C(r,t)=[w_{Cs}(r)+w_{Ct}(r,t)]H(t),$$

(26)

in which

$$\begin{array}{l}{w}_{Cs}(r)=r-2(1+\alpha K){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{[1+\alpha (r_n^2+K)](r_n^2+K_{eff})J_2(r_n)}},\end{array}$$

(27)

$$w_{Ct}(r,t)=-2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{[1+\alpha (r_n^2+K)](r_n^2+K_{eff})J_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right]\hspace{0.17em}.$$

(28)

Direct computations show that the dimensionless steady velocity $w_{Cs}(r)$ can be also written in the simpler form

$$w_{Cs}(r)=r-2K_{eff}{\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{r_n(r_n^2+K_{eff})J_2(r_n)}},$$

(29)

which is identical to the steady velocity field corresponding to the incompressible Newtonian fluids performing the same motion. This result is not surprising, because the governing equations corresponding to steady flows of incompressible Newtonian and non-Newtonian fluids are identical. A new equivalent form for $w_{Cs}(r)$, namely

$$w_{Cs}(r)={\displaystyle \frac{I_1(r\sqrt{K_{eff}})}{I_1(\sqrt{K_{eff}})}},$$

(30)

has been obtained, taking $\omega =0$ in Equality (25)₁ (first relation from Equations (25)).

5. Application

Let us now consider the MHD flow of the same fluids through a porous medium generated by the infinite horizontal circular cylinder of radius a that applies a time-dependent longitudinal shear stress $Sg(t)$ to the fluid. The function $g(\cdot )$, as well as the function $f(\cdot )$ from the previous sections, are piecewise continuous, and $g(0)=0$, while S is a constant shear stress. The velocity vector corresponding to this motion is given by the relation

$$\mathsf{v}=\mathsf{v}(r,t)=u(r,t){\mathit{e}}_z;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(31)

in the same system of cylindrical coordinates, in which ${\mathit{e}}_z$ is the unit vector in the z-direction. Introducing the vector $\mathsf{v}(r,t)$ from Equation (31) in (1), one finds that the non-trivial shear stress $\eta (r,t)=T_{rz}(r,t)$ is given by the relation

$$\eta (r,t)=\left(\mu +{\alpha }_1{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right){\displaystyle \frac{\mathsf{\partial }u(r,t)}{\mathsf{\partial }r}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(32)

In the same conditions as in the previous sections, the balance of linear momentum reduces to the next relevant partial differential equation:

$$\rho {\displaystyle \frac{\mathsf{\partial }u(r,t)}{\mathsf{\partial }t}}={\displaystyle \frac{\mathsf{\partial }\eta (r,t)}{\mathsf{\partial }r}}+{\displaystyle \frac{1}{r}}\eta (r,t)-\sigma B^{2}u(r,t)-{\displaystyle \frac{\varphi }{k}}\left(\mu +{\alpha }_1{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)u(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(33)

The corresponding initial and boundary conditions are

$$u(r,0)=\eta (r,0)=0,\hspace{0.17em}\hspace{0.17em}0<r<a;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\eta (a,t)=Sg(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(34)

The dimensionless forms of the governing Equations (32) and (33), namely

$$\eta (r,t)=\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right){\displaystyle \frac{\mathsf{\partial }u(r,t)}{\mathsf{\partial }r}};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(35)

$${\displaystyle \frac{\mathsf{\partial }u(r,t)}{\mathsf{\partial }t}}={\displaystyle \frac{\mathsf{\partial }\eta (r,t)}{\mathsf{\partial }r}}+{\displaystyle \frac{1}{r}}\eta (r,t)-Mu(r,t)-K\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)u(r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<a,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,$$

(36)

have been obtained using the next non-dimensional variables and functions

$$r^{\ast }={\displaystyle \frac{1}{a}}r,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{t}^{\ast }={\displaystyle \frac{\nu }{a^2}}t,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{u}^{\ast }={\displaystyle \frac{\mu }{aS}}u,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\eta }^{\ast }={\displaystyle \frac{1}{S}}\eta ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{g}^{\ast }(\hspace{0.17em}{t}^{\ast })=g\left({\displaystyle \frac{a^2}{\nu }}{t}^{\ast }\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\alpha ={\displaystyle \frac{{\alpha }_1}{\rho a^2}}$$

(37)

and giving up the star notation.

Eliminating the velocity $u(r,t)$ between the Equalities (35) and (36), one finds the following partial differential equation,

$$\begin{array}{l}{\displaystyle \frac{\mathsf{\partial }\eta (r,t)}{\mathsf{\partial }t}}=\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)\left({\displaystyle \frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{r}^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }r}}-{\displaystyle \frac{1}{r^2}}\right)\eta (r,t)\\ -M\eta (r,t)-K\left(1+\alpha {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }t}}\right)\eta (r,t);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0<r<1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0,\end{array}$$

(38)

for the shear stress $\eta (r,t)$. The corresponding initial and boundary conditions are

$$\eta (r,0)=0,\hspace{0.17em}\hspace{0.17em}0\le r\le 1;\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\eta (a,t)=g(t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t>0.$$

(39)

Since the governing Equations (10) and (38) and the boundary conditions (11) and (39) are identical in form, the dimensionless shear stress $\eta (r,t)$ corresponding to this motion of ECISGFs is given by the relation (see equality (17))

$$\begin{array}{l}\eta (r,t)=rg(t)-2(1+\alpha K)g(t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{{[1+\alpha (r_n^2+K)]}^2{J}_2(r_n)}}{\displaystyle \underset{0}{\overset{t}{\int }}g(s)}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}(t-s)\right]ds.\end{array}$$

(40)

Once the dimensionless shear stress $\eta (r,t)$ is known, the corresponding velocity field $u(r,t)$ can be determined, solving the linear differential Equation (36) with the initial condition $u(r,0)=0$.

5.1. The Case When the Cylinder Applies an Oscillatory Shear Stress to the Fluid

Replacing the function $g(t)$ by $H(t)\cos (\omega t)$ or $H(t)\sin (\omega t)$ in Equation (40), one obtains the dimensionless starting shear stresses ${\eta }_c(r,t)$ and ${\eta }_s(r,t)$ corresponding to MHD flows of ECISGFs through a porous medium induced by the infinite circular cylinder that applies oscillatory longitudinal shear stresses to the fluid. Of course, these shear stresses can be also written as the sum of their steady state and transient components, whose expressions are given by the relations

$$\begin{array}{l}{\eta }_{cs}(r,t)=r\cos (\omega t)-2(1+\alpha K)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}+2\omega (1-\alpha M)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}},\end{array}$$

(41)

$${\eta }_{ct}(r,t)=-2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right],$$

(42)

$$\begin{array}{l}{\eta }_{ss}(r,t)=r\sin (\omega t)-2(1+\alpha K)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M)\sin (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n(r_n^2+K_{eff})J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]a_n{J}_2(r_n)}}-2\omega (1-\alpha M)\cos (\omega t){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}},\end{array}$$

(43)

$${\eta }_{st}(r,t)=2\omega (1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{a_n{J}_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right],$$

(44)

which are also new in the literature. Equivalent forms for the dimensionless steady state shear stresses ${\eta }_{cs}(r,t)$ and ${\eta }_{ss}(r,t)$ are given by the relations

$${\eta }_{cs}(r,t)=\mathrm{Re}\left\{{\displaystyle \frac{I_1(r\sqrt{\gamma })}{I_1(\sqrt{\gamma })}}{e}^{i\omega t}\right\}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\eta }_{ss}(r,t)=\mathrm{Im}\left\{{\displaystyle \frac{I_1(r\sqrt{\gamma })}{I_1(\sqrt{\gamma })}}{e}^{i\omega t}\right\}\hspace{0.17em}.$$

(45)

5.2. The Cylinder Applies a Constant Shear Stress S to the Fluid

Substituting the function $g(t)$ by $H(t)$ in Equation (40), or making $\omega =0$ in Equations (41) and (42), one obtains the dimensionless starting shear stress ${\eta }_C(r,t)$ corresponding to the MHD motion of ECISGFs through a porous medium induced by the infinite circular cylinder that applies a constant shear stress S to the fluid. Its steady and transient components are given by the relations

$$\begin{array}{l}{\eta }_{Cs}(r)=r-2(1+\alpha K){\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{[1+\alpha (r_n^2+K)]r_n{J}_2(r_n)}}\\ +2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{[1+\alpha (r_n^2+K)](r_n^2+K_{eff})J_2(r_n)}},\end{array}$$

(46)

$${\eta }_{Ct}(r,t)=-2(1-\alpha M){\displaystyle \sum _{n=1}^{\infty }\frac{r_n{J}_1(r{r}_n)}{[1+\alpha (r_n^2+K)](r_n^2+K_{eff})J_2(r_n)}}\exp \left[-{\displaystyle \frac{r_n^2+K_{eff}}{1+\alpha (r_n^2+K)}}t\right]\hspace{0.17em}.$$

(47)

In both cases, i.e., the two oscillatory motions or motion due to a constant shear stress on the boundary, the dimensionless similar tensions for electrical conducting incompressible Newtonian fluids performing the same motions, namely ${\eta }_{Ncs}(r)$ and ${\eta }_{Nct}(r),$ are immediately obtained, taking $\alpha =0$ in the corresponding relations. New equivalent forms for the dimensionless steady shear stress ${\eta }_{NCs}(r)$ are given by relations

$${\eta }_{NCs}(r)=r-2K_{eff}{\displaystyle \sum _{n=1}^{\infty }\frac{J_1(r{r}_n)}{r_n(r_n^2+K_{eff})J_2(r_n)}} \mathrm{or}{\eta }_{NCs}(r)=I_1(r\sqrt{K_{eff}})/I_1(\sqrt{K_{eff}}).$$

(48)

In all cases, the corresponding velocity fields can be easily determined, solving the linear ordinary differential Equation (10) with the initial condition (11).

6. Some Numerical Results and Conclusions

In this work, the isothermal MHD motion problem of ECISGFs through a porous medium in an infinite circular cylinder that moves along its symmetry axis is completely solved. Exact general expressions have been established for the dimensionless velocity field $w(r,t)$ using the finite Hankel transform only. 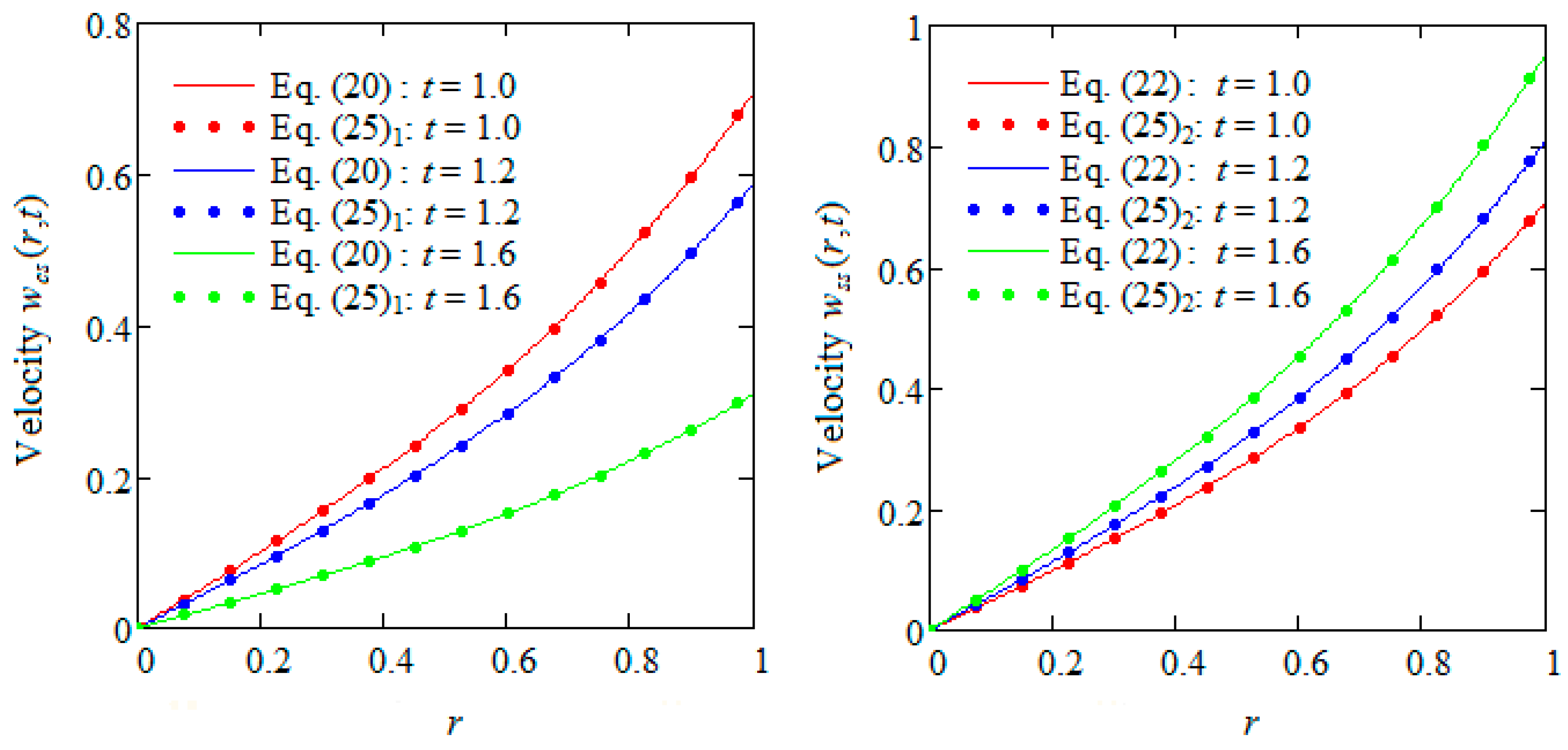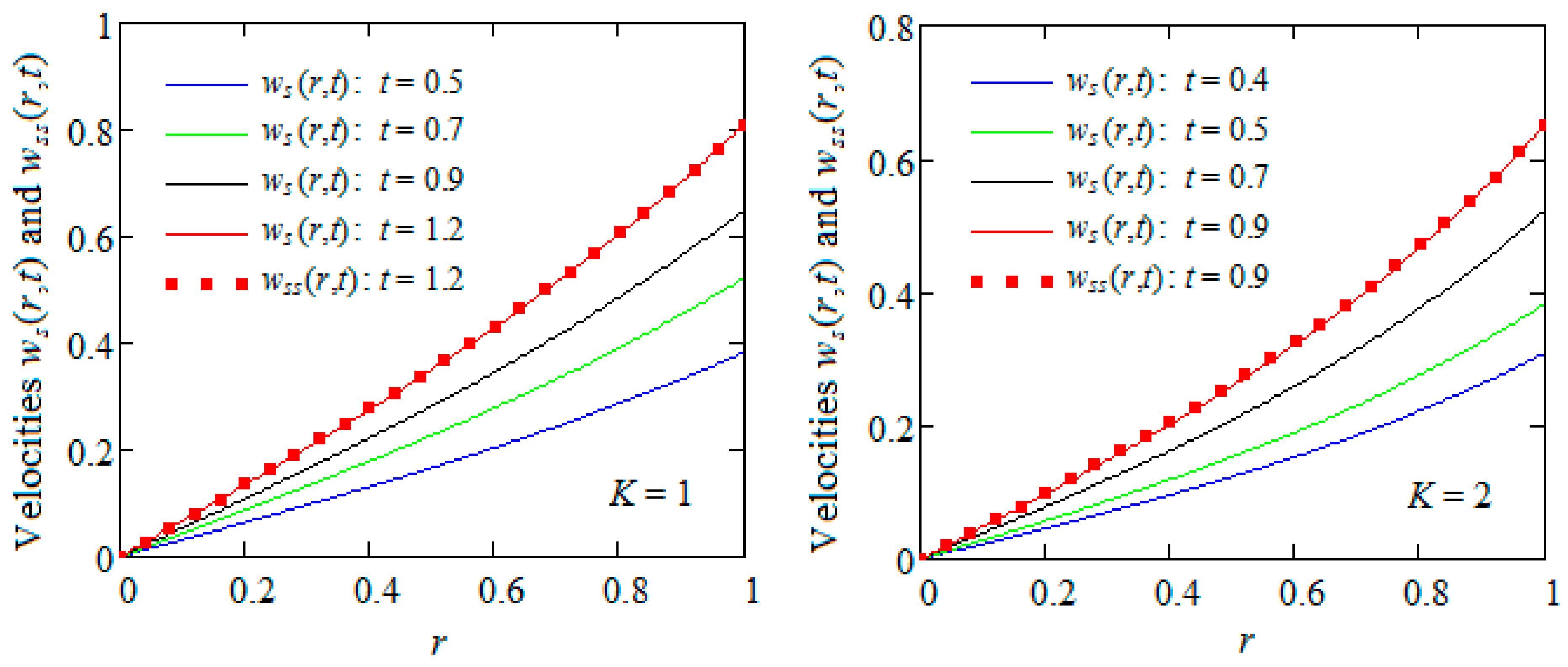One of these expressions is used to determine the dimensionless shear stress $\eta (r,t)$ corresponding to the MHD motion of the same fluids through a porous medium in an infinite circular cylinder that applies an arbitrary time-dependent shear stress $Sg(t)$ to the fluid. Actually, this is the first exact solution for MHD motions of ECISGFs through a porous medium in cylindrical domains when the shear stress is prescribed on the boundary. For illustration, as well as to bring to light some characteristics of the fluid motion, some particular cases are considered, and the corresponding velocity fields are provided. In addition, the correctness of results that have been obtained was graphically proved by Figure 2 and Figure 3.

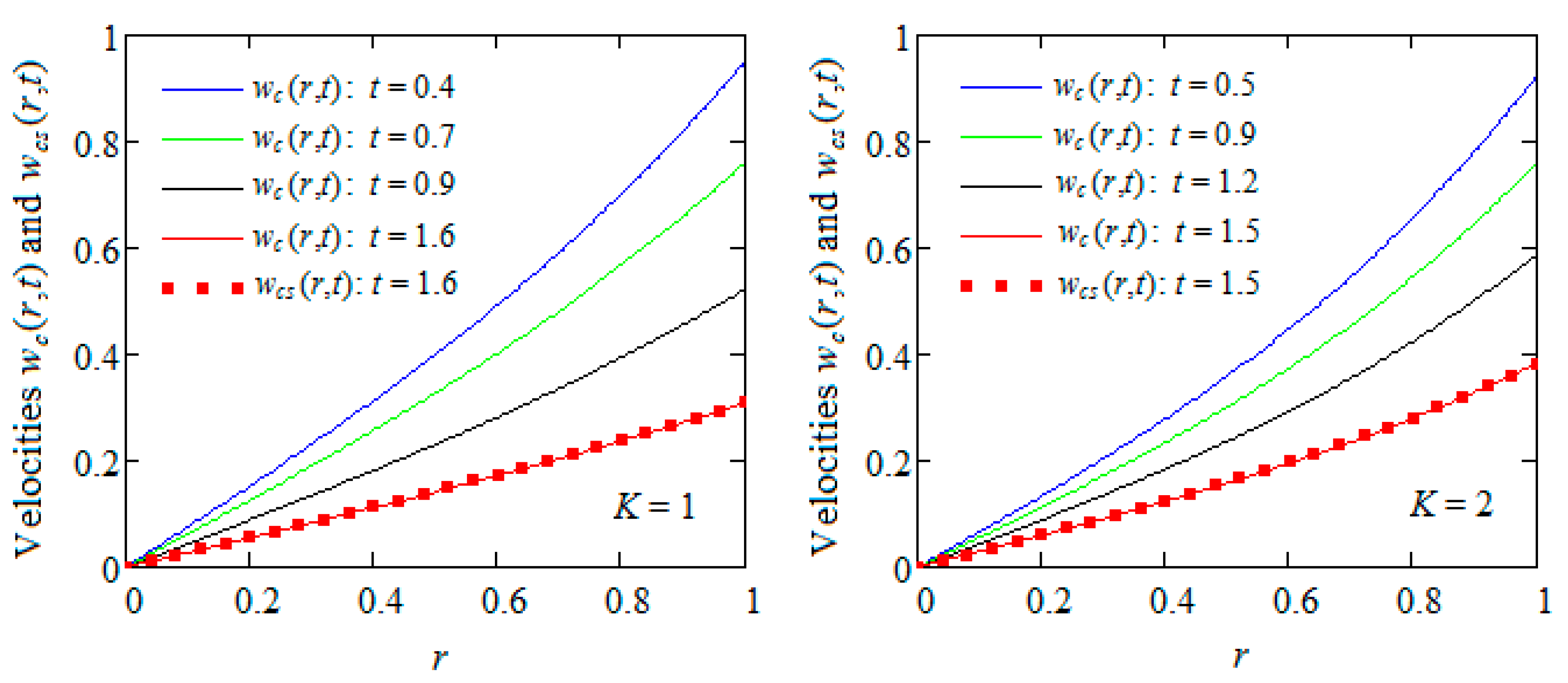
The three unsteady motions of ECISGFs whose dimensionless velocity fields have been provided in Section 3 become steady in time, and a very important problem for experimental researchers is to determine the time after which the steady state is reached. From a mathematical point of view, this is the time after which the diagrams of starting velocities superpose with those of their steady state components. In order to bring to light the influence of the magnetic field and porous medium on this time, Figure 4, Figure 5, Figure 6 and Figure 7 depict the fixed values of the parameters $\alpha ,\hspace{0.17em}\hspace{0.17em}\omega$, distinct values of the magnetic and porous parameters M and K, and increasing values of the time t. From these figures, it is clear that the need time to reach the steady state declines for increasing values of M or K. Consequently, the steady state for such unsteady motions of ECISGFs is rather obtained in the presence of a magnetic field or porous medium.

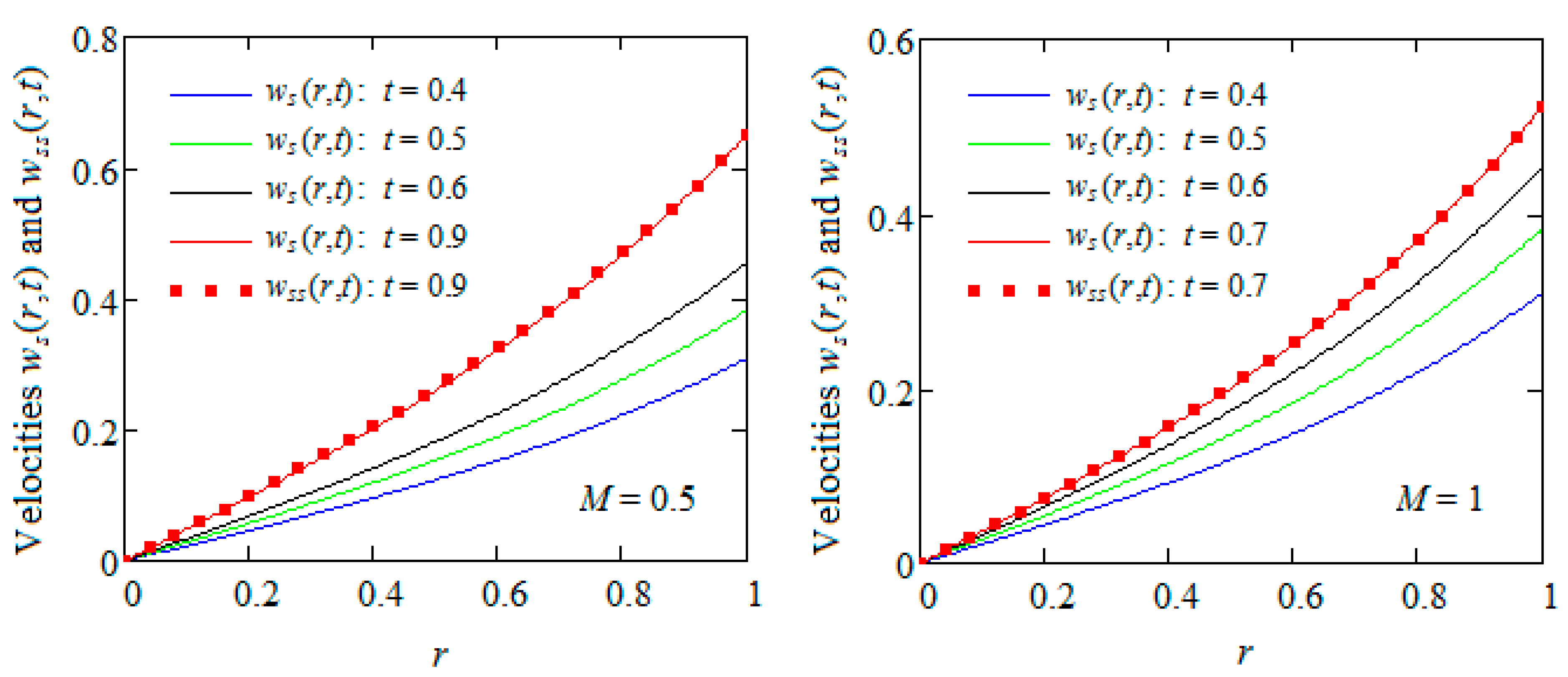
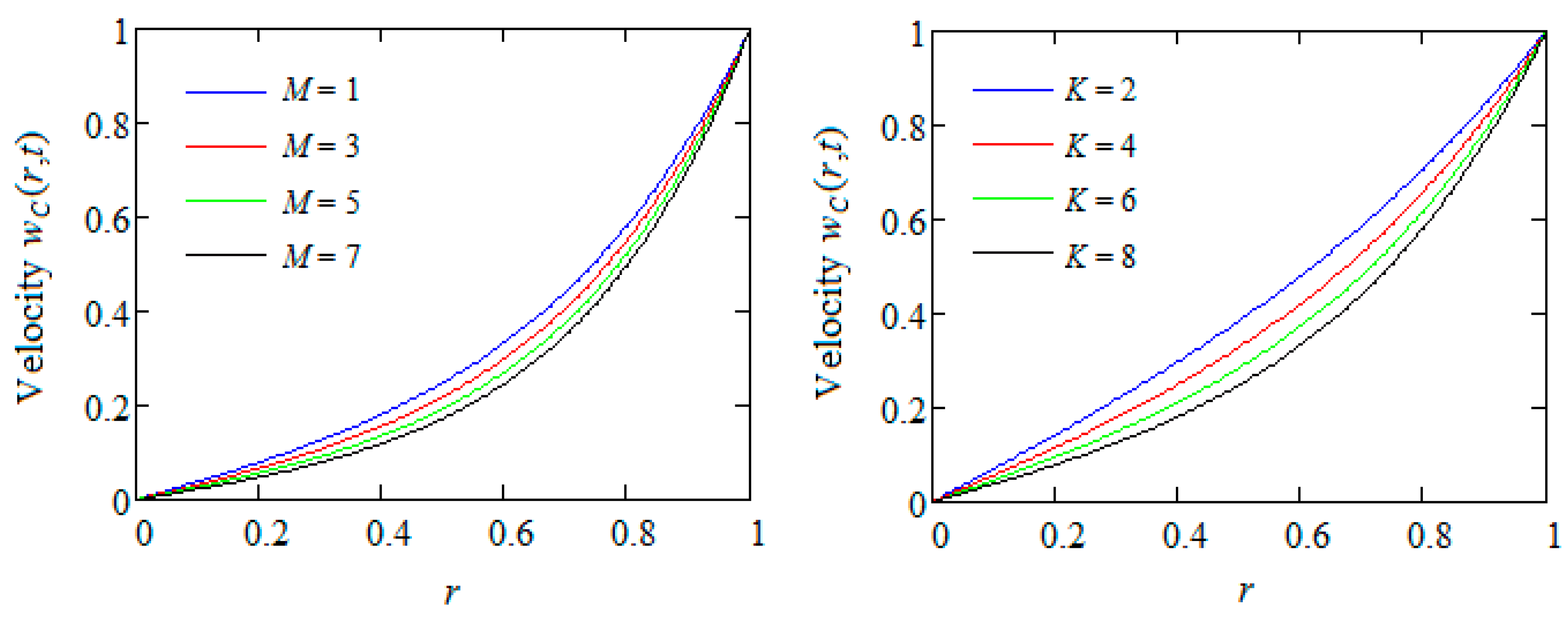
In Figure 8, the profiles of the starting velocity $w_C(r,t)$ are depicted for increasing values of the parameters M or K and fixed values of the other parameters and of the time t. From these figures, it is clear that the dimensionless fluid velocity $w_C(r,t)$ is a decreasing function with respect to the two parameters. Consequently, the fluid flows slower in the presence of a magnetic field or porous medium.

Lastly, Figure 9 presents comparisons between the dimensionless starting velocity fields $w_C(r,t)$ and $w_{CN}(r,t)$ corresponding to the motion of incompressible second-grade and Newtonian fluids, respectively. The expression of the velocity $w_{CN}(r,t)$ can be immediately obtained, taking $\alpha =0$ in equality (26). From this Figure, it is clear that the second-grade fluid flows faster in comparison with the Newtonian fluid and the boundary condition is clearly satisfied. Furthermore, after the value 3 (three) of the dimensionless time t, the diagrams of the two velocities are identical. This is not a surprise because, as it is known from the literature, the non-Newtonian effects disappear in time.

The main results that have been obtained by means of this study are as follows:

1. General expressions have been established for the dimensionless velocity of ECISGFs in MHD motions through a porous medium induced by an infinite circular cylinder that moves along its symmetry axis with a time-dependent velocity $Vf(t)$.

2. One of these expressions has been used to give the dimensionless shear stress for MHD motions of same fluids through a porous medium in an infinite circular cylinder that applies an arbitrary longitudinal shear stress $Sg(t)$ to the fluid.

3. It is worth mentioning that the general expression (17) for the dimensionless fluid velocity $w(r,t)$ was obtained in a simple way using the finite Hankel transform only.

4. As the boundary conditions (5) and (34) contain arbitrary functions $f(\cdot )$ and $g(\cdot )$, the two MHD motion problems of incompressible second-grade fluids through a porous medium in an infinite circular cylinder are completely solved.

5. For the results’ validation and in order to bring to light some characteristics of the fluid motion, three study cases with technical relevance were considered and the correctness of the respective velocity fields has been graphically proved.

6. Graphical representations showed that, in the absence of the magnetic field or of the porous medium, the fluid flows faster and the steady state is later touched.

Finally, we mention the fact that the governing Equation (38) for the dimensionless shear stress $\eta (r,t)$ can be useful for readers who want to investigate other MHD motion problems of ECISGFs through a porous medium in cylindrical domains. In addition, the dimensionless shear stresses corresponding to the studied motions can be easily obtained substituting the respective velocity fields in Equation (7).