Non-Relativistic and Relativistic Lagrangian Pairing in Fluid Mechanics Inspired by Quantum Theory

Abstract

The pairing of non-relativistic and relativistic Lagrangians within the context of fluid mechanics, advancing methodologies for constructing Poincare-invariant Lagrangians, is explored. Through leveraging symmetries and Noether’s theorem in an inverse framework, three primary cases are investigated: potential flow, barotropic flow expressed in terms of Clebsch variables, and an extended Clebsch Lagrangian incorporating thermodynamic effects. To ensure physical correctness, the eigenvalue relation of the energy–momentum tensor, together with velocity normalisation, are applied as key criteria. The findings confirm that the relativistic Lagrangians successfully reduce to their non-relativistic counterparts in the limit $c\to \infty$. These results demonstrate a systematic approach that enhances the relationship between symmetries and variational formulations, providing the advantage of deriving Lagrangians that unify non-relativistic and relativistic theories.

1. Introduction

Lagrange formalism (LF) is one of the most sophisticated ways of describing the dynamics of physical systems, encapsulating their behaviour within a single scalar function. The Lagrangian gives rise to Hamilton’s action principle: real processes are distinguished from virtual processes by variation of the action integral. For discrete systems, particularly in the realm of conservative Newtonian mechanics, this framework has been rigorously formalised, providing a systematic and universal approach [1]. However, extending this methodology to continuum systems and field theories, for example, Schrödinger’s theory [2], the thermodynamics of irreversible processes [3] or fluid mechanics [4], presents significant challenges. A general prescription for constructing Lagrangians is not well known in such cases, for either non-relativistic or relativistic scenarios.

An early contribution to this area is the work of Lin [5], who showed that a variational principle for ideal compressible flow could be formulated with a Lagrangian density defined as the kinetic energy minus the potential energy. However, it was found that the resulting velocity field cannot be rotational in the case of isentropic flow, implying it to be irrotational. To eliminate this problem, Bateman [6] introduced additional scalar fields, often referred to as Clebsch potentials [7,8,9]. First, proposed by Clebsch in the 1850s, the Clebsch variables prove to be a useful mathematical tool for formulating fluid mechanics within the framework of LF. In fact, Scholle [10], Scholle et al. [11] found a mathematical proof that the Clebsch representation of the velocity field in a Clebsch form is nothing but a compelling consequence of Galilean symmetry and the application of Noether’s theorem to the same: by which densities and current densities of the respective physical observables—namely energy, momentum and mass—are well defined and thus ultimately so too is the flow field, which can be understood as the quotient of momentum density and mass density. The Clebsch formulation therefore results naturally from a canonical framework for describing fluid mechanics in LF. Later, Lin [12] incorporated more scalar fields than those introduced in the work of Bateman [6], which Seliger and Whitham [4]—who applied the Clebsch transformation to many applications within continuum mechanics, but still with the restriction that the flow is inviscid—and Schutz Jr [13] deemed to be redundant, while initially applied to inviscid flows, a generalised Clebsch transformation for viscous fluid mechanics was explored by Scholle and Marner [14] and Cartes and Descalzi [15]. Over time, the Clebsch transformation has found applications in a variety of fields, including electrodynamics [16], magnetohydrodynamics [17], and even quantum theory, particularly in the quantisation of vortex tubes [18].

The question arises as to how the above approaches, in general, and the construction scheme of [10] for Lagrangians with Galilean invariance, can be modified and applied also to relativistic systems that are subject to Lorentz invariance? A first step toward this aim was achieved recently [19] in the field of quantum theory, involving an extension of the scheme developed in [10] to assign a Lorentz-invariant Lagrangian to each Lagrangian with Galilean invariance, and vice versa via simple substitution rules, applicable to a common ’blueprint Lagrangian’. This was exemplified for Schrödinger’s and Klein–Gordon’s (KG) Lagrangians, showing that both form an associated pair, i.e., they can be considered as just two different manifestations—one with Galilean, the other with Lorentz, invariance—of the same blueprint Lagrangian. This remarkable result from quantum theory serves as inspiration with respect to fluid mechanics, forming the main framework of the work reported here. The specific aim was to obtain a Lorentz-invariant Lagrangian density from a known Lagrangian density with Galilean invariance, exemplified through the problem of simple potential flow, Clebsch’s Lagrangian for barotropic flow and finally Seliger and Whitham [4]’s Lagrangian, incorporating thermodynamic effects. While the motivation for this study is the completion of the physical picture, large-scale fluid flows under relativistic conditions do indeed occur, for example, in astrophysical flows such as accretion disks around black holes [20,21,22,23].

This paper is structured as follows: Section 2 provides a brief review of how the concept of associated pairs has been applied previously to quantum theory. In Section 3, this platform concept is modified and advanced for application in the fields of non-relativistic and relativistic fluid mechanics, highlighting the challenges of constructing universal variational formulations. The focus is on formulating velocity normalisation and the eigenvalue relation of the energy–momentum tensor to obtain differential equations for the Lagrangian by leveraging symmetries through Noether’s theorem. In Section 4, the three non-relativistic Lagrangians mentioned above are derived via the respective blueprint form of their associated relativistic counterparts, ensuring consistency between the two. Section 5 consists of a detailed discussion of the findings’ implications, a comparison with the existing literature, potential limitations, and a summary of the key contributions to the field. Conclusions and future perspectives of this work are provided in Section 6.

2. A Short Review of Associated Pairs in Quantum Theory

2.1. General Scheme for Lagrangians Based on Galilean Invariance

In the paper [10] a general scheme for Lagrangians was established via an inverse treatment of Noether’s theorem, starting purely from the requirement of Galilean invariance and the constitutive relation:

$$\overrightarrow{p}=\varrho \overrightarrow{u},$$

(1)

between momentum density $\overrightarrow{p}$ and mass flux density $\overrightarrow{j}=\varrho \overrightarrow{u}$, both Noether observables. Any Lagrangian satisfying Galilean invariance and the equivalence via (1) of momentum density and mass flux density, without loss of generality written in terms of N independent fields, ${\psi }_i=(\varphi ,{\vartheta }^1,\cdots ,{\vartheta }^{N-1})$, is specified according to

$$\ell \left({\psi }_i,{\partial }_t\psi ,\nabla \psi \right)=L\left(\omega ,{\vartheta }^j,\stackrel{\odot }{{\vartheta }^j},\partial {\vartheta }^j\right) ,$$

(2)

as a function L, subsequently termed a blueprint Lagrangian [19], of the following expressions:

$$\begin{array}{cc}\hfill \omega & \to {\displaystyle \frac{\partial \varphi }{\partial t}}+{\displaystyle \frac{1}{2}}{(\nabla \varphi )}^2,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \stackrel{\odot }{{\vartheta }^j}& \to {\displaystyle \frac{\partial {\vartheta }^j}{\partial t}}+\nabla \psi ·\nabla {\vartheta }^j ,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \partial {\vartheta }^j& \to \nabla {\vartheta }^j ,\hfill \end{array}$$

(5)

and invariant with respect to the Galilean group, as well as the fields ${\vartheta }^j$ themselves.

Moreover, although not initially required, the gauge transformation

$$\varphi \to {\varphi }^{\prime }=\varphi -\epsilon ,$$

(6)

with an arbitrary constant $\epsilon$ is a further symmetry, since it has no effect on the expressions (3)–(5) and therefore on the Lagrangian. Since this symmetry is not part of the Galilean group, it is nevertheless a consequence of the same; because the above scheme follows from it, (6) is called the induced gauge transformation. This symmetry is crucial, since it gives rise for the definition of the mass density $\varrho$ and flux density $\varrho \overrightarrow{u}$ via Noether’s theorem as

$$\begin{array}{cc}\hfill \varrho & =-{\displaystyle \frac{\partial L}{\partial \omega }} ,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \varrho \overrightarrow{u}& =\overrightarrow{p}=\varrho \nabla \varphi -\varrho \nabla \varphi -{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{{\vartheta }^j}}}\nabla {\vartheta }^i .\hfill \end{array}$$

(8)

According to (8), the velocity field takes a Clebsch-like form, $\overrightarrow{u}=\nabla \varphi +\left(\cdots \right)\nabla {\vartheta }^i$, automatically.

2.2. Modified Scheme for Relativistic Lagrangians

More recently, the above framework was modified toward encompassing relativistic systems [19] where Lorentz boosts the fundamental symmetry of spacetime in relativistic theories and replaces the Galilei boosts. This is achieved by modifying the substitution rules (3)–(5) for the expressions $\omega$, $\stackrel{\odot }{{\vartheta }^j}$ and $\partial {\vartheta }^j$, streamlining the construction process as follows:

$$\begin{array}{cc}\hfill \omega & \to {\displaystyle \frac{c^2}{2}}-{\displaystyle \frac{1}{2}}{\partial }^{\alpha }\varphi {\partial }_{\alpha }\varphi ,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \stackrel{\odot }{{\vartheta }^j}& \to -{\partial }^{\alpha }\varphi {\partial }_{\alpha }{\vartheta }^j ,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \partial {\vartheta }^j& \to \left\{\begin{array}{cc}{\partial }_{\nu }{\vartheta }^j ,\hfill & \mathrm{covariant} \mathrm{use}\hfill \\ -{\partial }^{\nu }{\vartheta }^j ,\hfill & \mathrm{contravariant} \mathrm{use}\hfill \end{array}\right. ,\hfill \end{array}$$

(11)

where $(+,-,-,-)$ is used as a metric signature. Note that the Lagrangian resulting from the above substitutions is a Lorentz-scalar. Since it also has no explicit dependence on the coordinates $x^{\alpha }$ it is, more generally, Poincaré-invariant.

As a result of the above adjustments, (9)–(11), the analytical calculation formulae for the Noether observables also change compared to the Galilean case: with respect to the induced gauge transformation (6), which remains a symmetry of the Lagrangian in the relativistic case also, the particle current density is obtained as

$$j^{\mu }={\displaystyle \frac{\partial L}{\partial \omega }}{\partial }^{\mu }\varphi +{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{{\vartheta }^j}}}{\partial }^{\mu }{\vartheta }^j ,$$

(12)

while with respect to space–time translations $x^{\mu }\to {x\prime }^{\mu }=x^{\mu }+{\epsilon }^{\mu }$ the energy–momentum tensor becomes

$$T^{\mu \nu }={\displaystyle \frac{\partial L}{\partial \left({\partial }_{\mu }{\vartheta }^j\right)}}{\partial }^{\nu }{\vartheta }^j-{\partial }^{\mu }\varphi j^{\nu }-{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{{\vartheta }^j}}}{\partial }^{\mu }{\vartheta }^j{\partial }^{\nu }\varphi -{\eta }^{\mu \nu }L .$$

(13)

In contrast to the Galilean case, where the identity $\overrightarrow{p}=\varrho \overrightarrow{u}$ is an automatic outcome of the Lagrangian’s analytic form, there is no obvious relationship between the particle current density (12) and the energy–momentum tensor (13) in the relativistic case.

Thus, starting from a blueprint Lagrangian $L\left(\omega ,{\vartheta }^j,\stackrel{\odot }{{\vartheta }^j},\partial {\vartheta }^j\right)$, a pairing of two Lagrangians can be generated, one with Galilean invariance from utilising the substitution rules (3)–(5), the other one with Poincaré invariance from utilising the substitution rules (9)–(11), as illustrated schematically in Figure 1.

2.3. Application to Schrödinger and KG Theory

To exemplify the use of the above methodical approach, the following result from [19] is reviewed. Consider Schrödinger’s Lagrangian for a free particle [24]:

$$\ell \left(\psi ,\overline{\psi },\partial \psi ,\partial \overline{\psi }\right)={\displaystyle \frac{\hslash }{2\mathrm{i}}}\left(\psi {\partial }_t\overline{\psi }-\overline{\psi }{\partial }_t\psi \right)-{\displaystyle \frac{{\hslash }^2}{2m}}\nabla \psi ·\nabla \overline{\psi } ,$$

(14)

in terms of the state function $\psi$ and its complex conjugate, $\overline{\psi }$. By applying polar decomposition to the complex state function,

$$\psi =\sqrt{{\displaystyle \frac{\varrho }{m}}}exp\left(\mathrm{i}{\displaystyle \frac{m}{\hslash }}\varphi \right) , \overline{\psi }=\sqrt{{\displaystyle \frac{\varrho }{m}}}exp\left(-\mathrm{i}{\displaystyle \frac{m}{\hslash }}\varphi \right) ,$$

(15)

the so-called Madelung picture [25] is established as an alternative form, also known as the hydrodynamic picture of quantum theory:

$$\ell =-\varrho \left[{\displaystyle \frac{\partial \varphi }{\partial t}}+{\displaystyle \frac{1}{2}}{\left(\nabla \varphi \right)}^2\right]-{\displaystyle \frac{{\hslash }^2}{8m^2}}{\displaystyle \frac{{\left(\nabla \varrho \right)}^2}{\varrho }} .$$

(16)

By identifying the equivalent three expressions, (3)–(5), in the above Lagrangian, its blueprint form is determined straight-forwardly as

$$L\left(\omega ,\varrho ,\partial \varrho \right)=-\varrho \omega -{\displaystyle \frac{{\hslash }^2}{8m^2}}{\displaystyle \frac{{\left(\partial \varrho \right)}^2}{\varrho }} .$$

(17)

Conversely, by applying the replacement rules, (9)–(11), to the blueprint Lagrangian (17), the Poincaré invariant Lagrangian

$$\ell ={\displaystyle \frac{1}{2}}\varrho {\partial }^{\alpha }\varphi {\partial }_{\alpha }\varphi +{\displaystyle \frac{{\hslash }^2}{8m^2}}{\displaystyle \frac{{\partial }^{\alpha }\varrho {\partial }_{\alpha }\varrho }{\varrho }}-{\displaystyle \frac{\varrho c^2}{2}}$$

(18)

is obtained. By inversion of transformation (15), a corresponding form in terms of a complex state function $\psi$ and its complex conjugate results:

$$\ell ={\displaystyle \frac{{\hslash }^2}{2m}}{\partial }^{\alpha }\overline{\psi }{\partial }_{\alpha }\psi -{\displaystyle \frac{m{c}^2}{2}}\overline{\psi }\psi ,$$

(19)

which is obviously the Klein–Gordon Lagrangian [26], apart from a factor of 2.

The above framework, successfully applied to quantum mechanics, identifies the Schrödinger and the Klein–Gordon (KG) Lagrangians as an associated pair of non-relativistic and relativistic Lagrangians, respectively [19].

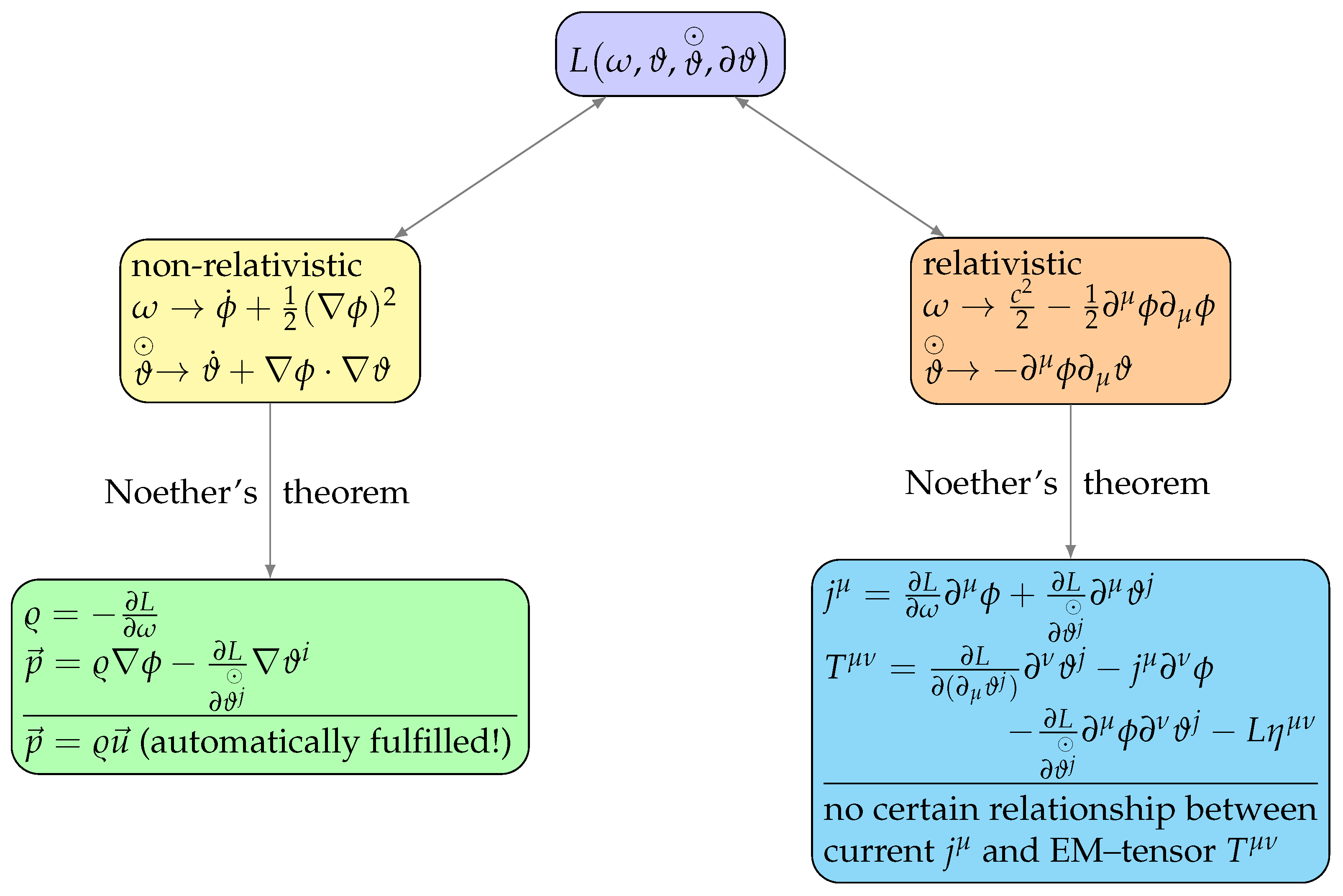
3. Methodical Approach for Fluid Mechanics

3.1. Motivation

One obvious potential use of the above methodology is to identify an as yet unknown conjugate counterpart to a known Lagrangian with either Galilean or Lorentz invariance. In this sense, the focus of this paper is on the Lagrangian proposed by Seliger and Whitham [4] for inviscid, compressible fluid flow, without heat conduction, which in the general scheme (2) is, according to [10], given by the following blueprint form:

$$\begin{array}{c}\hfill L=-mn\left[\omega +\alpha \stackrel{\odot }{\beta }-s\stackrel{\odot }{\vartheta }+{\displaystyle \frac{1}{2}}{\left(\alpha \nabla \beta -s\nabla \vartheta \right)}^2-e(n,s)\right] ,\end{array}$$

(20)

in terms of the Clebsch variables $\alpha ,\beta$, the specific entropy s and another potential field $\vartheta$, termed the thermasy [27] the material time derivative of which is the temperature. The aim is to build on the foundational contributions of [10,19] and identify a relativistic counterpart to this well-known classical, non-relativistic, Lagrangian. However, a direct application of the methodology from [19] can be used by applying the transformation rules to (20), would not achieve the intended outcome. Unlike in quantum mechanical systems such as the Klein–Gordon theory, where charge flux rather than matter flux is considered, fluid mechanics imposes additional constraints: in the case of Galilean invariance, the momentum density resulting from Noether’s theorem must coincide with Noether’s mass flux density according to (1), which is automatically fulfilled by the scheme (2).

In relativistic fluid mechanics, the conventional approach, which primarily relies on the energy-momentum tensor [28,29], is not entirely rigorous, as the definition of an energy-momentum tensor assumes the existence of an explicit Lagrangian density. Also, current relativistic fluid approaches typically use Lagrange multipliers to incorporate the mass conservation, velocity normalisation and form of the perfect fluid energy–momentum tensor. Alternatively, these constraints are incorporated when taking variations of the Lagrangian to obtain the Euler–Lagrange equations, or a combination of both methods is used [30,31,32,33,34]. In contrast, the approach here is to integrate these vital physical constraints directly into the Lagrangian formulation, by deriving the Lagrangian using an inverse Noether approach, constructed based on the required conservation laws and symmetries. By formulating the eigenvalue relation for the energy–momentum tensor and its associated eigenvector velocity, a more consistent and fundamental connection between the energy–momentum tensor and the Lagrangian density is established. The constitutive relation (1) is replaced by the eigenvalue relationship:

$$\begin{array}{c}\hfill T^{\mu \nu }{U}_{\nu }=n(m{c}^2+e)U^{\mu } ,\end{array}$$

(21)

associated with the energy–momentum tensor $T_{\mu \nu }$, with the velocity $U^{\nu }$ as its associated eigenvector and the eigenvalue $n(m{c}^2+e)$, which corresponds to the energy density as measured in the rest frame of the fluid [35,36,37].

Physically, this ensures that the flow of energy–momentum along the direction of the fluid’s 4-velocity is consistent with the system’s dynamics and that thermodynamic principles are respected. Thermodynamic properties, such as pressure and density, are encoded in the energy–momentum tensor. Without condition (21), the energy–momentum tensor could describe arbitrary distributions that are physically inconsistent with the flow of matter, or violate causality. Additionally, a normalisation condition on the velocity, $U^{\mu }{U}_{\mu }=1$, is introduced to preserve the invariant spacetime interval, maintain proper time parametrisation, and enforce causality.

The outcome is a novel method for constructing Lagrangians that preserve both non-relativistic and relativistic correspondences. In order to address the above-mentioned shortcomings, the framework is generalised by introducing c as an additional parameter in the blueprint Lagrangian, which replaces the following:

$$L=L\left(\omega ,{\vartheta }^j,\stackrel{\odot }{{\vartheta }^j},\partial {\vartheta }^j\right) ,$$

by the more general form:

$$L=L\left(\omega ,{\vartheta }^j,\stackrel{\odot }{{\vartheta }^j},\partial {\vartheta }^j;c\right) ,$$

such that the limit $c\to \infty$ exists and delivers the Galilean blueprint form. The generalised approach derives the analytical structure of the Lagrangian from first principles by leveraging symmetries and the inverse Noether theorem. The translation invariance is employed to obtain the canonical energy–momentum tensor, while the “induced gauge” symmetry (6) is used to define the particle density and the canonical velocity. Noether’s theorem [38] assigns to each parameter of a symmetry of the Lagrangian is represented by a Lie group, a homogeneous balance equation. Moreover, the conservation equation related to the induced gauge takes the following form for Lagrangians represented by the general scheme (2):

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \varrho }{\partial t}}+\nabla ·\overrightarrow{j}=0 ,\end{array}$$

(22)

where $j^{\alpha }=-{\displaystyle \frac{\partial \mathcal{L}}{\partial \left({\partial }_{\alpha }\varphi \right)}},$ mass flux density $\overrightarrow{j}=(j^1,j^2,j^3)$, with the mass density given by $\varrho ={\displaystyle \frac{j^0}{c}}$. Following the established relativity theory, the mass density is expressed as $\varrho =mn$, where n and m are the particle density and rest mass, respectively.

3.2. The Canonical Velocity and Normalisation

Considering that the square of the norm of the canonical particle current density (12) gives

$$j^{\mu }{j}_{\mu }={\left(mn\right)}^2{u}^{\mu }{u}_{\mu }={\left(mn\right)}^2 ,$$

where the second equality uses the following normalisation: $u^{\mu }{u}_{\mu }=1$. By defining the canonical velocity as

$$\begin{array}{c}\hfill U^{\mu }:={\displaystyle \frac{j^{\mu }}{c\sqrt{j^{\mu }{j}_{\mu }}}} ,\end{array}$$

(23)

it is automatically normalised. Alternatively, in terms of the variables given by Equations (9) and (10), we have

$$U^{\mu }=-{\displaystyle \frac{1}{cnm}}\left({\displaystyle \frac{-\partial L}{\partial \omega }}{\partial }^{\mu }\varphi -{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{{\vartheta }_j}}}{\partial }^{\mu }{\vartheta }_j\right) .$$

(24)

For the analysis of compressible flow, the Lagrangian is simplified by assuming it does not depend on density gradients: ${\displaystyle \frac{\partial \ell }{\partial \left({\partial }_{\mu }n\right)}}=0$. This approach is consistent with non-relativistic, fluid mechanics formulations, such as [4,39,40,41]. An overview of the extended framework is illustrated schematically in Figure 2.

Compared to the framework for quantum theories in Figure 1, the differences are outlined as follows: (i) the normalisation condition for the velocity, (ii) the eigenvalue relationship, (iii) the explicit dependence of the blueprint Lagrangian on c, and (iv) the consideration of the gauge symmetry of the Clebsch variables. The latter is explained in detail in Section 4.2.2.

4. Results

To demonstrate the utility and ease of use of the analysis established in Section 3, three fluid mechanics examples of increasing complexity are considered below.

4.1. A Potential Flow Lagrangian

The aim is to construct a Lagrangian for potential flow that is $u^{\alpha }={\partial }^{\alpha }\varphi$, which satisfies (24), (21) and is Poincaré-invariant. In the case of potential flow, $L=L({\partial }^{\mu }\varphi ,mn)$. The standardised normalised velocity $U^{\mu }$ is initially assumed to be

$$U^{\mu }={\displaystyle \frac{-{\partial }^{\mu }\varphi }{\mid \partial \varphi \mid }}={\displaystyle \frac{-{\partial }^{\mu }\varphi }{\sqrt{{\partial }_{\alpha }\varphi {\partial }^{\alpha }\varphi }}}={\displaystyle \frac{-{\partial }^{\mu }\varphi }{\sqrt{c^2-2\omega }}} .$$

(25)

Equating the above to (24), since it is common in relativistic formulations to assume the canonical velocity equals the physical velocity (and the same with the energy–momentum tensor), gives

$$U^{\mu }=-{\displaystyle \frac{{\partial }^{\mu }\varphi }{\sqrt{c^2-2\omega }}}=-\left(-{\displaystyle \frac{1}{nmc}}{\displaystyle \frac{\partial L}{\partial \omega }}{\partial }^{\mu }\varphi \right) ,$$

which, when integrating with respect to $\omega$, leads to

$$L=nmc\sqrt{c^2-2\omega }+L_1\left(mn\right) ,$$

with an integration function $L_1\left(mn\right)$ to be determined. The latter is achieved via the eigenvalue relationship (21). The canonical energy–momentum tensor (13) results in

$$T^{\mu \nu }=mnc\sqrt{{\partial }_{\gamma }\varphi {\partial }^{\gamma }\varphi }\left[U^{\mu }{U}^{\nu }-{\eta }^{\mu \nu }\right]-L_1\left(mn\right){\eta }^{\mu \nu } ,$$

(26)

and the associated eigenvalue relationship (21) yields, considering the normalisation of velocity, the following:

$$-L_1\left(mn\right)U^{\mu }=n\left(m{c}^2+e\left(n\right)\right)U^{\mu } ,$$

(27)

thus implying

$$\begin{array}{c}\hfill f\left(mn\right)=-n\left(m{c}^2+e\left(n\right)\right) .\end{array}$$

(28)

Therefore, the blueprint Lagrangian for a potential flow results in

$$L=mnc\sqrt{c^2-2\omega }-n\left(m{c}^2+e\left(n\right)\right) .$$

(29)

The individual form of the inner energy per particle, $e\left(n\right)$, is subject to thermodynamic considerations and not discussed here. The non-relativistic limit and its interpretation, along with the physical significance of the terms, are discussed as part of the third example investigated subsequently, since the limit can be obtained as a simplified case of the latter.

4.2. Barotropic Inviscid Flow in Clebsch Variables

The Clebsch formulation for baratropic flow, in its simplest form, excludes thermodynamic effects, such as variations in entropy, and provides a useful stepping stone to the ultimate example considered.

4.2.1. Initial Assumptions and Integration

The Lagrangian presented here is constructed to respect the symmetries (24), (21), to be Poincaré-invariant. Additionally, it is required of the Lagrangian that it satisfies the Clebsch gauge conditions, specified below in Section 4.2.2. Extending the variables which describe the velocity from $\varphi$ to incorporate the Clebsch variables, $\alpha$ and $\beta$, the Lagrangian can be expressed as a function of the following variables:

$$\begin{array}{c}\hfill \ell (\varphi ,\partial \varphi ,\alpha ,\beta ,\partial \beta ,mn)=L(\omega ,\alpha ,\beta ,\stackrel{\odot }{\beta },\partial \beta ,mn) ,\end{array}$$

(30)

since in the Clebsch parametrisation it is often assumed that the gradient of one of the conjugate variables vanishes, it has been taken here that ℓ has no dependence on $\partial \alpha$. The velocity expression, (24) becomes

$$\begin{array}{c}\hfill U^{\mu }=-{\displaystyle \frac{1}{cmn}}\left(-{\displaystyle \frac{\partial L}{\partial \omega }}{\partial }^{\mu }\varphi -{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{\beta }}}{\partial }^{\mu }\varphi \right) .\end{array}$$

(31)

The starting assumed form of $U^{\mu }$ for the standardised, normal velocity is

$$\begin{array}{c}\hfill U^{\mu }={\displaystyle \frac{-\left({\partial }^{\mu }\varphi +\alpha {\partial }^{\mu }\beta \right)}{\sqrt{\left({\partial }^{\alpha }\varphi +\alpha {\partial }^{\alpha }\beta \right)\left({\partial }_{\alpha }\varphi +\alpha {\partial }_{\alpha }\beta \right)}}} .\end{array}$$

(32)

Using (9) and (10), the term in the denominator of the above can be expressed as:

$$\left({\partial }_{\lambda }\varphi +\alpha {\partial }_{\lambda }\beta \right)\left({\partial }^{\lambda }\varphi +\alpha {\partial }^{\lambda }\beta \right)=c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta ,$$

(33)

and Equation (32) becomes

$$U^{\mu }=-{\displaystyle \frac{{\partial }^{\mu }\varphi +\alpha {\partial }^{\mu }\beta }{\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }}} .$$

(34)

Equating (34) and (31) gives

$$\begin{array}{c}\hfill -{\displaystyle \frac{{\partial }^{\mu }\varphi +\alpha {\partial }^{\mu }\beta }{\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }}}={\displaystyle \frac{1}{cnm}}\left({\displaystyle \frac{\partial L}{\partial \omega }}{\partial }_{\mu }\varphi +{\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{\beta }}}{\partial }_{\mu }\beta \right) .\end{array}$$

(35)

Since ${\partial }^{\mu }\varphi$ and ${\partial }^{\mu }\beta$ are 4-gradients of independent fields, the above equation implies the following two identities via a comparison of coefficients:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial L}{\partial \omega }}& =-{\displaystyle \frac{mnc}{\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }}} ,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial L}{\partial \stackrel{\odot }{\beta }}}& =-{\displaystyle \frac{mnc\alpha }{\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }}} ,\hfill \end{array}$$

(37)

and the solution of which is obviously

$$L=mnc\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }+L_2\left(\alpha ,\beta ,\partial \beta ,mn\right) ,$$

(38)

with an integration function $L_2\left(\alpha ,\beta ,\partial \beta ,mn\right)$. In order to determine the latter, additional considerations regarding the gauge symmetry of the Clebsch variables are required (see the grey box in Figure 2), which are set out below.

4.2.2. Gauge Condition

In addition to the Poincaré group and the induced gauge symmetry, the Lagrangian has to be invariant with respect to the symmetry group of Clebsch variables’ gauge conditions. The analysis is based on Schönberg [42]’s finding for the Clebsch transformation $\overrightarrow{u}=\nabla \varphi +\alpha \nabla \beta$ of the classical velocity field, namely that this potential representation is not unique because one can redefine $\varphi ,\alpha$ and $\beta$ using the following transformations:

$$\begin{array}{cc}\hfill \varphi & \to \varphi +f(\alpha ,\beta ) ,\hfill \\ \hfill \alpha & \to g(\alpha ,\beta ) ,\hfill \\ \hfill \beta & \to h(\alpha ,\beta ) ,\hfill \end{array}$$

(39)

leading to an identical velocity field if and only if the following differential equations are satisfied [42]:

$${\displaystyle \frac{\partial f}{\partial \beta }}+g{\displaystyle \frac{\partial h}{\partial \beta }}=\alpha ,$$

(40)

$${\displaystyle \frac{\partial f}{\partial \alpha }}+g{\displaystyle \frac{\partial h}{\partial \alpha }}=0 .$$

(41)

Note that as long as the velocity field of classical physics is considered, the three functions $f,g,h$ should also depend explicitly on time. However, since this would obviously lead to problems with the relativistic formulation, this is ruled out from the outset.

The analysis is directed at how the above transformation acts on the Lagrangian (38), particularly focusing on the key term, as follows:

$$\begin{array}{cc}\hfill {\partial }_{\lambda }\varphi +\alpha {\partial }_{\lambda }\beta \to & {\partial }_{\lambda }\left[\varphi +f(\alpha ,\beta )\right]+g(\alpha ,\beta ){\partial }_{\lambda }h(\alpha ,\beta )\hfill \\ & ={\partial }_{\lambda }\varphi +{\displaystyle \frac{\partial f}{\partial \alpha }}{\partial }_{\lambda }\alpha +{\displaystyle \frac{\partial f}{\partial \beta }}{\partial }_{\lambda }\beta +g\left[{\displaystyle \frac{\partial h}{\partial \alpha }}{\partial }_{\lambda }\alpha +{\displaystyle \frac{\partial h}{\partial \beta }}{\partial }_{\lambda }\beta \right] ,\hfill \\ & ={\partial }_{\lambda }\varphi +\underset{\alpha }{\underbrace{\left[{\displaystyle \frac{\partial f}{\partial \beta }}+g{\displaystyle \frac{\partial h}{\partial \beta }}\right]}}{\partial }_{\lambda }\beta +\underset{0}{\underbrace{\left[{\displaystyle \frac{\partial f}{\partial \alpha }}+g{\displaystyle \frac{\partial h}{\partial \alpha }}\right]}}{\partial }_{\lambda }\alpha ,\hfill \end{array}$$

recognising that the latter is invariant. As a consequence of this and Equation (33), the expression $c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta$ under the root sign of the Lagrangian (38) is also invariant and therefore the entire first term in (38). Thus, the same gauge transformation applies in the relativistic case as in the non-relativistic one.

For the overall invariance of the Lagrangian (38), the second term $L_2\left(\alpha ,\beta ,\partial \beta ,mn\right)$ must also be invariant in its own right, as follows:

$$L_2\left(h\left(\alpha ,\beta \right),g\left(\alpha ,\beta \right),{\displaystyle \frac{\partial h}{\partial \alpha }}\partial \alpha +{\displaystyle \frac{\partial h}{\partial \alpha }}\partial \beta ,mn\right)=L_2\left(\alpha ,\beta ,\partial \beta ,mn\right) .$$

(42)

By taking the derivative of above gauge condition with respect to $\partial \alpha$, $\partial L_2/\partial (\partial \beta )=0$ eventually follows. Therefore, $L_2=L_2\left(\alpha ,\beta ,mn\right)$. Since, obviously, no pure algebraic combination of $\alpha$ and $\beta$ can be invariant with respect to the above gauge group, the conclusion is

$$L_2=L_2\left(mn\right) .$$

(43)

Note that the fulfilment of the gauge symmetry guarantees the equations of motion and the physical observables, such as the velocity and energy–momentum tensor, which are also invariant with respect to the gauge transformation of Clebsch variables.

4.2.3. Eigenvalue Relationship and Solution

According to (13), the energy–momentum tensor for the Lagrangian (38), with reference to (43), reads

$$T^{\mu \nu }=nmc\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta } \left[U^{\mu }{U}^{\nu }-{\eta }^{\mu \nu }\right]-{\eta }^{\mu \nu }{L}_2\left(mn\right) ,$$

(44)

and the eigenvalue relationship (21) takes the same form (27) as in case of potential flow analysed above, implying the following:

$$L_2\left(mn\right)=-n\left(m{c}^2+e\left(n\right)\right) ,$$

and, therefore, the final form of the Lagrangian is

$$\begin{array}{c}\hfill L=nmc\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+{\alpha }^2{\partial }_{\lambda }\beta {\partial }^{\lambda }\beta }-n\left(m{c}^2+e\left(n\right)\right) .\end{array}$$

(45)

The non-relativistic limit of the above, its interpretations, and the physical significance of terms, are discussed together with analysis of the more general example explored below.

4.3. A Lagrangian for Thermo-Fluid Dynamics

Here, thermal degrees of freedom are included by the introduction of an additional pair of variables, entropy, s, and thermasy $\vartheta$. In [43], thermasy was considered as entering the Lagrangian via a Lagrange multiplier corresponding to the entropy–conservation constraint. The term thermasy was coined by [27], as the material time integral of the temperature T: ${\displaystyle \frac{D}{t}}\vartheta =T$. With these additional two variables, the Lagrangian is a function of $L(\omega ,\alpha ,\beta ,\stackrel{\odot }{\beta },\partial \beta ,\stackrel{\odot }{\vartheta },\partial \vartheta ,s,mn)$. Even without modelling heat conduction or dissipation, the inclusion of entropy and thermasy in the Lagrangian enables the description of isentropic but thermodynamically influenced flows. These are flows where the entropy of each fluid element remains constant along its trajectory, while different fluid elements can have varying entropy values. Therefore, thermal effects can still impact the flow through baroclinic pressure–density relationships that depend on entropy, and internal energy changes are accounted for. As was the case with $\alpha$, s is treated in a similar way in that it is assumed that ${\displaystyle \frac{\partial L}{\partial \left({\partial }_{\mu }s\right)}}=0$. The assumed form of $U^{\mu }$ for the standardised, normalised velocity is

$$\begin{array}{cc}\hfill U^{\mu }=& {\displaystyle \frac{-\left({\partial }^{\mu }\varphi +\alpha {\partial }^{\mu }\beta -s{\partial }^{\mu }\vartheta \right)}{\sqrt{\left({\partial }^{\alpha }\varphi +\alpha {\partial }^{\alpha }\beta -s{\partial }^{\alpha }\vartheta \right)\left({\partial }_{\alpha }\varphi +\alpha {\partial }_{\alpha }\beta -s{\partial }_{\alpha }\vartheta \right)}}} .\hfill \end{array}$$

(46)

Note that using Equations (9) and (10) leads to

$$\begin{array}{cc}\hfill \left({\partial }^{\alpha }\varphi +\alpha {\partial }^{\alpha }\beta -s{\partial }^{\alpha }\vartheta \right)& \left({\partial }_{\alpha }\varphi +\alpha {\partial }_{\alpha }\beta -s{\partial }_{\alpha }\vartheta \right)\hfill \\ & =-(2\omega -c^2+2\alpha \stackrel{\odot }{\beta }-{\alpha }^2{\partial }_{\nu }\beta {\partial }^{\nu }\beta -s^2{\partial }_{\nu }\vartheta {\partial }^{\nu }\vartheta -2s\stackrel{\odot }{\vartheta })+2\alpha s{\partial }_{\nu }\beta {\partial }^{\nu }\vartheta \hfill \\ & =c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+2s\stackrel{\odot }{\vartheta }+\left(\alpha {\partial }^{\mu }\beta -s{\partial }^{\mu }\vartheta \right)\left(\alpha {\partial }_{\mu }\beta -s{\partial }_{\mu }\vartheta \right) ,\hfill \end{array}$$

Equation (46) can be expressed as

$$\begin{array}{cc}\hfill U^{\mu }=& {\displaystyle \frac{-\left({\partial }^{\mu }\varphi +\alpha {\partial }^{\mu }\beta -s{\partial }^{\mu }\vartheta \right)}{\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+2s\stackrel{\odot }{\vartheta }+\left(\alpha {\partial }^{\mu }\beta -s{\partial }^{\mu }\vartheta \right)\left(\alpha {\partial }_{\mu }\beta -s{\partial }_{\mu }\vartheta \right)}}} .\hfill \end{array}$$

(47)

Since the mathematical problem to be solved here corresponds largely to that of the previous Section 4.2, except for an additional pair of fields, the following steps are essentially the same as before. For details, see Appendix A.1. The resulting Lagrangian is shown as follows:

$$\begin{array}{c}L=nmc\sqrt{c^2-2\omega -2\alpha \stackrel{\odot }{\beta }+2s\stackrel{\odot }{\vartheta }+\left(\alpha {\partial }^{\mu }\beta -s{\partial }^{\mu }\vartheta \right)\left(\alpha {\partial }_{\mu }\beta -s{\partial }_{\mu }\vartheta \right)}\hfill \\ -n\left(m{c}^2+e(n,s)\right) ,\hfill \end{array}$$

(48)

has a similar structure to the examples discussed above, fulfilling all requirements, particularly the eigenvalue relationship and gauge invariance. In contrast to the barotropic example outlined before, the inner energy per particle is a function of both n and s (baroclinic flow). Its individual form is subject to thermodynamics.

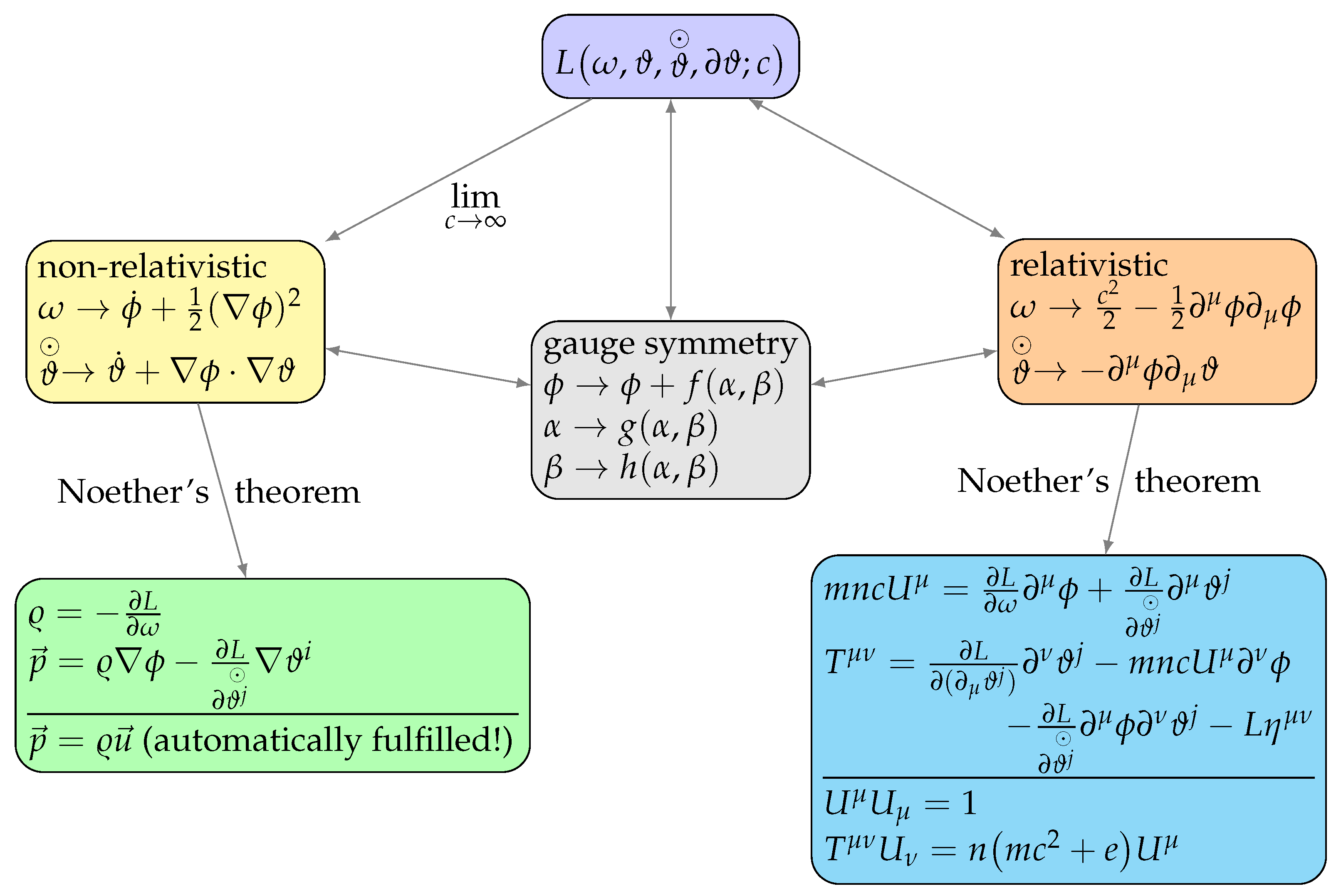
4.4. Non-Relativistic Limit

The non-relativistic limit, $c\to \infty$, is now taken to ensure that the Lagrangian behaves consistently. By factoring out $c^2$ and using a Taylor expansion in the form of $\sqrt{1+x}\approx 1+{\displaystyle \frac{x}{2}}$, since all terms divided by $c^2$ are small, the first term in the Lagrangian can be approximated as

$$\begin{array}{cc}\hfill L& =nm{c}^2\sqrt{1-2{\displaystyle \frac{\omega }{c^2}}-2{\displaystyle \frac{\alpha }{c^2}}\stackrel{\odot }{\beta }+2{\displaystyle \frac{s}{c^2}}\stackrel{\odot }{\vartheta }+{\displaystyle \frac{1}{c^2}}\left(\alpha {\partial }_{\nu }\beta -s{\partial }_{\nu }\vartheta \right)\left(\alpha {\partial }^{\nu }\beta -s{\partial }^{\nu }\vartheta \right)}-n\left(m{c}^2+e(n,s)\right)\hfill \\ & \approx nm{c}^2\left[1-{\displaystyle \frac{\omega }{c^2}}-{\displaystyle \frac{\alpha \stackrel{\odot }{\beta }}{c^2}}+{\displaystyle \frac{s\stackrel{\odot }{\vartheta }}{c^2}}+{\displaystyle \frac{1}{2c^2}}\left(\alpha {\partial }_{\nu }\beta -s{\partial }_{\nu }\vartheta \right)\left(\alpha {\partial }^{\nu }\beta -s{\partial }^{\nu }\vartheta \right)\right]-n\left(m{c}^2+e(n,s)\right) .\hfill \end{array}$$

Now, writing out the four-derivative ${\partial }^{\nu }\varphi {\partial }_{\nu }\varphi ={\displaystyle \frac{1}{c^2}}{\left({\partial }_t\varphi \right)}^2-{(\nabla \varphi )}^2$ in the non-relativistic limit leads to ${\partial }^{\nu }\varphi {\partial }_{\nu }\varphi \to -{(\nabla \varphi )}^2.$ Substituting this into the above expression gives

$$\begin{array}{cc}\hfill L& \approx nm{c}^2\left(1-{\displaystyle \frac{\omega }{c^2}}-{\displaystyle \frac{\alpha \stackrel{\odot }{\beta }}{c^2}}+{\displaystyle \frac{s\stackrel{\odot }{\vartheta }}{c^2}}+{\displaystyle \frac{\alpha s\nabla \beta \nabla \vartheta }{c^2}}-{\displaystyle \frac{{\alpha }^2{(\nabla \beta )}^2}{2c^2}}-{\displaystyle \frac{s^2{\partial }_{\nu }\vartheta {\partial }^{\nu }\vartheta }{2c^2}}\right)\hfill \\ & -n\left(m{c}^2+e(n,s)\right)\hfill \\ & =-mn\left[\omega +\alpha \stackrel{\odot }{\beta }-s\stackrel{\odot }{\vartheta }+{\displaystyle \frac{1}{2}}{\left(\alpha \nabla \beta -s\nabla \vartheta \right)}^2-e(n,s)\right] ,\hfill \end{array}$$

(49)

and, therefore, we obtain the reproduction of the Galilean blueprint form (20) of Seliger and Whitham [4]’s Lagrangian. This confirms that in the non-relativistic limit, the Lagrangian reduces appropriately to a kinetic term and an internal energy term, with the rest energy naturally being cancelled out. This is in agreement with [4], confirming that the two Lagrangians form an associated pair, supporting the validity of the methodology. Naturally, the same holds for the Clebsch parametrisation case, obtained by setting $\vartheta ,s=0$, as well as for the potential velocity case, where $\alpha ,\beta =0$, with both recovering their expected non-relativistic counterparts.

5. Discussion

The results obtained demonstrate the efficacy of the approach adopted across three important cases: (1) potential flow, (2) barotropic flow with Clebsch variable parametrisations, and (3) thermodynamically influenced flows. This highlights the adaptability of the methodology. Notably, the inclusion of entropy and thermal variables enriches the description to allow thermodynamic effects to be catered for. In Lagrangian formulations for phenomenological or thermodynamic systems, extremising an entropy functional [44,45,46,47,48] is a common method, with quantities like entropy being typically treated as external variables or introduced in an ad hoc manner. The approach worked out here, however, provides a more unified and dynamic description, incorporating these quantities intrinsically into the system’s dynamics.

Comparisons to earlier work confirm that the Lagrangians derived here recover their non-relativistic counterparts in the appropriate limits $c\to \infty$. For a more thorough investigation, the stability of the dynamics associated with the Lagrangians can be analysed, including the impact of the energy term $e(n,s)$, the analytical form of which is subject to thermodynamics and not discussed here. The variational approach facilitates a stability analysis, as a second-order expansion of the Lagrangian for potential flow (as shown in [49] for a non-relativistic potential flow), where the compression modulus,

$$K:=n^2\left[2{\displaystyle \frac{\partial e}{\partial n}}+n{\displaystyle \frac{{\partial }^{2}e}{\partial n^2}}\right] ,$$

as a decisive quantity, has to be positive to guarantee the stability of fluid flow. This analysis can easily be extended from non-relativistic to the relativistic Lagrangians considered here, both for barotropic Clebsch and thermodynamic Lagrangian cases.

The preservation of Poincaré invariance, induced gauge invariance, and, in Section 4.2, Clebsch gauge invariance emphasises the robustness of the models, while the conservation of induced gauge and Poincaré invariance might initially appear trivial—given that the energy–momentum tensor is derived under Poincaré symmetry constraints and the canonical velocity comes from the induced gauge framework—the non-trivial aspect lies in how these invariances are maintained when the coupled differential equations are solved. In a similar manner, the Clebsch gauge symmetry—although not being a Lie symmetry and therefore not being subject of Noether’s theorem—is associated with Helmholtz’s conservation equation for vorticity [50], which is the local form of Kelvin’s circulation theorem [51,52] and implies that in an ideal fluid, the circulation around a closed loop moving with the fluid remains constant. By demonstrating that the final Lagrangians fulfil these symmetries, the reliability of the methodology is firmly established.

Furthermore, it is noted that, in the literature, different signs in front of the Clebsch differential form are used for representing velocity. The motivation for choosing the negative sign in the representations (25), (32) and (46) of the velocity was to recover their non-relativistic counterparts, $\overrightarrow{u}=\nabla \varphi$, $\overrightarrow{u}=\nabla \varphi +\alpha \nabla \beta$ and $\overrightarrow{u}=\nabla \varphi +\alpha \nabla \beta -s\nabla \vartheta$, respectively. These findings align with prior work, particularly the results of [53], lending further credence to the presented framework.

6. Conclusions

A systematic approach for constructing relativistic Lagrangians that are associated counterparts to their non-relativistic equivalents was derived. By addressing key challenges in extending non-relativistic formulations—such as the requirement of velocity normalisation and the eigenvalue relation of the energy-momentum tensor, which constrain the form Lagrangians can take—this work introduced a novel and systematic framework, extending the methodology proposed by [10,19]. These two conditions, by modifying the eigenvalue appropriate to the system in (21), provide generalised, universal criteria for constructing relativistic Lagrangians concerned with a system describing matter flux. It is also highly advantageous in that, in contrast to traditional methods where canonical quantities are used as mathematical tools, all canonical quantities (mass flux/velocity and the energy–momentum tensor) in the paper were inherently tied to Noether’s theorem, giving them a clear physical significance. They were built into the methodology of constructing the Lagrangian via an inverse Noether procedure. Therefore, velocity normalisation, the form of the energy–momentum tensor, mass conservation, and symmetry of the induced gauge do not need to be treated separately, as is often the case in much of the literature. This makes the approach more systematic and universal. It not only improves the construction of Lagrangians in relativistic contexts but also provides a deeper insight into the interplay between symmetries, momentum densities, and the structure of relativistic theories.

The present framework assumes inviscid and non-dissipative conditions, simplifying the analysis in a first approach but limiting direct applicability to systems where viscosity is significant. Viscous forces become important where the gathering of mass due to gravity occurs, for example, in accretion discs [54,55]. Similarly, a combination of both viscous and relativistic effects arises in such discs around neutron stars and black holes [20,21,23,56]. Nevertheless, the methodology remains structurally unchanged even in such cases, as shown in Appendix A.2, for the eigenvalue relation associated with dissipative effects. Gravitational effects naturally enter through the metric, which is already incorporated in the canonical energy–momentum tensor and velocity normalisation condition. Thus, the methodology does not require modification for curved backgrounds, specifying the appropriate metric suffices. Coupling to additional fields (for example, electromagnetic or scalar) may alter the energy–momentum tensor eigenvalue relationship but does not affect the underlying formulation of obtaining differential equations for the Lagrangian by the canonical velocity and using the energy–momentum tensor relation by an inverse application of Noether’s theorem. One conceivable problem could be shock waves in hypersonic flows, as these call the continuity of the fields into question. To address this problem, however, an approach is shown in [19,57] as to how discontinuous phenomena can also be treated in LF, which is an advantageous feature compared to the usual formulation of fluid mechanics in terms of PDEs.

The broader approach outlined in the present work can, in principle, be extended to other systems that satisfy the necessary symmetries. The Clebsch transformation has been applied in magnetohydrodynamics (MHD) [58,59]. Extending the relativistic Clebsch–Lagrangian approach to MHD would involve incorporating electromagnetic corrections, modifying the energy–momentum eigenvalue relationship, but the structural formulation of using this and the canonical velocity to obtain differential equations for the Lagrangian by an inverse Noether method would remain the same.

Clebsch potentials have been used in a Madelung framework; for example, they were used in [60] to describe quantum–fluid correspondence in relativistic fluids with spin and in [18] to describe vortex dynamics in superfluids. Given this, the Lagrangian structure developed here could provide a foundation for extending relativistic quantum fluid formulations, particularly in fluid mechanic analogues of quantum mechanics. Indeed, since Clebsch variables describe velocity fields in all relativistic, non-relativistic and quantum fluids, and have already been employed in Madelung–based approaches, an extension to quantum fluid mechanics using a relativistic Clebsch representation appears plausible. This could establish a variational principle for quantum fluid mechanics with applications in relativistic superfluid theories in, for example, Bose–Einsein condensates or relativistic fluid mechanics in high–energy quantum chromodynamics (QCD). However, although this remains speculative at this stage, it represents an interesting future research direction. Quantisation also remains an interesting perspective future research avenue. A number of authors, for example, [61,62], have quantised the motion of an inviscid fluid.

If the methodology was applied to a fundamental quantum field theory (QFT), operator correspondence would need to be established—how classical quantities translate into quantum operators obeying commutation relations. Another interesting QFT application would be an extension to a Proca-type action, which could be a useful example for testing classical correspondence for a massive vector field theory. This requires, as it were, a generalisation of the scalar fields to a spinor form. However, considerations in this direction exist not only in the field of quantum theory but also in continuum theory, where a spinor-form of the Clebsch representation suggests itself for representing the distortion tensor of a crystalline material with dislocations.