Resolving the Open Problem by Proving a Conjecture on the Inverse Mostar Index for c-Cyclic Graphs

Abstract

Inverse topological index problems involve determining whether a graph exists with a given integer as its topological index. One such index, the Mostar index, $Mo\left(G\right)$, is defined as $Mo\left(G\right)={\sum }_{uv\in E\left(G\right)}|n_u\left(e\right|G)-n_v\left(e\right|G)|,$ where $n_u\left(e\right|G)$ and $n_v\left(e\right|G)$ represent the number of vertices closer to vertex u than v and closer to v than u, respectively, for an edge $e=uv$. The inverse Mostar index problem has gained significant attention recently. In their work, Alizadeh et al. [Solving the Mostar index inverse problem, J. Math. Chem. 62 (5) (2024) 1079–1093] proposed the following open problem: “Which nonnegative integers can be realized as Mostar indices of c-cyclic graphs, for a given positive integer c?”. Subsequently, one of the present authors [On the inverse Mostar index problem for molecular graphs, Trans. Comb. 14 (1) (2024) 65–77] conjectured that, except for finitely many positive integers, all other positive integers can be realized as the Mostar index of a c-cyclic graph, where $c\ge 3$. In this paper, we address the inverse Mostar index problem for c-cyclic graphs. Specifically, we construct infinitely many families of symmetric c-cyclic structures, thereby demonstrating a solution to the inverse Mostar index problem using an infinite family of such symmetric structures. By providing a comprehensive proof of the conjecture, we fully resolve this longstanding open problem.

1. Introduction

Let $G=(V,E)$ be a simple, connected graph with vertex set $V\left(G\right)\left(\right|V\left(G\right)|=n)$ and edge set $E\left(G\right)\left(\right|E\left(G\right)|=m)$. For $u,v\in V\left(G\right)$, the length of the shortest path between the vertices u and v is their distance, $d_G(u,v)$. Let $e=uv$ be an edge of the graph G (which may contain cycles or be acyclic), connecting the vertices u and v. Define two sets $N_u\left(e\right|G)$ and $N_v\left(e\right|G)$ as

$$\begin{array}{cc}\hfill N_u\left(e\right|G)& =\{w\in V\left(G\right)|d_G(w,u)<d_G(w,v)\},\hfill \\ \hfill N_v\left(e\right|G)& =\{w\in V\left(G\right)|d_G(w,v)<d_G(w,u)\}.\hfill \end{array}$$

The number of elements of $N_u\left(e\right|G)$ and $N_v\left(e\right|G)$ is denoted by $n_u\left(e\right|G)$ and $n_v\left(e\right|G)$, respectively. Thus, $n_u\left(e\right|G)$ counts the vertices of G lying closer to the vertex u than to vertex v. The meaning of $n_v\left(e\right|G)$ is analogous. Vertices equidistant from both ends of the edge $uv$ belong neither to $N_u\left(e\right|G)$ nor to $N_v\left(e\right|G)$. Note that for any edge $e=uv$ of G, $n_u\left(e\right|G)\ge 1$ and $n_v\left(e\right|G)\ge 1$, because $u\in N_u\left(e\right|G)$ and $v\in N_v\left(e\right|G)$.

Topological indices are numerical quantities associated with graphs that remain invariant under graph isomorphisms. The Mostar index, introduced in [1], is a recently developed bond-additive topological index. The Mostar index $Mo\left(G\right)$ is defined as

$$\begin{array}{c}\hfill Mo\left(G\right)=\sum _{e=uv\in E\left(G\right)}|n_u\left(e\right|G)-n_v\left(e\right|G)|.\end{array}$$

(1)

We use the notation $\varphi \left(e\right|G)=|n_u\left(e\right|G)-n_v\left(e\right|G)|$ to represent the contribution of the edge $e=uv$ to the Mostar index. Thus, we have

$$\begin{array}{c}\hfill Mo\left(G\right)=\sum _{e=uv\in E\left(G\right)}\varphi \left(e\right|G).\end{array}$$

(2)

In recent years, numerous studies have explored the Mostar index and its associated variants. For further literature on the subject, see [1,2,3,4,5,6,7,8,9].

The inverse topological index problem involves the realization of integers as topological indices within various classes of graphs. It is closely related to several similar problems in other fields [10]. The first version of this problem was introduced by Gutman in [11], and since then, several variants have been investigated for different topological indices [12,13,14,15,16,17,18]. Recently, the inverse Mostar index problem for various classes of graphs has been studied extensively [12,13,19]. In [19], Alizadeh et al. proposed the following problem on inverse Mostar index for c-cyclic graphs.

Problem 1. 

Which nonnegative integers can be realized as Mostar indices of c-cyclic graphs, for a given positive integer c?

This problem was thoroughly resolved for c-cyclic graphs when $c\in \{0,1,2,3\}$ in [12,13,14]. Building on these findings and after an in-depth study of Problem 1 as discussed in [12], one of the present authors proposed the following conjecture concerning the inverse problem of the Mostar index for c-cyclic graphs.

Conjecture 1. 

For any fixed $c\ge 3$, there exists a c-cyclic graph with the Mostar index $Mo\left(G\right)=p$, where $p\in \mathbb{N}\setminus A$, and A is a finite set.

In this paper, we address the inverse Mostar index problem for c-cyclic graphs. Specifically, we construct infinitely many families of symmetric c-cyclic structures, providing a solution to the inverse Mostar index problem through an infinite family of such symmetric graphs. Specifically, for each given Mostar index value, we systematically design a corresponding family of symmetric c-cyclic graphs that realize this index, ensuring that every possible target value has at least one structural realization. By utilizing symmetry properties and cyclic arrangements, we generate these graph families with a consistent and reliable construction. This approach not only offers a constructive solution to the inverse Mostar index problem but also highlights the intricate relationship between graph symmetry and topological indices, providing deeper insights into the role of cyclic structures in shaping graph invariants. By providing a comprehensive proof of Conjecture 1, we fully resolve this longstanding open problem, Problem 1.

2. Main Results

In this section, we provide a complete resolution of Problem 1 by proving Conjecture 1. We use the following constructions to prove the result. In each case, we present multiple constructions to address both Conjecture 1 and Problem 1. We begin by examining the case of c-cyclic graphs when c is even.

• Construction I. Consider a cycle $C=u_1{u}_2\cdots u_{2c+2}{u}_1$ of length $2c+2$. Starting from $i=1$, for each path $u_i{u}_{i+1}{u}_{i+2}$ of length 2 in C, take a vertex $v_{{\displaystyle \frac{i+1}{2}}}$ and form a 4-cycle by attaching the edges $u_i{v}_{{\displaystyle \frac{i+1}{2}}}$ and $u_{i+2}{v}_{{\displaystyle \frac{i+1}{2}}}$ for $i=1,3,5,\cdots c-1$. Next, starting from $i=c+4$, take the path $u_i{u}_{i+1}{u}_{i+2}$ and a new vertex $v_{{\displaystyle \frac{i-2}{2}}}$, forming a 4-cycle by attaching the edges $u_i{v}_{{\displaystyle \frac{i-2}{2}}}$ and $u_{i+2}{v}_{{\displaystyle \frac{i-2}{2}}}$ for $i=c+4,c+6\cdots 2c$. Let the resultant graph be denoted by $G_{E,E}$ (see, Figure 1). In $G_{E,E}$, let $C_i$ denote the 4-cycle containing the vertex $v_i$. Now, let $G_{E,E}^1$ (see, Figure 1) be the graph obtained by inserting a new edge between the cycles $C_{{\displaystyle \frac{c}{2}}}$ & $C_{{\displaystyle \frac{c}{2}}+1}$, and $C_{c-1}$ & $C_1$ in C (or by subdividing the edges $u_{c+1}{u}_{c+2}$ and $u_{2c+2}{u}_1$). Relabel the vertices of the cycle C as $u_1{u}_2\cdots u_{2c+3}{u}_{2c+4}$. Proceeding in this manner, let $G_{E,E}^k$ denote the graph obtained from $G_{E,E}^{k-1}$ by inserting a new edge between the cycles $C_{{\displaystyle \frac{c}{2}}}$ & $C_{{\displaystyle \frac{c}{2}}+1}$, and $C_{c-1}$ & $C_1$ in C (or by subdividing the edges $u_{c+1}{u}_{c+2}$ and $u_{2c+2}{u}_1$k-times in $G_{E,E}$). Clearly, $G_{E,E}$ is a c-cyclic graph with $3c+1$ vertices and $4c$ edges, while $G_{E,E}^k$ is a c-cyclic graph with $3c+2k+1$ vertices and $4c+2k$ edges. In all the graphs considered, let $e_{i,j}$ denote the edge connecting the vertices $u_i$ and $u_j$, where $i\le j$. Similarly, let $e_{i,j}^{\prime }$ denote the edge connecting the vertices $u_i$ and $v_j$, where $i\ge j$.
  

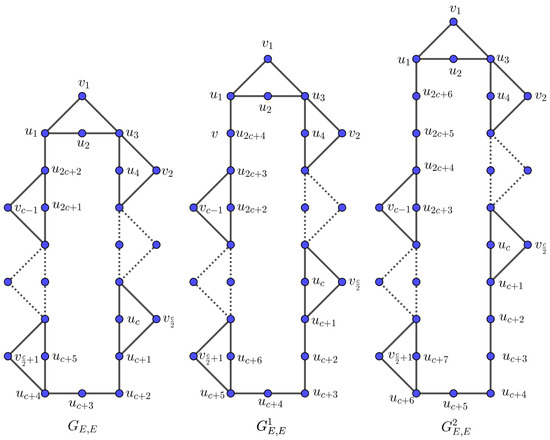  Figure 1. The graphs mentioned in Construction I.

Proposition 1. 

For an even $c\ge 4$, $\left(a\right)$$Mo\left(G_{E,E}\right)=8c-8$, $\left(b\right)$$Mo\left(G_{E,E}^1\right)=Mo\left(G_{E,E}\right)+2$ and $Mo\left(G_{E,E}^k\right)=Mo\left(G_{E,E}^{k-1}\right)+2,k=2,3,\dots$.

Proof. 

$\left(a\right)$ In $G_{E,E}$, consider any 4-cycle $C_i(i=2,3,\cdots ,{\displaystyle \frac{c}{2}})$. For the edges $e_{2i-1,i}^{\prime }=u_{2i-1}{v}_i$ and $e_{2i-1,2i}=u_{2i-1}{u}_{2i}$, we obtain

$$n_{u_{2i-1}}\left(e_{2i-1,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+4}{2}}\mathrm{and}{n}_{v_i}\left(e_{2i-1,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c-2}{2}},$$

$$n_{u_{2i-1}}\left(e_{2i-1,2i}\right|G_{E,E})={\displaystyle \frac{3c+4}{2}}\mathrm{and}{n}_{u_{2i}}\left(e_{2i-1,2i}\right|G_{E,E})={\displaystyle \frac{3c-2}{2}}.$$

Therefore, there are exactly two edges with the contribution

$$\varphi \left(e_{2i-1,2i}\right|G_{E,E})=\varphi \left(e_{2i-1,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+4}{2}}-{\displaystyle \frac{3c-2}{2}}=3.$$

For the other two edges $e_{2i+1,i}^{\prime }=u_{2i+1}{v}_i$ and $e_{2i,2i+1}=u_{2i}{u}_{2i+1}$, the following holds:

$$n_{u_{2i+1}}\left(e_{2i+1,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}\mathrm{and}{n}_{v_i}\left(e_{2i+1,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c}{2}},$$

$$n_{u_{2i+1}}\left(e_{2i,2i+1}\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}\mathrm{and}{n}_{u_{2i}}\left(e_{2i,2i+1}\right|G_{E,E})={\displaystyle \frac{3c}{2}}.$$

Therefore, these two edges have the contribution

$$\varphi \left(e_{2i+1,i}^{\prime }\right|G_{E,E})=\varphi \left(e_{2i,2i+1}\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c}{2}}=1.$$

Next, we consider any 4-cycle $C_i(i={\displaystyle \frac{c}{2}}+1,\cdots ,c-1)$. For the edges $e_{2i+2,i}^{\prime }=u_{2i+2}{v}_i$ and $e_{2i+2,2i+3}=u_{2i+2}{u}_{2i+3}$, we obtain

$$n_{u_{2i+2}}\left(e_{2i+2,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}\mathrm{and}{n}_{v_i}\left(e_{2i+2,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c}{2}},$$

$$n_{u_{2i+2}}\left(e_{2i+2,2i+3}\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}\mathrm{and}{n}_{u_{2i+3}}\left(e_{2i+2,2i+3}\right|G_{E,E})={\displaystyle \frac{3c}{2}}.$$

Therefore, there are exactly two edges with the contribution

$$\varphi \left(e_{2i+2,2i+3}\right|G_{E,E})=\varphi \left(e_{2i+2,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c}{2}}=1.$$

For the other two edges $e_{2i+4,i}^{\prime }=u_{2i+4}{v}_i$ and $e_{2i+3,2i+4}=u_{2i+3}{u}_{2i+4}$, the following holds:

$$n_{u_{2i+4}}\left(e_{2i+4,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c+4}{2}},\mathrm{and}{n}_{v_i}\left(e_{2i+4,i}^{\prime }\right|G_{E,E})={\displaystyle \frac{3c-2}{2}},$$

$$n_{u_{2i+4}}\left(e_{2i+3,2i+4}\right|G_{E,E})={\displaystyle \frac{3c+4}{2}},\mathrm{and}{n}_{u_{2i+3}}\left(e_{2i+3,2i+4}\right|G_{E,E})={\displaystyle \frac{3c-2}{2}}.$$

Therefore, these two edges have the contribution

$$\varphi \left(e_{2i+4,i}^{\prime }\right|G_{E,E})=\varphi \left(e_{2i+3,2i+4}\right|G_{E,E})={\displaystyle \frac{3c+4}{2}}-{\displaystyle \frac{3c-2}{2}}=3.$$

For all the remaining edges $e=uv$ of $G_{E,E}$,

$$n_u\left(e\right|G_{E,E})={\displaystyle \frac{3c+2}{2}},n_v\left(e\right|G_{E,E})={\displaystyle \frac{3c}{2}}.$$

Therefore, these edges have the contribution

$$\varphi \left(e\right|G_{E,E})=|n_u\left(e\right|G_{E,E})-n_v\left(e\right|G_{E,E})|={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c}{2}}=1.$$

Using the above results, from (2), we obtain

$$Mo\left(G_{E,E}\right)=8(c-2)+8=8c-8.$$

$\left(b\right)$ In $G_{E,E}^1$, the contribution of a new edge $e=uv$ is calculated as follows:

$$\varphi \left(e\right|G_{E,E}^1)=|n_u\left(e\right|G_{E,E}^1)-n_v\left(e\right|G_{E,E}^1)|={\displaystyle \frac{3c+4}{2}}-{\displaystyle \frac{3c+2}{2}}=1.$$

For each of the other edges $e=uv\in E\left(G_{E,E}^1\right)$, the contribution is

$$\varphi \left(e\right|G_{E,E}^1)=|n_u\left(e\right|G_{E,E})+1-n_v\left(e\right|G_{E,E})-1|=|n_u\left(e\right|G_{E,E})-n_v\left(e\right|G_{E,E})|.$$

This means that all the other edges have the same contribution as in $G_{E,E}$. Therefore,

$$Mo\left(G_{E,E}^1\right)=Mo\left(G_{E,E}\right)+2.$$

Similarly, in $G_{E,E}^k$ and $G_{E,E}^{k-1}$, all the edges except the new edges have the same contribution. The two new edges in $G_{E,E}^k$ each have a contribution $\varphi \left(e\right|G_{E,E}^k)=1$. Thus, it follows that

$$Mo\left(G_{E,E}^1\right)=Mo\left(G_{E,E}\right)+2.$$

In a similar manner, we can establish

$$Mo\left(G_{E,E}^k\right)=Mo\left(G_{E,E}^{k-1}\right)+2\mathrm{for}k=2,3,\cdots$$

□

We can also provide several classes of constructions to obtain the same value of the Mostar index as in Proposition 1. A general version of the construction is as follows.

• General Construction I. Consider the base graph $G_{E,E}$ as in Construction I. For $j=3,5,\cdots ,c-1$, let $u_j$ and $u_{c+j+1}$ be vertices positioned between the 4-cycles $C_{{\displaystyle \frac{j+1}{2}}},C_{{\displaystyle \frac{j-1}{2}}}$ and $C_{{\displaystyle \frac{c+j-1}{2}}},C_{{\displaystyle \frac{c+j-3}{2}}}$, respectively. Define $G_{E,E}^{j,1}$ as the graph obtained from $G_{E,E}$ by deleting the edges $u_j{v}_{{\displaystyle \frac{j+1}{2}}}$ and $u_{c+j+1}{v}_{{\displaystyle \frac{c+j-1}{2}}}$, subdividing the edges $u_j{u}_{j+1}$ and $u_{c+j+1}{u}_{c+j+2}$, relabeling the vertices of the cycle C as $u_1,u_2,\cdots ,u_{2c+4}$, and adding an edge between $u_{j+1}{v}_{{\displaystyle \frac{j+1}{2}}}$ and $u_{c+j+3}{v}_{{\displaystyle \frac{c+j-1}{2}}}$. This effectively inserts an edge between the cycles $C_{{\displaystyle \frac{j+1}{2}}},C_{{\displaystyle \frac{j-1}{2}}}$ and $C_{{\displaystyle \frac{c+j-1}{2}}},C_{{\displaystyle \frac{c+j-3}{2}}}$ in C. Proceeding iteratively, define $G_{E,E}^{j,k}$ (see, Figure 2) as the graph obtained from $G_{E,E}^{j,k-1}$ by subdividing the edges $u_{j+k-1}{u}_{j+k}$ and $u_{c+j+2k-1}{u}_{c+j+2k}$, thereby inserting k edges between the cycles $C_{{\displaystyle \frac{j+1}{2}}},C_{{\displaystyle \frac{j-1}{2}}}$ and $C_{{\displaystyle \frac{c+j-1}{2}}},C_{{\displaystyle \frac{c+j-3}{2}}}$. At each step, relabel the vertices of C in $G_{E,E}^{j,k}$. Clearly, $G_{E,E}^{j,k}$ is a c-cyclic graph with $3c+2k+1$ vertices and $4c+2k$ edges for each $j=3,5,\cdots ,c-1$.
  

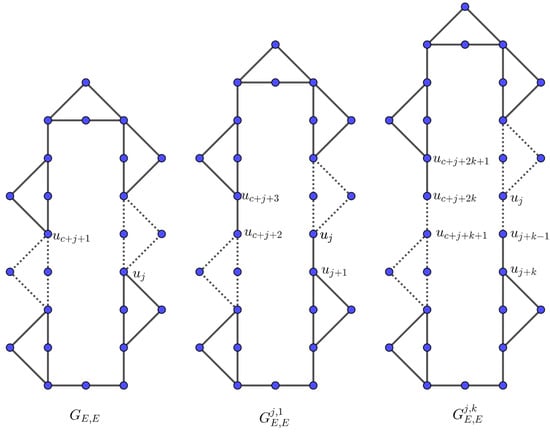  Figure 2. The graphs mentioned in General Construction I.

Proposition 2. 

For each fixed even integer $c\ge 4$, $Mo\left(G_{E,E}^{j,k}\right)=Mo\left(G_{E,E}^{j,k-1}\right)+2$, where $j=3,5,\cdots ,c-1$ and $k=2,3\cdots$.

Proof. 

From direct computation in $G_{E,E}^{j,k}$, the contribution of the new edges is 1 each, and the contribution of every other edge remains the same as in $G_{E,E}^{j,k-1}$. Therefore,

$$\begin{array}{cc}\hfill Mo\left(G_{E,E}^{j,k}\right)& =Mo\left(G_{E,E}^{j,k-1}\right)+2\mathrm{and}Mo\left(G_{E,E}^{j,1}\right)=Mo\left(G_{E,E}\right)+2\mathrm{for}j=3,5,\cdots ,c-1\mathrm{and}\hfill \\ \hfill k=2,3,\cdots .\end{array}$$

□

• Construction II. Consider a cycle $C=u_1{u}_2\cdots u_{2c+1}{u}_1$ of length $2c+1$. Select the vertex $u_2$ and its diametrically opposite edge $u_{c+2}{u}_{c+3}$ in C. From the path $u_1{u}_2{u}_3$ in C, attach the end vertices $u_1$ and $u_3$ to a new vertex $v_1$, forming a 4-cycle $C_1$. Additionally, attach a pendant edge $v_{1}w$ at $v_1$. Starting from $i=4$, for each path $u_i{u}_{i+1}{u}_{i+2}$ of length 2 with $i=4,6,\cdots ,c$, take a new vertex $v_{{\displaystyle \frac{i}{2}}}$ and attach $u_i$ and $u_{i+2}$ to $v_{{\displaystyle \frac{i}{2}}}$ to form a 4-cycle. Similarly, starting from $i=c+3$, for each path $u_i{u}_{i+1}{u}_{i+2}$ of length 2 with $i=c+3,c+5,\cdots ,2c-1$, take a vertex $v_{{\displaystyle \frac{i-1}{2}}}$ and attach $u_i$ and $u_{i+2}$ to $v_{{\displaystyle \frac{i-1}{2}}}$ to form a 4-cycle. The resulting graph is denoted by $G_{E,O}$, which is a c-cyclic graph with order $3c+1$ and size $4c$ (see, Figure 3). Let the 4-cycle in $G_{E,O}$ containing the vertex $v_i$ be denoted as $C_i$, for $i=1,2,\cdots ,c-1$. Define $G_{E,O}^1$ (see, Figure 3) as the graph obtained from $G_{E,O}$ by subdividing the edge $u_1{u}_{2c+1}$ and attaching a new edge between the cycles $C_{{\displaystyle \frac{c}{2}}}$ and $C_{{\displaystyle \frac{c}{2}}-1}$, relabeling the vertices of C as $u_1{u}_2\cdots u_{2c+3}$. Next, let $G_{E,O}^2$ (see, Figure 3) be the graph obtained from $G_{E,O}^1$ by inserting a new edge between the cycles $C_{c-1}\&C_1$, and another edge between $C_{{\displaystyle \frac{c}{2}}}\&C_{{\displaystyle \frac{c}{2}}-1}$. Proceeding iteratively, define $G_{E,O}^k$ as the graph obtained from $G_{E,O}^{k-1}$ by inserting edges between the cycles $C_{c-1}\&C_1$, and between $C_{{\displaystyle \frac{c}{2}}}\&C_{{\displaystyle \frac{c}{2}}-1}$. Clearly, $G_{E,O}^k$ is a c-cyclic graph with $3c+1+2k$ vertices and $4c+2k$ edges for each $k=1,2,\cdots$. In all these graphs, let $e_{i,j}$ denote the edge connecting the vertex $u_i$ and $u_j$, where $i\le j$ and $e_{i,j}^{\prime }$ denote the edge connecting the vertex $u_i$ and $v_j$, where $i\ge j$.
  

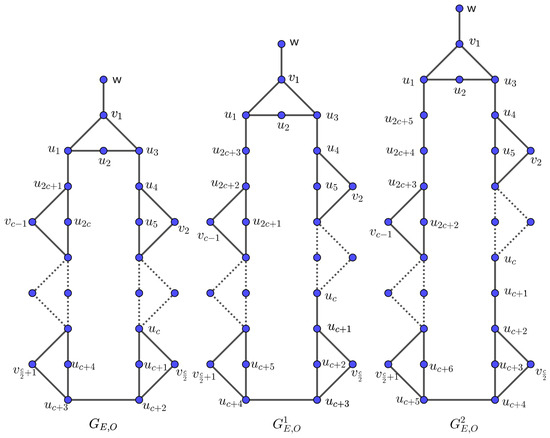  Figure 3. The graphs mentioned in Construction II.

Proposition 3. 

For an even $c\ge 4$, $\left(a\right)$$Mo\left(G_{E,O}\right)=9c-11,$$\left(b\right)$$Mo\left(G_{E,O}^1\right)=Mo\left(G_{E,O}\right)+2$, and $Mo\left(G_{E,O}^k\right)=Mo\left(G_{E,O}^{k-1}\right)+2$, $j=2,3,\cdots$.

Proof. 

$\left(a\right)$ Since $G_{E,O}$ has $3c+1$ vertices, the pendant edge $e=v_{1}w$ has the contribution $\varphi \left(e\right|G_{E,O})=3c-1$. Now, in the cycle $C_1$, for the edges $e_{1,1}^{\prime }=u_1{v}_1$ and $e_{3,1}^{\prime }=u_3{v}_1$, we have

$$n_{u_1}\left(e_{1,1}^{\prime }\right|G_{E,O})=n_{v_1}\left(e_{1,1}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}},\mathrm{and}{n}_{u_3}\left(e_{3,1}^{\prime }\right|G_{E,O})=n_{v_1}\left(e_{3,1}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}}.$$

There are exactly two edges with the contributions $\varphi \left(e_{1,1}^{\prime }\right|G_{E,O})=\varphi \left(e_{3,1}^{\prime }\right|G_{E,O})=0$, and for the other two edges $e_{1,2}=u_1{u}_2,$ and $e_{2,3}=u_2{u}_3$, we have

$$\begin{array}{cc}\hfill & n_{u_1}\left(e_{1,2}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{u_2}\left(e_{1,2}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},\hfill \\ \hfill \mathrm{and}& n_{u_3}\left(e_{2,3}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{u_2}\left(e_{2,3}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.\hfill \end{array}$$

Therefore,

$$\varphi \left(e_{1,2}\right|G_{E,O})=\varphi \left(e_{2,3}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c-2}{2}}=2.$$

Similarly, in $C_{{\displaystyle \frac{c}{2}}}$, there are two edges, $e_{c+2,{\displaystyle \frac{c}{2}}}^{\prime }=u_{c+2}{v}_{{\displaystyle \frac{c}{2}}}$ and $e_{c+1,c+2}=u_{c+1}{u}_{c+2}$, with

$$\begin{array}{cc}\hfill & n_{u_{c+2}}\left(e_{c+2,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}},n_{v_{{\displaystyle \frac{c}{2}}}}\left(e_{c+2,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}},\hfill \\ \hfill \mathrm{and}& n_{u_{c+2}}\left(e_{c+1,c+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}},n_{u_{c+1}}\left(e_{c+1,c+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}}.\hfill \end{array}$$

Therefore, the contribution is

$$\varphi \left(e_{c+2,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})=\varphi \left(e_{c+1,c+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}}-{\displaystyle \frac{3c}{2}}=0,$$

and for the other two edges, $e_{c,{\displaystyle \frac{c}{2}}}^{\prime }=u_c{v}_{{\displaystyle \frac{c}{2}}},$ and $e_{c,c+1}=u_c{u}_{c+1}$, we have

$$n_{u_c}\left(e_{c,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{v_{{\displaystyle \frac{c}{2}}}}\left(e_{c,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},$$

$$n_{u_c}\left(e_{c,c+1}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{u_{c+1}}\left(e_{c,c+1}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.$$

Thus, the contribution is

$$\varphi \left(e_{c,{\displaystyle \frac{c}{2}}}^{\prime }\right|G_{E,O})=\varphi \left(e_{c,c+1}\right|G_{E,O})=|n_u\left(e_{c,c+1}\right|G_{E,O})-n_v\left(e_{c,c+1}\right|G_{E,O})|={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c-2}{2}}=2.$$

Similarly, in $C_{{\displaystyle \frac{c}{2}}+1}$, there are two edges, each incident at $u_{c+5}$, with the contribution $\varphi \left(e\right|G_{E,O})=2,$ and the other two edges incident at $u_{c+3}$ have the contribution $\varphi \left(e\right|G_{E,O})=0$. For the remaining cycles $C_i,i=2,\cdots {\displaystyle \frac{c}{2}}-1$, for the edges $e_{2i,i}^{\prime }=u_{2i}{v}_i$ and $e_{2i,2i+1}=u_{2i}{u}_{2i+1}$, we have

$$n_{u_{2i}}\left(e_{2i,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{v_i}\left(e_{2i,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},$$

$$n_{u_{2i}}\left(e_{2i,2i+1}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},n_{u_{2i+1}}\left(e_{2i,2i+1}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.$$

Therefore,

$$\varphi \left(e_{2i,i}^{\prime }\right|G_{E,O})=\varphi \left(e_{2i,2i+1}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c-2}{2}}=2.$$

Now, for the edge $e_{2i+2,i}^{\prime }=u_{2i+2}{v}_i$, we have

$$n_{u_{2i+2}}\left(e_{2i+2,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}},n_{v_i}\left(e_{2i+2,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},$$

and for the edge $e_{2i+1,2i+2}=u_{2i+1}{u}_{2i+2}$, we have

$$n_{u_{2i+2}}\left(e_{2i+1,2i+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}},n_{u_{2i+1}}\left(e_{2i+1,2i+2}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.$$

Therefore,

$$\varphi \left(e_{2i+2,i}^{\prime }\right|G_{E,O})=\varphi \left(e_{2i+1,2i+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}}-{\displaystyle \frac{3c-2}{2}}=1.$$

Similarly, on the cycle $C_i$, where $i={\displaystyle \frac{c}{2}}+2,\cdots ,c-1$, for the edge $e_{2i+1,i}^{\prime }=u_{2i+1}{v}_i$, we have

$$n_{u_{2i+1}}\left(e_{2i+1,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c}{2}},\mathrm{and}{n}_{v_i}\left(e_{2i+1,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},$$

and for the edge $e_{2i+1,2i+2}=u_{2i+1}{u}_{2i+2}$, we obtain

$$n_{u_{2i+1}}\left(e_{2i+1,2i+2}\right|G_{E,O})={\displaystyle \frac{3c}{2}},\mathrm{and}{n}_{u_{2i+2}}\left(e_{2i+1,2i+2}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.$$

Therefore, $\varphi \left(e_{2i+1,i}^{\prime }\right|G_{E,O})=\varphi \left(e_{2i+1,2i+2}\right|G_{E,O})=1$. For the other two edges, $e_{2i+3,i}^{\prime }=u_{2i+3}{v}_i$, we have

$$n_{u_{2i+3}}\left(e_{2i+3,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},\mathrm{and}{n}_{v_i}\left(e_{2i+3,i}^{\prime }\right|G_{E,O})={\displaystyle \frac{3c-2}{2}},$$

and for the edge $e_{2i+2,2i+3}=u_{2i+2}{u}_{2i+3}$, we obtain

$$n_{u_{2i+3}}\left(e_{2i+2,2i+3}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}},\mathrm{and}{n}_{u_{2i+2}}\left(e_{2i+2,2i+3}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}.$$

Therefore, $\varphi \left(e_{2i+3,i}^{\prime }\right|G_{E,O})=\varphi \left(e_{2i+2,2i+3}\right|G_{E,O})={\displaystyle \frac{3c+2}{2}}-{\displaystyle \frac{3c-2}{2}}=2$. Now, for the edges $e_{1,2c+1}=u_1{u}_{2c+1}$ and $e_{3,4}=u_3{u}_4$, the contribution is

$$\varphi \left(u_{1,2c+1}\right|G_{E,O})=\varphi \left(e_{3,4}\right|G_{E,O})={\displaystyle \frac{3c}{2}}-{\displaystyle \frac{3c-2}{2}}=1,$$

and the remaining edge has the contribution $\varphi \left(e_{c+2,c+3}\right|G_{E,O})={\displaystyle \frac{3c-2}{2}}-{\displaystyle \frac{3c-2}{2}}=0$. Using the above results, from (2), we obtain

$$\begin{array}{c}\hfill Mo\left(G_{E,O}\right)=6(c-4)+12+2+3c-1=9c-11.\end{array}$$

$\left(b\right)$ In $G_{E,O}^k$ and $G_{E,O}^{k-1}$, the pendant edges contribute $\varphi \left(e\right|G_{E,O}^k)=3c+2k-1$ and $\varphi \left(e\right|G_{E,O}^{k-1})=3c+2k-3$, respectively. Two new edges in $G_{E,O}^k$ each contribute $\varphi \left(e\right|G_{E,O}^k)=0$ to the Mostar index. For the remaining edges $e=uv$ of $G_{E,O}^k$, we have

$$\varphi \left(e\right|G_{E,O}^k)=|n_u\left(e\right|G_{E,O}^{k-1})+1-n_v\left(e\right|G_{E,O}^{k-1})-1|=|n_u\left(e\right|G_{E,O}^{k-1})-n_v\left(e\right|G_{E,O}^{k-1})|=\varphi \left(e\right|G_{E,O}^{k-1}).$$

Therefore, the remaining edges of $G_{E,O}^k$ and $G_{E,O}^{k-1}$ contribute the same amount. Thus, we conclude that

$$\begin{array}{c}\hfill Mo\left(G_{E,O}^k\right)=Mo\left(G_{E,O}^{k-1}\right)+2.\end{array}$$

□

We can also provide several classes of constructions that yield the same value of the Mostar index as in Proposition 3. A general version of the construction is as follows.

• General Construction II. Consider the base graph $G_{E,O}$ as described in Construction II. For $j=6,8,\cdots ,c-2$, let $u_j$ and $u_{c+j+1}$ be vertices such that $u_j$ lies between the 4-cycles $C_{{\displaystyle \frac{j}{2}}}$ and $C_{{\displaystyle \frac{j}{2}}-1}$, and $u_{c+j+1}$ lies between the cycles $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$. Define $G_{E,O}^{j,1}$ as the graph obtained by deleting the edges $u_j{v}_{{\displaystyle \frac{j}{2}}}$ and $u_{c+j+1}{v}_{{\displaystyle \frac{c+j}{2}}}$, subdividing the edges $u_j{u}_{j+1}$ and $u_{c+j+1}{u}_{c+j+2}$, relabeling the vertices of C as $u_1,u_2,\cdots ,u_{2c+3}$, and adding edges $u_{j+1}{v}_{{\displaystyle \frac{j}{2}}}$ and $u_{c+j+3}{v}_{{\displaystyle \frac{c+j}{2}}}$. This process effectively connects the cycles $C_{{\displaystyle \frac{j}{2}}}$ and $C_{{\displaystyle \frac{j}{2}}-1}$, as well as $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$, through the newly added edges. Proceeding iteratively, let $G_{E,O}^{j,k}$ denote the graph obtained by subdividing the edges $u_{j+k-2}{u}_{j+k-1}$ and $u_{c+j+2k-2}{u}_{c+j+2k-1}$ of $G_{E,O}^{j,k-1}$ exactly once, or equivalently, inserting $k-1$ edges between the cycles $C_{{\displaystyle \frac{j}{2}}}$ and $C_{{\displaystyle \frac{j}{2}}-1}$, and between $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$ in C of $G_{E,O}^{j,1}$, like in Figure 2. After each step, relabel the vertices of the cycle C in $G_{E,O}^{j,k}$. Clearly, $G_{E,O}^{j,k}$ is a c-cyclic graph with $3c+2k+1$ vertices and $4c+2k$ edges, where $k=1,2,\cdots ,$ and $j=6,8,\cdots ,c-2$.

Proposition 4. 

For every fixed even integer $c\ge 4$, $Mo\left(G_{E,O}^{j,k}\right)=Mo\left(G_{E,O}^{j,k-1}\right)+2,$ where $j=6,8,\cdots ,c-2$ and $k=1,2,\cdots$.

Proof. 

In $G_{E,O}^{j,k}$ and $G_{E,O}^{j,k-1}$, the pendant edges contribute $\varphi \left(e\right|G_{E,O}^{j,k})=3c+2k-1$ and $\varphi \left(e\right|G_{E,O}^{j,k-1})=3c+2k-3$, respectively. Two new edges in $G_{E,O}^{j,k}$ each contribute $\varphi \left(e\right|G_{E,O}^{j,k})=0$ to the Mostar index. The remaining edges of $G_{E,O}^{j,k}$ and $G_{E,O}^{j,k-1}$ contribute the same amount. Therefore, $Mo\left(G_{E,O}^{j,k}\right)=Mo\left(G_{E,O}^{j,k-1}\right)+2$. □

Next, we consider the case when c is odd.

• Construction III. Consider a cycle $C=u_1{u}_2\cdots u_{2c-1}{u}_1$ of length $2c-1$. Add a vertex $v_1$ and connect it to $u_1$ and $u_2$ to form a 3-cycle $u_1{u}_2{v}_1{u}_1$. For each path $u_i{u}_{i+1}{u}_{i+2}$ in C where $i=3,5,\cdots ,2c-3$, introduce a vertex $v_{{\displaystyle \frac{i+1}{2}}}$ and connect it to $u_i$ and $u_{i+2}$, forming a 4-cycle $u_i{u}_{i+1}{u}_{i+2}{v}_{{\displaystyle \frac{i+1}{2}}}{u}_i$. Let the resultant graph be denoted as $G_{O,E}$ (see, Figure 4). Define $C_1$ as the 3-cycle $u_1{u}_2{v}_1{u}_1$, and for $i=2,3,\cdots ,c-1$, let $C_i$ denote the 4-cycle containing the vertex $v_i$. Now, construct $G_{O,E}^1$ (see, Figure 4) from $G_{O,E}$ by deleting the edge $u_c{v}_{{\displaystyle \frac{c-1}{2}}}$, subdividing the edges $u_1{u}_{2c-1}$ and $u_{c-1}{u}_c$, relabeling the vertices of C as $u_1,u_2,\cdots ,u_{2c+1}$, and adding the edge $v_{{\displaystyle \frac{c-1}{2}}}{u}_c$. Alternatively, this can be described as inserting a new edge between the cycles $C_1$ and $C_{c-1}$, as well as between $C_{{\displaystyle \frac{c-1}{2}}}$ and $C_{{\displaystyle \frac{c+1}{2}}}$ in C. Proceeding recursively, $G_{O,E}^k$ is obtained from $G_{O,E}^{k-1}$ by inserting new edges between $C_1$ and $C_{c-1}$, and between $C_{{\displaystyle \frac{c-1}{2}}}$ and $C_{{\displaystyle \frac{c+1}{2}}}$ in C, or equivalently by subdividing the edges $u_1{u}_{2c-1+2(k-1)}$ and $u_c{u}_{c+1}$ exactly once, or by subdividing the edges $u_1{u}_{2c+1}$ and $u_c{u}_{c+1}$ in $G_{O,E}^1$ exactly $k-1$ times. Clearly, $G_{O,E}$ is a c-cyclic graph of the order $3c-2$ and size $4c-3$, while $G_{O,E}^k$ is a c-cyclic graph of the order $3c-2+2k$ and size $4c-3+2k$ for $k=1,2,\cdots$. In all these graphs, let $e_{i,j}$ denote the edge connecting vertices $u_i$ and $u_j$ (where $i\le j$), and let $e_{i,j}^{\prime }$ denote the edge connecting $u_i$ and $v_j$ (where $i\ge j$).
  

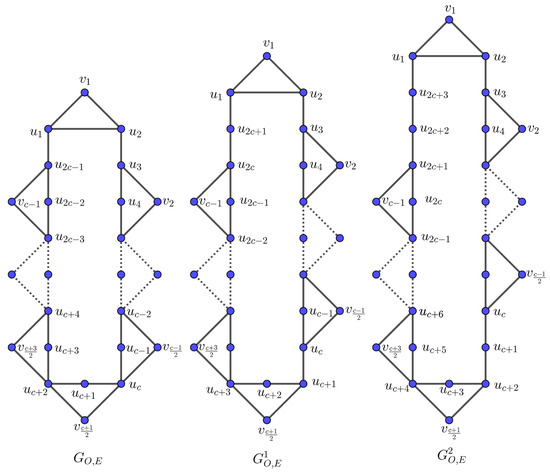  Figure 4. The graphs mentioned in Construction III.

Proposition 5. 

For an odd $c\ge 3$, $\left(a\right)$$Mo\left(G_{O,E}\right)=9c-13$, $\left(b\right)$$Mo\left(G_{O,E}^1\right)=Mo\left(G_{O,E}\right)+2$ and $Mo\left(G_{O,E}^k\right)=Mo\left(G_{O,E}^{k-1}\right)+2$, $j=2,3,\cdots$.

Proof. 

$\left(a\right)$ In $G_{O,E}$, two edges $e_{1,1}^{\prime }=u_1{v}_1$ and $e_{2,1}^{\prime }=u_2{v}_1$ contribute the following:

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,E})=\varphi \left(e_{2,1}^{\prime }\right|G_{O,E})={\displaystyle \frac{n-1}{2}}={\displaystyle \frac{3c-3}{2}}.$$

The edge $e_{1,2}=u_1{u}_2$ contributes

$$\varphi \left(e_{1,2}\right|G_{O,E})=|n_{u_1}\left(e_{1,2}\right|G_{O,E})-n_{u_2}\left(e_{1,2}\right|G_{O,E})|={\displaystyle \frac{3c-5}{2}}-{\displaystyle \frac{3c-5}{2}}=0.$$

In each of the cycles $C_i$ for $i=2,3,\cdots c-1,$ where $i\ne {\displaystyle \frac{c+1}{2}}$, two edges $e_{2i-1,i}^{\prime }=u_{2i-1}{v}_i$ and $e_{2i-1,2i}=u_{2i-1}{u}_{2i}$ contribute the following:

$$n_{u_{2i-1}}\left(e_{2i-1,i}^{\prime }\right|G_{O,E})={\displaystyle \frac{3c-3}{2}}{n}_{v_i}\left(e_{2i-1,i}^{\prime }\right|G_{O,E})={\displaystyle \frac{3c-5}{2}},$$

$$n_{u_{2i-1}}\left(e_{2i-1,2i}\right|G_{O,E})={\displaystyle \frac{3c-3}{2}}{n}_{u_{2i}}\left(e_{2i-1,2i}\right|G_{O,E})={\displaystyle \frac{3c-5}{2}}.$$

Therefore, the contribution of these two edges are

$$\varphi \left(e_{2i-1,i}^{\prime }\right|G_{O,E})=\varphi \left(e_{2i-1,2i}\right|G_{O,E})={\displaystyle \frac{3c-3}{2}}-{\displaystyle \frac{3c-5}{2}}=1.$$

For the edges, $e_{2i,2i+1}=u_{2i}{u}_{2i+1}$ and $e_{2i+1,i}^{\prime }=u_{2i+1}{v}_i$, we have

$$n_{u_{2i+1}}\left(e_{2i,2i+1}\right|G_{O,E})={\displaystyle \frac{3c-1}{2}}{n}_{u_{2i}}\left(e_{2i,2i+1}\right|G_{O,E})={\displaystyle \frac{3c-5}{2}},$$

$$n_{u_{2i+1}}\left(e_{2i+1,i}^{\prime }\right|G_{O,E})={\displaystyle \frac{3c-1}{2}}{n}_{v_i}\left(e_{2i+1,i}^{\prime }\right|G_{O,E})={\displaystyle \frac{3c-5}{2}}.$$

Thus, the contributions of these two edges are $\varphi \left(e_{2i+1,i}^{\prime }\right|G_{O,E})=\varphi \left(e_{2i,2i+1}\right|G_{O,E})={\displaystyle \frac{3c-1}{2}}-{\displaystyle \frac{3c-5}{2}}=2$. In $C_{{\displaystyle \frac{c+1}{2}}}$, each of the four edges $e=uv$ contributes:

$$n_u\left(e\right|G_{O,E})={\displaystyle \frac{3c-1}{2}}\mathrm{when}u=u_c,u_{c+2},$$

$$n_v\left(e\right|G_{O,E})={\displaystyle \frac{3c-5}{2}}\mathrm{when}v=u_{c+1},v_{{\displaystyle \frac{c+1}{2}}}.$$

Therefore, each of these four edges contributes

$$\varphi \left(e\right|G_{O,E})={\displaystyle \frac{3c-1}{2}}-{\displaystyle \frac{3c-5}{2}}=2.$$

The remaining edges in $G_{O,E}$ have zero contribution. Using the above results, from (2), we obtain

$$\begin{array}{c}\hfill Mo\left(G_{O,E}\right)=2\left({\displaystyle \frac{3c-3}{2}}\right)+6(c-3)+8=9c-13.\end{array}$$

$\left(b\right)$ In $G_{O,E}^k$ and $G_{O,E}^{k-1}$, two edges $e_{1,1}^{\prime }=u_1{v}_1$ and $e_{2,1}^{\prime }=u_2{v}_1$ contribute

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,E}^k)=\varphi \left(e_{2,1}^{\prime }\right|G_{O,E}^k)={\displaystyle \frac{3c-3+2k}{2}},$$

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,E}^{k-1})=\varphi \left(e_{2,1}^{\prime }\right|G_{O,E}^{k-1})={\displaystyle \frac{3c-3+2(k-1)}{2}}.$$

The edge $e_{1,2}=u_1{u}_2$ contributes $\varphi \left(e_{1,2}\right|G_{O,E}^k)=\varphi \left(e_{1,2}\right|G_{O,E}^{k-1})=0$. Two new edges $e\in E\left(G_{O,E}^k\right)$ have the contribution $\varphi \left(e\right|G_{O,E}^k)=0$. For all remaining edges $e=uv$ in $G_{O,E}^k$, we have

$$n_u\left(e\right|G_{O,E}^k)=n_u\left(e\right|G_{O,E}^{k-1})+1\mathrm{and}{n}_v\left(e\right|G_{O,E}^k)=n_v\left(e\right|G_{O,E}^{k-1})+1.$$

Therefore,

$$\varphi \left(e\right|G_{O,E}^k)=|n_u\left(e\right|G_{O,E}^{k-1})+1-n_v\left(e\right|G_{O,E}^{k-1})-1|=|n_u\left(e\right|G_{O,E}^{k-1})-n_v\left(e\right|G_{O,E}^{k-1})|=\varphi \left(e\right|G_{O,E}^{k-1}).$$

Thus, all the remaining edges of $G_{O,E}^k$ have the same contribution as in $G_{O,E}^{k-1}$. Consequently,

$$\begin{array}{c}\hfill Mo\left(G_{O,E}^k\right)=Mo\left(G_{O,E}^{k-1}\right)+2.\end{array}$$

□

We can also provide several classes of constructions to obtain the same value of the Mostar index as in Proposition 5. A general version of the construction is as follows.

• General Construction III. Consider the base graph $G_{O,E}$ as in Construction III. For $j=3,5,\cdots ,c-2$, consider the vertices $u_j$ and $u_{c+j-1}$. The vertex $u_j$ lies between the 4-cycles $C_{{\displaystyle \frac{j+1}{2}}}$ and $C_{{\displaystyle \frac{j+1}{2}}-1}$, while $u_{c+j-1}$ lies between the cycles $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$. For each $j=3,5,\cdots ,c-2$, let $G_{O,E}^{j,1}$ be the graph obtained by deleting the edges $u_j{v}_{{\displaystyle \frac{j+1}{2}}}$ and $u_{c+j-1}{v}_{{\displaystyle \frac{c+j}{2}}}$, subdividing the edges $u_j{u}_{j+1}$ and $u_{c+j-1}{u}_{c+j}$, relabeling the vertices $u_1,u_2,\cdots ,u_{2c-1}$ of C as $u_1,u_2,\cdots ,u_{2c+1}$, and attaching the edges $u_{j+1}{v}_{{\displaystyle \frac{j+1}{2}}}$ and $u_{c+j+3}{v}_{{\displaystyle \frac{c+j}{2}}}$ (or equivalently, adding an edge between the cycles $C_{{\displaystyle \frac{j+1}{2}}}$ and $C_{{\displaystyle \frac{j+1}{2}}-1}$, as well as between the cycles $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$). Proceeding in this manner, let $G_{O,E}^{j,k}$ be the graph obtained by subdividing the edges $u_{j+k-2}{u}_{j+k-1}$ and $u_{c+j+2k-2}{u}_{c+j+2k-1}$ of $G_{O,E}^{j,k-1}$ exactly once (or equivalently, inserting $k-1$ edges between the cycles $C_{{\displaystyle \frac{j+1}{2}}}$ and $C_{{\displaystyle \frac{j+1}{2}}-1}$, as well as between the cycles $C_{{\displaystyle \frac{c+j}{2}}}$ and $C_{{\displaystyle \frac{c+j}{2}}-1}$ in $G_{O,E}^{j,1}$). At each step, relabel the vertices of the cycle C in $G_{O,E}^{j,k}$. Clearly, $G_{O,E}^{j,k}$ is a c-cyclic graph with $3c-2+2k$ vertices and $4c-3+2k$ edges, where $k=2,3,\cdots$ and $j=3,5,\cdots ,c-2$.

Proposition 6. 

For every fixed odd integer $c\ge 3$, $Mo\left(G_{O,E}^{j,k}\right)=Mo\left(G_{O,E}^{j,k-1}\right)+2$, where $j=3,5,\cdots ,c-2$ and $k=2,3,\cdots$.

Proof. 

In $G_{O,E}^{j,k}$ and $G_{O,E}^{j,k-1}$, the two edges $e_{1,1}^{\prime }=u_1{v}_1$ and $e_{2,1}^{\prime }=u_2{v}_1$ contribute

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,E}^{j,k})=\varphi \left(e_{2,1}^{\prime }\right|G_{O,E}^{j,k})={\displaystyle \frac{3c-3+2k}{2}}$$

and

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,E}^{j,k-1})=\varphi \left(e_{2,1}^{\prime }\right|G_{O,E}^{j,k-1})={\displaystyle \frac{3c-3+2(k-1)}{2}}.$$

The edge $e_{1,2}=u_1{u}_2$ contributes $\varphi \left(e_{1,2}\right|G_{O,E}^{j,k})=\varphi \left(e_{1,2}\right|G_{O,E}^{j,k-1})=0$. Two new edges $e\in E\left(G_{O,E}^{j,k}\right)$ have the contribution $\varphi \left(e\right|G_{O,E}^{j,k})=0$. All remaining edges in $G_{O,E}^{j,k}$ have the same contribution as in $G_{O,E}^{j,k-1}$. Therefore, $Mo\left(G_{O,E}^{j,k}\right)=Mo\left(G_{O,E}^{j,k-1}\right)+2$. □

• Construction IV. Consider a cycle $C=u_1{u}_2\cdots u_{2c}{u}_1$ of length $2c$, where c is odd. Introduce a vertex $v_1$ and connect $u_1{v}_1$ and $u_2{v}_1$ to form a 3-cycle $u_1{u}_2{v}_1{u}_1$. For each path $u_i{u}_{i+1}{u}_{i+2}$ in C starting from $i=2$ and incrementing by 2, add a vertex $v_{{\displaystyle \frac{i+2}{2}}}$, and connect $u_i{v}_{{\displaystyle \frac{i+2}{2}}}$ and $u_{i+2}{v}_{{\displaystyle \frac{i+2}{2}}}$ to form a 4-cycle $u_i{u}_{i+1}{u}_{i+2}{v}_{{\displaystyle \frac{i+2}{2}}}{u}_i$ for $i=2,4,\cdots ,c-1$. Similarly, for $i=c+2,c+4,\cdots ,2c-3$, add a vertex $v_{{\displaystyle \frac{i+1}{2}}}$, and connect $u_i{v}_{{\displaystyle \frac{i+1}{2}}}$ and $u_{i+2}{v}_{{\displaystyle \frac{i+1}{2}}}$ to form a 4-cycle $u_i{u}_{i+1}{u}_{i+2}{v}_{{\displaystyle \frac{i+1}{2}}}{u}_i$. Denote the resulting graph by $G_{O,O}$. Let $C_1$ denote the 3-cycle $u_1{u}_2{v}_1{u}_1$, and let $C_i$ denote the 4-cycle containing $v_i$ for $i=2,3,\cdots ,c-1$. Define $G_{O,O}^1$ as the graph obtained from $G_{O,O}$ by deleting the edge $u_{c-1}{v}_{{\displaystyle \frac{c-1}{2}}}$ and subdividing the edges $u_{c-2}{u}_{c-1}$ and $u_1{u}_{2c}$ exactly once. Relabel the vertices of C as $u_1{u}_2\cdots u_{2c+2}$, and reattach the edge $u_{c-1}{v}_{{\displaystyle \frac{c-1}{2}}}$ (or insert a new edge between the cycles $C_1$ and $C_{c-1}$ in C, and another new edge between $C_{{\displaystyle \frac{c-1}{2}}}$ and $C_{{\displaystyle \frac{c+1}{2}}}$ in C). Iteratively, define $G_{O,O}^k$ as the graph obtained from $G_{O,O}^{k-1}$ by inserting new edges between $C_1$ and $C_{c-1}$ and between $C_{{\displaystyle \frac{c-1}{2}}}$ and $C_{{\displaystyle \frac{c+1}{2}}}$, or equivalently, by subdividing the edges $u_1{u}_{2c+2(k-1)}$ and $u_{c-1}{u}_c$ of $G_{O,O}^{k-1}$ exactly once. Thus, $G_{O,O}$ is a c-cyclic graph of the order $3c-1$ and size $4c-2$, and $G_{O,O}^k$ is a c-cyclic graph of the order $3c-1+2k$ and size $4c-2+2k$ for $k=1,2,\cdots$. In these graphs, let $e_{i,j}$ denote the edge connecting $u_i$ and $u_j$ (where $i\le j$), and $e_{i,j}^{\prime }$ denote the edge connecting $u_i$ and $v_j$ (where $i\ge j$).

Proposition 7. 

For an odd $c\ge 3$, $\left(a\right)$$Mo\left(G_{O,O}\right)=11c-20$, $\left(b\right)$$Mo\left(G_{O,O}^1\right)=Mo\left(G_{O,O}\right)+2$ and $Mo\left(G_{O,O}^k\right)=Mo\left(G_{O,O}^{k-1}\right)+2$, $j=2,3,\cdots$.

Proof. 

$\left(a\right)$ In the cycle $C_1$, two edges incident on $v_1$ have the contribution

$$\varphi \left(e_{1,1}^{\prime }\right|G_{O,O})=|n_{u_1}\left(e_{1,1}^{\prime }\right|G_{O,O})-n_{v_1}\left(e_{1,1}^{\prime }\right|G_{O,O})|={\displaystyle \frac{3c-3}{2}}-1={\displaystyle \frac{3c-5}{2}},$$

$$\varphi \left(e_{2,1}^{\prime }\right|G_{O,O})=|n_{u_2}\left(e_{2,1}^{\prime }\right|G_{O,O})-n_{v_1}\left(e_{2,1}^{\prime }\right|G_{O,O})|={\displaystyle \frac{3c-1}{2}}-1={\displaystyle \frac{3c-3}{2}}.$$

The remaining edge in the cycle, $e_{1,2}=u_1{u}_2$ has the contribution:

$$\varphi \left(e_{1,2}\right|G_{O,O})=|n_{u_2}\left(e_{1,2}\right|G_{O,O})-n_{u_1}\left(e_{1,2}\right|G_{O,O})|={\displaystyle \frac{3c-1}{2}}-{\displaystyle \frac{3c-3}{2}}=1.$$

Now, except for the cycle $C_{{\displaystyle \frac{c+1}{2}}}$, in all other cycles $C_i$ (for $i=2,3,\cdots {\displaystyle \frac{c-1}{2}}$), we have the following contributions for the edges $e_{2i-2,2i-1}=u_{2i-2}{u}_{2i-1}$ and $e_{2i-2,i}^{\prime }=u_{2i-2}{v}_i$:

$$n_{u_{2i-2}}\left(e_{2i-2,2i-1}\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{u_{2i-1}}\left(e_{2i-2,2i-1}\right|G_{O,O})={\displaystyle \frac{3c-3}{2}},$$

$$n_{u_{2i-2}}\left(e_{2i-2,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{v_i}\left(e_{2i-2,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c-3}{2}}.$$

For the edges $e_{2i-1,2i}=u_{2i-1}{u}_{2i}$ and $e_{2i,i}^{\prime }=u_{2i}{v}_i$, we have

$$n_{u_{2i}}\left(e_{2i-1,2i}\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{u_{2i-1}}\left(e_{2i-1,2i}\right|G_{O,O})={\displaystyle \frac{3c-3}{2}},$$

$$n_{u_{2i}}\left(e_{2i,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{v_i}\left(e_{2i,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c-3}{2}}.$$

Therefore, all four edges have the contribution $\varphi \left(e_{2i-1,2i}\right|G_{O,O})=\varphi \left(e_{2i,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}}-{\displaystyle \frac{3c-3}{2}}=2$ each. For $i={\displaystyle \frac{c+3}{2}},\cdots ,c-1$, the edges $e_{2i-1,2i}=u_{2i-1}{u}_{2i}$ and $e_{2i-1,i}^{\prime }=u_{2i-1}{v}_i$, we have

$$n_{u_{2i-1}}\left(e_{2i-1,2i}\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{u_{2i}}\left(e_{2i-1,2i}\right|G_{O,O})={\displaystyle \frac{3c-3}{2}},$$

$$n_{u_{2i-1}}\left(e_{2i-1,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}},n_{v_i}\left(e_{2i-1,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c-3}{2}}.$$

For the edges $e_{2i,2i+1}=u_{2i}{u}_{2i+1}$ and $e_{2i+1,i}^{\prime }=u_{2i+1}{v}_i$, we have

$$n_{u_{2i+1}}\left(e_{2i,2i+1}\right|G_{O,O})={\displaystyle \frac{3c+1}{2}}\mathrm{and}{n}_{u_{2i}}\left(e_{2i,2i+1}\right|G_{O,O})={\displaystyle \frac{3c-3}{2}},$$

$$n_{u_{2i+1}}\left(e_{2i+1,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}}\mathrm{and}{n}_{v_i}\left(e_{2i+1,i}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c-3}{2}}.$$

Therefore, all four edges have the contribution $\varphi \left(e\right|G_{O,O})={\displaystyle \frac{3c+1}{2}}-{\displaystyle \frac{3c-3}{2}}=2$. In $C_{{\displaystyle \frac{c+1}{2}}}$, two edges, $e_{c-1,{\displaystyle \frac{c+1}{2}}}^{\prime }=u_{c-1}{v}_{{\displaystyle \frac{c+1}{2}}}$ and $e_{c-1,c}=u_{c-1}{u}_c$, have the contributions

$$\varphi \left(e_{c-1,c}\right|G_{O,O})=\varphi \left(e_{c-1,{\displaystyle \frac{c+1}{2}}}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c+1}{2}}-{\displaystyle \frac{3c-3}{2}}=2.$$

The other two edges, $e_{c+1,{\displaystyle \frac{c+1}{2}}}^{\prime }=u_{c+1}{v}_{{\displaystyle \frac{c+1}{2}}}$ and $e_{c,c+1}=u_c{u}_{c+1}$, have the contributions

$$\varphi \left(e_{c,c+1}\right|G_{O,O})=\varphi \left(e_{c+1,{\displaystyle \frac{c+1}{2}}}^{\prime }\right|G_{O,O})={\displaystyle \frac{3c-1}{2}}-{\displaystyle \frac{3c-1}{2}}=0.$$

Among the remaining edges,

$$\varphi \left(e_{1,2c}\right|G_{O,O})=2,\varphi \left(e_{2c-1,2c}\right|G_{O,O})=0\mathrm{and}\varphi \left(e_{c+1,c+2}\right|G_{O,O})=1.$$

Using the above results, from (2), we obtain

$$Mo\left(G_{O,O}\right)=8(c-3)+8+{\displaystyle \frac{3c-3}{2}}+{\displaystyle \frac{3c-5}{2}}=11c-20.$$

$\left(b\right)$ In $G_{O,O}^k$ and $G_{O,O}^{k-1}$, the edges incident on $v_1$ contribute

$$\varphi \left(e\right|G_{O,O}^k)={\displaystyle \frac{3c-1+2k}{2}}-1={\displaystyle \frac{3c-3+2k}{2}},$$

$$\varphi \left(e\right|G_{O,O}^k)={\displaystyle \frac{3c-3+2k}{2}}-1={\displaystyle \frac{3c-5+2k}{2}},$$

$$\varphi \left(e\right|G_{O,O}^{k-1})={\displaystyle \frac{3c-1+2(k-1)}{2}}-1={\displaystyle \frac{3c-3+2(k-1)}{2}},$$

and

$$\varphi \left(e\right|G_{O,O}^{k-1})={\displaystyle \frac{3c-3+2(k-1)}{2}}-1={\displaystyle \frac{3c-5+2(k-1)}{2}},$$

respectively. Two new edges in $G_{O,O}^k$ each contribute $\varphi \left(e\right|G_{O,O}^k)=0$ to the Mostar index. For the remaining edges of $G_{O,O}^k$ and $G_{O,O}^{k-1}$, we have

$$\varphi \left(e\right|G_{O,O}^k)=|n_u\left(e\right|G_{O,O}^{k-1})+1-n_v\left(e\right|G_{O,O}^{k-1})-1|=|n_u\left(e\right|G_{O,O}^{k-1})-n_v\left(e\right|G_{O,O}^{k-1})|=\varphi \left(e\right|G_{O,O}^{k-1}).$$

Therefore, the remaining edges of $G_{O,O}^k$ and $G_{O,O}^{k-1}$ have the same contribution. Thus, $Mo\left(G_{O,O}^k\right)=Mo\left(G_{O,O}^{k-1}\right)+2$. □

We can also provide several classes of constructions for obtaining the same value of the Mostar index as in Proposition 7. A general version of the construction is as follows.

• General Construction IV. Consider the base graph $G_{O,O}$ as in Construction IV. For $j=2,4,\cdots ,c-3$, consider the vertices $u_j$ and $u_{c+j}$. Then, $u_j$ is in between the 4-cycles $C_{{\displaystyle \frac{j+2}{2}}}$ and $C_{{\displaystyle \frac{j+2}{2}}-1}$, and $u_{c+j}$ is in between the cycles $C_{{\displaystyle \frac{c+j+1}{2}}}$ and $C_{{\displaystyle \frac{c+j+1}{2}}-1}$. Now, for each $j=2,4,\cdots ,c-3$, let $G_{O,O}^{j,1}$ be the graph obtained by deleting the edges $u_j{v}_{{\displaystyle \frac{j+2}{2}}}$, $u_{c+j}{v}_{{\displaystyle \frac{c+j-1}{2}}}$ and subdividing the edges $u_j{u}_{j+1}$, $u_{c+j}{u}_{c+j+1}$, and relabeling the vertices of C as $u_1,u_2,\cdots ,u_{2c+2}$. Also, attach the edges $u_{j+1}{v}_{{\displaystyle \frac{j+2}{2}}}$ and $u_{c+j+3}{v}_{{\displaystyle \frac{c+j+1}{2}}}$ (or add an edge between the cycles $C_{{\displaystyle \frac{j+2}{2}}}$, $C_{{\displaystyle \frac{j+2}{2}}-1}$ and $C_{{\displaystyle \frac{c+j+1}{2}}}$, $C_{{\displaystyle \frac{c+j+1}{2}}-1}$ in C). Proceeding in this manner, let $G_{O,O}^{j,k}$ be the graph obtained by subdividing the edges $u_{j+k-2}{u}_{j+k-1}$, $u_{c+j+2k-2}{u}_{c+j+2k-1}$ of $G_{O,O}^{j,k-1}$ exactly once (or inserting $k-1$ edges between the cycles $C_{{\displaystyle \frac{j+2}{2}}}$, $C_{{\displaystyle \frac{j+2}{2}}-1}$ and $C_{{\displaystyle \frac{c+j+1}{2}}}$, $C_{{\displaystyle \frac{c+j+1}{2}}-1}$ in C of $G_{O,O}^{j,1}$). As shown in Figure 2, in each of the steps, relabel the vertices of the cycle C in $G_{E,O}^{j,k}$. Clearly, $G_{O,O}^{j,k}$ is a c-cyclic graph with $3c-1+2k$ vertices and $4c-2+2k$ edges, where $k=2,3,\cdots$ and $j=2,4,\cdots ,c-3$.

Proposition 8. 

For every fixed odd integer $c\ge 3$, $Mo\left(G_{O,O}^{j,k}\right)=Mo\left(G_{O,O}^{j,k-1}\right)+2$, where $j=2,4,\cdots ,c-3$ and $k=2,3,\cdots$.

Proof. 

In $G_{O,O}^{j,k}$ and $G_{O,O}^{j,k-1}$, the edges incident on $v_1$ contribute

$$\varphi \left(e\right|G_{O,O}^{j,k})={\displaystyle \frac{3c-3+2k}{2}},\varphi \left(e\right|G_{O,O}^{j,k})={\displaystyle \frac{3c-5+2k}{2}}$$

and

$$\varphi \left(e\right|G_{O,O}^{j,k-1})={\displaystyle \frac{3c-3+2(k-1)}{2}},\varphi \left(e\right|G_{O,O}^{j,k-1})={\displaystyle \frac{3c-5+2(k-1)}{2}},$$

respectively. Two new edges in $G_{O,O}^{j,k}$ each contribute $\varphi \left(e\right|G_{O,O}^{j,k})=0$ to the Mostar index. The remaining edges have the same contribution in $G_{O,O}^{j,k}$ as in $G_{O,O}^{j,k-1}$. Therefore, $Mo\left(G_{O,O}^{j,k}\right)=Mo\left(G_{O,O}^{j,k-1}\right)+2$. □

Using these constructions, we are ready to resolve Problem 1 by proving Conjecture 1. The proof of Conjecture 1 is as follows. Here, we denote ${\mathbb{Z}}_{\ge 0}$ as the set of non-negative integers, and the set of integers is represented by the letter $\mathbb{Z}$.

Theorem 1. 

For any fixed $c\ge 3$, there exists a c-cyclic graph with the Mostar index $Mo\left(G\right)=p$, where $p\in {\mathbb{Z}}_{\ge 0}\setminus A$, and A is given by $A=A_1\cup A_2$ when c is even, and $A=A_3\cup A_4$ when c is odd, with

$$\begin{array}{cc}\hfill A_1& =\left\{2x\in \mathbb{Z}|0\le x\le 4c-5,\mathbf{c}is even\right\},\hfill \\ \hfill A_2& =\left\{2x+1\in \mathbb{Z}|1\le x\le {\displaystyle \frac{9c}{2}}-7,\mathbf{c}is even\right\},\hfill \\ \hfill A_3& =\left\{2x\in \mathbb{Z}|0\le x\le {\displaystyle \frac{11c-15}{2}},\mathbf{c}is odd\right\},\hfill \\ \hfill A_4& =\left\{2x+1\in \mathbb{Z}|1\le x\le {\displaystyle \frac{11c-23}{2}},\mathbf{c}is odd\right\}.\hfill \end{array}$$

Proof. 

We consider the following two cases:

• Case 1: $\mathbf{c}$ is even. The graph $G_{E,E}$ (see, Figure 1) is a c-cyclic graph (even $c\ge 4$) described in Construction I. According to Proposition 1, we have

  $$\begin{array}{c}\hfill Mo\left(G_{E,E}\right)=8c-8,Mo\left(G_{E,E}^1\right)=Mo\left(G_{E,E}\right)+2,Mo\left(G_{E,E}^k\right)=Mo\left(G_{E,E}^{k-1}\right)+2\mathrm{for}k=2,3\cdots \end{array}$$

  From the above, we conclude that every even number greater than or equal to $8c-8$ can be the Mostar index of some c-cyclic graph for every fixed c (even $c\ge 4$). Thus we have $Mo\left(G_{E,E}\right)\ge 2k$, where k is a positive integer with $k\ge 4c-4$ (even $c\ge 4$).
  The graph $G_{E,O}$ (see, Figure 3) is a c-cyclic graph (even $c\ge 4$) described in Construction II. According to Proposition 3, we have

  $$\begin{array}{c}\hfill Mo\left(G_{E,O}\right)=9c-11,Mo\left(G_{E,O}^1\right)=Mo\left(G_{E,O}\right)+2,Mo\left(G_{E,O}^k\right)=Mo\left(G_{E,O}^{k-1}\right)+2\mathrm{for}k=2,3\cdots \end{array}$$

  From the above, we conclude that every odd number greater than or equal to $9c-11$ can be the Mostar index of some c-cyclic graph for every fixed c (even $c\ge 4$). Thus we have $Mo\left(G_{E,E}\right)\ge 2k+1$, where k is a positive integer with $k\ge {\displaystyle \frac{9c}{2}}-6$ (even $c\ge 4$).
  For the c-cyclic graph for every fixed c (even $c\ge 4$), we obtain $Mo\left(G\right)=p$, where $p\in {\mathbb{Z}}_{\ge 0}\setminus A$, and A is given by

  $$A=A_1\cup A_2,$$

  with

  $$\begin{array}{cc}\hfill A_1& =\{2x\in \mathbb{Z}|0\le x\le 4c-5,\mathbf{c}\mathrm{is} \mathrm{even}\},\hfill \\ \hfill A_2& =\{2x+1\in \mathbb{Z}|1\le x\le {\displaystyle \frac{9c}{2}}-7,\mathbf{c}\mathrm{is} \mathrm{even}\}.\hfill \end{array}$$
• Case 2: $\mathbf{c}$ is odd. The graph $G_{O,E}^k$ (see, Figure 4) is a c-cyclic graph (odd $c\ge 3$) described in Construction III. According to Proposition 5, we have

  $$\begin{array}{c}\hfill Mo\left(G_{O,E}\right)=11c-13,Mo\left(G_{O,E}^1\right)=Mo\left(G_{O,E}\right)+2,Mo\left(G_{O,E}^k\right)=Mo\left(G_{O,E}^{k-1}\right)+2\mathrm{for}k=2,3\cdots \end{array}$$

  From the above, we conclude that every even number greater than or equal to $11c-13$ can be the Mostar index of some c-cyclic graph for every fixed c when c is odd. Thus we have $Mo\left(G_{E,E}\right)\ge 2k$, where k is a positive integer with $k\ge {\displaystyle \frac{11c-13}{2}}$ (c is odd).
  The graph $G_{O,O}$ (see, Figure 5) is a c-cyclic graph (odd $c\ge 3$) described in Construction IV. According to Proposition 7, we have

  $$\begin{array}{cc}\hfill & Mo\left(G_{O,O}\right)=11c-20,Mo\left(G_{O,O}^1\right)=Mo\left(G_{O,O}\right)+2\hfill \\ \hfill \mathrm{and}& \\ \hfill & Mo\left(G_{O,O}^k\right)=Mo\left(G_{O,O}^{k-1}\right)+2\mathrm{for}k=2,3\cdots \hfill \end{array}$$

  From the above, we conclude that every odd number greater than or equal to $11c-20$ can be the Mostar index of some c-cyclic graph for every fixed c when c is odd. Thus we have $Mo\left(G_{O,O}\right)\ge 2k+1$, where k is a positive integer with $k\ge {\displaystyle \frac{11c-21}{2}}$ (odd $c\ge 3$).
  

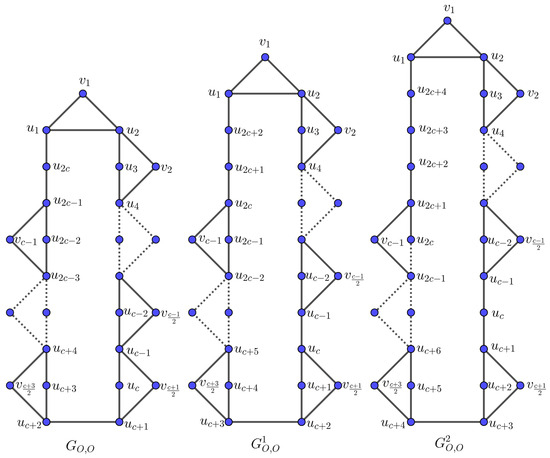  Figure 5. The graphs mentioned in Construction IV.
  For the c-cyclic graph for every fixed c (odd $c\ge 3$), we obtain $Mo\left(G\right)=p$, where $p\in {\mathbb{Z}}_{\ge 0}\setminus A$, and A is given by

  $$A=A_3\cup A_4,$$

  with

  $$\begin{array}{cc}\hfill A_3& =\{2x\in \mathbb{Z}|0\le x\le {\displaystyle \frac{11c-15}{2}},\mathbf{c}\mathrm{is} \mathrm{odd}\},\hfill \\ \hfill A_4& =\{2x+1\in \mathbb{Z}|1\le x\le {\displaystyle \frac{11c-23}{2}},\mathbf{c}\mathrm{is} \mathrm{odd}\}.\hfill \end{array}$$

This completes the proof of the theorem. □

Remark 1. 

Using Theorem 1, we provide a solution to Problem 1.

Using Theorem 1, we can also solve the inverse Mostar index problem for connected graphs.

Corollary 1. 

For every positive integer $p\ge 19$, there exists a graph G with the Mostar index $Mo\left(G\right)=p$.

Proof. 

For $c=4$, from Theorem 1, we have

$$\begin{array}{cc}\hfill A_1& =\{2x\in \mathbb{Z}|0\le x\le 11\},A_2=\{2x+1\in \mathbb{Z}|1\le x\le 11\},\hfill \end{array}$$

that is,

$$A_1=\{0,2,4,6,\dots ,20,22\},A_2=\{1,3,5,\dots ,21,23\}.$$

Similarly, for $c=3$, from Theorem 1, we have

$$A_3=\{0,2,4,\dots ,16,18\},A_4=\{1,3,5,\dots ,9,11\}.$$

This completes the proof of the result. □

Remark 2. 

We can also prove Theorem 1, using General Constructions I, II, III, and IV and Proposition 2, Proposition 4, Proposition 6, and Proposition 8.

3. Conclusions

Several variants of the Mostar index have been proposed recently, including the edge Mostar index $M{o}_e\left(G\right)$, the total Mostar index $M{o}^{\ast }\left(G\right)$, and the total edge Mostar index $M{o}_e^{\ast }\left(G\right)$ [3]. For a graph G, these indices are defined as follows:

$$M{o}^{\ast }\left(G\right)=\sum _{\{u,v\}\subseteq V}|n_u\left(e\right|G)-n_v\left(e\right|G)|,$$

$$M{o}_e\left(G\right)=\sum _{uv\in E\left(G\right)}|m_u\left(e\right|G)-m_v\left(e\right|G)|,$$

$$M{o}_e^{\ast }\left(G\right)=\sum _{\{u,v\}\subseteq V}|m_u\left(e\right|G)-m_v\left(e\right|G)|,$$

where $m_u\left(e\right|G)$ is the number of edges closer to u than to v, and similarly for $m_v\left(e\right|G)$. In this paper, we have resolved an open problem and conjecture related to the inverse Mostar index problem for c-cyclic graphs with $c\ge 3$. Despite this significant progress, several open problems remain in this area. For instance, the inverse edge Mostar index problem for c-cyclic graphs with $c\ge 4$ has yet to be explored. Additionally, the infinite realizability of odd integers for both the Mostar index and the edge Mostar index remains an open question. Future research opportunities include addressing analogous problems for other bond-additive indices, such as the total Mostar index and the total edge Mostar index. These extensions represent promising directions for further studies in this field.