Four-Module Cascaded Downsampling Filter for Phasemeter in Space Gravitational Wave Detection
Abstract
1. Introduction
2. Downsampling of the Phase Information
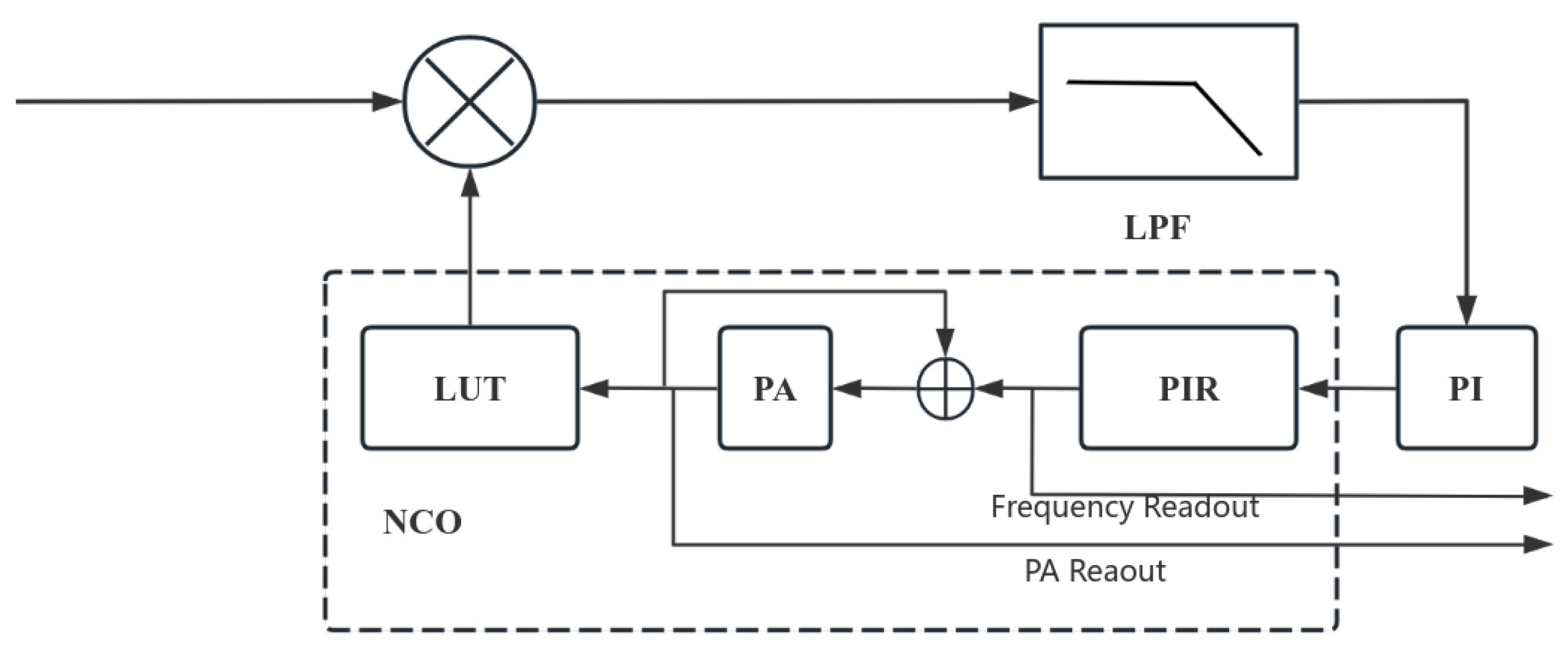
2.1. Digital Phase-Locked Loop-Based Phase Measurement
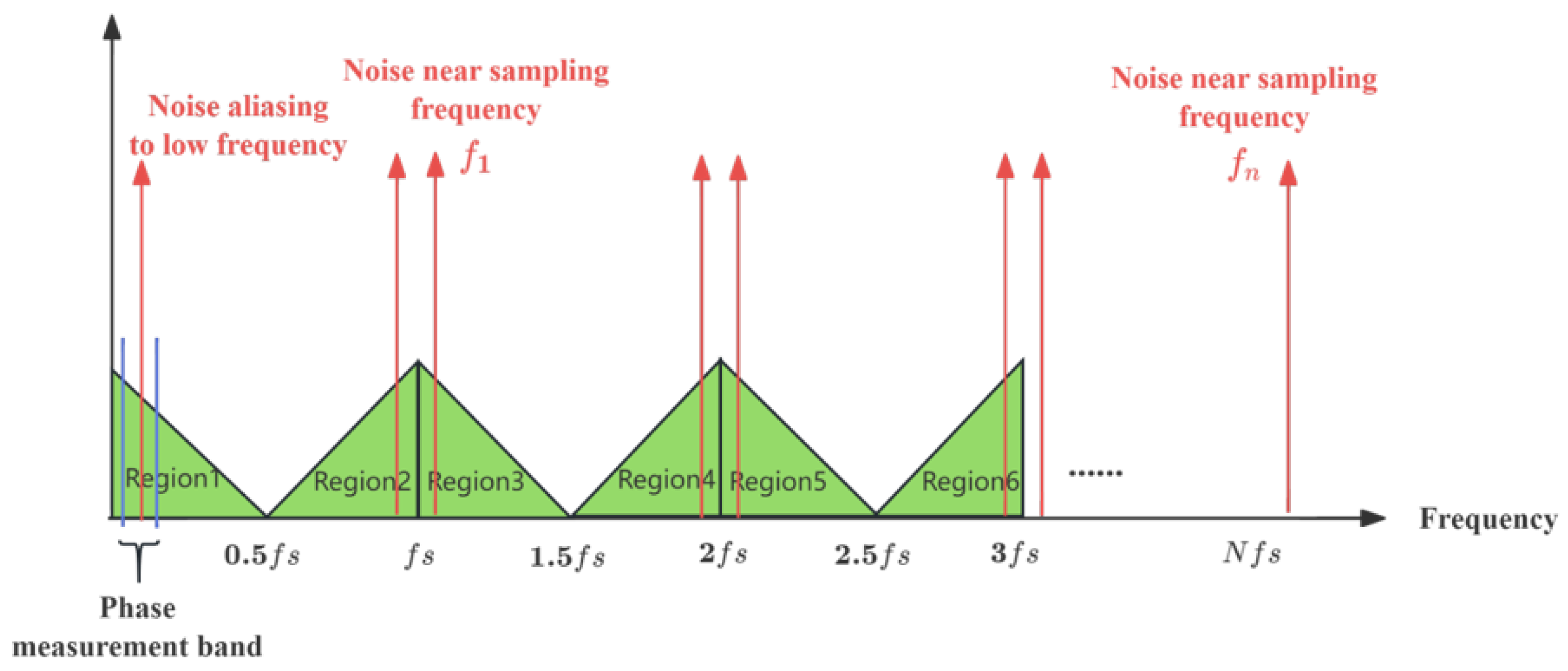
2.2. Spectral Aliasing Impact Analysis
3. Downsampling Filter Design
3.1. Structural Design of Downsampling Filter
3.2. Parameter Design of Downsampling Filter
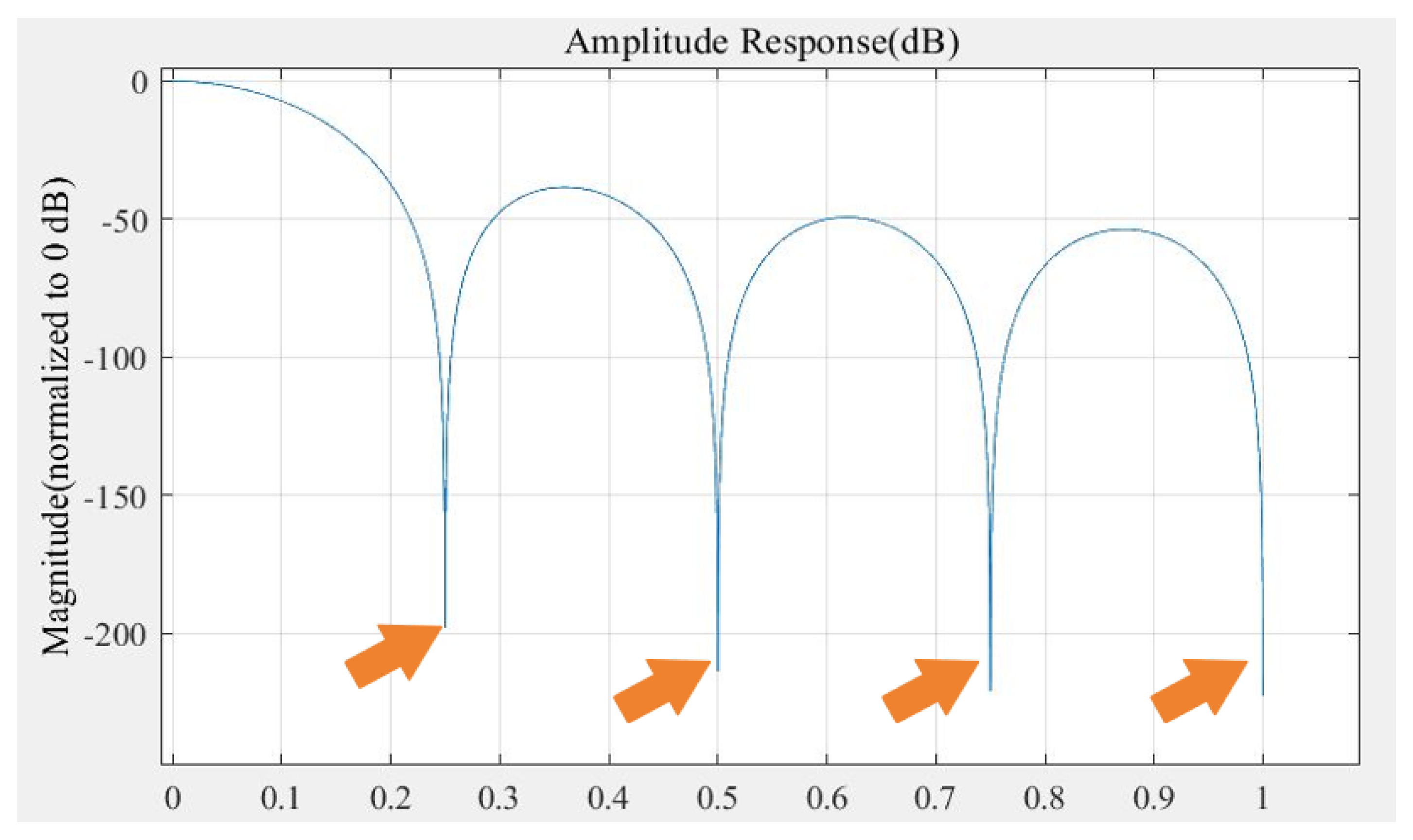
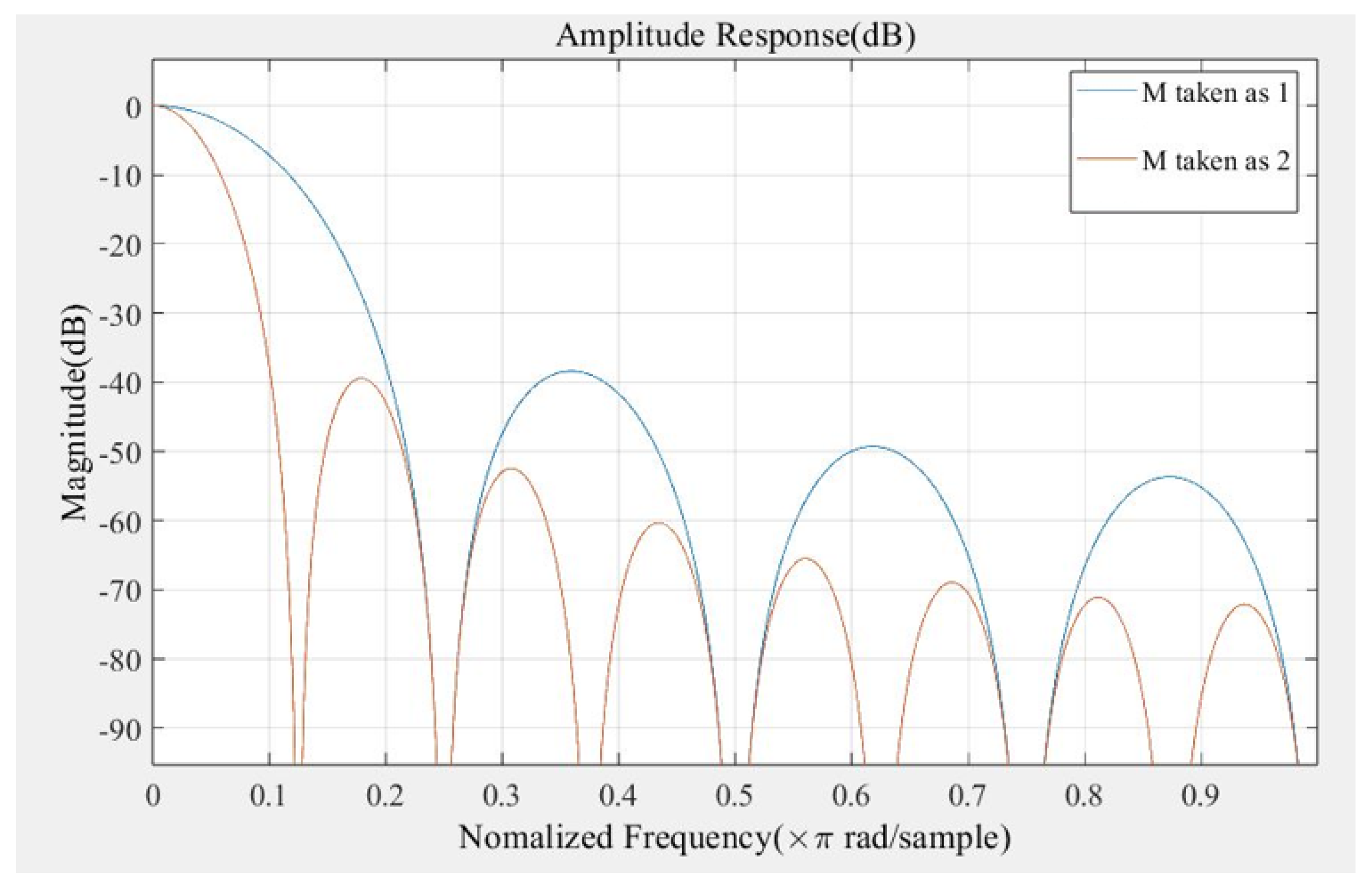
3.2.1. CIC Filter Bank Parameter Design
3.2.2. Compensation Filter Parameter Design
3.2.3. Multi-Rate FIR, HB Filter Bank Parameter Design
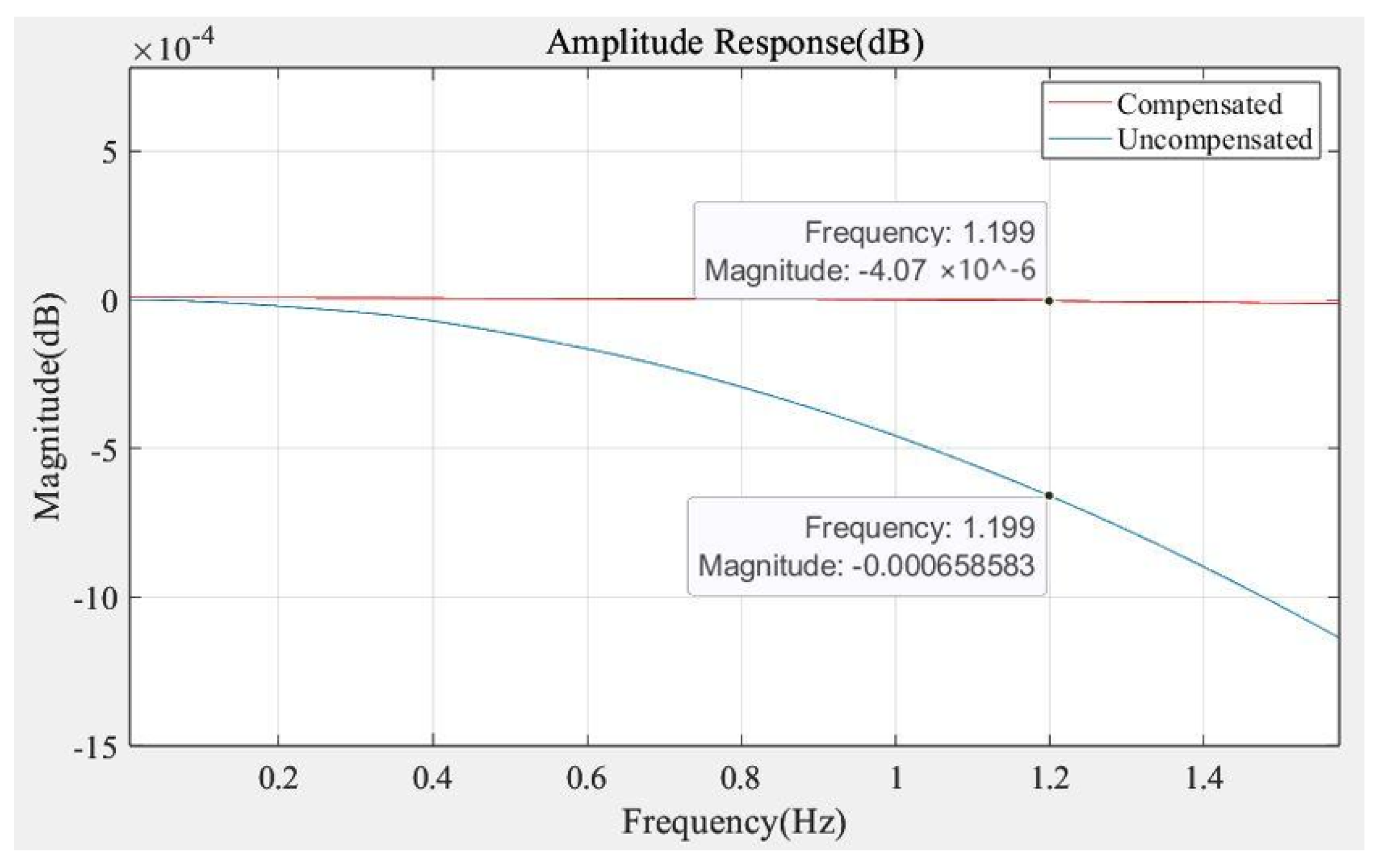
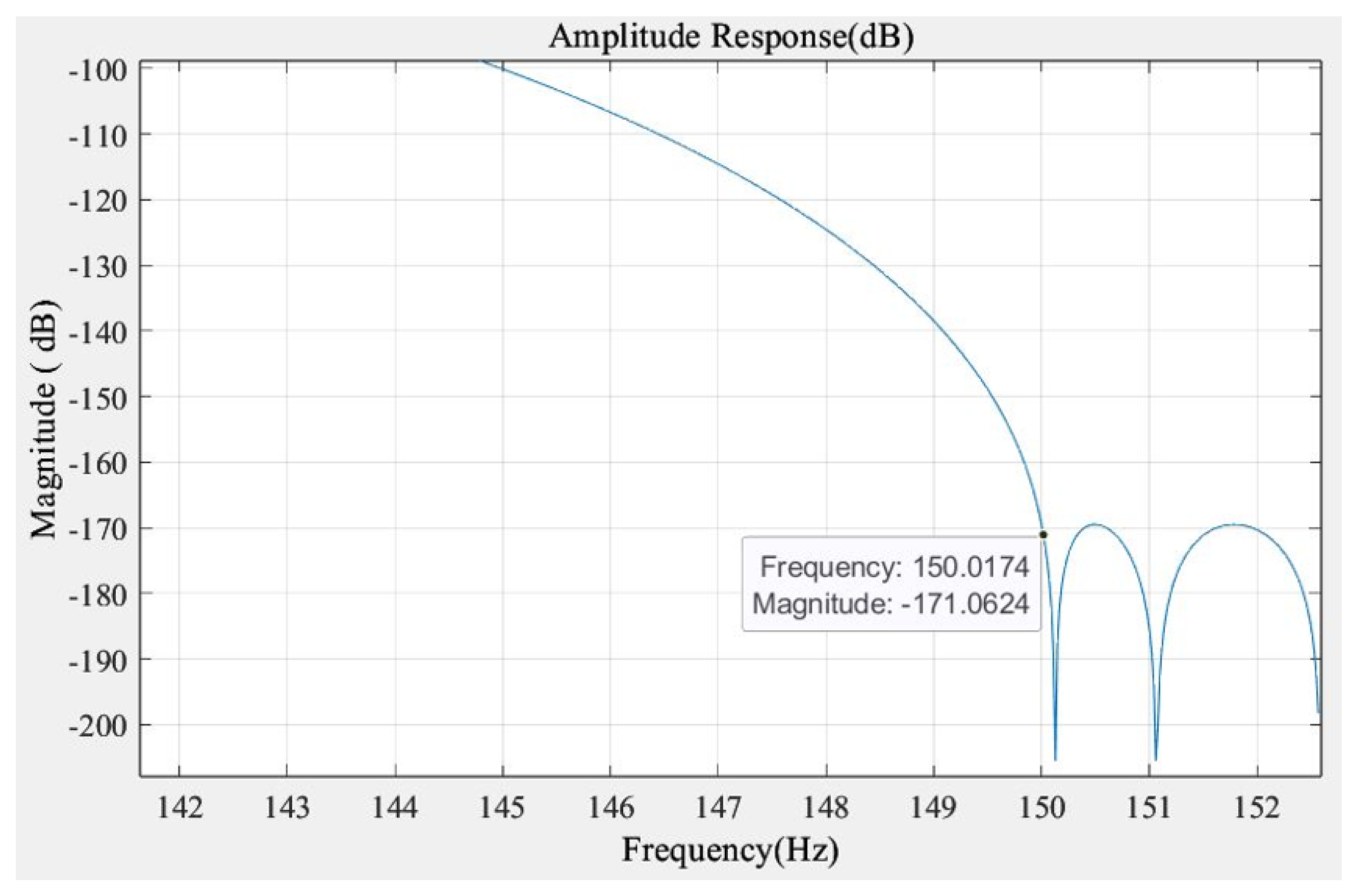
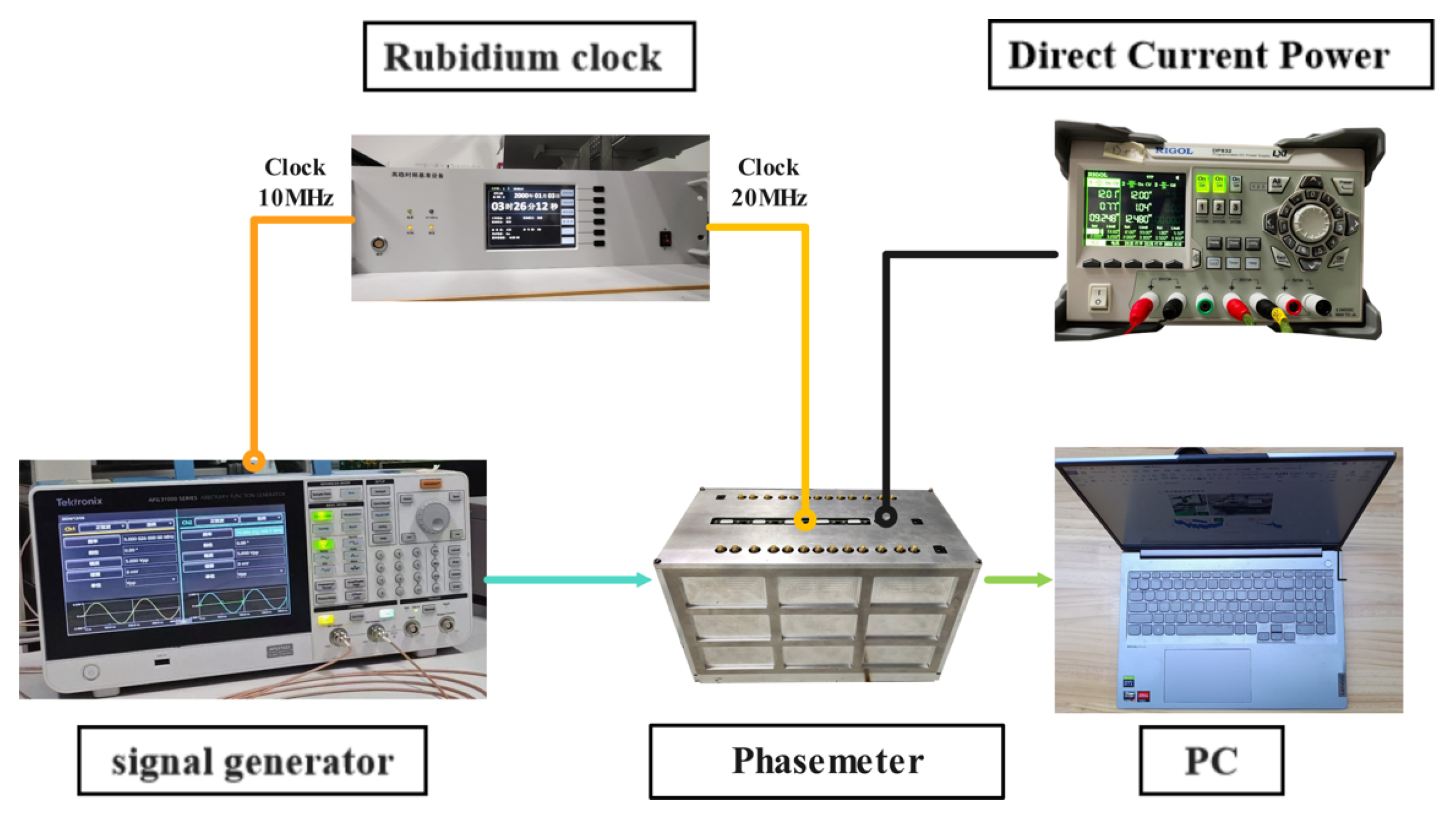
4. Experimental Testing of Downsampling Filter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LISA | Laser Interferometer Space Antenna |
| DPLL | Digital Phase-Locked Loop |
| NCO | Numerically Controlled Oscillator |
| FIR | Finite Impulse Response |
| IIR | Infinite Impulse Response |
| CIC | Cascade Intergrator Comb |
| HB | Half Band |
| VHDL | Very-High-Speed Integrated Circuit Hardware Description Language |
| FPGA | Field-Programmable Gate Array |
| FCDF | Four-module Cascaded Downsampling Filter |
References
- Danzmann, K. LISA and its pathfinder. Nat. Phys. 2015, 11, 613–615. [Google Scholar]
- Hu, W.R.; Wu, Y.L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, Y.; Wu, Y.; Hu, W.; Jin, G. The Taiji program: A concise overview. Prog. Theor. Exp. Phys. 2020, 2021, 05A108. [Google Scholar] [CrossRef]
- Hu, Y.; Mei, J.; Luo, J. TianQin project and international collaboration. Chin. Sci. Bull. 2019, 64, 2475–2483. [Google Scholar] [CrossRef]
- Mei, J.; Bai, Y.Z.; Bao, J.; Barausse, E.; Cai, L.; Canuto, E.; Cao, B.; Chen, W.M.; Chen, Y.; Ding, Y.W.; et al. The TianQin project: Current progress on science and technology. Prog. Theor. Exp. Phys. 2021, 2021, 05A107. [Google Scholar] [CrossRef]
- Luo, Z.R.; Zhang, M.; Jin, G. Overall discussion on the key problems of a space-borne laser interferometer gravitational wave antenna. Chin. Sci. Bull. 2019, 64, 2468–2474. [Google Scholar] [CrossRef]
- Liu, H.S.; Dong, Y.H.; Li, Y.Q.; Luo, Z.R.; Jin, G. The evaluation of phasemeter prototype performance for the space gravitational waves detection. Rev. Sci. Instrum. 2014, 85, 024503. [Google Scholar] [CrossRef]
- Gerberding, O.; Sheard, B.; Bykov, I.; Kullmann, J.; Delgado, J.J.; Danzmann, K.; Heinzel, G. Phasemeter core for intersatellite laser heterodyne interferometry: Modelling, simulations and experiments. Class. Quantum Gravity 2013, 30, 235029. [Google Scholar] [CrossRef]
- Staab, M.; Lilley, M.; Bayle, J.B.; Hartwig, O. Laser noise residuals in LISA from onboard processing and time-delay interferometry. Phys. Rev. D 2024, 109, 043040. [Google Scholar] [CrossRef]
- Liang, Y.R. High Precision Phase Measurement for Heterodyne Laser Interferometer. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2013. [Google Scholar]
- Zhang, J.; Yang, Z.; Ma, X.; Peng, X.; Liu, H.; Tang, W.; Zhao, M.; Gao, C.; Qiang, L.E.; Han, X.; et al. Inter-spacecraft offset frequency setting strategy in the Taiji program. Appl. Opt. 2022, 61, 837–843. [Google Scholar] [CrossRef]
- Luo, Z.R.; Yu, T.; Liu, H.S. Taiji Scientific Collaboration. The phasemeter of Taiji-1 experimental satellite. Int. J. Mod. Phys. A 2021, 36, 2140005. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Z.; Jin, G. The Development of Phasemeter for Taiji Space Gravitational Wave Detection. Microgravity Sci. Technol. 2018, 30, 775–781. [Google Scholar] [CrossRef]
- Kullmann, J. Development of a Digital Phase Measuring System with Microradian Precision for LISA. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 2012. [Google Scholar]
- Liang, Y.R.; Ye, X.J. High-precision phasemeter for inter-satellite laser ranging. In Proceedings of the 8th Annual Academic Meeting of the Deep Space Exploration Technology Committee of the Chinese Society of Astronautics, Shanghai, China, 26 October 2011. [Google Scholar]
- Ware, B.; Folkner, W.M.; Shaddock, D.; Spero, R.; Halverson, P.; Harris, I.; Rogstad, T. Phase Measurement System for Inter-Spacecraft Laser Metrology. 2006. Available online: https://www.researchgate.net/publication/242087596_Phase_Measurement_System_for_Inter-Spacecraft_Laser_Metrology (accessed on 29 June 2006).
- Li, S. Research and Design of Digital Decimation Filter in Audio Sigma-Delta ADC. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Yu, Z. Design of A CIC digital filter in sigma-delta ADC. China Integr. Circuit 2024, 33, 34–36. [Google Scholar]
- Yang, R.; Liu, H.; Luo, Z. Optimization Design of Decimation Filter for the Phasemeter in the Space Gravitational Wave Detection. IEEE Trans. Instrum. Meas. 2024, 73, 7006508. [Google Scholar] [CrossRef]
- Tian, D.; Chen, Y.Z. Research and Performance Analysis of CIC Filter Compensation Method. In Proceedings of the 12th National Conference on Signal and Intelligent Information Processing and Application, Nanjing, China, 8–10 March 2024. [Google Scholar]
- Shen, Z.S.; Liu, Y.T.; Fang, S.; Wang, Y. A Digital Decimation Filter of Σ-ΔADC with Ultra-Low power and Small Area. Microelectronics 2022, 52, 555–561. [Google Scholar]
- Wan, R.; Li, Y.; Tian, C.; Yang, F.; Deng, W.; Tang, S.; Wang, J.; Zhang, W. Design and Implementation of Sigma-Delta ADC Filter. Electronics 2022, 11, 4229. [Google Scholar] [CrossRef]






| Variable Decimation Factor Filter Bank | Fixed Decimation Factor Filter Bank |
|---|---|
| Decimation multiplier: 2/4/8 | Decimation multiplier: 16 |
| Diffierential delay: 2 | Diffierential delay: 1 |
| Order: 3 | Order: 3 |
| Passband cutoff frequency | 1.2 Hz |
| Stopband cutoff frequency | 150 Hz |
| Passband maximum attenuation | dB |
| Stopband minimum attenuation | 170 dB |
| Multi-Rate FIR Filter | HB Fliter |
|---|---|
| Passband cutoff frequency: 1.2 Hz | Passband cutoff frequency: 1.2 Hz |
| Stopband cutoff frequency: 100/19/2.4 Hz | Stopband cutoff frequency: 8.8 Hz |
| Decimation factor: 3/5/3 | Decimation factor: 2 |
| Passband max attenuation: dB | Passband max attenuation: dB |
| Stopband minimum attenuation: 160 dB | Stopband minimum attenuation: 160 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Yu, T.; Xue, K.; Pan, M.; Long, H.; Wang, Z.; Zhou, J. Four-Module Cascaded Downsampling Filter for Phasemeter in Space Gravitational Wave Detection. Symmetry 2025, 17, 258. https://doi.org/10.3390/sym17020258
Yang P, Yu T, Xue K, Pan M, Long H, Wang Z, Zhou J. Four-Module Cascaded Downsampling Filter for Phasemeter in Space Gravitational Wave Detection. Symmetry. 2025; 17(2):258. https://doi.org/10.3390/sym17020258
Chicago/Turabian StyleYang, Peng, Tao Yu, Ke Xue, Mingzhong Pan, Hongyu Long, Zhi Wang, and Jun Zhou. 2025. "Four-Module Cascaded Downsampling Filter for Phasemeter in Space Gravitational Wave Detection" Symmetry 17, no. 2: 258. https://doi.org/10.3390/sym17020258
APA StyleYang, P., Yu, T., Xue, K., Pan, M., Long, H., Wang, Z., & Zhou, J. (2025). Four-Module Cascaded Downsampling Filter for Phasemeter in Space Gravitational Wave Detection. Symmetry, 17(2), 258. https://doi.org/10.3390/sym17020258







