Symmetry Study on Damage Inversion of Wharf Pile Foundation in Three Gorges Reservoir Area Under Ship Impact
Abstract
1. Introduction
2. Uncertainty and Quantification of Ship Berthing
2.1. Quantification of Ship Tonnage Uncertainty
2.2. Quantification of Ship Impact Position Uncertainty
3. Establishment of Sample Data Set for Damage Inversion
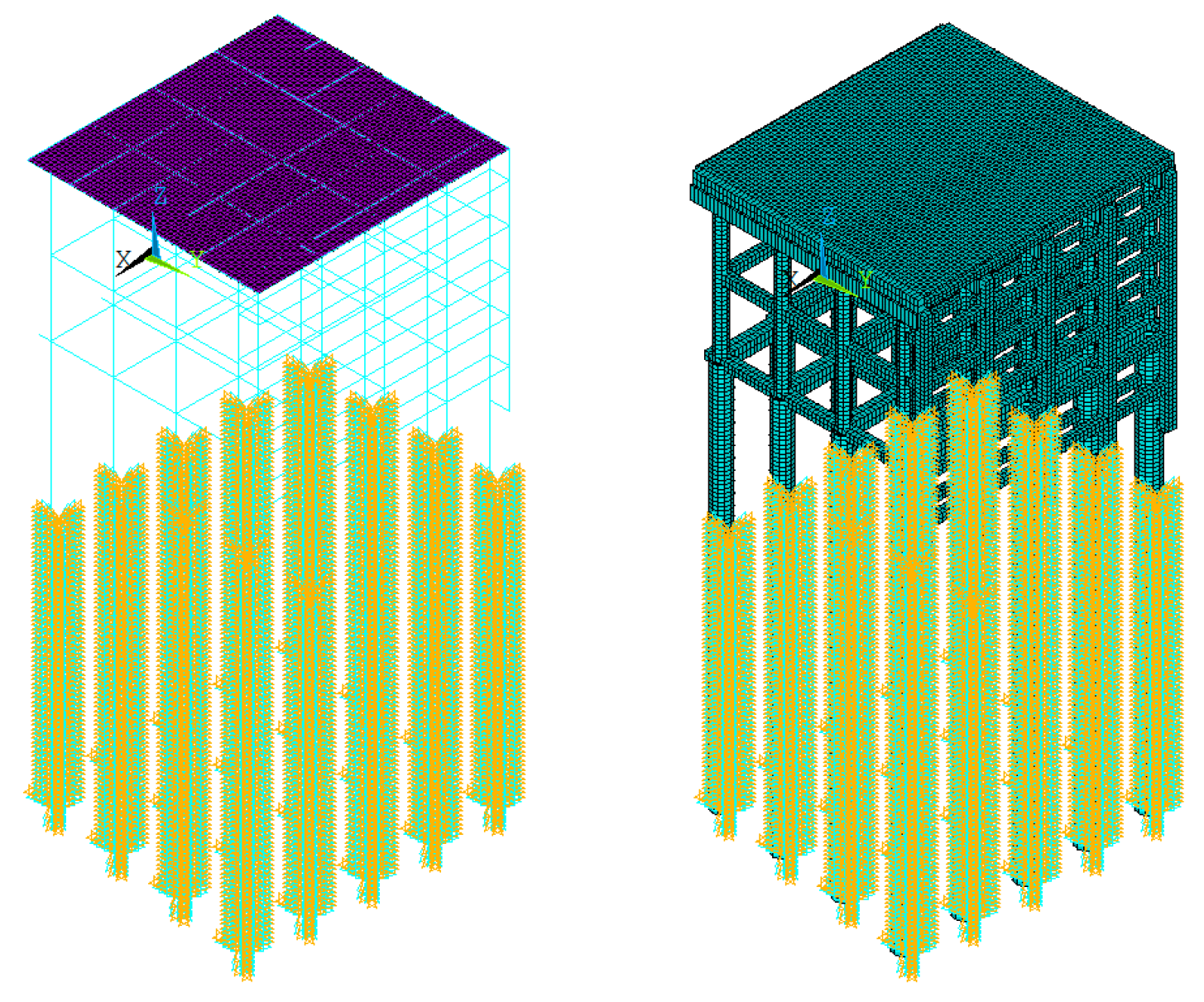
3.1. Establishment of Parametric Model
3.2. Data Collection and Sample Set Construction
4. Establishment of Damage Inducement Inversion Model
- (1)
- Collect stress characteristic data of finite element model pile groups under different working conditions.
- (2)
- Fuse and reconstruct the stress sample data; calculate the range, mean, variance, and discrete coefficient of the extracted stress features of each pile; and use the calculated results as a supplement to the sample features to construct a sample data set D, which contains features x and corresponding labels y, where X ∈ Rm × n, X ∈ Rm × q, m is the number of samples, and n is the number of features.
- (3)
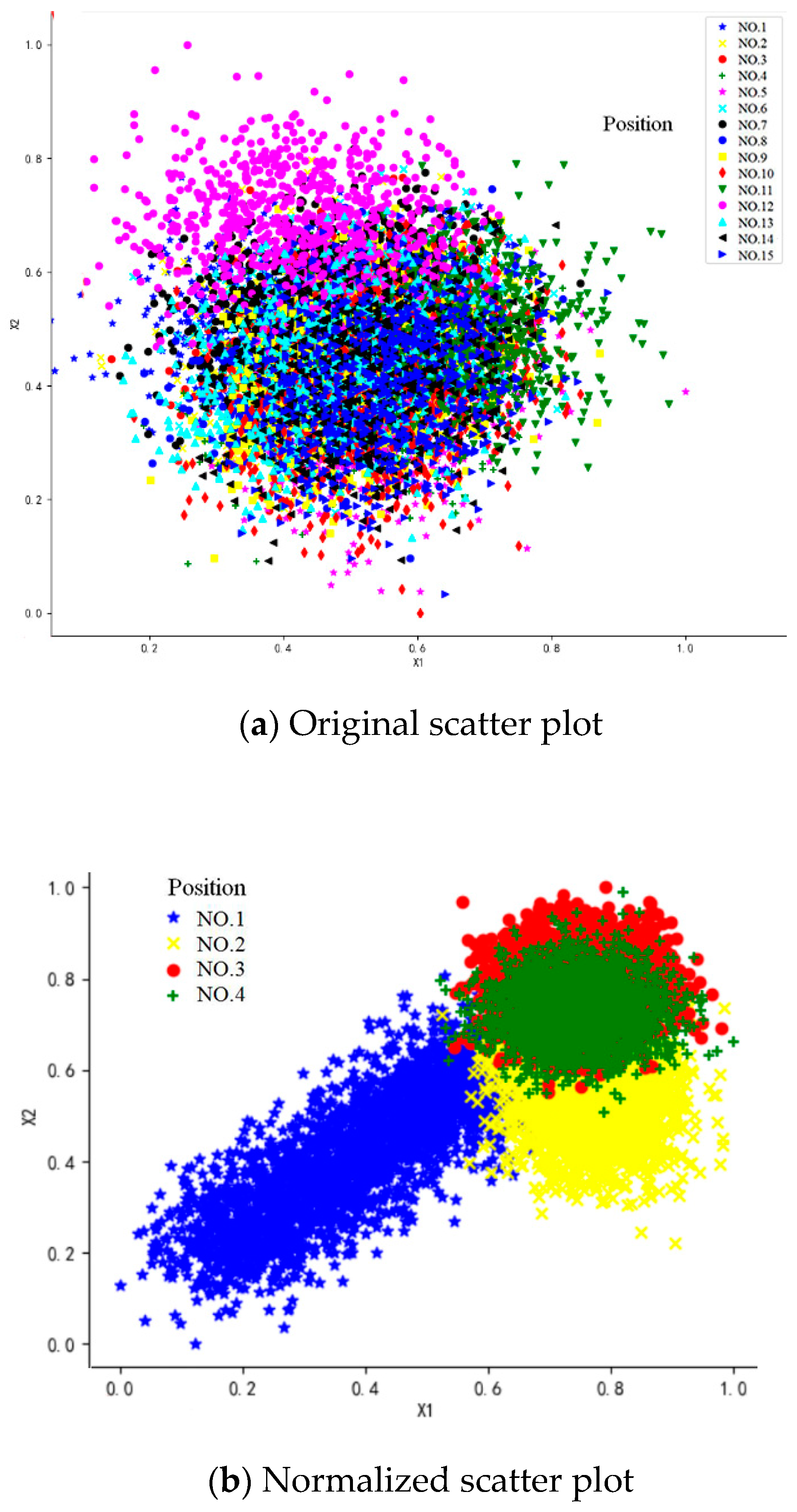
- Information fusion is carried out on the sample data set by the normalization method, and the first principal components, x_PCA ∈ RM × a, are extracted.
- (4)
- The data set is randomly divided into a training set S and a test set T according to a ratio of 3:1 by adopting a set-aside method.
- (5)
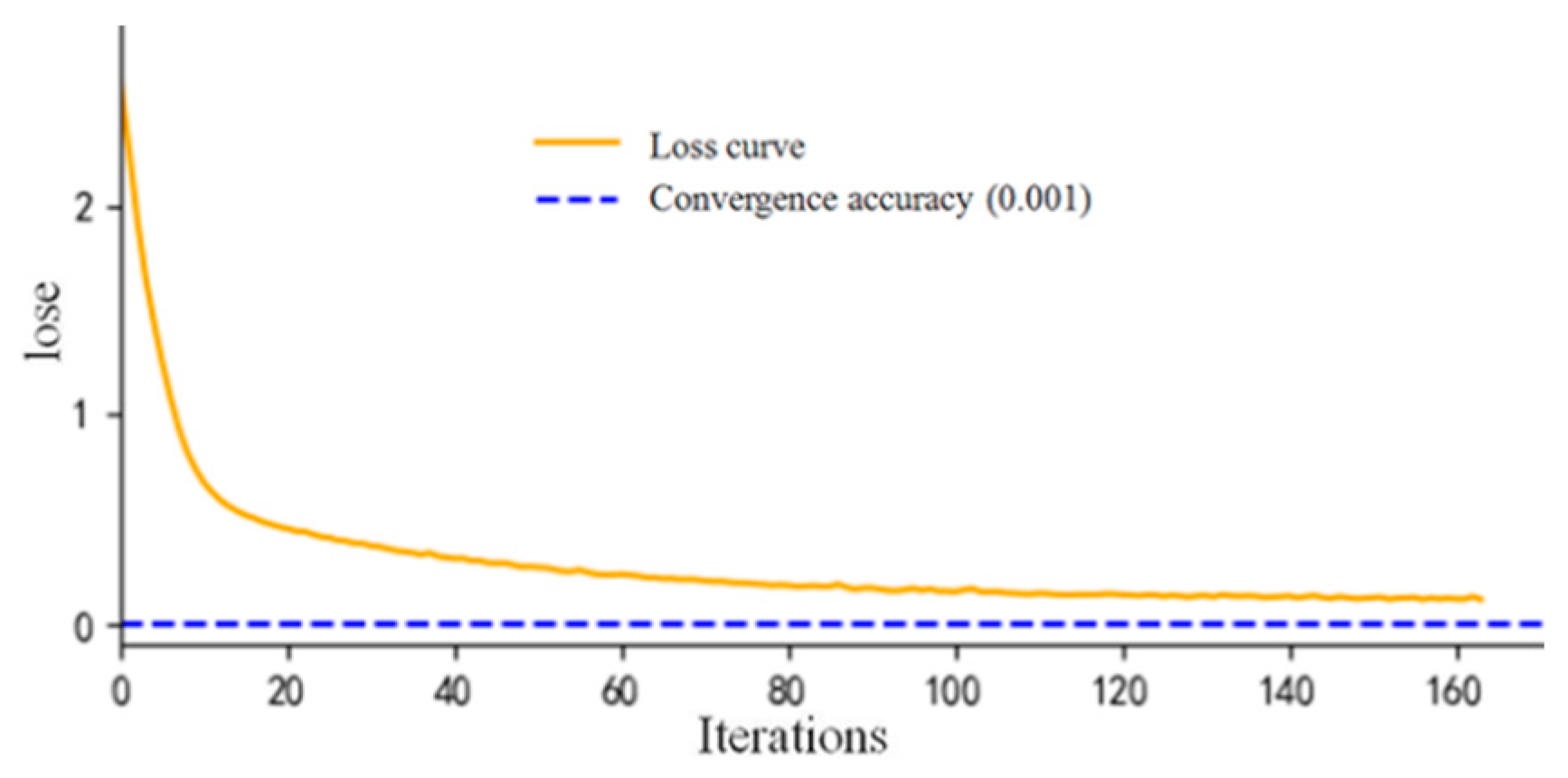
- Construct the neural network full connection model ANN with three hidden layers. The model optimizer adopts adam algorithm, the activation function adopts {“identity”, “logistic”, “tanh”, “relu”}, the damage function of classification learner in the output layer adopts cross entropy loss, the loss function of regression learner adopts the mean square error function, and the range of penalty factor α is set (0.0001–10). Set the maximum iteration number and model convergence accuracy, set k-fold cross-validation, split the training set s and load it into the ANN model for self-adaptive training, train the classification problem and regression problem, respectively, and cross-validate the training to obtain the model score to evaluate the performance of the model. The performance metrics mainly adopt precision accuracy and average absolute error MAE, and the low score means the model is unreliable, so the next step of optimization and parameter adjustment is carried out. Parameter optimization is carried out through the Gridsearch toolkit, and the parameters searched include the optimal parameters of the model, such as the number of hidden layers of neural network, the number of hidden layer nodes, and penalty factors.
- (6)
- After training and verifying the training set S, load the test set T into the model to further evaluate the generalization ability of the model.
5. Inversion Analysis of Damage Inducement
5.1. Artificial Neural Network Model Training
5.2. Damage Inversion Analysis Results
- (1)
- Ship impact location identification
- (2)
- Identification of ship impact strength
6. Conclusions
- (1)
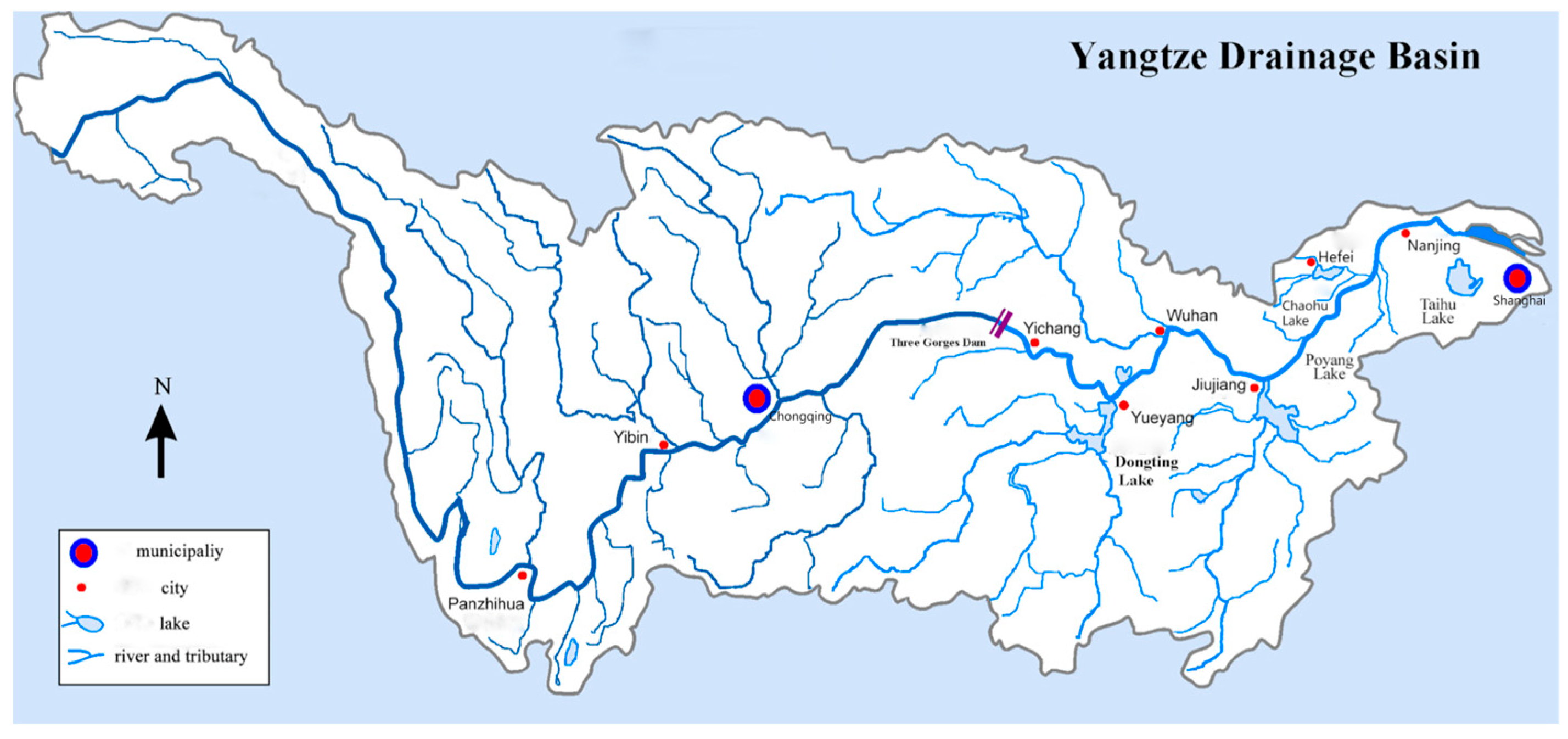
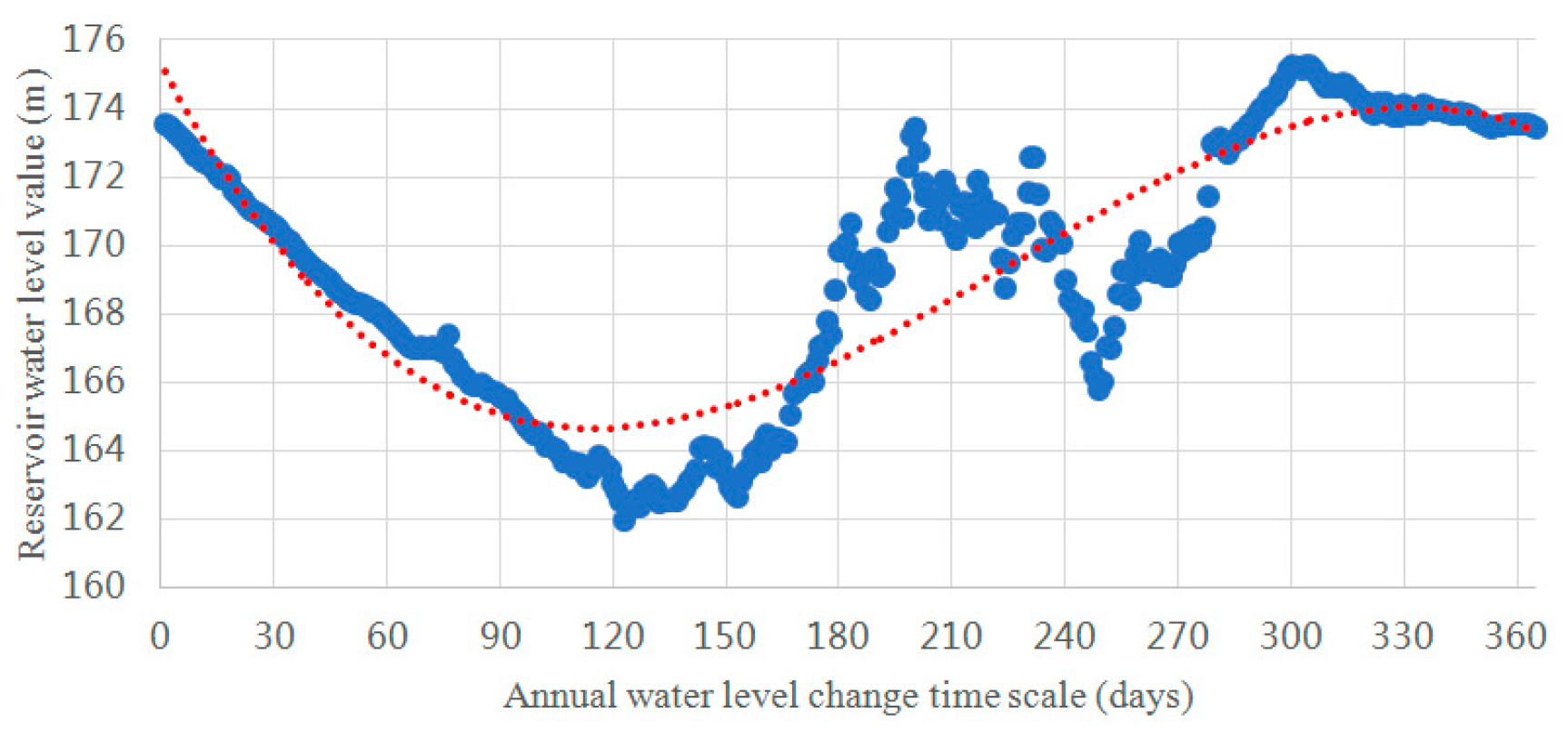
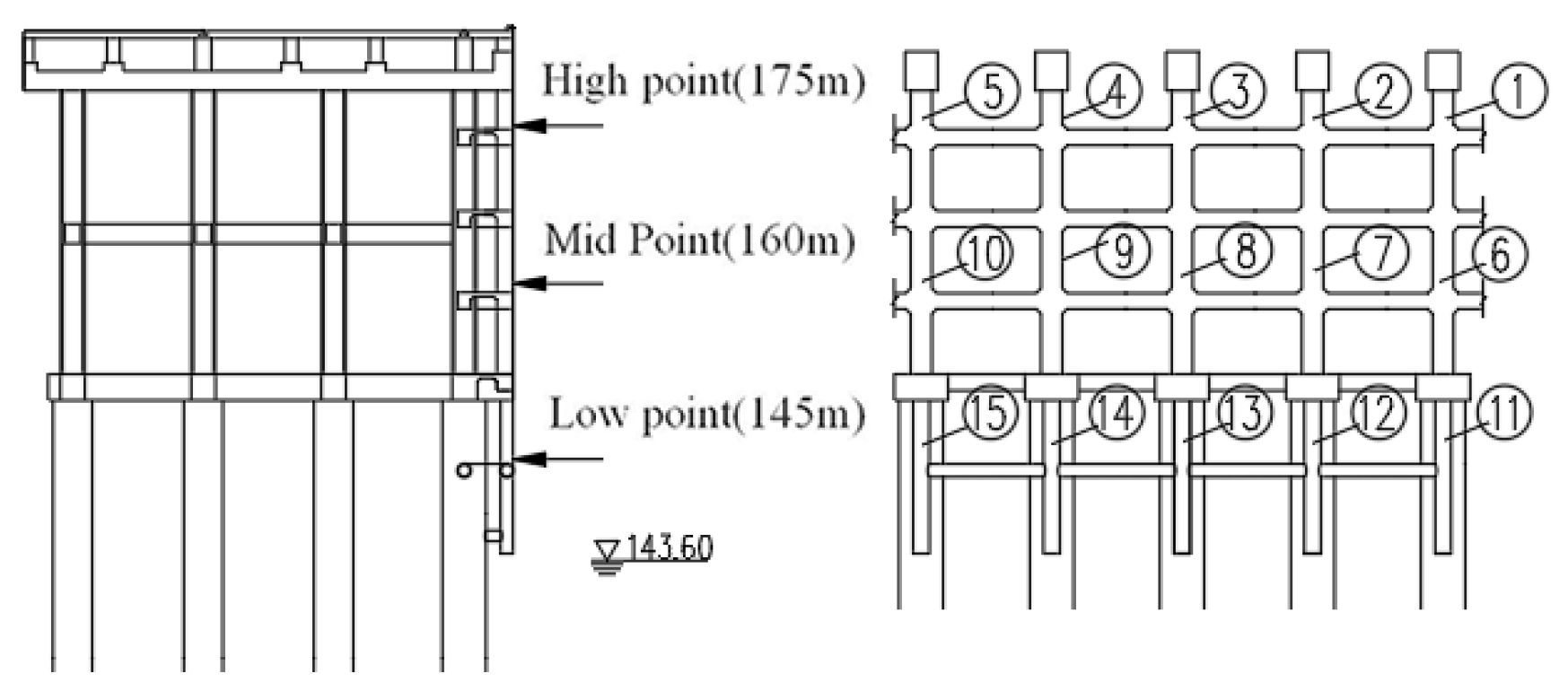
- Based on the statistical data of ships operating in the Three Gorges Reservoir area and water level, through the quantitative analysis of uncertainty, using probability density function and polynomial fitting method, the analysis parameters of ship impact damage incentives in the fluctuating backwater area in the Three Gorges Reservoir area are obtained, which are 6000 tons in size and 145 m, 160 m, and 175 m in position.
- (2)
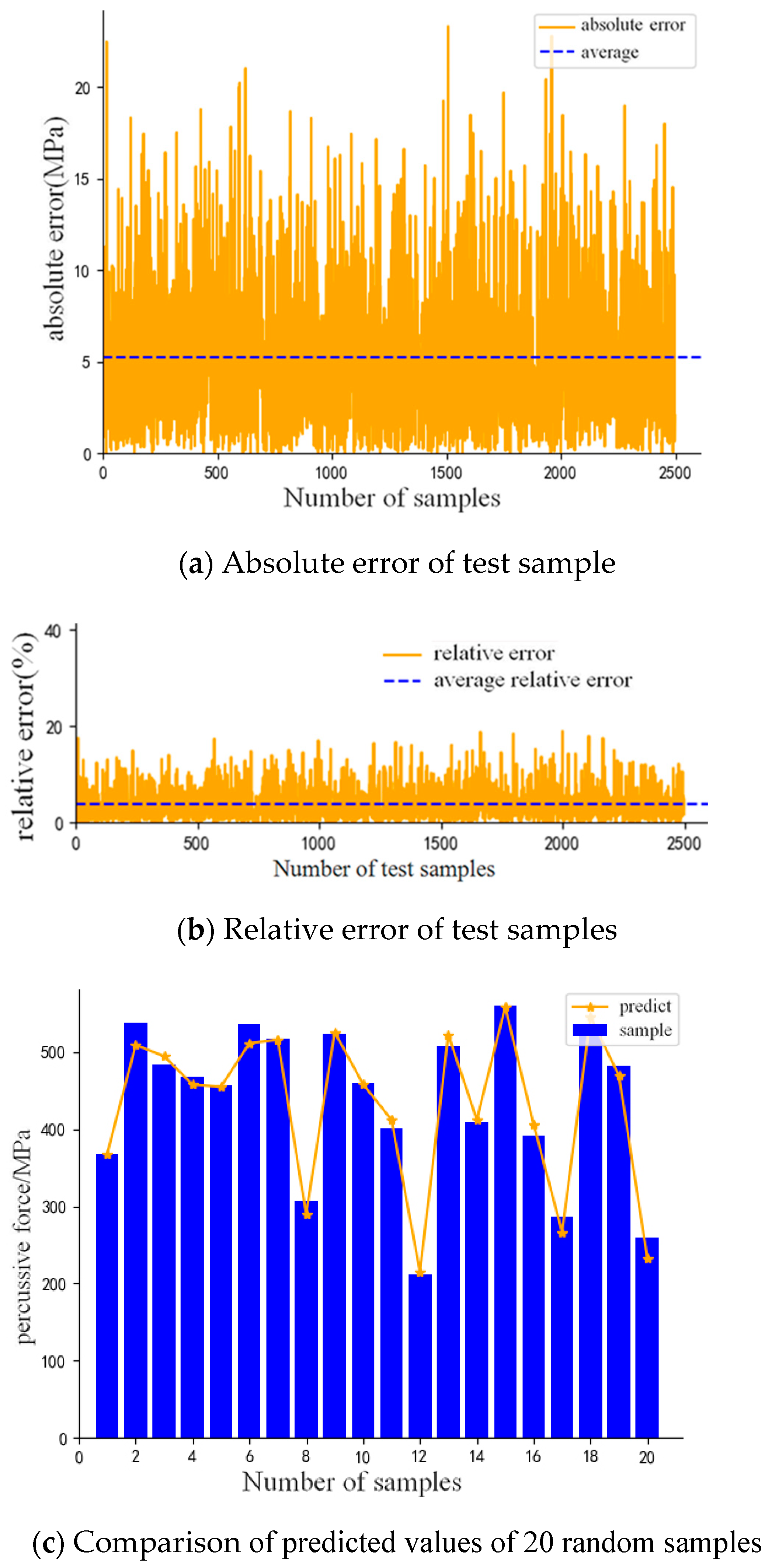
- The optimal parameters of the neural network model are searched by a grid search, the scores of the evaluation indexes of the model are cross-verified, and the inducement of ship collision damage is analyzed. After analysis, the location recognition accuracy of ship collision is 0.94, and the average absolute error of size recognition is 5.5 kN. The inversion model has a very good generalization ability for ship collision injury inducement samples.
- (3)
- The finite element simplified analysis model is established, and the MANSYS module is called by Python’s subprocess module for analysis, which proves the feasibility of batch calculation of pile foundation stress in the complex structure of the overhead vertical high-pile wharf. By comparing the stress characteristics with the solid element model, the calculation results of the simplified analysis model are verified to be correct, so that the sample space for inversion analysis can be obtained by using the simplified model calculation results.
- (4)
- After analysis, compared with the strength and position of the ship’s pile foundation, the pile foundation of the inland river overhead high-pile wharf is more sensitive to the strength and the position of the pile foundation at low water level. Therefore, in the process of wharf pile foundation design and health inspection, attention should be paid to the structural state under the conditions of large tonnage and low water level.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Q. Numerical Simulation Study on Siltation Characteristics of Fluctuating Backwater Area Basin in Three Gorges Project; Chongqing Jiaotong University: Chongqing, China, 2020; pp. 11–15. [Google Scholar]
- Zhao, T. Study on Damage Prediction of High-Piled Wharf Under Ship Impact Force; Tianjin University: Tianjin, China, 2018; pp. 131–135. [Google Scholar]
- Liu, S.; Zheng, Y.; Zhu, P. Damage diagnosis and reliability research of high-piled wharf structure under ship impact load. Port Sci. Technol. 2016, 5, 57–62. [Google Scholar]
- Liu, X.; Zhang, Y. Safety assessment of high-piled wharf under ship impact force. Waterw. Eng. 2016, 4, 17–22. [Google Scholar]
- Wang, J.; Gong, J.; Zhang, Y. Statistical Analysis of Ship Impact Forces on Light Wharf Structures. China Ocean. Eng. 2010, 3, 146–151. [Google Scholar]
- Ye, B. Study on Pile Foundation Damage Behavior of Continuous Beam Bridge with High Pile Caps Under Barge Impact; Chongqing Jiaotong University: Chongqing, China, 2020; pp. 31–35. [Google Scholar]
- Zhu, R. Research on damage identification of high-piled wharf based on dynamic test. In Proceedings of the 19th China Offshore Engineering Symposium (Part Two), Chongqing, China, 11–13 October 2019; pp. 1150–1156. [Google Scholar]
- Qin, F. Analysis of multimodal distribution probability model of vehicle load for reliability evaluation of highway bridges. Traffic World 2016, 401, 50–51. [Google Scholar]
- Tian, W.; Wan, H.; Wu, Y.; Meng, B.; Zhu, X. Study on the statistical law of ship collision accidents in Jiangsu section of Yangtze River trunk line. J. Beibu Gulf Univ. 2019, 34, 8–13. [Google Scholar]
- Cai, D.; Duan, X.; Gao, H. Detection and tracking of water sports ships. Comput. Math. Eng. 2017, 7, 1313–1317. [Google Scholar]
- Zhu, Z. Expectation Maximization (EM) algorithm and its application in Gaussian mixture model. Mod. Electron. Technol. 2003, 24, 88–90. [Google Scholar]
- 2020 Port Operation Ship Information Monthly Report (January–December); Chongqing Port Logistics Group: Chongqing, China, 2020.
- Yangtze River Water Level Information Report (2016–2020); Hydrological Bureau of Upper Yangtze River: Chongqing, China, 2020.
- Liu, P. Python programming in LabVIEW and TestStand. Comput. Times 2020, 18, 54–58. [Google Scholar]
- Ayer, J.E.B.; Lämmle, L.; Mincato, R.L.; Donadio, C.; Avramidis, P.; Pereira, S.Y. Three-dimensional model and environmental fragility in the Guarani Aquifer system, SE-Brazil. Groundw. Sustain. Dev. 2024, 26, 101285. [Google Scholar] [CrossRef]
- Zuo, L.; Cao, S.; Zhou, S.; Wu, J. Inversion of damage inducement of wharf pile foundation under heaped load based on parametric model. SN Appl. Sci. 2022, 4, 69. [Google Scholar] [CrossRef]
- Zuo, L.; Shiliang, Z.; Cao, S.; Wu, J. Inversion of damage inducement of overhead vertical wharf based on parametric model. Waterw. Eng. 2022, 2, 61–67. [Google Scholar]
- Zuo, L.; Shiliang, Z.; Quan, J. Analysis of factors affecting the stress of wharf pile foundation in reinforced high fill area. Waterw. Eng. 2022, 5, 170–177. [Google Scholar]
- Shiliang, Z.; Chunru, K.; Fan, W. Prediction Model of Ship Impact Force on Overhead Vertical Wharf Based on Support Vector Machine. Waterw. Eng. 2023, 8, 21–27+126. [Google Scholar]
- Cai, X.; Ji, C.; Zhao, T. A Constrained Many-Objective Mobile Crowd Sensing Task Allocation Method Considering Latent Workers. IEEE Internet Things J. 2024, 12, 4065–4077. [Google Scholar] [CrossRef]
- Cai, J.; Chen, B.; Wen, J.; Cui, Z.; Chen, J.; Zhang, W. A joint vehicular device scheduling and uncertain resource management scheme for Federated Learning in Internet of Vehicles. Inf. Sci. 2025, 690, 121552. [Google Scholar] [CrossRef]
- Wen, J.; Cui, Z.; Zhang, H.; Chen, J. A Many-objective Joint Device Selection and Aggregation Scheme for Federated Learning in IoV. ACM Trans. Sens. Netw. 2024; in press. [Google Scholar] [CrossRef]
- Cui, Z.; Qu, C.; Zhang, Z.; Jin, Y.; Cai, J.; Zhang, W.; Chen, J. An adaptive interval many-objective evolutionary algorithm with information entropy dominance. Swarm Evol. Comput. 2024, 91, 101749. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, L.; Cui, Z.; Qin, A.K. An adaptive strategy based multi-population multi-objective optimization algorithm. Inf. Sci. 2025, 686, 120913. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, Y.; Li, M.; Wu, L.; Zhang, W.; Chen, J. Dynamic deadline constrained multi-objective workflow scheduling in multi-cloud environments. Expert Syst. Appl. 2024, 258, 125168. [Google Scholar] [CrossRef]
- Cui, Z.; Wu, Y.; Zhao, T.; Zhang, W.; Chen, J. A two-stage accelerated search strategy for large-scale multi-objective evolutionary algorithm. Inf. Sci. 2025, 686, 121347. [Google Scholar] [CrossRef]
- Qin, J.; Pei, D.; Guo, Q.; Cai, X.; Xie, L.; Zhang, W. Intersection-union dual-stream cross-attention Lova-SwinUnet for skin cancer hair segmentation and image repair. Comput. Biol. Med. 2024, 180, 108931. [Google Scholar] [CrossRef]
- Zhao, B.; Cui, Z.; Yang, J.; Cai, X.; Cai, J.; Chen, J. A multi-task evolutionary algorithm for solving the problem of transfer targets. Inf. Sci. 2024, 681, 121214. [Google Scholar] [CrossRef]
- Cui, Z.; Shi, Z.; Li, Q.; Zhao, T.; Zhang, W.; Chen, J. Cooperative interference to achieve interval many-objective evolutionary algorithm for association privacy secure computing migration. Expert Syst. Appl. 2024, 255, 124662. [Google Scholar] [CrossRef]


| Statistical Object | Gaussian Component | Weight | Average Value | Standard Deviation |
|---|---|---|---|---|
| Ship tonnage | 1 | 0.191 | 5.98 | 2.55 |
| 2 | 0.233 | 12.55 | 7.25 | |
| 3 | 0.456 | 1.98 | 0.89 | |
| 4 | 0.009 | 50.15 | 11.21 |
| Parameter | Parameter | |
|---|---|---|
| Classification Learner | Regression Learner | |
| Optimizer | Adam | Adam |
| Hidden layer | 2 | 2 |
| Number of hidden layer nodes | [50, 30] | [100, 50] |
| Activate function | Relu | Identity |
| Convergence error | 0.001 | 0.001 |
| Penalty factor | 0.01 | 0.2 |
| Maximum number of iterations | 500 | 500 |
| Location | Training Data Set | Test Data Set | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample Number | Precision | F1 | Hamming Loss | Sample Number | Precision | F1 | Hamming Loss | |
| 1 | 526 | 0.95 | 0.949 | 0.049 | 169 | 0.899 | 0.888 | 0.1 |
| 2 | 493 | 0.937 | 0.933 | 0.063 | 166 | 0.903 | 0.901 | 0.096 |
| 3 | 497 | 0.974 | 0.998 | 0.026 | 163 | 0.975 | 0.975 | 0.024 |
| 4 | 534 | 0.949 | 0.95 | 0.051 | 159 | 0.905 | 0.91 | 0.0943 |
| 5 | 473 | 0.858 | 0.832 | 0.141 | 165 | 0.8 | 0.815 | 0.211 |
| 6 | 513 | 0.988 | 0.987 | 0.012 | 160 | 0.969 | 0.952 | 0.0312 |
| 7 | 499 | 0.952 | 0.949 | 0.048 | 177 | 0.949 | 0.948 | 0.0508 |
| 8 | 480 | 0.885 | 0.882 | 0.114 | 158 | 0.829 | 0.831 | 0.17 |
| 9 | 487 | 0.944 | 0.94 | 0.055 | 176 | 0.937 | 0.925 | 0.0625 |
| 10 | 478 | 0.971 | 0.969 | 0.029 | 166 | 0.957 | 0.955 | 0.032 |
| 11 | 522 | 0.998 | 0.989 | 0.001 | 167 | 0.998 | 0.986 | 0.001 |
| 12 | 530 | 0.999 | 0.989 | 0.01 | 179 | 0.969 | 0.971 | 0.0287 |
| 13 | 507 | 0.999 | 0.995 | 0.011 | 179 | 0.98 | 0.985 | 0.015 |
| 14 | 466 | 0.989 | 0.985 | 0 | 157 | 0.971 | 0.979 | 0.0215 |
| 15 | 495 | 0.99 | 0.995 | 0.02 | 159 | 0.982 | 0.985 | 0.0122 |
| total | 7500 | 0.942 | 0.942 | 0.057 | 2500 | 0.943 | 0.941 | 0.0576 |
| Location | Training Data Set | Test Data Set | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample Number | R2 | MSE | MAE | Sample Number | R2 | MSE | MAE | |
| 1 | 526 | 0.997 | 33.476 | 4.601 | 169 | 0.997 | 37.917 | 5.016 |
| 2 | 493 | 0.996 | 46.082 | 5.394 | 166 | 0.996 | 43.113 | 5.132 |
| 3 | 497 | 0.997 | 40.894 | 5.006 | 163 | 0.997 | 39.684 | 5.019 |
| 4 | 534 | 0.997 | 41.190 | 5.240 | 159 | 0.996 | 43.729 | 5.351 |
| 5 | 473 | 0.996 | 51.385 | 5.789 | 165 | 0.995 | 66.184 | 6.395 |
| 6 | 513 | 0.997 | 39.907 | 4.901 | 160 | 0.997 | 38.344 | 4.964 |
| 7 | 499 | 0.997 | 40.407 | 5.077 | 177 | 0.996 | 56.719 | 5.907 |
| 8 | 480 | 0.996 | 47.118 | 5.448 | 158 | 0.996 | 44.238 | 5.165 |
| 9 | 487 | 0.996 | 53.087 | 5.900 | 176 | 0.996 | 49.533 | 5.739 |
| 10 | 478 | 0.994 | 71.079 | 6.999 | 166 | 0.994 | 76.648 | 7.475 |
| 11 | 522 | 0.997 | 35.147 | 4.738 | 167 | 0.998 | 34.737 | 4.732 |
| 12 | 530 | 0.997 | 43.386 | 5.276 | 179 | 0.996 | 54.646 | 6.054 |
| 13 | 507 | 0.997 | 39.084 | 5.051 | 179 | 0.996 | 46.148 | 5.428 |
| 14 | 466 | 0.997 | 38.028 | 4.971 | 157 | 0.997 | 39.069 | 5.063 |
| 15 | 495 | 0.997 | 39.171 | 5.022 | 159 | 0.997 | 43.802 | 5.331 |
| total | 7500 | 0.992 | 43.963 | 5.294 | 2500 | 0.996 | 47.781 | 5.527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, L.; Wang, Q.; Liu, J.; Li, J. Symmetry Study on Damage Inversion of Wharf Pile Foundation in Three Gorges Reservoir Area Under Ship Impact. Symmetry 2025, 17, 215. https://doi.org/10.3390/sym17020215
Zuo L, Wang Q, Liu J, Li J. Symmetry Study on Damage Inversion of Wharf Pile Foundation in Three Gorges Reservoir Area Under Ship Impact. Symmetry. 2025; 17(2):215. https://doi.org/10.3390/sym17020215
Chicago/Turabian StyleZuo, Liangdong, Quanbao Wang, Jia Liu, and Jie Li. 2025. "Symmetry Study on Damage Inversion of Wharf Pile Foundation in Three Gorges Reservoir Area Under Ship Impact" Symmetry 17, no. 2: 215. https://doi.org/10.3390/sym17020215
APA StyleZuo, L., Wang, Q., Liu, J., & Li, J. (2025). Symmetry Study on Damage Inversion of Wharf Pile Foundation in Three Gorges Reservoir Area Under Ship Impact. Symmetry, 17(2), 215. https://doi.org/10.3390/sym17020215





