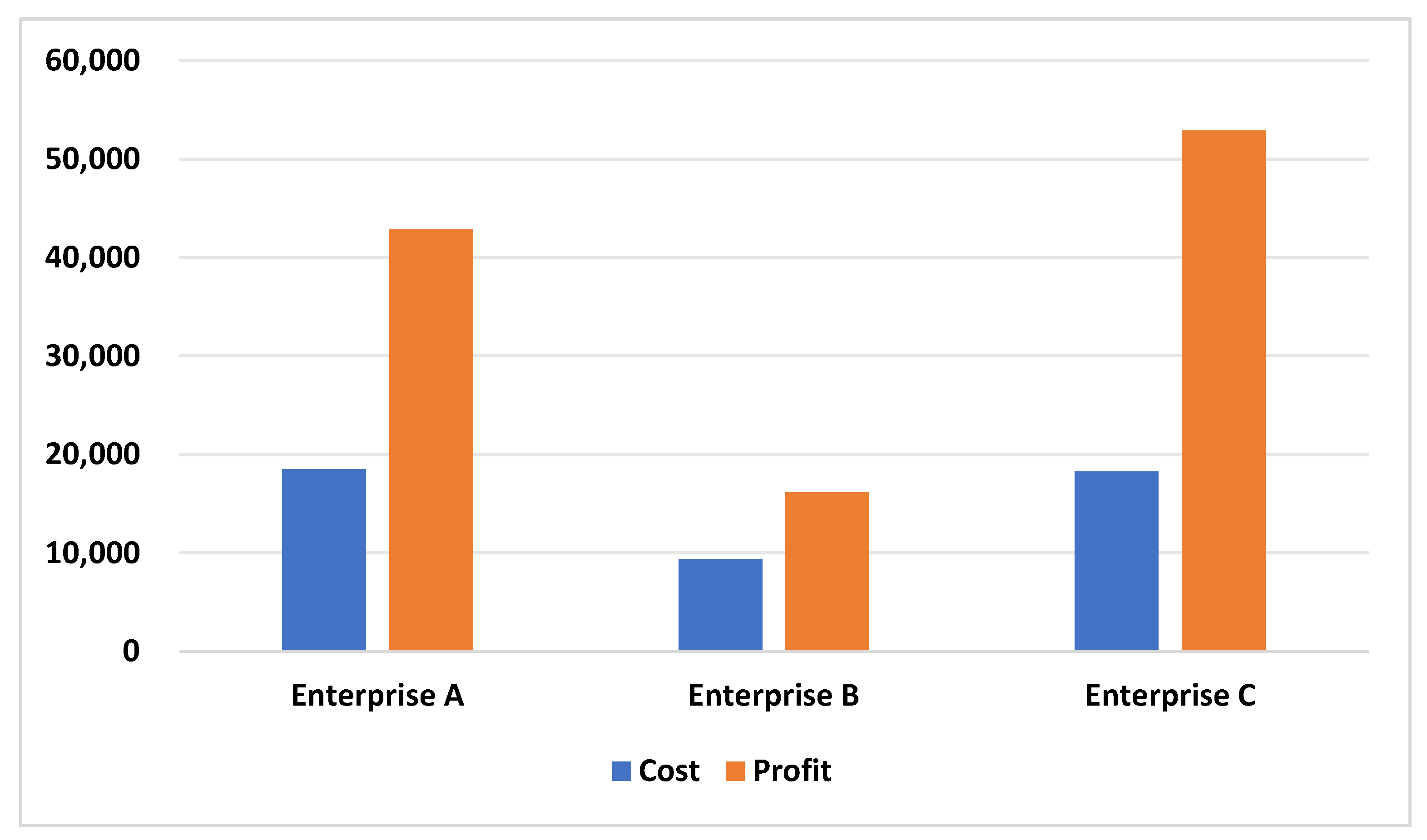
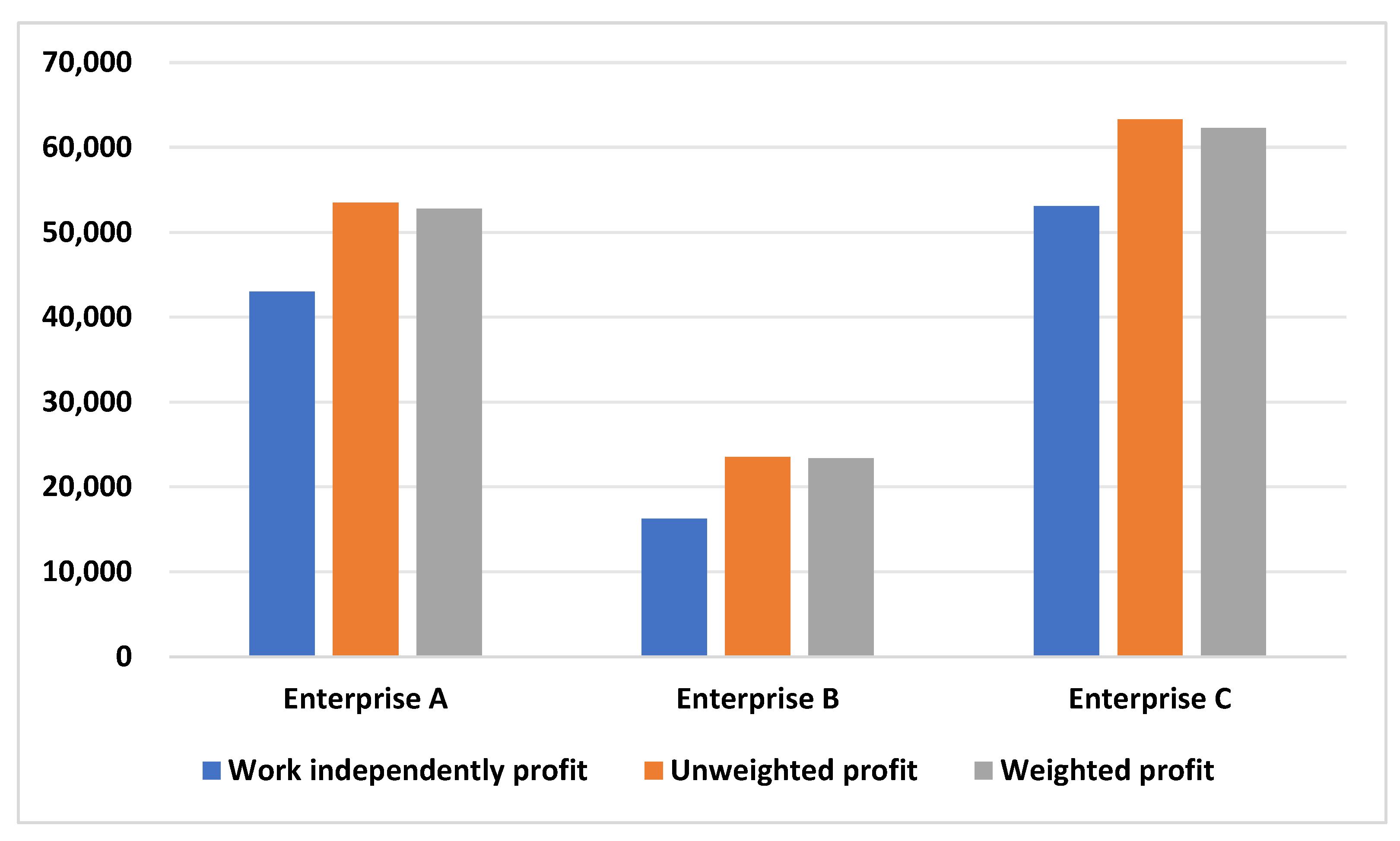
4.1. Equal Division Contribution Values of Trapezoidal Fuzzy Numbers
Whether the result of the allocation strategy can be adopted by the cooperative coalition depends most importantly on whether the players participating in the coalition can accept the allocation result of the cooperative profit of the coalition. Obviously, if the profit of the coalition does not change, one of the enterprises receiving one more unit of profit will necessarily result in the other enterprises receiving one less unit of profit. It is easy to maximize the profit and satisfaction for only one or several enterprises, but this is absolutely unreasonable. In order for each player to be satisfied with the allocation result, we need to minimize the sum of all players’ dissatisfaction with the allocation result as much as possible.
From the analysis in
Section 3.4, it can be seen that the square contribution excess is an indicator that is used to measure the dissatisfaction of players. Therefore, in order for the profit allocation strategy of a cooperative coalition to be acceptable to every player participating in it, it is necessary to find an equilibrium point so that the overall dissatisfaction of all players within the coalition with the coalition’s allocation strategy can be minimized. The following quadratic programming model is established.
In Equation (4),
,
,
, and
are respectively the lower limit value, the upper limit value, the left mean value, and the right mean value of the trapezoidal fuzzy number profit values obtained by players after participating in the coalition. These differs from the non-fuzzy equal division contribution value:
The non-fuzzy value only uses the precise number as the calculated value.
The allocation strategy obtained by solving Equation (4) is called the equal division contribution value of the trapezoidal fuzzy number. The following will introduce the derivation process.
Phase 1.
We construct the Lagrange function of Equation (4), and we obtain
According to Equation (5), we calculate the partial derivatives of the function
with respect to
,
,
,
,
,
,
, and
, respectively, and make them all equal to 0. Then, we can obtain
For the sake of making the expression more concise, we abbreviate the remainder terms, which are obtained by taking the partial derivatives of Equation (5) with respect to the independent variables , , , and , respectively, as , , , and .
Phase 2.
Taking the lower limit value of the equal division contribution value of the trapezoidal fuzzy number as an example, we continue to calculate its solution.
According to Equation (6), we can obtain
It can be observed from Equations (6) and (7) that
By rewriting Equation (8) into another form, we obtain
Let
represent the contribution value of player
to the coalition. Substituting Equation (9) into Equation (7), the lower limit value of the equal division contribution value of the trapezoidal fuzzy number is obtained as
Phase 3.
We apply the process of calculating the lower limit value
with respect to the calculation of the upper limit value
, the left mean value
, and the right mean value
of the equal division contribution value of the trapezoidal fuzzy number. Finally, the complete equal division contribution value of the trapezoidal fuzzy number
is obtained as
Using the equal division contribution value of the trapezoidal fuzzy number as the allocation strategy can ensure, to a greater extent, that each player participating in the coalition can be rewarded according to their efforts. It can be said that the greater the contribution made by a player after joining the coalition, the more profit they can obtain through allocation.
Different from this solution, the non-fuzzy equal division contribution value is
This method can also make players satisfied with the allocation result. However, in a complex and changeable game environment, this solution may become invalid at any time. It is easy to see that the allocation method in this paper must be adapted to a variety of game environments.
4.2. Weighted Equal Division Contribution Values of Trapezoidal Fuzzy Numbers
The equal division contribution value of a trapezoidal fuzzy number is allocated based on the contributions made by players after participating in the coalition. However, in practical cooperative games, we still need to take more situations into account. For instance, some enterprises, due to their own positive brand effects, still expand the influence of the coalition even if they do not make too many actual contributions after joining the coalition. In order to not ignore the potential value brought by these enterprises, we need to introduce player weights.
The weighted equal division contribution value of the trapezoidal fuzzy number also aims at minimizing the overall dissatisfaction of players. Therefore, the following quadratic programming model is established.
The allocation strategy obtained by solving this model is called the weighted equal division contribution value of the trapezoidal fuzzy number. In Equation (12), represents the player weight of player in the coalition, while , , , and are respectively the lower limit value, the upper limit value, the left mean value, and the right mean value of the trapezoidal fuzzy number profit values allocated to the players after participating in the coalition.
The non-fuzzy weighted value is also only a precise number; it is
For the purpose of simplifying the Equation (12), we use to represent . As a result, Equation (12) can be rewritten as follows.
The calculation process for the weighted equal division contribution value of a trapezoidal fuzzy number is similar to that for the unweighted value. The detailed phases will be introduced.
Phase 1.
We construct the Lagrange function of Equation (13), and we obtain
According to Equation (14), we calculate the partial derivatives of the function
with respect to
,
,
,
,
,
,
, and
respectively, and set them all equal to 0. Then, we obtain
In Equation (15), , , , and respectively represent the remainder terms obtained by taking the partial derivatives of the independent variables , , , and with respect to Equation (14).
Phase 2.
We take the lower limit value of the weighted equal division contribution value of the trapezoidal fuzzy number as an example and continue to calculate its solution.
Based on Equation (15), we can obtain
According to Equations (15) and (16), we can observe
By rewriting Equation (17) into another form, we obtain
Suppose
denotes the contribution value of player
to the coalition. By substituting Equation (9) into Equation (7), the lower limit value of the weighted equal division contribution value of the trapezoidal fuzzy number can be obtained as
Phase 3.
We apply the process of deriving the lower limit value
to calculate the upper limit value
, the left mean value
, and the right mean value
of the weighted equal division contribution value of the trapezoidal fuzzy number. It can thus be seen that if the sum of the contributions made by players is less than the coalition’s profit, the weighted equal division contribution value of the trapezoidal fuzzy number
is
If the sum of the contributions made by players is more than the coalition’s profit, the weighted equal division contribution value of the trapezoidal fuzzy number
is
Different from this solution, the non-fuzzy weighted equal division contribution is
Obviously, like the unweighted value, the non-fuzzy weighted equal division contribution value struggles to cope with the effects arising from changes in the game environment.
4.3. Some Properties of the Solution
Since the unweighted equal division contribution value of the trapezoidal fuzzy number and the weighted value have the same properties, only the unweighted equal division contribution value of the trapezoidal fuzzy number is taken as an example here, and the properties of the weighted value will not be elaborated on any further.
Theorem 1. (Validity) Let denote the set of cooperative games with players. For any trapezoidal fuzzy number cooperative game ,after applying the equal division contribution value of the trapezoidal fuzzy number as the allocation strategy, all players can exactly divide up the profit of the grand coalition .
Proof of Theorem 1. According to the addition operation rule of the trapezoidal fuzzy number, we can obtain
It can be determined from Equation (22) that , which indicates that the sum of the profit values allocated to all players from the grand coalition is exactly the coalition profit . Therefore, all players can exactly divide up the total profit of the grand coalition.
Theorem 2. (Additivity) Let denote the set of cooperative games with players. For any cooperative games and with equal division contribution values of the trapezoidal fuzzy numbers, it always holds that
Proof of Theorem 2. According to Equation (10) and the addition operation rule of trapezoidal fuzzy numbers, we can obtain Through the same method, other values can be calculated as
Therefore, we can obtain .
Theorem 3. (Symmetry) Let denote the set of cooperative games with players. If any two players and
in the cooperative game with an equal division contribution value of the trapezoidal fuzzy number have equal status within the coalition, then the allocated profit value .
Proof of Theorem 3. According to Equation (10), for players and with the same status, it holds that If players
and
have equal status within the coalition, it indicates that
, and then
also holds. Through a similar method, we can obtain
According to the operation rule of trapezoidal fuzzy number, it can be known that .