Experimental Study on the Symmetry of the Soil-Arching Effect of a Pile Foundation in a Reinforced High-Fill Area
Abstract
1. Introduction
2. Model Test Scheme
2.1. Test Program
2.2. Model Pile Pouring
2.3. Fabrication of Reinforced Slope
- (1)
- Cohesive soil, taken from alluvial soil on the terrace of the Chongqing section of the Three Gorges reservoir area of the Yangtze River.
- (2)
- Stone powder: sand rock powder with particle size of 0.5~3.0 mm was selected.
- (3)
- Gravel: limestone gravel aggregate with particle size of 14~18 mm was selected.
2.4. Loading and Data Monitoring
- (1)
- A vibrating wire earth pressure gauge with a diameter of 108 mm, a thickness of 26 mm, and a maximum range of 0.2 MPa was used to monitor the earth pressure of the slope in the reinforced high-fill area.
- (2)
- The stress of the pile foundation in the reinforced high-fill slope area was obtained using a pre-embedded strain.
3. Analysis of Test Results
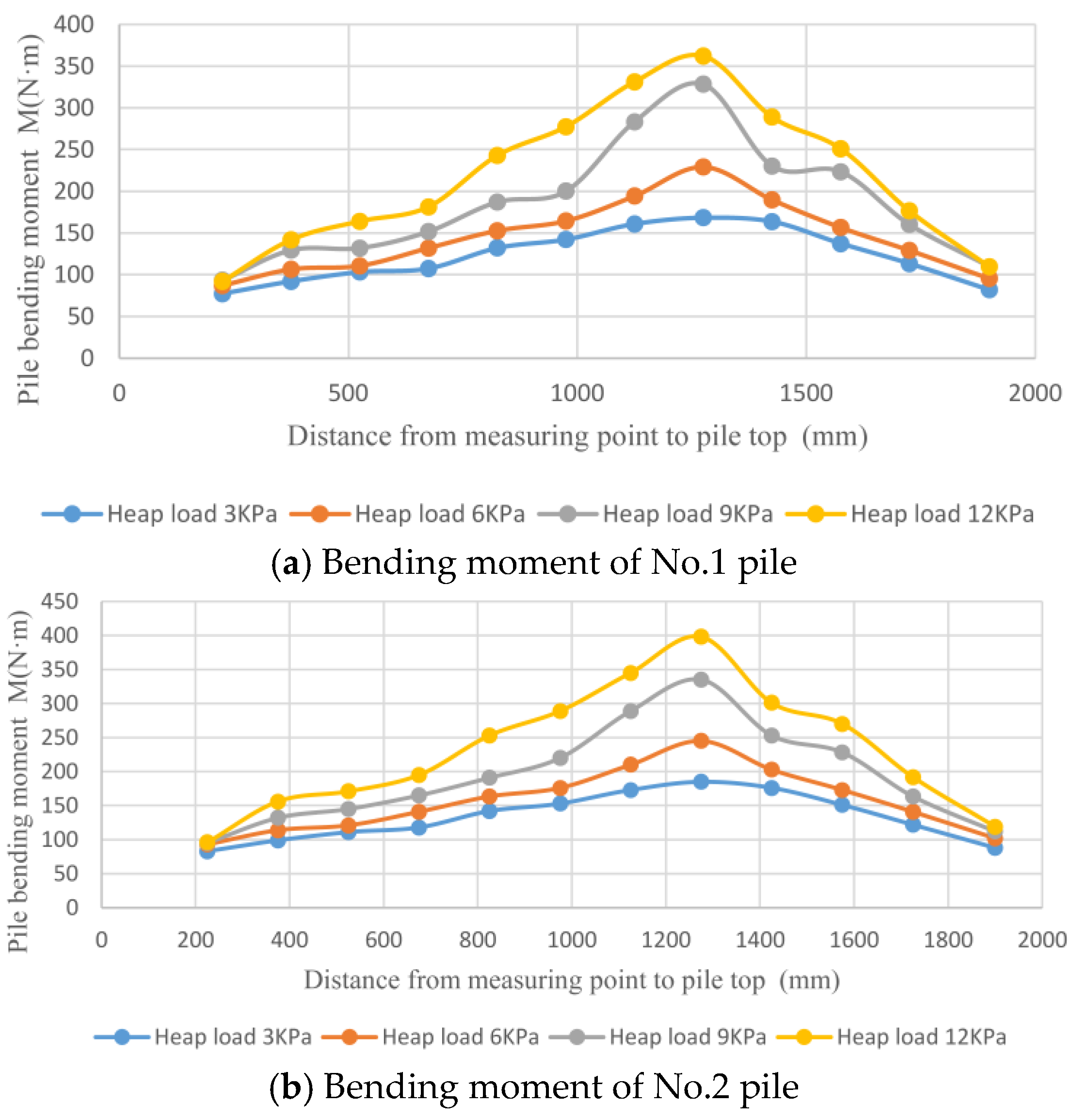
3.1. Bending Moment Analysis of Pile
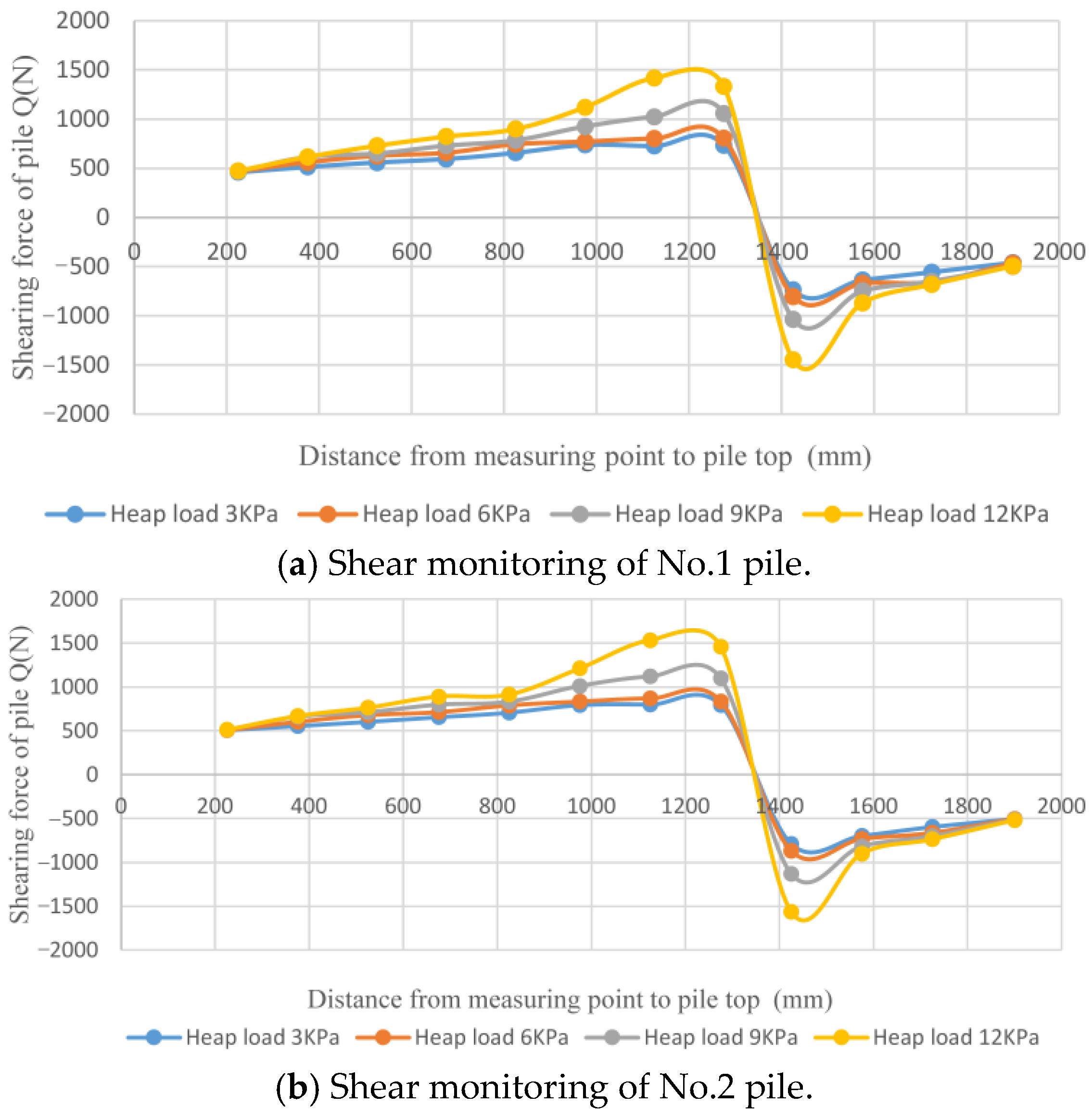
3.2. Shear Analysis of Pile
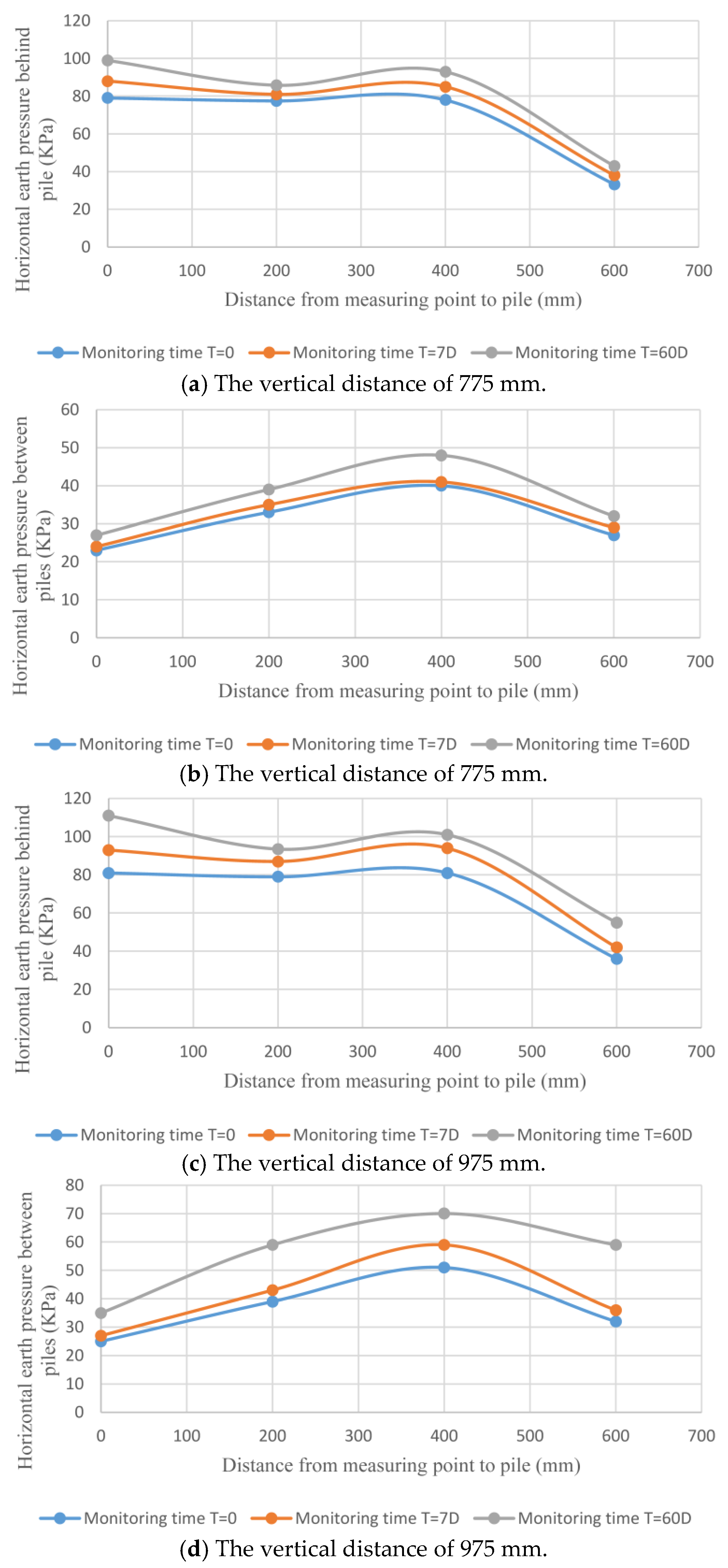
3.3. Analysis of Earth Pressure in Fill Area
4. Mechanism Analysis of the Soil Arch Behind the Pile
- (1)
- Compressive stress concentration stage: At the initial stage of surcharge loading, the reinforced-fill slope tends to move forward under the action of the horizontal earth pressure caused by surcharge loading at the top of the slope, which has the effect of compacting the soil behind the pile and forming a compressive stress concentration area behind the pile.
- (2)
- Formation of a soil arch between piles: With the gradual increase in stacking load at the top of the slope and the increase in stacking time, the stress becomes more concentrated. As it is not retained, the soil between piles undergoes a certain horizontal displacement under the action of horizontal pressure, and a friction soil arch is formed between piles.
- (3)
- Formation of soil arch behind piles: With the continuous increase in horizontal earth pressure and the limited bearing capacity of the friction soil arch, the stress concentration area of the arch foot behind the pile further expands until an arch-bearing structure is formed behind the adjacent arch foot; that is, a direct soil arch is formed behind the pile.
- (4)
- Extrusion of soil arch between piles: Under the long-term effect of surcharge, the soil arch between piles and behind piles enters a stable development stage. Because of the weak bearing capacity of the soil arch between piles, with the further increase in stress, the soil between piles shows signs of spalling. After the friction arch foot is destroyed, the soil between piles is squeezed out and the soil arch effect between piles disappears.
- (5)
- Stable development of soil arch: After the collapse of the soil arch between piles, the soil arch behind the piles enters a stable development stage. If the surcharge on the top of the slope continues to increase, after the horizontal stress reaches the bearing capacity limit of the soil arch behind the pile, cracks occur behind the arch ring, and soil will flow around the pile body.
5. Conclusions
- (1)
- There is an obvious soil-arching effect in the slope behind the pile and the soil-arching effect is obviously enhanced by an increase in depth.
- (2)
- The soil arch formed in the reinforced-soil slope behind the model pile is composed of two parts, namely, the friction arch between the piles and the direct soil arch behind the pile. The spatial distribution of the two parts is different and there is a difference in normal stress. The direct soil arch behind the pile bears most of the horizontal stress, which plays a decisive role in the stability of the soil behind the pile and the stress of the pile.
- (3)
- The maximum bending moment of the pile body is basically consistent with the position of the potential sliding surface of the reinforced-fill slope, and should be calculated as the control point of the pile foundation design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuang, L. Study on Soil Nailing Based on Soil Arching. Ph.D. Thesis, Central South University, Changsha, China, 2002. [Google Scholar]
- Chen, Z. Study on the Properties of Composite Foundation with Immersed Tube and Pile Under Embankment Load. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Zhang, Z.-H.; Chen, Q.-N.; Wang, J.; Li, S. Method for determining spacing of supporting piles based on soil arching effect. J. Hunan Univ. Sci. Technol. (Nat. Sci. Ed.) 2010, 25, 72–75. [Google Scholar]
- Hui, W.; Wu, Y.; Zhao, Y. Reasonable pile spacing analysis of curtain piles based on soil arching effect. J. Yangtze River Sci. Res. Inst. 2015, 32, 67–71+86. [Google Scholar]
- Zheng, J.; Luo, X.; Fu, H.; Cao, W. Pile-supported reinforced embankment analysis based on H&R soil arch model. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2019, 47, 50–54. [Google Scholar]
- Liu, H.; Han, Y.; Yang, J. Large deflection of curved elastic beams made of Ludwick type material. Appl. Math. Mech. (Engl. Ed.) 2017, 38, 909–920. [Google Scholar] [CrossRef]
- Qin, S.; Wang, Y.; Ren, L. Study on the essential attributes and fitting of a class of Lorentz curves. Math. Pract. Cogn. 2014, 44, 86–91. [Google Scholar]
- Zhao, M.; Peng, W.; Yang, C.; Xiao, Y. Finite difference decomposition of internal force calculation of double piles in high and steep cross slope section. China J. Highw. Transp. 2019, 32, 87–96. [Google Scholar]
- Zhao, M.; Peng, W.; Yang, C.; Xiao, Y. Study on the spacing of anti-slide piles considering the combined action of soil and arch behind piles. Highw. Traffic Sci. Technol. 2019, 36, 87–94+116. [Google Scholar]
- Jiang, T.; Lei, J.; Wang, R.; Zhang, J. Comparative model test study on reinforcement effect of anti-slide piles with different pile arrangement methods. J. Basic Sci. Eng. 2019, 27, 404–417. [Google Scholar]
- Ye, J.; Yu, J.; Lin, Z.; Zhou, X.Q.; Liu, S.Y.; Tu, B.X. Experimental study on horizontal push pile model of cantilever double-row anti-slide pile with variable stiffness. J. Civ. Eng. 2019, 52, 193–201. [Google Scholar]
- Chen, G.; Chen, Y.h.; Xu, K.; Qi, C.G.; Cai, R. Field test of soil arching effect of pile-supported reinforced embankment. J. Chang. Univ. (Nat. Sci. Ed.) 2016, 36, 41–47. [Google Scholar]
- Jin, L.; Hu, X.; Tan, F.; He, C.; Zhang, H.; Zhang, Y. Experimental study on soil arching effect of anti-slide pile based on infrared thermal imaging technology. Rock Soil Mech. 2016, 37, 2332–2340. [Google Scholar]
- Liang, Y.; Jiang, C.; Li, Q.; Li, F.; Zhao, X. Experimental study on soil arching effect and stress mechanism of composite structures between piles. J. Rock Mech. Eng. 2014, 33, 3825–3828. [Google Scholar]
- Chen, Q.; Guo, S.; Xu, C.; Liang, L.; Liu, X. Experimental study on the failure modes of loose earth pressure and displacement in loose zone in sandy soil. J. Cent. South Univ. (Nat. Sci. Ed.) 2019, 50, 108–117. [Google Scholar]
- Gu, H.; Luo, C. Model test on soil arching effect of foundation pit supported by sparse piles and soil nailing wall. J. Jilin Univ. (Eng. Ed.) 2018, 48, 1712–1724. [Google Scholar]
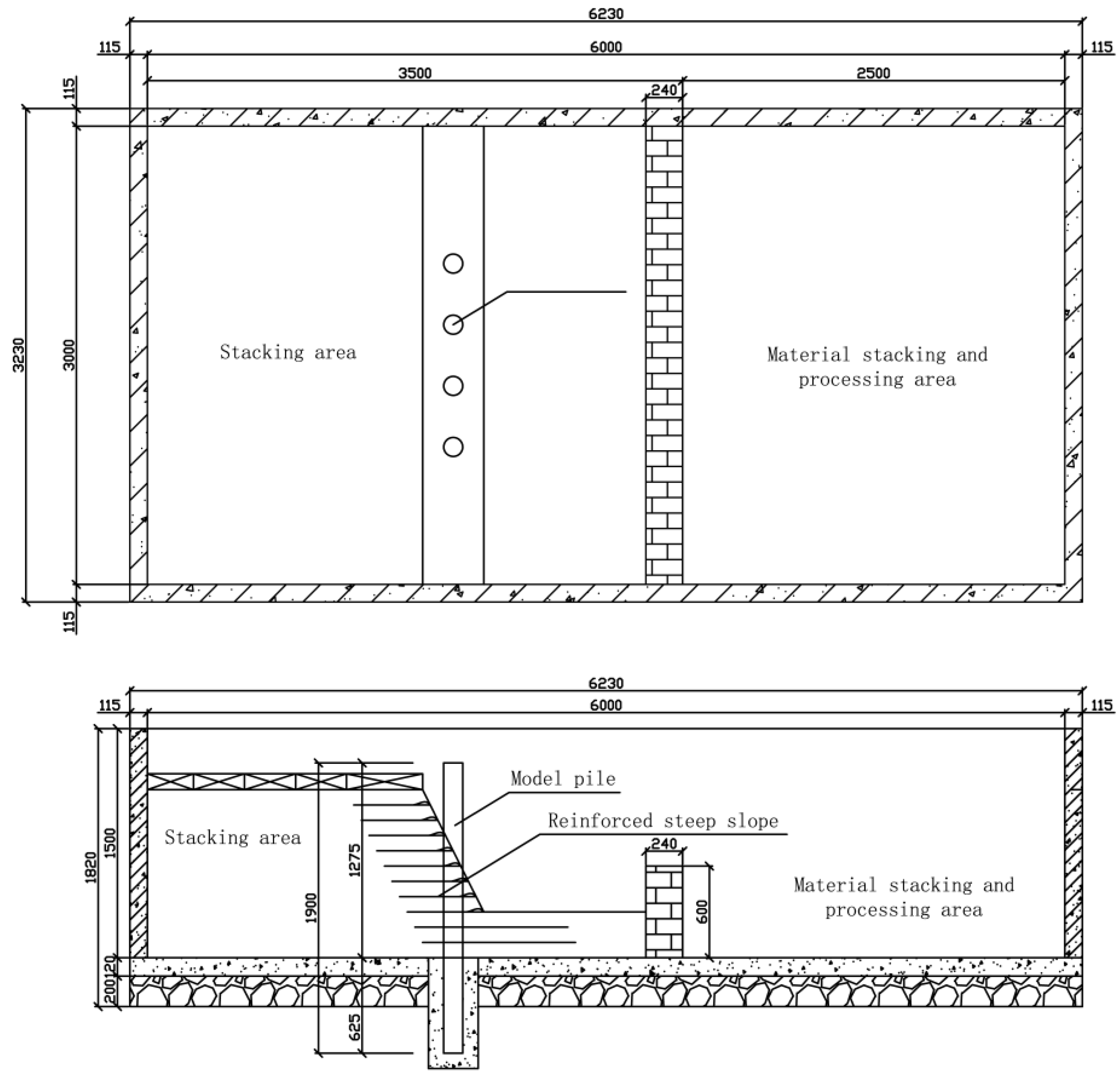


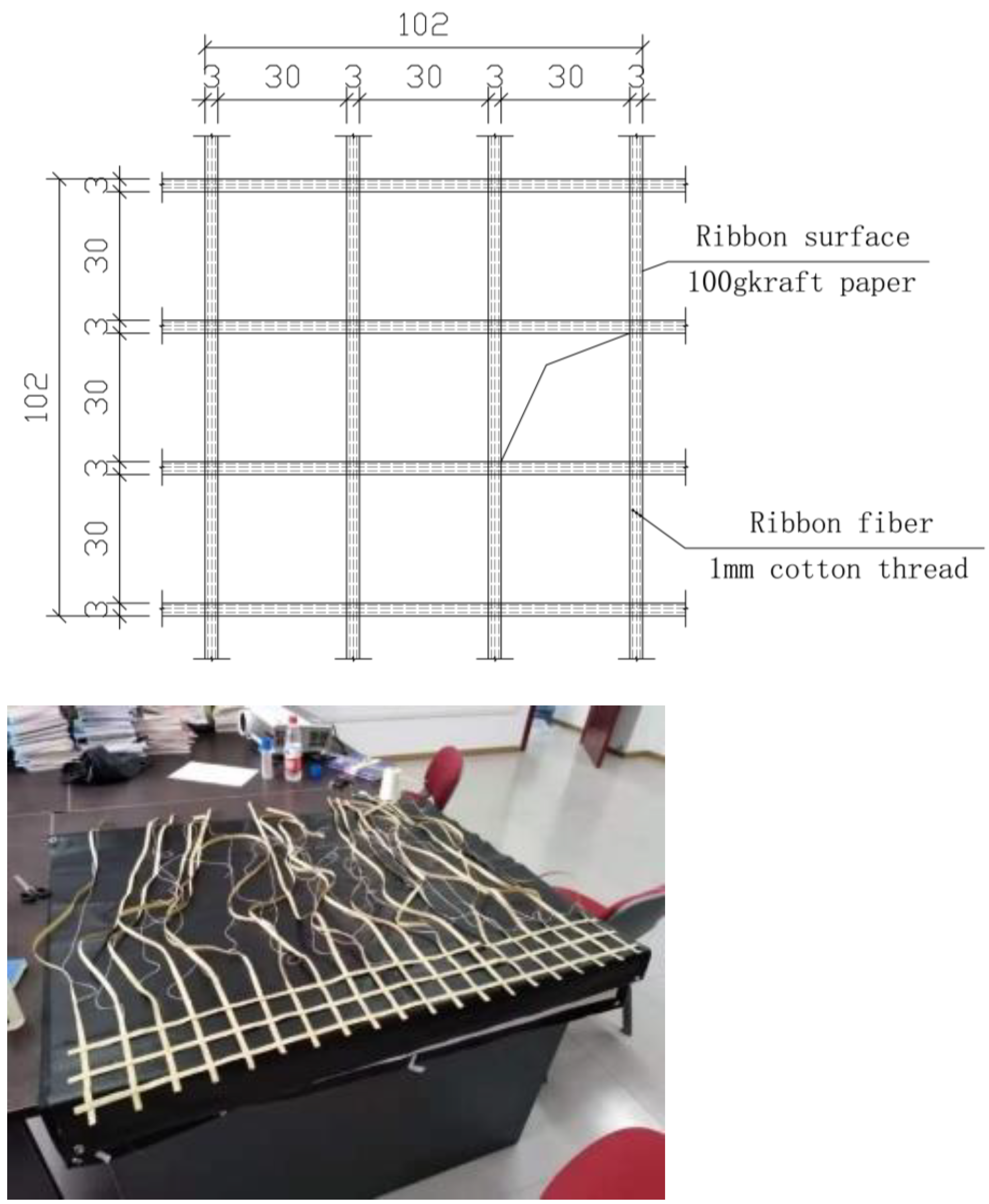

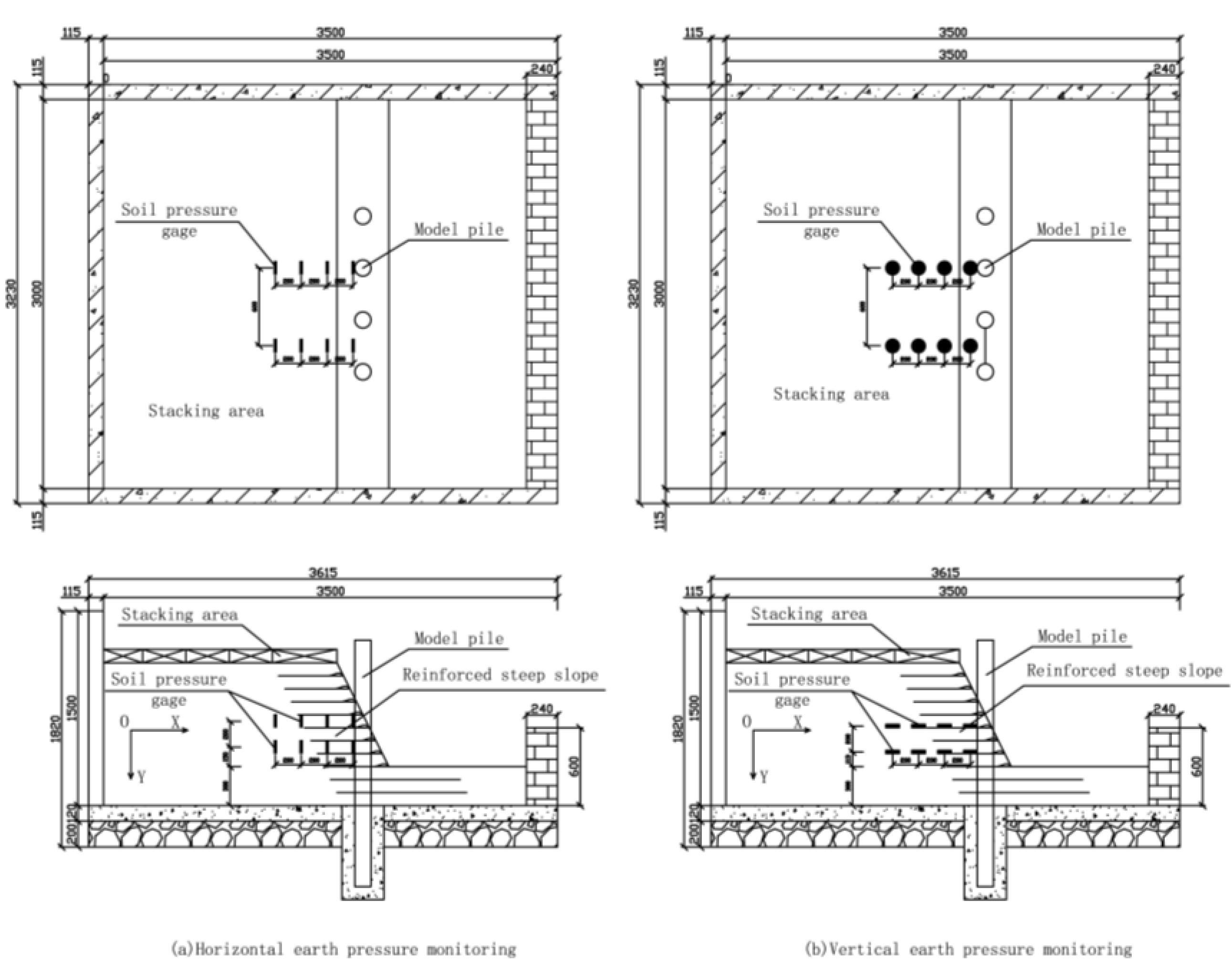

| Serial Number | Parameter | Prototype | Calculation Parameter | Model Parameter |
|---|---|---|---|---|
| 1 | Pile length (mm) | 38000 | 1900 | 1900 |
| 2 | Pile diameter (mm) | 2500 | 125 | 125 |
| 3 | Pile spacing (mm) | 8000 | 400 | 400 |
| 4 | Rock-embedded depth (mm) | >5 D | 625 | 625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, L.; Wang, Q.; Liu, J. Experimental Study on the Symmetry of the Soil-Arching Effect of a Pile Foundation in a Reinforced High-Fill Area. Symmetry 2025, 17, 188. https://doi.org/10.3390/sym17020188
Zuo L, Wang Q, Liu J. Experimental Study on the Symmetry of the Soil-Arching Effect of a Pile Foundation in a Reinforced High-Fill Area. Symmetry. 2025; 17(2):188. https://doi.org/10.3390/sym17020188
Chicago/Turabian StyleZuo, Liangdong, Quanbao Wang, and Jia Liu. 2025. "Experimental Study on the Symmetry of the Soil-Arching Effect of a Pile Foundation in a Reinforced High-Fill Area" Symmetry 17, no. 2: 188. https://doi.org/10.3390/sym17020188
APA StyleZuo, L., Wang, Q., & Liu, J. (2025). Experimental Study on the Symmetry of the Soil-Arching Effect of a Pile Foundation in a Reinforced High-Fill Area. Symmetry, 17(2), 188. https://doi.org/10.3390/sym17020188







