A Technique for Image Encryption Using the Modular Multiplicative Inverse Property of Mersenne Primes
Abstract
1. Introduction
- This work primarily contributes to the identification of a novel modular multiplicative inverse property of Mersenne primes.
- An image encryption technique using this property is proposed that employs symmetric block processing with a secret key in the cipher block chaining mode.
- Shannon’s confusion and diffusion are achieved using simple logic operations such as XOR, circular shift, negation, and modular inversion, rather than the complicated techniques used in other popular algorithms.
- The proposed encryption technique does not employ S-boxes, which in turn reduces the design complexity and computational complexity introduced by them.
- This work offers a highly scalable and spatially efficient technique for encryption, which can be further extended to the efficient hardware implementation of a secure cryptosystem with optimization.
2. Related Works
3. The Novel Modular Multiplicative Inverse Property of Mersenne Primes
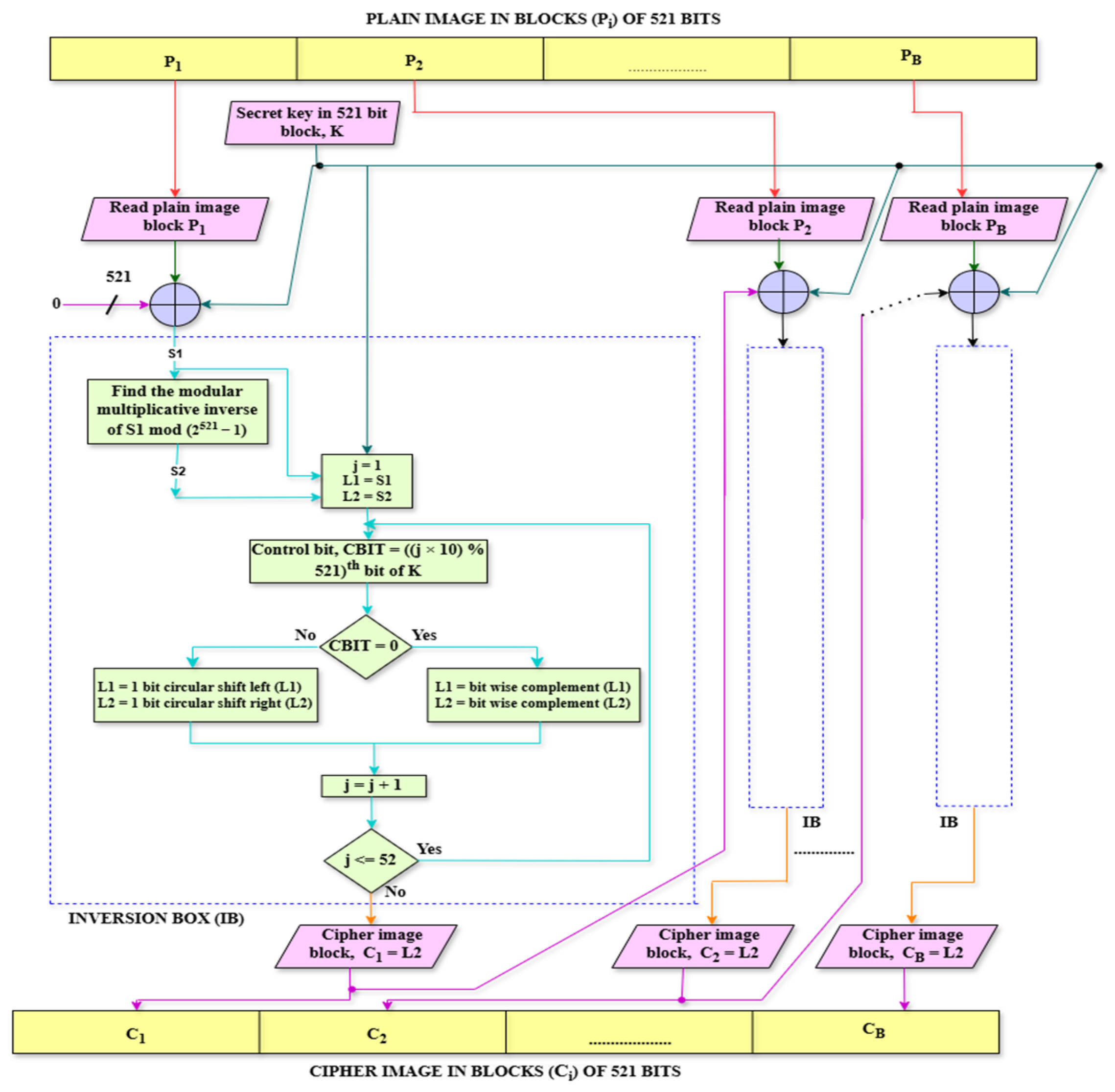
4. Image Encryption Technique Using the Proposed Property of Mersenne Primes
| Algorithm 1 Image encryption algorithm using the proposed technique |
| Input: Plain image P in 521-bit blocks denoted by Pi, i = 1,2,3… B, B = (size of P in bits)/521, Secret key K in a 521-bit block, Last_Sequence = LS. |
| 1: for (i = 1, i ≤ B, i++) 2: { 3: if i = 1, LS = 0; 4: else, LS = Ci−1; 5: S1 = XOR (Pi, K, LS); 6: S2 = S1−1 mod (2521 − 1); 7: Assign L1 = S1; 8: L2 = S2; 9: for j in 1 to 52 10: { 11: Control bit, CBIT = ((j × 10) % 521)th bit of K; 12: if (CBIT = 0) 13: { 14: L1 = bit wise complement (L1); 15: L2 = bit wise complement (L2); 16: } 17: else 18: { 19: L1 = Circular_Left_shift (L1,1); 20: L2 = Circular_Right_shift (L2,1); 17: } 18: } 19: Ci = L2; 20: } 21: C = Ci, Ci+1,…, CB; |
| Output: Cipher image C in binary generated. |
Features of the Proposed Encryption Technique
| Algorithm 2 Image decryption algorithm using the proposed technique |
| Input: Cipher image C in 521-bit blocks denoted by Ci, i = 1, 2, 3… B, B = (size of C in bits)/521, Secret key K in a 521 bit block, Last_Sequence = LS. |
| 1: for (i = 1, i ≤ B, i++) 2: { 3: S1 = Ci−1 mod (2521 − 1); 4: Assign L1 = Ci; 5: L2 = S1; 6: for j in 1 to 52 7: { 8: Control bit, CBIT = ((j × 10) % 521)th bit of K; 9: if (CBIT = 0) 10: { 11: L1 = bit wise complement (L1); 12: L2 = bit wise complement (L2); 13: } 15: else 16: { 17: L1 = Circular_Left_shift (L1,1); 18: L2 = Circular_Right_shift (L2,1); 19: } 20: } 21: S2 = L2; 22: if i = 1, LS = 0; 23: else, LS = Ci-1; 24: Pi = XOR (S2, K, LS); 25: } 26: P = Pi, Pi+1, …, PB; |
| Output: Plain image P in binary is recovered. |
5. Results and Discussions
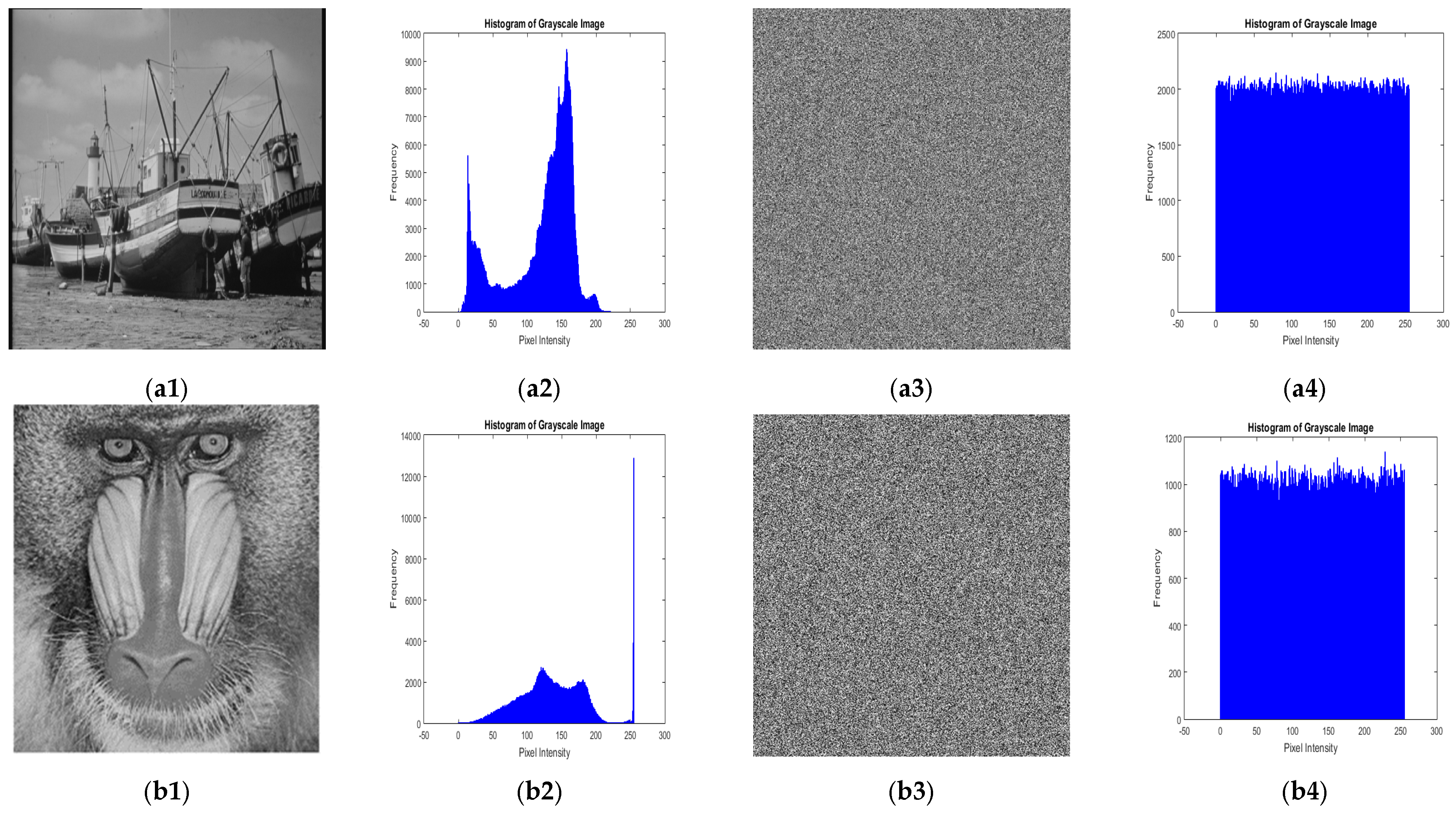
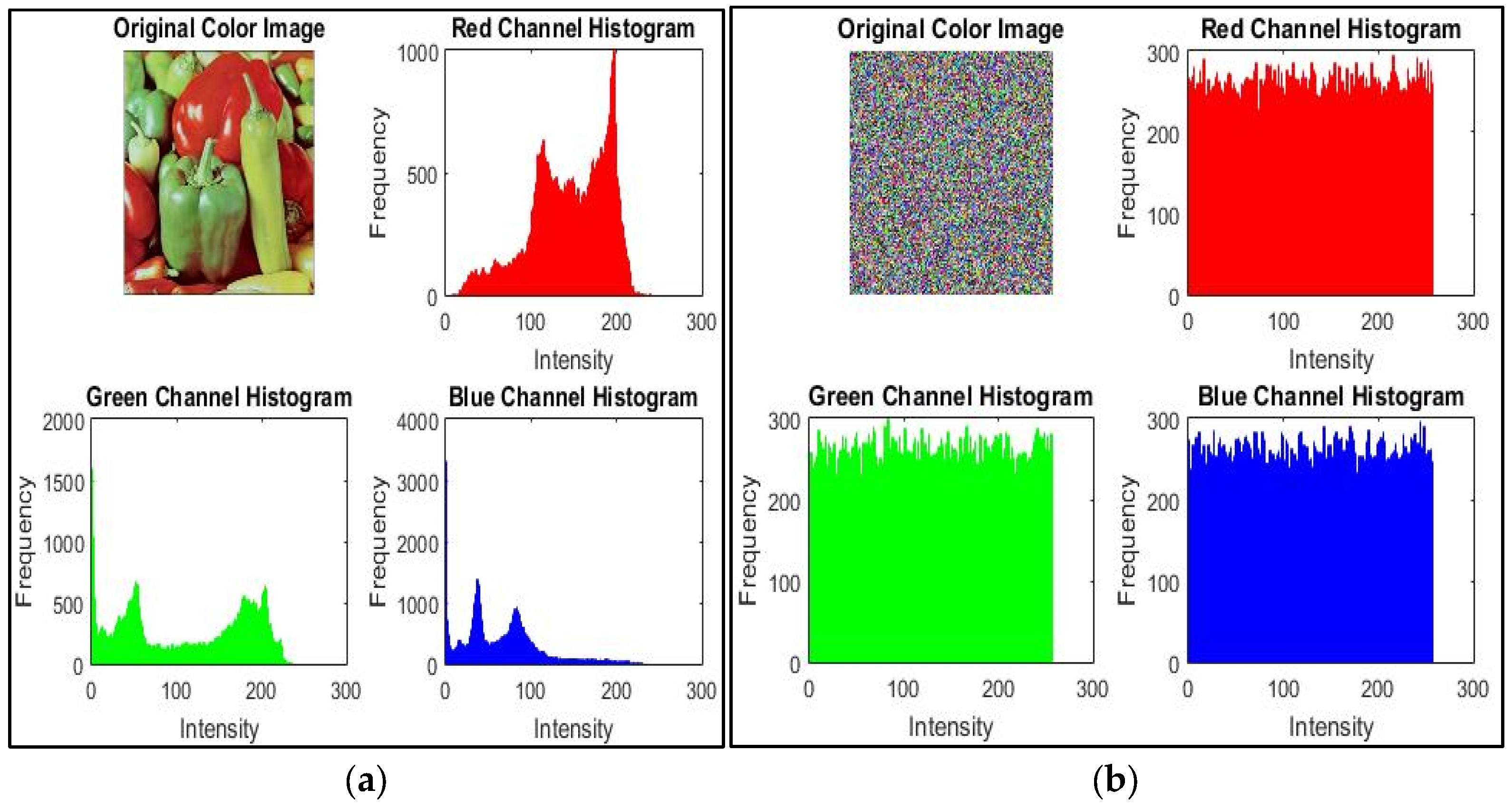
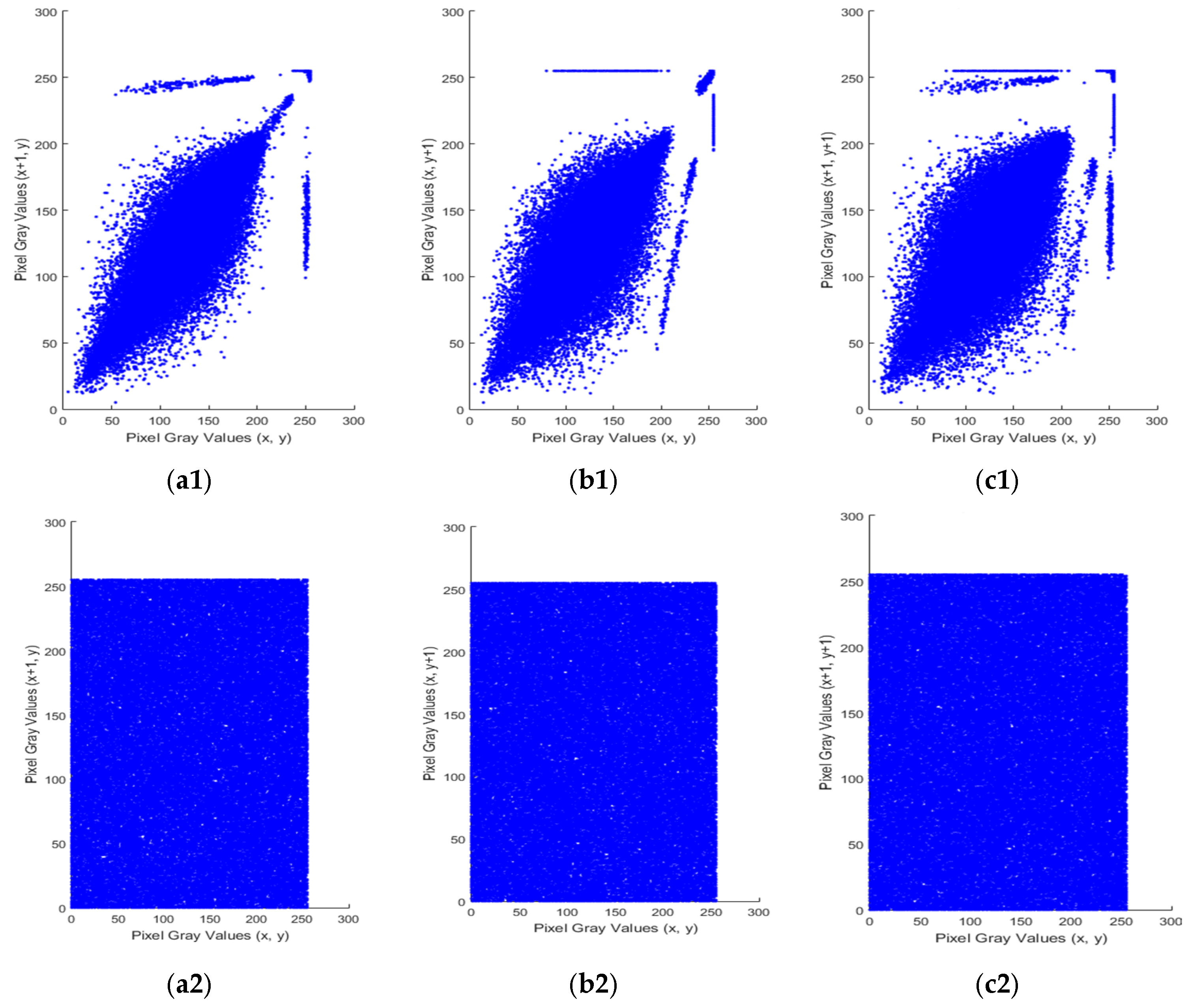
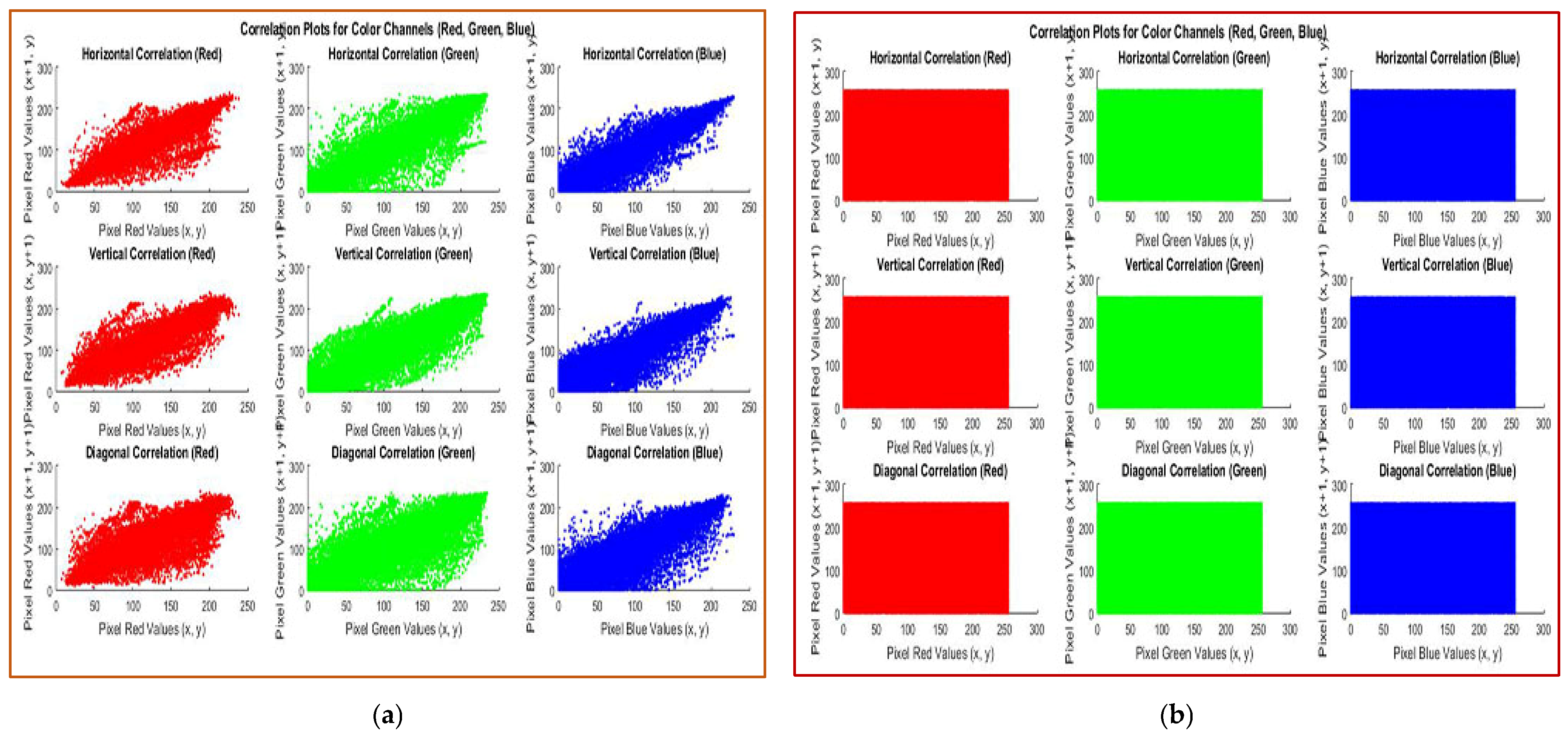
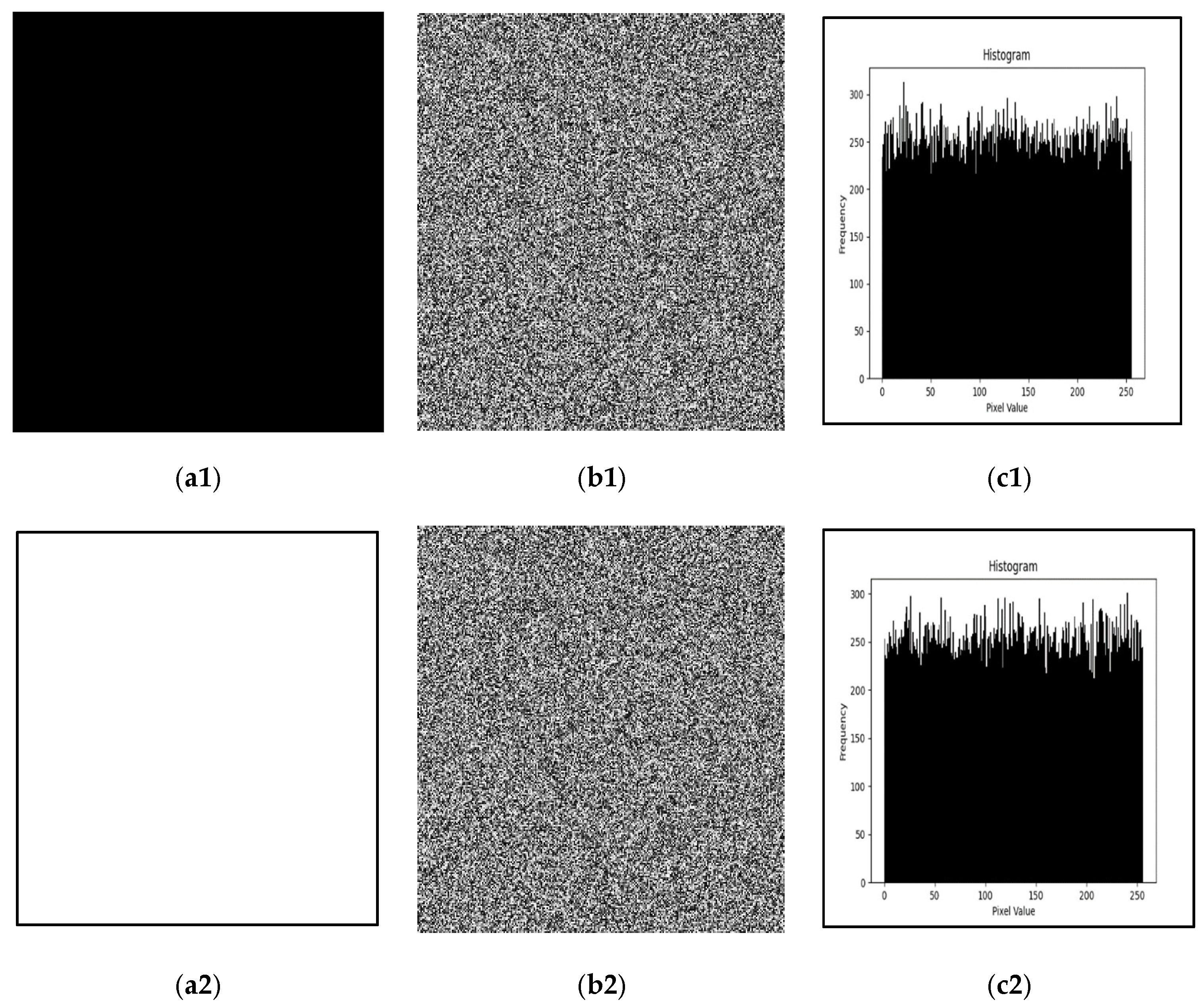
5.1. Visual Inspection
5.2. Statstical Analysis
5.2.1. Histogram Analysis
5.2.2. Correlation Coefficient Analysis
5.3. Security Analysis
5.3.1. Key Space
5.3.2. Key Sensitivity
- K1 = D9 DA 7B EA 1A 31 D8 AB E2 A2 7B 4E 85 5C 5C 5C 50 ED 00 C4 83 88 EA 9B 0F B7 C2 04 C2 C1 2D 39 97 15 7A 6F C8 E4 BB E4 32 C4 0D 35 F2 71 60 92 EB A0 2E 37 98 17 D6 36 A1 44 55 1D F4 9A DE 37 F0 0
- K2 = 59 DA 7B EA 1A 31 D8 AB E2 A2 7B 4E 85 5C 5C 5C 50 ED 00 C4 83 88 EA 9B 0F B7 C2 04 C2 C1 2D 39 97 15 7A 6F C8 E4 BB E4 32 C4 0D 35 F2 71 60 92 EB A0 2E 37 98 17 D6 36 A1 44 55 1D F4 9A DE 37 F0 0
- K3 = D9 9A 7B EA 1A 31 D8 AB E2 A2 7B 4E 85 5C 5C 5C 50 ED 00 C4 83 88 EA 9B 0F B7 C2 04 C2 C1 2D 39 97 15 7A 6F C8 E4 BB E4 32 C4 0D 35 F2 71 60 92 EB A0 2E 37 98 17 D6 36 A1 44 55 1D F4 9A DE 37 F0 0
5.4. Quantitative Analysis
5.4.1. Information Entropy
5.4.2. Mean Squared Error
5.4.3. Peak Signal-to-Noise Ratio
5.4.4. Structural Similarity Index
5.5. Differential Attack Analysis
5.6. Computational Complexity, Efficiency, and Peak Memory Usage
5.7. Chosen Plaintext Attack Analysis
6. Conclusions and Future Scope
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Great Internet Mersenne Prime Search (GIMPS). Available online: https://www.mersenne.org (accessed on 1 April 2022).
- Hoque, A.; Saikia, H.K. On generalized Mersenne prime. SeMA J. 2014, 66, 1–7. [Google Scholar] [CrossRef]
- Kraft, J.; Washington, L. An Introduction to Number Theory with Cryptography; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wojciechowski, J. Mersenne Primes, an Introduction and Overview, 2003, Academia.edu. Available online: https://www.academia.edu/9995980/Mersenne_Primes_An_Introduction_and_Overview (accessed on 22 March 2022).
- FIPS 186-5; Digital Signature Standard (DSS), Federal Information Processing Standards 186-5. National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023.
- Ding, J.; Li, S.; Gu, Z. High-speed ECC processor over NIST prime fields applied with Toom–Cook multiplication. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 66, 1003–1016. [Google Scholar] [CrossRef]
- Alrimeih, H.; Rakhmatov, D. Pipelined modular multiplier supporting multiple standard prime fields. In Proceedings of the 2014 IEEE 25th International Conference on Application-Specific Systems, Architectures and Processors, Zurich, Switzerland, 18–20 June 2014; pp. 48–56. [Google Scholar]
- Shin, S.-H.; Yoo, W.S.; Choi, H. Development of modified RSA algorithm using fixed Mersenne prime numbers for medical ultrasound imaging instrumentation. Comput. Assist. Surg. 2019, 24, 73–78. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, D.; Joux, A.; Prakash, A.; Santha, M. A new public-key cryptosystem via Mersenne numbers. In Proceedings of the Advances in Cryptology–CRYPTO 2018: 38th Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2018; pp. 459–482. [Google Scholar]
- Yang, X.B.; Boussakta, S.; Al-Gailani, M.; Ngadiran, R. A new development of cryptosystem using New Mersenne Number Transform. In Proceedings of the 2010 7th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP 2010), Newcastle Upon Tyne, UK, 21–23 July 2010; pp. 701–705. [Google Scholar]
- Maetouq, A.; Daud, S.M. HMNT: Hash function based on new Mersenne number transform. IEEE Access 2020, 8, 80395–80407. [Google Scholar] [CrossRef]
- Vostrikov, A.; Sergeev, M.; Balonin, N.; Sergeev, A. Use of symmetric Hadamard and Mersenne matrices in digital image processing. Procedia Comput. Sci. 2018, 126, 1054–1061. [Google Scholar] [CrossRef]
- Masood, F.; Boulila, W.; Ahmad, J.; Sankar, S.; Rubaiee, S.; Buchanan, W.J. A novel privacy approach of digital aerial images based on Mersenne twister method with DNA genetic encoding and chaos. Remote Sens. 2020, 12, 1893. [Google Scholar] [CrossRef]
- Alexan, W.; Gabr, M.; El-Aasser, M.; Maher, E.A.; El-Damak, D.; Aboshousha, A. Anteater: When Arnold’s cat meets Langton’s ant to encrypt images. IEEE Access 2023, 11, 106249–106276. [Google Scholar] [CrossRef]
- El-Damak, D.; Alexan, W.; Mamdouh, E.; El-Aasser, M.; Fathy, A.; Gabr, M. Fibonacci Q-Matrix, Hyperchaos, and Galois Field (28) for augmented medical image encryption. IEEE Access 2024, 12, 102718–102744. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Yang, K.; Chen, Y.; Liu, X. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations. Signal Process. Image Commun. 2017, 52, 6–19. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, X.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Process. 2018, 148, 124–144. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; He, S.; Zhu, C. An effective image encryption algorithm based on compressive sensing and 2D-SLIM. Opt. Lasers Eng. 2020, 134, 106178. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. A comprehensive review on image encryption techniques. Arch. Comput. Methods Eng. 2020, 27, 15–43. [Google Scholar] [CrossRef]
- Crandall, R.; Pomerance, C. “Primes!” Prime Numbers: A Computational Perspective; Springer: New York, NY, USA, 2005; pp. 1–82. [Google Scholar]
- Goy, T. On new identities for Mersenne numbers. Appl. Math. E-Notes 2018, 18, 100–105. [Google Scholar]
- Sreehari, S.; Wu, H.; Ahmadi, M. Application of new classes of Mersenne primes for fast modular reduction for large-integer multiplication. Int. J. Cyber-Secur. Digit. Forensics (IJCSDF) 2012, 1, 15–19. [Google Scholar]
- Sridhar, V.; Kumar, A. A Technique to Speed up the Modular Multiplicative Inversion over GF(P) Applicable to Elliptic Curve Cryptography. Int. J. Comput. Appl. 2012, 47, 16. [Google Scholar] [CrossRef]
- Choi, P.; Lee, M.-K.; Kong, J.-T.; Kim, D.K. Efficient design and performance analysis of a hardware right-shift binary modular inversion algorithm in GF(P). J. Semicond. Technol. Sci. 2017, 17, 425–437. [Google Scholar]
- Lu, J.; Li, S. A multibit left-shift modular inverse hardware algorithm and its implementation. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; pp. 1–5. [Google Scholar]
- Choi, P.; Kong, J.-T.; Kim, D.K. Analysis of hardware modular inversion modules for elliptic curve cryptography. In Proceedings of the 2015 International SoC Design Conference (ISOCC), Gyeongju, Republic of Korea, 2–5 November 2015; pp. 313–314. [Google Scholar]
- Hars, L. Modular inverse algorithms without multiplications for cryptographic applications. EURASIP J. Embed. Syst. 2006, 2006, 032192. [Google Scholar] [CrossRef]
- Kumari, M.; Gupta, S.; Sardana, P. A survey of image encryption algorithms. 3D Res. 2017, 8, 37. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inf. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Feng, W.; Yang, J.; Zhao, X.; Qin, Z.; Zhang, J.; Zhu, Z.; Wen, H.; Qian, K. A Novel Multi-Channel Image Encryption Algorithm Leveraging Pixel Reorganization and Hyperchaotic Maps. Mathematics 2024, 12, 3917. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Sun, Y.; Deng, Z.; Yang, G. Memristive tabu learning neuron generated multi-wing attractor with FPGA implementation and application in encryption. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 72, 300–311. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image Encryption Algorithm Based on Plane-Level Image Filtering and Discrete Logarithmic Transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Wen, H.; Lin, Y. Cryptanalyzing an Image Cipher Using Multiple Chaos and DNA Operations. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101612. [Google Scholar] [CrossRef]
- Feng, W.; Qin, Z.; Zhang, J.; Ahmad, M. Cryptanalysis and improvement of the image encryption scheme based on Feistel network and dynamic DNA encoding. IEEE Access 2021, 9, 145459–145470. [Google Scholar] [CrossRef]
- Feng, W.; He, Y.; Li, H.; Li, C. Cryptanalysis and improvement of the image encryption scheme based on 2D logistic-adjusted-sine map. IEEE Access 2019, 7, 12584–12597. [Google Scholar] [CrossRef]
- Chai, X.; Yang, K.; Gan, Z. A new chaos-based image encryption algorithm with dynamic key selection mechanisms. Multimed. Tools Appl. 2017, 76, 9907–9927. [Google Scholar] [CrossRef]
- Wang, X.; Xu, D. A novel image encryption scheme based on Brownian motion and PWLCM chaotic system. Nonlinear Dyn. 2014, 75, 345–353. [Google Scholar] [CrossRef]
- Shaista, M.; Parsa, S.; Parah, S.A.; Ullah, H.; Hijji, M.; Muhammad, K. Adaptive color image encryption scheme based on multiple distinct chaotic maps and DNA computing. Mathematics 2022, 10, 2004. [Google Scholar] [CrossRef]
- Li, N.; Xie, S.; Zhang, J. A color image encryption algorithm based on double fractional order chaotic neural network and convolution operation. Entropy 2022, 24, 933. [Google Scholar] [CrossRef]
- Alghafis, A.; Firdousia, F.; Khan, M.; Batool, S.I.; Amin, M. An efficient image encryption scheme based on chaotic and Deoxyribonucleic acid sequencing. Math. Comput. Simul. 2020, 177, 441–466. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Wang, W. A new image encryption algorithm based on chaos and secure hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef] [PubMed]
- Zhou, N.; Zhang, A.; Zheng, F.; Gong, L. Novel image compression–encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing. Opt. Laser Technol. 2014, 62, 152–160. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. A secure image encryption algorithm based on chaotic maps and SHA-3. Secur. Commun. Netw. 2016, 9, 2015–2023. [Google Scholar] [CrossRef]
- Younas, I.; Khan, M. A new efficient digital image encryption based on inverse left almost semi group and Lorenz chaotic system. Entropy 2018, 20, 913. [Google Scholar] [CrossRef] [PubMed]
- Alexan, W.; Chen, Y.-L.; Por, L.Y.; Gabr, M. Hyperchaotic maps and the single neuron model: A novel framework for chaos-based image encryption. Symmetry 2023, 15, 1081. [Google Scholar] [CrossRef]
- Ye, G.; Zhao, H.; Chai, H. Chaotic image encryption algorithm using wave-line permutation and block diffusion. Nonlinear Dyn. 2016, 83, 2067–2077. [Google Scholar] [CrossRef]
- Mohamed, H.I.; Alhammad, S.M.; Khafaga, D.S.; Hosny, K.M. A new image encryption scheme based on the hybridization of Lorenz Chaotic map and Fibonacci Q-matrix. IEEE Access 2023, 12, 14764–14775. [Google Scholar] [CrossRef]
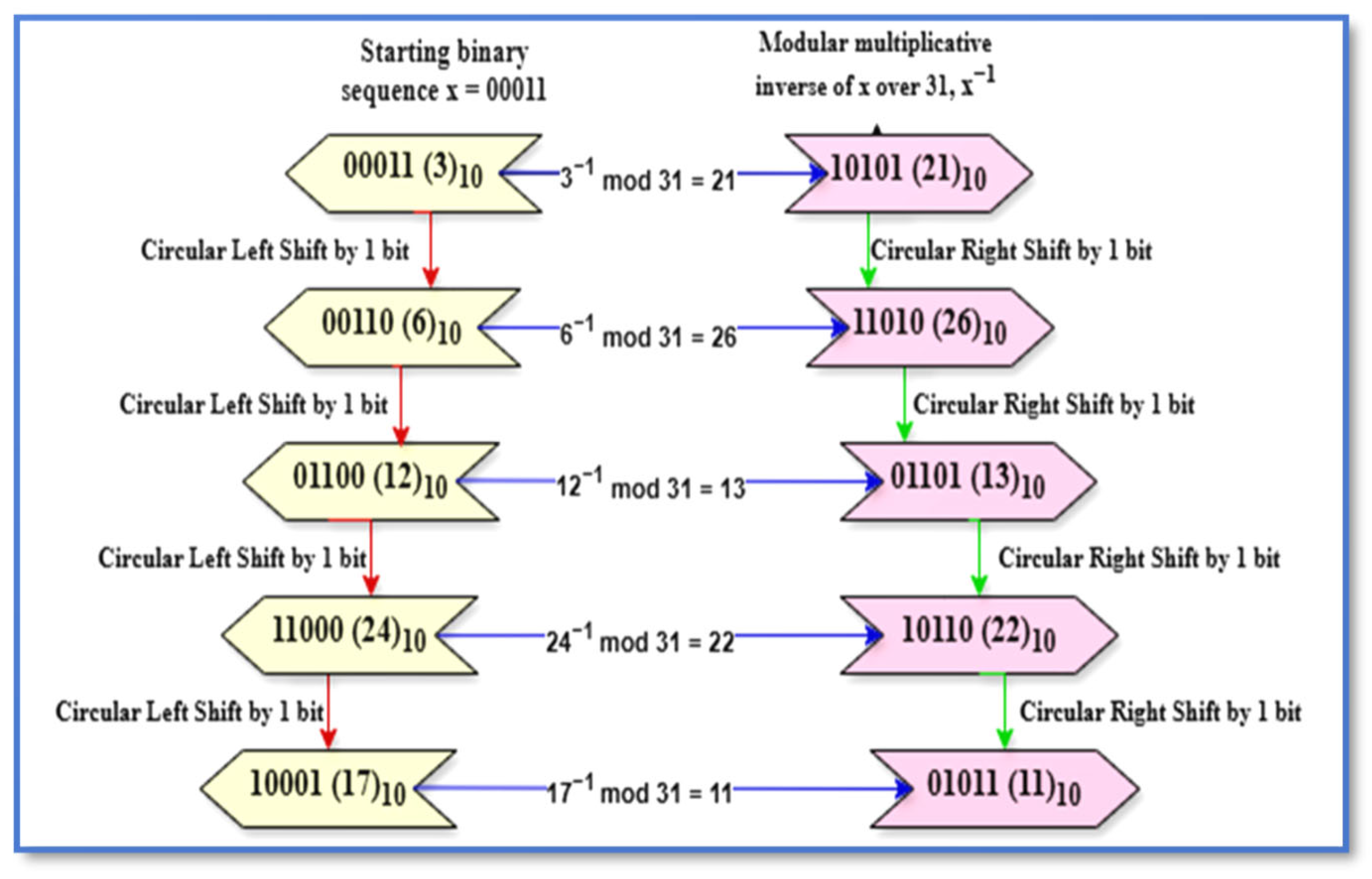

| x in Decimal | x in Binary | x−1 in Decimal | x−1 in Binary | x in Decimal | x in Binary | x−1 in Decimal | x−1 in Binary |
|---|---|---|---|---|---|---|---|
| 1 | 00001 | 1 | 00001 | 16 | 10000 | 2 | 00010 |
| 2 | 00010 | 16 | 10000 | 17 | 10001 | 11 | 01011 |
| 3 | 00011 | 21 | 10101 | 18 | 10010 | 19 | 10011 |
| 4 | 00100 | 8 | 01000 | 19 | 10011 | 18 | 10010 |
| 5 | 00101 | 25 | 11001 | 20 | 10100 | 14 | 01110 |
| 6 | 00110 | 26 | 11010 | 21 | 10101 | 3 | 00011 |
| 7 | 00111 | 9 | 01001 | 22 | 10110 | 24 | 11000 |
| 8 | 01000 | 4 | 00100 | 23 | 10111 | 27 | 11011 |
| 9 | 01001 | 7 | 00111 | 24 | 11000 | 22 | 10110 |
| 10 | 01010 | 28 | 11100 | 25 | 11001 | 5 | 00101 |
| 11 | 01011 | 17 | 10001 | 26 | 11010 | 6 | 00110 |
| 12 | 01100 | 13 | 01101 | 27 | 11011 | 23 | 10111 |
| 13 | 01101 | 12 | 01100 | 28 | 11100 | 10 | 01010 |
| 14 | 01110 | 20 | 10100 | 29 | 11101 | 15 | 01111 |
| 15 | 01111 | 29 | 11101 | 30 | 11110 | 30 | 11110 |
| Sequence Ordering | x in Binary | x in Decimal | Sequence Ordering | x−1 in Binary | x−1 in Decimal |
|---|---|---|---|---|---|
| Start | 00001 | 1 | Start | 00001 | 1 |
| LS-1 | 00010 | 2 | RS-1 | 10000 | 16 |
| LS-2 | 00100 | 4 | RS-2 | 01000 | 8 |
| LS-3 | 01000 | 8 | RS-3 | 00100 | 4 |
| LS-4 | 10000 | 16 | RS-4 | 00010 | 2 |
| Start | 00011 | 3 | Start | 10101 | 21 |
| LS-1 | 00110 | 6 | RS-1 | 11010 | 26 |
| LS-2 | 01100 | 12 | RS-2 | 01101 | 13 |
| LS-3 | 11000 | 24 | RS-3 | 10110 | 22 |
| LS-4 | 10001 | 17 | RS-4 | 01011 | 11 |
| Start | 00101 | 5 | Start | 11001 | 25 |
| LS-1 | 01010 | 10 | RS-1 | 11100 | 28 |
| LS-2 | 10100 | 20 | RS-2 | 01110 | 14 |
| LS-3 | 01001 | 9 | RS-3 | 00111 | 7 |
| LS-4 | 10010 | 18 | RS-4 | 10011 | 19 |
| Start | 00111 | 7 | Start | 01001 | 9 |
| LS-1 | 01110 | 14 | RS-1 | 10100 | 20 |
| LS-2 | 11100 | 28 | RS-2 | 01010 | 10 |
| LS-3 | 11001 | 25 | RS-3 | 00101 | 5 |
| LS-4 | 10011 | 19 | RS-4 | 10010 | 18 |
| Start | 01111 | 15 | Start | 11101 | 29 |
| LS-1 | 11110 | 30 | RS-1 | 11110 | 30 |
| LS-2 | 11101 | 29 | RS-2 | 01111 | 15 |
| LS-3 | 11011 | 27 | RS-3 | 10111 | 23 |
| LS-4 | 10111 | 23 | RS-4 | 11011 | 27 |
| Start | 10101 | 21 | Start | 00011 | 3 |
| LS-1 | 01011 | 11 | RS-1 | 10001 | 17 |
| LS-2 | 10110 | 22 | RS-2 | 11000 | 24 |
| LS-3 | 01101 | 13 | RS-3 | 01100 | 12 |
| LS-4 | 11010 | 26 | RS-4 | 00110 | 6 |
| Sequence Ordering | x in Binary | x in Decimal | Sequence Ordering | x−1 in Binary | x−1 in Decimal |
|---|---|---|---|---|---|
| Start | 0000001 | 1 | Start | 0000001 | 1 |
| LS-1 | 0000010 | 2 | RS-1 | 1000000 | 64 |
| LS-2 | 0000100 | 4 | RS-2 | 0100000 | 32 |
| LS-3 | 0001000 | 8 | RS-3 | 0010000 | 16 |
| LS-4 | 0010000 | 16 | RS-4 | 0001000 | 8 |
| LS-5 | 0100000 | 32 | RS-5 | 0000100 | 4 |
| LS-6 | 1000000 | 64 | RS-6 | 0000010 | 2 |
| Start | 0000011 | 3 | Start | 1010101 | 85 |
| LS-1 | 0000110 | 6 | RS-1 | 1101010 | 106 |
| LS-2 | 0001100 | 12 | RS-2 | 0110101 | 53 |
| LS-3 | 0011000 | 24 | RS-3 | 1011010 | 90 |
| LS-4 | 0110000 | 48 | RS-4 | 0101101 | 45 |
| LS-5 | 1100000 | 96 | RS-5 | 1010110 | 86 |
| LS-6 | 1000001 | 65 | RS-6 | 0101011 | 43 |
| Start | 0000101 | 5 | Start | 0110011 | 51 |
| LS-1 | 0001010 | 10 | RS-1 | 1011001 | 89 |
| LS-2 | 0010100 | 20 | RS-2 | 1101100 | 108 |
| LS-3 | 0101000 | 40 | RS-3 | 0110110 | 54 |
| LS-4 | 0010000 | 80 | RS-4 | 0011011 | 27 |
| LS-5 | 0100001 | 33 | RS-5 | 1001101 | 77 |
| LS-6 | 1000010 | 66 | RS-6 | 1100110 | 102 |
| Start | 0010111 | 23 | Start | 1110100 | 116 |
| LS-1 | 0101110 | 46 | RS-1 | 0111010 | 58 |
| LS-2 | 1011100 | 92 | RS-2 | 0011101 | 29 |
| LS-3 | 0111001 | 57 | RS-3 | 1001110 | 78 |
| LS-4 | 1110010 | 114 | RS-4 | 0100111 | 39 |
| LS-5 | 1100101 | 101 | RS-5 | 1010011 | 83 |
| LS-6 | 1001011 | 75 | RS-6 | 1101001 | 105 |
| Sequence Ordering | x in Binary | x in Decimal | Sequence Ordering | x−1 in Binary | x−1 in Decimal |
|---|---|---|---|---|---|
| Start | 0000000000001 | 1 | Start | 0000000000001 | 1 |
| LS-1 | 0000000000010 | 2 | RS-1 | 1000000000000 | 4096 |
| LS-2 | 0000000000100 | 4 | RS-2 | 0100000000000 | 2048 |
| LS-3 | 0000000001000 | 8 | RS-3 | 0010000000000 | 1024 |
| LS-4 | 0000000010000 | 16 | RS-4 | 0001000000000 | 512 |
| LS-5 | 0000000100000 | 32 | RS-5 | 0000100000000 | 256 |
| LS-6 | 0000001000000 | 64 | RS-6 | 0000010000000 | 128 |
| LS-7 | 0000010000000 | 128 | RS-7 | 0000001000000 | 64 |
| LS-8 | 0000100000000 | 256 | RS-8 | 0000000100000 | 32 |
| LS-9 | 0001000000000 | 512 | RS-9 | 0000000010000 | 16 |
| LS-10 | 0010000000000 | 1024 | RS-10 | 0000000001000 | 8 |
| LS-11 | 0100000000000 | 2048 | RS-11 | 0000000000100 | 4 |
| LS-12 | 1000000000000 | 4096 | RS-12 | 0000000000010 | 2 |
| Start | 0000000000011 | 3 | Start | 1010101010101 | 5461 |
| LS-1 | 0000000000110 | 6 | RS-1 | 1101010101010 | 6826 |
| LS-2 | 0000000001100 | 12 | RS-2 | 0110101010101 | 3413 |
| LS-3 | 0000000011000 | 24 | RS-3 | 1011010101010 | 5802 |
| LS-4 | 0000000110000 | 48 | RS-4 | 0101101010101 | 2901 |
| LS-5 | 0000001100000 | 96 | RS-5 | 1010110101010 | 5546 |
| LS-6 | 0000011000000 | 192 | RS-6 | 0101011010101 | 2773 |
| LS-7 | 0000110000000 | 384 | RS-7 | 1010101101010 | 5482 |
| LS-8 | 0001100000000 | 768 | RS-8 | 0101010110101 | 2741 |
| LS-9 | 0011000000000 | 1536 | RS-9 | 1010101011010 | 5466 |
| LS-10 | 0110000000000 | 3072 | RS-10 | 0101010101101 | 2733 |
| LS-11 | 1100000000000 | 6144 | RS-11 | 1010101010110 | 5462 |
| LS-12 | 1000000000001 | 4097 | RS-12 | 0101010101011 | 2731 |
| Variance | ||
|---|---|---|
| Test Image | Original | Encrypted |
| Pepper (128 × 128) | 2081.9766 | 57.8828 |
| Baboon (256 × 256) | 85,201.6875 | 271.5781 |
| Cameraman (256 × 256) | 110,973.3047 | 265.7656 |
| Pepper (512 × 512) | 507,986.90 | 1013.9141 |
| Baboon (512 × 512) | 1,258,830.9531 | 993.9063 |
| Boat (720 × 720) | 3,708,691.3438 | 1912.7188 |
| Correlation Coefficients | ||||
|---|---|---|---|---|
| Test Image | Type | Horizontally | Vertically | Diagonally |
| Pepper (128 × 128) | Original | 0.9171 | 0.9355 | 0.8808 |
| Encrypted | −0.0085 | 0.0005 | −0.0085 | |
| Mandrill Baboon (256 × 256) | Original | 0.9027 | 0.8850 | 0.8393 |
| Encrypted | 0.0010 | 0.0008 | 0.0001 | |
| Cameraman (256 × 256) | Original | 0.9333 | 0.9565 | 0.9145 |
| Encrypted | −0.0044 | −0.0027 | 0.0035 | |
| Pepper (512 × 512) | Original | 0.9730 | 0.9711 | 0.9480 |
| Encrypted | 0.0020 | −0.0021 | −0.0019 | |
| Mandrill Baboon (512 × 512) | Original | 0.9313 | 0.8985 | 0.8628 |
| Encrypted | −0.0031 | 0.0018 | −0.0010 | |
| Boat (720 × 720) | Original | 0.9693 | 0.9818 | 0.9549 |
| Encrypted | 0.0035 | 0.0020 | −0.0004 | |
| Correlation Coefficients | ||||
|---|---|---|---|---|
| Algorithm | Type | Horizontal | Vertical | Diagonal |
| Proposed | Original | 0.9333 | 0.9565 | 0.9145 |
| Encrypted | −0.0044 | −0.0027 | 0.0035 | |
| [43] | Encrypted | 0.0639 | 0.0539 | 0.0848 |
| [44] | Encrypted | 0.0093 | 0.0159 | 0.0097 |
| [18] | Encrypted | 0.0040 | −0.0027 | −0.0084 |
| [42] | Encrypted | −0.0017 | −0.0279 | 0.0047 |
| Correlation Coefficients | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Red | Green | Blue | ||||||||
| Algorithm | Type | H | V | D | H | V | D | H | V | D |
| Proposed | Plain | 0.9525 | 0.9559 | 0.9205 | 0.9742 | 0.9748 | 0.9555 | 0.9484 | 0.9594 | 0.9223 |
| Encrypted | 0.0069 | 0.0019 | 0.0003 | −0.0004 | −0.0026 | 0.0070 | −0.0028 | −0.0012 | 0.0052 | |
| [39] | Encrypted | −0.0027 | −0.0174 | 0.0022 | 0.0002 | 0.0105 | −0.0017 | −0.0008 | −0.0732 | −0.0029 |
| [40] | Encrypted | 0.0043 | −0.0006 | −0.0013 | 0.0019 | −0.0009 | 0.0026 | 0.0024 | −0.0001 | 0.0017 |
| [41] | Encrypted | 0.003 | −0.001 | 0.006 | −0.009 | −0.004 | −0.0002 | −0.003 | −0.0002 | −0.0008 |
| Correlation Coefficients | ||||
|---|---|---|---|---|
| Algorithm | Type | Horizontal | Vertical | Diagonal |
| Proposed | Plain | 0.95836 | 0.96336 | 0.93266 |
| Encrypted | 0.001225 | −0.00062716 | 0.0041962 | |
| [14] | Encrypted | 0.00157365 | 0.00494262 | −0.0067555 |
| [45] | Encrypted | −0.0028 | −0.0090 | −0.0007 |
| [46] | Encrypted | 0.00301689 | 0.00419115 | −0.00012237 |
| Image | NPCR (%) | UACI (%) |
|---|---|---|
| Pepper (128 × 128) | 99.6399 | 33.2911 |
| Baboon (256 × 256) | 99.6323 | 33.4907 |
| Cameraman (256 × 256) | 99.588 | 33.4892 |
| Baboon (512 × 512) | 99.6155 | 33.5034 |
| Algorithm | Color Channel | NPCR (%) | UACI (%) |
|---|---|---|---|
| Proposed | Red | 99.6292 | 33.3968 |
| Green | 99.6033 | 33.4858 | |
| Blue | 99.6282 | 33.589 | |
| Avg | 99.6206 | 33.4805 | |
| [40] | Red | 99.5636 | 33.5139 |
| Green | 99.6185 | 33.5660 | |
| Blue | 99.5972 | 33.5406 | |
| Avg | NA | NA | |
| [41] | Red | NA | NA |
| Green | NA | NA | |
| Blue | NA | NA | |
| Avg | 99.56 | 33.48 |
| Image | Type | Entropy |
|---|---|---|
| Pepper (128 × 128) | Plain | 7.5585 |
| Encrypted | 7.9897 | |
| Baboon (256 × 256) | Plain | 7.2202 |
| Encrypted | 7.9973 | |
| Cameraman (256 × 256) | Plain | 7.0097 |
| Encrypted | 7.9971 | |
| Pepper (512 × 512) | Plain | 7.5712 |
| Encrypted | 7.9993 | |
| Baboon (512 × 512) | Plain | 7.2871 |
| Encrypted | 7.9993 | |
| Boat (720 × 720) | Plain | 7.0955 |
| Encrypted | 7.9997 | |
| Pepper color (256 × 256) | Plain | 7.3291 |
| Encrypted | 7.9973 |
| Algorithm | Type | Entropy |
|---|---|---|
| Proposed | Original | 7.2871 |
| Encrypted | 7.9993 | |
| [16] | Encrypted | 7.9992 |
| [38] | Encrypted | 7.9993 |
| [29] | Encrypted | 7.99928 |
| [47] | Encrypted | 7.992 |
| Entropy | ||||
|---|---|---|---|---|
| Algorithm | Type | Red | Green | Blue |
| Proposed | Original | 7.3192 | 7.5999 | 7.0684 |
| Encrypted | 7.9975 | 7.9971 | 7.9975 | |
| [45] | Encrypted | 7.9976 | 7.9971 | 7.9971 |
| [39] | Encrypted | 7.9974 | 7.9971 | 7.9972 |
| [40] | Encrypted | 7.9973 | 7.9977 | 7.9969 |
| Image | MSE | PSNR | SSIM |
|---|---|---|---|
| Pepper (128 × 128) | 8226.2297 | 8.9788 | 0.0058 |
| Baboon (256 × 256) | 7954.4622 | 9.1247 | 0.0117 |
| Cameraman (256 × 256) | 9433.4528 | 8.3841 | 0.0101 |
| Pepper (512 × 512) | 8467.4397 | 8.8533 | 0.0092 |
| Baboon (512 × 512) | 8171.2378 | 9.0079 | 0.0092 |
| Pepper color (256 × 256) | 10010.122 | 8.1912 | 0.000788 |
| Algorithm | MSE | PSNR |
|---|---|---|
| Proposed | 10,010.122 | 8.1912 |
| [15] | 10,023.7 | 8.12053 |
| [38] | 7274.44 | 9.55 |
| [46] | 10,074.0 | 8.09877 |
| Algorithm | Color Channel | PSNR | SSIM |
|---|---|---|---|
| Proposed | R | 9.2709 | 0.001892 |
| G | 7.745 | 0.000363 | |
| B | 7.5579 | 0.000109 | |
| [39] | R | 9.4346 | 0.0118 |
| G | 7.7963 | 0.0092 | |
| B | 8.2885 | 0.0083 | |
| [41] | R | 8.2465 | 0.0093 |
| G | 7.4135 | 0.0070 | |
| B | 7.3602 | 0.0074 |
| Algorithm | Proposed | [48] | [14] | [42] |
|---|---|---|---|---|
| 128 × 128 Gray | 0.1286 s | NA | NA | 0.06 s |
| 256 × 256 Gray | 0.5018 s | NA | NA | 0.22 s |
| 512 × 512 Gray | 2.0043 s | NA | NA | 0.85 s |
| 256 × 256 Color | 1.5120 s | 3.3978 s | 0.427 s | NA |
| Machine Specification | Intel Core i5, 1.6 GHz, 8 GB RAM | NA | AMD Ryzen 5600H Mobile, 3.3 GHz, 16 GB | Intel Pentium dual core, 2.3 GHz, 2 GB |
| Correlation Coefficient | ||||
|---|---|---|---|---|
| Image (256 × 256) | Entropy | Horizontal | Vertical | Diagonal |
| Encrypted pure black image | 7.9970 | −0.0012 | −0.0108 | −0.0003 |
| Encrypted pure white image | 7.9969 | −0.0003 | −0.0121 | 0.0011 |
| Attributes | Proposed Encryption Technique | AES | Chaotic-Based Encryption Schemes |
|---|---|---|---|
| Encryption quality | Demonstrated high randomness, non-linearity and good diffusion due to modular inversion and XOR operations. | Proved to be strong and highly optimized with high diffusion and confusion properties through the use of substitution–permutation rounds. | High randomness is achieved through the proper selection of chaotic maps and techniques, such as dynamic scrambling and compressive sensing. |
| Key space | Large key space of 2521 is obtained. | Key space up to 2256 can be achieved. | Key spaces are normally large, but can be extremely large for some schemes incorporating the Mersenne Twister. |
| Key management | Fixed key sequence and hence less complex. | Established key expansion. | Sensitive to the initial condition but key management can be complex. |
| General structure and complexity of technique | Symmetric block cipher with a block size of 521 bits, simple yet efficient technique without the use of S-box. | Symmetric block cipher with a block size of 128 bits and the algorithm comprises the use of complex S-boxes. | Use chaotic maps like logistics maps or Arnold’s cat map to generate a random sequence for encryption and use pixel scrambling techniques for diffusing the image, which may or may not include S-boxes. |
| Computational complexity | Moderate based on modular inversion. | Quite high but highly optimized. | Moderate to high based on the maps used number of iterations performed. |
| Memory usage | Low to moderate and can be further optimized on hardware. | Even though it depends on implementation, typically low to moderate. | Can be high based on the chaotic system complexity. |
| Resilience to attacks | Proven to resist brute force, known/chosen plaintext attacks, and differential attacks. | Resistant to all possible cryptographic attacks. | Resistant to most of the attacks but the chaotic map weakness must be monitored. |
| Encryption time and scalability | Encryption time is comparable with other popular schemes but can be further optimized and is highly scalable. | Good encryption time and highly scalable. | Encryption time is comparable with other popular schemes and is scalable. |
| Hardware implementation | Efficient on hardware; memory usage and computational speed can be further improved. | Very efficient in hardware. | Can be complex unless optimized. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
A., S.M.; N., A.K.M. A Technique for Image Encryption Using the Modular Multiplicative Inverse Property of Mersenne Primes. Symmetry 2025, 17, 166. https://doi.org/10.3390/sym17020166
A. SM, N. AKM. A Technique for Image Encryption Using the Modular Multiplicative Inverse Property of Mersenne Primes. Symmetry. 2025; 17(2):166. https://doi.org/10.3390/sym17020166
Chicago/Turabian StyleA., Shanooja M., and Anil Kumar M. N. 2025. "A Technique for Image Encryption Using the Modular Multiplicative Inverse Property of Mersenne Primes" Symmetry 17, no. 2: 166. https://doi.org/10.3390/sym17020166
APA StyleA., S. M., & N., A. K. M. (2025). A Technique for Image Encryption Using the Modular Multiplicative Inverse Property of Mersenne Primes. Symmetry, 17(2), 166. https://doi.org/10.3390/sym17020166






