Abstract
The minimalist approach in the study of perturbations in fluid dynamics and magnetohydrodynamics involves describing their evolution in the linear regime using a single first-order ordinary differential equation, dubbed the principal equation.The dispersion relation is determined by requiring that the solution of the principal equation be continuous and satisfy specific boundary conditions for each problem. The formalism is presented for flows in Cartesian geometry and applied to classical cases such as the magnetosonic and gravity waves, the Rayleigh–Taylor instability, and the Kelvin–Helmholtz instability. For the latter, we discuss the influence of compressibility and the magnetic field, and also derive analytical expressions for the growth rates and the range of instability in the case of two fluids with the same characteristics.
1. Introduction
The study of perturbations in any physical system sheds light on the mechanisms responsible for maintaining equilibrium and offers a way to predict temporal behavior in response to variations. Although this task is generally difficult, simplifying each case and focusing on the most critical ingredients determining its evolution is essential. Classical waves and instabilities represent such simplified structures. For example, acoustic compressible perturbations, attributed to sound or magnetosonic waves, can be identified even in systems with complex dynamics. Alfvén waves play a significant role in magnetized plasmas. When gravity or buoyancy forces are important, differences in density drive gravity waves. By “gravity” we may also refer to fictitious forces in non-inertial frames, such as the effective gravity in a decelerating system or centrifugal forces. In cases of heavy-over-light fluid stratifications, the Rayleigh–Taylor instability comes to mind. Similarly, a relative velocity between two fluids triggers the Kelvin–Helmholtz instability. These are only a few examples of simplified structures that are crucial for understanding more complicated and realistic settings. They are often connected to temporal behaviors in laboratory experiments or specific features observed in astrophysical systems.
The full study of perturbation evolution in most cases can only be achieved through numerical simulations. Linearizing the system of equations is a simpler way to understand the conditions under which the system is unstable, although it does not cover nonlinear evolution. Normal mode analysis is a further simplification, allowed only in symmetric unperturbed states, and can be used to find wave frequencies or instability growth rates. This approach allows for simpler parametric studies or even the derivation of analytic expressions that directly reveal the physics of the mechanisms involved.
Since we are discussing classical problems, there are many books, e.g., [1,2,3,4,5], that provide the most basic information. There have also been a plethora of related works in the literature over the years, e.g., [6,7,8,9,10,11], to name but a few. Nevertheless, these problems continue to be an active area of research, e.g., [12,13,14], and there is always room—and need—to improve our understanding.
The goal of this paper is to present the methodology to determine the dispersion relation in each case, following the minimalist approach introduced in Ref. [15]. This novel approach simplifies the procedure as much as possible by using a single first-order ordinary differential equation, dubbed the principal equation. Firstly, we derive this equation through linearization and discuss the necessary boundary conditions (Section 2). Next, we apply the method to determine the dispersion relation for magnetohydrodynamic (MHD) waves (Section 3), gravity waves and the Rayleigh–Taylor instability (Section 4), gravito-acoustic waves (Section 5), and the Kelvin–Helmholtz instability (Section 6). We provide a more extensive analysis of the Kelvin–Helmholtz instability, deriving analytical expressions for the growth rate in the magnetized case and discussing the factors that most significantly affect the results.
2. Linear Analysis, the Principal Equation, and Boundary Conditions
Fluid dynamics is governed by the conservation laws of mass, momentum, and energy. To include cases of a conducting magnetized fluid (plasma), we combine these laws with Maxwell’s equations to obtain the system of magnetohydrodynamic equations. In the non-relativistic limit, and neglecting non-ideal effects such as viscosity, resistivity, and surface tension while using Lorentz–Heaviside units, these equations are as follows:
We are interested in exploring the perturbations of a steady state that depends only on one spatial Cartesian coordinate. In particular, we assume that the unperturbed state has density , pressure , bulk velocity , magnetic field , and the acceleration of gravity is . Introducing the total pressure
the zeroth-order equations are satisfied provided that
Adding perturbations of the form
defining the wavevector in the plane
and the Doppler-shifted frequency
we linearize the equations as shown in Appendix A; the main steps and related comments follow.
The linearized system reduces to two differential equations for the perturbations of the velocity in the direction and the total pressure (there are algebraic relations for all the other perturbations, connecting them to , , and their derivatives). Instead of and , it is more convenient to use two other quantities.
The first, replacing , is the Lagrangian displacement in the direction. The relation between the Lagrangian displacement and the velocity perturbation results from the expression of the velocity in the perturbed location of each fluid element , which equals , yielding . The component gives , with .
The second quantity, replacing , is the perturbation of the total pressure in the perturbed location of each fluid element .
The advantage of these replacements is that the new functions and are everywhere continuous, even at locations where the unperturbed state has contact discontinuities.
2.1. The System for ,
The resulting system is
To simplify the expressions we define the following quantities that have important physical meanings and effects in the resulting dispersion relations through their appearance in the array elements .
The is connected to the angle between the wavevector and the unperturbed magnetic field. Its presence in a dispersion relation represents the influence of the magnetic tension, which acts like a spring with restoring force per mass . This is evident in the pure Alfvén waves (in a static homogeneous plasma without gravity), for which the displacement satisfies , with .
The appears in the denominator of the resulting system of differential equations, and its zeros correspond to the Alfvén waves.
The is related to the density perturbation in the perturbed location of each fluid element . It is interesting to note that the incompressible limit corresponds to .
The defined through represents the local wavenumber in the direction. Indeed, the latter equation is equivalent to the dispersion relation of the slow/fast magnetosonic waves if we define the total wavevector and the angle between and through .
Another way to see the connection between and the wavenumber in the direction is to consider the homogeneous fluid case without gravity. In this scenario, system (14) with constant coefficients has solutions . The equation gives two opposite solutions for , corresponding to oppositely moving waves in the direction. Note that, in general, is complex, and its imaginary part corresponds to exponential variation of the eigenfunctions, since . In the incompressible limit, where and , it simplifies to purely exponential dependence , without sinusoidal dependence on x. More details on these waves will be discussed later; they offer a way to understand the physics of the solutions even in non-homogeneous fluids and are directly related to the boundary conditions when the fluid extends up to large distances or .
The cases , , and need to be studied separately, something that can be easily achieved since they lead to simplified equations. These cases correspond to waves and are not necessary for instability studies in which is real and complex.
2.2. The Principal Equation
Since the system (14) is linear, only the ratio is uniquely defined. Using the equations of the system we directly find that Y satisfies the principal equation
Following the minimalist approach [15], it is sufficient to work with the ratio Y and solve the principal equation in order to find the dispersion relation of the wave or instability. We just need to integrate this single, first-order differential equation, requiring Y to be everywhere continuous and satisfying the correct boundary conditions at the extreme values of x.
Knowing Y, we can find all the other perturbations from
and the relations (A20)–(A27) given in Appendix A. We emphasize though that these are not needed to find the dispersion relation.
2.3. Boundary Conditions
The linearization was based on the functions and , which are everywhere continuous. The same holds for their ratio. Therefore, in the case of discontinuities in the unperturbed state, we simply continue the integration of the principal equation when passing from one medium to another, keeping Y continuous.
In cases where the fluid ends at some extreme value of x, we always know the value of Y at that boundary and use it as a boundary condition. One example is the case of a solid wall at the boundary; here, Y vanishes on the wall since the Lagrangian displacement vanishes. Another example is when a medium with constant total pressure exists outside the fluid, such as a hydrodynamic atmosphere with negligible density. In this case, vanishes at the interface since the perturbation of the total pressure vanishes. (We arrive at the same result if we consider a nonzero perturbation in the atmosphere, solve the problem on both sides while requiring the continuity of Y, and ultimately take the limit of zero density outside.)
The nontrivial boundary conditions that need closer examination correspond to cases where the fluid extends to theoretically infinite distances or . At these distances the unperturbed fluid is homogeneous, and the solutions of the principal equation are given in Appendix B. These solutions correspond to two waves moving oppositely in the direction, with one wave’s amplitude increasing exponentially with x and the other’s decreasing. To avoid the wave with the diverging amplitude (there is a way to automatically find the non-diverging solution following the Schwarzian approach of Ref. [16]; to obtain analytical expressions though, as we attempt here, we can directly find the asymptotic solutions), the solution of the principal equation should approach one of the constant values that correspond to complex wavenumbers , respectively. Assuming that is the principal value of the root (with positive real part), we choose the upper sign at and the lower sign at .
In the case that (i.e., is a negative real number), the wave’s amplitude remains constant at infinity, and we can choose the solution whose sign of corresponds to the desired propagation.
Note that . In the presence of gravity, this is not constant since the unperturbed total pressure is variable, with its gradient balancing gravity. However, in cases where the fluid extends to theoretically infinite distances (in which since the total pressure also reaches theoretically infinite values), and uniform gravity, it approaches a constant corresponding to the incompressible limit.
In the absence of gravity, and without loss of generality we can choose the sign such that (taking the principal value of the root and the upper/lower sign at , respectively).
Summary of Equations and Boundary Conditions
The equations needed to apply the minimalist approach are summarized in Table 1.

Table 1.
Minimalist approach equations and boundary conditions.
In addition, the following forms of the principal equation may be useful, especially if one looks for analytical solutions:
with
Note that in cases with real oscillating eigenfunctions the Y is real and becomes infinite at some points; this problem can be easily handled numerically by working with an angular variable instead of Y (or more generally with , where are given functions of our choice), as described in Section 2 of Ref. [16].
3. MHD Waves
A simple case of disturbances inside a homogeneous magnetized plasma involves magnetohydrodynamic waves, which are analyzed in most plasma textbooks, e.g., Ref. [2].
3.1. Slow/Fast Magnetosonic Waves
For a homogeneous unperturbed state and zero gravity , , , the principal equation becomes .
Its constant solutions are (both signs are allowed). According to Equation (18) , i.e., is the wavenumber. The solutions correspond to the continuous spectrum of the slow/fast magnetosonic waves and, as already stated, the equation is equivalent to the dispersion relation of these waves .
The variable solution of the principal equation corresponds to a superposition of waves, as discussed in Appendix B.
3.2. Alfvén Waves
The continuous spectrum of Alfvén waves corresponds to the singular case of the principal equation . In that case, could be any function of x, (and ), with finite and . (Note that for Alfvén waves is given by , and does not represent a wavenumber.)
3.3. Two Semi-Infinite Incompressible Plasmas
As another example on how to use the minimalist approach, let us consider two semi-infinite incompressible, homogeneous, static, magnetized plasmas in the regimes (subscript “1”) and (subscript “2”), and zero gravity.
With in both regimes, we have , , . The principal equation is and has constant solutions . According to the boundary conditions given in Table 1 (or directly checking the sign of ) the upper sign should be used for and the lower for . Thus, for and for .
The continuity of Y gives the dispersion relation , representing a stable Alfvén wave whose amplitude drops exponentially as we move away from the contact discontinuity at . (We recall that , , and that all the unperturbed states considered in the paper have the form described in Section 2.)
3.4. Effect of Finite Depth
Following the previous example, suppose now that the bottom plasma has finite depth H (there is a solid wall at ). Then, in the bottom part the solution of the principal equation that vanishes at is . (In the upper part, the accepted solution corresponding to vanishing amplitude at continues to be as before.)
The continuity of Y at gives the dispersion relation . Evidently the relation describes a stable Alfvén wave, modified by the presence of the wall at and the reflections from that wall.
4. Gravity Waves and Rayleigh–Taylor Instability
Density discontinuities in fluids within a gravitational field can drive gravity waves. These include disturbances at the interface between two fluids, such as between the atmosphere and the ocean. When a heavier fluid lies above a lighter fluid, the perturbation becomes unstable, leading to what is known as the Rayleigh–Taylor instability. This phenomenon was first described in the pioneering research papers by Rayleigh [17] and Taylor [18].
Consider two semi-infinite incompressible, static, magnetized plasmas, the first (subscript “1”) in the region and the second (subscript “2”) in the region , inside uniform gravity , as in the left panel of Figure 1.
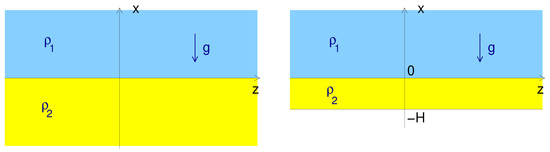
Figure 1.
The unperturbed state of two fluids in contact at . Left panel: semi-infinite fluids. Right panel: the bottom part has finite depth H.
With in both regimes, we have , , . The principal equation is and has constant solutions . (Although these parts are not homogeneous, since there must be a gradient of the total pressure balancing gravity, the incompressibility assumption allows them to have constant solutions, provided that and A are constant in both parts.)
Choosing the correct sign in each part following Table 1 (or directly using ), we conclude that for and for .
The continuity of Y gives the dispersion relation , a result derived in Ref. [1].
This relation includes as subcases the surface gravity waves corresponding to zero magnetic fields and , for which , and the classical Rayleigh–Taylor instability corresponding to zero magnetic fields and heavier fluid on top of lighter, for which the growth rate is . It also shows the stabilizing effect of the magnetic field through its magnetic tension manifest in the dispersion relation in the presence of and . It always reduces the growth rate, and if it is sufficiently strong it makes positive, converting the disturbance from an instability to an Alfvén wave.
Effect of Finite Depth
If the bottom plasma has finite depth H (there is a solid wall at ; see the right panel of Figure 1), we need to consider the variable solution of the principal equation with (given in Appendix B). Requiring Y to vanish at , we find for .
As a specific example, suppose the upper part is a hydrodynamic medium with negligible density. In that case for and the continuity of Y gives the dispersion relation for gravity waves , modified by the presence of the magnetic field. (The same can be found considering the constant solution in the upper part, requiring the continuity of Y at , and then taking the limit .) In the shallow water approximation , we obtain .
5. Gravito-Acoustic Waves
In the examples presented up to now, the fluids were homogeneous, at least partially, allowing us to easily solve the principal equation. In inhomogeneous cases, we rely on the numerical integration of the principal equation. An exception to that, where it is possible to analytically solve the differential equation although the fluid is not homogeneous, is the case of gravito-acoustic waves, analyzed, e.g., in Ref. [5]. In addition, this case serves as a nice example showing the interplay between acoustic and gravity waves.
For a hydrodynamic fluid between two solid walls at and , inside homogeneous gravity , with unperturbed density , pressure satisfying the hydrostatic equilibrium condition , and the constant scale height, we obtain , , , and the principal equation can be written as
Its general solution is with , and the square of the Brunt–Väisälä (or buoyancy) frequency. The boundary condition specifies C and gives . The boundary condition requires , and the dispersion relation is .
The equation for is , with solution . (The cases and need to be examined separately. The former gives and the latter gives . Neither can satisfy the boundary conditions, so they cannot be accepted.)
6. Kelvin–Helmholtz Instability
Relative motion between two fluids induces an instability known as Kelvin–Helmholtz, as first described in the seminal papers by Lord Kelvin [19] and Hermann von Helmholtz [20].
6.1. Incompressible Limit
For the incompressible case and two semi-infinite plasmas, similarly to the Rayleigh–Taylor instability (Section 4) we find that for and for . The only difference is that and now depend on the velocities.
The continuity of Y gives the dispersion relation with solutions
a result derived in Ref. [1]. The three terms within the square root have obvious physical meaning. The first is due to relative velocity and always leads to instability. The second is due to gravity and leads to stability/instability in the case of stable/unstable stratification (lighter fluid above heavier or the opposite). The third term is due to the magnetic field stress and is always stabilizing.
6.2. Compressible Kelvin–Helmholtz Instability
Taking into account compressibility and neglecting gravity, we have , , , and the constant solutions of the principal equation are with . According to Table 1 we need to choose the upper sign for and the lower for . Thus, and for , and for . The dispersion relation is or
We recall that we need to take the principal values of both square roots, i.e., the ones with positive real parts.
6.3. On the Physics of the Kelvin–Helmholtz Instability
A relatively simple case for which we can find analytical results will help to understand the physics of the instability. We consider two hydrodynamic fluids with the same unperturbed characteristics (same density , same pressure as required from the equilibrium at the contact discontinuity, and same sound velocity ) and work in the frame where the two fluids move with opposite velocities (with positive and the upper sign corresponding to ).
The dispersion relation becomes , where . Unstable modes (with ) exist for , with purely imaginary . One way to find this result is to substitute when the dispersion relation reduces to with solutions . Actually, the angle has an important meaning connected to the argument of the resulting complex wavenumbers in the direction, which are .
Although the results apply for any angle between and , to simplify the expressions, from now on we restrict ourselves to the case , i.e., we consider a disturbance with (with positive ). The characteristics of the unstable mode, the Lagrangian displacement, and the perturbations of the pressure, density, and velocity (written in a way to show the phase difference between each quantity with ) are
Suppose we initially disturb the interface between the two fluids by . The Lagrangian displacement along at any later time and for any other fluid element has the form ; the goal is to find and . Using the Lagrangian displacement and the Lagrangian perturbations of the velocity, pressure, density, which are , , and , respectively, the equations that lead to that goal are the momentum and the continuity (coming from ). Since all perturbations are proportional to , a time derivative has the meaning , and the divergence , with the total wavenumber in the two fluids (their components are the same, but the components differ).
The momentum equation along connects the displacement with the pressure perturbation . Requiring and to be continuous at the interface between the two fluids, we arrive at a first relation between the unknowns .
The pressure gradient along the interface is connected to the corresponding Lagrangian displacement through the momentum equation along , which gives . (The latter means that , a characteristic of longitudinal waves.)
The continuity also connects the two components of the displacement. It gives . Substituting and , we arrive at the second relation between the unknowns (one for each fluid) .
The perturbation essentially consists of two sound waves in the two fluids, with wavenumbers . In the fluid rest frames, the two waves move with different velocities, satisfying , a relation equivalent to , with . The two waves meet at the contact discontinuity and as a consequence they have the same and such that their phases are continuous at the interface. As already presented, for the case of fluids with the same density, in a frame in which they move with opposite velocities , and is parallel to the relative velocity, the resulting unstable mode has and , with , .
The value of the complex wavenumber (in each part) is directly connected to compressibility through S. In the incompressible limit it is purely imaginary, since in that limit , , and . (Note that in the incompressible limit the continuity gives . Since the two vectors are complex, this does not mean . It rather means , using from the momentum equation. In addition, the relation does not mean that the vector is zero.) If we consider cases with decreasing S, i.e., decreasing keeping the same, in which the compressibility becomes more and more important, the first part of the expression of affects the value of in two ways. Firstly, the imaginary part decreases, meaning that the perturbation survives at longer distances from the interface. Secondly, the increases, contributing more to the phase of the perturbation, which is . Both effects are expressed through the angle , which decreases with decreasing S (increasing M). The growth rate is also connected to S through . It decreases as the result of compressibility, from in the limit to zero when , corresponding to the minimum S for which the perturbation is unstable.
The vorticity is a key quantity in the Kelvin–Helmholtz instability. Its undisturbed value is the reason behind the development of the instability. Even with the perturbation included it is nonzero only in the interface between the two fluids. Nevertheless, the motion of the fluids along the interface redistributes the vorticity compared to the unperturbed state. The related velocity inside the upper/lower fluid, just above/below the interface , is . The mean value shows that fluid accumulates near the positions of lower pressure, where the vorticity increases (in the direction) by . This accumulation of vorticity further increases the displacement , leading to instability. It becomes stronger for larger , i.e., smaller M, since the mean value of increases with .
Three example solutions are shown in Figure 2. The upper panel corresponds to an incompressible case with , for which and . (For the approximate expression for is .) The exponential decrease in the perturbation as we move away from the interface is evident. The perturbed interface is shown, along with the circulation around points of minimum pressure (the mean velocity of the fluids on the interface points toward these minimum pressure points).
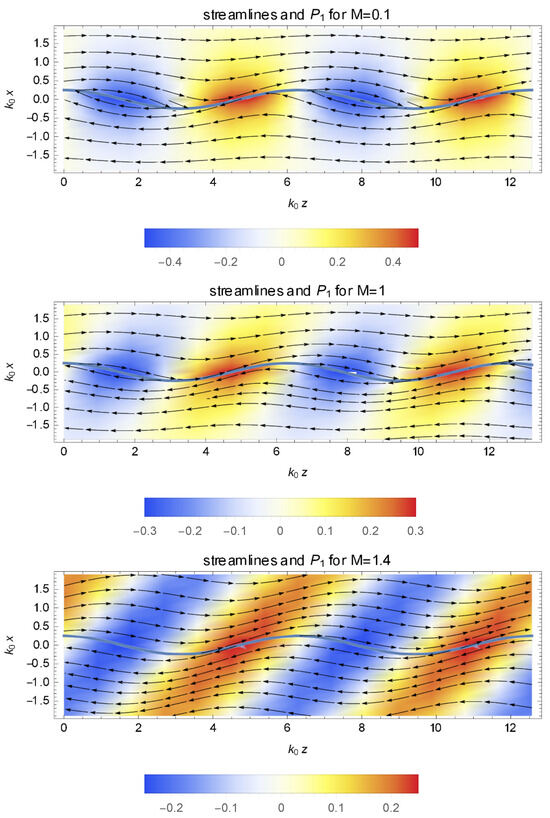
Figure 2.
The streamlines and the pressure perturbation for three cases: (upper panel), (middle panel), and (lower panel).
The two other panels correspond to cases in which compressibility is important. The solution in the middle panel has , , and , and in the lower panel , , and . The now has a nonnegligible part and as a result the iso-phase planes are constant, tilted as shown in the panels.
For cases approaching the maximum value of M for which the perturbation is unstable (the ), the values of , , and approach zero, and the perturbation practically consists of two standing sound waves (one in each fluid) with real wavenumbers. (For the approximate expression for is .)
6.4. Influence of Magnetic Field
For simplicity we consider again two homogeneous fluids with the same unperturbed characteristics, and work in the frame where the fluids move with opposite velocities . Now, there is also a constant magnetic field in the unperturbed state, the same in both fluids.
Inspecting the dispersion relation (22), we see that the magnetic field enters in two ways. Firstly, through its pressure , or equivalently the square of the Alfvén velocity . Secondly, through its tension, manifest in the terms , i.e., its component parallel to , or equivalently the component of the Alfvén velocity .
The magnetic pressure enters in the expression of S and increases its value. Thus, it moves the dynamics toward the incompressible limit and, according to the discussion of the previous section, destabilizes (the second terms inside the square roots equal , so an increase in leads to the square roots being closer to unity). Actually, if we include magnetic field normal to only, the dispersion relation is exactly equivalent to its hydrodynamic analogue, with the only difference that M now represents the fast magnetosonic Mach number . Figure 3 shows the resulting growth rates. Notably it includes as subcases the purely hydrodynamic case () considered in the previous section, and the cold case (), with only the component of the magnetic field.
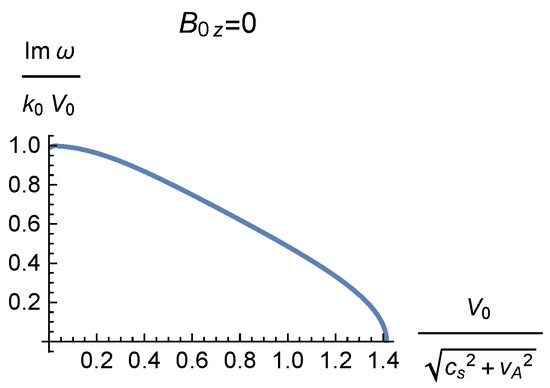
Figure 3.
The growth rate (normalized to ) of the Kelvin–Helmholtz instability for two homogeneous fluids moving with , with the same unperturbed density , sound velocity , magnetic field , and disturbance with .
The magnetic tension enters in the dispersion relation through (essentially the component of the magnetic field along ) in two places: inside A and S. It always has a stabilizing effect since the tension is a restoring force; we have seen that in the previous examples of Alfvén waves and the Rayleigh–Taylor instability, even in the incompressible limit. It also affects incompressibility through its appearance inside S. Since it decreases S, it moves the dynamics away from the incompressible limit, something that also, in general, stabilizes.
Another related connection is that the magnetic tension affects the perturbation of the vorticity inside each fluid, which, using the expressions of the velocity perturbations given in Appendix A, can be expressed as .
In the following, we present the methodology to find numerical results.
The dispersion relation (22) in the case under consideration can be written as
and can be solved numerically. However, for the case of fluids with the same characteristics considered here it is possible to proceed analytically. As shown in Appendix C, the dispersion relation can be transformed to the following quartic polynomial equation for the square of the growth rate,
using the parametrization
Note that the angle is connected to the angle between the magnetic field and the wavenumber since .
The left panel of Figure 4 shows the growth rate for cases where the magnetic field has only component along . In general, the field decreases the growth rate, and if it is sufficiently strong it completely suppresses the instability. Similar behavior is shown in the right panel of Figure 4 for the cold case. For all strengths of the magnetic field, if its orientation is sufficiently close to the wavevector, the magnetic tension completely suppresses the instability.
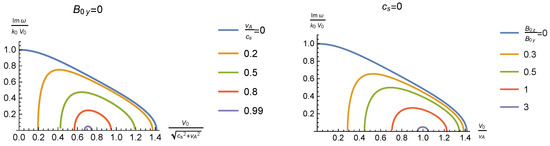
Figure 4.
Same as Figure 3, but in the left panel for magnetic field along with various strengths corresponding to the shown values of the ratio , and in the right panel for cold cases () and magnetic field with various strengths and orientations corresponding to the shown values of the ratio (in all cases ).
6.5. Range of Instability
It is interesting to explore the regions of M for which the Kelvin–Helmholtz instability is present, as shown in Figure 4. The question is: Under what conditions does the dispersion relation (27) have purely imaginary roots? For simplicity, we consider a disturbance with parallel to the velocities. The results can be easily generalized.
One might naively think that the extreme values of these instability regions can be found by setting in the dispersion relation (27) and requiring both numerators to vanish (since the denominators are opposite real numbers). However, this implies , resulting in no x-dependence of the disturbance. This case corresponds to magnetosonic waves in the frame of each fluid with total wavevectors and , with (see Section 3.1). The absence of x-dependence makes these cases unrelated to the unstable modes.
However, there are two other possibilities. The vanishing of both denominators in the dispersion relation (27) for needs to be considered as a possible limiting case. This corresponds to Alfvén waves with , with (see Section 3.2). Note that does not appear in the dispersion relation. Nevertheless, its value is nonzero, given by . The x-dependence of the disturbance allows for a possible connection with unstable modes.
A third possibility is that the limiting values may correspond to bifurcations of the dispersion relation. It is actually evident from inspecting Figure 3 that the slope becomes infinity when . In general, a dispersion relation depends on various parameters, and the slope is defined as the derivative with respect to one of these parameters, while keeping all others constant. For a dispersion relation of the form constant, its differential shows that bifurcation corresponds to . Thus, extreme values of the instability regions may be connected to the condition .
In our case, there are three parameters, and we can choose , , . The algebra gives that leads to or the following cubic for :
or .
For the left panel of Figure 4 we have , , and the extreme values of M are given by . The roots of this cubic are , , , and the corresponding wavenumbers , , , respectively. Thus, the value corresponds to a magnetosonic wave without x-dependence (unrelated to instability), while the other two solutions , are the extreme values of M related to the unstable modes.
The result is that for the Kelvin–Helmholtz instability occurs only if and for velocities in the interval . As we approach the limits, the wavenumbers approach real values and the instability is transformed to magnetosonic waves with constant amplitudes and wavenumbers .
For the right panel of Figure 4 we have and and the maximum value of M corresponds to bifurcation for which . The nontrivial root is , and the corresponding wavenumbers .
The lower limit of the instability region corresponds to Alfvén waves , so .
The result is that for the cold case the Kelvin–Helmholtz instability occurs only if . As we approach the limits, the wavenumbers approach real values and the instability is transformed to waves (Alfvén waves in the lower limit and magnetosonic in the upper) with constant amplitudes and wavenumbers .
6.6. Bifurcations in the General Case
The dispersion relation in the general case is , and taking its logarithmic derivative we conclude that bifurcations occur when is continuous at the interface. Equivalently, since is also continuous, is continuous. Substituting S and , this quantity equals
In the hydrodynamic case, the latter simplifies to , while in the cold case to .
7. Summary
The primary objective of this paper is to illustrate how the minimalist approach, as introduced in Ref. [15], can be applied to stability problems in planar geometry using Cartesian coordinates. This method highlights the approach’s efficacy in determining the dispersion relation by integrating a single first-order differential equation, the principal equation.
Although the mathematical formalism is quite cumbersome, it can be simplified by defining intermediate quantities with important physical meanings. For example, the complex has a direct connection to wave propagation and simultaneous amplitude variation. The function S is related to compressibility, which depends on both thermal and magnetic pressure, and shows how the wave propagation and the growth rate of the instability depend on these factors. The function F signifies the stabilizing nature of magnetic tension. All these aspects are discussed and reviewed when applying the method to classical instabilities.
A more extensive analysis was conducted on the Kelvin–Helmholtz instability, resulting in new findings. Specifically, analytical solutions of the dispersion relation in certain cases were derived, along with a study of bifurcations and their connection to the ranges of instability. These tools facilitate parametric studies, which are far from being considered complete even in classical instabilities.
Detailed studies of specific problems in hydrodynamics or magnetohydrodynamics will benefit from the examples and formalism presented, as well as from the ideas on how to explore the possible existence of analytical solutions and specify the range of instability. Applications in other geometries and more general theoretical frameworks are also possible and will be presented in future works.
Funding
This research received no external funding.
Data Availability Statement
This research is analytical; no new data were generated or analyzed. If needed, more details on the study and the numerical results will be shared on reasonable request to the author.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Linearization
The linearized Equations (1)–(4) are (for ) as follows:
with , the sound velocity (only the unperturbed is needed and is assumed to be a known function of x), , , and . In the above expressions, the relation was used. This can be seen as a consequence of the induction Equation (4), but shows more directly that the relation holds.
We can use Equations (A4)–(A8) of the system, together with the definitions of and , to express the perturbations of the density, velocity, and the magnetic field as functions of , , and :
where .
We introduce the perturbation of the total pressure in the perturbed position , a quantity that is continuous everywhere (similarly to ).
The substitution of , in Equation (A17), also using the equilibrium of the unperturbed state , gives
where .
After solving this system and finding , we return to the rest of the equations and find all other perturbations. We summarize the expressions below (in which the left-hand sides represent the Lagrangian perturbation of each quantity, i.e., the perturbation in the perturbed position).
Appendix B. Solutions of the Principal Equation in the Homogeneous Case
If the array elements are constants, the principal equation has two kinds of solutions. Either constants , satisfying with , or variable , with a constant of integration.
Each of the former corresponds to one-way wave propagation in the (or )-direction and the latter to a superposition of these two waves. This becomes clear if we find and using Equations (18). It is even simpler to look for solutions of the system (14), which is linear with constant coefficients in this case and admits solutions of the form with . The general solution is , .
We can simplify the expressions of the eigenfunctions to , , substituting , and their ratio agrees with the solution of the principal equation given above . Note that the last expression for Y can also be written as with , and we obtain the equivalent expressions of the eigenfunctions , .
The constant Y solutions correspond to , giving , .
The complex wavenumbers of the two waves are . Taking the principal value of the square root (with positive real part), the upper/lower sign corresponds to a wave whose amplitude decreases with increasing/decreasing x.
Appendix C. Analytical Solutions of the Magnetized Kelvin–Helmholtz Instability
With the parametrization , , , , , the dispersion relation (27) becomes
We can analytically find purely imaginary solutions of that equation, which is the continuity of the ratio . First, we observe that if the fluid characteristics are the same in the two parts and the velocities opposite, for purely imaginary , i.e., real , the relations and hold. This means that the dispersion relation is equivalent to the requirement that the ratio is real.
We can write the numerator as , with such that the amplitude vanishes at . In order for the ratio to be real, should be real.
- Substituting the expressions of and A, the previous two relations mean that the imaginary parts of and are zero.
Thus we arrive at the two relations that give in parametric form, with parameter
Eliminating , we find a single relation for the growth rate, the quartic polynomial Equation (28).
Note that Equation (28) can also be derived by squaring Equation (A28), since the substitution helps to exclude the trivial solutions of the resulting polynomial. This proves that indeed the solution is purely imaginary and verifies the above derivation, which has the advantage of connecting the solution with the correct sign of and its argument .
References
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Bateman, G. MHD Instabilities; MIT Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Boyd, T.J.M.; Sanderson, J.J. The Physics of Plasmas; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Freidberg, J.P. Ideal MHD; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Goedbloed, H.; Keppens, R.; Poedts, S. Magnetohydrodynamics of Laboratory and Astrophysical Plasmas; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Ferrari, A.; Trussoni, E.; Zaninetti, L. Relativistic Kelvin-Helmholtz instabilities in extragalactic radio sources. Astron. Astrophys. 1978, 64, 43. [Google Scholar]
- Hardee, P.E.; Norman, M.L. Spatial Stability of the Slab Jet. I. Linearized Stability Analysis. Astrophys. J. 1988, 334, 70. [Google Scholar] [CrossRef]
- Osmanov, Z.; Mignone, A.; Massaglia, S.; Bodo, G.; Ferrari, A. On the linear theory of Kelvin-Helmholtz instabilities of relativistic magnetohydrodynamic planar flows. Astron. Astrophys. 2008, 490, 493–500. [Google Scholar] [CrossRef]
- Matsumoto, J.; Aloy, M.A.; Perucho, M. Linear theory of the Rayleigh-Taylor instability at a discontinuous surface of a relativistic flow. Mon. Not. R. Astron. Soc. 2017, 472, 1421–1431. [Google Scholar] [CrossRef]
- Papadopoulos, D.B.; Contopoulos, I. The magnetic Rayleigh-Taylor instability around astrophysical black holes. Mon. Not. R. Astron. Soc. 2019, 483, 2325–2336. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Komissarov, S.S. Relativistic centrifugal instability. Mon. Not. R. Astron. Soc. 2018, 475, L125–L129. [Google Scholar] [CrossRef]
- Chow, A.; Rowan, M.E.; Sironi, L.; Davelaar, J.; Bodo, G.; Narayan, R. Linear analysis of the Kelvin-Helmholtz instability in relativistic magnetized symmetric flows. Mon. Not. R. Astron. Soc. 2023, 524, 90–99. [Google Scholar] [CrossRef]
- Karampelas, K.; Van Doorsselaere, T.; Guo, M.; Duckenfield, T.; Pelouze, G. Kelvin-Helmholtz instability and heating in oscillating loops perturbed by power-law transverse wave drivers. Astron. Astrophys. 2024, 688, A80. [Google Scholar] [CrossRef]
- Nykyri, K. Giant Kelvin-Helmholtz (KH) Waves at the Boundary Layer of the Coronal Mass Ejections (CMEs) Responsible for the Largest Geomagnetic Storm in 20 Years. Geophys. Res. Lett. 2024, 51, e2024GL110477. [Google Scholar] [CrossRef]
- Vlahakis, N. Linear Stability Analysis of Relativistic Magnetized Jets: The Minimalist Approach. Universe 2024, 10, 183. [Google Scholar] [CrossRef]
- Vlahakis, N. The Schwarzian Approach in Sturm-Liouville Problems. Symmetry 2024, 16, 648. [Google Scholar] [CrossRef]
- Rayleigh. Investigation of the Character of the Equilibrium of an Incompressible Heavy Fluid of Variable Density. Proc. Lond. Math. Soc. 1882, s1-14, 170–177. [Google Scholar] [CrossRef]
- Taylor, G.I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 201, 192–196. [Google Scholar] [CrossRef]
- Thomson, W. XLVI. Hydrokinetic solutions and observations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1871, 42, 362–377. [Google Scholar] [CrossRef]
- Helmholtz. XLIII. On discontinuous movements of fluids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1868, 36, 337–346. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).