Traveling Wave Solutions and Symmetries of Reverse Space-Time Nonlocal Nonlinear Schrödinger Equations

Abstract

This paper investigates the reverse space-time nonlocal nonlinear Schrödinger (NNLS) equation, which arises in nonlinear optics, Bose–Einstein condensation, integrable systems, and plasma physics. Several classes of exact solutions are constructed using multiple analytical techniques. First, traveling wave solutions of Jacobi elliptic, hyperbolic, and trigonometric function types are ultimately obtained by employing a traveling wave transformation combined with a Weierstrass-type Riccati equation expansion method. Second, Lie symmetry analysis is applied to the NNLS equation, and the corresponding infinitesimal generators are determined. Using these generators, the original equation is reduced to local and nonlocal ordinary differential equations (ODEs), whose invariant solutions are subsequently obtained through integration. Finally, the NNLS equation is generalized to a multi-component system, for which the general form of the infinitesimal symmetries is derived. Symmetry reductions of the extended system yield further classes of reduced ODEs. In particular, the general form of the multi-component solutions is derived.

1. Introduction

Nonlinear Schrödinger (NLS) equations have been central to nonlinear science, with broad applications in optical fiber communications, Bose–Einstein condensates, and plasma physics. Their ability to model complex physical phenomena, balanced between nonlinearity and dispersion, has made them foundational in both theoretical and applied research [1,2,3,4].

In 2013, Ablowitz and Musslimani proposed reverse space-time and reverse-time nonlocal integrable systems, respectively, in which nonlocality manifests in both space and time or solely in time [5,6]. These equations differ from classical local forms by incorporating nonlocal interactions, reflecting the influence of spatially and temporally reflected points on the dynamics at a given location. In recent years, the research focus of the academic community has gradually shifted to nonlocal equations. Relevant studies have not only invested considerable efforts but also adopted various analytical methods to obtain their exact solutions. Representative approaches include the inverse scattering transform [7,8,9,10], Darboux transformations [11,12,13,14,15], and the Hirota bilinear method [16,17,18]. Among these, Darboux transformations have been used most extensively for nonlocal systems. Recent work has led to a growing body of results on the NNLS equation [19,20,21,22,23,24,25], especially in the reverse-time case [26,27,28,29,30].

The reverse-time and reverse space-time NNLS equations, which are $\mathcal{PT}$(parity-time)-symmetric and integrable, form part of an infinite-dimensional Hamiltonian framework [5,6]. To study the relation between solutions at $(x,t)$ and $(-x,-t)$, one is naturally led to consider the reverse space-time reduction. The reverse space-time NNLS equation is given by

$$i{q}_t(x,t)-q_{xx}(x,t)+2q^2(x,t)q(-x,-t)=0,$$

(1)

where the presence of the term $q(-x,-t)$ implies that $q(x,t)$ is no longer determined locally, resulting in behavior distinct from standard NLS-type equations.

The study of Equation (1) has yielded important results such as soliton solutions and elliptic function solutions through methods like inverse scattering and Darboux transformations [7,31]. Despite these advances, a systematic Lie symmetry analysis of this equation remains unexplored. This approach can not only reduce the nonlocal partial differential equations (PDEs) to ODEs but also reveal invariant structures and conserved quantities that are difficult to obtain through traditional methods. By systematically applying this method, we aim to construct new types of exact solutions and to enhance our understanding of nonlocal integrable systems. Methods like inverse scattering and Darboux transformation focus on solving equations, while the Lie symmetry method directly explores equations’ invariance via infinitesimal transformation group analysis. Unlike Weierstrass-type Riccati equation expansion method [32] and the enhanced algebraic method [33], it requires no preset solution form and simplifies solving by reducing high-dimensional PDEs to low-dimensional ones through symmetry reduction.

In this work, we analyze Equation (1) using Lie symmetry techniques and obtain invariant solutions by integrating the resulting ordinary differential equations. Furthermore, we consider the following multi-component extension of the NNLS equation:

$$i{q}_{j,t}(x,t)-q_{j,xx}(x,t)+2\left(\sum _{l=1}^n{q}_l(x,t)q_l(-x,-t)\right)q_j(x,t)=0,(j=1,2,\cdots ,n).$$

(2)

which describes a system with $\mathcal{PT}$ symmetry, multiple components, and reverse space-time nonlocality.

This paper is structured as follows: Section 2 constructs traveling wave solutions via traveling wave transformations combined with the Weierstrass-type Riccati equation expansion method. Section 3 conducts Lie symmetry analysis and reductions of Equation (1), and obtains the corresponding invariant solutions. Section 4 extends the study to the multi-component system (2) and derives invariant solutions of certain reduced equations. Section 5 analyzes the dynamic characteristics of the solutions and performs graphical characterization. Section 6 summarizes the full text and presents the conclusions.

2. Traveling Wave Solutions of the NNLS Equation

Within this section, Equation (1) is converted to an ODE through a traveling wave transformation. Exploiting the parity of the solution, the derived ODE is solved via the Weierstrass-type Riccati equation expansion method [32], thereby deriving several novel traveling wave solutions to Equation (1).

2.1. Traveling Wave Transformation

This section focuses on constructing traveling wave solutions of Equation (1) via the introduction of a transformation:

$$\begin{array}{cc}\hfill q(x,t)& =u(x,t)exp\left(i\eta \right),\eta =\alpha x+\beta t,\hfill \\ \hfill q(-x,-t)& =u(-x,-t)exp(-i\eta ),-\eta =-\alpha x-\beta t.\hfill \end{array}$$

(3)

$\alpha$ and $\beta$ are real constants.

Substituting (3) into Equation (1) yields

$${\alpha }^{2}u(x,t)-\beta u(x,t)+2u(-x,-t)u^2(x,t)+i{u}_t(x,t)-2i\alpha u_x(x,t)-u_{xx}(x,t)=0.$$

(4)

Separating the real and imaginary parts of Equation (4) gives the following system:

$$\left\{\begin{array}{c}{\alpha }^{2}u(x,t)-\beta u(x,t)+2u(-x,-t)u^2(x,t)-u_{xx}(x,t)=0,\hfill \\ u_t(x,t)-2\alpha u_x(x,t)=0.\hfill \end{array}\right.$$

(5)

Applying the traveling wave transformation

$$u(x,t)=u\left(\vartheta \right),\vartheta =x+2\alpha t,$$

(6)

reduces the system to an ordinary differential equation:

$${\alpha }^{2}u\left(\vartheta \right)-\beta u\left(\vartheta \right)+2u(-\vartheta )u^2\left(\vartheta \right)-u^{″}\left(\vartheta \right)=0.$$

(7)

Assuming $u\left(\vartheta \right)$ is an odd function, i.e., $u(-\vartheta )=-u\left(\vartheta \right)$, Equation (7) reduces to

$${\alpha }^{2}u\left(\vartheta \right)-\beta u\left(\vartheta \right)-2u^3\left(\vartheta \right)-u^{″}\left(\vartheta \right)=0.$$

(8)

Using symbolic computation software (e.g., Maple), the Jacobi elliptic function solution to Equation (8) is found to be

$$u\left(\vartheta \right)=c_2\sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{c_2^2+{\alpha }^2-\beta -1}}}\mathrm{Jacobisn}\left(\left(\sqrt{(-{\alpha }^2+\beta +1)}\vartheta +c_1\right)\sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{c_2^2+{\alpha }^2-\beta -1}}},{\displaystyle \frac{c_2}{\sqrt{({\alpha }^2-\beta -1)}}}\right)$$

(9)

where $c_1$ and $c_2$ are integral constants. Since $u\left(\vartheta \right)$ is an odd function, it directly follows that $c_1=0$.

For $\mathrm{sn}(x,k)$, when $k\to 1$, it degenerates as

$$\mathrm{sn}(x,1)\to tanh\left(x\right)$$

Thus, in Equation (9), when $k\to 1$, we have $c_2\to \sqrt{({\alpha }^2-\beta -1)}$, and Equation (9) degenerates into the hyperbolic tangent-type solution:

$$u\left(\vartheta \right)=\sqrt{({\alpha }^2-\beta -1)}\sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{2{\alpha }^2-2\beta -2}}}tanh\left(\sqrt{(-{\alpha }^2+\beta +1)}\vartheta \sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{2{\alpha }^2-2\beta -2}}}\right).$$

(10)

By substituting Equation (10) into (3), the corresponding solution to Equation (1) is given by

$$\begin{array}{cc}\hfill q_1(x,t)& =\sqrt{({\alpha }^2-\beta -1)}\sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{2{\alpha }^2-2\beta -2}}}tanh\left(\sqrt{(-{\alpha }^2+\beta +1)}\left(2\alpha t+x\right)\right.\hfill \\ \hfill & \left.\sqrt{{\displaystyle \frac{{\alpha }^2-\beta }{2{\alpha }^2-2\beta -2}}}\right)exp\left(i\left(\alpha x+\beta t\right)\right)\hfill \end{array}$$

(11)

where $\alpha ,\beta$ are arbitrary real constants and ${\alpha }^2-\beta \ne 1$.

2.2. Overview of the Weierstrass-Type Riccati Equation Expansion Method

Step 1. Consider a PDE involving two independent variables x and t:

$$\begin{array}{c}\hfill R(u,u_x,u_t,u_{xx},u_{xt},u_{tt},\cdots )=0,\end{array}$$

(12)

Step 2. Apply the following traveling wave transformation:

$$u(x,t)=u\left(\vartheta \right),\vartheta =x-wt,$$

(13)

where w is the wave speed. Substituting (13) into (12) reduces it to an ODE of the form

$$W(u\left(\vartheta \right),u^{\prime }\left(\vartheta \right),u^{″}\left(\vartheta \right),\cdots )=0,$$

(14)

where W denotes the resulting ODE in terms of $\vartheta$.

Step 3. For the solution of Equation (14), suppose it assumes the form below:

$$u\left(\vartheta \right)=\sum _{i=0}^n{c}_i{f}^i\left(\vartheta \right),$$

(15)

where $c_i$ ($i=0,1,\cdots ,n$) are undetermined constants, balancing the highest derivative term against the highest nonlinear term in Equation (14) yields the determination of n. The function $f\left(\vartheta \right)$ complies with the Riccati equation

$$f^{\prime }\left(\vartheta \right)=c_0+c_{1}f\left(\vartheta \right)+c_2{f}^2\left(\vartheta \right),$$

(16)

where $f^{\prime }={\displaystyle \frac{df}{d\vartheta }}$, and $c_0$, $c_1$, $c_2$ are arbitrary constants.

Step 4. The Weierstrass elliptic function can be used to represent the general solution of Riccati Equation (16):

$$f\left(\vartheta \right)=\left\{\begin{array}{c}\hfill \begin{array}{cc}\hfill & -{\displaystyle \frac{c_1}{2c_2}}+{\displaystyle \frac{{\wp }^{\prime }(\vartheta ,g_2,g_3)}{2c_2(\wp (\vartheta ,g_2,g_3)-\frac{\delta }{12})}},\hfill \\ \hfill & -{\displaystyle \frac{(2c_0+c_1)(\wp (\vartheta ,g_2,g_3)-\frac{\delta }{12})-{\wp }^{\prime }(\vartheta ,g_2,g_3)}{(c_1+2c_2)(\wp (\vartheta ,g_2,g_3)-\frac{\delta }{12})+{\wp }^{\prime }(\vartheta ,g_2,g_3)}},\hfill \\ \hfill & {\displaystyle \frac{\frac{1}{2}{c}_0{c}_1(\wp (\vartheta ,g_2,g_3)-\frac{\delta }{12})-\frac{1}{2}{c}_0{\wp }^{\prime }(\vartheta ,g_2,g_3)}{{(\wp (\vartheta ,g_2,g_3)-\frac{c_0{c}_2}{6}-\frac{c_1^2}{12})}^2-{\left(\frac{c_0{c}_2}{2}\right)}^2}},\hfill \end{array}\end{array}\right.$$

(17)

where $\delta =c_1^2-4c_0{c}_2$, and the invariants of the Weierstrass elliptic function are given by $g_2={\displaystyle \frac{{\delta }^2}{12}}$, $g_3=-{\displaystyle \frac{{\delta }^3}{216}}$. The function $\wp (\vartheta ,g_2,g_3)$ fulfills the differential equation

$${\left({\wp }^{\prime }\right)}^2=4{\wp }^3-g_2\wp -g_3,$$

and it exhibits double periodicity in the complex plane, with a pole of the second order at $\vartheta =0$. When degenerate conditions occur, $\wp \left(\vartheta \right)$ collapses to trigonometric, hyperbolic, or rational functions.

The formula for converting the Weierstrass elliptic functions $\wp (\vartheta ,{\displaystyle \frac{{\theta }^2}{12}},-{\displaystyle \frac{{\theta }^3}{216}})$ into hyperbolic and trigonometric functions is given by

$$\wp \left(\vartheta ,{\displaystyle \frac{{\theta }^2}{12}},-{\displaystyle \frac{{\theta }^3}{216}}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\theta }{12}}-{\displaystyle \frac{\theta }{4}}{\mathrm{sech}}^2\left({\displaystyle \frac{\sqrt{\theta }}{2}}\vartheta \right),\hfill & \theta >0,\hfill \\ {\displaystyle \frac{\theta }{12}}+{\displaystyle \frac{\theta }{4}}{\mathrm{csch}}^2\left({\displaystyle \frac{\sqrt{\theta }}{2}}\vartheta \right),\hfill & \theta >0,\hfill \\ {\displaystyle \frac{\theta }{12}}-{\displaystyle \frac{\theta }{4}}{\sec }^2\left({\displaystyle \frac{\sqrt{-\theta }}{2}}\vartheta \right),\hfill & \theta <0,\hfill \\ {\displaystyle \frac{\theta }{12}}-{\displaystyle \frac{\theta }{4}}{\csc }^2\left({\displaystyle \frac{\sqrt{-\theta }}{2}}\vartheta \right),\hfill & \theta <0.\hfill \end{array}\right.$$

(18)

Step 5. Substituting the ansatz (15) into the ODE (14), and employing the Riccati Equation (16), we collect coefficients of like powers $f^l\left(\vartheta \right)$ ($l=0,1,2,\dots$) and equate them to zero. This yields an algebraic system for the parameters $c_i$ and the wave speed w.

Step 6. Through solving the algebraic system and inserting the Riccati Equation (17) solution into ansatz (15), we construct explicit solutions for the original nonlinear Equation (12).

2.3. Solutions of Equation (8) via the Weierstrass-Type Riccati Equation Expansion Method

By applying the homogeneous balance principle, the nonlinear term $u^3$ and the second-order derivative $u^{″}$ in Equation (8) are balanced to determine the value of n in the ansatz. Specifically, equating the leading orders $O\left(u^3\right)=3n$ and $O\left(u^{″}\right)=n+2$ yields $n=1$.

We therefore assume a solution of the form

$$u\left(\vartheta \right)=c_0+c_{1}f\left(\vartheta \right),$$

(19)

with $c_0$ and $c_1$ as undetermined constants, $f\left(\vartheta \right)$ fulfills Riccati Equation (16).

By inserting Equations (19) and (16) into Equation (8) and gathering terms according to the powers of $f\left(\vartheta \right)$, we set the coefficients of $f^l\left(\vartheta \right)$ (for $l=0,1,2,3$) to zero. The system is as follows:

$$\left\{\begin{array}{c}-2c_0^3-c_0{c}_1^2+c_0{\alpha }^2-c_0\beta =0,\hfill \\ -6c_0^2{c}_1-c_1^3-2c_0{c}_1{c}_2+c_1{\alpha }^2-c_1\beta =0,\hfill \\ -6c_0{c}_1^2-3c_1^2{c}_2=0,\hfill \\ -2c_1^3-2c_1{c}_2^2=0\hfill \end{array}\right.$$

(20)

By solving the above system using a symbolic computation tool (e.g., Mathematica or Maple), we derive the following results:

Output 1

$$c_0=-{\displaystyle \frac{\sqrt{\beta -{\alpha }^2}}{\sqrt{2}}},c_1=-\sqrt{2}\sqrt{{\alpha }^2-\beta },c_2=\sqrt{2}\sqrt{\beta -{\alpha }^2}.$$

(21)

Output 2

$$c_0={\displaystyle \frac{\sqrt{\beta -{\alpha }^2}}{\sqrt{2}}},c_1=-\sqrt{2}\sqrt{{\alpha }^2-\beta },c_2=-\sqrt{2}\sqrt{\beta -{\alpha }^2}.$$

(22)

Output 3

$$c_0=-{\displaystyle \frac{\sqrt{\beta -{\alpha }^2}}{\sqrt{2}}},c_1=\sqrt{2}\sqrt{{\alpha }^2-\beta },c_2=\sqrt{2}\sqrt{\beta -{\alpha }^2}.$$

(23)

Output 4

$$c_0={\displaystyle \frac{\sqrt{\beta -{\alpha }^2}}{\sqrt{2}}},c_1=\sqrt{2}\sqrt{{\alpha }^2-\beta },c_2=-\sqrt{2}\sqrt{\beta -{\alpha }^2}.$$

(24)

According to output (21), we obtained $\delta =2\left({\alpha }^2-\beta \right)+4\left(\beta -{\alpha }^2\right),g_2={\displaystyle \frac{1}{12}}{\left(2\left({\alpha }^2-\beta \right)+4\left(\beta -{\alpha }^2\right)\right)}^2,g_3=-{\displaystyle \frac{1}{216}}{\left(2\left({\alpha }^2-\beta \right)+4\left(\beta -{\alpha }^2\right)\right)}^3$. Substituting the output (21) into Equation (18) gives the transformation formulas for the Weierstrass elliptic function over the complex field.

$$\wp \left(\vartheta ,g_2,g_3\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{6}}\left({\alpha }^2-\beta \right)\left(3{\mathrm{sech}}^2\left({\displaystyle \frac{\vartheta \sqrt{\beta -{\alpha }^2}}{\sqrt{2}}}\right)-1\right),\hfill & \\ -{\displaystyle \frac{1}{6}}\left({\alpha }^2-\beta \right)\left(3{\mathrm{csch}}^2\left({\displaystyle \frac{\vartheta \sqrt{\beta -{\alpha }^2}}{\sqrt{2}}}\right)+1\right),\hfill & \\ {\displaystyle \frac{1}{6}}\left({\alpha }^2-\beta \right)\left(3{sec}^2\left({\displaystyle \frac{\vartheta \sqrt{{\alpha }^2-\beta }}{\sqrt{2}}}\right)-1\right),\hfill & \\ {\displaystyle \frac{1}{6}}\left({\alpha }^2-\beta \right)\left(3{csc}^2\left({\displaystyle \frac{\vartheta \sqrt{{\alpha }^2-\beta }}{\sqrt{2}}}\right)-1\right).\hfill \end{array}\right.$$

(25)

Subsequently, substituting system (25) into Equations (17) and (19) gives a series of solutions. Since $u\left(\vartheta \right)$ is an odd function, only the odd function cases are retained, leading to the following solutions:

$$u\left(\vartheta \right)={\displaystyle \frac{\sqrt{{\alpha }^2-\beta }tanh\left(\frac{\vartheta \sqrt{\beta -{\alpha }^2}}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(26)

$$u\left(\vartheta \right)={\displaystyle \frac{\sqrt{{\alpha }^2-\beta }coth\left(\frac{\vartheta \sqrt{\beta -{\alpha }^2}}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(27)

$$u\left(\vartheta \right)={\displaystyle \frac{\sqrt{\beta -{\alpha }^2}tan\left(\frac{\vartheta \sqrt{{\alpha }^2-\beta }}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(28)

$$u\left(\vartheta \right)=-{\displaystyle \frac{\sqrt{\beta -{\alpha }^2}cot\left(\frac{\vartheta \sqrt{{\alpha }^2-\beta }}{\sqrt{2}}\right)}{\sqrt{2}}}.$$

(29)

The solutions to Equation (1) are

$$q_2(x,t)={\displaystyle \frac{\sqrt{{\alpha }^2-\beta }\exp \left(i(\beta t+\alpha x)\right)tanh\left(\frac{\sqrt{\beta -{\alpha }^2}(2\alpha t+x)}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(30)

$$q_3(x,t)={\displaystyle \frac{\sqrt{{\alpha }^2-\beta }\exp \left(i(\beta t+\alpha x)\right)coth\left(\frac{\sqrt{\beta -{\alpha }^2}(2\alpha t+x)}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(31)

$$q_4(x,t)={\displaystyle \frac{\sqrt{\beta -{\alpha }^2}\exp \left(i(\beta t+\alpha x)\right)tan\left(\frac{\sqrt{{\alpha }^2-\beta }(2\alpha t+x)}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(32)

$$q_5(x,t)=-{\displaystyle \frac{\sqrt{\beta -{\alpha }^2}\exp \left(i(\beta t+\alpha x)\right)cot\left(\frac{\sqrt{{\alpha }^2-\beta }(2\alpha t+x)}{\sqrt{2}}\right)}{\sqrt{2}}},$$

(33)

where $\alpha ,\beta$ are arbitrary real constants. The solutions to Equation (8) corresponding to outputs (22)–(24) can be derived in the same manner, leading to further solutions to Equation (1).

3. Symmetry Reductions of the NNLS Equation

3.1. Symmetry Analysis

Symmetry is fundamental in the analysis of differential equations, having been extended from classical local systems to nonlocal frameworks [34,35,36,37].

To analyze the symmetries of Equation (1), we now focus on the following one-parameter infinitesimal transformations:

$$\begin{array}{cc}\hfill & x\to x+\epsilon \xi (x,t,q(x,t))+\mathcal{O}\left({\epsilon }^2\right),\hfill \\ \hfill & t\to t+\epsilon \tau (x,t,q(x,t))+\mathcal{O}\left({\epsilon }^2\right),\hfill \\ \hfill & q\to q+\epsilon \varphi (x,t,q(x,t))+\mathcal{O}\left({\epsilon }^2\right),\hfill \end{array}$$

(34)

where $\epsilon$ is a small parameter, and $\vartheta$, $\tau$, and $\varphi$ are the infinitesimals associated with x, t, and q, respectively. The relevant vector field has the following form:

$$Z=\xi (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial x}}+\tau (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial t}}+\varphi (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial q(x,t)}}.$$

(35)

To handle the nonlocal terms in Equation (1), the following reflections are introduced:

$$\begin{array}{cc}\hfill R^x\circ R^t& =R^{x,t},\hfill \\ \hfill R^{x,t}:(x,t)& \to (-x,-t),\hfill \\ \hfill R^{x,t}:q(x,t)& \to q(-x,-t).\hfill \end{array}$$

(36)

Accordingly, the second prolongation of the vector field incorporating the reflections takes the form

$$Z_R^{\left(2\right)}=Z+{\varphi }_{\left[t\right]}{\displaystyle \frac{\partial }{\partial q_t}}+{\varphi }_{\left[xx\right]}{\displaystyle \frac{\partial }{\partial q_{xx}}}+\left(R^{x,t}\varphi \right){\displaystyle \frac{\partial }{\partial \left(R^{x,t}q\right)}}.$$

(37)

where

$${\varphi }_{\left[t\right]}=D_t\varphi -\left(D_t\xi \right)q_x-\left(D_t\tau \right)q_t,{\varphi }_{\left[xx\right]}=D_x{\varphi }_{\left[x\right]}-\left(D_x\xi \right)q_{xx}-\left(D_t\tau \right)q_{xt}.$$

(38)

For Equation (1) to admit Lie point symmetries, the invariance condition must be satisfied:

$$Z_R^{\left(2\right)}\left(i{q}_t(x,t)-q_{xx}(x,t)+2q^2(x,t)q(-x,-t)\right)=0.$$

(39)

Expanding the above expression, we obtain its explicit form as

$$\begin{array}{cc}\hfill & \left[\xi (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial x}}+\tau (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial t}}+\varphi (x,t,q(x,t)){\displaystyle \frac{\partial }{\partial q(x,t)}}\right.\hfill \\ \hfill & +\varphi (-x,-t,q(-x,-t)){\displaystyle \frac{\partial }{\partial q(-x,-t)}}+{\varphi }_{\left[t\right]}{\displaystyle \frac{\partial }{\partial q_t}}\hfill \\ \hfill & +{\varphi }_{\left[xx\right]}{\displaystyle \frac{\partial }{\partial q_{xx}}}\left(i{q}_t(x,t)-q_{xx}(x,t)+2q^2(x,t)q(-x,-t)\right)=0.\hfill \end{array}$$

(40)

Simplifying the left-hand side of Equation (39) yields

$$i{\varphi }_{\left[t\right]}-{\varphi }_{\left[xx\right]}+4q(x,t)q(-x,-t)\varphi (x,t,q)+2q^2(x,t)\varphi (-x,-t,q(-x,-t))=0.$$

(41)

Substituting (38) into the above yields

$$\begin{array}{cc}\hfill & i\left[D_t\varphi -\left(D_t\xi \right)q_x-\left(D_t\tau \right)q_t\right]-D_x^2\varphi +\left(D_x^2\xi \right)q_x+2\left(D_x\xi \right)q_{xx}\hfill \\ \hfill & +\left(D_x^2\tau \right)q_t+2\left(D_x\tau \right)q_{xt}+4q(x,t)q(-x,-t)\varphi (x,t,q)\hfill \\ \hfill & +2q^2(x,t)\varphi (-x,-t,q(-x,-t))=0.\hfill \end{array}$$

(42)

The term $q_t$ is eliminated using the original Equation (1):

$$q_t(x,t)=i(2q^2(x,t)q(-x,-t)-q_{xx}(x,t)).$$

Substituting this expression into Equation (42) and collecting terms results in a polynomial in $q_x$ and $q_{xx}$. By matching the coefficients of linearly independent terms to zero, we obtain the following determining system:

$$\begin{array}{cc}\hfill & D_x\tau =0,{\xi }_q=0,{\tau }_q=0,{\varphi }_{qq}=0,2{\xi }_x-{\tau }_t=0,\hfill \\ \hfill & {\xi }_{xx}-i{\xi }_t-2{\varphi }_{xq}(x,t,q(x,t))=0,\hfill \\ \hfill & 2q^2(x,t)\varphi (-x,-t,q(-x,-t))+4q(x,t)q(-x,-t)\varphi (x,t,q(x,t))\hfill \\ \hfill & +2q^2(x,t)q(-x,-t)({\tau }_t-{\varphi }_q(x,t,q(x,t)))+i{\varphi }_t(x,t,q(x,t))-{\varphi }_{xx}(x,t,q(x,t))=0.\hfill \end{array}$$

(43)

Solving this system gives

$$\xi =c_{1}x+i{c}_{2}t+c_3,\tau =2c_{1}t+c_4,\varphi (x,t,q(x,t))=\left({\displaystyle \frac{c_2}{2}}x-c_1\right)q(x,t),$$

(44)

with $c_1$, $c_2$, $c_3$, and $c_4$ being constant values. Hence, the Lie point symmetries of Equation (1) are generated from the following vector fields:

$${\displaystyle \frac{\partial }{\partial x}},{\displaystyle \frac{\partial }{\partial t}},x{\displaystyle \frac{\partial }{\partial x}}+2t{\displaystyle \frac{\partial }{\partial t}}-q(x,t){\displaystyle \frac{\partial }{\partial q(x,t)}},it{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{x}{2}}q(x,t){\displaystyle \frac{\partial }{\partial q(x,t)}}.$$

(45)

3.2. Symmetry Reductions and Invariant Solutions

The Lie point symmetries obtained above are now employed to reduce the NNLS equation. By introducing appropriate similarity variables, the original nonlocal partial differential equation is transformed into either a nonlocal or a local ODE.

We now turn to the consideration of the general infinitesimal generator

$$a{\displaystyle \frac{\partial }{\partial x}}+b{\displaystyle \frac{\partial }{\partial t}}+c\left(it{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{x}{2}}q{\displaystyle \frac{\partial }{\partial q}}\right)+e\left(x{\displaystyle \frac{\partial }{\partial x}}+2t{\displaystyle \frac{\partial }{\partial t}}-q{\displaystyle \frac{\partial }{\partial t}}\right),$$

(46)

with a, b, c, and e being arbitrary constant parameters.

Solving the corresponding characteristic equations gives rise to the similarity variables

$${\displaystyle \frac{dx}{a+ict+ex}}={\displaystyle \frac{dt}{b+2et}}={\displaystyle \frac{dq}{\frac{c}{2}xq-eq}}.$$

(47)

We present the following representative cases for discussion:

• Case 1: $a=b=e=0$

The similarity variables take the form

$$\begin{array}{cc}\hfill y& =t,\hfill \\ \hfill q(x,t)& =\exp \left({\displaystyle \frac{x^2}{4it}}\right)p\left(y\right).\hfill \end{array}$$

(48)

Reduction to a nonlocal ODE. Substituting $q(x,t)=exp\left({\displaystyle \frac{x^2}{4it}}\right)p\left(t\right)$ into Equation (1) and using $q(-x,-t)=exp\left(-{\displaystyle \frac{x^2}{4it}}\right)p(-t)$, the reduced nonlocal ODE is derived:

$${\displaystyle \frac{i}{2y}}p\left(y\right)+2p(-y)p^2\left(y\right)+i{p}^{\prime }\left(y\right)=0.$$

(49)

Reduction to a local ODE. Choosing $y=t^2$ yields $q(-x,-t)=exp\left(-{\displaystyle \frac{x^2}{4it}}\right)p\left(y\right)$, resulting in the local ODE:

$${\displaystyle \frac{i}{2\sqrt{y}}}p\left(y\right)+2p^3\left(y\right)+2i\sqrt{y}{p}^{\prime }\left(y\right)=0.$$

(50)

A specific solution is provided as

$$p\left(y\right)=\pm {\displaystyle \frac{1}{\sqrt{c_1\sqrt{y}-2i\sqrt{y}lny}}},$$

(51)

where $c_1$ denotes an integral constant. Therefore, the solution to Equation (1) reads

$$q_6(x,t)=\pm {\displaystyle \frac{\exp \left(-\frac{i{x}^2}{4t}\right)}{\sqrt{c_1\sqrt{t^2}-2i\sqrt{t^2}ln{t}^2}}}.$$

(52)

• Case 2: $e=0$

From the characteristic equations, we obtain

$$\begin{array}{cc}\hfill y& =bx-{\displaystyle \frac{1}{2}}ic{t}^2-at,\hfill \\ \hfill q(x,t)& =\exp \left({\displaystyle \frac{c{x}^2}{4(a+ict)}}\right)p\left(y\right).\hfill \end{array}$$

(53)

Setting $c=0$, we simplify the similarity variables as

$$\begin{array}{cc}\hfill y& =bx-at,\hfill \\ \hfill q(x,t)& =p\left(y\right).\hfill \end{array}$$

(54)

Reduction to a nonlocal ODE. Using $q(x,t)=p\left(y\right)$ and $q(-x,-t)=p(-y)$, Equation (1) reduces to

$$2p(-y)p^2\left(y\right)-ia{p}^{\prime }\left(y\right)-b^2{p}^{″}\left(y\right)=0.$$

(55)

A specific solution is provided as

$$p\left(y\right)=c_1\exp \left(c_{2}y\right),$$

(56)

where $a={\displaystyle \frac{i\left(b^2{c}_2^2-2{c_1}^2\right)}{c_2}}$, and $c_1$, $c_2$ denote arbitrary constants. Hence, the corresponding solution to Equation (1) becomes

$$q_7(x,t)=c_1\exp \left(b{c}_2(x-ib{c}_{2}t)+2i{c}_1^{2}t\right).$$

(57)

Reduction to a local ODE. Choosing $y={(bx-at)}^2$ and using the same ansatz, the reduced local ODE becomes

$$p^3\left(y\right)-b^2{p}^{\prime }\left(y\right)-ia\sqrt{y}{p}^{\prime }\left(y\right)-2b^{2}y{p}^{″}\left(y\right)=0.$$

(58)

Introducing the change of variable $y=z^2$, $p\left(y\right)=f\left(z\right)$, the equation simplifies to

$$b^2{f}^{″}\left(z\right)+ia{f}^{\prime }\left(z\right)-2f^3\left(z\right)=0.$$

(59)

Setting $a=b=0$, we obtain

$$\begin{array}{cc}\hfill y& =-{\displaystyle \frac{1}{2}}ic{t}^2,\hfill \\ \hfill q(x,t)& =exp\left({\displaystyle \frac{x^2}{4it}}\right)p\left(y\right),\hfill \end{array}$$

(60)

and the corresponding reduced ODE is

$${\displaystyle \frac{i\sqrt{c}}{2\sqrt{2iy}}}p\left(y\right)+2p^3\left(y\right)+\sqrt{2ciy}{p}^{\prime }\left(y\right)=0.$$

(61)

A particular solution is

$$p\left(y\right)=\pm {\displaystyle \frac{\sqrt{y}}{\sqrt{c_1{y}^{3/2}-2\sqrt{2}c{\left(\frac{iy}{c}\right)}^{3/2}lny}}},$$

(62)

which gives

$$q_8(x,t)=\pm {\displaystyle \frac{\sqrt{-2ic{t}^2}exp\left(-\frac{i{x}^2}{4t}\right)}{\sqrt{\sqrt{2}{c}_1{(-ic{t}^2)}^{3/2}-4c{\left(t^2\right)}^{3/2}ln\left(-\frac{1}{2}ic{t}^2\right)}}}.$$

(63)

• Case 3: $e\ne 0$

Solving the characteristic equations yields

$$\begin{array}{cc}\hfill y& ={\displaystyle \frac{x+\frac{a}{e}-\frac{ic}{e}\left(\frac{b}{e}+t\right)}{\sqrt{b+2et}}},\hfill \\ \hfill q(x,t)& =exp\left({\displaystyle \frac{cx-2e}{4e}}ln(b+2et)\right)p\left(y\right).\hfill \end{array}$$

(64)

Taking $a=b=c=0$, we find

$$\begin{array}{cc}\hfill y& ={\displaystyle \frac{x}{\sqrt{2et}}},\hfill \\ \hfill q(x,t)& =exp\left(-{\displaystyle \frac{1}{2}}ln\left(2et\right)\right)p\left(y\right).\hfill \end{array}$$

(65)

Reduction to a nonlocal ODE. Substituting into Equation (1) and using $q(-x,-t)=exp\left(-{\displaystyle \frac{1}{2}}ln(-2et)\right)p\left(iy\right)$, we derive the reduced nonlocal ODE:

$$-{\displaystyle \frac{1}{2e}}{p}^{″}\left(y\right)-{\displaystyle \frac{i}{e}}p\left(iy\right)p^2\left(y\right)-{\displaystyle \frac{i}{2}}y{p}^{\prime }\left(y\right)-{\displaystyle \frac{i}{2}}p\left(y\right)=0.$$

(66)

A constant solution is

$$p\left(y\right)=\pm {\displaystyle \frac{i\sqrt{2e}}{2}},$$

(67)

leading to

$$q_9(x,t)=\pm {\displaystyle \frac{i\sqrt{t}}{2t}}.$$

(68)

Reduction to a local ODE. Choosing $y={\displaystyle \frac{x^4}{4e^2{t}^2}}$, we find the reduced local ODE:

$$-{\displaystyle \frac{6}{e}}\sqrt{y}{p}^{\prime }\left(y\right)-{\displaystyle \frac{i}{e}}{p}^3\left(y\right)-y^{3/2}{p}^{″}\left(y\right)-2iy{p}^{\prime }\left(y\right)-{\displaystyle \frac{i}{2}}p\left(y\right)=0.$$

(69)

The classification of solutions for $q_1$–$q_9$ is presented in Table A1 of the Appendix.

4. The Nonlocal Multi-Component System

In this section, the Lie symmetry analysis and reduction techniques are extended to the nonlocal multi-component system (2), and a unified symmetry analysis and solution scheme is proposed for such systems with complex coupling characteristics.

4.1. Symmetry Analysis

Take into account the one-parameter Lie group of infinitesimal transformations that preserve the invariance of system (2), defined by

$$\begin{array}{cc}\hfill x& \to x+\epsilon \xi (x,t,q_1,q_2,\dots ,q_n)+\mathcal{O}\left({\epsilon }^2\right),\hfill \\ \hfill t& \to t+\epsilon \tau (x,t,q_1,q_2,\dots ,q_n)+\mathcal{O}\left({\epsilon }^2\right),\hfill \\ \hfill q_j& \to q_j+\epsilon {\varphi }_j(x,t,q_1,q_2,\dots ,q_n)+\mathcal{O}\left({\epsilon }^2\right),j=1,2,\dots ,n.\hfill \end{array}$$

(70)

where $\xi$, $\tau$, and ${\varphi }_j$ denote the infinitesimals relating to x, t, and $q_j$ correspondingly.

The corresponding vector field is expressed as

$$\begin{array}{c}\hfill Z=\xi {\displaystyle \frac{\partial }{\partial x}}+\tau {\displaystyle \frac{\partial }{\partial t}}+\sum _{j=1}^n{\varphi }_j{\displaystyle \frac{\partial }{\partial q_j(x,t)}}.\end{array}$$

(71)

The second prolongation of Z is given by

$$Z^{\left(2\right)}=Z+\sum _{j=1}^n\left({\varphi }_{j,\left[t\right]}{\displaystyle \frac{\partial }{\partial q_{j,t}}}+{\varphi }_{j,\left[xx\right]}{\displaystyle \frac{\partial }{\partial q_{j,xx}}}\right),$$

(72)

where ${\varphi }_{j,\left[t\right]}$ and ${\varphi }_{j,\left[xx\right]}$ are the prolonged coefficients.

In order for Z to be a symmetry of system (2), the invariance condition must be satisfied:

$$Z_R^{\left(2\right)}\left(i{q}_{j,t}-q_{j,xx}+2\left(\sum _{l=1}^n{q}_l(x,t)q_l(-x,-t)\right)q_j(x,t)\right)=0,j=1,2,\dots ,n.$$

(73)

Expanding the left side of system (73) yields

$$\begin{array}{cc}\hfill & i\left(D_t{\varphi }_j-\left(D_t\xi \right)q_{j,x}-\left(D_t\tau \right)q_{j,t}\right)-D_x^2{\varphi }_j+\left(D_x^2\xi \right)q_{j,x}+2\left(D_x\xi \right)q_{j,xx}\hfill \\ \hfill & +\left(D_x^2\tau \right)q_{j,t}+2\left(D_x\tau \right)q_{j,xt}+2{\varphi }_j\sum _{l=1}^n{q}_l(x,t)q_l(-x,-t)\hfill \\ \hfill & +2q_j(x,t)\sum _{l=1}^n\left[{\varphi }_l(x,t,\dots )q_l(-x,-t)+q_l(x,t){\varphi }_l(-x,-t,\dots )\right]=0.\hfill \end{array}$$

(74)

Substituting the original system (2) into system (74) by replacing $q_{j,t}$ with

$$q_{j,t}(x,t)=i\left(-q_{j,xx}(x,t)+2\left(\sum _{l=1}^n{q}_l(x,t)q_l(-x,-t)\right)q_j(x,t)\right),$$

and the infinitesimal generators are derived by resolving the determining equations:

$$\begin{array}{cc}\hfill Z_1& ={\displaystyle \frac{\partial }{\partial x}},\hfill \\ \hfill Z_2& ={\displaystyle \frac{\partial }{\partial t}},\hfill \\ \hfill Z_3& =it{\displaystyle \frac{\partial }{\partial x}}+{\displaystyle \frac{x}{2}}\sum _{j=1}^n{q}_j(x,t){\displaystyle \frac{\partial }{\partial q_j(x,t)}},\hfill \\ \hfill Z_4& =x{\displaystyle \frac{\partial }{\partial x}}+2t{\displaystyle \frac{\partial }{\partial t}}-\sum _{j=1}^n{q}_j(x,t){\displaystyle \frac{\partial }{\partial q_j(x,t)}}.\hfill \end{array}$$

(75)

4.2. Symmetry Reductions

In this section, we apply the infinitesimal generators obtained in the previous subsection to reduce the nonlocal multi-component system (2).

• Case 1: $Z_3$.

The characteristic equations associated with $Z_3$ are

$${\displaystyle \frac{dx}{it}}={\displaystyle \frac{dt}{0}}={\displaystyle \frac{d{q}_1}{\frac{x}{2}{q}_1}}={\displaystyle \frac{d{q}_2}{\frac{x}{2}{q}_2}}=\cdots ={\displaystyle \frac{d{q}_n}{\frac{x}{2}{q}_n}}.$$

(76)

The corresponding similarity transformation takes the form

$$\begin{array}{cc}\hfill y& =t,\hfill \\ \hfill q_j& =\exp \left({\displaystyle \frac{x^2}{4it}}\right)v_j\left(y\right),(j=1,2,\cdots ,n).\hfill \end{array}$$

(77)

Reduction to Nonlocal ODEs. Substituting into system (2), we obtain

$${\displaystyle \frac{i}{2y}}{v}_j\left(y\right)+2\left(\sum _{l=1}^n{v}_l(-y)v_l\left(y\right)\right)v_j\left(y\right)+i{v}_j^{\prime }\left(y\right)=0,j=1,2,\dots ,n.$$

(78)

Reduction to Local ODEs. By choosing $y=t^2$, the ansatz remains $q_j=exp\left({\displaystyle \frac{x^2}{4it}}\right)v_j\left(y\right)$, and we obtain

$${\displaystyle \frac{i}{2\sqrt{y}}}{v}_j\left(y\right)+2\left(\sum _{l=1}^n{v}_l^2\left(y\right)\right)v_j\left(y\right)+2i\sqrt{y}{v}_j^{\prime }\left(y\right)=0,j=1,2,\dots ,n.$$

(79)

When $n=1$, the solution to Equation (79) coincides with the solution of Equation (50), which reads

$$v_1\left(y\right)=\pm {\displaystyle \frac{1}{\sqrt{c_1\sqrt{y}-2i\sqrt{y}lny}}}.$$

where $c_1$ denotes an integral constant.

For $n\ge 2$, the solutions of system (79) are given by

$$\begin{array}{cc}\hfill v_1\left(y\right)& =\pm {\displaystyle \frac{1}{\sqrt{2c_1\sqrt{y}lny-2c_0\sqrt{y}}}},\hfill \\ \hfill v_k\left(y\right)& =c_{k-1}{v}_1\left(y\right),k=2,3,\dots ,n-1,\hfill \\ \hfill v_n\left(y\right)& =\mp {\displaystyle \frac{\sqrt{-v_1\left(y\right)\sqrt{y}\left(4v_1\left(y\right)\sqrt{y}{\sum }_{l=2}^{n-1}{v}_l^2\left(y\right)+4iy{v}_1^{\prime }\left(y\right)+4v_1^3\left(y\right)\sqrt{y}+i{v}_1\left(y\right)\right)}}{2v_1\left(y\right)\sqrt{y}}}.\hfill \end{array}$$

(80)

Thus, the corresponding exact solutions read

$$\begin{array}{cc}\hfill q_1(x,t)& =\pm exp\left({\displaystyle \frac{x^2}{4it}}\right){\displaystyle \frac{1}{\sqrt{2c_1\sqrt{t^2}ln{t}^2-2c_0\sqrt{t^2}}}},\hfill \\ \hfill q_k(x,t)& =c_{k-1}{q}_1(x,t),k=2,3,\dots ,n-1,\hfill \\ \hfill q_n(x,t)& =\mp exp\left({\displaystyle \frac{x^2}{4it}}\right){\displaystyle \frac{\sqrt{-v_1\left(t^2\right)t\left(4v_1\left(t^2\right)t{\sum }_{l=2}^{n-1}{v}_l^2\left(t^2\right)+4i{t}^2{v}_1^{\prime }\left(t^2\right)+4v_1^3\left(t^2\right)t+i{v}_1\left(t^2\right)\right)}}{2v_1\left(t^2\right)t}}.\hfill \end{array}$$

(81)

where $c_0,c_1,c_{k-1}$ are arbitrary constants.

• Case 2: $Z_4$.

The characteristic equations associated with $Z_4$ are

$${\displaystyle \frac{dx}{x}}={\displaystyle \frac{dt}{2t}}={\displaystyle \frac{d{q}_1}{-q_1}}={\displaystyle \frac{d{q}_2}{-q_2}}=\cdots ={\displaystyle \frac{d{q}_n}{-q_n}}.$$

(82)

Solving the above system yields the similarity form

$$y={\displaystyle \frac{x^2}{t}},q_j(x,t)={\displaystyle \frac{1}{x}}{v}_j\left(y\right),j=1,2,\dots ,n.$$

(83)

Reduction to Nonlocal ODEs.

$$-2v_j\left(y\right)-2\left(\sum _{l=1}^n{v}_l(-y)v_l\left(y\right)\right)v_j\left(y\right)+(2y-i{y}^2)v_j^{\prime }\left(y\right)-4y^2{v}_j^{″}\left(y\right)=0,j=1,2,\dots ,n.$$

(84)

Reduction to Local ODEs. By choosing $y={\displaystyle \frac{x^4}{t^2}}$, we obtain

$$v_j\left(y\right)+\left(\sum _{l=1}^n{v}_l^2\left(y\right)\right)v_j\left(y\right)+(2y+i{y}^{3/2})v_j^{\prime }\left(y\right)+8y^2{v}_j^{″}\left(y\right)=0,j=1,2,\dots ,n.$$

(85)

• Case 3: $a{Z}_1+b{Z}_2$.

The characteristic equations are

$${\displaystyle \frac{dx}{a}}={\displaystyle \frac{dt}{b}}={\displaystyle \frac{d{q}_1}{0}}={\displaystyle \frac{d{q}_2}{0}}=\cdots ={\displaystyle \frac{d{q}_n}{0}}.$$

(86)

Solving yields the similarity form

$$y=bx-at,q_j(x,t)=v_j\left(y\right),j=1,2,\dots ,n.$$

(87)

Reduction to Nonlocal ODEs.

$$2\left(\sum _{l=1}^n{v}_l(-y)v_l\left(y\right)\right)v_j\left(y\right)-ia{v}_j^{\prime }\left(y\right)-b^2{v}_j^{″}\left(y\right)=0,j=1,2,\dots ,n.$$

(88)

A class of explicit solutions to (88) reads

$$v_j\left(y\right)=c_{2j-1}exp\left(c_{2}y\right),j=1,2,\dots ,n,$$

(89)

where the parameter a satisfies $a={\displaystyle \frac{i(b^2{c}_2^2-2{\sum }_{j=1}^n{c}_{2j-1}^2)}{c_2}}$, and $c_{2j-1}$ are arbitrary constants.

Substituting yields the explicit solutions

$$q_j(x,t)=c_{2j-1}exp\left(c_2\left(bx-{\displaystyle \frac{i(b^2{c}_2^2-2{\sum }_{l=1}^n{c}_{2l-1}^2)}{c_2}}t\right)\right),j=1,2,\dots ,n.$$

(90)

Reduction to Local ODEs. By choosing $y={(bx-at)}^2$, the system reduces to

$$\left(\sum _{l=1}^n{v}_l^2\left(y\right)\right)v_j\left(y\right)-b^2{v}_j^{\prime }\left(y\right)-ia\sqrt{y}{v}_j^{\prime }\left(y\right)-2b^{2}y{v}_j^{″}\left(y\right)=0,j=1,2,\dots ,n.$$

(91)

Explanations of the relevant symbols are provided in Table A2 of the Appendix.

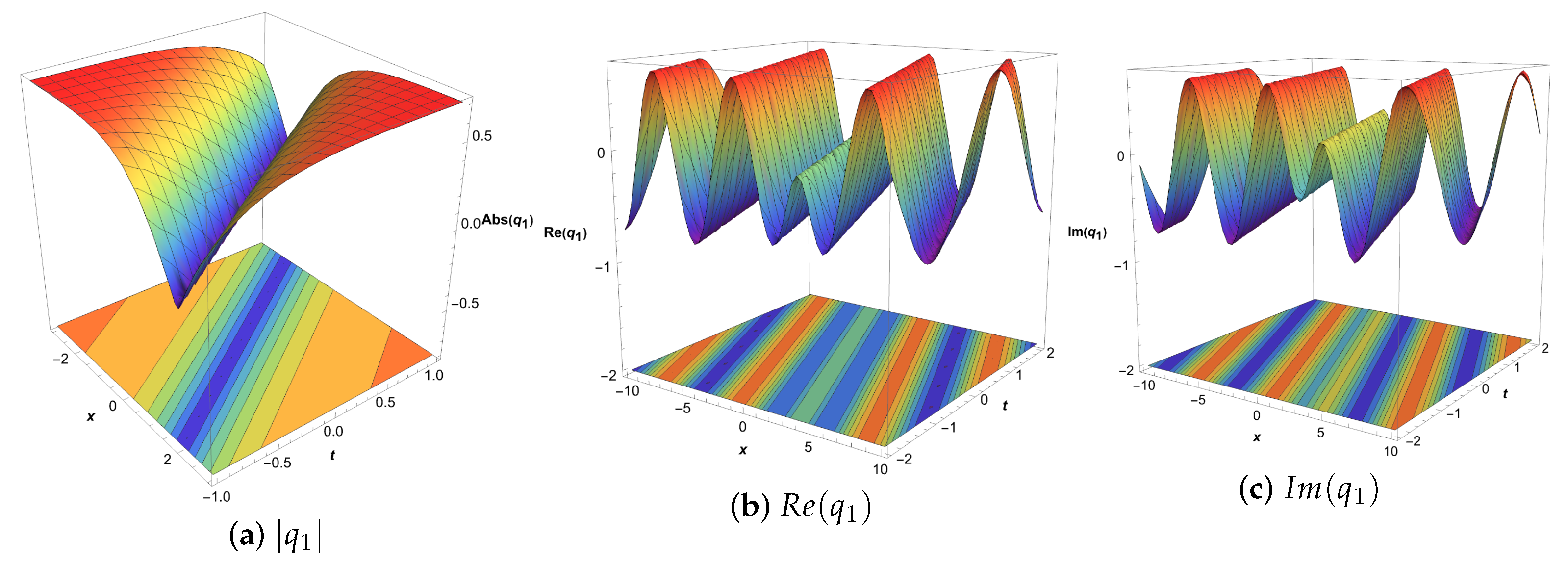
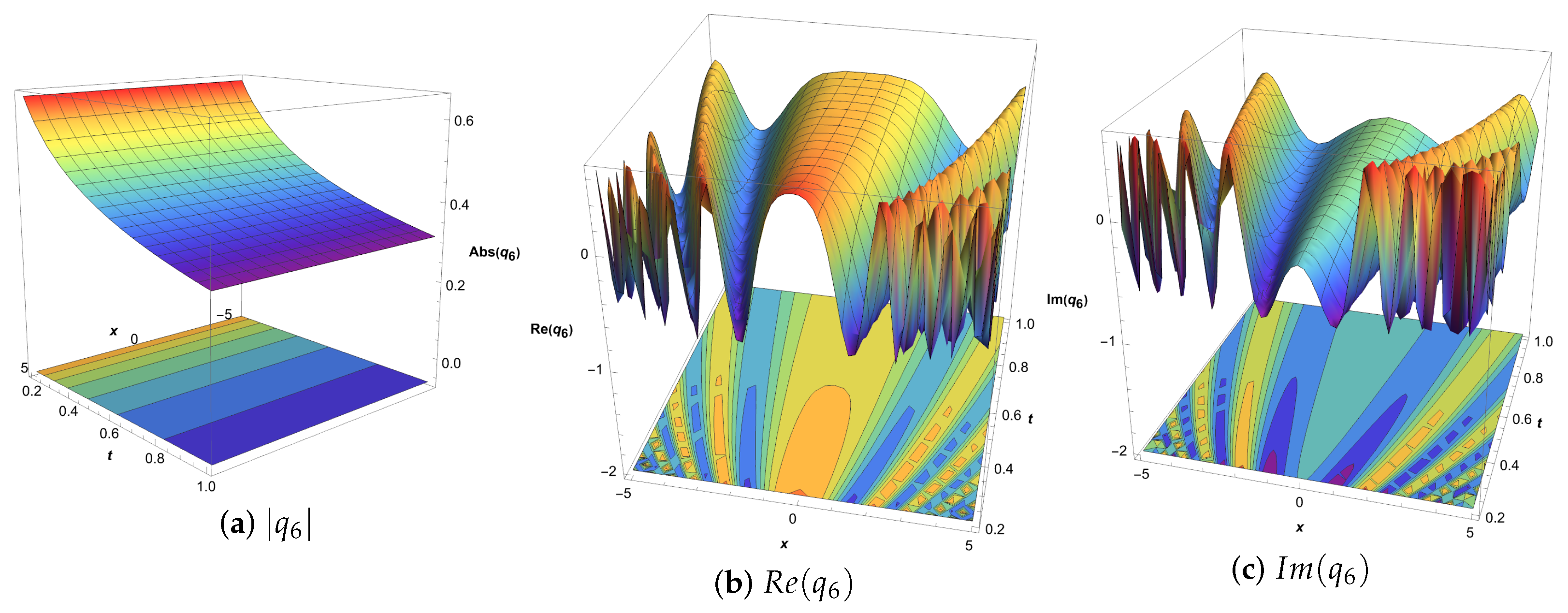
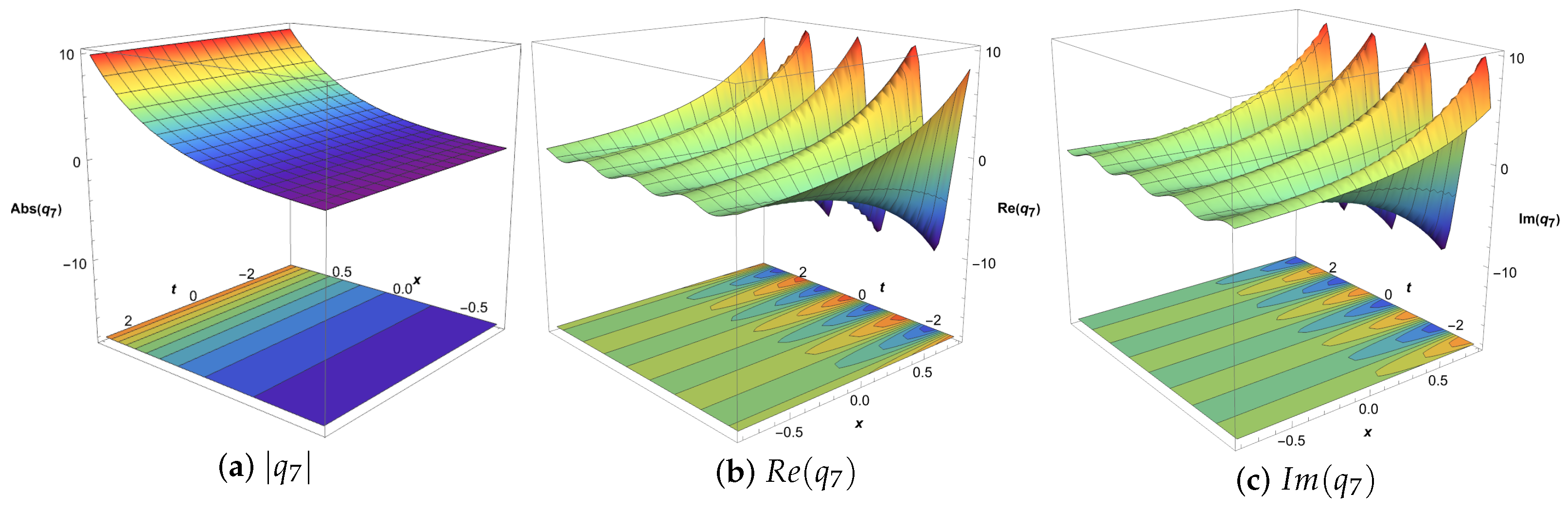
5. Dynamical Characteristics and Graphical Analysis of Solutions

To clarify the dynamic characteristics of the derived solutions, we present 3D surface and 2D contour plots for exemplary cases.

Figure 1 shows the profile of $q_1$, the solution to Equation (11). Panel (a) presents the modulus of $q_1$, which corresponds to a canonical dark soliton, a localized amplitude dip on a uniform background that forms a spatially confined envelope. Amplitude is concentrated and shape is preserved during propagation. Panels (b) and (c) correspond to the real part and the imaginary part, respectively, both exhibiting significant periodic oscillations. Such oscillatory characteristics, combined with a phase difference of ${\displaystyle \frac{\pi }{2}}$, collectively form the complete coherent structure of the complex field, intuitively reflecting the core dynamic traits of solitons: localized stability and coherent propagation.

Figure 2 illustrates the solution $q_6$ given by Equation (52). Panels (b) and (c) present the real and imaginary components of $q_6$, both symmetric with respect to $x=0$. As the time parameter $t\to 0$, the amplitude of $q_6$ increases sharply and tends to infinity, while the phase exhibits increasingly rapid oscillations. This behavior indicates that, at $t=0$, the solution becomes singular due to the divergence of the denominator. In this complex field solution, the singularity acts as an indicator of three core physical features: initial strong-field excitation, the critical state of nonlinear-dispersion interaction competition, and the physical validity boundary of the solution. It corresponds to the key processes of intense excitation and effect transition in practical nonlinear systems. A similar behavior is observed in Figure 3.

Figure 4 shows the solution $q_7$ from Equation (57). Panels (b) and (c), representing the real and imaginary parts respectively, both exhibit prominent periodic oscillations. In this coherent field solution, periodic oscillations serve as a core physical indicator that sustains the temporal coherence of the field, characterizes the linear phase shift and dispersion effects of the medium, and defines the characteristic time scale for the dynamical evolution of the field. Analysis of the wave structure confirms that $q_7$ is a time-periodic solution with period

$$T={\displaystyle \frac{2\pi }{|2c_1^2-b^2{c}_2^2|}},\mathrm{provided}\mathrm{that}2c_1^2-b^2{c}_2^2\ne 0.$$

6. Conclusions

This work investigates the reverse space-time NNLS equation for the first time by combining the traveling wave transformation with the Weierstrass-type Riccati expansion method. The nonlocal term is effectively converted into a local form through exploiting the parity of the solution, which facilitates the construction of explicit traveling wave solutions. We derive a variety of exact solutions, including those expressed by means of Jacobi elliptic and hyperbolic functions.

A Lie symmetry analysis of the NNLS equation is performed, where the infinitesimal generators are identified, leading to a reduction of the equation to both local and nonlocal ordinary differential equations. Exponential-type invariant solutions are obtained via direct integration, which emphasizes the critical role of properly handling the space-time reflection term $q(-x,-t)$ in nonlocal system symmetries.

The dynamic behavior of the obtained solutions is examined through three-dimensional surface plots and two-dimensional contour maps. The modulus of certain solutions reveals characteristic dark soliton profiles, while others exhibit finite-time blow-up with exponential amplitude growth or sustained periodic oscillations over time.

Additionally, the NNLS equation is extended to a nonlocal multi-component system. Lie symmetries of this system are derived, and reductions to systems of ordinary differential equations are performed. The resulting solutions capture the coupling induced by spatiotemporal reflection terms, offering valuable analytical insights into multi-mode nonlocal systems, such as those encountered in multi-component fiber optic transmission.

The discovery of exact solutions is of great significance for physics research. The core work of this paper is to construct the exact solutions of the NNLS equation through mathematical methods. In the future, we will further expand the relevant research on high-dimensional and variable-coefficient equations [38,39], and deepen the exploration of the physical significance and application scenarios of the solutions. The referenced literature [40,41] can serve as reference directions for subsequent research and provide strong support for related work.