Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives
Abstract
1. Introduction
2. Physical Structure and Problem Formulation
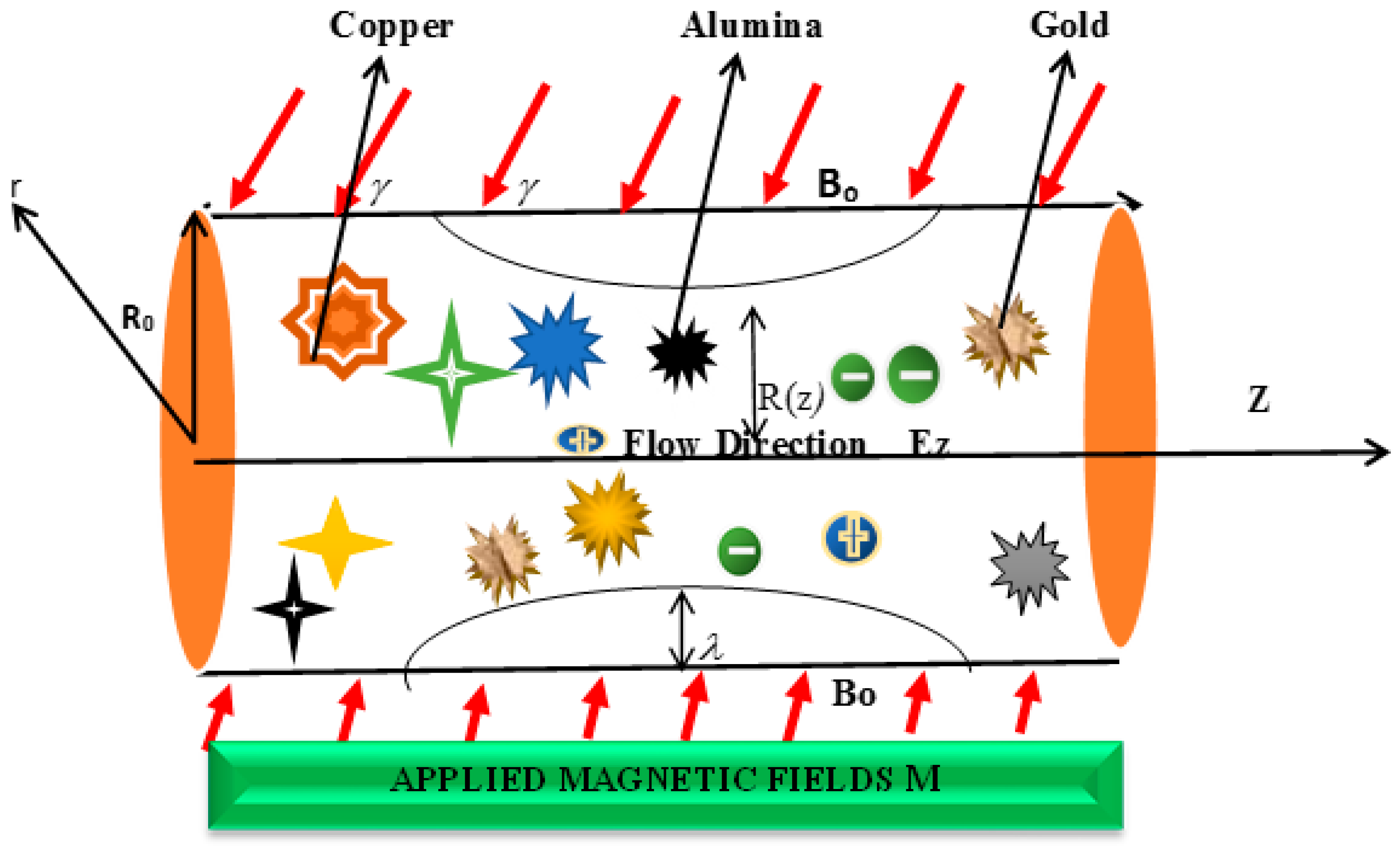
2.1. Flow Geometry
2.2. Basic Flow Equations
2.3. External Applied Electric Field
3. Solution Techniques
3.1. Fractional-Time Derivatives of Modeled Equations
3.2. Analytical Analysis
3.2.1. Velocity Profile
3.2.2. Temperature Profile
4. Numerical Procedure
4.1. Numerical Results and Discussion
4.2. Analysis of the Main Results
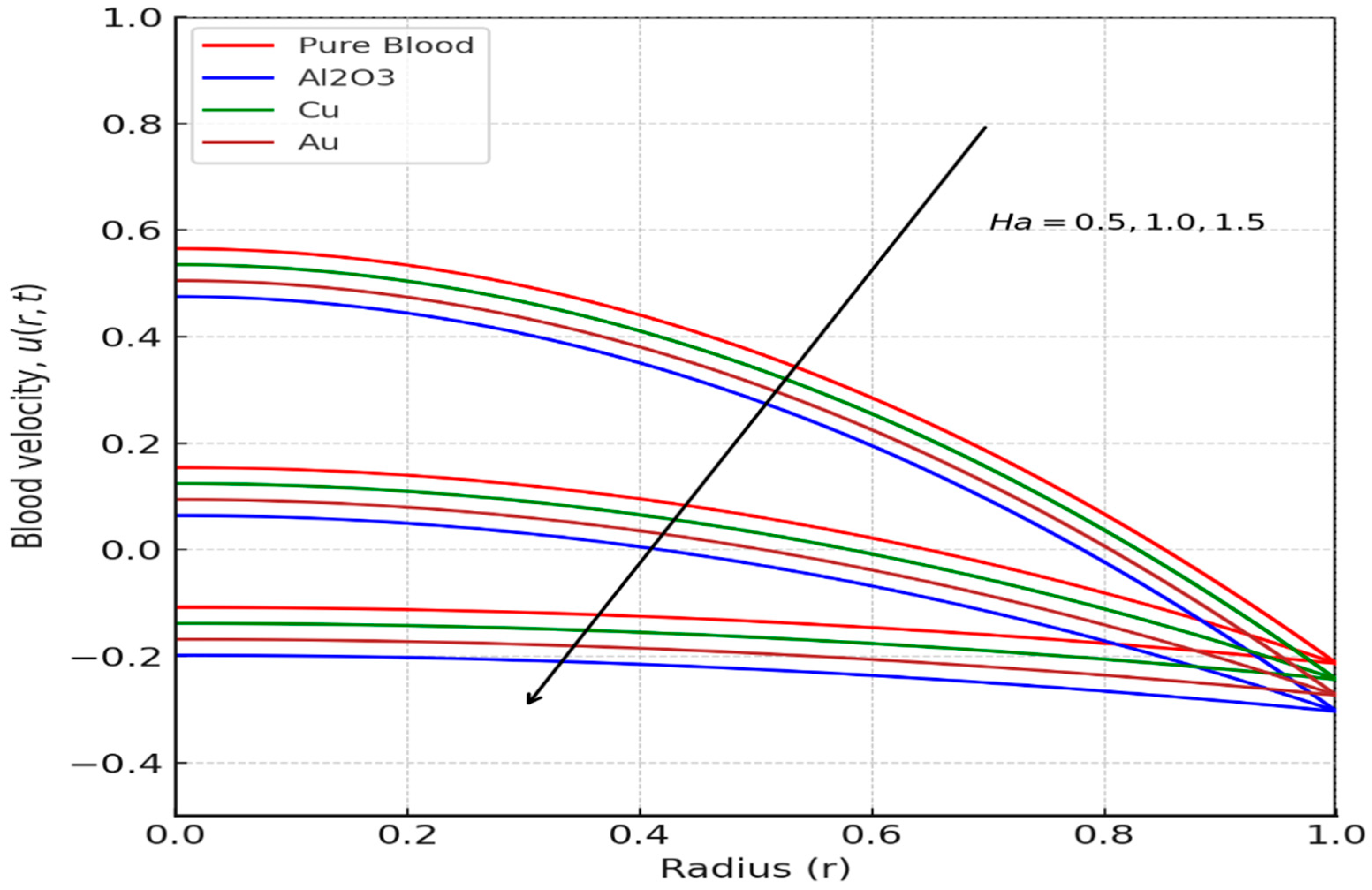
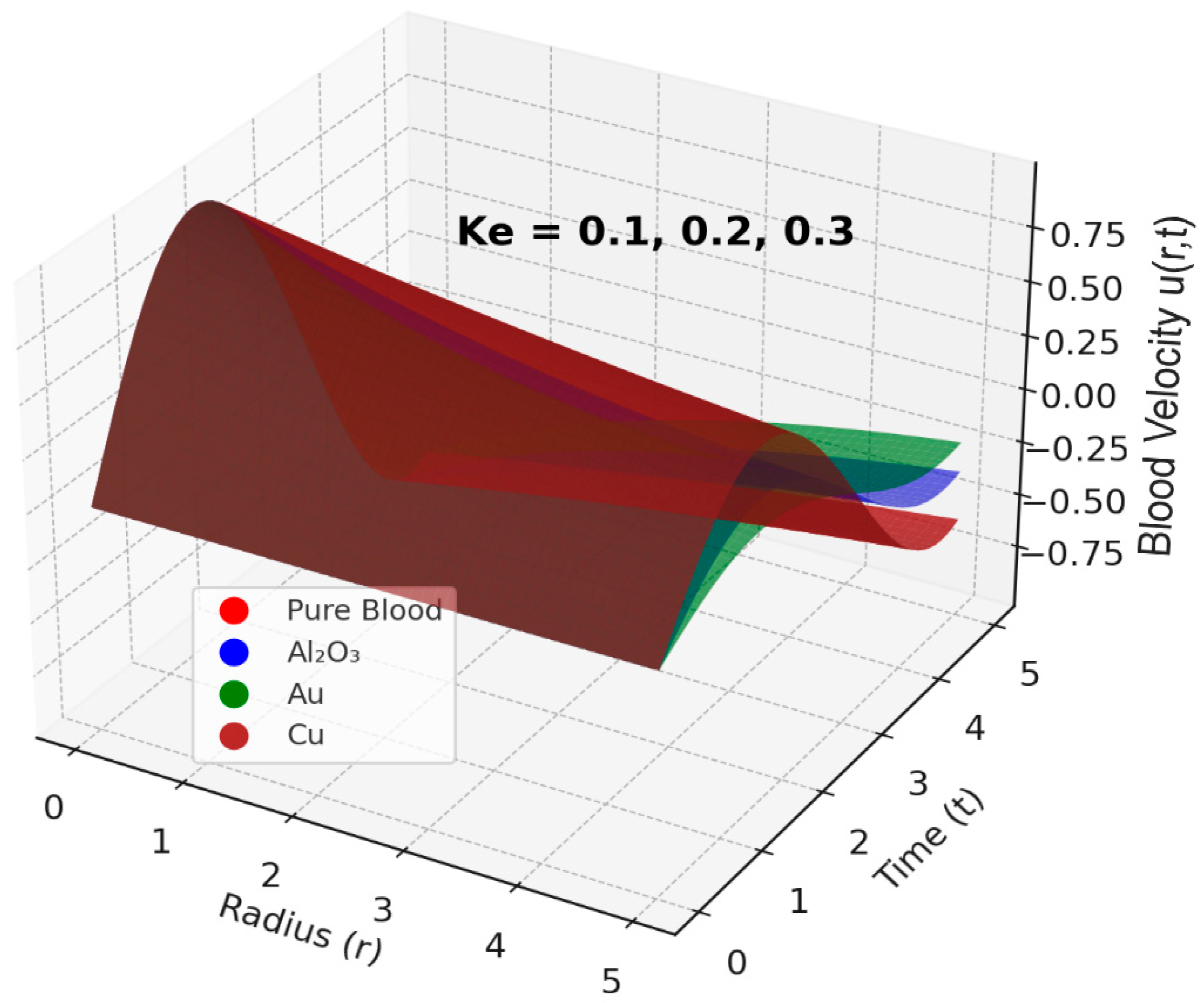
4.2.1. Results of Velocity Profile of the Blood Flow
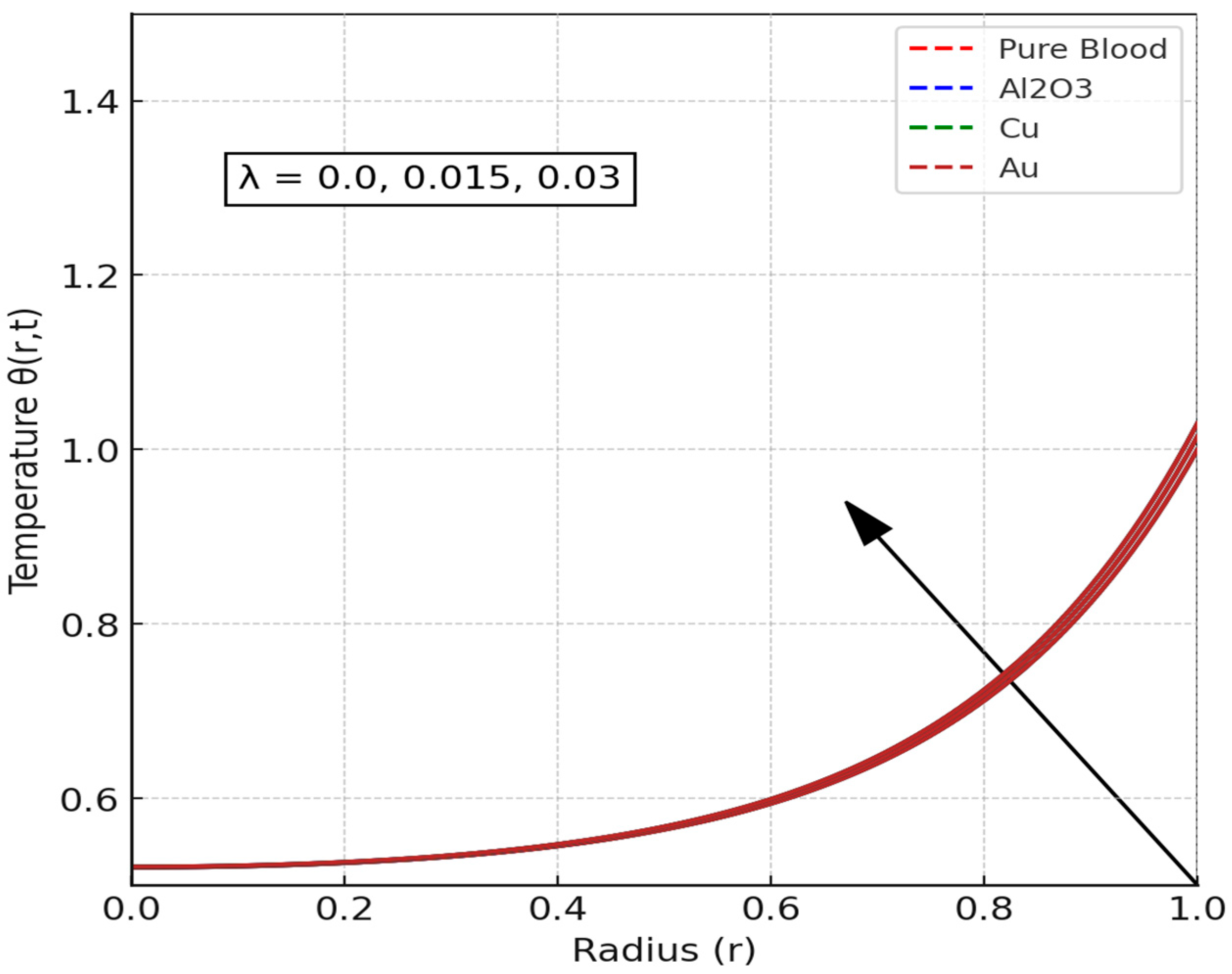
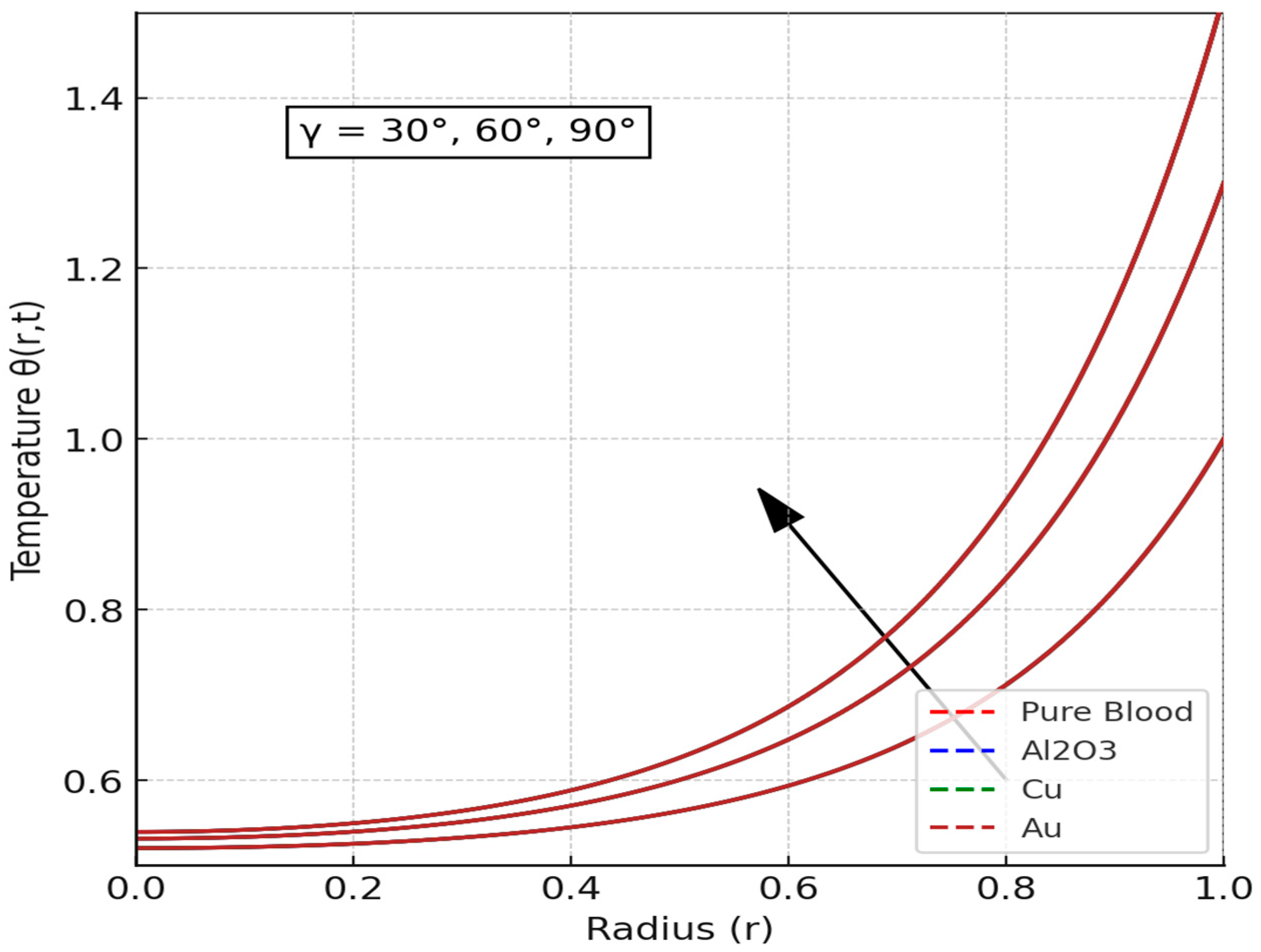
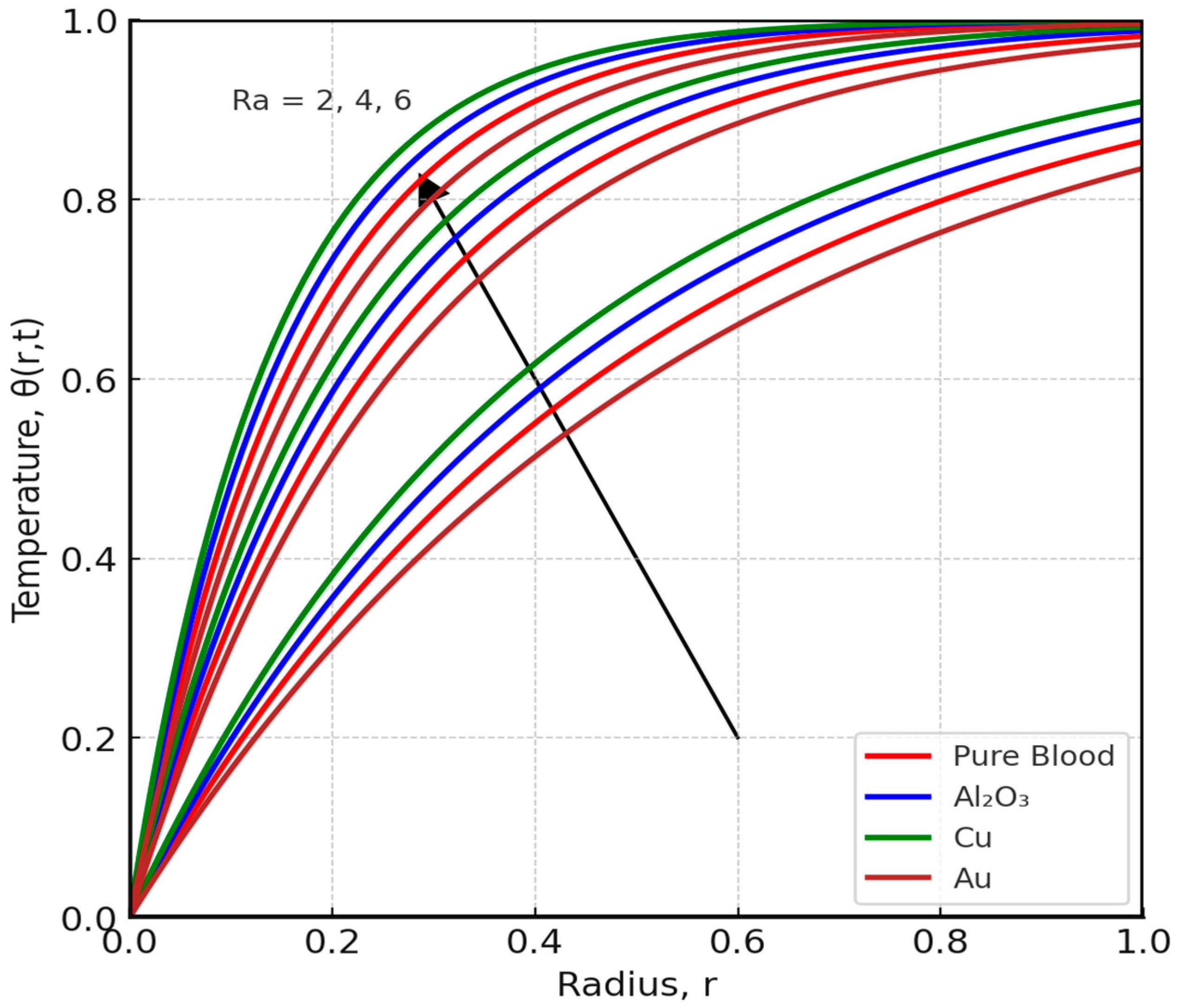
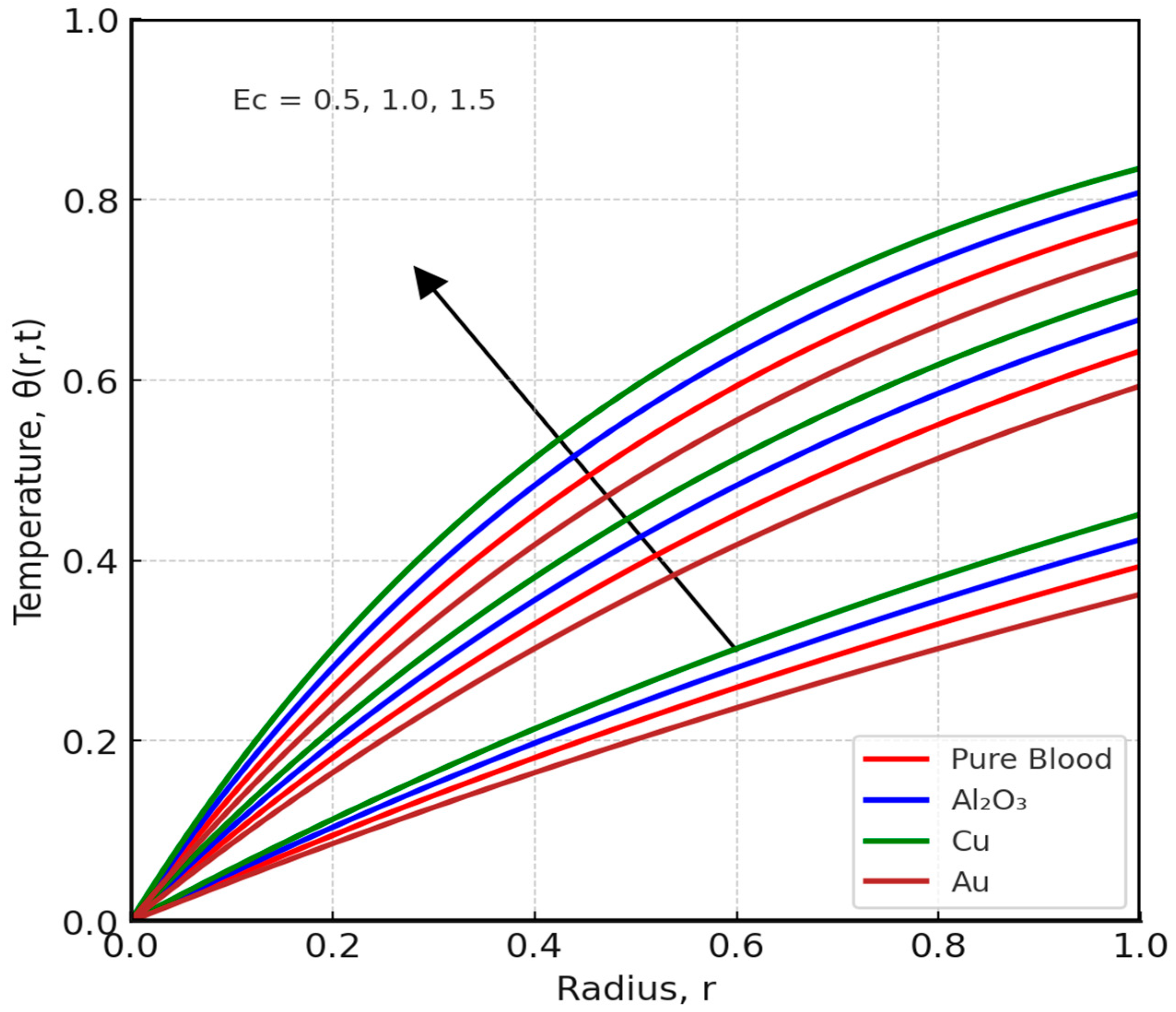
4.2.2. Results of Temperature Profile of the Blood
4.2.3. Effects of Pertinent Parameter on Skin Friction, Nusselt Number and Sherwood Number
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Mass diffusivity | ||
| Specific heat capacity | ||
| Reference velocity | ||
| thermal conductivity | ||
| Dimensionless temperature | ||
| Dimensionless concentration | ||
| Density | ||
| Electrical Conductivity | ||
| Dynamic viscosity | ||
| Gravitational acceleration | ||
| Thermal expansion | ||
| Mass expansion | ||
| Magnetic field | T | |
| Radial Coordinate | m | |
| Axial Coordinate | m | |
| Hight of the stenosis | m | |
| Axial Electric field | V/m | |
| Dielectric constant | V | |
| Boltzmann constant | J/K | |
| Kinetic width parameter | - | |
| Stenosis amplitude parameter | - | |
| Dimensional amplitude of applied field | A/m |
Appendix A
References
- Leon, M.B.; Smith, C.R.; Mack, M.; Miller, D.C.; Moses, J.W.; Svensson, L.G.; Tuzcu, E.M.; Webb, J.G.; Fontana, G.P.; Makkar, R.R.; et al. Transcatheter Aortic-Valve Implantation for Aortic Stenosis in Patients Who Cannot Undergo Surgery. N. Engl. J. Med. 2010, 363, 1597–1607. [Google Scholar] [CrossRef] [PubMed]
- Sankar, D.S.; Lee, U.; Ismail, A.I.M. Mathematical analysis for MHD flow of blood in constricted arteries. Int. J. Nonlinear Sci. Numer. Simul. 2013, 14, 195–204. [Google Scholar] [CrossRef]
- Nandal, J.; Kumari, S.; Rathee, R. The effect of slip velocity on unsteady peristalsis MHD blood flow through a constricted artery experiencing body acceleration. Int. J. Appl. Mech. Eng. 2019, 24, 645–659. [Google Scholar] [CrossRef]
- Azzouz, R.; Hamida, M.B.B. Natural convection in two different enclosures filled with nanohybrid under magnetic field: Application to heat exchanger. Therm. Sci. 2025, 29, 593–606. [Google Scholar] [CrossRef]
- Hussain, A.; Sarwar, L.; Rehman, A.; Al Mdallal, Q.; Almaliki, A.H.; El-Shafay, A.S. Mathematical analysis of hybrid mediated blood flow in stenosis narrow arteries. Sci. Rep. 2022, 12, 12704. [Google Scholar] [CrossRef]
- Nazar, T.; Shabbir, M. Irreversibility analysis in the ternary nanofluid flow through an inclined artery via Caputo-Fabrizio fractional derivatives. Results Phys. 2023, 53, 106992. [Google Scholar] [CrossRef]
- Jalili, P.; Ghahare, A.S.; Jalili, B.; Ganji, D.D. Analytical and numerical investigation of thermal distribution for hybrid nanofluid through an oblique artery with mild stenosis. SN Appl. Sci. 2023, 5, 95. [Google Scholar] [CrossRef]
- Alam, J.; Murtaza, M.; Tzirtzilakis, E.; Ferdows, M. Application of Biomagnetic Fluid Dynamics modeling for simulation of flow with magnetic particles and variable fluid properties over a stretching cylinder. Math. Comput. Simul. 2022, 199, 438–462. [Google Scholar] [CrossRef]
- Misra, J.C.; Sinha, A. Effect of thermal radiation on MHD flow of blood and heat transfer in a permeable capillary in stretching motion. Heat Mass Transf. 2013, 49, 617–628. [Google Scholar] [CrossRef]
- Kahshan, M.; Lu, D.; Rahimi-Gorji, M.; Do, H.-T. A mathematical model of blood flow in a permeable channel: Application to flat plate dialyzer. Phys. Scr. 2020, 95, 045202. [Google Scholar] [CrossRef]
- Changdar, S.; De, S. Analytical solution of mathematical model of magnetohydrodynamic blood nanofluid flowing through an inclined multiple stenosed artery. J. Nanofluids 2017, 6, 1198–1205. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Khan, N.B.; Jameel, M. Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second-order slip and entropy generation. Comput. Methods Programs Biomed. 2020, 189, 105294. [Google Scholar] [CrossRef]
- Tian, Y.; Shao, Y.; Shen, Y.; He, J.-H. A variational principle of an electrohydrodynamic fluid. Mod. Phys. Lett. A 2025, 40, 2450223. [Google Scholar] [CrossRef]
- Huang, H.; Shan, C.; Long, F.; Zeng, Z.; Xie, L.; Zou, F.; Xu, P. The adoption of novel cooling liquids for enhancing heat transfer performance of 3-d integrated circuits with embedded micro-channel. Therm. Sci. 2025, 29, 227–250. [Google Scholar] [CrossRef]
- Kumari, S.; Rathee, R.; Nanda, J. Unsteady peristaltic transport of MHD fluid through an inclined stenosed artery with slip effect. Int. J. Appl. Eng. Res. 2019, 14, 1881–1891. [Google Scholar] [CrossRef]
- Omamoke, E.; Amos, E. Treatment and slip effect on MHD blood flow through a stenotic artery: A mathematical model. Asian Res. J. Math. 2023, 19, 61–76. [Google Scholar] [CrossRef]
- Prakash, J.; Makinde, O.D. Radiative heat transfer to blood flow through a stenotic artery in the presence of magnetic field. Latin Am. Appl. Res. 2011, 41, 273–277. [Google Scholar]
- Chinyoka, T.; Makinde, O.D. Computational dynamics of arterial blood flow in the presence of magnetic field and thermal radiation therapy. Adv. Math. Phys. 2014, 2014, 915640. [Google Scholar] [CrossRef]
- Isah, A.; Musa, A.; Yakubu, G.; Adamu, G.T.; Mohammed, A.; Baba, A.; Kadas, S.; Mahmood, A. The impact of heat source and chemical reaction on MHD blood flow through permeable bifurcated arteries with tilted magnetic field in tumor treatments. Comput. Methods Biomech. Biomed. Eng. 2023, 27, 558–569. [Google Scholar] [CrossRef]
- Younis, O.; Abderrahmane, A.; Ali, A.B.; Rashad, A.; Ahmed, S.E.; Mourad, A.; Salahshour, S.; Hekmatifar, M.; Guedri, K. Heat transfer and entropy investigation of non-Newtonian nanofluid mixed convection in a cubic cavity with a wavy bottom wall under the influence of a magnetic field. Case Stud. Therm. Eng. 2025, 71, 106222. [Google Scholar] [CrossRef]
- Yin, D.; Wang, P.; Hao, Y.; Yue, W.; Jiang, X.; Yao, K.; Wang, Y.; Hang, X.; Xiao, A.; Zhou, J.; et al. A battery-free nanofluidic intracellular delivery patch for internal organs. Nature 2025, 642, 1051–1061. [Google Scholar] [CrossRef] [PubMed]
- Bansi, C.; Tabi, C.; Motsumi, T.; Mohamadou, A. Fractional blood flow in oscillatory arteries with thermal radiation and magnetic field effects. J. Magn. Magn. Mater. 2018, 456, 38–45. [Google Scholar] [CrossRef]
- Yadeta, H.B.; Shaw, S. Analysis of unsteady non-Newtonian Jeffrey blood flow and transport of magnetic nanoparticles through an inclined porous artery with stenosis using the time fractional derivative. J. Appl. Phys. 2023, 134, 104701. [Google Scholar] [CrossRef]
- Jamil, D.F.; Saleem, S.; Roslan, R.; Al-Mubaddel, F.S.; Rahimi-Gorji, M.; Issakhov, A.; Din, S.U. Analysis of non-Newtonian magnetic Casson blood flow in an inclined stenosed artery using Caputo-Fabrizio fractional derivatives. Comput. Methods Programs Biomed. 2021, 203, 106044. [Google Scholar] [CrossRef]
- Abdullah, M.; Butt, A.R.; Raza, N.; Alshomrani, A.S.; Alzahrani, A. Analysis of blood flow with nanoparticles induced by uniform magnetic field through a circular cylinder with fractional Caputo derivatives. J. Magn. Magn. Mater. 2018, 446, 28–36. [Google Scholar] [CrossRef]
- Maiti, S.; Shaw, S.; Shit, G. Fractional order model for thermochemical flow of blood with Dufour and Soret effects under magnetic and vibration environment. Colloids Surf. B Biointerfaces 2021, 197, 111395. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Fataf, N.; Banerjee, S.; Sun, K. Complexity in the muscular blood vessel model with variable fractional derivative and external disturbances. Physics A 2019, 526, 120904. [Google Scholar] [CrossRef]
- Imoro, I.; Etwire, C.J.; Musah, R. MHD Flow of Blood-Based Hybrid Nanofluid Through a Stenosed Artery with Thermal Radiation Effect. Case Stud. Therm. Eng. 2024, 59, 104418. [Google Scholar] [CrossRef]
- He, J.-H.; Moatimid, G.M.; Mohamed, M.A.A.; Elagamy, K. A stretching cylindrical Carreau nanofluid border layer movement with motile microorganisms and variable thermal characteristics. Int. J. Mod. Phys. B 2024, 38, 2450223. [Google Scholar] [CrossRef]
- Wang, X.; Popel, A.S. Modeling the combined effects of joule heating and viscous dissipation on blood flow in microvessels. Microvasc. Res. 2013, 87, 46–52. [Google Scholar] [CrossRef]
- Sharma, P.R.; Sinha, S. Combined effects of viscous dissipation and joule heating on unsteady MHD flow and heat transfer over a stretching sheet saturated in porous medium. Ann. Pure Appl. Math. 2017, 14, 387–399. [Google Scholar] [CrossRef]
- Rasheed, H.U.; Al-Zubaidi, A.; Islam, S.; Saleem, S.; Khan, Z.; Khan, W. Effects of joule heating and viscous dissipation on magnetohydrodynamic boundary layer flow of jeffrey nanofluid over a vertically stretching cylinder. Coatings 2021, 11, 353. [Google Scholar] [CrossRef]
- Al-Zahrani, A.A.; Adnan; Mahmood, I.; Rahman, K.U.; Bani-Fwaz, M.Z.; Tag-Eldin, E. Analytical study of (ag-graphene)/blood hybrid nanofluid influenced by (plateletscylindrical) nanoparticles and joule heating via VIM. ACS Omega 2023, 8, 19926–19938. [Google Scholar] [CrossRef]
- Manikandan, S.; Nanthakumar, A. Development of a predictive model for thermal conductivity in graphene nanoplatelets infused damper oil using ANN/RSM. Therm. Sci. 2024, 28, 4235–4247. [Google Scholar] [CrossRef]
- Bouaraour, K.; Lalmi, D.; Sidi Mohamed, M.S. Mixed convection analysis of nanofluid flow inside an indented micro-channel. Therm. Sci. 2024, 28, 4321–4331. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Chu, Y.-M.; Qushairi, A.; Shafie, S.; Nisar, K.S. Multiple fractional solutions for magnetic bio-nanofluid using Oldroyd-B model in a porous medium with ramped wall heating and variable velocity. Appl. Sci. 2020, 10, 3886. [Google Scholar] [CrossRef]
- Bit, A.; Alblawi, A.; Chattopadhyay, H.; Quais, Q.A.; Benim, A.C.; Rahimi-Gorji, M.; Do, H.-T. Three dimensional numerical analysis of hemodynamic of stenosed artery considering realistic outlet boundary conditions. Comput. Methods Programs Biomed. 2019, 185, 105163. [Google Scholar] [CrossRef] [PubMed]
- Yakubu, D.G.; Abdullahi, I.; Musa, A. The dynamic flow of ternary nanofluids with magnetic nanoparticles in an inclined artery exposed to thermal radiation and magnetic fields. Alex. Eng. J. 2025, 123, 231–241. [Google Scholar] [CrossRef]
- Shit, G.; Majee, S. Pulsatile flow of blood and heat transfer with variable viscosity under magnetic and vibration environment. J. Magn. Magn. Mater. 2015, 388, 106–115. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Mei, Y.; Tian, X.; Li, X.; Gepreel, K. Fractal Space-Based Dimensionless Analysis of the Surface Settlement Induced by Shield Tunneling. Facta Univ. Ser. Mech. Eng. 2023, 21, 737–749. [Google Scholar] [CrossRef]
- Basha, H.T.; Rajagopal, K.; Ahammad, N.A.; Sathish, S.; Gunakala, S.R. Finite difference computation of Au-Cu/magneto-bio-hybrid nanofluid flow in an inclined uneven stenosis artery. Complexity 2022, 2022, 2078372. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.-L.; Li, Z.-Y. A high-precision numerical approach to solving space fractional gray-Scott model. Appl. Math. Lett. 2022, 125, 1077596. [Google Scholar] [CrossRef]
- Che, H.; Wang, Y.-L.; Li, Z.-Y. Novel patterns in a class of fractional reaction-diffusion models with the Riesz fractional derivative. Math. Comput. Simul. 2022, 202, 149–163. [Google Scholar] [CrossRef]
- Alhachami, A.S.K.; Asadi, Z.; Jalili, B.; Khan, Y.; ShayanMehr, M.; Jalili, P.; Ganji, D.D. Hydrothermal analysis of time-fractional magneto hydrodynamic viscous fluid flow on a plate. ZAMM-Z. Für Angew. Math. Und Mech. 2024, 104, e202300369. [Google Scholar] [CrossRef]
- Wikipedia. Fractional Calculus. 2023. Available online: https://en.wikipedia.org/wiki/Fractional_calculus (accessed on 8 February 2023).
- Algehyne, E.A.; Lone, S.A.; Raizah, Z.; Eldin, S.M.; Saeed, A.; Galal, A.M. Analysis of the electrically conducting magnetohydrodynamic hybrid nanofluid flow past a convectively heated stretching surface with suction/injection and non-linear thermal radiation. Front. Mater. 2023, 10, 1179189. [Google Scholar]
- Zar, P.M.; Shateri, A.; Jalili, P.; Al-Yarimi, F.A.M.; Jalili, B.; Ganji, D.D.; Ben Khedher, N. Radiative effects on 2d unsteady mhd Al2O3-water nanofluid flow between squeezing plates: A comparative study using agm and hpm in python. ZAMM-Z. Für Angew. Math. Und Mech. 2025, 105, e202400546. [Google Scholar] [CrossRef]
- Moussa, B.; Youssouf, M.; Wassiha, N.A.; Youssouf, P. Homotopy perturbation method to solve Duffing-Van der Pol equation. Adv. Differ. Equ. Control Processes 2024, 31, 299–315. [Google Scholar] [CrossRef]
- He, J.-H.; He, C.-H.; Alsolami, A.A. A good initial guess for approximating nonlinear oscillators by the homotopy perturbation method. Facta Univ. Ser. Mech. Eng. 2023, 21, 21–29. [Google Scholar] [CrossRef]
- Liu, Y.-P.; He, J.-H. A fast and accurate estimation of amperometric current response in reaction kinetics. J. Electroanal. Chem. 2024, 978, 118884. [Google Scholar] [CrossRef]
- He, J.-H. An Old Babylonian Algorithm and Its Modern Applications. Symmetry 2024, 16, 1467. [Google Scholar] [CrossRef]
- Sharma, M.; Gaur, R.; Sharma, B. Radiation effect on mhd blood flow through a tapered porous stenosed artery with thermal and mass diffusion. Int. J. Appl. Mech. Eng. 2019, 24, 411–423. [Google Scholar] [CrossRef]
- Zamfirache, I.A.; Precup, R.-E.; Petriu, E.M. Q-learning, policy iteration and actor-critic reinforcement learning combined with metaheuristic algorithms in servo system control. Facta Univ. Ser. Mech. Eng. 2023, 21, 615–630. [Google Scholar] [CrossRef]
- Shateri, A.; Ganji, A.M.; Jalili, P.; Jalili, B.; Ganji, D.D. Utilizing python for numerical analysis of bioconvection in magnetized casson-maxwell nanofluid systems with gyrotactic microorganisms: An investigation of dominant factors. Results Eng. 2024, 25, 103760. [Google Scholar] [CrossRef]
- Jalili, B.; Zar, P.M.; Liu, D.; Ji, C.-H.; Jalili, P.; Abdelmohimen, M.A.; Ganji, D.D. Thermal study of mhd hybrid nano fluids confined between two parallel sheets: Shape factors analysis. Case Stud. Therm. Eng. 2024, 63, 105229. [Google Scholar] [CrossRef]
- Ganji, D.D.; Mahboobtosi, M.; Jalili, B.; Jalili, P. Heat transfer analysis of magnetized fluid flow through a vertical channel with thin porous surfaces: Python approach. Case Stud. Therm. Eng. 2024, 60, 104643. [Google Scholar] [CrossRef]
- Hajizadeh, S.; Jalili, P.; Jalili, B.; Alam, M.M.; Ali, M.R.; Hendy, A.S.; Ganji, D.D. Innovative binary nanofluid approach with copper (Cu-EO) and magnetite (Fe3O4-EO) for enhanced thermal performance. Case Stud. Therm. Eng. 2024, 63, 105191. [Google Scholar] [CrossRef]
- Darvesh, A.; Boukhris, I.; Santisteban, L.J.C.; Al-Buriahi, M.; Elqahtani, Z.M.; Akgül, A.; García, L.K.O.; Hassani, M.K. Radiative heat transfer in mhd copper-based polymer nanofluid over a sphere using larger radius and inter particle spacing of nanoparticles. Results Eng. 2025, 26, 105012. [Google Scholar] [CrossRef]
- Jalili, P.; Afifi, M.D.; Jalili, B.; Mirzaei, A.M.; Ganji, D.D. Numerical study and comparison of two-dimensional ferrofluid flow in semi-porous channel under magnetic field. Int. J. Eng. 2023, 36, 2087–2101. [Google Scholar] [CrossRef]
- Roshani, H.; Jalili, B.; Mirzaei, A.; Jalili, P.; Ganji, D.D. The effect of buoyancy force on natural convection heat transfer of nanofluid flow in triangular cavity with different barriers. Heliyon 2024, 10, e35690. [Google Scholar] [CrossRef]
- Jalili, B.; Shateri, A.; Akgül, A.; Bariq, A.; Asadi, Z.; Jalili, P.; Ganji, D.D. An investigation into a semi-porous channel’s forced convection of nano fluid in the presence of a magnetic field as a result of heat radiation. Sci. Rep. 2023, 13, 18505. [Google Scholar] [CrossRef]
- Zhang, P.; Roshani, H.; Jalili, P.; Jalili, B.; Alotaibi, H.; Ganji, D.D. Thermal analysis of transient mhd ferrofluid flow and natural convection in a porous cavity with a cylindrical barrier. Case Stud. Therm. Eng. 2024, 66, 105693. [Google Scholar] [CrossRef]
- He, J.-H.; Bai, Q.; Luo, Y.-C.; Kuangaliyeva, D.; Ellis, G.; Yessetov, Y.; Skrzypacz, P. Modeling and numerical analysis for an MEMS graphene resonator. Front. Phys. 2025, 13, 1551969. [Google Scholar] [CrossRef]
- He, C.-H.; Cui, Y.; He, J.-H.; Buhe, E.; Bai, Q.; Xu, Q.; Ma, J.; Alsolam, A.A.; Gao, M. Nonlinear Dynamics in MEMS Systems: Overcoming Pull-in Challenges and Exploring Innovative Solutions. J. Low Freq. Noise Vib. Act. Control 2025. [Google Scholar] [CrossRef]
- He, J.H. Periodic solution of a micro-electromechanical system. Facta Univ. Ser. Mech. Eng. 2024, 22, 187–198. [Google Scholar] [CrossRef]
- He, J.-H.; Cheng, Y.; Luo, C.-L.; Zhong, C.; Lin, H.; Marinkovic, D. Differential equation-driven intelligent control: Integrating AI, Quantum computing, and adaptive strategies for next-generation industrial automation. Adv. Differ. Equ. Control Process. 2025, 32, 3096. [Google Scholar] [CrossRef]
- Abbas, Z.; Abdullah, A.R.; Malik, M.F.; Shah, S.A.A. Artificial Neural Network Modeling of Darcy–Forchheimer Nanofluid Flow over a Porous Riga Plate: Insights into Brownian Motion, Thermal Radiation, and Activation Energy Effects on Heat Transfer. Symmetry 2025, 17, 1582. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Alshammari, F.S.; Malik, M.F.; Batool, S. Numerical–ANN Framework for Thermal Analysis of MHD Water-Based Prandtl Nanofluid Flow over a Stretching Sheet Using Bvp4c. Symmetry 2025, 17, 1347. [Google Scholar] [CrossRef]
- Vaferi, B.; Dehbashi, M.; Alibak, A.H. Cutting-Edge Machine Learning Techniques for Accurate Prediction of Agglomeration Size in Water–Alumina Nanofluids. Symmetry 2024, 16, 804. [Google Scholar] [CrossRef]


| Blood | Au | Cu | Al2O3 | Physical Properties |
|---|---|---|---|---|
| 1060 | 19,320 | 8933 | 3971 | |
| 0.492 | 314.0 | 401.0 | 40.0 | |
| 1.80 | 14.00 | 16.70 | 8.60 | |
| 3594.0 | 129.0 | 385.0 | 765.0 | |
| 0.667 | 4.10 10−7 | 5.96 10−7 | 35.00 10−6 |
| Radius (r) | [16] | [28] | This Paper | MSE |
|---|---|---|---|---|
| 0.2 | 0.809 | 0.807 | 0.815 | 0.000064 |
| 0.4 | 0.700 | 0.702 | 0.710 | 0.000064 |
| 0.6 | 0.538 | 0.527 | 0.540 | 0.000169 |
| 0.8 | 0.303 | 0.281 | 0.290 | 0.000081 |
| 1.0 | 0.000 | 0.000 | 0.000 | 0.000000 |
| Ha | Ke | Cf | Nu | |
|---|---|---|---|---|
| 0.2 | 1.5498 | −0.1854 | ||
| 0.4 | 1.5973 | −0.1772 | ||
| 0.6 | 1.6470 | −0.1689 | ||
| 0.5 | 1.7175 | −0.1423 | ||
| 1.0 | 1.685 | −0.1396 | ||
| 1.5 | 1.6420 | −0.1344 | ||
| 1.0 | 0.8594 | −0.1753 | ||
| 1.2 | 0.8589 | −0.1692 | ||
| 1.4 | 0.8585 | −0.1564 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.-H.; Adamu, M.Y.; Abdullahi, I.; Xu, N.; He, C.-H. Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives. Symmetry 2025, 17, 2024. https://doi.org/10.3390/sym17122024
He J-H, Adamu MY, Abdullahi I, Xu N, He C-H. Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives. Symmetry. 2025; 17(12):2024. https://doi.org/10.3390/sym17122024
Chicago/Turabian StyleHe, Ji-Huan, Magaji Yunbunga Adamu, Isah Abdullahi, Nuo Xu, and Chun-Hui He. 2025. "Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives" Symmetry 17, no. 12: 2024. https://doi.org/10.3390/sym17122024
APA StyleHe, J.-H., Adamu, M. Y., Abdullahi, I., Xu, N., & He, C.-H. (2025). Magnetohydrodynamic Flow and Transport Behaviors of Blood-Based Ternary Nanofluids in Stenosed Arteries with Axial Symmetry: Effects of Thermal Radiation and Caputo Fractional Derivatives. Symmetry, 17(12), 2024. https://doi.org/10.3390/sym17122024







