Symmetry-Inspired Design and Full-Coverage Path Planning for a Multi-Arm NDT Robot on a Reactor Pressure Vessel
Abstract
1. Introduction
- (1)
- Symmetrical Deployment for Enhanced Coverage: A four-arm, radially symmetric configuration with redundant degrees of freedom (DOF) and modular joint design achieves full-pose coverage in complex geometries, improving inspection efficiency by 40–60% over single-arm systems.
- (2)
- Comprehensive Kinematics Analysis: An improved Denavit–Hartenberg (D-H) parameter model coupled with multi-arm collaborative control enables submillimeter-level positioning accuracy, effectively mitigating kinematic singularities inherent in single-arm systems.
- (3)
- Hierarchical Zonal Algorithm: Geometric feature-based partitioning divides the inspection area into seven sub-regions—including circumferential weld zones, flange regions, and nozzle-to-shell and nozzle-to-safe end areas. The simulation results demonstrate that the proposed full-coverage traversal inspection method effectively improves the detection coverage rate.
2. Design of NDT Robot
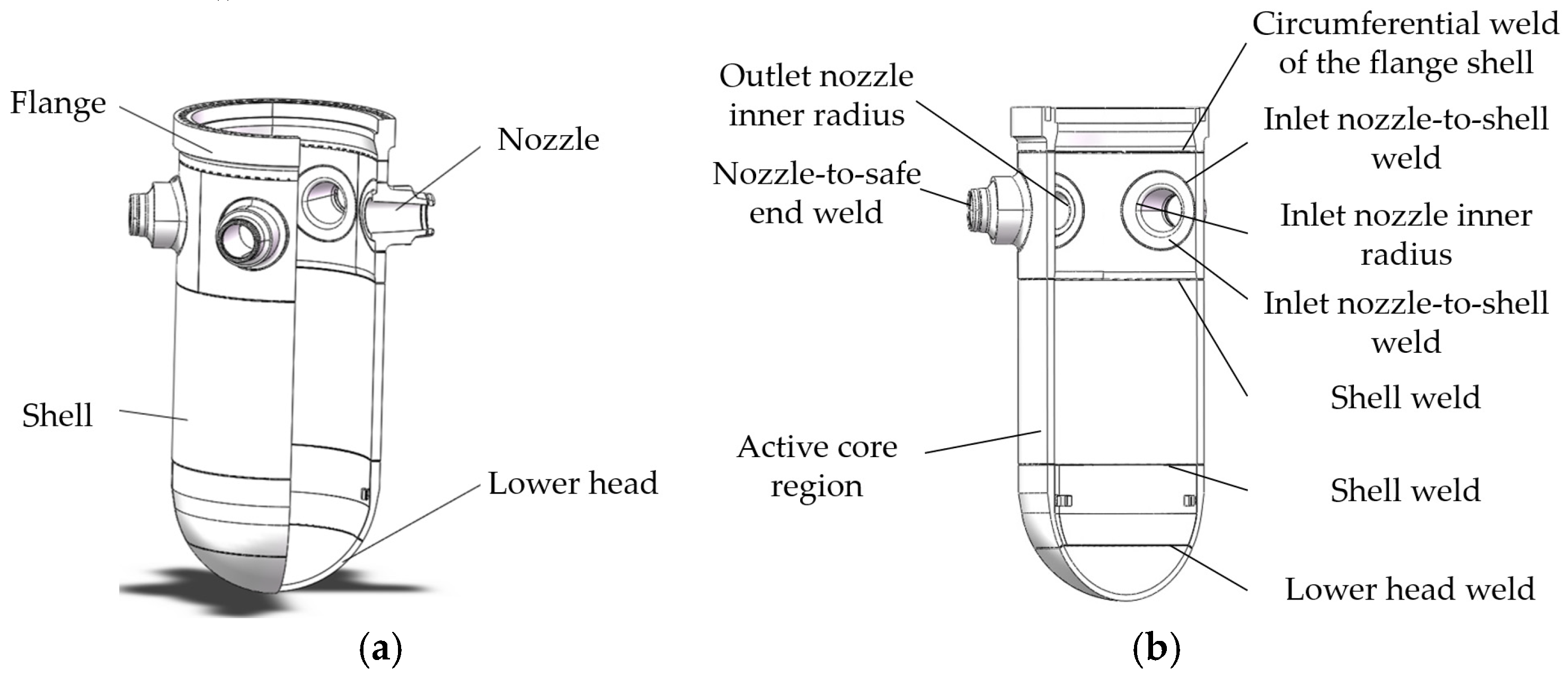
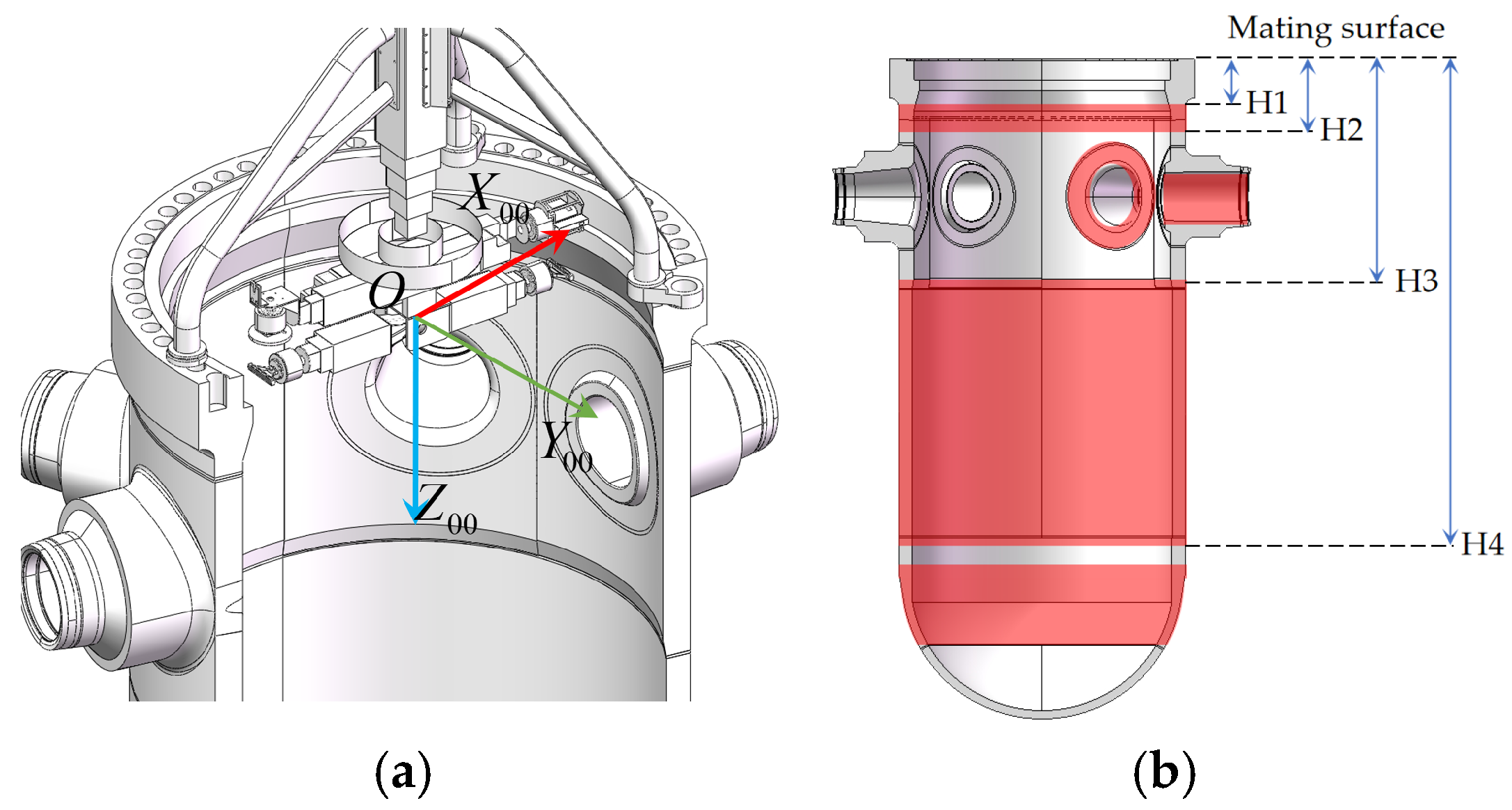
2.1. Introduction to Robot’s Working Environment
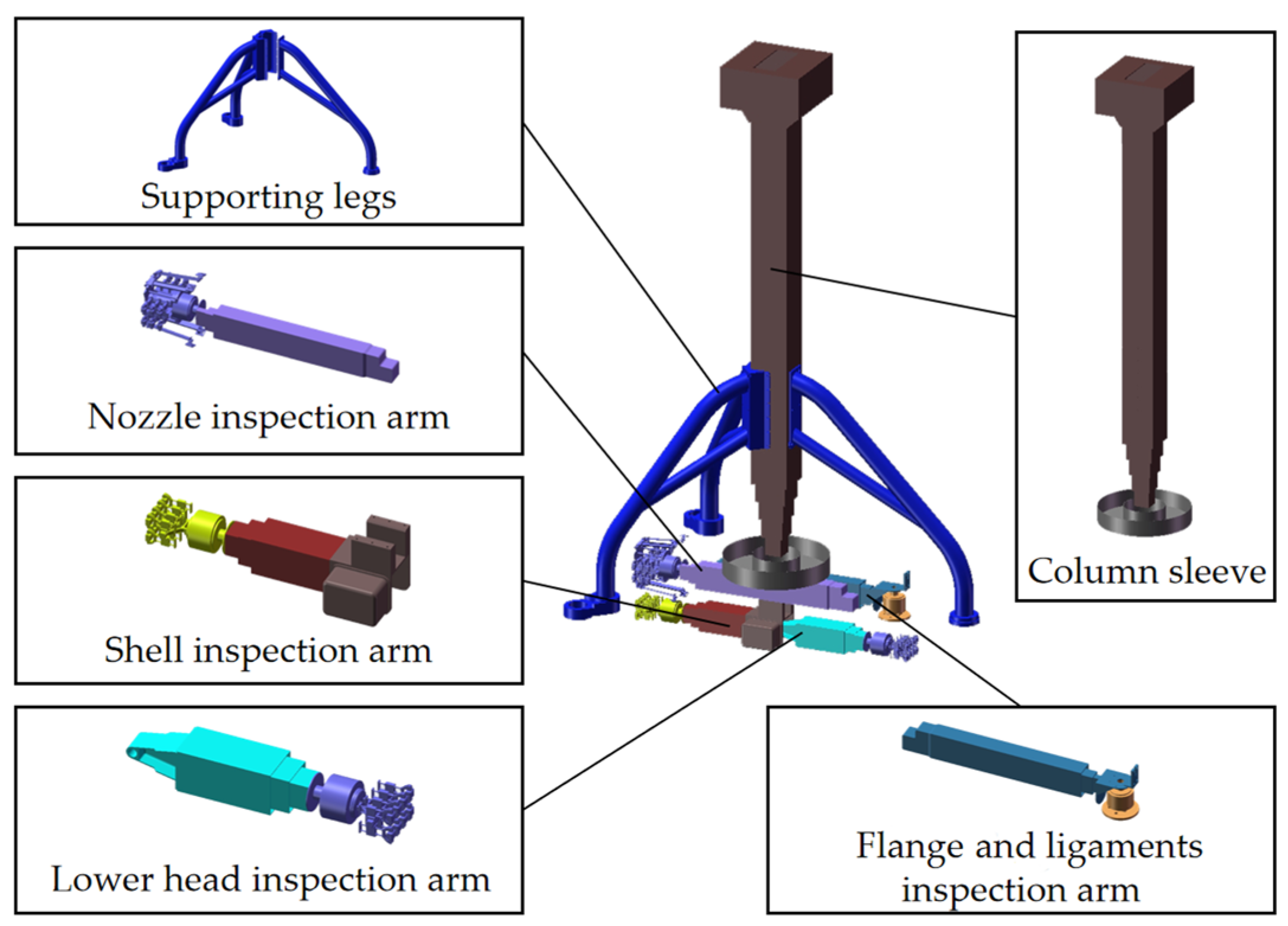
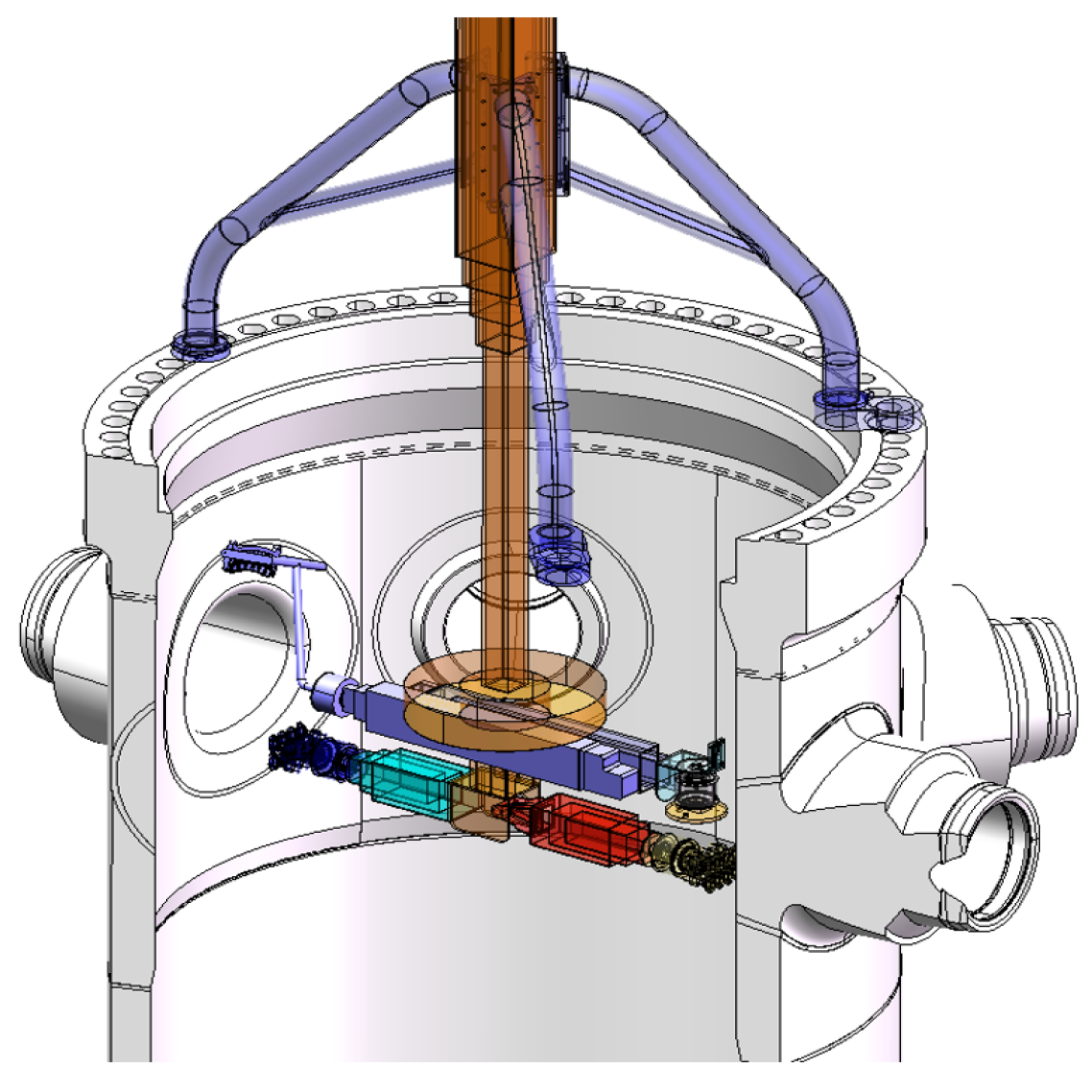
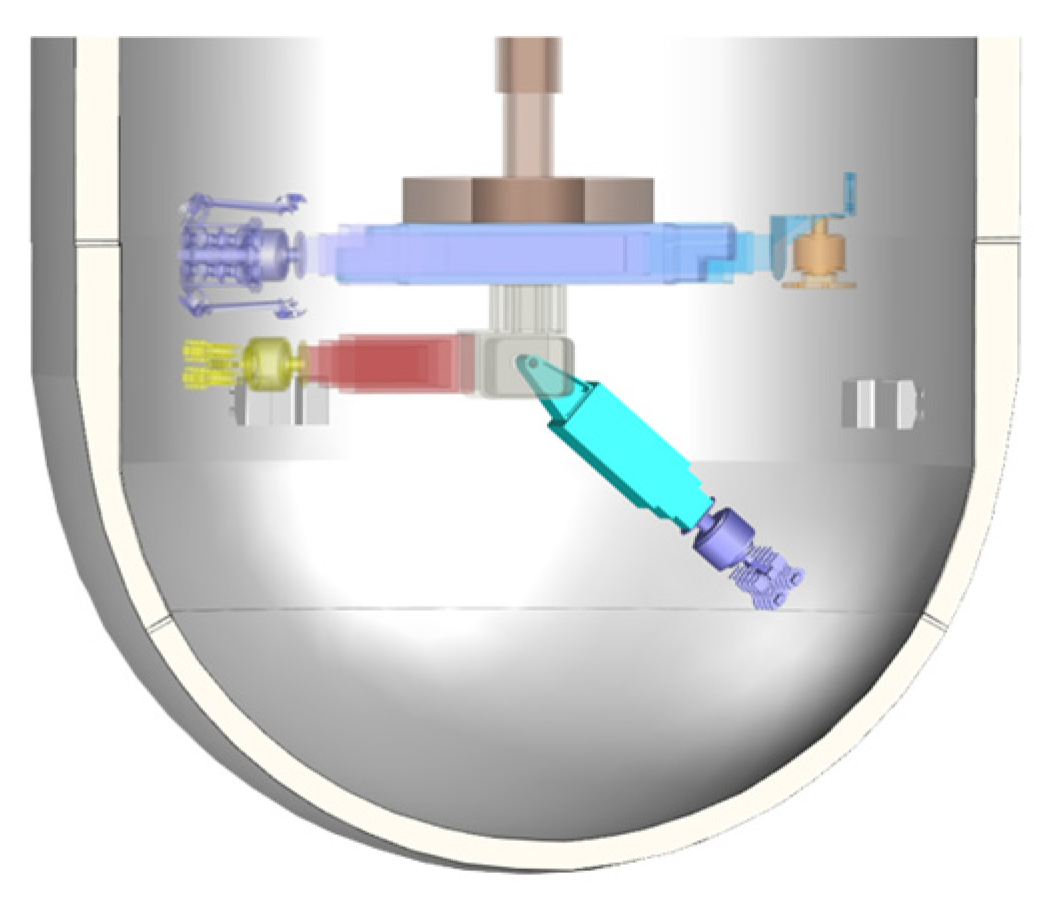
2.2. Introduction to Nondestructive Inspection Robot
2.3. Control System Architecture
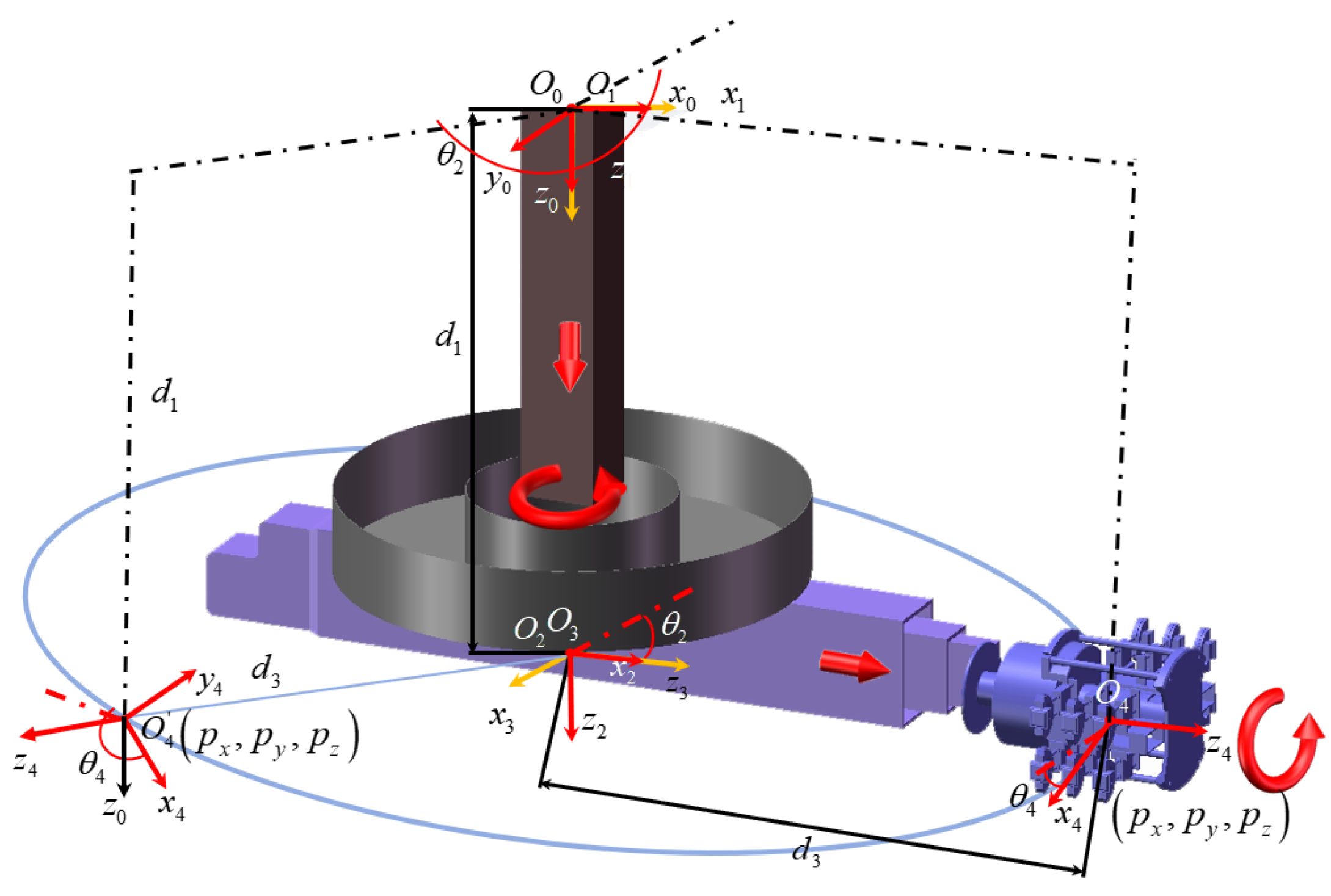
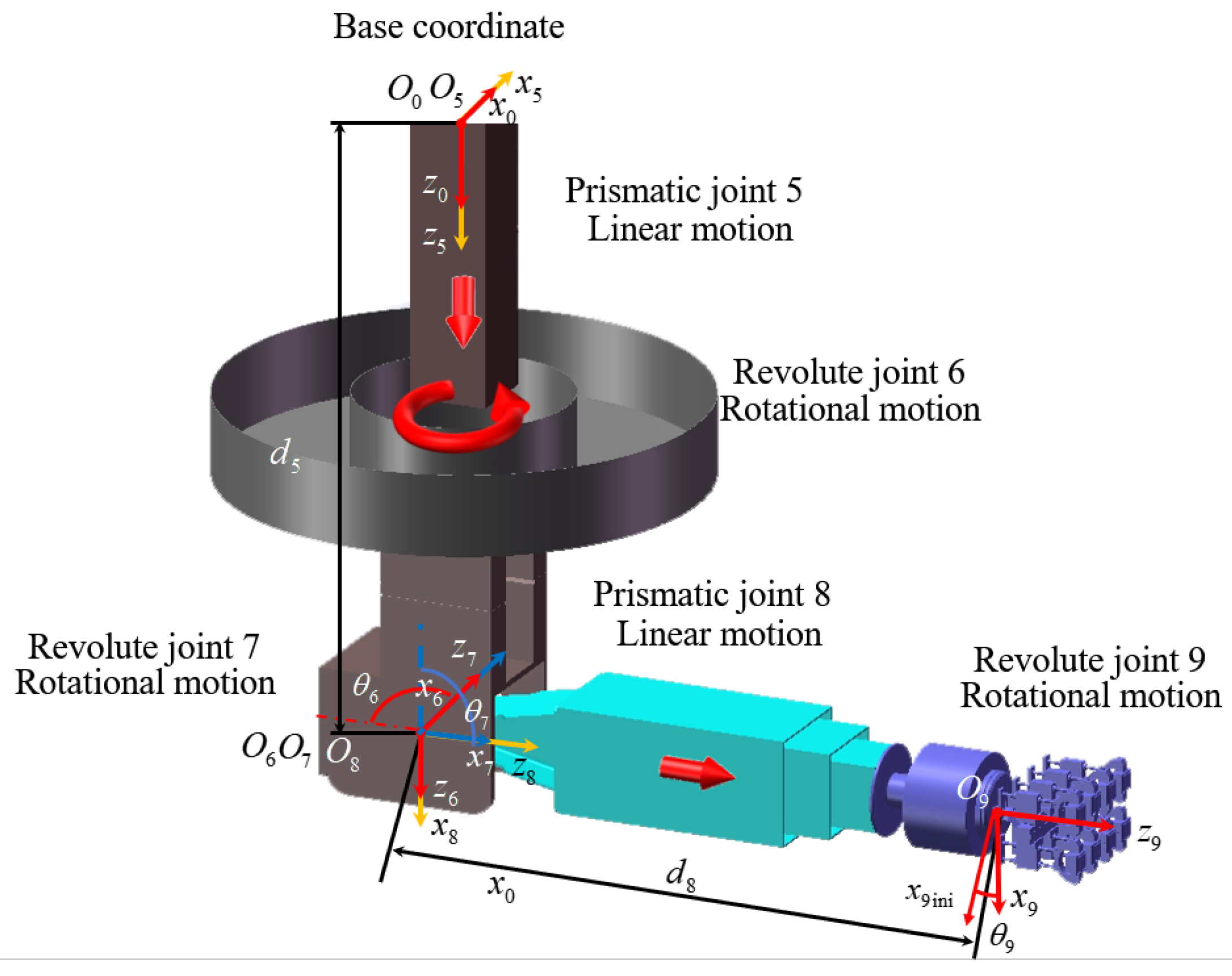
3. Kinematic Analysis of the Inspection Arm
3.1. The Type I Inspection Arm
- (1)
- Forward Kinematics Modeling
- (2)
- Inverse Kinematics Modeling
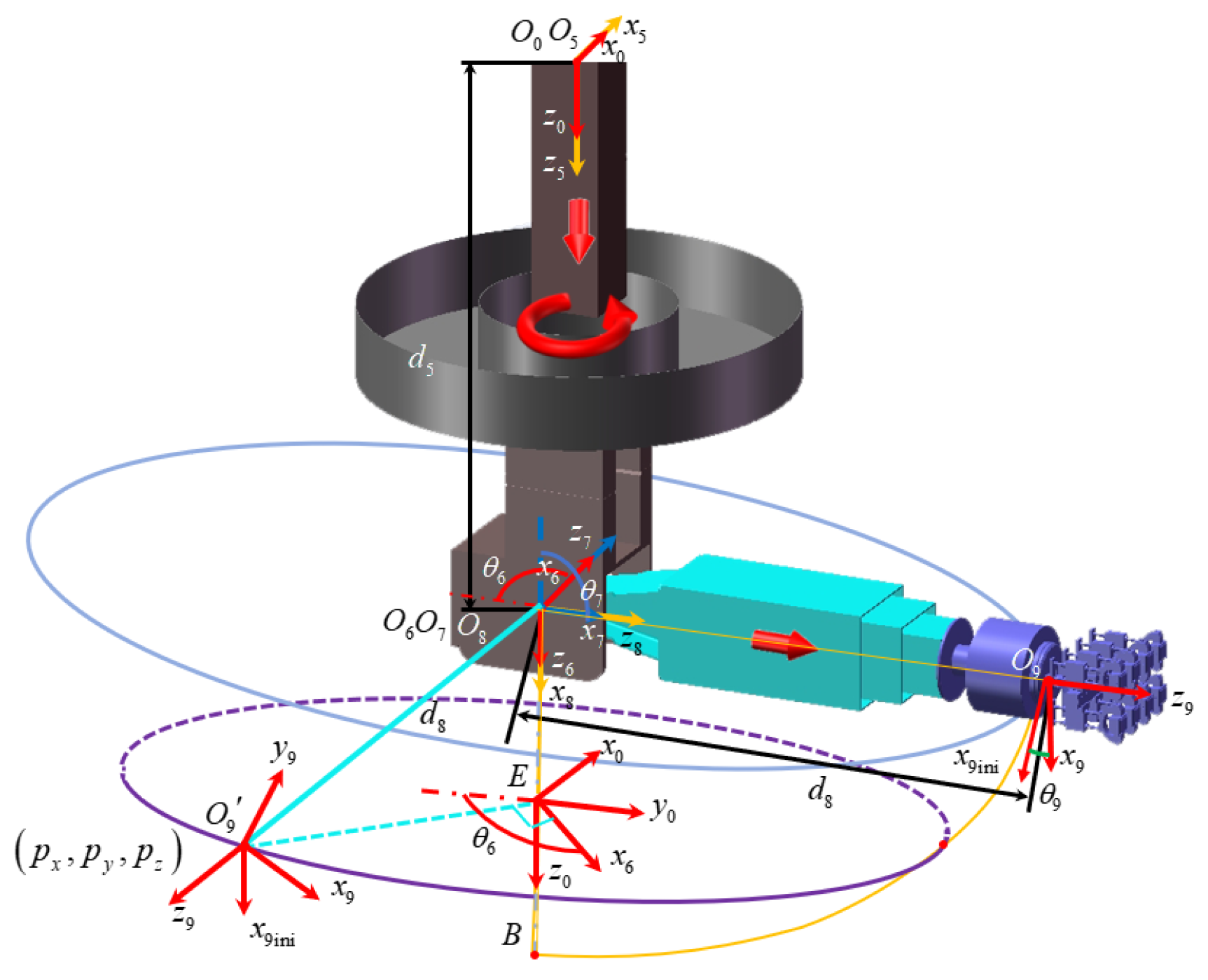
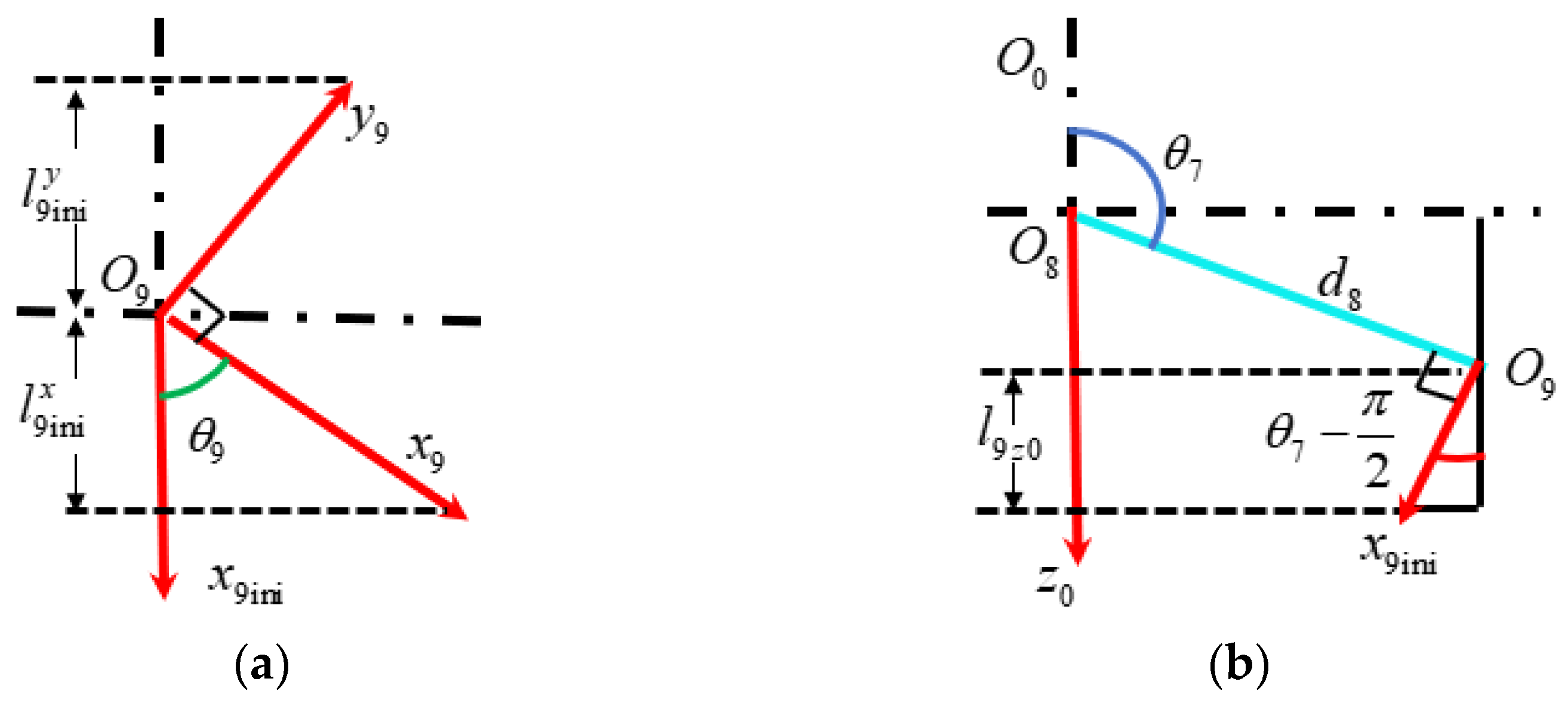
3.2. The Type II Inspection Arm
- (1)
- Forward Kinematics Modeling
- (2)
- Inverse Kinematics Modeling
4. Adaptive Exhaustive Inspection
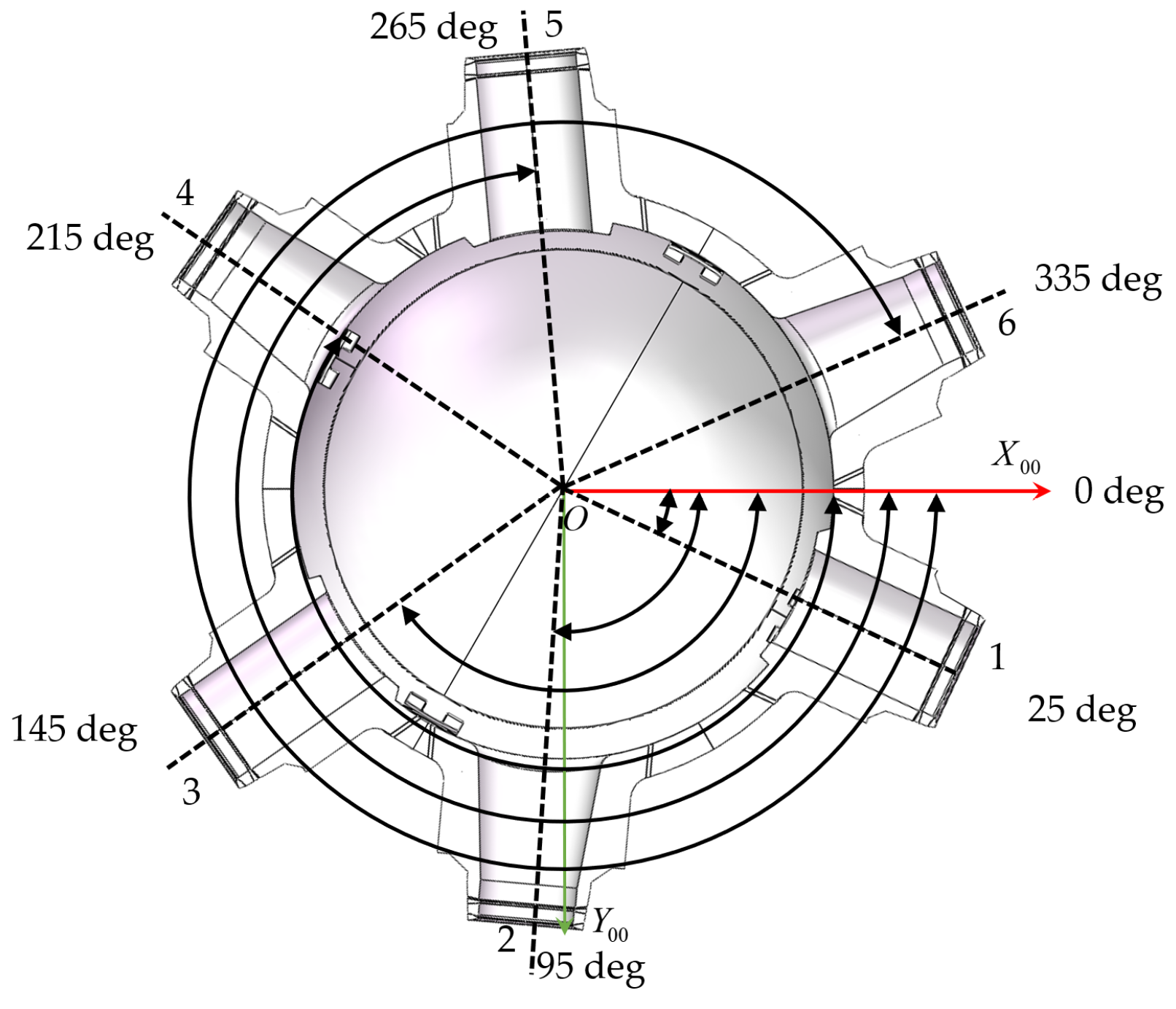
4.1. The Inspection Region Division
4.2. The Traversing Evaluation Indicators
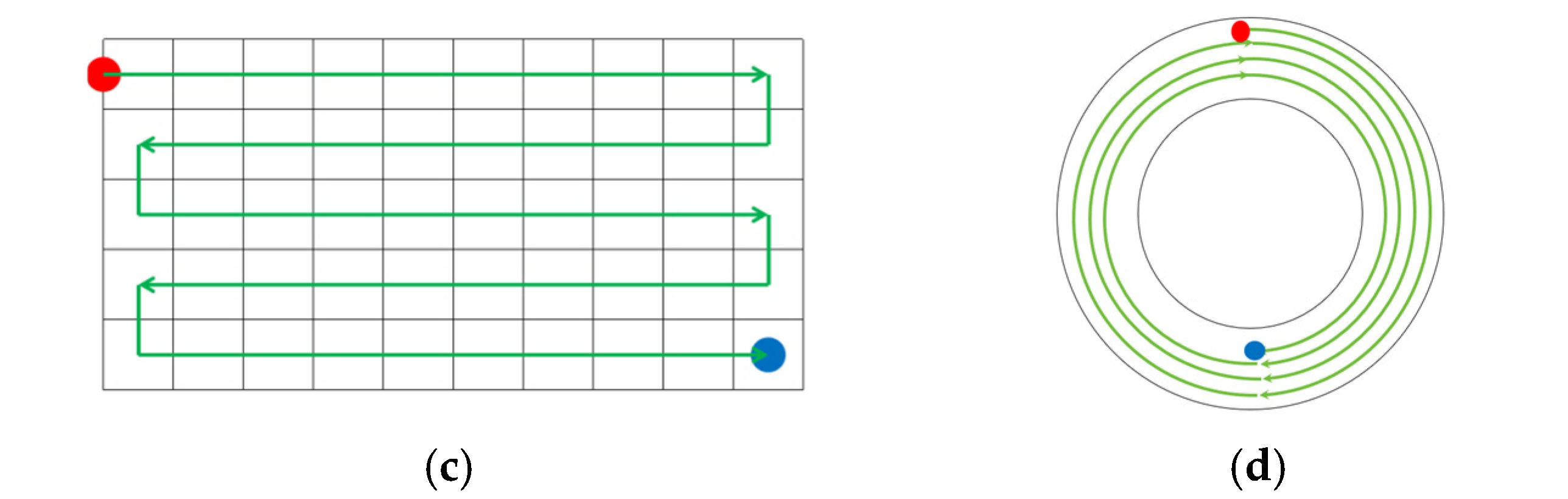
4.3. The Comparison of Traversal Methods
4.4. The Inspection Path Planning Method
4.5. The Inspection Trajectory Interpolation Method
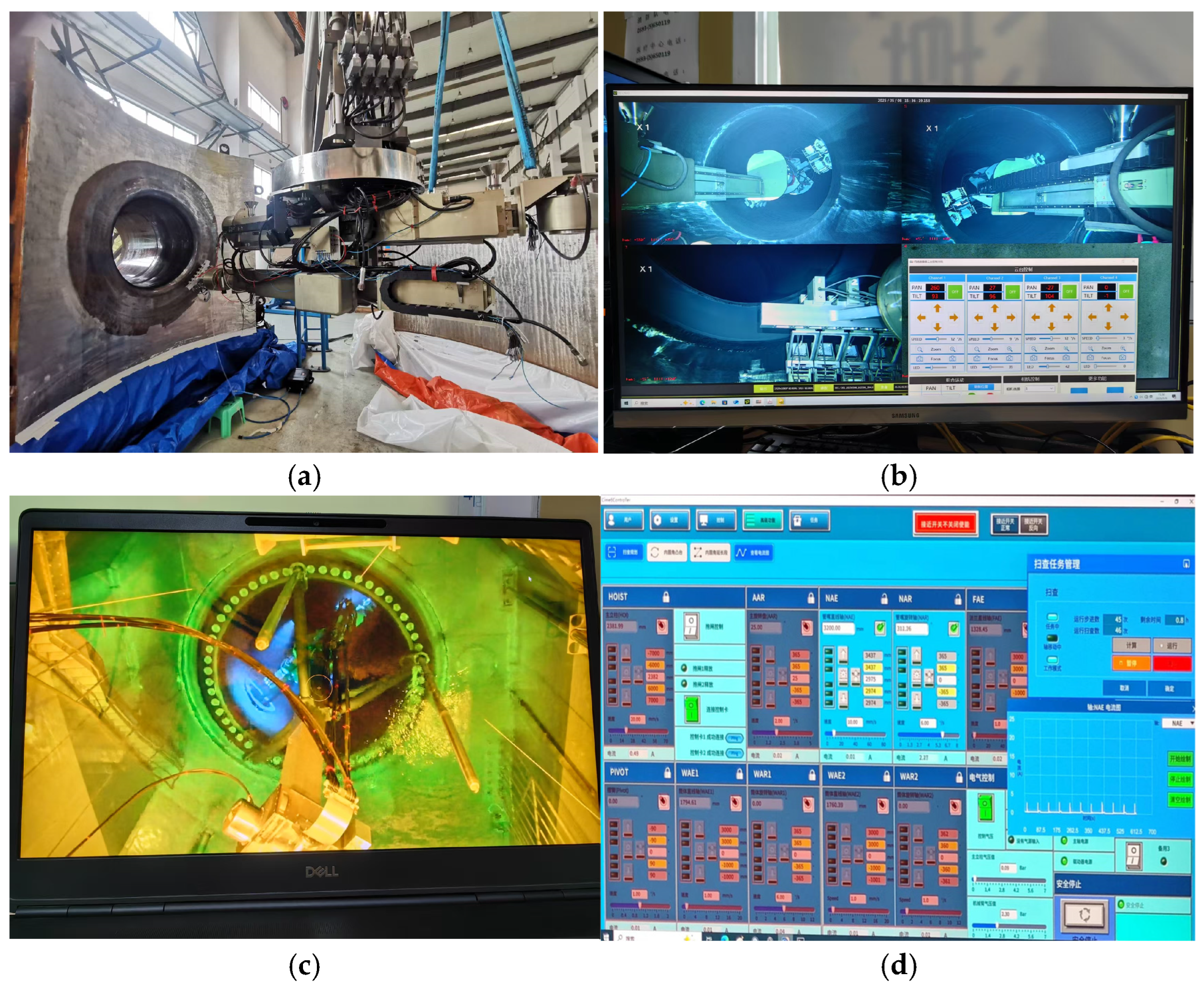
5. Experiments and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernandez-Arias, P.; Vergara, D.; Orosa, J.A. A Global Review of PWR Nuclear Power Plants. Appl. Sci. 2020, 10, 4434. [Google Scholar] [CrossRef]
- Huang, S.; Sun, H.; Wang, K.; Zhao, W.; Peng, L. Nondestructive Testing and Condition Monitoring of Pressurized Water Reactor Nuclear Power Plants: A Review. J. Mech. Eng. 2022, 58, 1–13. [Google Scholar]
- Wen, S.; Gao, X.; Zhang, R.; Fan, K.; Jia, B.; Jing, J.; Liu, F.; Tian, X. Study on the influences of RPV deformation on CHF under IVR conditions. Front. Energy Res. 2023, 11, 1087135. [Google Scholar] [CrossRef]
- Aksenov, P.L.; Komolov, I.A.; Molodov, P.A. Development of a Risk Monitoring Model for NPPs with a VVER-440 Reactor. At. Energy 2023, 133, 136–141. [Google Scholar] [CrossRef]
- Emerson, J.N.; Marrero-Jackson, E.H.; Nemets, G.A.; Okuniewski, M.A.; Wharry, J.P. Nuclear Reactor Pressure Vessel Welds: A Critical and Historical Review of Microstructures, Mechanical Properties, Irradiation Effects, and Future Opportunities. Mater. Des. 2024, 244, 113134. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, M.; Li, Y.; Liu, W.; Wang, B.; Meng, X.; Ouyang, X. Influence of interaction among multiple cracks on crack propagation in nozzle corner of reactor pressure vessel. Ann. Nucl. Energy 2023, 194, 110142. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. ASME BPVC Section XI: Rules for Inservice Inspection of Nuclear Power Plant Components; ASME: New York, NY, USA, 2023. [Google Scholar]
- Ducros, C.; Hauser, G.; Mahjoubi, N.; Girones, P.; Boisset, L.; Sorin, A.; Jonquet, E.; Falciola, J.M.; Benhamou, A. RICA: A Tracked Robot for Sampling and Radiological Characterization in the Nuclear Field. J. Field Robot. 2017, 34, 583–599. [Google Scholar] [CrossRef]
- Kim, J.H. Reactor nozzle inspection based on the laser-guided mobile robot. J. Field Robot. 2018, 35, 1155–1172. [Google Scholar] [CrossRef]
- Hong, M.; Li, Y.; Yan, J.; Ma, G.; Ye, X.; Chen, H.; Zhang, X. Simulation and analysis of full-coverage ultrasonic signal detection for reinforcement part of nuclear reactor pressure vessel outlet nozzle. Int. J. Press. Vessel. Pip. 2025, 216, 105462. [Google Scholar] [CrossRef]
- Sung, M.; Choi, Y. Algorithmic Modified Denavit–Hartenberg Modeling for Robotic Manipulators Using Line Geometry. Appl. Sci. 2025, 15, 4999. [Google Scholar] [CrossRef]
- Wang, J.; Liang, F.; Zhou, H.; Yang, M.; Wang, Q. Analysis of position, pose and force decoupling characteristics of a 4-UPS/1-RPS parallel grinding robot. Symmetry 2022, 14, 825. [Google Scholar] [CrossRef]
- Zhong, F.; Liu, G.; Lu, Z.; Han, Y.; Liu, F.; Ye, T. Inverse kinematics analysis of humanoid robot arm by fusing denavit-hartenberg and screw theory to imitate human motion with kinect. IEEE Access 2023, 11, 67126–67139. [Google Scholar] [CrossRef]
- Shin, H.; Jeong, K.M.; Jung, S.; Kim, S. Development of a steam generator tube inspection robot with a supporting leg. Nucl. Eng. Technol. 2009, 41, 125–134. [Google Scholar] [CrossRef]
- Zheng, C.; Zou, L.; Zheng, Z.; Xue, X. Kinematics modeling and singularity analysis of a 6-DOF all-metal vibration isolator based on dual quaternions. Symmetry 2023, 15, 562. [Google Scholar] [CrossRef]
- Cho, Y.; Do, H.M.; Cheong, J. Screw based kinematic calibration method for robot manipulators with joint compliance using circular point analysis. Robot. Comput. Integr. Manuf. 2019, 60, 63–76. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, Y.; Li, S.; Yang, J.; Xie, H.; Lu, X. Research on kinematics modeling and path planning of a hyper-redundant continuum robot. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 5880–5890. [Google Scholar] [CrossRef]
- Yang, H.; Xia, C.; Wang, X.; Xu, W.; Liang, B. An efficient solver for the inverse kinematics of cable-driven manipulators with pure rolling joints using a geometric iterative approach. Mech. Theory 2024, 196, 105611. [Google Scholar] [CrossRef]
- Park, S.O.; Lee, M.C.; Kim, J. Trajectory Planning with Collision Avoidance for Redundant Robots Using Jacobian and Artificial Potential Field-based Real-time Inverse Kinematics. Int. J. Control Autom. Syst. 2020, 18, 2095–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, X.; Han, B.; Jia, Y.; Liang, G.; Wang, X. A general approach based on Newton’s method and cyclic coordinate descent method for solving the inverse kinematics. Appl. Sci. 2019, 9, 5461. [Google Scholar] [CrossRef]
- Dereli, S.; Köker, R. A meta-heuristic proposal for inverse kinematics solution of 7-DOF serial robotic manipulator: Quantum behaved particle swarm algorithm. Artif. Intell. Rev. 2020, 53, 949–964. [Google Scholar] [CrossRef]
- Lan, L.; Li, H.; Yang, W.; Qiao, Y.; Qi, Z. Learning the Kinematics of a Manipulator Based on VQTAM. Symmetry 2020, 12, 519. [Google Scholar] [CrossRef]
- Liu, F.; Gao, C.; Liu, L. SK-PSO: A Particle Swarm Optimization Framework with SOM and K-Means for Inverse Kinematics of Manipulators. Symmetry 2024, 16, 1667. [Google Scholar] [CrossRef]
- Hassan, A.A.; El-Habrouk, M.; Deghedie, S. Inverse kinematics of redundant manipulators formulated as quadratic programming optimization problem solved using recurrent neural networks: A review. Robotica 2020, 38, 1495–1512. [Google Scholar] [CrossRef]
- Vertesy, G.; Rabung, M.; Gasparics, A.; Uytdenhouwen, I.; Griffin, J.; Algernon, D.; Gronroos, S.; Rinta-Aho, J. Evaluation of the embrittlement in reactor pressure-vessel steels using a hybrid nondestructive electromagnetic testing and evaluation approach. Materials 2024, 17, 1106. [Google Scholar] [CrossRef]
- Vasiljevic, G.; Brkic, V.; Postruzin, Z.; Kovaxix, Z. 3D Model-Based Nondestructive Scanning of Reactor Pressure Vessels with 6DoF Robotic Arms. In Proceedings of the 2022 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Sevilla, Spain, 8–10 November 2022. [Google Scholar]





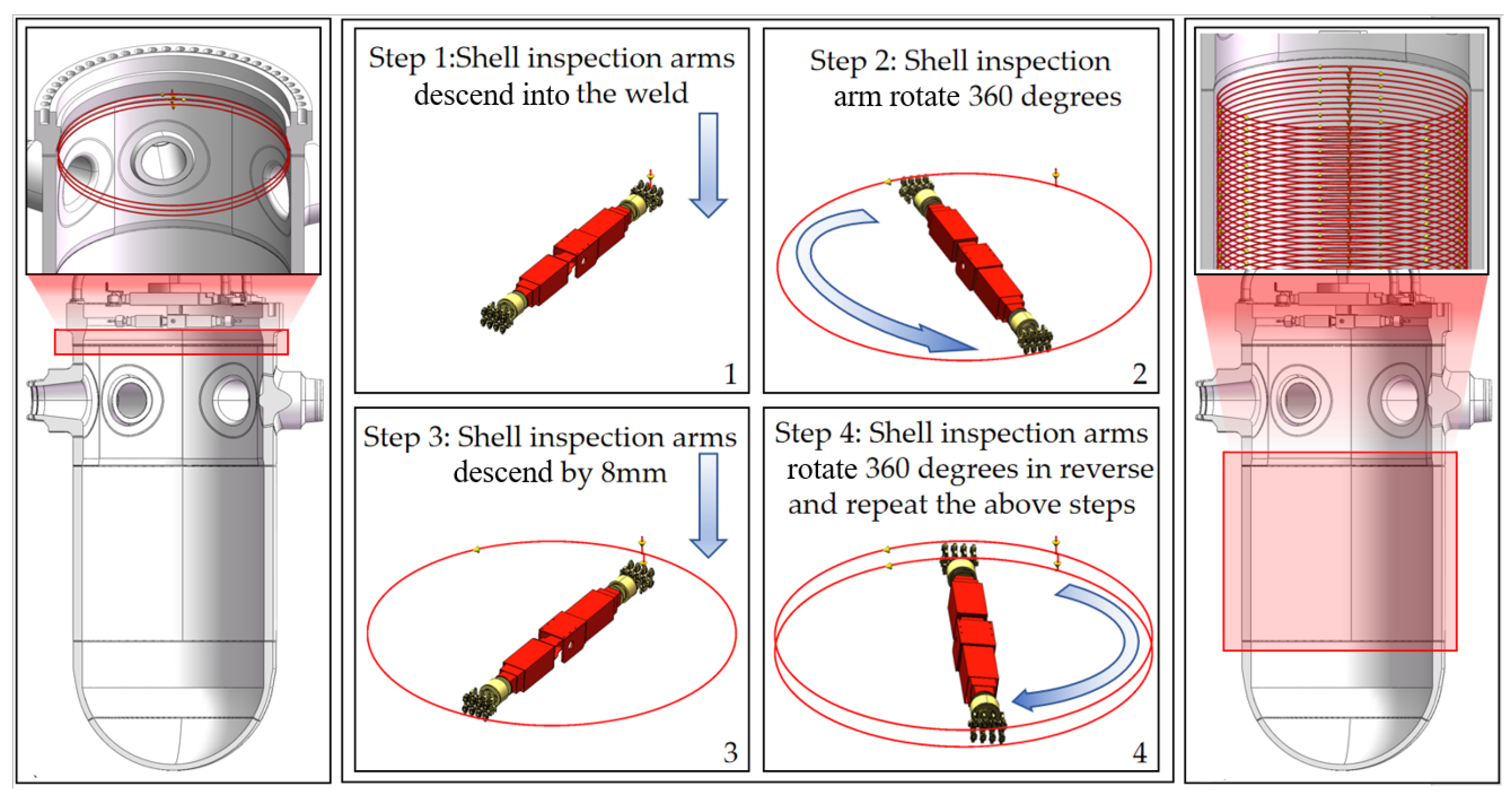

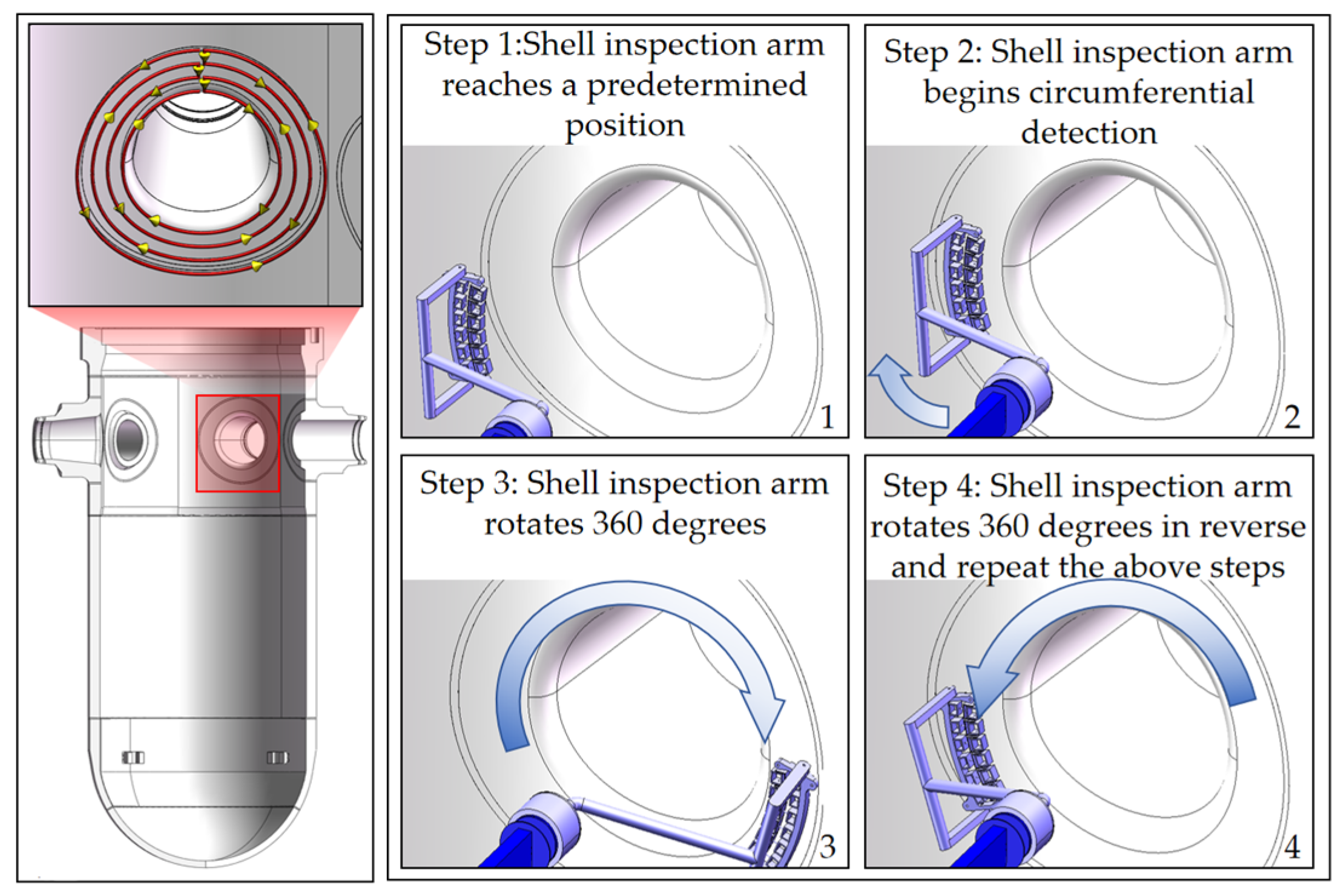
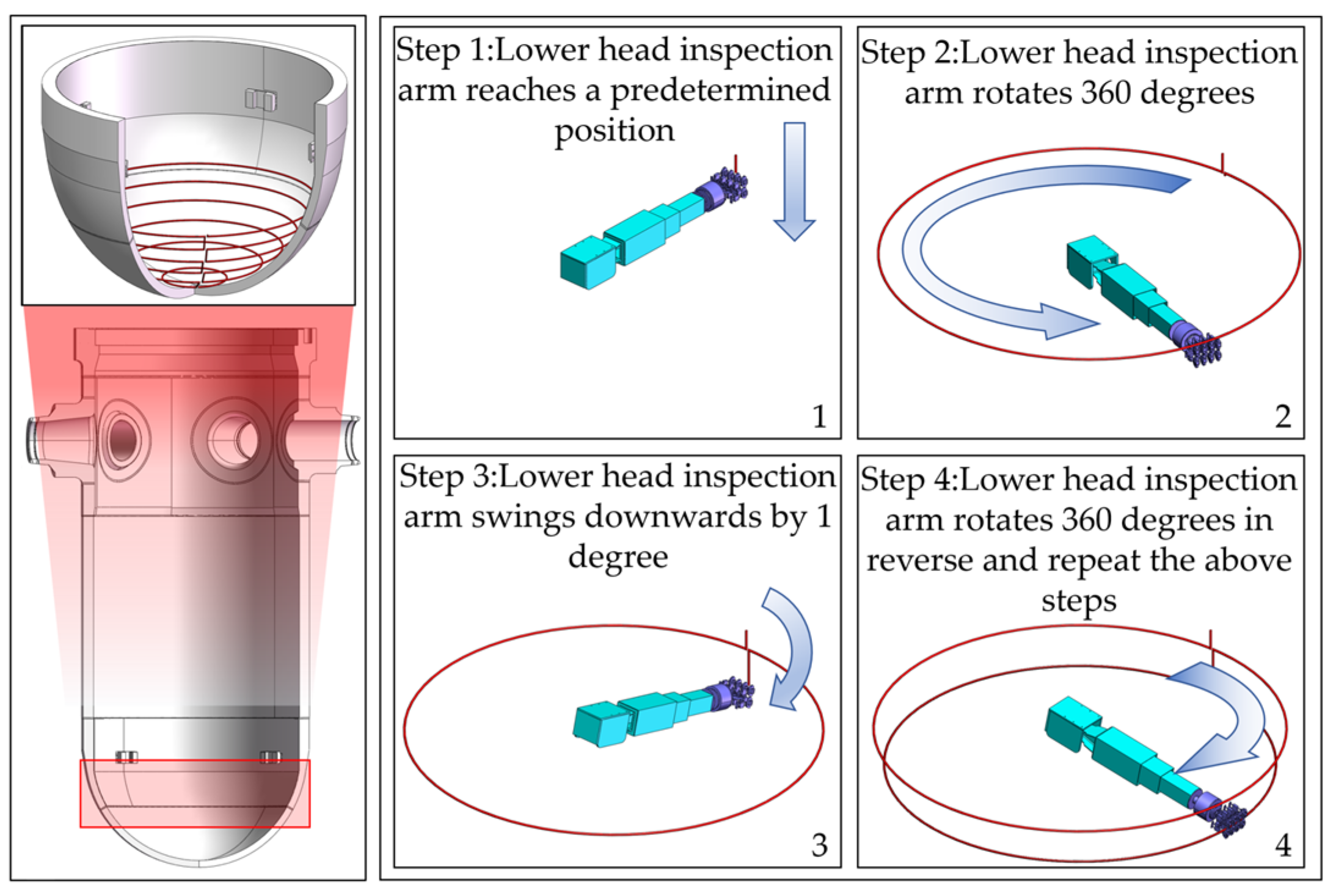
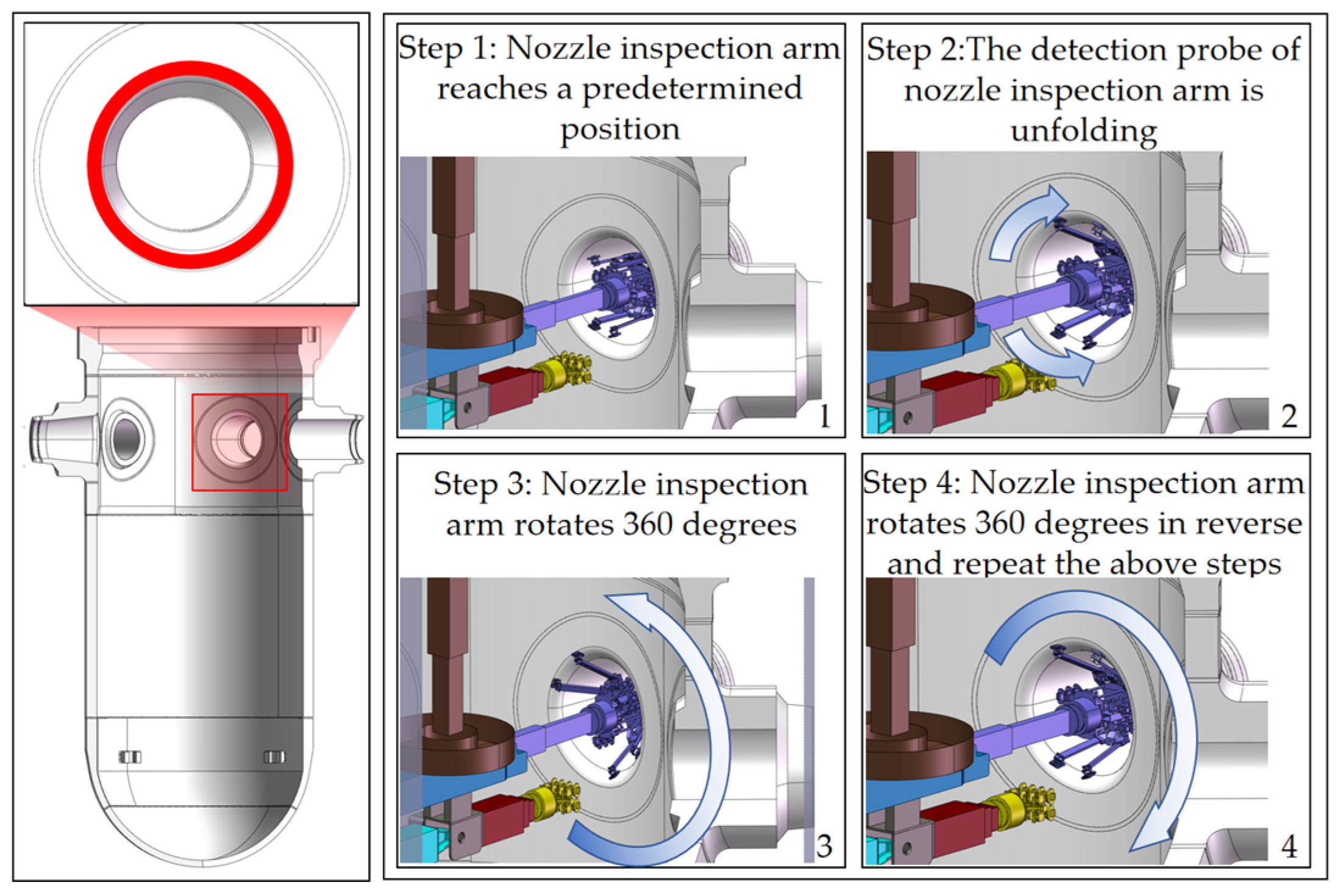
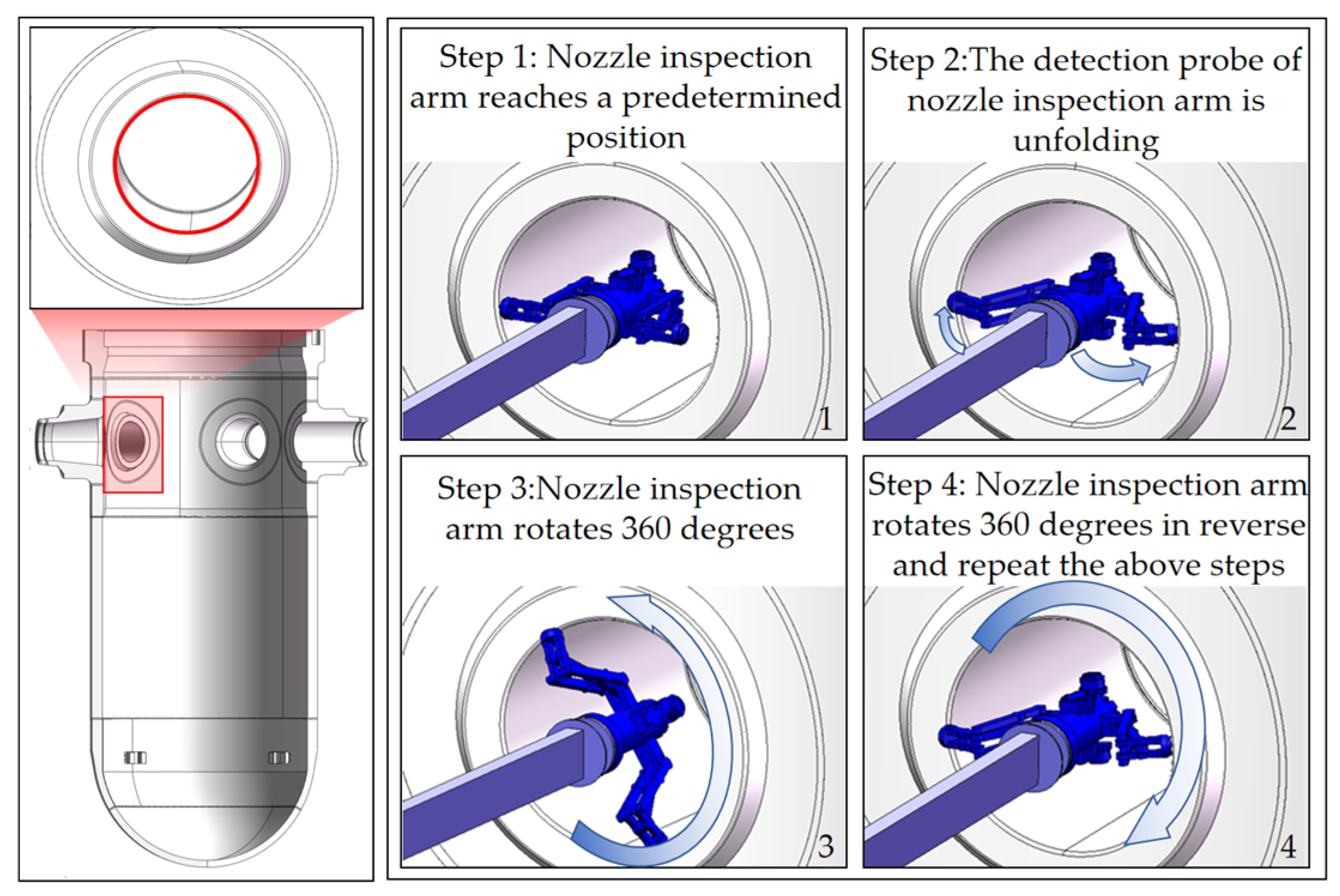

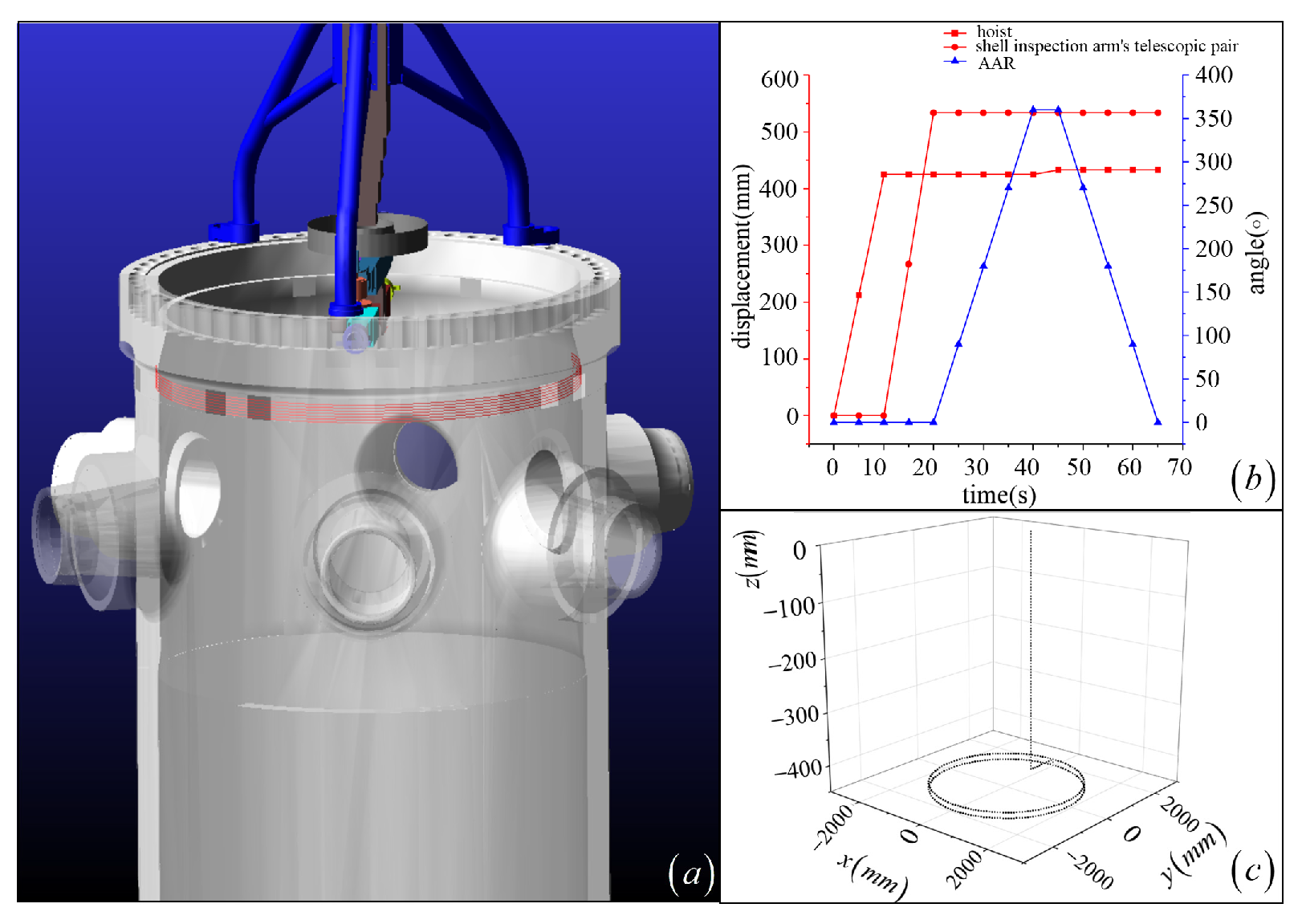

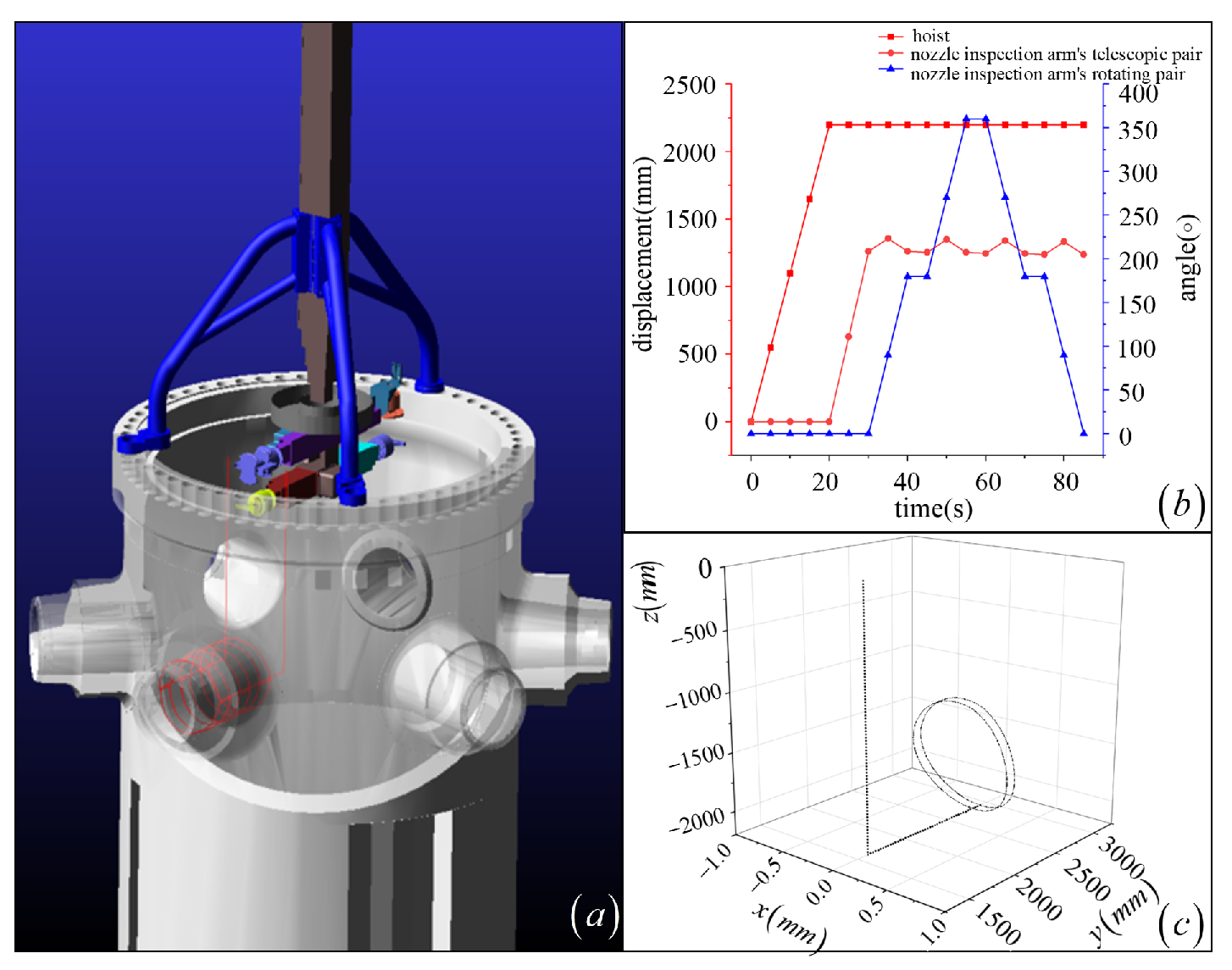
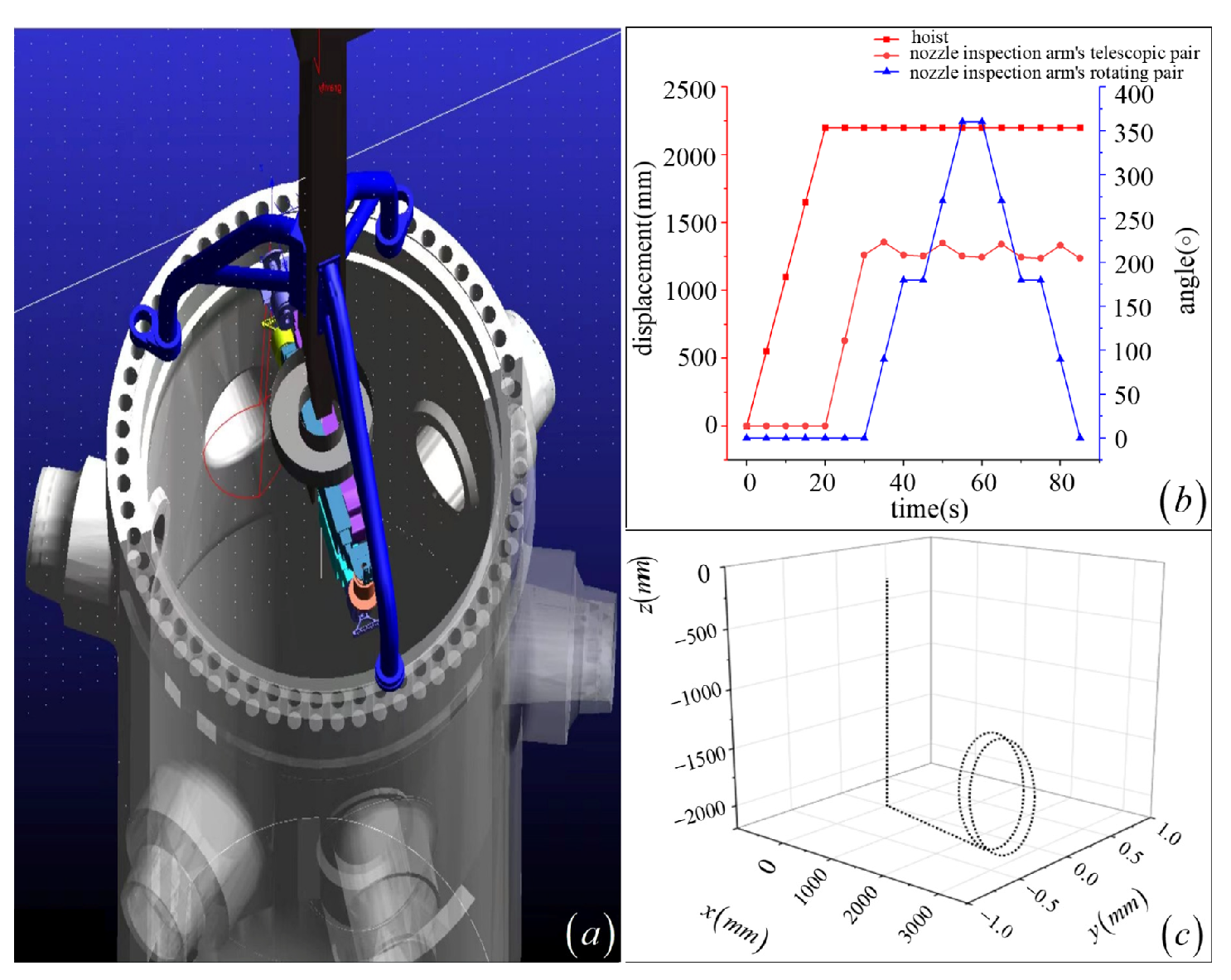
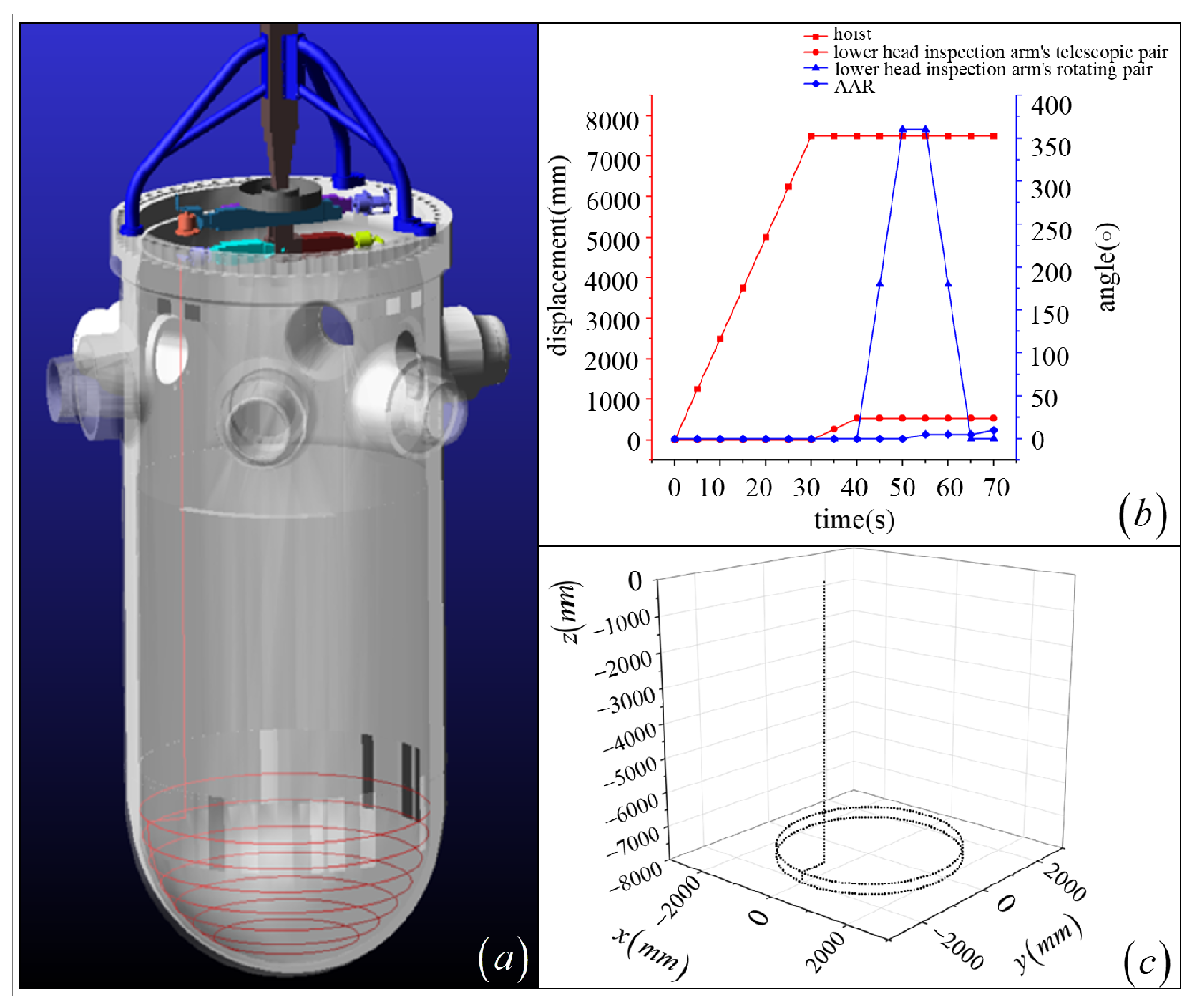
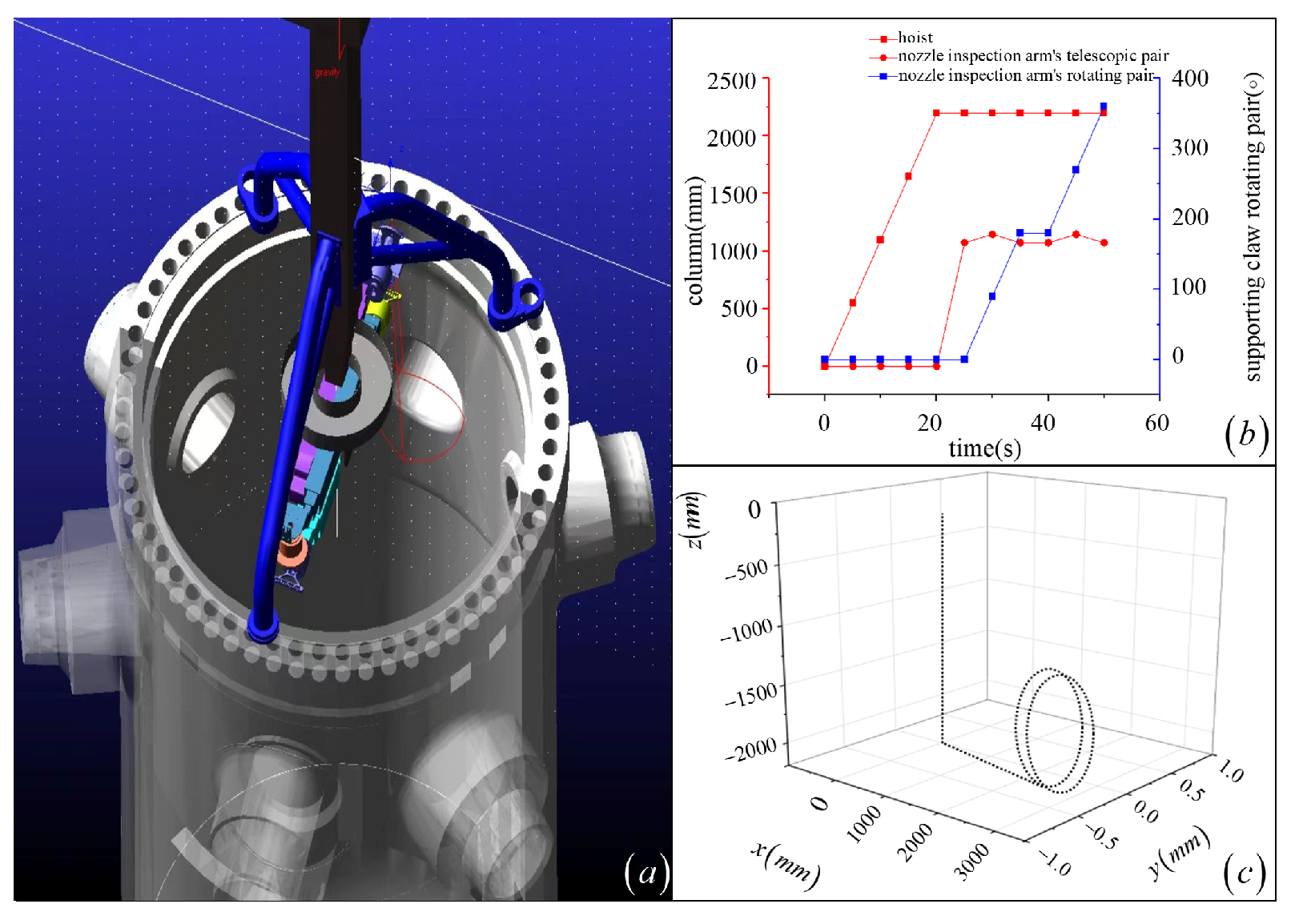
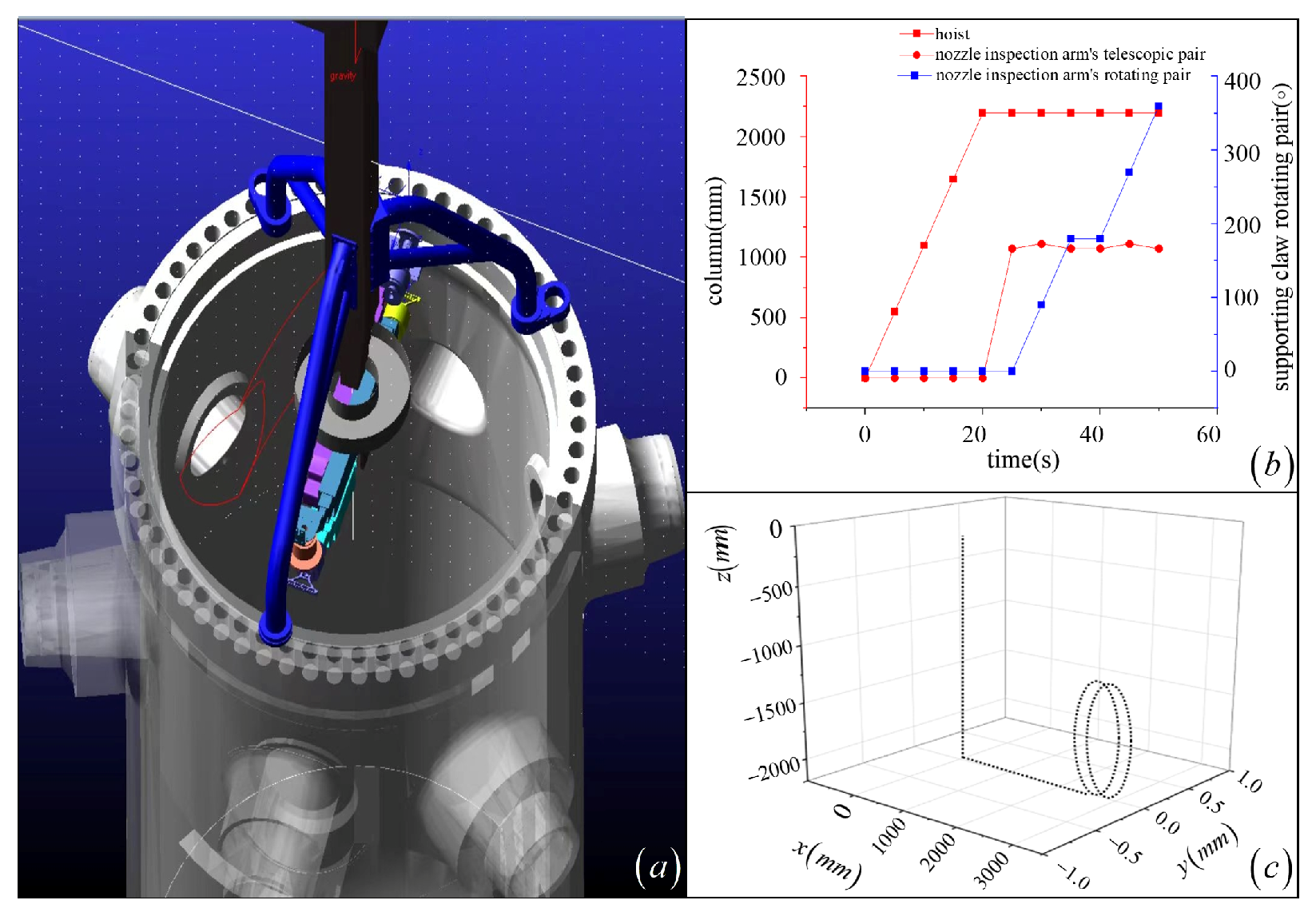
| Joint No. | Joint Type | (mm) | (Rad) | (mm) | (Rad) | Initial Value of Joint Variable | Range of Joint Variables |
|---|---|---|---|---|---|---|---|
| 1 | Prismatic Joint | 0 | 0 | 0 | 3300 mm | ||
| 2 | Revolute Joint | 0 | 0 | ||||
| 3 | Prismatic Joint | 0 | 0 | 0 | 1100 mm | ||
| 4 | Revolute Joint | 0 | 0 | 0 | 0 |
| Joint No. | Joint Type | (mm) | (Rad) | (mm) | (Rad) | Initial Value of Joint Variable | Range of Joint Variables |
|---|---|---|---|---|---|---|---|
| 5 | Prismatic Joint | 0 | 0 | 0 | 3800 mm | ||
| 6 | Revolute Joint | 0 | 0 | ||||
| 7 | Revolute Joint | 0 | 0 | ||||
| 8 | Prismatic Joint | 0 | 0 | 0 | 1200 mm | ||
| 9 | Revolute Joint | 0 | 0 | 0 | 0 |
| Region No. | |||
|---|---|---|---|
| Traditional Method | New Method | Coverage Improvement | |
| Region 1 | 100% | 100% | Optimized for higher operational efficiency |
| Region 2 | 100% | 100% | Optimized for higher operational efficiency |
| Region 3 | 94% | 100% | Eliminated inspection blind spots |
| Region 4 | 0% (Not Required) | 100% | Enabled full coverage as per new standards |
| Region 5 | 100% | 100% | Optimized for higher operational efficiency |
| Region 6 | 0% (Not Required) | 100% | Enabled full coverage as per new standards |
| Region 7 | 0% (Not Required) | 100% | Enabled full coverage as per new standards |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, M.; Zhao, Z.; Jiang, J.; Zhao, X.; Yan, J.; Chen, H.; Zhang, X. Symmetry-Inspired Design and Full-Coverage Path Planning for a Multi-Arm NDT Robot on a Reactor Pressure Vessel. Symmetry 2025, 17, 1995. https://doi.org/10.3390/sym17111995
Hong M, Zhao Z, Jiang J, Zhao X, Yan J, Chen H, Zhang X. Symmetry-Inspired Design and Full-Coverage Path Planning for a Multi-Arm NDT Robot on a Reactor Pressure Vessel. Symmetry. 2025; 17(11):1995. https://doi.org/10.3390/sym17111995
Chicago/Turabian StyleHong, Maocheng, Zhengyang Zhao, Jianxiang Jiang, Xiaoyang Zhao, Jingli Yan, Huaidong Chen, and Xiaobing Zhang. 2025. "Symmetry-Inspired Design and Full-Coverage Path Planning for a Multi-Arm NDT Robot on a Reactor Pressure Vessel" Symmetry 17, no. 11: 1995. https://doi.org/10.3390/sym17111995
APA StyleHong, M., Zhao, Z., Jiang, J., Zhao, X., Yan, J., Chen, H., & Zhang, X. (2025). Symmetry-Inspired Design and Full-Coverage Path Planning for a Multi-Arm NDT Robot on a Reactor Pressure Vessel. Symmetry, 17(11), 1995. https://doi.org/10.3390/sym17111995







